(完整word版)巧数图形题目

九图形的计数 ( 一)年级班姓名得分一、填空题1．下列图中一共有（）条线段.2.以下列图 , O 为三角形 A1A6A12的边 A1A12上的一点 , 分别连接 OA2,OA3, OA11，这样图中共有 _____个三角形 .A12A11A10OA9A8A7A6A1A2A3A4A53.下列图中有 _____个三角形 .ADB C4.下列图中共有 _____个梯形 .5.数一数(1)一共有 ( ) 个长方形 .(2)一共有 ( ) 个三角形 .DA(1)(2)C B6.在下列图中 , 全部正方形的个数是 ______.7.在一块画有 4 4 方格网木板上钉上了 25 颗铁钉 ( 以下列图 ), 假如用线绳围正方形 , 最多能够围出 _____个.A P O NMB QX W LC R Y V KD S T UJEF G H I8.一块相邻的横竖两排距离都相等的钉板 , 上边有 4 4 个钉 ( 如右图 ). 以每个钉为极点 , 你能用皮筋套出正方形和长方形共 _____个 .9.以下列图,方格纸上放了20枚棋子,以棋子为极点的正方形共有_____个.10.数一数 , 下列图是由 _____个小立方体堆成的 . 要注意那些看不见的 .二、解答题11.右图中共有 7 层小三角形，求白色小三角形的个数与黑色小三角形的个数之比.123456712.下列图中 ,AB、CD、EF、MN 相互平行，则图中梯形个数与三角形个数的差是多少？OA BC DE FM13．此刻都是由边长为 1 厘米的红色、白色两种正方形分别构成边长为N2厘米、 4 厘米、 8 厘米、 9 厘米的大小不一样的正方形、它们的特色都是正方形的四边的小正方形都是涂有红颜色的小正方形，除此之外，都是涂有白色的小正方形，要构成这样 4 个大小不一样的正方形，总合需要红色正方形多少个？白色正方形多少个？14．将 ABC 的每一边 4 平分，过各分点作边的平行线，在所得下列图中有多少个平行四边形？———————————————答案——————————————————————1．30由例 1 注可知图形中每边有 3+2+1=6（条）线段，所以整个图形中共有 6 5=30 条线段 .2. 37将 A1A6A12分解成以 OA6为公共边的两个三角形 . OA1A6中共有5+4+3+2+1=15(个) 三角形 , OA6A12中共有 6+5+4+3+2+1=21(个)三角形 , 这样 , 图中共有 15+21+1=37(个)三角形 .3.15这样的问题应当经过分类计数求解 . 本题中的三角形可先分红含极点C 的和不含极点C 的两大类 . 含极点 C 的又可分红此外两极点在线段AB 上的和在线段BD 上的两小类 . 分类图解以下 :A ADB C B CADB DCB所以原图有(3+2+1)+(3+2+1)+3=15( 个) 三角形 .4. 18梯形一共有三行 , 每行都有 3+2+1=6(个), 所以一共有 63=18(个) 梯形 .5. 108,36(1)因为长方形是由长和宽构成的 , 所以可分别考虑全部长方形的长和宽的可能种数 . 依据前面所介绍的线段的计数方法可分别求出长和宽的线段条数 , 将它们相乘就是全部长方形的个数 .98因为 AB 边上有 8+7+6+ +2+1==36 条线段， AD 边上有 2+1=3 条线段，所以图中一共有363=108 个长方形 .(2) 三角形一共有 6 行, 每行都有 3+2+1=6(个), 所以一共有 6 6=36(个) 三角形 .6. 30由例 5 注可知整个图形中共有12+22+32 +42=30 个正方形 .7. 50此类问题一般用分类方法计数. 对正方形的边长分八类计数以下:边长为 AB 的正方形有 16 个；边长为 AC 的正方形有 9 个；边长为 AD 的正方形有 4 个；边长为 AE 的正方形有 1 个；边长为 DF 的正方形有 9 个；边长为 CF 的正方形有 8 个；边长为 BF 的正方形有 2 个；边长为 CG 的正方形有 1 个 .所以 , 最多可围出 50 个正方形 .8. 44因为正方形是特别的长方形 , 所以能够把正方形当作长方形 , 这样就不用分别求正方形和长方形的个数 , 仍用分类计数的方法求解 .先考虑有一组对边平行于BC 的长方形有多少个 . 这一类按其水平边的地点可分为 6 小类 , 即地点在 BF、FE、EC、FC、BE、BC. 相同 , 其竖直边也分为 6 类 . 所以这一类有 6 6=36 个长方形 .A DB CF E另一类是没有边平行于 BC 的 . 这一类又分类两小类 , 分解图以下页图所示 , 此中分别有 6 个和 2 个长方形 .所以，一共可套出正方形和长方形 36+6+2=44个. 9． 21以正方形的面积大小分类计数 .设相邻两点的距离为 1，则正方形面积为 1 的有 9 个； 面积为 2的有 4个； 面积为 5的有 2个； 面积为 8的有 4个； 面积为 13 的有 2 个；所以，共有 9+4+2+4+2=21个正方形 . 10． 30将原立体图形从左至右分类计算，共有 11+7+5+7=30个. 11. 白色小三角形个数 =1+2+3+ +6=(1 6)6=21，2黑色小三角形个数 =1+2+3+ +7=(1 7)7=28，2所以它们的比 =21= 3.28 412. 解法一本图中三角形的个数为 (1+2+3+4) 4=40(个). 下边求梯形的个数 . 梯形由两底独一确立 . 第一在 AB, CD, EF, MN 中, 考虑两底所在的线段 , 共有(4 3) 2=6( 种) 选法；对上述四条线段中确立的两条线段， 共有 10（10=4+3+2+1）个梯形 . 共 60 个梯形 . 故所求差为 20.解法二 在图 中可数出 4 个三角形 ,6 个梯形 , 梯形比三角图形图形多 2 个. 而在题图中 , 这类恰有 10 个. 故题图中 , 梯形个数与三角形的个数之差为 2 10=20(个).13. 边长 2 厘米的正方形 : 2 2=4(个) 红色边长 4 厘米的正方形(4-1) 4=12(个 )红色(4-2)(4-2)=4( 个 )白色边长 8 厘米的正方形(8-1) 4=28(个 )红色(8-2)(8-2)=36( 个)白色边长 9 厘米的正方形(9-1)4=32(个 )红色(9-2)(9-2)=49( 个)白色所以 , 红色小正方形共有4+12+28+32=76(个)白色小正方形共有4+36+49=89(个)[ 注] 本题的要求是由边长为 1 厘米的红色和白色两种正方形, 分别构成边长是 2 厘米 ,4 厘米 ,8 厘米 ,9 厘米的大小不一样的正方形 , 能够看作方阵问题来解 . 周围的小正方形是涂红色的 , 可当作是空心方阵 , 所以 , 涂红色正方形的个数等于4 ( n-1). 其余小正方形是涂白色的，可看作实心方阵，所以，涂白色的正方形的个数等于 ( n-2) ( n-2). 比方 , 由边长为 1 厘米的正方形构成边长为 9 厘米的正方形 , 涂红色的小正方形的个数是 :4 (9-1)=32( 个 ), 涂白色的小正方形的个数是 :(9-2) (9-2)=49( 个 ).14.将平行四边形分为三类 : ①尖角在上、下方；②尖角在左下、右上方；③尖角在左上、右下方 .就第①类而言 :型6个；型型 1 个，与其对称的 1 个；分别含 15 个，故上述三类平行四边形共3 个，与其对称的 3 个；型 1 个；共 15 个. 同理 , 第②、③类也45 个.[ 注 ] 这样数平行四边行, 很麻烦 , 又易犯错 . 我们试图找到一种对应关系: 先考虑任一边不与 BC 平行的平行四边形, 延伸各边必与BC 有 4 个交点 , 特别状况下 , 第二个交点与第三个交点重合；反过来， BC 上的随意四点或三点决定一个平行四边形，也就是说，边不与BC 平行的平行四边形的个数与BC 上的四交点组和三交点组的数量相同多。

巧数图形练习题一、选择题1. 下列图形中，边数最多的是哪一个？A. 三角形B. 四边形C. 五边形D. 六边形2. 如果一个多边形有10条边，那么它有多少个内角？A. 10B. 20C. 30D. 403. 一个正方形有几条对称轴？A. 1B. 2C. 4D. 84. 一个圆有多少条对称轴？A. 1B. 无数条C. 360D. 无法确定5. 下列图形中，哪一个是中心对称图形？A. 等边三角形B. 长方形C. 等腰梯形D. 正五边形二、填空题6. 一个n边形的内角和是_________度。

7. 如果一个多边形的外角和为360度，那么它有_________条边。

8. 一个正六边形的每个内角是_________度。

9. 一个圆的周长是其直径的_________倍。

10. 一个图形的对称轴越多，其对称性越_________。

三、计算题11. 一个八边形的每个内角是多少度？如果将其每个内角增加10度，形成的新多边形是什么形状？12. 一个圆的半径是5厘米，计算它的周长和面积。

13. 一个正三角形的边长是6厘米，计算其周长和面积。

14. 一个长方形的长是10厘米，宽是5厘米，计算其周长和面积。

15. 一个正方形的边长是8厘米，计算其周长和面积。

四、简答题16. 描述如何判断一个图形是否为轴对称图形。

17. 解释什么是图形的旋转对称性，并给出一个例子。

18. 说明什么是图形的平移对称性，并给出一个例子。

19. 描述如何计算一个正多边形的边长，如果已知其周长。

20. 解释什么是图形的相似性，并给出两个相似图形的例子。

五、应用题21. 在一个平面上，有5个点，这些点不共线也不共面。

通过这些点，最多可以画出多少条直线？22. 一个班级有30名学生，如果每两名学生之间都画一条线段，表示他们之间的友谊，那么一共可以画出多少条线段？23. 一个圆内接于一个正方形，已知正方形的边长是10厘米，求圆的半径。

24. 如果一个多边形的每个外角都是45度，求这个多边形的边数。

第二讲图形的计数问题一、知识点：几何图形计数问题常常没有不言而喻的次序，并且要数的对象往常是重叠交织的，要正确计数就需要一些智慧了．实质上，图形计数问题，往常采纳一种简单原始的计数方法－一列举法．详细而言，它是指把所要计数的对象一一列举出来，以保证列举时无一重复、．无一遗漏，而后计算其总和．正确地解答较复杂的图形个数问题，有助于培育同学们思想的有序性和优秀的学习习惯．二、典例解析：例（ 1）数出右中共有多少个角解析：在∠ AOB内有三条角分线 OC1、OC2、OC3，∠ AOB被这三条角分线分红 4 个基本角，那么∠ AOB内总合有多少个角呢？第一有这 4 个基本角，其次是包括有 2 个基本角构成的角有 3 个（即∠ AOC2、∠ C1OC3、∠ C2OB），而后是包括有 3 个基本角构成的角有 2 个（即∠ AOC3、∠C1OB），最后是包括有 4 个基本角构成的角有 1 个（即∠ AOB），所以∠ AOB内总合有角：4＋3＋2＋1＝10（个）解：4＋3＋ 2＋ 1＝10（个）答：中共有10 个角。

一：数一数右中共有多少个角？答案 :共有角：10+9+8+⋯ +4+3+2+1=55（个）例（ 2）数一数共有多少条线段？共有多少个三角形？解析：①要数多少条线段：先看线段3 条基本线段，再看 BC、 MN、GH 这AB、AD、 AE、AF、 AC、上各有3 条线段上各有 3 个分点，各分红2 个分点，各分红4 条基本线段 .所以图中总合有线段是：（3+2+1）× 5+（ 4+3+2+1）× 3=30+30=60（条） .②要数有多少个三角形，先看在△ AGH中，在 GH上有 3 个分点，分红基本小三角形有 4 个. 所以在△ AGH中共有三角形 4+3+2+1=10（个） . 在△ AMN与△ ABC中，三角形有相同的个数，所以在△ ABC中三角形个数总合：（4+3+2+1）× 3=10× 3=30（个）解：：①在△ ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ ABC中共有三角形是：（4+3+2+1）× 3=10× 3=30（个）答：在△ ABC中共有线段60 条，共有三角形30 个。

第六讲角（巧数图形的个数）例题精讲
例1. 数一数右图中有多少条线段。

例2. 数一数右图中有几个角。

O 例3.数一数右图中共有多少个三角形。

例4. 数一数右图中有多少个三角形。

同步练习
2. 下图中，一共有（）个角。

3. 下图中，大大小小的长方形一共有（）个。

4. 数一数下图共有几条线段。

5. 下图中有（）个三角形。

（）条（）条（）条
（）条
（）条
b c
6. 下图中有多少个不同的正方形？
7. 在下面点子图上，以这些点为顶点的正方形可画几个？
···
···
···
8. 再添一条线段，使下图中三角形的个数为12，想一想，应该怎样添呢？
9. 数一数包含涂色的正方形有多少个？
10. 数一数图中三角形的个数。

拓展提高
1. 在一线段上任取21个点（包括两端点），则一共有（ ）条线段。

2. 下图一共有（ ）条线段。

3. 数一数，下列图中一共有（ ）个角。

4. 一条直线上共有50个点，可以数出（ ）条线段。

5. 从一点引出10条射线，可以数出（
）个小于180º的角。

6. 平面上有10个点，没有三点在一条直线上的情况。

这些点可以连成（ ）条线段。

7. 下图中有几个三角形？
8. 数一数图中长方形的个数。

一年级数学巧数图形练习题请先确保你提供的题目是“一年级数学巧数图形练习题”。

然后，我将为你撰写一篇2000字的文章，按照数学练习题的格式来呈现。

请阅读以下内容：
一年级数学巧数图形练习题
题一：巧数填方格
请将1到10的巧数填入下面的方格中，每个数字只能填写一次，使得每行、每列和对角线上的数字之和均相等。

1 |
2 | 3
12| 4 | 6
8 | 5 | ?
题二：巧数蛇形路径
请你沿着蛇形路径，将1到12的巧数填入下面的图形中，从1开始，依次填入空白的圆圈中，使得相邻数字之间的和始终为巧数。

3
/ \
2 4
/ \
1 5
\ /
6 8
\ /
7
题三：巧数的面积
下面是一张巧数图形，其中每个小格子上标有1至8的数字。

请你计算图形中各个三角形的面积，并将计算结果写在对应的空白处。

1
2 3
4 5 6
7 8 9 10
...
（具体图形请自行绘制）
题四：巧数梯形求和
下面是一个梯形，其中标有1至8的巧数。

请你计算梯形中所有小方格中的数字之和。

1
2 3
4 5 6
7 8
（具体图形请自行绘制）
题五：巧数的对角线
给定一个4x4的方格，在每个小方格中填入1至16的巧数，使得每条对角线上的数字之和相等。

以上是一年级数学巧数图形练习题的内容。

通过解决这些题目，你可以提高自己对巧数的理解，并且提升数学思维能力。

希望这些题目能让你感到有趣并且有所收获。

如果你还需要其他帮助，请随时告诉我。

巧数图形数图形包括：数线段、数角、数长方形、数正方形、数三角形等，这看似简单，其实其中学问可大了．为了能准确地数出结果，我们必须有次序、有条理地数，既不能遗漏，也不能重复．只要我们掌握了数的方法，就能数得又对又快．例1．下图中有多少条线段？（1）思路分析：每条线段均有两个端点，可以根据左端点进行分类．以A为左端点的线段为AB、AC，共有2条；以B点为左端点的线段为BC，只有1条；以C点为左端点的线段不存在．因此共有2＋1＝3(条)．答：图中共有3条线段．(2)这题中左端点是A的线段有：AB、AC、AD、AE，共有4条；左端点是B的线段有BC、BD、BE，共有3条；左端点是C的线段有C D、CE，共有2条；左端点是D的线段有DE；左端点是E的线段不存在．所以共有4＋3＋2＋1＝10(条)．答：图中共有10条线段．例2．数出下面图中共有多少条线段？思路分析：线段有一个重要特征：线段都是笔直的．所以我们在数的时候，必须将这幅图分成四个部分，每一部分分别采用以线段左端点分类数的方法，然后把四部分算得结果加起来．例题解答：第一部分从A到E共有4＋3＋2＋1＝10条线段．第二部分从G到J共有4＋3＋2＋1＝10条线段．第三部分是FG一条线段．第四部分是JK一条线段．10＋10＋1＋1＝22(条)答：这幅图共有22条线段．方法指导：数线段可以根据左端点将线段分类，数出每一类有多少条线段，然后再相加得出线段的总的条数．例3．一条线段上共有10个点，以这10个点为端点的不同线段共有多少条？思路分析：将这条线段上的10个点从左到右依次标为、、…、、以为左端点的线段为、、、、、、、、共有9条；为左端点的线段为、、、…、，共有8条；…；以为左端点的线段为，只有1条；以为左端点的线段不存在．因此，共有线段：9＋8＋…＋3＋2＋1＝(9＋1)×9÷2＝45(条)答：一共有45条线段．方法指导：一般地，如果线段上有几个点(其中n是大于或等于2的自然数)，那么以这n个点为端点的线段共有：(n－1)＋(n－2)＋…＋3＋2＋1＝n×(n－1)÷2例4．下面图形中有几个角？思路分析：数角的个数为了不遗漏、不重复，也需要按一定的顺序去数，可以采用与数线段相同的方法．以OA为一边的角有：∠AOB、∠AOC、∠AOD，共3个；以OB为一边的角有：∠BOC、∠BOD，共2个．以OC为一边的角有：∠COD，只有1个．3＋2＋1＝6(个)答：图中共有6个角．例5．数出下面图中共有多少个三角形？思路分析：数三角形个数的方法与数线段的方法差不多．以AB为边的三角形有：△ABD、△ABE、△ABC，共有3个．以AD为边的三角形有：△ADE、△ADC，共有2个．以AE为边的三角形有：△AEC，只有1个．所以，图中一共有三角形：3＋2＋1＝6(个)．我们还可以发现，可以抓住底边BC来考虑，底边BC中所包含的每一条线段都恰好对应一个三角形．底边左端点是B的三角形共有△BDA、△BEA、△BCA三个．底边左端点是D的三角形共有△DEA、△DCA两个．底边左端点是E的三角形只有△ECA一个．所以一共有三角形：3＋2＋1＝6(个)．方法指导：数角的个数和三角形个数这些基本图形时，所采用的方法与数线段的方法相同．即角的个数＝射线数×(射线数－1)÷2．即三角形个数就是底边上的线段数．例6．数一数图中共有多少个三角形？思路分析：我们可以将这幅图分成三个部分来数，即下面三幅图．在△ABC中，一共有5＋4＋3＋2＋1＝15(个)三角形，在△ABD中，一共有5＋4＋3＋2＋1＝15(个)三角形；在△BDC中，一共有5个三角形．15＋15＋5＝35(个)答：图中共有35个三角形．例7．图中共有多少个不同的三角形？思路分析：将本题分成(1)、(2)两部分来数：第(1)部分中共有三角形：3＋2＋1＝6(个)；第(2)部分中共有3＋2＋1＝6(个)三角形．所以，共有三角形6＋6＝12(个)．例8．数出下图中共有多少个三角形？思路分析：这题我们可以采用按基本图形组合的方法来数．把图中最小的一个三角形看作基本图形．由一个基本三角形构成的三角形共有8个；由两个基本三角形构成的三角形共有4个；由四个基本三角形构成的三角形共有4个．因此：8＋4＋4＝16(个)，所以，图中共有16个三角形．例9．数出下面图形中共有多少个三角形？思路分析：这题采用把其中最小的三角形作为一个基本图形，然后分类相加的方法．由一个基本三角形构成的三角形共有9个；由四个基本三角形构成的三角形共有3个；由九个基本三角形构成的三角形只有1个．因此9＋3＋1＝13(个)，所以，图形中共有13个三角形．例10．下面两幅图中各有多少个长方形？思路分析：(1)中长方形都是竖向的，可以利用对应的方法来数．因为每个长方形都和底边上的一条线段对应，因此用数长边上的线段条数来数长方形的个数．所以，图中长方形共有4＋3＋2＋1＝10(个)．(2)我们可用按基本图形组合的方法来数．由一个基本长方形构成的长方形共有6个；由两个基本长方形构成的长方形共有7个；由三个基本长方形构成的长方形共有2个；由四个基本长方形构成的长方形共有2个；由六个基本长方形构成的长方形有1个；所以，图中共有长方形6＋7＋2＋2＋1＝18(个)．本题还可以结合数线段的方法，这题中长方形的长被分成了3段，线段总数为3＋2＋1＝6条，宽被分成了2段，线段总数为2＋1＝3 (条)．由此可见，长方形的个数＝6×3＝18(个)．于是，可以整理出数长方形个数的方法：长方形的个数等于原长方形长上的线段数乘以宽上的线段数．例11．数出各图中正方形的个数．思路分析：(1)中最基本的正方形有9个，即边长为1的正方形有9个(9＝3×3)；由4个基本正方形组成的正方形，即边长为2的正方形有4个(4＝2×2)；由9个基本正方形组成的正方形，即边长为3的正方形有1个(1＝1×1)所以共有正方形9＋4＋1＝14(个)．(2)中边长为1的正方形有16个，即16＝4×4；边长为2的正方形有9个，即9＝3×3；边长为3的正方形有4个，即4＝2×2；边长为4的正方形有1个，即1＝1×1．所以共有正方形有16＋9＋4＋1＝30(个)．因此，如果一个正方形的各边被分成几个等份，那么正方形的个数便是1×1＋2×2＋3×3＋…＋n×n．方法指导：正确数出图形的个数，首先要弄清图形中包含的基本图形是什么，有多少个．然后再从各图形中所包含基本图形的个数多少出发，依次数出它们的个数，并求出它们的和是多少．有些图形被分成了几个部分，可以先从各部分的基本图形出发，数出所含图形的个数，再求各部分的总和．例12．图中共有多少个正方形？思路分析：将正方形分类，将每一类的总数相加，就可得到所有正方形的个数．由两块小三角形构成的正方形有4个；由四块小三角形构成的正方形有4个；由八块小三角形构成的正方形有1个；由十六块小三角形构成的正方形有1个．由一、三、五、七、六、九、十、十一、十二、十三、十四、十五块小三角形不能构成正方形．所以，图中共有4＋4＋1＋1＝10(个)正方形．例13．数出图中共有多少个正方形？思路分析：根据正方形边长的大小，我们将它们分成四类：第1类：边长为1的正方形有24个；第2类：边长为2的正方形有13个；第3类：边长为3的正方形有4个；第4类：边长为4的正方形有1个．所以图中共有24＋13＋4＋1＝42(个)正方形．这题如果把四条边长多出的8个小正方形去掉，很容易得出共有1×1＋2×2＋3×3＋4×4＝30(个)正方形，添上了去掉的小正方形后，这8个小正方形还能再和其他图形组成4个新的正方形．所以，图中共有30＋8＋4＝42(个)正方形．例14．下图中共有多少个长方形？思路分析：我们可以先将大长方形中的5小块编上号：这5块都是符合要求的长方形．然后数由两小块拼成的长方形，共有4个，即①＋②，②＋③，③＋④，④＋⑤；再数由三小块拼成的长方形，共有2个，即①＋③＋④，③＋④＋⑤；没有由四小块拼成的长方形；最后数由5小块拼成的长方形只有最大的一个．所以，图中共有5＋4＋2＋1＝12(个)长方形．例15．数出下图中共有多少个三角形？思路分析：首先将大三角形中六小块分别编上号．通过观察，我们可以发现这6小块中，④和⑤不是三角形，因此，由一块形成的三角形有4个；由两块拼成的三角形有5个，即分别是①＋②，①＋③，③＋④，②＋④，⑤＋⑥；由三块拼成的三角形有两个，分别为①＋③＋⑤，②＋④＋⑥；由四块拼成的三角形有1个，即是①＋②＋③＋④；没有由五块拼成的三角形；由六块拼成的三角形有1个，即最大的三角形．所以，图中三角形一共有4＋5＋2＋1＋1＝13(个)．方法指导：数长方形、正方形、三角形以及一些不规则的图形都可以采用编号数图形的方法，就是将原来图中的每一小块都编上号，先看每一小块是否符合要求的图形，接着数由两个小块相拼成的图形中有几个是符合要求的图形，再依次数由三小块、四小块……拼成的图形中各有几个是符合要求的图形，最后将每一步数得的结果加起来．。

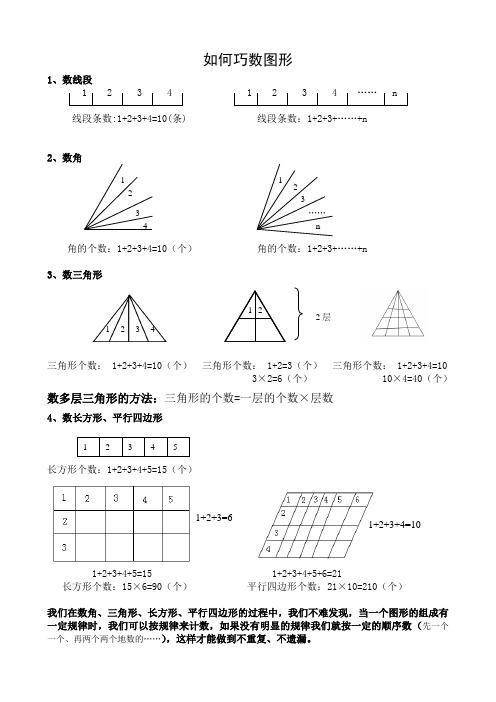
如何巧数图形
1、数线段 1 2 3 4 1 2 3 4 …… n
线段条数:1+2+3+4=10(条) 线段条数：1+2+3+……+n
2、数角
角的个数：1+2+3+4=10（个） 角的个数：1+2+3+……+n
3、数三角形
三角形个数： 1+2+3+4=10（个） 三角形个数： 1+2=3（个） 三角形个数： 1+2+3+4=10 3×2=6（个） 10×4=40（个） 数多层三角形的方法：三角形的个数=一层的个数×层数
4、数长方形、平行四边形
长方形个数：1+2+3+4+5=15（个）
1+2+3+4+5=15 1+2+3+4+5+6=21
长方形个数：15×6=90（个） 平行四边形个数：21×10=210（个）
我们在数角、三角形、长方形、平行四边形的过程中，我们不难发现，当一个图形的组成有一定规律时，我们可以按规律来计数，如果没有明显的规律我们就按一定的顺序数（先一个一个、再两个两个地数的……），这样才能做到不重复、不遗漏。

1 2 3 4 1 2 3 ……
n 1 2 3 4
1 2
2层 1 2 3 4 5 1+2+3=6 1+2+3+4=10
5、数不规则图形。

（1+2+3+4+5+6）×（1+2+3）＋（1+2+3）×（1+2+3+4）－（1+2+3）×（1+2+3）=150。

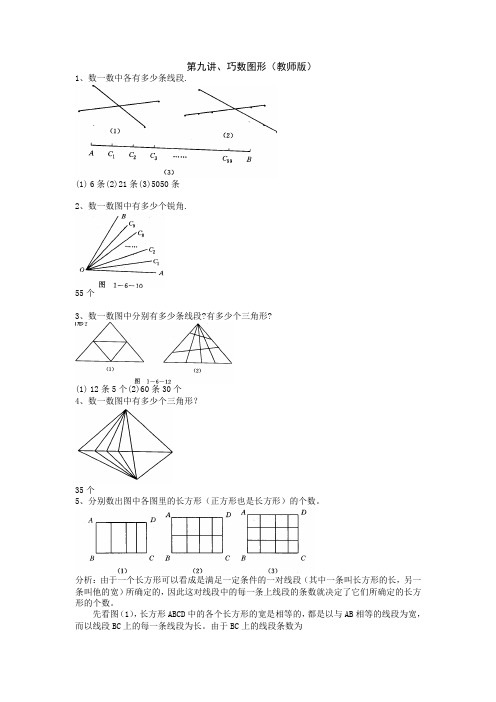
第九讲、巧数图形（教师版）1、数一数中各有多少条线段.(1)6条(2)21条(3)5050条2、数一数图中有多少个锐角.55个3、数一数图中分别有多少条线段?有多少个三角形?(1)12条5个(2)60条30个4、数一数图中有多少个三角形？35个5、分别数出图中各图里的长方形（正方形也是长方形）的个数。

分析：由于一个长方形可以看成是满足一定条件的一对线段（其中一条叫长方形的长，另一条叫他的宽）所确定的，因此这对线段中的每一条上线段的条数就决定了它们所确定的长方形的个数。

先看图（1），长方形ABCD中的各个长方形的宽是相等的，都是以与AB相等的线段为宽，而以线段BC上的每一条线段为长。

由于BC上的线段条数为4+3+2+1=10(条)所以长方形的个数是:(4+3+2+1)×1=10(个)再看图 (2),它可以看成是由图 (1)中的两个图形拼接起来的.那么又多了多少个长方形呢?如果说多了10个就错了.应该同上面的思考方法一样,先看AB上有几条线段,就相当于有几个不同的宽,再把BC上不同的线段当作长,1个长配一个宽,就得到1个长方形.所以长方形的个数为(4+3+2+1)×(2+1)=30(个)再看图 (3),用同样的方法,容易得出图中的长方形个数为(4+3+2+1)×(3+2+1)=60(个)解:长方形的个数分别为:(1)(4+3+2+1)×1=10(个)(2)(4+3+2+1)×(2+1)=30(个)(3)(4+3+2+1)×(3+2+1)=60(个)观察上面3个式子,想一想:算式中被乘数和乘数分别与AB边及BC边上的线段有什么关系?或者说与AB边及BC边上的小格有什么关系?从5的分析中,我们发现,可以将数长方形的问题归结成数线段的问题.一般的,长方形的总数等于长方形的长上的线段总数乘以宽上的线段总数:或者说当长方形的一边上有n个小格,另一边上有m个小格时,长方形的总数为:(n+ +3+2+1)×(m+ +3+2+1)我们通过对长方形自身的构成规律的分析,以及与数线段之间的联系,找到了数长方形的规律.今后,找规律是我们解决数学问题是经常要用到的思考方法6、数出图中有多少个梯形？分析：首先要知道什么是梯形?图中的四边形好像一个梯子，而且一组对边平行，另一组对边不平行。

小学三年级奥数巧数图形（一）数线段例1数出下图中共有多少条线段。

巩固练习：（1)数一数，下图中一共有多少条线段？（2)下图中,如果这条直线上有101个点。

那么这些点一共可以形成了多少条线段？101个（3)数一数，下图中一共有多少条线段？（4）数一数，下图中一共有多少条线段？（二）数三角形例2 下列各图形中，三角形的个数各是多少?例3下列图形中各有多少个三角形?例4右图中有多少个三角形？（三）数锐角例5数出下页左上图中锐角的个数。

巩固练习：（1)数一数，右图中有多少个锐角？（2）数一数，右图中有多少个角？（四)数长方形的个数例6。

数一数，下图中有多少个长方形? (五）数正方形的个数例7数一数，右图中有多少个正方形？(六）数包含特殊符号图形的个数例6下图中有多少长方形中含有长方形a？a综合练习1。

下图有多少线段？有多少三角形？2。

下面16个点可以连成多少个正方形?＊* * ＊＊* ＊＊＊* * ＊＊* * *3。

正方形边长是1厘米，，六个叠在一起组成的图形，周长是多少？如果100个这样的正方形叠在一起，周长是多少？5。

下列图形中各有多少个长方形？6。

下列图形中，包含“＊”号的三角形或长方形各有多少？7.下列图形中，不含“＊”号的三角形或长方形各有几个？答案与提示练习111。

（1）28；（2）210.2.(1）36；（2)8。

3.（1）10；(2)15。

4。

（1）9个；(2)16个；（3）21个。

5.(1）60个；(2）66个。

6.（1)12个;（2)32个。

7。

（1)21个；(2)62个。

提示:4～7题均采用按所含小块的个数分类（见下表)，表中空缺的为0。

第2讲 巧数图形知识要点同窗们，咱们常常会碰到数图形的问题，关于较复杂的图形，常常会显现数重复或数漏掉的错误。

如何才能不重复也不遗漏地数出图形的个数呢？这节课，咱们将一路来寻觅好的方式。

要正确数出图形的个数，关键是要从大体图形入手。

第一要弄清图形中包括的大体图形是什么，有多少个，然后再数出由大体图形组成的新的图形，并求出它们的和。

精典例题例1: 数出以下图中有多少条线段？仿照练习数一数，每种图形有多少个？有（ ）条线段 有（ ）个三角形有（ ）个角 有（ ）个长方形 有（ ）个正方形例2: 数出图中共有多少个三角形？从短的线段入手，再两条两条拼接起来数，你发现规律了吗？还能用刚才的方法来数吗？EABCDODC B A FEA仿照练习数一数，每幅图里有多少个三角形？ （1） （2）有（ ）个三角形 有（ ）个三角形例3:下面的图形中有多少个三角形？（第九届中国青青年数学论坛趣味数学解题技术展现大赛试题）仿照练习数一数，图中共有几个正方形？（2020武汉明心数学资优生水平测试题）精典例题例4: 数出以下图中有多少个长方形？多少个正方形？三角形很多，可以尝试按三角形的方向和大小尝试分类数。

KG I H G A仿照练习1.数一数，图中有多少个长方形？2.数一数图中有多少个正方形？家庭作业1.数一数每幅图里面图形的个数（能计算的写出算式）。

（1） （2）前面学习的数长方形的方法还有用吗？怎么能用上呢？DCBA D CBA有（ ）条线段 有（ ）个角2.右图中有多少个三角形？3.图中有多少个长方形？（把你的方式分享给你的爸爸妈妈听，你能教会他们吗？分享后让爸爸妈妈给你打星，最多5颗星）4.数一数，右图中有多少个正方形？5.数一数，其中共有多少个包括“（2020年“陈省身杯”国际青青年数学邀请赛试题）。

巧数图形月 日 姓 名知识要点：1．巧数图形问题包括：数线段、数三角形、数正方形、数长方形等。

2．数图形的个数，不但要有一双好眼睛，还要善于开动脑筋，仔细观察，按顺序分类去做，做到不重复，不遗漏，这样才能数得又快又准。

通过数线段、数三角形、数角等总结出共用的方法：（n －1）＋(n －2)＋(n －3)＋…＋2＋1经典例题：例1．（1）图4-1中有多少条线段？（2）图4-2中共有多少个角？（3）数一数图4-3中共有多少个三角形？例2．图4-4中一共有多少条线段？图4-1图4-2图4-3图4-4例3．数一数图4-5有多少个正方形？例4．图4-6中一共有多少个长方形？就地练兵1．如图4-7所示图中共有条线段。

2．数一数图4-8中有多少个三角形？3．如图4-9所示，图中共有多少条线段？4．数一数图4-10中有多少条线段？图4-5图4-6图4-7图4-8123C图4-10图4-95．图4-11中共有多少锐角？6．如图4-12所示，图中共有 线段，共有 个三角形。

7．图4-13中共有 个三角形。

8．（1）数一数图4-14中有多少个正方形。

（2）数一数图4-15中共有多少个正方形？9．数一数图4-16中有多少个长方形？A OC 1 C 2 C 20B图4-11· · · 图4-12C图4-13 图4-14图4-15图4-16课后大考验姓 名 成 绩1．如图4-17中共有 条线段。

2．数一数，图4-18中有多少条线段？3．图4-19中共有多少个角？4．数一数图4-20有多少个正方形？5．图4-21中共有多少个长方形？AB C D EF G图4-172 3 4 56图4-19图4-20图4-21图4-18。