四年级数学-巧数图形
- 格式：doc
- 大小：174.80 KB
- 文档页数：5
文档推荐
-
四年级上册数学读数写数平面图形练习试题页数:6
-
北师大版四年级数学上册《数图形的学问》课件页数:12
-
北师大版数学四年级上册《数图形的学问》数学好玩页数:11
-
四年级上册数学《数图形的学问》教案设计页数:2
-
四年级数学上册《数图形的学问》练习题页数:2
下载文档原格式
合集下载
四年级下数学-思维拓展训练- 巧数图形 全国通用PPT课件(10张)
7、巧数图形
在每个图形中，分别有多少条线段？ 多少个角？多少个三角形？
例1：图中有多少个三角形？
0 12 3 4 0 12 3 4 5
0+1+2+3+4=10（个） 0+1+2+3+4+5=15（个） 10+15=25（个）
例2：数一数，图中有多少个三角形？
单个△：16个 由4个△组成的：6个 共16+6=22（个）
共16+6=22（个）
18个△组成的正方形：1个
共9+8+4+2+1=24（个）
2个△组成的正方形：9个 4个△组成的正方形：8个 8个△组成的正方形：4个 16个△组成的正方形：2个 18个△组成的正方形：1个
共9+8+4+2+1=24（个）
例7 包含两个“ ”在内的小正方形组成的长方形（含正方 形）共有多少个？
例5：数一数，下图中有多少个正方形中包含两个阴影方格？
2×2的正方形：2个 3×3的正方形：4个 4×4的正方形：1个 共2+4+1=7（个）
例6：图中有多少个正方形？
2个△组成的正方形：9个
例1：图中有多少个三角形？
例3：下图中有多少个长方形？
例2：数一数，图中有多少个三角形？
多少个角？多少个三角形？
3 × 4 × 2 × 2 = 48（个）
图123原、、、形理按按弄计计顺单清数数序个楚： 。编图构号形成，的特运组殊用成图加个形法数的原有每理序一或计条乘数边法。有原几理种计选数择。，再用乘法 1多例多2例例 238例28例 多2多例例例共例共例0例多例0880+6+++、 个 个 个 个 个少2少3427少少21226233少6++2211++： ： ：： ： ： ： ： ： ： ：按△△△△△1+3+++个 个 个 个 个44562222包数单下数 组数组组数图数图下下图组组++=-++++角角角角角1112含2233一个图出 成一成成一中一中图图中成成===5++++？？？？？7两77（7744数图中图 的数的的数有数有中中有的的1（（多多多多多11=+（个个，形有中 正，正正，多，多有有多正正==15个个少少少少少770=个“）图的多含 方图方方图少图少多多少方方99（1））个个个个个（（5）中组少形中形形中个中个少少个形形个*（三三三三三个个的有成个：有：：有三有正个个正：：）个角角角角角”））长多 个 长 多 多 角 多 方 长 长 方49444）形形形形形在个个个个个方少数方少少形少形方方形？？？？？内形个有形个个？个？形形？的（三序？三三三？？小包角计角角角正括形数形形形方正？。？？？形方组形成）的的长个方数形。（含正方形）共有多少个？
在每个图形中，分别有多少条线段？ 多少个角？多少个三角形？
例1：图中有多少个三角形？
0 12 3 4 0 12 3 4 5
0+1+2+3+4=10（个） 0+1+2+3+4+5=15（个） 10+15=25（个）
例2：数一数，图中有多少个三角形？
单个△：16个 由4个△组成的：6个 共16+6=22（个）
共16+6=22（个）
18个△组成的正方形：1个
共9+8+4+2+1=24（个）
2个△组成的正方形：9个 4个△组成的正方形：8个 8个△组成的正方形：4个 16个△组成的正方形：2个 18个△组成的正方形：1个
共9+8+4+2+1=24（个）
例7 包含两个“ ”在内的小正方形组成的长方形（含正方 形）共有多少个？
例5：数一数，下图中有多少个正方形中包含两个阴影方格？
2×2的正方形：2个 3×3的正方形：4个 4×4的正方形：1个 共2+4+1=7（个）
例6：图中有多少个正方形？
2个△组成的正方形：9个
例1：图中有多少个三角形？
例3：下图中有多少个长方形？
例2：数一数，图中有多少个三角形？
多少个角？多少个三角形？
3 × 4 × 2 × 2 = 48（个）
图123原、、、形理按按弄计计顺单清数数序个楚： 。编图构号形成，的特运组殊用成图加个形法数的原有每理序一或计条乘数边法。有原几理种计选数择。，再用乘法 1多例多2例例 238例28例 多2多例例例共例共例0例多例0880+6+++、 个 个 个 个 个少2少3427少少21226233少6++2211++： ： ：： ： ： ： ： ： ： ：按△△△△△1+3+++个 个 个 个 个44562222包数单下数 组数组组数图数图下下图组组++=-++++角角角角角1112含2233一个图出 成一成成一中一中图图中成成===5++++？？？？？7两77（7744数图中图 的数的的数有数有中中有的的1（（多多多多多11=+（个个，形有中 正，正正，多，多有有多正正==15个个少少少少少770=个“）图的多含 方图方方图少图少多多少方方99（1））个个个个个（（5）中组少形中形形中个中个少少个形形个*（三三三三三个个的有成个：有：：有三有正个个正：：）个角角角角角”））长多 个 长 多 多 角 多 方 长 长 方49444）形形形形形在个个个个个方少数方少少形少形方方形？？？？？内形个有形个个？个？形形？的（三序？三三三？？小包角计角角角正括形数形形形方正？。？？？形方组形成）的的长个方数形。（含正方形）共有多少个？
如何巧数图形
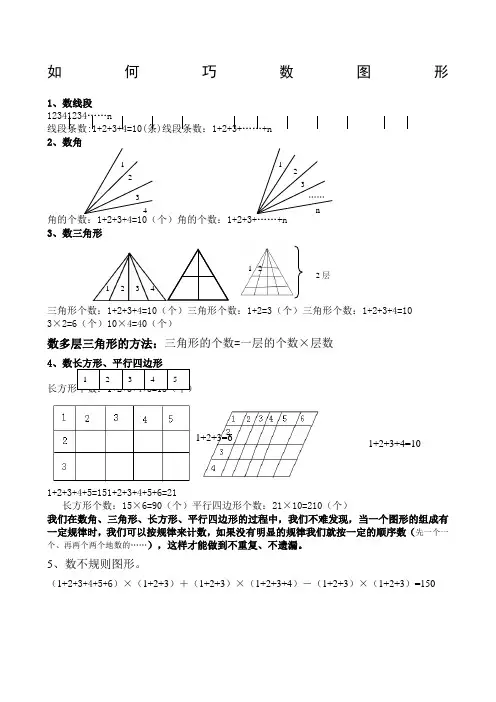
如何巧数图形
1、数线段
12341234……n
线段条数:1+2+3+4=10(条)线段条数：1+2+3+……+n
2、数角
角的个数：1+2+3+4=10（个）角的个数：1+2+3+……+n
3、数三角形 三角形个数：1+2+3+4=10（个）三角形个数：1+2=3（个）三角形个数：1+2+3+4=10 3
×2=6（个）10×4=40（个）
数多层三角形的方法：三角形的个数=一层的个数×层数
4
1+2+3+4+5=151+2+3+4+5+6=21
长方形个数：15×6=90（个）平行四边形个数：21×10=210（个）
我们在数角、三角形、长方形、平行四边形的过程中，我们不难发现，当一个图形的组成有一定规律时，我们可以按规律来计数，如果没有明显的规律我们就按一定的顺序数（先一个一个、再两个两个地数的……），这样才能做到不重复、不遗漏。
5、数不规则图形。
（1+2+3+4+5+6）×（1+2+3）＋（1+2+3）×（1+2+3+4）－（1+2+3）×（1+2+3）=150 1 2 3 4 1 2 3
……
n
1 2 3 4
1 2
2层
1+2+3=6 1+2+3+4=10。
四年级数学寒假教材班第2次课 巧数图形
巧数图形
月日姓名
【知识要点】
图形的计数问题包括：数线段，数角，数长方形，数正方形，数三角形，数综合图形等。要做到数的时候既不重复，又不遗漏，就必须有次序，有条理地数，从基本图形入手，找出规律。
有些图形若没有规律，则一定要按照分类的思想数。
【热身训练】
按要求数图形。
【例题放映】
例1请你数一数图中有多少个正方形？
例2请你计算图中有多少个长方形？
例3数一数图中有多少个三角形？
例4数一数，图中共有多少个三角形？
【随堂练习】
姓名成绩
1．2．
3．
53．
☆4．
家长签字留言处：
我们的工作离不开您的支持与配合，感谢您的合作！
月日姓名
【知识要点】
图形的计数问题包括：数线段，数角，数长方形，数正方形，数三角形，数综合图形等。要做到数的时候既不重复，又不遗漏，就必须有次序，有条理地数，从基本图形入手，找出规律。
有些图形若没有规律，则一定要按照分类的思想数。
【热身训练】
按要求数图形。
【例题放映】
例1请你数一数图中有多少个正方形？
例2请你计算图中有多少个长方形？
例3数一数图中有多少个三角形？
例4数一数，图中共有多少个三角形？
【随堂练习】
姓名成绩
1．2．
3．
53．
☆4．
家长签字留言处：
我们的工作离不开您的支持与配合，感谢您的合作！
巧数图形教案
备课人：教学目标：1、学会按照一定的顺序和类别数出某种图形的个数，数图形时能做到有条理，不重复，不遗漏。
2、会从组合图形中辨认出正方形和长方形。
3、帮助孩子在写作业时养成良好的握笔习惯。
教学重点和难点：1、学生能正确区分正方形和长方形。
2、数图形不重复不遗漏。
教学对策：带着学生一个一个地数清楚。
教学准备：PPT、多媒体教学过程：一、导入（回忆上节课内容）（3’）师：上节课我们学习了如何把一个复杂的图形简单化，只要把它分成小的我们熟悉的图形，数一数每种图形的个数，那么复杂的图形就会简单化。
今天我们继续研究这样的复杂图形。
可是，今天的复杂图形是由一种图形组成的，也就是组合图形。
我们看例1。
例1：下图中有多少个三角形？师：如果老师要求你们自己画出这幅图，你有什么简单的方法吗？预设1：学生可能会说出由两个三角形组成。
预设2：学生可能会说出有6个小三角形。
师：小朋友们从这幅图中看出了2个大三角形，也看出了有6个小三角形，还有没有其他的三角形了？生：没有了。
师：从这幅图中，我们很容易就看出三角形，有大的，也有小的，那我们就可以根据三角形的大小来分别数一数有多少个。
再请2名同学上黑板指一指大三角形和小三角形分别是哪几个。
（板书过程）学生跟着老师写下过程。
师：我们数过了三角形，你还知道哪些图形吗？生：圆，正方形，长方形......师：接下来我们就一起来数一数正方形。
出示例2。
例2：数一数，一共有多少个正方形？师：谁能说一说正方形是什么样子的？预设1：有四条边。
预设2：方方正正的。
预设3：四条边都是一样的。
师：正方形和哪个图形很像呢？生：长方形。
师：那怎么区分正方形和长方形呢？或者提问：谁能说一说正方形和长方形有什么相同和不同的地方吗？根据学生的回答进行总结：相同点：都有四条边，都是方方正正的。
不同点：正方形的四条边都是一样长的，而长方形不一定，只要对边一样长即可。
师：谁来说一说你的方法？根据学生的回答进行评价，可能会出现根据大小分、根据组成的块数分。
北师大四年级数学巧数图形
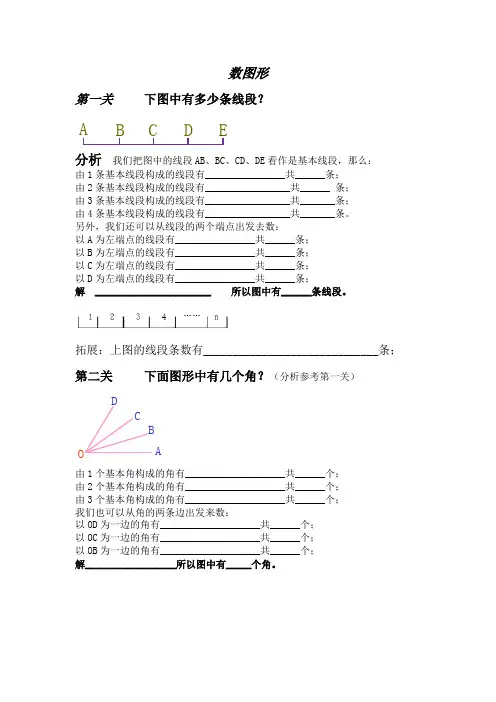
数图形第一关下图中有多少条线段？A B C D E分析我们把图中的线段AB、BC、CD、DE看作是基本线段，那么：由1条基本线段构成的线段有________________共______条；由2条基本线段构成的线段有_________________共______ 条；由3条基本线段构成的线段有_________________共_______条；由4条基本线段构成的线段有_________________共_______条。
另外，我们还可以从线段的两个端点出发去数：以A为左端点的线段有________________共______条；以B为左端点的线段有________________共______条；以C为左端点的线段有________________共______条；以D为左端点的线段有________________共______条；解_______________________ 所以图中有______条线段。
拓展：上图的线段条数有______________________________条；第二关下面图形中有几个角？（分析参考第一关）O DCBA由1个基本角构成的角有____________________共______个；由2个基本角构成的角有____________________共______个；由3个基本角构成的角有____________________共______个；我们也可以从角的两条边出发来数：以OD为一边的角有____________________共______个；以OC为一边的角有____________________共______个；以OB为一边的角有____________________共______个；解__________________所以图中有_____个角。
拓展1：上图有________________________个角；拓展2：上图中共有________________个三角形？拓展3：上图中共有________________个三角形？第三关下面图形中有几个长方形？解_______________________ 所以图中有______个长方形。
2024年苏教版四年级上册数学期末极速提分法第16招巧数图形
第16招 巧数图形
图形计数常用的方法有按顺序数和分类数。要准确、 迅速地数出图形的个数需要注意两点：一是弄清被数图 形的特征和变化规律，找出基本图形；二是要按一定的 顺序数，做到不重复、不遗漏。
经典例题 例 数一数，下图中一共有多少个三角形？
经典例题
思路分析：数这个图中一共有多少个三角形，可以 分两个步骤进行，先不看中间那条横向的线段，这 个图中共有1＋2＋3＝6(个)三角形；加上那条横向 的线段后，上半部分与前面类似，也一共有1＋2＋ 3＝6(个)三角形。应注意下半部分没有三角形。所 以这个图中一共有12 个三角形。
经典例题 规范解答： (1＋2＋3)×2＝12(个)
分类训练
技 巧 1 数线段
规律：先数基本线段，若条数是n，则总条数是n＋(n－ 1)＋(n－2)＋…＋1。
1. 下面各图中分别有多少条线段？
(1)
(2)
4＋3＋2＋1＝10(条) 3＋2＋1＋5＋4＋3＋2＋1＝21(条)
分类训练
技 巧 2 数有同一顶点的角或三角形的个数
分类训练
5. 下面各图中分别有多少个正方形？
(1)
(2)
2×2＋1×1＝5(个)
4×4＋3×3＋2×2＋1×1＝ 30(个)
(1)
(2)
(4＋3＋2＋1)×(3＋2＋1)＝ (2＋1)×(4＋3＋2＋1)＝
Байду номын сангаас
60(个)
30(个)
分类训练
技 巧 4 数大正方形中小正方形的个数
规律： n×n 个相同的小正方形组成的n 行n 列的大正方 形 中 所 含 的 正 方 形 的 总 个 数 是 n × n ＋ (n － 1) × (n－1)＋……＋1×1。
图形计数常用的方法有按顺序数和分类数。要准确、 迅速地数出图形的个数需要注意两点：一是弄清被数图 形的特征和变化规律，找出基本图形；二是要按一定的 顺序数，做到不重复、不遗漏。
经典例题 例 数一数，下图中一共有多少个三角形？
经典例题
思路分析：数这个图中一共有多少个三角形，可以 分两个步骤进行，先不看中间那条横向的线段，这 个图中共有1＋2＋3＝6(个)三角形；加上那条横向 的线段后，上半部分与前面类似，也一共有1＋2＋ 3＝6(个)三角形。应注意下半部分没有三角形。所 以这个图中一共有12 个三角形。
经典例题 规范解答： (1＋2＋3)×2＝12(个)
分类训练
技 巧 1 数线段
规律：先数基本线段，若条数是n，则总条数是n＋(n－ 1)＋(n－2)＋…＋1。
1. 下面各图中分别有多少条线段？
(1)
(2)
4＋3＋2＋1＝10(条) 3＋2＋1＋5＋4＋3＋2＋1＝21(条)
分类训练
技 巧 2 数有同一顶点的角或三角形的个数
分类训练
5. 下面各图中分别有多少个正方形？
(1)
(2)
2×2＋1×1＝5(个)
4×4＋3×3＋2×2＋1×1＝ 30(个)
(1)
(2)
(4＋3＋2＋1)×(3＋2＋1)＝ (2＋1)×(4＋3＋2＋1)＝
Байду номын сангаас
60(个)
30(个)
分类训练
技 巧 4 数大正方形中小正方形的个数
规律： n×n 个相同的小正方形组成的n 行n 列的大正方 形 中 所 含 的 正 方 形 的 总 个 数 是 n × n ＋ (n － 1) × (n－1)＋……＋1×1。
巧数图形教案
巧数图形教案篇一：巧数图形巧数图形1、教材地位及作用《数图形中的学问》是第八册书中第一个专题性活动。
在第二单元认识各种图形之后，本课设计了数简单图形个数的活动，使学生初步体会有序思考的必要性，培养学生有序思考的习惯。
为后面学习“图形中的规律”打下坚实的基础。
2、教学目标：1、体会到按一定规律去数，可以做到不重复，不遗漏，发展有序思维。
2、引导学生在按一定规律数的基础上发现数图形的规律。
3、教学重点：有规律地数，不重复不遗漏。
教学难点：引导学生在按一定规律数的基础上发现数图形的规律。
【学情分析】学生们能够数出简单的图形的个数，但是不一定做到按着一定的顺序来数。
只有极少数学生知道数图形的规律并用算式来计数，绝大多数同学并没有发现数图形的规律，更不会用算式来计数。
设计中注意兼顾各层面学生的不同需求，做到有层次、有梯度。
【教学策略】1、留出空白，放手探究。
课堂教学中在以下几个环节中留出“空白”，让学生去探索、思考。
⑴在寻找新旧知识的衔接点时留“空白”；⑵在提问后留“空白”；⑶当学生对知识认识模糊时留“空白”；⑷在概括结论之前留“空白”；⑸在出现错误之后留“空白”；⑹在出现难题时留“空白”。
2、群体互动，合作探究。
在数较复杂的图形的个数时，有计划地组织他们进行合作探究，以形成集体探究的氛围，培养学生的合作精神。
【教学过程】一、激趣导入。
同学们，今天这节数学课有一些老朋友要和我们一起来上课，欢迎吗？快来看看它们是谁吧！（出示图一）（图一）这些老朋友是谁呀？（指名回答：梯形、三角形、长方形??）今天他们不仅自己来到了课堂，还带来了各自的兄弟姐妹，快来看看向我们提出了什么问题？（出示图二）?共()个共()个（图二）原来让我们数他们兄弟姐妹的个数，也就是数图形的个数。
同学们，你们会数吗？（生有答会数，有答不会数）好，今天这节课我们就一起来研究——数图形中的学问。
（板书课题）咱们先从简单的图形数起吧，这么多图形，你觉得谁的兄弟姐妹的个数最好数呀？（角）（设计意图：引发学生认知冲突，激发学生学习兴趣）二、探索规律。
巧数图形(1)
《巧数图形》微课教学设计教学目标：1、体会有条理数法的多样性，并能运用有序的数法数出给定图形的个数。
2、经历数图形的过程，渗透有序、转化、化繁为简等数学思想，进一步开展空间观念。
3、提高对数学学科的兴趣，增强学习自信心。
教学重点：有规律地数，不重复不遗漏。
教学难点：引导学生在按一定规律数的根底上发现数图形的规律。
一、问题导入，引发兴趣。
在教学四年级下册三角形一知识点时，书上出现了一道找规律数三角形的题目。
如何教学呢？如何引导学生探讨其中的规律呢？我想就结合数线段、数角，由简到繁，由浅入深，引导学习一起来自主学习。
二、数线段，构建数学模型。
我们先从简单的开始。
1、巧数线段〔1〕出示图一共有几条线段？线段上一共有5个点，如何数出线段呢？我们可以按一下思路来理解。
（2）这样一共就有：4+3+2+1=10(条〕2、那么我增加两个点，线段上一共有7个点呢？生自主数，展示方法。
用同样的方法，我们可以列出算式：6+5+4+3+2+1=21(条〕3、师小结：通过以上两道题，大家掌握了规律和诀窍吗？引出：有序、不重复、不遗漏。
三、应用规律：数角我们通过数线段了解了规律，那么可以用这个规律来数角吗？引导学生列式：4+3+2+1=10四、知识迁移：数三角形数线段和角我们都会了，那数三角形是否也可以这样分类来数呢？以上三幅图，能否用刚刚的方法列式数出三角形的个数？你知道怎样列式吗？列式： 3+2+1=6〔个〕 5+4+3+2+1=15〔个〕 6+5+4+3+2+1=21〔个〕五、深化提高：数三角形学会了规律，大家有信心来挑战一下自己吗？运用规律尝试用数三角形的方法数复杂一些的图形中的三角形个数。
师：数完后，你发现了什么？运用分层计数法，就是把刚刚的规律多用几次，用乘法原理就可以很快的数出三角形的个数了。
你学会了吗？它们数的方法与数线段的方法是一样的。
六、归纳总结，拓展提升，开展思维1、归纳总结：数图形时，我们要按照一定的顺序，有条理有方案有方法地去解答，由单个根本图形数起，再数两个图形合成的图形，依次规律一个一个往下数。
巧数图形详解-小学奥数
题目三：数长方形
总结词
数长方形是巧数图形中的高级题目，主要考 察学生的空间想象力和细致的观察能力。
详细描述
题目通常会给出一张由不同形状组成的图形 ，其中包含长方形。学生需要通过空间想象 和细致的观察，数出长方形的数量。在数长 方形的过程中，学生需要注意长方形的定义 ，即两组相对边等长。此外，学生还需要注 意长方形可能存在不同的方向和旋转，确保
枚举法
总结词
逐一列举所有可能的情况，找出符合条件的结果。
详细描述
枚举法适用于图形数量较少、情况较为简单的问题。在解题时，需要逐一列举出 所有可能的情况，并逐一检验是否符合题目要求。通过排除不符合条件的情况， 最终找出符合条件的结果。
排除法
总结词
通过排除不符合条件的情况，逐步缩小范围，最终找出答案。
常见类型与实例
类型
常见的巧数图形题目包括数线段、数三角形、数正方形、数 立方体等。
实例
如数线段，给定一条直线段，在直线段上任意取n个点，将线 段分成n+1段，求这些小段的线段长度之和。
巧数图形的解题思路
观察
首先观察题目所给的图 形，寻找其中的规律或
特征。
分析
分析图形的构成和数量 关系，确定解进行逻 辑推理，得出正确的答
案。
计算
进行必要的计算，得出 最终答案。
02 巧数图形的解题技巧
观察法
总结词
通过细致观察图形特点，找出规律，解决问题。
详细描述
观察法是解决巧数图形问题的一种常用方法。在解题过程中，首先要仔细观察 图形，注意图形的形状、大小、对称性等特征，以及各图形之间的相互关系。 通过观察找出规律，从而解决问题。
详细描述
排除法是解决巧数图形问题的一种常用方法。在解题过程中，首先根据题目的要求和图形的特征，排除一些不可 能的情况。然后逐步缩小范围，最终找出符合条件的结果。排除法可以有效地减少计算量，提高解题效率。
四年级数学巧数图形
进入，但其他的人每题至少 答对六人以上才能算过关。
闯关二：有10个老朋友见面，每两人 要握一次手，一共要握几次手？
10×9÷2=45（次）
答: 一共要握45次手。
大家好，我是童话王国的国
民小蚂蚁。前面两关都被你们闯 过啦！ 好吧，我为你们打开门， 你们通过吧！
闯关三： 数一数，图中有多少个长方形？
6+6+3=15个
五级工程师：下面图形中有多少个三角 形？
拆走2条线后有3个三角形。 返回第1条线后增5个三角形。 返回第2条线后增8个三角形。 总共3+5+8=16个三角形。
或6+3+6+1=16
单2 3 整 个 个个个
大工程师：售票员需要准备几种车票？
钟楼 易 初 莲 唐兴
花
路
学校
回顾探究的经历
数线段和 角的个数
？
数一数，下图中有多少个角？
1
11
2
3
4
2
4+3+2+1=10 个
数线段
31542
共5+4+3+2+1=15 条线段
6×5÷2=15（条） 线段总数=端点数×基本线段数÷2
升级考试: 你能一口报出有多少条线段吗？
A B C D E F GHI J K L 12×11÷2=66（条）
一级工程师:
15 6
总共15+6-1= 20个 （6+5+4+2+1）× （3+2+1）= 126个
闯关四. 数一数，图中有多少个正方形？
15+6+1= 22个
9+2= 11 个
闯关二：有10个老朋友见面，每两人 要握一次手，一共要握几次手？
10×9÷2=45（次）
答: 一共要握45次手。
大家好，我是童话王国的国
民小蚂蚁。前面两关都被你们闯 过啦！ 好吧，我为你们打开门， 你们通过吧！
闯关三： 数一数，图中有多少个长方形？
6+6+3=15个
五级工程师：下面图形中有多少个三角 形？
拆走2条线后有3个三角形。 返回第1条线后增5个三角形。 返回第2条线后增8个三角形。 总共3+5+8=16个三角形。
或6+3+6+1=16
单2 3 整 个 个个个
大工程师：售票员需要准备几种车票？
钟楼 易 初 莲 唐兴
花
路
学校
回顾探究的经历
数线段和 角的个数
？
数一数，下图中有多少个角？
1
11
2
3
4
2
4+3+2+1=10 个
数线段
31542
共5+4+3+2+1=15 条线段
6×5÷2=15（条） 线段总数=端点数×基本线段数÷2
升级考试: 你能一口报出有多少条线段吗？
A B C D E F GHI J K L 12×11÷2=66（条）
一级工程师:
15 6
总共15+6-1= 20个 （6+5+4+2+1）× （3+2+1）= 126个
闯关四. 数一数，图中有多少个正方形？
15+6+1= 22个
9+2= 11 个
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第1讲巧数图形
数出某种图形的个数是一类有趣的图形问题。
由于图形千变万化，
错综复杂，所以准确地数出其中包含的某种图形的个数，可以培养我们
认真，仔细，做事耐心有条理的好习惯。
要想有条理、不重复、不遗漏地数出所要图形的个数，最常用的方法就是分类数。
例1数出下图中共有多少条线段。
分析与解：1.我们可以按照线段的左端点的位置分为A，B，C三类。
如下图
所示，以A为左端点的线段有______条，以B为左端点的线段有________
条，
以C为左端点的线段有_______条。
所以共有_________＝6(条)。
2. 我们也可以按照一条线段是由几条小线段构成的来分类。
如下图所示，AB，BC，CD是最基本的小线段，由一条线段构成的线段有_______条，由两条
小线段构成的线段有_______条，由三条小线段构成的线段有________条。
所以，共有_____________＝6(条)。
由例1看出，数图形的分类方法可以不同，关键是分类要科学，所分的类型
要包含所有的情况，并且相互不重叠，这样才能做到不重复、不遗漏。
例2 下列各图形中，三角形的个数各是多少？
分析与解：因为底边上的任何一条线段都对应一个三角形(以顶点及这条线段
的两个端点为顶点的三角形)，
所以各图中最大的三角形的底边所包含的线段的条数就是三角形的总个数。
由前面数线段的方法知，
图(1)中有三角形1＋2＝3(个)。
图(2)中有三角形________(个)。
图(3)中有三角形_________(个)。
图(4)中有三角形_______________＝15(个)。
图(5)中有三角形______________=21(个)。
例3下列图形中各有多少个三角形？
分析与解：(1)只需分别求出以AB，ED为底边的三角形中各有多少个三角形。
以AB为底边的三角形ABC中，有三角 1＋2＋3＝6(个)。
以ED为底边的
三角形CDE中，有三角形___________(个)。
所以共有三角形___________________(个)。
这是以底边为标准来分类计算的方法。
它的好处是可以借助“求底边线段数”而
得出三角形的个数。
我们也可以以小块个数作为分类的标准来计算：图中共有6个小块。
由1个小块组成的三角形有3个；由2个小块组成的三角形有5个；
由3个小块组成的三角形有1个；由4个小块组成的三角形有________个；
由6个小块组成的三角形有_________个。
所以，共有三角形3＋5＋1＋2＋1＝12(个)。
(2)如果以底边来分类计算，各种情况较复杂，因此我们采用以“小块个数”为
分类标准来计算：
由1个小块组成的三角形有4个；由2个小块组成的三角形有______个；
由3个小块组成的三角形有________个；
由4个小块组成的三角形有_______个；
由6个小块组成的三角形有________个。
所以，共有三角形___________________＝15(个)。
例4右图中有多少个三角形？
解：假设每一个最小三角形的边长为1。
按边的长度来分类计算三角形的个数。
边长为1的三角形，从上到下一层一层地数，有1＋3＋5＋7=16(个)；
边长为2的三角形(由________个小三角形组成)(注意，有一个尖朝下的三角形) 有______________7(个)；边长为3的三角形有___________(个)；边长为
4的三角形有__________ 个。
所以，共有三角形16＋7＋3＋1＝27(个)。
例5数出下页左上图中锐角的个数。
分析与解：在图中加一条虚线，如下页右上图。
容易发现，所要数的每个角
都对应一个三角形(这个角与它所截的虚线段构成的三角形)，这就回到例2，
从而回到例1的问题，即所求锐角的个数，就等于从O点引出的6条射线将
虚线截得的线段的条数。
虚线上线段的条数有________________________
例6在下图中，包含“*”号的长方形和正方形共有多少个？
解：按包含的小块分类计数(
如何数一定数量的长方形小块有多少？有规则吗？) 包含1小块的有1个；包含2小块的有___个；
包含3小块的有4个；包含4小块的有____个；包含5小块的有2个；
包含6小块的有___个；包含8小块的有4个；包含9小块的有____个；
包含10小块的有____个；包含12小块的有4个；包含15小块的有___个。
所以共有1＋4＋4＋7＋2＋6＋4＋3＋2＋4＋2=______(个)。
练习
1.下列图形中各有多少条线段？
2.下列图形中各有多少个三角形？
3.下列图形中，各有多少个小于180°的角？
4.下列图形中各有多少个三角形？
5.下列图形中各有多少个长方形？
6.下列图形中，包含“*”号的三角形或长方形各有多少？
7.下列图形中，不含“*”号的三角形或长方形各有几个？。