第十章 球函数
- 格式:ppt
- 大小:8.57 MB
- 文档页数:60

第十章球函数1000)(',)(0)()()(')()(''c z w c z w z w z q z w z p z w 级数解法一、二阶常微分方程的二阶常微分方程:数。
定解条件,逐个确定系幂级数,并代入方程和的为中心,带有待定系数表示为以级数解法:将方程的解0z ,sin cos 0'"x B x A y y y 的通解为例如:都可展为幂级数。
、处,在x x x sin cos 0 、方程的常点和奇点1为方程的常点。
点解析,则在和)常点:如果(00)()(1z z z q z p 为方程的奇点。
的非解析点,则和是)奇点:如果(00)()(2z z q z p z 否则,为非正则奇点。
为正则奇点;的二阶极点,则的一阶极点,最多是若00)()(z z q z p z00)()(k kk z z c z w 条件确定系数。
递推关系,再根据定解为零,找出系数之间的,令合并后各系数分别代入方程,合并同幂项将00)()(k kk z z c z w 法、常点邻域内的级数解2域内单值解析。
件的解存在,并在此区这个区域中满足定解条内单值解析,则方程在在、)定理:若(R z z z q z p ||)()(10)确定系数(2)0()ln()()()()()0()()()(00,1002000012121b z z z Aw z z b z z z w a z z a z z z w n s s k kks k kks 数解、正则奇点邻域中的级3两个线性无关解为:002010001)()()()()()()()(k kk k kk z z q z q z z z q z z p z p z z z p0)()(k sk k z z c z w 设解的形式为:20)(0)()()(')()(''z z z w z q z w z p z w 两边方程0)()()()(')()()('')(202020 z w z q z z z w z p z z z w z z 0)()()(')()()('')(11020 z w z q z w z p z z z w z z)()()()()()()1)((00000000k sk kk kk k s k k k kk k sk kz z c z z q z z c s k z z p z z c s k s k 零,可得判定方程:令最低次幂项的系数为0)1(00 q sp s s 是较小的根。



求函数解析式的几种方法山东 胡大波求()f x 解析式方法多,难度大.只有正确求出函数解析式才能进一步研究函数性质,因此本文介绍几种求()f x 解析式的方法,供同学们参考.1.配凑法例1 已知2(1)2f x x -=+,求()f x .解:22(1)2(1)2(1)3f x x x x -=+=-+-+,即2()23f x x x =++.2.换元法例2 若2(1)21f x x +=+,求()f x .解:令1t x =+,则1x t =-,22()2(1)1243f t t t t ∴=-+=-+. 2()243f x x x ∴=-+.3.解方程组法若已知()f x 满足某个等式,这个等式除()f x 是未知量外,还出现其他未知量(如()f x -,1f x ⎛⎫ ⎪⎝⎭等).可以利用相互代换得到方程组,消去()f x -或1f x ⎛⎫ ⎪⎝⎭,进而得到()f x 的解析式.例3 若2()()1f x f x x --=+,求()f x .解: 2()()1f x f x x --=+,用x -去替换式中的x , 得2()()1f x f x x --=-+,即有2()()12()()1f x f x x f x f x x --=+⎧⎨--=-+⎩,, 解方程组消去()f x -,得 ()13x f x =+. 4.待定系数法当题设给出函数特征,求函数的解析式时,可用此种方法,如函数为一次函数,可设()(0)f x ax b a =+≠,再利用恒等原理确定其系数.例4 设方程210x x -+=的两根为αβ,,试求满足()f αβ=,()f βα=,(1)1f = 的二次函数()f x 的解析式.解:由已知条件,可得1αβ+=,1αβ= ,显然αβ≠,即0αβ-≠.设二次函数2()(1)f x a x x bx c =-+++.αβ ,为方程210x x -+=的两根,210αα∴-+=且210ββ-+=.222()(1)()(1)(1)(111)1f a b c f a b c f a b c ααααβββββα⎧=-+++=⎪=-+++=⎨⎪=-+++=⎩,,, 可得1b c b c a b c αββα+=⎧⎪+=⎨⎪++=⎩,,, 故111a b c =⎧⎪=-⎨⎪=⎩,,,22()(1)122f x x x x x x ∴=-+-+=-+.5.特值法此法适用于所给的关系式中,无论自变量在定义域内取何值,关系式均成立,通过取某些特殊值代入题设的等式中,有时能使问题具体化、简单化,顺利找出规律,求出解析式.例5 已知(0)1f =,()()(21)()f p q f p q p q p q -=--+∈R ,,求()f x . 解法1:令0p =,得(0)(0)(1)f q f q q -=--+,即()1(1)f q q q -=--+.又令q x -=,代入上式,得2()1()(1)1f x x x x x =--+=++,2()1f x x x ∴=++.解法2:令p q =,得(0)()(1)f f p p p =-+,即2()1(1)1f p p p p p =++=++, 2()1f x x x ∴=++.。
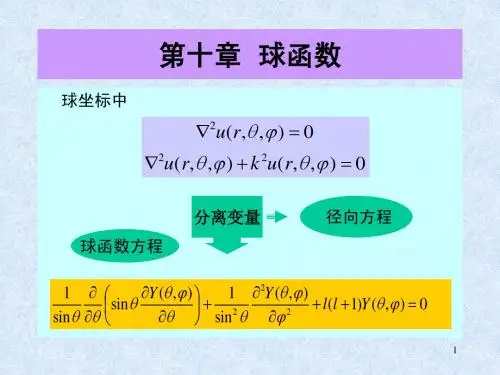





球函数柱函数一、球函数球函数是一类特殊的函数,它们在三维空间中描述了一个点到原点的距离。
球函数通常用于物理学和数学中,用于描述三维空间中的某些物理量或几何量。
1. 球坐标系球坐标系是一种描述三维空间中点的坐标系。
它由径向距离r、极角θ和方位角φ组成。
其中,极角θ表示与z轴的夹角,范围为0到π;方位角φ表示与x轴的夹角,范围为0到2π。
2. 球面积分球面积分是对三维空间中某个区域上的函数进行积分。
球面积分可以用球坐标系来描述,并且可以通过改变极角θ和方位角φ来改变积分区域。
3. 球谐函数球谐函数是一种特殊的函数,它们在球坐标系下具有良好的性质。
球谐函数通常用于描述量子力学中的波函数、电磁场等物理量。
二、柱函数柱函数是另一类特殊的函数,它们在二维平面上描述了一个点到x轴或y轴的距离。
柱函数通常用于数学和工程学中,用于描述平面上的某些物理量或几何量。
1. 柱坐标系柱坐标系是一种描述二维平面上点的坐标系。
它由径向距离r和极角θ组成。
其中,极角θ表示与x轴的夹角,范围为0到2π。
2. 柱面积分柱面积分是对二维平面上某个区域上的函数进行积分。
柱面积分可以用柱坐标系来描述,并且可以通过改变极角θ来改变积分区域。
3. 柱谐函数柱谐函数是一种特殊的函数,它们在柱坐标系下具有良好的性质。
柱谐函数通常用于描述声波、电磁波等在圆形管道中传播时的特性。
三、球函数和柱函数之间的关系球函数和柱函数之间存在着一定的关系。
具体来说,球谐函数可以通过对柱谐函数进行变换得到。
1. 球谐函数与柱谐函数之间的关系球谐函数Ylm(θ,φ)可以表示为:Ylm(θ,φ) = ClmPlm(cosθ)eimφ其中Plm(x)是勒让德多项式,Clm是一个常数,m是一个整数。
柱谐函数Flm(ρ,θ)可以表示为:Flm(ρ,θ) = Dlm(ρ)eimθ其中Dlm(ρ)是柱贝塞尔函数,m是一个整数。
通过对Plm(x)和Dlm(ρ)进行变换,可以得到球谐函数和柱谐函数之间的关系。
数学物理方法第十章球函数参考教材:梁昆淼《数学物理方法》(第四版)球函数♦轴对称问题和勒让德多项式♦转动对称问题和连带勒让德函数♦一般问题和球函数♦本章小结轴对称问题和勒让德多项式♦轴对称拉普拉斯方程的求解♦勒让德多项式♦勒让德多项式的母函数和递推公式♦勒让德多项式的性质♦勒让德多项式的应用轴对称拉普拉斯方程的求解0=∆u 0)1()''(2=+−R l l R r 0)1('2"2=+−+R l l rR R rΘΘ=Θ++Θ有界)(),0(0sin )1()''(sin πθθl l±Θ=Θ++Θ−有界)1(0)1(]'')1[(2l l x θcos =x )(|θf u a r ==1−−+=l l l l rB r A R )(x P l =Θ∑∞==)(cos )(l l l P r R u θ∑∞==)(cos )()(l l l P a R f θθ勒让德多项式♦定义♦一般表示♦具体形式♦级数表示♦微分表示♦积分表示的本征函数有界刘问题—斯±Θ=Θ++Θ−)1(0)1(]'')1[(2l l x ∑−−−−−=kl l k l xk l k l k k l x P 2)!2()!(!2)!22()1()(l lll lx dx d l x P )1(!21)(2−=∫+−−=dz x z z i x P l lll 12)()1(2121)(π♦代数表达式♦图象勒让德多项式的代数表达式)92cos 204cos 35()33035()()cos 33cos 5()35()()12cos 3()13()(cos )(1)(6412481481321341221210++=+−=+=−=+=−====θθθθθθx x x P x x x P x x P x x P x P llll k l l kl x dxd l x k l k l k k l x P )1(!21)!2()!(!2)!22()1()(22−=−−−−=∑−勒让德多项式的图象勒让德多项式的图象母函数和递推公式♦母函数–定义:u(x, r) =∑ P l (x) r l–形式:u(x, r) = ( 1-2rx + r2 )-1/2–推导–应用♦递推公式–基本递推公式–证明–应用母函数的推导∑∞=)(),(ll rx P r x u ∑∫∞+−−=12)()1(2121),(lCl l lrdz x z z i r x u π∑∫∞−−−=2)(2)1(21ll l l Cx z r z xz dz iπ)(2)1(11221x z r z Cxz dz i−−−∫−=πr z x z dziC)1()(21221−−−=∫π2211|11221r xr zri i z z +−=−=−=ππ)211(12r xr rz +−±=±奇点:母函数的应用2211)(),(r rx r x P r x u ll +−==∑∞1)1(11)1(),1(00=⇒=−==∑∑∞∞l l ll P r rr P r u ll l l ll P r rr P r u )1()1()1(11)1(),1(00−=−⇒−=+=−=−∑∑∞∞∑∑∞∞−−=+==22!)!2(!)!12()1(11)0(),0(kkll rk k rr P r u+===⇒−−12,02,)0(!)!2(!)!12()1(k l k l P k k l k 1!)!1(!!0)12(531!)!12()2(642!)!2(=−=−⋅⋅=−⋅⋅=k k k k基本递推公式)()()12()()1(11x kP x xP k x P k k k k −+−+=+)(')()1()('1x xP x P k x P k k k ++=+)(')(')(1x P x xP x kP k k k −−=)()()(')1(12x kP x kxP x P x k k k −−=−0)(0=<x P k递推公式的证明20211)(),(rrx r x P r x u ll +−==∑∞2/3201)21()(),(r rx r x rl x P r x u l l r +−−==∑∞−∑∑∞−∞+−=+−+−−=−0122/3220)()21()21()21)()()(l l ll r l x P r rx r rx r rx r x r x P r x ([][]∑∑∞+−∞++−=−01112l l l l l ll l llr P l r lxP rP l rP rxP 111)1(2)1(−+−−+−+=−k k k k k P k kxP P k P xP 0)12()1(11=++−+−+k k k P k xP k P k递推公式的应用)()()12()()1(11x kP x xP k x P k k k k −+−+=+xx xP x P k =−=⇒=0)()(00113)()(3)(212012−=−=⇒=x x P x xP x P k x x x P x xP x P k 293215123)(2)(5)(32−=−=⇒=勒让德多项式的性质♦奇偶性P l(-x) = (-1)l P l(x)♦零点定理L阶勒让德多项式为L次多项式,有L个零点。
球函数Legendre 多项式Helmholtz 方程球坐标下分离变量得到连带Legendre 方程21d d sin 0sin d d sin μθλθθθθΘ⎛⎫⎡⎤+-Θ= ⎪⎢⎥⎝⎭⎣⎦作变换cos x θ=,()y θ=Θ改写为()22101d dy x y dx dx x μλ⎡⎤⎡⎤-+-=⎢⎥⎢⎥-⎣⎦⎣⎦讨论0μ=情况:1. 三个正则奇点:1,z =±∞,其余全平面解析 z=0邻域内两个线性无关解()2210122212!22n n n n n w z n νννν∞=+⎛⎫⎛⎫Γ-Γ+ ⎪ ⎪⎝⎭⎝⎭=+⎛⎫⎛⎫Γ-Γ ⎪ ⎪⎝⎭⎝⎭∑21n w +n 1,-1对数发散:21ln 1z-,在设()()()11nn n w z z c z ρ∞==--∑。
得到指标方程解120ρρ==得到两个线性无关解()()()()2011112!nn n z P z n n ννν∞=Γ++-⎛⎫= ⎪Γ-+⎝⎭∑()()()()()()2211ln 22121111111 (12)2!z Q z P z z n z n n n ννγψννν+⎡⎤=--+⎢⎥-⎣⎦Γ++-⎛⎫⎛⎫++++ ⎪⎪Γ-+⎝⎭⎝⎭∑2. 方程条件改变球内区域Laplace 方程轴对称边值问题20|u u f ∇==∑其中∑代表球面上的变点i ii令最下两个构成本征值问题,作变换()cos ,x y θθ==Θ,()1λνν=+变为同之前的两个结果,可以得到在0或1的邻域出发求解由于0出的解对数发散,要求ν取特殊值在1邻域得到()()()12y x c P x c Q x νν=+由于Q 发散,其系数为0,令1c 为1。
P 在1收敛,在-1对数发散3. ✧ ()11l P =✧2()()33532P x x x =- ✧ ✧✧✧✧ 由此得到的Legendre 多项式在0点的值:()()()()222!02!ll ll P l =-()2100l P +=✧ Legendre 多项式为l 次多项式,最高项系数为()22!2!l l l c l =4. Legendre 多项式的正交性Legendre 多项式为前述本征值问题的解 作为本征函数有正交性:()()110lkP x P x dx -=⎰证1:由本征值问题直接证明(仿照14.1,写出两个微分方程l 和k ,交叉相乘相减,分部积分得到相似的结果,由边界条件得到为0) 证2:求解积分()11k l x P x dx -=⎰当k l ±()(()111111121112!112!l kk l l l l l k l l d x P x dx x l dxd x x l dx ------=⎡=--⎢⎢⎣⎰⎰⎰前一项为0,继续分部积分l()12211ln x x dx --⎰ ()()()p q p q ΓΓΓ+得到结果为()!221!n l n ++5. Legendre 多项式的模方由之前的结论得到乘方求积分后,低次项全部为0,得到()()()11212!!!222!21!21l l l l l l l l c x P x dx l l l +-==++⎰6. Legendre 多项式的完备性任意在区间[-1,1]分段连续的函数f(x),在平均收敛的意义下,可以展开为级数7. Legendre 多项式生成函数将生成函数函数在0()0l l l P x t ∞==∑由此得到多项式递推关系 8. Legendre 多项式递推关系 ✧ ()()()1121()1l l l l xP x l P x lP +-+=++✧()()()()11'2''l l l l P x P x xP x P x +-=-+Laplace 方程在球坐标下求解1. 一般的Laplace 方程设在电场强度为E 0的均匀电场中放进一个接地导体球,球的半径为a 。
《数学物理方法》课程考试大纲2022-2023山东大学物理学院 数学物理方法期末试题一、 填空题(每题3分,共27分)1. 已知zz =cos (aa +iibb ),z 的代数表达式为________________2. 指出多值函数�(zz −aa )(zz −bb )的支点和阶数___________3. 已知级数∑aa nn xx nn ∞nn=0的收敛半径为A ,试问级数∑aa nn √1+bb nn nnxx nn ∞nn=0(|bb |<1)的收敛半径为_____________4.ssss nn 2zz zz 3的极点为_____,且为______ 阶极点5. 利用柯西公式计算∮zz 2−zz+1zz 2(zz−1)ddzz |zz |=2_______________6. 连带勒让德多项式的正交代数表达式为_______________7. 计算留数1(zz 2+1)2_________________________8. 从t=a 持续作用到t=b 的作用力ff (tt ),可以看作许多前后相继的瞬时力的总和,其数学表达形式为__________9. ∫3δδ(xx −ππ)[ee 2xx +cccccc xx ]ddxx 10−10=_________________ 二、 简算题(每题5分,共15分)1. 将函数ff (zz )=1zz 2−3zz+2,在区域0<|zz −1|<1上展开为洛朗级数 2. �cos mmxx(xx 2+aa 2)2d xx ∞−∞,m>03. 已知解析函数ff =uu +iiνν,而uu =xx 3−3xxyy 2,试求ff三、 (8分)用级数法解微分方程yy ′′+xxyy ′+yy =0四、 (10分)在圆域ρρ<ρρ0上求解泊松方程的边值问题�ΔΔuu =aa +bb (xx 2−yy 2)uu ρρ=pp 0=cc五、 (15分)设有一均匀球体,在球面上的温度为cos 2θθ,试在稳定状态下求球内的温度分布(已知,PP 0(xx )=1,PP 1(xx )=xx , PP 2(xx )=12(3xx 2−1))六、 (10分)利用拉普拉斯变换解RC 电路方程:�RRRR +1CC �RR dd tt tt=EE 0sin ωωttRR (0)=0七、 (15分)计算:⎩⎨⎧ðð2uu ððtt 2−aa 2ðð2uuððxx2=AA cos ππxx ll sin ωωttuu |xx=0=0, uu |xx=ll =0uu |tt=0=φφ(xx ), uu tt |tt=0=ψψ(xx )2022-2023 数学物理方法期末试题 参考答案一、 填空题(每题3分,共27分)1.【正解】 12(ee bb +ee −bb )cos aa +i2(ee −bb −ee bb )sin aa 【解析】cos (aa +i bb )=ee ss (aa+ss bb )+ee −ss (aa+ss bb )2=12(ee −bb ee ss aa+ee bb ee −ss aa )=12[e −bb(cos aa +isin aa )+e bb (cos aa −isin aa )]=12[(e bb+e −bb )cos aa +i(e −bb −e bb )sin aa ]=12(ee bb +ee −bb)cos aa +i 2(ee −bb−ee bb )sin aa 2.【正解】支点:z=a 、b 、∞;皆为一阶支点【解析】注意到函数为12次,且当z=a 、b 时函数置零,z=∞为熟知的支点,阶数皆为2−1=1 3.【正解】A【解析】由根值判别法,幂级数的收敛区间为ll ii ll nn→∞�aa nn ⋅(1+bb nn )nn⋅xxxx (−1,1)而|bb |<1⇒ll ii ll nn→∞√1+bb nn nn=1故收敛半径保持不变,仍为A 4.【正解】zz =0;一阶 【解析】ll ii llzz→0ssss nn 2zz zz 3→∞,且ll ii ll zz→0zz ⋅ssss nn 2zz zz 3=1故zz =0为一阶极点5.【正解】2πi注意到原函数的极点为zz =0和zz =1,且分别为2阶与一阶极点,故上述积分即为II =2ππii �Re cc�ff (zz ),0]+Re cc [ff (zz ),1]��而Re cc [ff (zz ),0]=ll ii ll zz→0dd �zz 2−zz +1zz −1�ddzz=0Re cc [ff (zz ),1]=ll ii ll zz→1zz 2−zz +1zz 2=1因此II =2ππii6.【正解】�PP ll mm (xx )⋅PP kk mm (xx )ddxx =01−1(ll ≠kk ) 7. 【正解】Re cc [ff (zz ),ii ]=ll ii ll zz→ss dd �1(zz +ii )2�ddzz=−2[2ii ]−3Re cc [ff (zz ),−ii ]=ll ii ll zz→−ss dd �1(zz −ii )2�ddzz=−2[−2ii ]−38.【正解】∫ff (ττ)1−1δδ(tt −ττ)ddττ 9.【正解】ee 2ππ−1【解析】由δδ函数的挑选性,上述积分即为 (ee 2xx +cccccc xx )|xx=ππ=ee 2ππ−1 二、 简算题(每题5分,共15分)1.【解析】在区域0<|zz −1|<1内ff (zz )=1zz 2−3zz +2=−12⋅11−zz 2−1zz −1=−12⋅11−zz 2−1zz ⋅11−1zzff (zz )=−�12kk+1zz kk ∞kk=0−�zz −(kk+1)∞kk=0 =−�zz kk−1kk=−∞−�12kk+1zz kk∞kk=02.【解析】由约旦引理,从上半平面的半圆弧补全围道,上半平面有一个二阶极点zz 0=iiaa ,该点的留数为RReeccff (zz 0) =limzz→zz 0d d zz e immzz(zz +aa i)2=lim zz→zz 0[i ll e immzz (zz +aa i)2−2e ss nn zz (zz +aa i)3] =−llaa +14aa 3ie −mmaaII =ππi ⋅(−llaa +14aa 3ie −mmaa )=llaa +14aa3ππe −mmaa 3.【解析】根据C-R 条件,有∂uu ∂xx =3xx 2−3yy 2=∂νν∂yy−∂uu ∂yy =6xxyy =∂νν∂xxddνν=−(−6xxyy )d xx +3(xx 2−yy 2)d yy =d(3xx 2yy −yy 3) 有νν=3xx 2yy −yy 3+CC ,代入得ff (zz )=xx 3−3xxyy 2+i(3xx 2yy −yy 3+CC ) =(xx +i yy )3+i CC =zz 3+i CC 0三、(8分)【解析】设 yy =�aa nn xx nn ∞nn=0 是方程的解,其中 aa 0,aa 1 是任意常数,则yy ′=�nnaa nn xx nn−1∞nn=1yy ′′=�nn (nn −1)aa nn xx nn−2∞nn=2=�(nn +2)(nn +1)aa nn+2xx nn ∞nn=0方程 yy ′′+xxyy ′+yy =0,得�[(nn +2)(nn +1)aa nn+2+nnaa nn +aa nn ]xx nn ∞nn=0=0故必有(nn +2)(nn +1)aa nn+2+(nn +1)aa nn =0即aa nn+2=−aa nnnn +2(nn =0,1,2,⋯ ) 可见,当 nn =2(kk −1) 时aa 2kk=(−12kk )aa 2kk−2=(−12kk )(−12kk −2)⋯(−12)aa 0=aa 0(−1)kkkk !2kk当nn =2kk −1时aa 2kk+1=(−12kk +1)aa 2kk−1=(−12kk +1)(−12kk −1)⋯(−13)aa 1=aa 1(−1)kk (2kk +1)!�aa 2nn xx 2nn ∞nn=0与�aa 2nn+1xx 2nn+1∞nn=0的收敛域均为(−∞,+∞) 故yy =�aa κκxx κκ∞κκ=0=�aa 2κκxx 2κκ∞κκ=0+�aa 2κκ+1xx 2κκ+1∞κκ=0=�aa 0(−1)nn nn !2nn xx 2nn∞nn=0+�aa 1(−1)nn (2nn +1)!xx 2nn+1∞ss=0即yy =aa 0e −xx 22+aa 1�(−1)nn (2nn +1)!xx 2nn+1∞nn=0,xx ∈(−∞,+∞)四、 (10分)【解析】 首先找到满足方程的特解vv =aa 4(xx 2+yy 2)+bb 12(xx 4−yy 4)=aa 4ρρ2+bb 12(xx 2+yy 2)(xx 2−yy 2) =aa 4ρρ2+bb 12ρρ4cos 2φφ 令uu =vv +ww =aa 4ρρ2+bb 12ρρ4cos 2φφ+ww对于齐次方程,且满足球心为有限值的泊松方程通解为ww (ρρ,φφ)=�ρρnn (AA mm cos ll φφ+BB nn sin llφφ)∞mm=0代入边界条件,有 �ρρ0nn (AA mmcos ll φφ+BB nn sin llφφ)∞mm=0=cc −aa 4ρρ02−bb 12ρρ04cos 2φφ比较系数解得uu =vv +ww =cc +aa 4(ρρ2−ρρ02)+bb 12ρρ2(ρρ2−ρρ02)cos 2φφ 五、(15分)【解析】对于满足球心处为有限值的拉普拉斯方程通解为uu (rr ,θθ)=�AA ll rr l P ll (cos θθ)∞ll=0代入边界条件有�AA ll rr 0l P ll (cos θθ)∞ll=0=cos 2θθ=xx 2由于P 2(xx ) =12(3xx 2−1) ,有xx 2=13[1+2P 2(xx )]=13P 0(xx )+23P 2(xx )即�AA ll rr 0lP ll (cos θθ)∞ll=0=cos 2θθ=xx 2=13P 0(xx )+23P 2(xx )对比系数可得uu (rr ,θθ)=13+23⋅1rr 02⋅rr 2P 2(cos θθ)六、(10分)【解析】对方程进行拉普拉斯变换,有jj ‾RR +jj ‾ppCC =EE 0ωωpp 2+ωω2 解得jj ‾=ωωEE 0(RR +1ppCC )(pp 2+ωω2)再进行反演RR (tt )=EE 0ωωRR (−RRCC e llRRRRωω2RR 2CC 2+1+RRCC cos ωωtt +ωωRR 2CC 2sin ωωtt ωω2RR 2CC 2+1) =EE 0RR 2+1/CC 2ωω2(RR sin ωωtt +1CCωωcos ωωtt )−EE 0/CCωωRR 2+1/CC 2ωω2e −tt /RRRR七、(15分)【解析】应用冲量定理法,先求解vv uu −aa 2vv xxxx =0ννxx ∣x=0=0,vv x ∣x=l =0vv ∣tt=ττ+0=0,vv t ∣t=ττ+0=AA cos ππxxllsin ωωττ根据通解的一般形式并代入边界条件,可得vv (xx ,tt ;ττ)=AAllππaasin ωωττsin ππaa (tt −ττ)ll cos ππxx ll uu (xx ,tt )=�vv (xx ,tt ;ττ)tt=AAll ππaa cos ππxx ll �sin ωωττsin ππaa (tt −ττ)ll d ττtt 0=AAll ππaa 1ωω2−ππ2aa 2/ll 2(ωωsin ππaa ll tt −ππaa ll sin ωωtt )cos ππxx ll。
第十章球函数§10.1 轴对称球函数§10.2 连带L多项式§10.3 一般球函数§10.1 轴对称球函数1. 球函数方程本征值问题)()(),(ϕθϕθΦΘ=Y 0]sin )1([sin sin 122=Θθ-++⎪⎭⎫ ⎝⎛θΘθθθm l l d d d d ϕ+ϕ=ϕΦm B m A sin cos )(0=Φλ+Φ'')()2(ϕΦ=π+ϕΦ0)1(2)1(222=Θ++Θ-Θ-l l dxd x dx d x 如果球坐标的极轴是对称轴m=0, Let θ=cos x )()(1100x y a x y a y +=通解0)1(sin 1sin sin 1222=++ϕ∂∂θ+⎪⎭⎫ ⎝⎛θ∂∂θθ∂∂θY l l Y Y 1)当l =0,1,2,3,….其中解的一个变为多项式P l (x ),另一个为无穷级数(在±1发散,舍去)。
⎪⎩⎪⎨⎧Θπ=+∞<±Θ=Θ++Θ-Θ-),0(,)1(012)1(222有界时)(l l dx d x dx d x 2)也称为轴对称球函数)()()(0x P Y l =ΦθΘ=θ本征值问题的本征值:l(l+1), l =0,1,2,3,….本征函数:P l (x )2. L 多项式的各种表达式1) 多项式表达式2)!(2)!2(l l a x l l l=系数为通常给定最高次项22)1)(()1)(2()1)(2()1)((++++-++=⇒++++-=k k k k a l k l k k k a a k k l k l k a 由)!2()!1(2)!22()1()!2)(1()!1(2)12(2)!22)(12(2)1()!(2)!2()12(2)1()12)(2()1(22----=-------=---=---=-l l l l l l l l l l l l l l l l l l l a l l l a l l l l l)!4()!2(2!2)!42()1()!4)(3)(2()!2)(1(2)32(4)!42)(32)(22)(3)(2()1()!2()!1(2)!22()32(4)3)(2()1()32)(4()3)(2(22224----=------------=-------=----=--l l l l l l l l l l l l l l l l l l l l a l l l a l l l l l )!2()!(2!)!22()1(2n l n l n n l a l n n l ----=-⎪⎪⎩⎪⎪⎨⎧-=⎥⎦⎤⎢⎣⎡----=-⎥⎦⎤⎢⎣⎡=∑)(21)(22)!2()!(2!)!22()1()(220为奇数为偶数l l l l l x k l k l k k l x P k l l k l k l kn 记为将)35(21),13(21cos ,1332210x x P x P xP P -=-===如因为只含奇次幂)即求常数项系数计算(0)0(?)0(12==+n l P P )022()!22()!2(2!)!24()1()0(022n k k n x n n n n n n n P n nn ==-----=次幂系数只含偶数项求[]!)!2(!)!12()1()!!2(!)!12(!)!2()1()!!2()!2()1(!2)!2()1(!!2)!2()1(2222n n n n n n n n n n n n n n n n n n n --=--=-=-=-=)()()(x P x P l-=-l l ll l x dxd l P )1(!212-=k k l l k l ba k k l lb a -=∑-=+0!)(!)(:证2,22,22l k l k l l k l ≤≥-<-即项求导过程中保留时求导为零当k l l k l k l l l x k k l k l k l k l x dx d l 22/02!)!(2)12()122)(22()1()1(!21-=∑-+-----=- k l lk l k k k l l k l l l x k k l x k k l l l x l 220202!)!(21)1()1()(!)(!!21)1(!21-=-=∑∑--=--=-)()!2()!(!2)!22()1(22/0x P x k l k l k k l l k l l k l k =----=-=∑按照柯西积分公式dz z z z f i n z f l n n ⎰+-π=100)()()(2!)(dzx z z i x P l l l l l ⎰+--π=12)()1(221)(ψ-=-+=<-=ψψd e x i dz e x x z x x x z l i i 22211)1(1,,半径圆心在若取圆周()[][]⎰⎰ππ-ψψψππ-+ψ+ψψ-ψ-+-π=ψ-⋅-⎥⎦⎤⎢⎣⎡--+π=d e x x i x e x d e x i e x e x x i x P l i li i l i l i l l )12(sin 1(12211)()1(11221)(2222112222施列夫利ψψ-+π=ψψ-+π=ψψ-+π=⎰⎰⎰πππ-ππ-d x x d x i x d x i x l l l )cos 1(1)cos 1(21)sin 1(210222l l l P d P )1()1(11)1(0-=-=ψπ=⎰π拉普拉斯11sin cos 1cos sin cos 1cos sin cos 1)(00222022220=ψπ=ψθ+θπ≤ψψθ+θπ≤ψψθ+θπ≤⎰⎰⎰⎰ππππd d d d i x P l l l l3. 第二类勒让德函数l 为零或整数时,一个解为P l ,另一个解为无穷级数:[]为第二类勒让德多项式dx x P ex P x Q l dxx xl l ⎰⎰=-212)()()(2发散在勒让德方程一般解1)()()(:21±=+=x x Q x Q c x P c y l l l4. L 多项式的正交关系为S —L 本征值问题的特例:)(0)()(11l k dx x P x P l k ≠=⎰-5. L 多项式的模值.122)(1122+==⎰-l dx x P N l l)(0sin )(cos )(cos 0l k d P P l k ≠=⎰θθθθπ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-----=--=⎰⎰⎰--------1122221111211222211222112)1()1()1()1()!(21)1()1()!(21)(dx x dx d dx d x dx d x dx d x dx d l dxx dx d x dx d l dx x P ll l l l l l l l l l ll ll l l l l 证明:)()1()1()!(2)1(211222222ll l lll lx x dx d x l ⎰----=最高次分部积分])1(1()1()11[2112的一阶零点阶零点,则是的)是(ll l l l l x dxd l x x x x --+=-±=--⎰-++-----=11211211221)1()1()!(2)1(dx x dxd x dx d l ll l l l l l ⎥⎦⎤⎢⎣⎡+--=+--=⎰⎰--112112)1()1()!2()!(2)1()!2()1()1()!(2)1(dx x x l l l dx x x l l l l ll l l l⎰⎰-+--+--++-+--=⎥⎦⎤⎢⎣⎡+--+-+-=1111211111112)1()1(1)1()!(2)!2()1()1()1()1()1(11)!2()!(2)1(dx x x l l l l dx x x l x x l l l l l l l l l l l l l2,1,012212212221)1(12121)1()1(21211)1()!(2)!2()1(12211122112022=+=+=+=++=+-+-+--=+-+-⎰l l N l l x l dx x x l l l l l l l l l l l l ll l l分部积分分部l 次6.广义傅里叶级数dxx P x f l dx x P x f N f x P f x f l l ll l l l ⎰⎰∑--∞=+===11112)()(212)()(1)()(θθθθ+=θ=θ⎰∑π∞=d P f l f P f f l l l l l sin )(cos )(212)(cos )(0勒让德多项式是完备的,可作为广义傅里叶级数展开的基,把定义在区间[一1,1]上的函数展开为广义傅里叶级数:)35(21)13(21432)(332210332211003x x f x f x f f P f P f P f P f x x x f -+-++=+++=++=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫==-=-=225230233214323120f f f f f f 3103545214432P P P x x ++=++∴例:⎪⎪⎪⎩⎪⎪⎪⎨⎧====54052143210f f f f 332231202523)23()21(x f x f x f f f f ++-+-=7. 轴对称问题应用⎪⎩⎪⎨⎧θ=<=∇=22cos )0(00r r u r u 例122222222sin 1)(sin sin 1)(1ϕ∂∂θ+θ∂∂θθ∂∂θ+∂∂∂∂=∇u r u r r u r r r u ⎪⎩⎪⎨⎧∞<Θ=Θ++∂Θ∂+=⇒=+-+=∂Θ∂Θ-=∂Θ∂+Θ=+πθθθθθθθθθθθθθ,01222220)1()(sin sin 10)1()()1()(sin sin 1)(1)(sin sin )(l l d drB Ar R R l l dr dR r dr d l l d d dr dR r dr d R d d r R dr dR r dr d r l l得到:令)()(),(θθΘ=r R r u)(cos 2,1,0),1(θ=+l P l l l 本征函数本征值 )(cos )(),(01θ+=θ∑∞=+l l l l ll P r B r A r u ∑∝===<∝→0l )(cos ),(0θθl ll l P r A r u B u r 220cos )(xx P r A lll ==∑θ)(cos 3231),(202θ+=θ∴lP r r r u []32313231)(2131)13(21020202222==∴+=+=⇒-=r A A P P x P x x PP287 例5 E求球内外电场介质球均匀静电场中放置均匀,)1()(000i 2r r u u r i <⎪⎩⎪⎨⎧∞<=∇=球内解:)(cos )(01θl l l lll i P r B r A u ∑∞=++=00=⇒∞<=l r B u 由)(cos 0θl l ll i P r A u ∑∞==∴)2()(cos cos )(00002⎪⎩⎪⎨⎧-=-=>=∇∞→θθl r e e rPE r E u r r u 球外)4()3(0r r er r i r r er r i ru ru u u ====∂∂=∂∂-=εεε球面上)(cos )()2(01θl l l lll e P r D r C u ∑∞=++=的一般解问题ll l l l l l l l l l l l l l ll P r D l D P E P r lA P r D P r E C P rA ∑∑∑∑∞=+∞=-∞=+∞=+--=εθ+-=θ0210010010100000)1()(cos )(cos )4)(3(由)(cos )(cos )1,0(00110001θθl l l le l P rD rPE C u l C E C ∑∞=++-=∴≠=-=∴)(cos cos 000θθl l l ll r e rP E r E P r C u -=-==∑∞=∞→⎪⎪⎩⎪⎪⎨⎧--=+-==⎪⎪⎩⎪⎪⎨⎧=+==3010*********0000002100r D E A r D r E r A l r D r D C A l ε1,0021230003010100≠⎩⎨⎧==⎪⎪⎩⎪⎪⎨⎧-ε-ε=+ε-=⎩⎨⎧==l D A Er D E A C D l l ⎪⎪⎩⎪⎪⎨⎧+-==≠+-+2010100)1(1,0l ll l l l ll r D l r lA r D r A l εθεcos 2300r E A u i +-=均匀极化)(2)1(3)1(230000+ε-εε=-εε=+ε=E E P E E i i )2)1(4(41cos cos 121cos 03003000203000+-=⋅+-=+-+-=εεπεπεθθεεθE r p rrp r E A rE r r E A u e设在单位球北极置4πε0单位的正电荷,则在球内任一点M 产生的静电势为:7. 母函数20cos 21141rr d q u +-==θπε1111)1(,00=⇒=-==θ∑∝=l l l l l A r A r P )1()(cos cos 21102<θ=+θ-∑∞=r P r rr l l l )(cos )(cos )(01θθll l ll l l lll P r A P r B r A ∑∑∞=∞=+=+=)(cos )1()1(cos 1211cos 211022θ=+θ-=+θ-∑∞=l l lP rr rr r rr )1()(cos 1cos 211012>θ=+θ-∑∞=+r P rrr ll l ⎪⎪⎩⎪⎪⎨⎧>θ<θ=+θ-∑∑∞=+∞=+010122)()(cos )()(cos cos 21n n n nn n n nR r P rR R r P R rr Rr R例6 在点电荷4πε0的电场中放置按地导体球,球的半径为a ,球心与点电荷相距r 1,[r 1>a].求解这个静电场.解:取球心为球坐标系的极点,极轴通过点电荷,则极轴是对称轴,问题与φ无关.假如没有导体球,则静电势本来应当是由于导体球的存在,静电势修正为+2121cos rr r r qθ2-),(cos ),(2121θθθr v rr r r qr u ++=2-以球面边界条件代入:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-==∇→∝=0lim cos 2-),(0),(21212v r r r r q r v r v r a r θθθ)(cos )(cos )(),(0101θθθl l l ll l l l ll P rB P r B r A r v ∑∑∞=+∞=+=+=)(cos cos 2-)(cos 011212101θθθl l l ll l l l P r aq aa r r qP a B ∑∑∞=+∞=+-=+-=比较两边的广义傅里叶系数,得最后解得:1112++-=l l l r aq B )(cos 1)(cos 2-),(0111122121θθθl l l l l P r r a q rr r r qr u ∑∞=+++-++=9. 递推公式)(21:)(211123202x P lr r rx r x r x P r rrx l l l l l l∑∑∞=-∞==+--=+-)(求导对)()21()()()21(21210121222x P lr r rx x P r r x x P lr r rx rrx r x rrx l l l l l ll l l ∑∑∑∞=-∞=∞=-+-=-+-=+--+-)或(两边同乘11)()(2)()()(+∞=∞=-∞=∞=+∞=∑∑∑∑∑+-=-l l l ll l l l l l il ll llrx P l r x P lx rx P l rx P r x xPll l ll l ll l l ll l llrx P l r x lxP r x P l r x Pr x xP )()1()(2)()1()()(111011-∞=∞=+∞=∞=-∞=-+-+=-∑∑∑∑∑11111)1()12()1(2)1(+--+-+=-+-+-+=-l l l l l l l l P l lP xP l P l lxP P l P xP 1211111)1()12(2---+-+-='-'-'='-'=+'+'-'=l l l l l l l l l l l l l lP lxP P x P P x lP P P P l P P x P P 其它:的系数得比较lr 11)()(2)()()(+∞=∞=-∞=∞=+∞=∑∑∑∑∑+-=-l l l ll l l l l l il ll llrx P l r x P lx rx P l rx P r x xP例p296. 4⎪⎩⎪⎨⎧⎩⎨⎧π<θ<ππ≤θ≤=<=∇=2/02/0)(00020u u r r u r r 解:定解问题ll l lll P rB r A r u ∑∝=++=θ01)1(),(⎰⎰∑+=+==⎩⎨⎧π<θ<ππ≤θ≤==<∝⇒-∝==101100000212)(212)(2/02/00dx P u l dx P x f l r A x f u P r A B u l l l l l l l l l r ])12[(11-+'-'=+l l l P P P l)]0()0()1()1([2)(2111101110-+-+-++--='-'=⎰l l l l l l P P P P u dx P P u ]22)1)(34(!)!22(!)!12()1()34(!)!22(!)!12()1(!)!22()12(!)!12()1(!)!22()22(!)!12()1()0()0(!)!22(!]!12[)1(!)!22(!]!1)1(2[)1()0()0(,!)!2(!)!12()1()0()0(!)!2(!)!12()1()0(,0)0(,1)1([010000120121111)1(21212121212u dx P u A r k k k A k k k k k k k k k P P k k k k P P k k P P n n P P P k k k k k k l l k k k k l l k k k l l nn l l ==++--=⇒++--=++--+++--=-++-=+-+-=−−→−--=−−→−--===⎰+++-++++=++=-+2))(34(!)!22(!)!12()1(201212000u P r r k k k u u k k k k+++--=++∝=∑§10.2 连带L 多项式1.连带L 函数1)在非轴对称的情况)1(0112)1(22222=Θ⎥⎦⎤⎢⎣⎡--++Θ-Θ-x m l l dx d x dx d x )()3()1(2()1)12)1)2()1)1)()1222212212222221222222yx x m m y x m y x x m y x dxd xyx m y x dxd x y x mm m m m m m ------+--'--''-=Θ--'-=Θ-=Θ)((((((令)]1()1([)1(2)11)3(),2(2=+-++'+-''-y m m l l y x m y x ()得代入(0]1(1[2)1(0]61[6)1(0]21[4)1(012)1(][][][2]4[222=+-++'-''-=''-++'''--='-++''-'''-=++'-''-m m m P m m l l P x P x m P l l P x P x P l l P x P x P l l P x P x ))(次,微分)(再微分一次,)(微分一次,得)(另一方面,将多项式连带可见,L )1()(][22][←-=Θ=m lm m P x Px y⎪⎩⎪⎨⎧Θπ=+∞<±Θ=Θ⎥⎦⎤⎢⎣⎡--++Θ-Θ-),0(,)1(0112)1(22222有界时)(x m l l dx d x dx d x 2)本征值问题ml P x x P l l l m lm ml ≥-==+][22)1()(,.....2,1,0),1(本征函数:本征值:θ=-=θ=-=θ=-=222221212021211sin 33)1(2sin 233)1(sin )1(x P x x P P x P 如3)微分表达式lml ml lm ml l m l ml l mml x dxd l x x P x dx d l x x P )1(!2)1()()1(!2)1()(222222--=--=----++,)()!()!()1()()()(x P m l m l x P x P x P ml mml ml m l +--=--线性相关:,可以证明4)正交完备关系⎰∑⎰-∝=-++-==⎪⎩⎪⎨⎧=+-+≠=11011)()(212)!()!()()(122)!()!(0dx x P x f l m l m l f x P f x f lk l m l m l l k dx P P ml l l m l l ml m k0)1(sin 1sin sin 1222=++ϕ∂∂θ+⎪⎭⎫ ⎝⎛θ∂∂θθ∂∂θY l l YY 0=Φλ+Φ'')()2(ϕΦ=π+ϕΦϕ+ϕ=ϕΦm B m A sin cos )(⎪⎩⎪⎨⎧Θπ=+∞<±Θ=Θ⎥⎦⎤⎢⎣⎡--++Θ-Θ-),0(,)1(0112)1(22222有界时)(x m l l dx d x dx d x ml P x x P m lm ml ≥-=][22)1()(⎪⎪⎭⎫ ⎝⎛==⎪⎩⎪⎨⎧θθθθ=ϕθ,......2,1,0,...2,1,0cos )(cos sin )(cos ),(l l m m P m P Y ml ml ml §10.3 一般球函数1.球函数为球函数,l 为球函数的阶,独立的l 阶球函数是2l +1个2cos ,2sin ϕϕϕϕϕϕim im im im e em ie em --+=-=2. 正交完备关系⎪⎩⎪⎨⎧≠=π+-+=π=πδ=ϕ=θθϕθϕθ⎰⎰⎰⎰⎰⎰---π-*ππk l k l l m l m l dx P P dx P P d edx P P d Y Ym k m l mnn km l n m i n km l n kml02122|)!|(|)!|(22sin ]),()[,(11||||11||||1120)(||||200[]ϕθθθϕθπ++-=θ=ϕθ*ϕππ∝=-=ϕ⎰⎰∑∑d d e P f l m l m l C eP C f im m l mll llm im m l m lsin )(cos ),(412|)!|(|)!|()(cos ),(||2000||⎪⎪⎭⎫ ⎝⎛=++--==........2,1,01....2,1,0,.....1,)(cos ),(||l l l l m eP Y im m l ml ϕθϕθ∑∑∑∑∝=-=∝=-=⇒+=0||0||)(cos )(cos )1(),,(l llm im m ll m l l llm im m l l m llm leP r A eP r B r A r u ϕϕθθϕθ)2,2,2(2612sin )sin 3(61)(cos sin cos sin 22220200||020-==-===-∝=-=∑∑m l iee P u u eP r A u i i l llm im m ll m l ϕϕϕϕθθϕϕθ⎪⎩⎪⎨⎧<∝=<=∇=)0(sin cos sin )(020020u u u r r u r r ϕϕθ例4.p314一般解:ϕθ=θ-θ=ϕθϕ-ϕ2sin )(cos 61)(cos 2161)(cos 2161),,(22020222200222200l i l i l P r u r eP r ir u e P r i r u r u ir u A i r u A i u r A i u r A 2161,21612161,216120022200220202202022-==-==--)2,2,2(2612sin )sin 3(61)(cos sin cos sin 22220200||020-==-===-∝=-=∑∑m l ie e P u u eP r A u i i l llm im m ll m l ϕϕϕϕθθϕϕθ。