现代控制理论(第二章)讲解
- 格式:ppt
- 大小:12.01 MB
- 文档页数:55




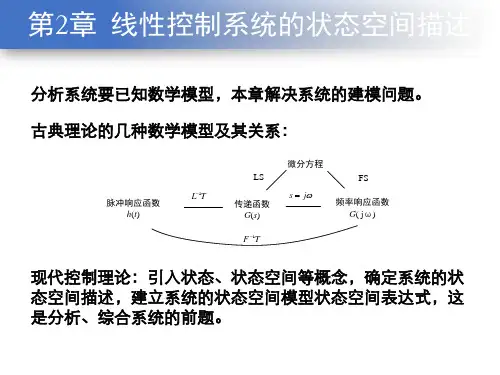
第二章现在控制理论线性系统的数学描述1第二章现在控制理论线性系统的数学描述1第二章线性系统的数学描述数学模型可以存有许多相同的形式,较常用的存有三种:第一种是:把系统的输入量和输出量之间的关系用数学方式表达出来,称之为输入输出描述,或外部描述;比如:微分方程式、传递函数和差分方程。
第二种是:不仅可以描述系统输入、输出之间的关系,而且还可以描述系统的内部特性,称之为状态空间描述或内部描述;它特别适用于于多输出、多输入系统,也适用于于时变系统、非线性系统和随机控制系统。
第三种是:用比较直观的方块图(结构图)和信号流图模型进行描述。
同一系统的数学模型可以表示为不同的形式,需要根据不同的情况对这些模型进行取舍,以利于对控制系统进行有效的分析。
许多表面上全然相同的系统(例如机械系统、电气系统、液压系统和经济学系统)有时却可能将具备完全相同的数学模型;从这个意义上讲,数学模型表达了这些系统的共性,所以只要研究透了一种数学模型,也就能完全了解具有这种数学模型形式的各式各样系统的本质特征。
92.1线性系统的时域数学模型对于单输出、单输入线性定常系统,使用以下微分方程去叙述:c(n)(t)?a1c(n?1)(t)?a2c?b0r(m)(n?2)?(t)?anc(t)(t)an?1c(m?1)(t)?b1r(t)?b2r(m?2)?(t)?bmr(t)(t)bm?1r(2.1)式中,r(t)和c(t)分别是系统的输入信号和输出信号,c(n)(t)为c(t)对时间t的n阶导数;ai(i?1,2,?n)和bj(j?0,1,?m)就是由系统的结构参数同意的系数。
通常情况下,列写控制系统运动方程的步骤就是(建模过程):首先,分析系统的工作原理及其各变量之间的关系,找出系统的输入量和输出量;其次,根据系统运动特性的基本定律,通常从系统的输出端的已经开始依次写下各元件的运动方程,在列写元件运动方程时,须要考量相连元件间的相互作用;最后,由组成系统各元件的运动方程中,消去中间变量,求取只含有系统输入和输出变量及其各阶导数的方程,并将其化为标准形式。




2.1 状态空间描述的基本概念系统一般可用常微分方程在时域内描述,对复杂系统要求解高阶微分方程,这是相当困难的。
经典控制理论中采用拉氏变换法在复频域内描述系统,得到联系输入-输出关系的传递函数,基于传递函数设计单输入-单输出系统极为有效,可从传递函数的零点、极点分布得出系统定性特性,并已建立起一整套图解分析设计法,至今仍得到广泛成功地应用。
但传递函数对系统是一种外部描述,它不能描述处于系统内部的运动变量;且忽略了初始条件。
因此传递函数不能包含系统的所有信息。
由于六十年代以来,控制工程向复杂化、高性能方向发展,所需利用的信息不局限于输入量、输出量、误差等,还需要利用系统内部的状态变化规律,加之利用数字计算机技术进行分析设计及实时控制,因而可能处理复杂的时变、非线性、多输入-多输出系统的问题,但传递函数法在这新领域的应用受到很大限制。
于是需要用新的对系统内部进行描述的新方法-状态空间分析法。
第一节基本概念状态变量指描述系统运动的一组独立(数目最少的)变量。
一个用阶微分方程描述含有个独立变量的系统,当求得个独立变量随时间变化的规律时,系统状态可完全确定。
若变量数目多于,必有变量不独立;若少于,又不足以描述系统状态。
因此,当系统能用最少的个变量完全确定系统状态时,则称这个变量为系统的状态变量。
选取状态变量应满足以下条件:给定时刻的初始值,以及的输入值,可唯一确定系统将来的状态。
而时刻的状态表示时刻以前的系统运动的历史总结,故状态变量是对系统过去、现在和将来行为的描述。
状态变量的选取具有非唯一性,即可用某一组、也可用另一组数目最少的变量。
状态变量不一定要象系统输出量那样,在物理上是可测量或可观察的量,但在实用上毕竟还是选择容易测量的一些量,以便满足实现状态反馈、改善系统性能的需要。
状态向量把描述系统状态的个状态变量看作向量的分量,则称为状态向量,记以,上标为矩阵转置记号。
若状态向量由个分量组成,则称维状态向量。


第二章 线性系统的状态空间分析法c§1 线性系统的状态空间描述§2 线性定常连续系统的分析e a第二章 线性系统的状态空间分析法§3 线性定常离散系统的分析 §4 系统的传递函数矩阵ty cc§1 线性系统的状态空间描述§2 线性定常连续系统的分析e a§3 线性定常离散系统的分析 §4 系统的传递函数矩阵ty c叠加 原理一、系统描述的基本概念 一、系统描述的基本概念1,输入、输出2,松弛性:若系统的输出y[t0,∞) 由输入u[t0,∞)唯一确定,则称系统在t0时刻是松弛的。
系统在t0 时刻不存储能量,初始条件为零!ce a4,线性: H (u1 + u 2 ) = Hu1 + Hu2 可加性5,定常性: Qa 为位移算子y = Hu算子,如传递函数3,因果性:系统在t 时刻的输出仅取决于t时刻和t 时刻之前的输入,与t 时刻之后的输入无关。
ty cy1 y2 yq输入延迟输出相应延迟 y = Hu = HQa u = Qa Hu = Qa y = y (t − a )u (t ) y (t ) u (t ) y (t )cH (αu1 ) = αH (u1 )e at齐次性a为实数u (t ) = Qa u (t ) = u (t − a )ty ct系统 数学描述cu1 u2 up外部描述(输入—输出描述)不完全描述微分方程、传递函数e aM二、状态空间的基本概念 二、状态空间的基本概念Mx 例:机械位移系统 依据牛顿定律: ∑ F = m&&(t )系 统x1 , x2 , L , xn内部描述(状态空间描述)状态方程+输出方程ty c完全描述ckmF (t )e ax (t )& ∴ F (t ) − kx(t ) − fx(t ) = m&&(t ) x微分方程:& m&&(t ) + fx(t ) + kx(t ) = F (t ) xf传递函数:X (s ) 1 = (s ) ms 2 + fs + k F经典控制理论中的数学模型(外部描述),反映 了输入输出的关系,不能反映内部变量的关系。