浮力的计算方法及例题

浮力知识点一、浮力（1）定义：一切浸在液体（气体）的物体都受到液体（气体）对它竖直向上的托力，这个力叫叫浮力。

（2）产生原因（本质）：液（气）体对物体向上的压力大于向下的压力，上下表面压力差即为浮力。

（3）浮力方向：竖直向上，施力物体是液（气）体。

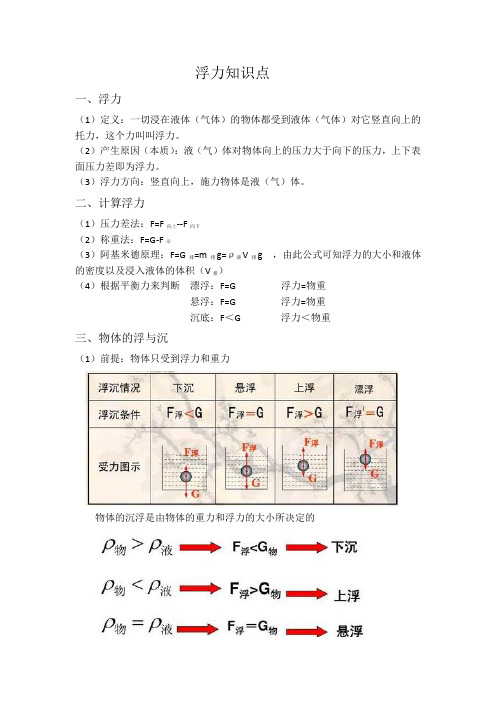
二、计算浮力（1）压力差法：F=F向上--F向下（2）称重法：F=G-F示（3）阿基米德原理：F=G排=m排g=ρ液V排g ，由此公式可知浮力的大小和液体的密度以及浸入液体的体积（V排）（4）根据平衡力来判断漂浮：F=G 浮力=物重悬浮：F=G 浮力=物重沉底：F＜G 浮力＜物重三、物体的浮与沉（1）前提：物体只受到浮力和重力物体的沉浮是由物体的重力和浮力的大小所决定的（2）几种特殊说明：①密度均匀的物体悬浮（或漂浮）在某液体中，若把物体切成大小不等的两块，则大块、小块都悬浮（或漂浮）。

②一物体漂浮在密度为ρ液的液体中，若露出体积为物体总体积的1/n ，则物体密度为ρ液（n -1）/n③悬浮与漂浮的比较相同： F 浮 = G不同：悬浮ρ液 =ρ物 ；V 排=V 物漂浮ρ液 >ρ物； V 排<V 物④冰或冰中含有木块、蜡块、等密度小于水的物体，且漂浮在水面上，化为水液面高度不变。

冰块中含有铁块，石头的等密度大于水的物体，溶化后液面高度降低。

四、关于密度的计算（1）漂浮物体漂浮时重力等于浮力，ρ液V 排g=ρ物V 物g ，∴ρ物/ρ液=V 排/V 物，根据上述公式可计算出漂浮物体的密度（2）密度大于液体的物体利用密度公式ρ=m/v 来计算，先求出质量m ，若物体全部浸没则V 排=V 物，可利用V 排=F 浮/（ρ液g ）来求解。

例如在空中重力为G,浸在密度为ρ的液体中，示数为F 则物体密度为：ρ物= G ρ/ (G -F)五、漂浮的几个特点（1）物体漂浮在液体中，所受的浮力等于它受的重力（2）同一物体在不同液体里漂浮，在密度大的液体里浸入的体积小 （3）同一物体在不同液体里漂浮，所受浮力相同（4）漂浮物体浸入液体的体积是它总体积的几分之几，物体密度就是液体密度 的几分之几（5）将漂浮物体全部浸入液体里，需加的竖直向下的外力等于液体对物体增大的浮力六、浮力的应用（1）轮船：要使密度大于水的材料能够漂浮在水面上的物体必须把它做成空心的，使它能够排开更多的水来增大浮力。

可编辑修改精选全文完整版浮力液面高度变化量计算方法与技巧一、原理分析如何计算液面高度变化量呢？关键是弄清液面变化所对应的体积和相应的底面积，如图所示。

1.高度关系：+h h h ∆=∆∆浸物液①V h S ∆∆=排液容②（ΔV 排=V ②+V ③+V ④）V h S ∆∆=排浸物③（ΔV 排=V ①+V ④）2.体积关系：①V ①=V ②+V ③ ⇒ S 物·Δh 物＝（S 容－S 物）·Δh 液⇒ S h h S S ⋅∆∆=-物物液物容 ②V ②+V ③+V ④= V ①+V ④ ⇒ S 容·Δh 液=S 物·Δh 浸 ⇒ S h h S ⋅∆∆=浸物液容3.递进关系：Δh 液 → Δp 液 → ΔF 液 → ΔF 浮 → ΔF 外二、例题分享如图所示，有一圆柱形容器和一个足够长的圆柱形金属块，容器底面积S 容=30cm 2，圆柱体底面积S柱=10cm 2，容器中盛有水，金属块吊在一根细线下，现将金属块慢慢放入水中，水未溢出，金属块上下底面始终和水面平行。

求：①若金属块浸入水中深度达到15cm时，容器底部受到水的压强增大了多少？②若绳子从金属块底部刚好接触到水面时开始向下放下15cm时，容器底部受到水的压强增了多少？1.第1小问分析过程：要求水对容器底部增加的压强，也就是求水位增加的高度。

如何求水位增加的高度呢？思维过程如下：当圆柱体浸入水中15cm时，实际上是一个动态过程，圆柱体一边下降，水位一边上升，圆柱体下降的深度加上水位上升的高度刚好为15cm。

由此可见，如何将动态变化过程转化为静态过程才是解题关键。

多数同学可能有这样的思维过程：假设原来水位不变，我们把圆柱体浸入水中后排开的水用容器接到，然后将排开的水再倒回容器中。

这个时候有两种思考：（1）倒入圆柱体两边的空白处，这样水位上升的高度，Δh=V排/(S容－S柱)。

显然，圆柱体浸入水中的深度就是15cm+Δh，跟题意矛盾。

浮力的计算专题一、浮力计算方法归纳（一）称重法先用弹簧称称出物体在空气中的重量G，再用弹簧称称出物体浸入液体中时的重量F，两次的示数差，就是物体受到的浮力，这种计算浮力的方法称为称重法。

公式为：F浮＝G－F例1．铝球挂在弹簧秤下，在空气中示数为4牛，将铝球浸没在水中示数为1.8牛，则铝球在水中受到的浮力是多大？（二）压力差法浮力的大小等于下表面受到的向上压力减去上表面受到的向下压力，这种计算浮力的方法称为压力差法。

公式：F＝F下表面－F上表面例2．一个长方体的木块浸没在水中，上表面受到水向下的压力20N，下表面受到水向上的压力50 N，求该木块在水中受到的浮力是多大？（三）原理法阿基米德原理：浸在液体（或气体）里的物体受到向上的浮力，浮力的大小等于被该物体排开的液体的重力，这种方法称为公式法，其公式为F浮=G排例3．“武汉号”导弹驱逐舰在亚洲处于领先水平，参加了我国海军首批赴亚丁湾﹑索马里海域的护航任务。

“武汉号”的排水量为7000t，是一种防空反潜反舰能力均衡的远洋驱逐舰。

满载时，“武汉号”受到的浮力有多大？（g=10牛/千克）（四）公式法F浮=ρ液V排g 这是浮力大小的决定式，浮力大小只与液体密度和物体排开液体体积有关，与物体的体积、物体的密度无关。

例4．一艘小船排开水的体积为10m?，求该小船受到的浮力多大？（g=10牛/千克）（五）平衡法当物体在液体表面或液体中静止时，有两种特殊的状态悬浮和漂浮，此时，在竖直方向上，物体受到向下的重力和向上的浮力是对平衡力，重力的大小等于浮力的大小，这种方法称为平衡法。

公式：F浮＝G例5．一艘重1000000 N的潜水艇，悬浮在水中，求该潜水艇在水中受到的浮力是多大？沉底问题“五规律”规律一：物体在液体中沉底，所受的浮力小于它受的重力；规律二：同一物体在不同液体里沉底，所受浮力不同，液体密度越大浮力越大；规律三：同一物体在不同液体里沉底，排开液体的体积相同，都等于物体的体积；规律四：物体沉底时，它排开液体的重力小于物体的重力，排开液体的质量小于物体的质量，排开液体的质量等于液体的密度乘以物体的体积。

课题名称：浮力专题训练知识点睛知识点 1．浮力的基本知识树叶漂在水面，是因为受到了水的浮力．在水中下沉的铁块，也受到浮力吗？用钢铁制造的轮船，为什么能浮在水面呢？1．定义：液体和气体对浸在其中的物体有向上的托力，物理学中把这个托力叫做浮力。

( F浮=G-F示：G表示物体所受的重力， F 示表示物体浸在液体中时弹簧测力计的求数。

)浮力的方向：竖直向上。

2．浮力产生的原因：浮力是由于液体对浸在它里面的物体向上和向下的压力差产生的，即： F 浮= F 上 -F 下，式中 F 上为物体下表面受到液体向上的压力， F 下为物体上表面受到液体向下的压力。

例题精讲【例 1】下列关于浮力的说法中正确的是（）A ．浮力都是由水产生的B ．在不同液体中浮力的方向会不同C．只有固体才会受到浮力作用 D ．浮力方向与重力方向相反【例 2】一个物体挂在竖直放置的弹簧测力计挂钩上，静止时弹簧测力计的示数是3N．若将物体浸到水中，静止的弹簧测力计的示数为 1.8N．由此可知物体重为N ，水对物体的浮力是N ．【例 3】一个盛有盐水的容器中悬浮着一个鸡蛋，容器放在斜面上，如图所示．图上画出了几个力的方向，你认为鸡蛋所受浮力的方向应是（）A ． F1B ． F2C． F3D． F4【例 4】如图，取一个瓶口内径略小于乒乓球直径的雪碧瓶，去掉其底部，把一只乒乓球放到瓶口处，然后向瓶里注水，会发现水从瓶口流出，乒乓球不上浮．若用手指堵住瓶口，不久就可观察到乒乓球上浮起来．此实验说明了（）A ．大气存在压强B．连通器原理C．浮力产生的原因D．液体的压强与液体的密度和深度有关【例 5】氢气球在空气中脱手后会上升，说明氢气球在空气中也受到力，方向为．【例 6】边长为 20cm的立方体，水平浸没在足够多的水中，如果上表面与水面间的距离为5cm，物体所受的浮力 (g 取 10 N/kg )( )A 80NB 60NC 100ND 80N或 60NF浮G课堂检测【课 1】以下说法中错误的是（）A ．在海滨游泳的人受到海水对他的浮力B．在空中漂浮的氢气球受到空气对它的浮力C．将一石块扔到水中，在其下沉过程中不受浮力D．在水中升起的木块受到浮力【课2】一正方体铁块，在水下某深度时，上表面受到15N 的压力，下表面受到20N 的压力，则此时铁块受到的浮力是N；当铁块下沉到某位置时，上表面受到的压力增大为20N时，下表面受到的压力是N．【课3】将一个物体挂在弹簧测力计上，静止时弹簧测力计的示数为 4.5N，将物体浸没到某种液体中静止时，弹簧测力计的指针恰好回到了零刻线，则此时物体受到的浮力为N．知识点睛知识点 2．阿基米德原理1．浸在液体中的物体受到向上的浮力，浮力的大小等于物体排开的液体所受的重力．2．公式：F浮=G排=m排g=ρ液V排g（说明：液指液体的密度，V排指物体排开液体的体积），当物体全部浸入时，V排＝ V物，受到的浮力最大，且与深度无关．当物体部分浸入时，V排V物，此时 V排等于物体浸入液体中的体积．阿基米德原理同样也适用于气体．节日里放飞的气球就是由于受到了空气对它的浮力而飞上天空的．3．浮力的大小与哪些因素有关当物体受到浮力时，浮力的大小只取决于液体（或气体）的密度和物体排开液体（或气体）的体积；与物体本身的重力、体积和密度无直接关系；且与物体浸没在液体中的深度无关．知识点 3．物体的沉浮条件（物体全部浸没在液体中）：1 、当浮力大于物体重力（）——物体上浮，最终浮在液面上（漂浮），根据二力平衡可知： F′浮 =G。

浮力计算：求解“浮力”最重要的三种方法一、教学目标：让学生掌握在不同已知条件下求解浮力的方法二、教学思路：知识教授→例题精讲→针对练习→综合练习→归纳总结三、教学过程：解法一：压差法该法利用浮力产生的原因：浸在液体中的物体受到液体对它的向上与向下的压力差。

即 F 浮=F 向上－F 向下【例题1】某物块浸没在水中时，下表面受到水的压力为2.5牛，上表面受到水的压力为1.5牛，则该物块受到水的浮力为 牛，方向为 。

【例题2】某物体漂浮在水中处于静状态，已知物体的底面积为1m 2，此时物体底面的压强为1000pa ，浮力为 。

【针对练习1】已知某正方体物块浸没在水中，物块的边长为10cm ，其上表面距液面2cm ，求物块的浮力 。

（水的密度1x103kg/m 3）【针对练习2】已知某物体在水中漂浮时的浮力为10N ，且物体的底面积为10cm 2,求物体底部的压强 。

【针对练习3】已知边长为1cm 正方体物体在水中所受的浮力为10N ，物体上表面的所受的压力为2N ，求物体下表面所受的压强 。

解法二：示重（差）法此法物体在空气中的重与物体在液体中的重的差值等于浮力。

即 浮液空F G G =-。

【例题1】弹簧秤下挂一铁块，静止时弹簧秤的示数是4N ，将铁块一半浸入水中时，弹簧秤的示数为3.5N ，这时铁块所受的浮力是_________N ，ρ铁：ρ水=_________ 。

【例题2】弹簧测力计下挂一长方物体，将物体从盛有适量水的烧杯上方离水面某一高度处缓缓下降，然后将其逐渐浸入水中如图甲，图乙是弹簧测力计示数F与物体下降高度h变化关系的图像，则下列说法中正确的是()A．物体的体积是500cm3B．物体受到的最大浮力是5NC．物体的密度是2.25×103kg/m3D．物体刚浸没时下表面受到水的压力是9N【针对练习1】在弹簧测力计下悬挂一个实心小球，弹簧测力计的示数是8N。

把实心小球浸没在密度为0.8×103kg/m3的油中，弹簧测力计的示数是6N，下列说法不正确．．．的是() A．小球受到的浮力是2NB．小球的质量是0.8 kgC．小球的体积是2.5×10－4m3D．小球的密度是3.2×103g/cm3【针对练习2】有一个实心球形物体，用弹簧测力计在空气中称重时，测力计的示数为12N；当把物体一半体积浸入水中时，测力计的示数为5N。

物理复习题1、浮力计算：（1）实验测量法F浮=G-F示①金属块挂在弹簧秤下端，其示数为7.2N，把它全部浸没在盛满水的烧杯中，弹簧秤示数为4.2N，请计算：①金属块在水中受到的浮力②金属块的密度方法: ①把物体挂在弹簧秤上,测出G物②让物体逐渐浸入液体中读出此时弹簧秤示数F示，则F浮=G-F示②一实心铜块挂在弹簧秤下示数为8.9N，把铜块浸没于某筒状液体中（g=10N/kg）,弹簧秤示数为8.1N，则铜块所受浮力为 N,铜块体积为，液体密度为（ρ铜=8.9g/cm³），当铜块逐渐浸入液体中时，液体对底的压强，最后②F浮=F向上-F向下3、如图③是边长为0.1m的正方体物体，他在离水面0.3m处。

悬浮，他的下a表面受到向上的压力为 N，上表面受到向下的压力为 N，物体受到的浮力 N，方向4、铝块沉在某煤油底部，受到煤油向上的压力为67N，受到向下压力为40N，则铝块受到浮力为 N，方向，铝块重力为 N，（g=10N/kg）③公式法：F浮=ρ液gV排5、把一重5N，体积为0.6dm³的物体投入水中，若不计水的阻力，当物体静止时，下列说法中正确的是（）A 物体上浮F浮=6N,B 物体悬浮，F浮=5N，C 物体漂浮，F浮=5N D物体沉于水底，F浮=6N6、有一块体积为100cm³的木块，把它放入水中，有2/5的体积露出水面，则木块排开水的体积为cm³，所受浮力为 N，木块所受的重力为 N，木块密度为kg/ m³，把它放入另一种液体中，有3/4的物体体积浸入液体中，则该液体密度为kg/ m³，（g=10N/kg）④悬浮式漂浮F浮= G物7、如何验证：F浮= G-F示（保鲜膜，弹簧秤，水建立模型法）8、水平地面上放一只木桶，桶里装满水，轻轻的向水里面放了一段2kg的圆木，它受到浮力 N，从桶中溢水的质量9、对于水中正在上升的气泡，下列说法正确的是（）A、气泡受到水的压强变小，浮力变小B、气泡受到水的压强变小，浮力变大C、气泡受到水的压强变大，浮力变小D、气泡受到水的压强变大，浮力变大5、用天平测浮力F浮=（m2-m1）g,由物体间的力的作用是相互的，水对物体的浮力F浮等于物体对水面向下压力F，而F等于天平增加的砝码所受重力（m2-m1）g，因此F浮=（m2-m1）g10、小红在海边拾到一块漂亮的小石块，她想测出小石块的密度，小红利用一架托盘天平，一个烧杯，适量的水和细线设计了一个测量小石块密度的实验方案，以下是她设计的部分实验步骤，请你按照小红的实验思路将实验步骤补充完整：①用调节好的天平称出小石块的质量m1②在烧杯中注入适量的水，用天平称出烧杯和水的质量m2③在天平右盘加适量砝码，移动游码，天平平衡后，读出砝码和游码的示数为m34在已知水的密度为ρ水，利用上述测量的物理量和已知量计算小石的密度，ρ石的表达式为ρ石=11、把质量相同的实心木块和实心铁球浸没于水中，放手后，木块上浮而铁球下沉。

八年级浮力经典例题一、浮力的基本概念与阿基米德原理相关例题1. 例题一个正方体金属块，边长为10cm，质量为5kg，将其浸没在水中，求它受到的浮力。

（g = 10N/kg）2. 解析（1）首先求出正方体金属块的体积V。

因为正方体边长a = 10cm=0.1m，根据正方体体积公式V=a^3，可得V=(0.1m)^3=1×10^-3m^3。

（2）根据阿基米德原理F_浮=ρ_液gV_排。

当金属块浸没在水中时，V_排=V = 1×10^-3m^3，水的密度ρ_水=1.0×10^3kg/m^3，g = 10N/kg。

则F_浮=ρ_水gV_排=1.0×10^3kg/m^3×10N/kg×1×10^-3m^3=10N。

二、物体浮沉条件相关例题1. 例题一个物体重为5N，体积为600cm^3，将其放入水中，求这个物体静止时受到的浮力。

（g = 10N/kg）2. 解析（1）先求出物体的密度ρ_物。

已知物体重力G = 5N，根据m=(G)/(g)，可得物体质量m=(5N)/(10N/kg)=0.5kg。

物体体积V = 600cm^3=6×10^-4m^3，根据密度公式ρ=(m)/(V)，可得ρ_物=(0.5kg)/(6×10^-4)m^{3}≈0.83×10^3kg/m^3。

（2）因为ρ_物<ρ_水(1.0×10^3kg/m^3)，所以物体在水中静止时漂浮。

（3）根据漂浮条件F_浮=G = 5N。

三、浮力的计算与多个物理量综合例题1. 例题有一个用细线系着的实心铜球，体积为100cm^3，将它缓慢浸没在某种液体中时，细线对球的拉力为0.98N，求这种液体的密度。

（ρ_铜=8.9×10^3kg/m^3，g = 9.8N/kg）2. 解析（1）先求出铜球的重力G。

根据m=ρ V，铜球体积V = 100cm^3=1×10^-4m^3，ρ_铜=8.9×10^3kg/m^3，可得铜球质量m=ρ_铜V = 8.9×10^3kg/m^3×1×10^-4m^3=0.89kg。