《函数》第10讲 函数的图象(2)

题目 高中数学复习专题讲座函数图象及图象性质的应用高考要求函数的图象与性质是高考考查的重点内容之一，它是研究和记忆函数性质的直观工具,利用它的直观性解题,可以起到化繁为简、化难为易的作用因此，考生要掌握绘制函数图象的一般方法，掌握函数图象变化的一般规律，能利用函数的图象研究函数的性质 重难点归纳1 熟记基本函数的大致图象，掌握函数作图的基本方法 (1)描点法 列表、描点、连线；(2)图象变换法 平移变换、对称变换、伸缩变换等2 高考中总是以几类基本初等函数的图象为基础来考查函数图象的题型多以选择与填空为主，属于必考内容之一，但近年来，在大题中也有出现，须引起重视典型题例示范讲解例1对函数y =f (x )定义域中任一个x 的值均有f (x +a )=f (a －x ), (1)求证y =f (x )的图象关于直线x =a 对称；(2)若函数f (x )对一切实数x 都有f (x +2)=f (2－x ),且方程f (x )=0恰好有四个不同实根，求这些实根之和命题意图 本题考查函数概念、图象对称问题以及求根问题 知识依托 把证明图象对称问题转化到点的对称问题错解分析 找不到问题的突破口，对条件不能进行等价转化技巧与方法 数形结合、等价转化(1)证明 设(x 0,y 0)是函数y =f (x )图象上任一点，则y 0=f (x 0),∵2)2(00x x a +-=a , ∴点(x 0,y 0)与(2a －x 0,y 0)关于直线x =a 对称，又f (a +x )=f (a －x ),∴f (2a －x 0)=f ［a +(a －x 0)］=f ［a －(a －x 0)］=f (x 0)=y 0, ∴(2a －x 0,y 0)也在函数的图象上，故y =f (x )的图象关于直线x =a 对称(2)解 由f (2+x )=f (2－x )得y =f (x )的图象关于直线x =2对称，若x 0是f (x )=0的根，则4－x 0也是f (x )=0的根， 若x 1是f (x )=0的根，则4－x 1也是f (x )=0的根， ∴x 0+(4－x 0)+ x 1+(4－x 1)=8 即f (x )=0的四根之和为8例2如图，点A 、B 、C 都在函数y =x 的图象上，它们的横坐标分别是a 、a +1、a +2 又A 、B 、C 在x 轴上的射影分别是A ′、B ′、C ′,记△AB ′C 的面积为f (a ),△A ′BC ′的面积为g (a )(1)求函数f (a )和g (a )的表达式；(2)比较f (a )与g (a )的大小，并证明你的结论命题意图 本题考查函数的解析式、函数图象、识图能力、图形的组合等知识依托 充分借助图象信息，利用面积问题的拆拼以及等价变形找到问题的突破口错解分析 图形面积不会拆拼技巧与方法 数形结合、等价转化 解 (1)连结AA ′、BB ′、CC ′,则f (a )=S △AB ′C =S 梯形AA ′C ′C －S △AA ′B ′－S △CC ′B =21(A ′A +C ′C )=21(2++a a ),g (a )=S △A ′BC ′=21A ′C ′·B ′B =B ′B1(2)()()2f a g a -=12=--102=-<∴f (a )<g (a )例3已知函数f (x )=ax 3+bx 2+cx +d 的图象如图，求b 的范围解法一 观察f (x )的图象，可知函数f (x )的图象过原点，即f (0)=0,得d =0,又f (x )的图象过(1，0)，∴f (x )=a +b +c ① 又有f (－1)＜0,即－a +b －c ＜0 ② ①+②得b ＜0,故b 的范围是(－∞,0)解法二 如图f (0)=0有三根0,1,2，∴f (x )=ax 3+bx 2+cx +d =ax (x －1)(x －2)=ax 3－3ax 2+2ax ,∴b =－3a ,∵当x>2时，f (x )>0，从而有a >0,∴b ＜0 学生巩固练习1 当a ≠0时，y =ax +b 和y =b ax的图象只可能是( )2某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了，再走余下的路，下图中y轴表示离学校的距离，x轴表示出发后的时间，则适合题意的图形是()3已知函数f(x)=log2(x+1)，将y=f(x)的图象向左平移1个单位，再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，得到函数y=g(x)的图象，则函数F(x)=f(x)－g(x)的最大值为_________三、解答题4如图，在函数y=lg x的图象上有A、B、C三点，它们的横坐标分别为m,m+2,m+4(m>1)(1)若△ABC面积为S，求S=f(m);(2)判断S=f(m)的增减性5如图，函数y=23|x|在x∈［－1,1］的图象上有两点A、B，AB∥Ox轴，点M(1，m)(m∈R且m>23)是△ABC的BC边的中点(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);(2)求函数S=f(t)的最大值，并求出相应的C点坐标6已知函数f(x)是y=1102+x－1(x∈R)的反函数，函数g(x)的图象与函数y=－21-x的图象关于y轴对称，设F(x)=f(x)+g(x)(1)求函数F(x)的解析式及定义域；(2)试问在函数F(x)的图象上是否存在两个不同的点A、B，使直线AB 恰好与y轴垂直？若存在，求出A、B的坐标；若不存在，说明理由7已知函数f1(x)=21x-,f2(x)=x+2,(1)设y =f (x )=⎩⎨⎧∈--∈]1,0[ ),(3)0,1[ ),(21x x f x x f ，试画出y =f (x )的图象并求y =f (x )的曲线绕x 轴旋转一周所得几何体的表面积；(2)若方程f 1(x +a )=f 2(x )有两个不等的实根，求实数a 的范围(3)若f 1(x )>f 2(x －b )的解集为［－1，21］，求b 的值8 设函数f (x )=x +x1的图象为C 1，C 1关于点A (2，1)对称的图象为C 2，C 2对应的函数为g (x )(1)求g (x )的解析表达式；(2)若直线y =b 与C 2只有一个交点，求b 的值，并求出交点坐标； (3)解不等式log a g (x )<log a 29 (0<a <1)参考答案1 解析 ∵y =b ax =(b a )x ,∴这是以b a 为底的指数函数 仔细观察题目中的直线方程可知 在选择支B 中a >0,b >1,∴b a >1,C 中a ＜0,b >1,∴0＜b a＜1,D 中a ＜0,0＜b ＜1,∴b a >1 故选择支B 、C 、D 均与指数函数y =(b a )x 的图象不符合答案 A2 解析 由题意可知，当x =0时，y 最大，所以排除A 、C 又一开始跑步，所以直线随着x 的增大而急剧下降答案 D3 解析 g (x )=2log 2(x +2)(x >－2)F (x )=f (x )－g (x )=log 2(x +1)－2log 2(x +2)=log 21441log441log)2(122222+++=+++=++x x x x x x x x)1(21111log2->++++=x x x ∵x +1>0,∴F (x )≤41log211)1(21log 22=++⋅+x x =－2当且仅当x +1=11+x ,即x =0时取等号∴F (x )max =F (0)=－2答案 －24 解 (1)S △ABC =S 梯形AA ′B ′B +S 梯形BB ′C ′C －S 梯形AA ′C ′C(2)S =f (m )为减函数5 解 (1)依题意，设B (t ,23 t ),A (－t ,23t )(t >0),C (x 0,y 0)∵M 是BC 的中点 ∴2x t +=1,2230y t + =m∴x 0=2－t ,y 0=2m －23t在△ABC 中，|AB |=2t ,AB 边上的高h AB =y 0－23t =2m －3t∴S =21|AB |·h AB =21·2t ·(2m －3t ),即f (t )=－3t 2+2mt ,t ∈(0,1)(2)∵S =－3t 2+2mt =－3(t －3m )2+32m ,t ∈(0,1],若⎪⎪⎩⎪⎪⎨⎧>≤<23130m m ，即23＜m ≤3,当t =3m 时，S max =32m ,相应的C 点坐标是(2－3m ,23m ),若3m >1,即m >3 S =f (t ) 在区间(0，1］上是增函数，∴S max =f (1)=2m －3,相应的C 点坐标是(1，2m －3)6 解 (1)y =1102+x－1的反函数为f (x )=lg xx +-11(－1＜x ＜1)由已知得g (x )=21+x ,∴F (x )=lgxx +-11+21+x ,定义域为(－1，1)(2)用定义可证明函数u =xx +-11=－1+12+x 是(－1，1）上的减函数，且y =lg u 是增函数∴f (x )是(－1，1）上的减函数，故不存在符合条件的点A 、B7 解 (1）y =f (x )=⎪⎩⎪⎨⎧∈+--∈-]1,0[,1)0,1[,12x x x x 的图像如图所示y =f (x )的曲线绕x 轴旋转一周所得几何体是由一个半径为1的半球及底面半径和高均为1的圆锥体组成，其表面积为(2+2)π(2)当f 1(x +a )=f 2(x )有两个不等实根时，a 的取值范围为2－2＜a ≤1(3)若f 1(x )>f 2(x －b )的解集为［－1，21］，则可解得b8 (1)g (x )=x －(2)b =4时，交点为(5，4)；b =0时，交点为(3，0)(3)不等式的解集为{x |4＜x ＜29或x >6}课前后备注。

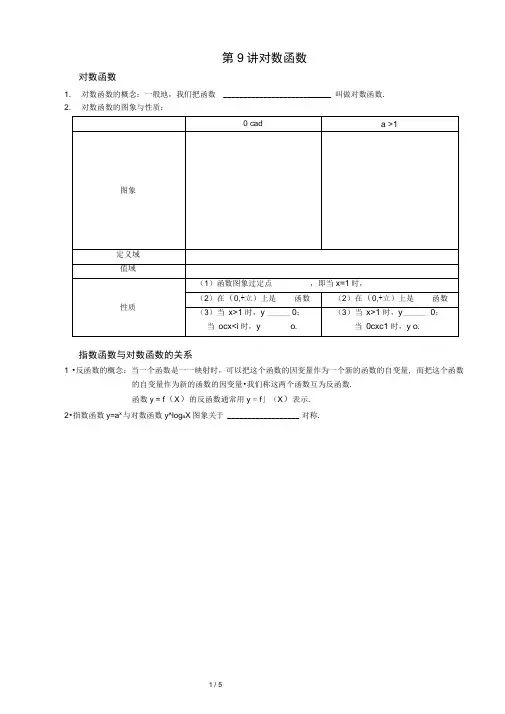
第9讲对数函数对数函数1. 对数函数的概念：一般地，我们把函数 ___________________________ 叫做对数函数.2. 对数函数的图象与性质：指数函数与对数函数的关系1 •反函数的概念：当一个函数是一一映射时，可以把这个函数的因变量作为一个新的函数的自变量, 而把这个函数的自变量作为新的函数的因变量•我们称这两个函数互为反函数.函数y = f（X）的反函数通常用y = f」（X）表示.2•指数函数y=a x与对数函数y^log a X图象关于 __________________ 对称.【例1】下列函数是对数函数的是 （ ）2A . y =log 3(x 1)B . y =log a (2x)(a .0 ,且 a =1)C . y =1 nxD . y =log a X (a . 0,且a =1)【例2】 函数f （x ） =（a 2 a -5）log a x 为对数函数，则f （-）等于（ ）8【例1】求下列函数的定义域：j^3x（1）f x二g x 1 ；【例3】(1)设 A =〈x|y = .1—X 2?,B =「y|y =ig(1-x 2)?，则 小B =() A . {( -1,1)} B . {(0,1)}C . [-1 , 0]D . [0 , 1](2)函数y =log (2xi) 3x —2的定义域是()2 1 ________________ 2 ________________ 1 __________A .(3,1)U (1，二)B . (-,1^J(1/::)C . (-，：：)D . (- , ■:：)【例2】a,b,c 是图中三个对数函数的底数，它们的大小关系是图中的曲线是y=log a x 的图象，已知a 的值为 2 , 次为（）.4 31一,—,一，则相应曲线 G ,C 2,C 3,C 4的a依3 10 5A . c > a > bB . c > b > aC . a > b > c1-51-53一10303一1014-33W1- 5XB . -3C . -log 3 6D . - log 3 8(2) y = 1 —Iog 2(4x_5).【例3】【例4】当o :::a ：：：1时，在同一坐标系中，函数y =a°与y =log a X 的图象是（)•x【例5】 已知f (x 3) =log 2 x,则f (8)的值等于( ).A . 1B . 2C . 8【例6】 若log 2a ::1，则a 的取值范围是3---------22A . 0 :: aB . a -332[例 7】 函数y=log i(x -6X 17)的值域是(2A . RB . [8,：：)下面结论中，不正确的是 _____________ A .若a > 1,贝U y=a x 与y=log a X 在定义域内均为增函数 B .函数y =3x 与y =log 3X 图象关于直线y =x 对称2C . y - log a x 与y=2logax 表示同一函数D .若 0 :: a <1,0 : ： m ：： n ：：1，则一定有 log a m log a n 0【例13】若log m 3 ::: log n 3，求m 和n 的关系.【例8】 比较两个对数值的大小：ln7 ln12 ; log °.5°.7 l o g . 5 0. . 8 【例9】 若 logm9 ：：：logn9 ：：：0，那么A . m n 1 【例10】 log 1 b :: log 1 a :: log 1 c 2 2 2 A . 2b 2a 2c 已知 【例11】 下列大小关系正确的是( 3 0.4A . 0.4：:3 :: log 4 0.3C . log 4 0.3 ：：0.43 ：：30.4m,n 满足的条件是（ ，则（ ).). C . 0 ：： n ::: m ：： 1 D . 0 ：： m ：： n ：： 1 C . 2c 2b 2a D . 2c 2a -2b30.40.4 :: log 4 0.3 :: 3log 4 0.3 ：：：30.4 ：：0.43 D . 122 C . a ：：：1 3D . 20 ■■： a或 a >).C .（」：，-3]D .[3,；)【例12】【例14】下列区间中，函数 f(x) =lg(2 —x)，在其上为增函数的是()【例15】设x i , X 2是方程lg 2x alg x ^0的两个根，则X 1X 2的值是 _________________ .2 2【例16】函数y =(log 1 x) -log 1 x 5在2剟x 4时的值域为 _________________________ .【例17】已知函数f (X) =lg(2 x 2)，则满足不等式f(2x 一1) ：：： f (3)的x 的取值范围为【例18】(1)若函数y =log 2(kx 亠4kx 亠5)的定义域为R ，则k 的取值范围( )5 55 5A . (0，;)B . [0，；)C . [0，； ]D .(」:，0)-(二，：■)4 44 42(2)已知函数f(x)=lg(ax -2x a)的值域为R ，则实数a 的取值范围为( )A . [/ , 1]B . [0 , 1]C ., -1)- (1 ,：：)D . (1,：：)__ Q【例19】已知函数f(x)=log 2X 的定义域是[2 , 16].设g(x) = f (2x) -[ f(x)].(1) 求函数g(x)的解析式及定义域； (2) 求函数g(x)的最值.A .(一打]C - [0,3)D . [1,2)课后作业C . (i ：二“山(-1 ,0)D . (-: ：，0)L/(0 ,，)A . f(x) =x 1与 g(x) =x 1x —1C . f (x)二x 与 g(x) =log 22x f (x)=2lg x 与 g(x) =lg x 2【练6】图中曲线分别表示y=log a X , y=log b X ,y=log d X 的图象，a, b, c, d 的关系是( A . 0 :: a::: b:: 1=: d:: c B . 0 :: b:: a ::: 1:: c:: d C.0 :: d :: c:: 1：：： a ::: bD . 0 :: c d ：：1：： a ::: b【练7】 函数y =log 2(x 2 2)的值域是 ______________________ 【练8】 已知函数f(x)=lg(2 x) lg(2-x).(1) 求函数f (x)的定义域；(2) 若不等式f(x) m 有解，求实数m 的取值范围.【练1】方程2log3x=4的解是()13A .-B .C . . 3D . 993【练2】已知 a =log 2 0.3,b =2° ',c =0.21'3，则 a,b,c 的大小关系是( : )A . a ::: b ::: cB . c ::: a ::: bC . a ::: c ::: bD . b ::: c ■ a【练3】如果f 人：：：1，求x o 的取值范围.【练4】若f(x)=応，则f(x)的定义域是(【练5】F 列各组函数中，表示同一个函数的是(设函数f(x)=[2「，x 兰log 2 (x +1 ),x >0A . (1, * ：：)B . (0讥(1，•:：) f (x)二■. x 2 与 g(x) =x log c x , )O。

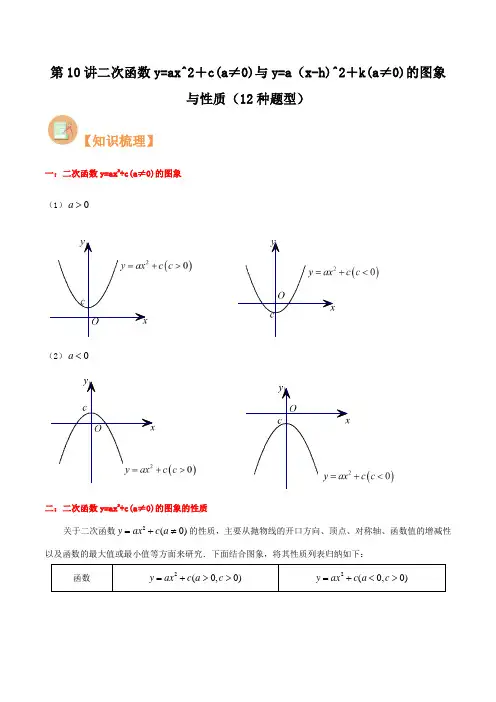
第10讲二次函数y=ax^2＋c(a ≠0)与y=a （x-h)^2＋k(a ≠0)的图象与性质（12种题型）【知识梳理】一：二次函数y=ax 2+c(a ≠0)的图象 （1）（2）二：二次函数y=ax 2+c(a ≠0)的图象的性质关于二次函数的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：函数0a >0a <2(0)y ax c a =+≠2(0,0)y ax c a c =+>>2(0,0)y ax c a c =+<>jjjj三：二次函数与之间的关系；（上加下减）.的图象向上（c ＞0）【或向下（c ＜0）】平移│c │个单位得到的图象. 要点诠释：抛物线的对称轴是y 轴，顶点坐标是(0，c)，与抛物线的形状相同． 函数的图象是由函数的图象向上（或向下）平移个单位得到的，顶点坐标为(0，c)．抛物线y ＝ax 2(a ≠0)的对称轴、最值与顶点密不可分，其对称轴即为过顶点且与x 轴垂直的一条直线，其顶点横坐标x ＝0，抛物线平移不改变抛物线的形状，即a 的值不变，只是位置发生变化而已． 四：二次函数()2y a x m =+的图像一般地，二次函数()2y a x m =+的图像是抛物线，称为抛物线()2y a x m =+，它可以通过将抛物线2y ax =向左（0m >时）或向右（0m <时）平移m 个单位得到．抛物线()2y a x m =+（其中a 、m 是常数，且0a ≠）的对称轴是过点（-m ，0）且平行（或重合）于y 轴的直线，即直线x = -m ；顶点坐标是（-m ，0）．当0a >时，开口向上，顶点是抛物线的最低点；当0a <时，开口向下，顶点是抛物线的最高点． 五：二次函数()2y a x m k =++的图像二次函数()2y a x m k =++（其中a 、m 、k 是常数，且0a ≠）的图像即抛物线()2y a x m k =++，可()20y ax a =≠()20y ax c a =+≠()20y ax a =≠()20y ax c a =+≠2(0)y ax c a =+≠2(0)y ax a =≠2(0)y ax c a =+≠2(0)y ax a =≠||c以通过将抛物线2y ax =进行两次平移得到．这两次平移可以是：先向左（0m >时）或向右（0m <时）平移m 个单位，再向上（0k >时）或向下（0k <时）平移k 个单位．利用图形平移的性质，可知：抛物线()2y a x m k =++（其中a 、m 、k 是常数，且0a ≠）的对称轴是经过点（m -，0）且平行于y 轴的直线，即直线x =m -；抛物线的顶点坐标是（m -，k ）．抛物线的开口方向由a 所取值的符号决定，当0a >时，开口向上，顶点是抛物线的最低点；当0a <时，开口向下，顶点是抛物线的最高点．【考点剖析】题型1：求二次函数y=ax 2+c(a ≠0)解析式例1.求下列抛物线的解析式：（1）与抛物线形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线； （2）顶点为（0，1），经过点（3，-2）并且关于y 轴对称的抛物线．题型2：二次函数y=ax 2+c(a ≠0)平移例2.在同一直角坐标系中，画出和的图象，并根据图象(如图所示)回答下列问题．(1)抛物线向________平移________个单位得到抛物线；2132y x =-+2y x =-21y x =-+21y x =-+2y x =-(2)抛物线，开口方向是________，对称轴为________，顶点坐标为________；(3)抛物线，当x________时，随x 的增大而减小；当x________时，函数y 有最________值，其最________值是________．【变式】(1)抛物线的开口方向 ，对称轴是 ，顶点坐标是 ． (2)抛物线与的形状相同，其顶点坐标为（0，1），则其解析式为 ． (3)抛物线向 平移 个单位后，得到抛物线. 题型3：二次函数y=ax 2+c(a ≠0)的实际应用例3.有一个抛物线形的拱形隧道，隧道的最大高度为6m ，跨度为8m ，把它放在如图所示的平面直角坐标系中．（1）求这条抛物线所对应的函数关系式；（2）若要在隧道壁上点P （如图）安装一盏照明灯，灯离地面高4.5m ．求灯与点B 的距离．题型4：二次函数y=ax 2+c(a ≠0)与一次函数的综合例4.在同一平面直角坐标系中，一次函数与二次函数 的图象大致为（ ）．【变式】在同一坐标系中，一次函数y=ax +b 与二次函数y=ax 2﹣b 的图象可能是（ ）21y x =-+21y x =-+225y x =--2y ax c =+23y x =2172y x =-+2132y x =--y ax c =+2y ax c =+A ．B ．C ．D ．题型5：二次函数()2y a x m =+平移例5.在同一平面直角坐标系中，画出函数()221y x =-+、22y x =-和()221y x =--的图像．【变式1】把抛物线213y x =-向左平移2个单位得到抛物线____________；若将它向下平移2个单位，得到抛物线____________．【变式2】将抛物线2y ax bx c =++（0a ≠）向下平移3个单位，再向左平移4个单位 得到抛物线2245y x x =--+，则原抛物线的顶点坐标是____________．题型6：二次函数()2y a x m =+开口方向、顶点坐标、对称轴及函数的最值例6.将函数()221y x =-+、()221y x =--与函数22y x =-的图像进行比较，函数()221y x =-+、()221y x =--【变式1】说出下列函数的图像如何由抛物线213y x =-平移得到，再分别指出图像的开口方向、对称轴和顶点坐标．（1）()2123y x =-+； （2）()2143y x =--．【变式2】说出抛物线()2213y x =+-的开口方向、对称轴和顶点坐标，并指出它是由抛物线22y x =通过怎样的平移得到的．【变式3】顶点坐标为（-5，0）且开口方向、形状与函数235y x =-相同的抛物线是____________．【变式4】已知函数223y x ⎛⎫=+ ⎪⎝⎭，当x = ______时，函数取得最______值，为______；已知函数()23y x =-+，当x = ______时，函数取得最______值，为______．【变式5】一个运动员打高尔夫球，若球的飞行高度y （米）与水平距离x （米）之间的函数表达式为()21301090y x =--+，则高尔夫球在飞行过程中的最大高度为（ ）A ．10米B ．20米C ．30米D ．60米【变式6】对于二次函数2288y x x =-+-：（1）求出图像的开口方向、对称轴、顶点坐标，这个函数有最大值还是最小值？这个值是多少？ （2）求出此抛物线与x 、y 轴的交点坐标； （3）当x 取何值时，y 随着x 的增大而减小．题型7：二次函数()2y a x m =+增减性问题例7.已知抛物线()21y x =--，当x > 1时，y 随着x 的增大而______；当x < 1时，y 随着x 的增大而______．题型8：二次函数()2y a x m =+与一次函数综合例8.如图，已知二次函数()2y a x m =+与一次函数y ax m =+，它们在同一直角坐标系中的图像大致是（ ）【变式1】已知二次函数()21y a x c =--的图像如图所示，则一次函数y ax c =+的大致图像 可能是（ ）【变式2】已知抛物线()22y x =-的顶点为C ，直线y = 2x + 4与抛物线交于A 、B 两点．试求ABC S ∆．题型9：二次函数()2y a x m =+对称性及其应用例9.若抛物线()2y a x m =+的对称轴为直线x = -1，且它与抛物线22y x =-的形状相同，开口方向相反，则点（a ，m ）关于原点的对称点为______．【变式1】已知二次函数23(1)y x k =-+的图像上有A （2，y 1）、B （2，y 2）、C （5-， y 3）三个点，则y 1、y 2、y 3的大小关系为（ ）A ．123y y y >>B ．213y y y >>xyO xyOxy OxyOA ．B ．C ．D ．OA ．B ．C ．D ．xy xy xyxy xy O O O OC ．312y y y >>D ．321y y y >>【变式2】已知抛物线()21y x b x c =+-+经过点P （1-，2b -）． （1）求b + c 的值；（2）若b = 3，求这条抛物线的顶点坐标；（3）若3b >，过点P 作直线P A ⊥y 轴，交y 轴与点A ，交抛物线于另一点B ，且BP = 2P A ，求这条抛物线所对应的解析式．题型10：求二次函数()2y a x m =+解析式例10.已知二次函数图像的顶点在x 轴上，且图像经过点（2，2）与（-1，8），求此函数解析式．题型11：与二次函数()2y a x m =+有关动态问题例11.已知二次函数()2y a x m =+的顶点坐标为()1,0-，且过点12,2A ⎛⎫-- ⎪⎝⎭．（1）求这个二次函数的解析式； （2）点()2,2B -在这个函数图像上吗？（3）如何通过左右平移函数图像，使它经过点B ？题型12：利用二次函数()2y a x m =+的图像与性质解决实际问题例12.为了参加科技节展览，同学们制作了一个截面为抛物线形的隧道模型，用了三种正方形钢筋支架．在如图所示的设计图中，如果在直角坐标系中，抛物线的函数解析式为2y x c =-+，正方形ABCD 的边长和正方形EFGH 的边长之比为5 : 1，求：（1）抛物线解析式中常数c 的值；（2）正方形MNPQ 的边长．【变式1】有一个抛物线形的桥洞，桥洞离水面的最大高度BM 为3米，跨度OA 为6米， 以OA 所在直线为x 轴，O 为原点建立直角坐标系，如图所示． （1）请直接写出O 、A 、M 三点的坐标；（2）一艘小船平放着一些长3米，宽2米且厚度均匀的矩形木板，要使该小船能通过此桥洞，问这些木板最高可堆放多少米（设船身底板与水面同一平面）？【过关检测】一、单选题1．抛物线245y x =-+的开口方向（ ） A ．向上；B ．向下；C ．向左；D ．向右；ABC DO E FPN M Q GH x y x yAB O M2．（2021·上海九年级一模）抛物线223y x =-的顶点坐标是（ ）A ．()2,3-B ．()2,3C ．()0,3-D ．()0,33．（2020·上海市静安区实验中学九年级课时练习）抛物线2()y x m =+的对称轴是直线x=-2，则m 的值是（ ） A ．12B ．-12C ．2D ．-24．（2020·上海市静安区实验中学九年级课时练习）函数y ＝x 2－4的图象与y 轴的交点坐标是（ ） A ．（2，0）B ．（－2，0）C ．（0，4）D ．（0，－4）5．（2020·上海九年级专题练习）已知二次函数23()y x =-+，那么这个二次函数的图象有（ ）A ．最高点(30)，B ．最高点(30)-，C ．最低点(30)，D ．最低点(30)-， 6．（2020·上海市青浦区第一中学九年级期中）点()()1122,,,x y x y 均在抛物线21y x =-上，下列说法正确的是（ ）A ．若12y y =，则12x x =B ．若12x x =-，则12y y =-C ．若120x x <<，则12y y >D ．若120x x <<，则12y y >7．（2019·上海市嘉定区唐行九年制学校九年级二模）将抛物线2112y x =+绕顶点旋转180︒，则旋转后的抛物线的解析式为（ ） A ．221y x =-+ B ．221y x =-- C ．2112y x =-+ D ．2112y x =-- 8．（2021·上海九年级专题练习）二次函数y ＝1﹣2x 2的图象的开口方向（ ） A ．向左B ．向右C ．向上D ．向下9．（2019·上海市天山初级中学九年级期中）若在同一直角坐标系中，作222,2,21y x y x y x ==+=+的图像，则他们（ ）A ．都关于y 轴对称B ．开口方向相同C ．都经过原点D ．互相可以通过平移得到 10．（2020·上海市静安区实验中学九年级课时练习）二次函数y ＝x 2＋1的图象大致是（ ） A ． B ．C ．D ．11．已知抛物线y=-（x+1）2上的两点A （x 1，y 1）和B （x 2，y 2），如果x 1＜x 2＜-1，那么下列结论一定成立的是（ ）A ．120y y <<B ．120y y <<C ．210y y <<D ．210y y <<．二、填空题12．（2021·上海九年级一模）抛物线223y x =-在y 轴左侧的部分是_______________．（填“上升”或“下降”）13．（2021·上海九年级专题练习）如果点A (﹣3，y 1)和点B (﹣2，y 2)是抛物线y ＝x 2+a 上的两点，那么y 1_____y 2．（填“＞”、“＝”、“＜”）．14．（2020·上海九年级一模）抛物线21(1)2y x =+的顶点坐标为_______________ 15．（2021·上海九年级一模）已知抛物线()211y a x =-+的开口向上，那么a 的取值范围是______．16．（2021·上海九年级一模）抛物线236y x =-的顶点坐标为____．17．（2021·上海九年级一模）如果(2，1y )、(3，2y )是抛物线()21y x =+上两点，那么1y ______2y ．（填“>”或“<”）18．（2021·上海九年级一模）沿着x 轴正方向看，抛物线22y x =-在y 轴左侧的部分是______的（填“上升”或“下降”）．19．（2021·上海九年级一模）如果抛物线()221y a x =-的开口向下，那么实数a 的取值范围是______． 三、解答题20．（2020·上海市静安区实验中学九年级课时练习）已知抛物线2()y a x m =+的对称轴是直线x=2，该抛物线与y 轴的交点坐标是(0，8)，求这个二次函数的解析式．21．（2020·上海市静安区实验中学九年级课时练习）二次函数2(0)y ax c a =+≠的图像经过A(2，1)，B(-1，-2)求这个二次函数的解析式．。

第10讲 函数的图像考试说明 1.掌握基本初等函数的图像特征,能熟练运用基本初等函数的图像解决问题. 2.掌握图像的作法:描点法和图像变换. 3.会运用函数的图像理解和研究函数性质.考情分析真题再现■ [2017-2013]课标全国真题再现1.[2017·全国卷Ⅲ] 函数y=1+x+的部分图像大致为 ( )A BC D[解析] D函数y=1+x+的图像可以看成是由y=x+的图像向上平移一个单位长度得到的,并且y'=1+x+'=1+,当x→∞时,y'→1,所以可确定答案为A或D,又当x=1时,y=1+1+sin 1>2,由图像可以排除A,故选D.2.[2016·全国卷Ⅱ]已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图像的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0B.mC.2mD.4m[解析] B由f(-x)=2-f(x)得f(x)的图像关于点(0,1)对称,∵y==1+的图像也关于点(0,1)对称,∴两函数图像的交点必关于点(0,1)对称,且对于每一组对称点(x i,y i)和(x'i,y'i)均满足x i+x'i=0,y i+y'i=2,∴(x i+y i)=x i+y i=0+2·=m.3.[2015·全国卷Ⅰ]设函数f(x)=e x(2x-1)-ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.B.C. D.[解析] D令g(x)=e x(2x-1),则g'(x)=e x(2x+1),由g'(x)>0得x>-,由g'(x)<0得x<-,故函数g(x)在上单调递减,在上单调递增.又函数g(x)在x<时,g(x)<0,在x>时,g(x)>0,所以其大致图像如图所示.直线y=ax-a过点(1,0).若a≤0,则f(x)<0的整数解有无穷多个,因此只能a>0.结合函数图像可知,存在唯一的整数x0,使得f(x0)<0,即存在唯一的整数x0,使得点(x0,ax0-a)在点(x0,g(x0))的上方,则x0只能是0,故实数a应满足即解得≤a<1.故实数a的取值范围是,1.4.[2015·全国卷Ⅱ]如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD 与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()[解析] B当点P在BC上时,=tan x,=,+=tan x+,即f(x)=tan x+,x∈,由正切函数的性质可知,函数f(x)在上单调递增,所以其最大值为1+,且函数y=f(x)的图像不可能是线段,排除选项A,C.当点P在CD上运动时,我们取P为CD的中点,此时x=,f=2,由于2<1+,即f<f,排除选项D.综上可知,只有选项B中图像符合题意.■ [2017-2016]其他省份类似高考真题[2017·山东卷]已知当x∈[0,1]时,函数y=(mx-1)2的图像与y=+m的图像有且只有一个交点,则正实数m的取值范围是 ()A.(0,1]∪[2,+∞)B.(0,1]∪[3,+∞)C.(0,]∪[2,+∞)D.(0,]∪[3,+∞)[解析] B应用排除法.当m=时,画出y=(x-1)2与y=+的图像,由图可知,两函数的图像在[0,1]上无交点,排除C,D;当m=3时,画出y=(3x-1)2与y=+3的图像,由图可知,两函数的图像在[0,1]上恰有一个交点.故选B.【课前双基巩固】知识聚焦2.f(x-a)f(x)+b -f(x)f(-x)-f(-x)log a x(a>0且a≠1)f(ax)af(x)y=y=f()对点演练1.y=0[解析] y=lo x=-log a x,故两个函数图像关于x轴,即直线y=0对称.2.x=0[解析] y==a-x,故两个函数的图像关于y轴,即直线x=0对称.3.y=x [解析] 两个函数互为反函数,故两个函数图像关于直线y=x对称.4.③[解析] 将y=两边平方,得y2=|1-x2|(y≥0),即x2+y2=1(y≥0)或x2-y2=1(y≥0),所以③正确.5.y=(2x+3)2[解析] 得到的是y=[2(x+1)+1]2=(2x+3)2的图像.6.y=ln[解析] 根据伸缩变换方法可得,所求函数解析式为y=ln.7.-log2(x-1)[解析] 与f(x)的图像关于直线y=x对称的图像所对应的函数为g(x)=-log2x,再将其图像右移1个单位得到h(x)=-log2(x-1)的图像.8.[解析] y=其图像如图所示:【课堂考点探究】例1[思路点拨] (1)利用图像的平移和翻折作图;(2)利用图像的平移作图;(3)利用偶函数的关系作图,先作出x≥0时的图像,再关于y轴对称作出另一部分的图像.解:(1)首先作出y=lg x的图像,然后将其向右平移1个单位,得到y=lg(x-1)的图像,再把所得图像在x轴下方的部分翻折到x轴上方,即得所求函数y=|lg(x-1)|的图像,如图①所示(实线部分).(2)将y=2x的图像向左平移1个单位,得到y=2x+1的图像,再将所得图像向下平移1个单位得到y=2x+1-1的图像,如图②所示.(3)y=x2-|x|-2=其图像如图③所示.变式题解:(1)先画出函数y=x2-4x+3的图像,再将其x轴下方的图像翻折到x轴上方,如图①所示.(2)y==2-的图像可由y=-的图像向左平移1个单位,再向上平移2个单位得到,如图②所示.(3)y=10|lg x|=其图像如图③所示.例2[思路点拨] 选用函数图像经过的几个特殊点验证排除.B[解析] 由f(0)=-1,得函数图像过点(0,-1),可排除D,由f(-2)=4-4=0,f(-4)=16-16=0,得函数图像过点(-2,0),(-4,0),可排除A,C,故选B.例3[思路点拨] 根据函数的奇偶性及单调性可作出判断.D[解析] 令f(x)=,则f(-x)===f(x),∴f(x)是偶函数,图像关于y轴对称,排除B,C.当x>1时,y==,显然y>0且函数单调递减,故D正确.例4[思路点拨] 对函数f(x)=2x的图像作相应的对称变换可得到图中所示的图像,再写出相应的解析式.C[解析] 题图中是函数y=-2-|x|的图像,即函数y=-f(-|x|)的图像,故选C.强化演练1.D[解析] 当x=1时,y=0,即函数图像过点(1,0),由选项中图像可知,只有D符合.2.A[解析] 由函数定义域知2x-2≠0,即x≠1,排除B,C;当x<0时,y=<0,排除D.故选A.3.C[解析] 由=>0,得x>0,又<1,故y<0,只能是选项C中的图像.4.A[解析] 先作出函数f(x)=log a x(0<a<1)的图像,当x>0时,y=f(|x|+1)=f(x+1),其图像由函数f(x)的图像向左平移1个单位得到,又函数y=f(|x|+1)为偶函数,所以再将函数y=f(x+1)(x>0)的图像关于y轴对称翻折到y轴左边,得到x<0时的图像,故选A.例5[思路点拨] 根据图像可判断其对应函数的定义域、奇偶性、单调性等情况,从而确定符合性质的相应函数的解析式.D[解析] 由函数的图像可知,函数的定义域为R,所以B不符合;又图像关于原点对称,可知函数是奇函数,排除C;函数在定义域内有增有减,不是单调函数,而选项A为增函数,不符合.所以选D.例6[思路点拨] (1)作出分段函数f(x)的图像,结合图像从单调性、最值角度考虑;(2)先化简函数的解析式,在同一坐标系中画出函数y=的图像与函数y=kx-2的图像,结合图像可得实数k的取值范围.(1)[-8,-1](2)(0,1)∪(1,4)[解析] (1)作出函数f(x)的图像,当x≤-1时,函数f(x)=log2单调递减,且最小值为f(-1)=-1,则令log2=2,解得x=-8;当x>-1时,函数f(x)=-x2+x+在(-1,2)上单调递增,在[2,+∞)上单调递减,则最大值为f(2)=2,又f(4)=<2,f(-1)=-1,故所求实数m的取值范围为[-8,-1].(2)y===函数y=kx-2的图像恒过点(0,-2).在同一坐标系中画出函数y=的图像与函数y=kx-2的图像,结合图像可得,实数k的取值范围是(0,1)∪(1,4).例7[思路点拨] 对这样一个非常规不等式应采用数形结合处理,不妨构建函数f(x)=3sin x,g(x)=lo x,将原不等式转化成两函数图像的位置关系,再进行研究.A[解析] 不等式3sin x-lo x<0,即3sin x<lo x.设f(x)=3sin x,g(x)=lo x,在同一坐标系中分别作出函数f(x)与g(x)的图像,由图像可知,当x为整数3或7时,有f(x)<g(x),所以不等式3sin x-lo x<0的整数解的个数为2.例8[思路点拨] 根据所给的条件可确定函数f(x)的图像,并作出函数y=log7|x-2|的图像,由两函数图像的交点个数确定方程解的个数.B[解析] 由函数f(x)是R上的奇函数,得f(0)=0,由f(x+2)=-f(x),可得f(1-x)=f(1+x),f(x+4)=f(x),∴函数f(x)的图像关于直线x=1对称,且f(x)是周期为4的周期函数.在同一坐标系中画出y=f(x)和y=log7|x-2|的图像(图略),由图像不难看出,其交点个数为7,即方程解的个数为7.故选B.强化演练1.C[解析] f(x)=画出函数f(x)的图像,观察图像可知,函数f(x)的图像关于原点对称,故函数f(x)为奇函数,且在(-1,1)上单调递减.2.5[解析] 方程2[f(x)]2-3f(x)+1=0的解为f(x)=或1.作出函数y=f(x)的图像,由图像知零点的个数为5.3.∪[解析] 在0,上,y=cos x>0,在,4上,y=cos x<0.由f(x)的图像知,在1,上,<0.因为f(x)为偶函数,y=cos x也是偶函数,所以y=为偶函数,所以<0的解集为-,-1∪1,.4.[解析] y=作出其图像,如图所示.此曲线与y轴交于点(0,a),最小值为a-,要使直线y=1与其有四个交点,只需a-<1<a,所以1<a<.【备选理由】例1考查分段函数,由各区间上的单调性及函数值确定函数图像;例2为依据函数图像判定相应函数图像,由所给函数图像反映的性质,探究所求函数的性质,有一定的技巧性;例3以新定义为背景,考查函数图像的应用,要注意图像对称性的应用.1[配合例3使用] [2018·南阳第一中学月考]函数f(x)=log2|2x-1|的图像大致是()[解析] C函数可化为f(x)=所以当x>0时,函数为增函数,当x<0时,函数为减函数,可排除A,B,结合图像可知,当x<0时,f(x)<0,排除D,故选C.2[配合例5使用] [2017·长沙长郡中学一模]已知函数y=f(x)的图像如图所示,则函数g(x)=f[f(x)]的图像可能是()[解析] C∵f[f(-x)]=f[f(x)],∴排除A,B;又g(1)=f(0)=-1,∴排除D,故选C.3[配合例8使用] 规定“⊗”表示一种运算,即a⊗b=a2+2ab-b2.设函数f(x)=x⊗2,且关于x的方程f(x)=lg|x+2|(x≠-2)恰有四个互不相等的实数根x1,x2,x3,x4,则x1+x2+x3+x4的值是()A.-4B.4C.8D.-8[解析] D函数f(x)=x2+4x-4,由于函数y=f(x),y=lg|x+2|的图像(如图)均关于直线x=-2对称,故四个实数根之和为-8.。