长方形和正方形周长和面积的复习

三年级数学下册长方形和正方形面积期末复习重点聪明出于勤奋，天才在于积累。

尽快地掌握科学知识，迅速提高学习能力,接下来查字典数学网为大家提供的三年级数学下册长方形和正方形面积期末复习重点。

《长方形和正方形的面积》期末复习设计教学内容：长方形、正方形的面积复习教学目标：1、学生能牢记常用的面积单位和面积单位间的进率，并能正确地化聚。

2、学生能比较熟练地计算长方形和正方形的周长和面积，并能解决简单的实际问题。

3、渗透变与不变的辨证唯物主义思想。

4、教学过程：一、课题引入：师：前天由于风比较大，把学校的一块玻璃窗给打碎了，老师打算到玻璃店去配一块新的玻璃。

想一想，老师该怎么做?那配上的玻璃有多大?这其实指的是什么?引出：今天，我们复习长方形、正方形的面积(板书课题) 二、知识整理：师：这学期，我们学习了有关面积的好多知识，想一想，你都学到了些什么?生：大体先说说师：你能把这些知识整理一下吗?以四人小组为单位，共同合作，整理知识，由组长执笔记录。

比比哪组整理得既完整又简洁。

学生活动反馈，展示，师根据学生交流板书。

(一)面积的含义：提问：面积是指物体的哪个部分?(物体的表面或平面图形的大小)周长是指物体的哪个部分?(物体的边线的总长)小结：面积是一整片，周长是一条线。

练习：1、画一个平面图，用黄色描周长，红色图面积。

2、判断(1)两个长方形面积相等，它们的周长也一定相等。

( )(2)周长大的图形，面积就一定大。

( )(3)长方形和正方形的周长相等，它们的面积也一定相等。

( )(4)两个相等的正方形拼成一个大长方形，面积和原来一样。

( )3、选择(1)下图中，长方形被分成甲、乙两部分，这两部分( )。

A、周长和面积都相等B、周长和面积都不等C、周长相等，面积不等(二)面积的单位：1)提问：计算面积要用什么单位?2)举例说明1平方厘米、1平方分米、1平方米的大小。

3)每相邻的两个面积单位的进率是多少?板书：平方米100平方分米100平方厘米10000练习：1、填空(1)1平方米的正方形里有( )个1平方分米的正方形。

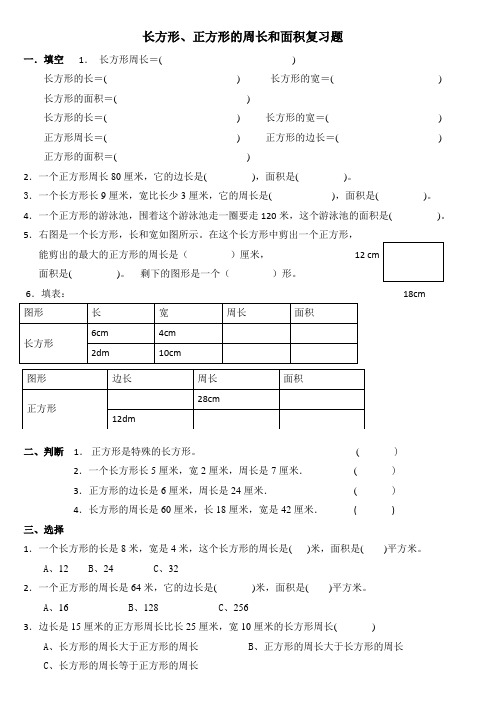
长方形、正方形的周长和面积复习题一．填空1．长方形周长＝()长方形的长＝() 长方形的宽＝() 长方形的面积＝()长方形的长＝() 长方形的宽＝() 正方形周长＝() 正方形的边长＝() 正方形的面积＝()2．一个正方形周长80厘米，它的边长是()，面积是()。

3．一个长方形长9厘米，宽比长少3厘米，它的周长是()，面积是()。

4．一个正方形的游泳池，围着这个游泳池走一圈要走120米，这个游泳池的面积是()。

5．右图是一个长方形，长和宽如图所示。

在这个长方形中剪出一个正方形，能剪出的最大的正方形的周长是（）厘米，面积是()。

剩下的图形是一个（）形。

6．填表：18cm二、判断1．正方形是特殊的长方形。

( )2．一个长方形长5厘米，宽2厘米，周长是7厘米．( )3．正方形的边长是6厘米，周长是24厘米．( )4．长方形的周长是60厘米，长18厘米，宽是42厘米．()三、选择1．一个长方形的长是8米，宽是4米，这个长方形的周长是()米，面积是()平方米。

A、12B、24C、322．一个正方形的周长是64米，它的边长是()米，面积是()平方米。

A、16B、128C、2563．边长是15厘米的正方形周长比长25厘米，宽10厘米的长方形周长()4、一个正方形剪成2个长方形后，两个长方形的周长和（）原来正方形的周长。

A、相等B、大于C、小于四．计算下面图形的周长和面积12cm 10dm五、解决问题1．一块长方形菜地，长18米，宽9米，一面靠墙（如下图），其它三面墙围上竹篱笆。

竹篱笆长多少米？菜地的面积时多少平方米？2．一个长方形操场，长是100米，宽40米，这个操场的面积是多少平方米?围着这个操场跑两圈，要跑多少米？3．一段长60厘米的铁丝围成一个最大的正方形，这个正方形的边长是多少厘米？面积时多少平方厘米？4．一个长方形和一个正方形的周长相等．长方形的长为12米，宽为8米，那么正方形的面积是多少平方米?5．长方形的长16分米，长是宽的2倍，周长是多少分米？6．把两个完全相同的长方形拼在一起，原来长方形的长是4厘米，宽是2厘米。

长方形和正方形的面积与周长知识点长方形和正方形是几何学中常见的两种形状，它们有不同的特点和性质。

本文将详细介绍长方形和正方形的面积与周长的计算方法以及相关知识点。

1. 长方形的面积与周长长方形是指拥有两对相等且平行的边的四边形。

其中，相邻边长度不同的称为长和宽，长和宽的度量单位一致。

长方形的面积即为长乘以宽，周长则是长和宽的两倍之和。

设长方形的长为L，宽为W，则长方形的面积S为 S = L * W，周长P为 P = 2 * (L + W)。

这是长方形面积与周长的基本计算公式。

2. 正方形的面积与周长正方形是一种特殊的长方形，它的四条边长度相等且每个角都为直角。

正方形的边长通常用a表示。

正方形的面积即为边长的平方，周长则是边长的四倍。

设正方形的边长为a，则正方形的面积S为S = a^2，周长P为P = 4a。

这是正方形面积与周长的基本计算公式。

3. 长方形和正方形的性质比较长方形和正方形面积与周长的计算方法不同，下面将对它们的性质进行比较。

（1）面积比较：相同周长下，正方形的面积最大。

这是因为正方形的四条边长度相等，而长方形的两条边可以有不同的长度，因此，给定周长情况下，正方形的边长最大，面积最大。

（2）周长比较：相同面积下，正方形的周长最小。

这是因为正方形的边长相等，而长方形的两条边可以有不同的长度，给定面积情况下，正方形的边长最小，周长最小。

综上所述，长方形和正方形在面积与周长上有不同的特点和计算方法。

在实际应用中，我们常常需要根据给定的条件计算长方形或正方形的面积和周长，以便解决相关问题。

例如，假设一块土地的形状是长方形，已知它的周长为40米，我们可以利用周长的计算方法求出长为10米。

如果要计算这块土地的面积，可以利用面积的计算方法得到100平方米。

又如，假设一块地的形状是正方形，已知它的面积为64平方米，我们可以利用面积的计算方法求出边长为8米。

如果要计算这块地的周长，可以利用周长的计算方法得到32米。

一：背诵：姓名：------------------------1、长方形的周长=（长+宽）×2（读作长加宽的和除以2），长方形的面积=长×宽。

2、知道长方形的周长和长（或宽），求宽或长：长=周长÷2-宽，宽=周长÷2-长。

3、知道长方形的面积各长或宽，求宽或长：长=面积÷宽，宽=面积÷长。

4、正方形的周长=边长×4，正方形的面积=边长×边长。

知道周长求边长：正方形的边长=周长÷4，知道面积求边长：看几×几=正方形面积，几就是正方形的边长。

二、应用：1、一个长方形周长是24厘米，长是7厘米，它的面积是多少？分析：本题是知道长方形的周长和长，求长方形的面积，要求长方形的面积，首先要求出长方形的宽，然后利用面积公式:长方形的面积=长×宽，求出面积。

（1）先求出长方形的宽：宽=周长÷2-长24÷2-7=5（厘米）（2）利用面积公式求出面积：长方形的面积=长×宽7×5=35（平方厘米）答：它的面积是35平方厘米。

2、一块长方形菜地，周长是70米，宽是15米，这块地的面积是多少？（1）（2）答：3、一个长方形面积是72平方厘米，宽是8厘米，它的周长是多少？分析：这道题是告诉了长方形的面积和宽，求周长。

首先要用长方形的面积÷宽=长这个公式求出长，再利用长方形的周长=（长+宽）×2公式求出周长。

（1）先求出长方形的长:长=面积÷宽72÷8=9（厘米）（2）利用周长公式求出周长：长方形的周长=（长+宽）×2 （9+8）×2 =34（厘米）答:它的周长是34厘米。

4、一个长方形花园，面积是105平方米，长是7米，花园的周长是多少米？（1）（2）答：5、一个正方形周长是48厘米，它的面积是多少？分析:这个题是知道正方形的周长，求正方形的面积，要求正方形的面积，必须知道正方形的边长，根据正方形的边长=周长÷4求出边长，再利用正方形的面积公式正方形的面积=边长×边长。

苏教版三年级数学上册第三单元
《长方形和正方形》知识整理及典型练习
一、长方形和正方形的特征
二、什么是周长
沿着封闭．．
图形的边线，从起点到起点的长度。

三、长方形和正方形周长计算的方法
1、计算下面图形的周长
注意：计算长方形的周长一般用第一种方法。

四、长方形的长或宽的求法，正方形边长的求法
1. 长方形的长宽和等于周长的一半。

长方形的周长÷2=长宽和（1条长和1条宽的长度）
长方形的长=周长÷2—宽 长方形的宽=周长÷2—长 2. 正方形的边长=周长÷4
五、长方形和正方形的画法
正方形有4个直角，有4条边，四条边都相等
1、长方形的画法
你能在方格纸上画出周长是20厘米的长方形或正方形吗？能画出不同的长方形吗？（每个小方格的边长表示1厘米）
2、正方形的画法
在方格纸上画周长20厘米的正方形
六、典型练习
1. 2. 3.
4.
5.
6.
10.用两个相同的长方形拼成了一个正方形，已知
正方形的周长是40厘米，每个长方形的周长是多
少厘米？
11把两个相同的长方形拼成了一个正方形，周长
减少了40厘米，每个长方形的周长是多少厘米？。

长方形和正方形的周长整理和复习教案一、教学目标：1. 让学生理解和掌握长方形和正方形的周长公式。

2. 培养学生运用周长公式解决实际问题的能力。

3. 帮助学生巩固长方形和正方形的性质，提高空间想象力。

二、教学内容：1. 长方形和正方形的周长公式。

2. 长方形和正方形的性质。

3. 运用周长公式解决实际问题。

三、教学重点与难点：1. 重点：长方形和正方形的周长公式及其应用。

2. 难点：运用周长公式解决实际问题，灵活运用长方形和正方形的性质。

四、教学方法：1. 采用讲解法、演示法、练习法、讨论法等相结合的教学方法。

2. 利用多媒体课件辅助教学，提高学生的空间想象力。

3. 组织学生进行小组合作学习，培养学生的团队协作能力。

五、教学过程：1. 导入新课：通过复习长方形和正方形的性质，引导学生思考周长与边长之间的关系。

2. 讲解周长公式：讲解长方形和正方形的周长公式，让学生理解和掌握。

3. 演示与练习：利用多媒体课件展示长方形和正方形，让学生直观地感受周长的计算过程。

布置练习题，让学生巩固所学知识。

4. 应用与拓展：引导学生运用周长公式解决实际问题，如计算生活中常见物体的周长。

5. 总结与反馈：对本节课的内容进行总结，了解学生的掌握情况，针对性地进行辅导。

6. 布置作业：布置适量作业，让学生进一步巩固周长公式和长方形、正方形的性质。

教案编辑专员：X日期：2024年月日六、教学评估：1. 课堂提问：通过提问了解学生对长方形和正方形周长公式的掌握程度。

2. 练习反馈：收集学生的练习作业，分析其解答过程和结果，评估学生对知识的掌握情况。

3. 小组讨论：观察学生在小组讨论中的参与程度和合作能力，了解其在团队中的表现。

七、教学反思：1. 对教学方法的反思：评估所采用的教学方法是否适合学生的学习需求，是否有助于学生对知识的理解和应用。

2. 对教学内容的反思：思考是否全面覆盖了长方形和正方形周长的相关知识点，是否需要补充或调整。

正方形长方形的面积公式和周长公式正方形和长方形是我们常见的两种几何图形，它们有着特定的面积公式和周长公式。

本文将分别介绍正方形和长方形的面积及周长公式，并举例说明其应用。

一、正方形的面积公式和周长公式1. 面积公式：正方形的面积可以通过边长的平方来计算。

设正方形的边长为a，则正方形的面积S为S = a^2。

2. 周长公式：正方形的周长等于4倍边长。

设正方形的边长为a，则正方形的周长P为P = 4a。

例如，若一个正方形的边长为5cm，则该正方形的面积为25cm^2，周长为20cm。

二、长方形的面积公式和周长公式1. 面积公式：长方形的面积可以通过长和宽的乘积来计算。

设长方形的长为L，宽为W，则长方形的面积S为S = L × W。

2. 周长公式：长方形的周长可以通过长和宽的两倍之和来计算。

设长方形的长为L，宽为W，则长方形的周长P为P = 2L + 2W。

例如，若一个长方形的长为6cm，宽为4cm，则该长方形的面积为24cm^2，周长为20cm。

正方形和长方形是我们日常生活中经常遇到的两种图形。

它们的面积和周长公式可以帮助我们计算它们的具体数值。

在实际应用中，这些公式可以帮助我们解决各种问题。

例如，假设我们要铺设一个正方形花坛，边长为3m，我们可以通过正方形的面积公式计算出花坛的面积为9m^2。

这样，我们就可以确定所需的土壤和花卉数量。

又如，假设我们要购买一个长方形的地毯，长为4m，宽为5m，我们可以通过长方形的面积公式计算出地毯的面积为20m^2。

这样，我们就可以确定所需的地毯尺寸和购买数量。

除了计算面积和周长，正方形和长方形还有其他有趣的特性。

1. 正方形的特性：- 所有边长相等，角度为90度；- 对角线相等且垂直于对边，可以互相平分；- 是所有边长相等的四边形中面积最大的。

2. 长方形的特性：- 有两对相等的对边；- 对角线相等但不垂直于对边；- 可以变换成正方形，使得面积最大。

正方形和长方形是我们常见的几何图形，它们有着特定的面积和周长公式。

长方形、正方形的周长［知识要点］同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

［范例解析］例1有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

思路与导航根据题意，我们可以把每个正方形的边长的一半同时向左、右、上、下平移（如图b），转化成一个大正方形，这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。

因此，所求周长是18×4=72厘米。

例2 一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？思路导航把截掉的192平方厘米分成A、B、C三块（如图），其中AB的面积是192－4×4=176（平方厘米）。

把A和B移到一起拼成一个宽4厘米的长方形，而此长方形的长就是这块木板剩下部分的周长的一半。

176÷4=44（厘米），现在这块木板的周长是44×2=88（厘米）。

例3求下列图形的周长。

（单位：厘米）思路导航：从图中可以看出，整个图形的周长由八条线段围成，其中四条横着，四条竖着。

其中上面三条横着的线段和是10厘米，那么这样四条横着的线段和是10+10=20（厘米），四条竖着的线段和是8×2+2×2=20（厘米）。

所以，整个图形的周长是20+20=40（厘米）。

例4下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

例5 如下图，阴影部分是正方形，DF=6厘米，AB=9厘米，求最大的长方形的周长。

分析根据题意可知，最大长方形的宽就是正方形的边长。

因为BC=EF，CF=DE，所以，AB＋BC＋CF=AB＋FE＋ED=9＋6=15（厘米），这正好是最大长方形周长的一半。

长方形正方形平行四边形三角形梯形的周长和面积公式我们要找出长方形、正方形、平行四边形、三角形、梯形的周长和面积的公式。

首先，我们需要了解这些几何形状的基本性质和公式。

1. 长方形：长方形有2个长边和2个短边。

周长= 2 × (长 + 宽)
面积 = 长× 宽
2. 正方形：正方形有4个等长的边。

周长= 4 × 边长
面积 = 边长^2
3. 平行四边形：平行四边形有2个等长的对边。

周长= 2 × (长 + 宽)
面积 = 长× 宽
4. 三角形：三角形有3条边。

周长 = a + b + c，其中a、b、c是三角形的三条边。

面积 = (底× 高) / 2
5. 梯形：梯形有2个平行的边和2个不平行的边。

周长 = a + b + c + d，其中a、b是上底和下底的长度，c、d是梯形的两条腰的长度。

面积 = ((上底 + 下底) × 高) / 2
计算结果如下：
长方形的周长公式为：2 × (长 + 宽)，面积公式为：长× 宽
正方形的周长公式为：4 × 边长，面积公式为：边长^2
平行四边形的周长公式为：2 × (长 + 宽)，面积公式为：长× 宽
三角形的周长公式为：a + b + c，面积公式为：(底× 高) / 2
梯形的周长公式为：a + b + c + d，面积公式为：((上底 + 下底) × 高) / 2。