深圳市悦晋教育_三角函数讲义(2)
- 格式:doc
- 大小:954.00 KB
- 文档页数:17

三角函数复习讲义知识要点:一、角的概念与推广:任意角的概念;角限角、终边相同的角; 二、弧度制:把长度等于半径的弧所对的圆心角叫做1弧度;弧长公式:r l α=扇形面积:S=α22121r r l =⋅三角函数线:如右图,有向线段AT 与MP OM 分别叫做α 的的正切线、正弦线、余弦线。
三、同角三角函数关系:即:平方关系、商数关系、倒数关系。
四、诱导公式:()ααπf n f '±=⎪⎭⎫⎝⎛±2 记忆:单变双不变,符号看象限。
单双:即看πn 中的n 是2π的单倍还是双倍,单倍后面三角函数名变,双不变则三角函数名不变;符号看象限:即把α看成锐角,加上2πn 终边落在第几象限则是第几象限角的符号。
五、有关三角函数单调区间的确定、最小正周期、奇偶性、对称性以及比较三角函数值的大小问题,一般先化简成单角三角函数式。
然后再求解。
六、三角函数的求值、化简、证明问题常用的方法技巧有:1、常数代换法:如:αααααα2222tan sec cot tan cos sin 1-=⋅=+= 2、配角方法:ββαα-+=)( ()βαβαα-++=)(2 22βαβαβ--+=3、降次与升次:22cos 1sin 2αα-= 22cos 1cos 22αα+= 以及这些公式的变式应用。
4、()θααα++=+sin cos sin 22b a b a (其中ab=θtan )的应用,注意θ的符号与象限。
5、常见三角不等式:(1)、若x x x x tan sin .2,0<<⎪⎭⎫⎝⎛∈则π (2)、若2cos sin 1.2,0≤+<⎪⎭⎫⎝⎛∈x x x 则π(3)、1c o s s i n ≥+x x6、常用的三角形面积公式:(1)、c b a ch bh ah S 212121===(2)、B ac A bc C ab S sin 21sin 21sin 21=== (3)、S = 七、三角函图象和性质:(1)正弦函数图象的变换:()()αωαωω+=−−−→−+=−−−→−=−−−→−=x A y x y x y x y sin sin sin sin 振幅变换平移变换横伸缩变换象关于轴对称在区间在区间在区间在区间考点一: 求三角函数的定义域、值域和最值、三角函数的性质(包括奇偶性、单调性、周期性)这类问题在选择题、填空题、解答题中出现较多,主要是考查三角的恒等变换及三角函数的基础知识。

《三角函数的简单应用》讲义一、引言三角函数是数学中的重要概念,在实际生活和众多领域中都有着广泛的应用。
通过学习三角函数的简单应用,我们能够更好地理解和解决与周期性、波动等相关的问题。
二、三角函数的基本概念在探讨三角函数的应用之前,我们先来回顾一下三角函数的基本概念。
三角函数包括正弦函数(sin)、余弦函数(cos)和正切函数(tan)等。
正弦函数sinθ 表示直角三角形中对边与斜边的比值;余弦函数cosθ 表示邻边与斜边的比值;正切函数tanθ 表示对边与邻边的比值。
这些函数的图像具有周期性,例如正弦函数和余弦函数的周期为2π,正切函数的周期为π。
三、三角函数在物理学中的应用1、简谐运动在物理学中,简谐运动是一种常见的运动形式,例如弹簧振子的运动。
其位移随时间的变化可以用正弦函数或余弦函数来描述。
假设一个弹簧振子的位移函数为 x =A sin(ωt +φ),其中 A 是振幅,ω 是角频率,t 是时间,φ 是初相位。
通过这个函数,我们可以计算出振子在不同时刻的位移,从而了解其运动规律。
2、交流电交流电的电压和电流随时间的变化也可以用正弦函数来表示。
比如,电压函数可以写成 U = U₀ sin(ωt),其中 U₀是电压的最大值,ω 是角频率。
通过三角函数,我们能够分析交流电的特性,如有效值、频率等,这对于电力系统的设计和运行至关重要。
四、三角函数在天文学中的应用1、天体的位置和运动在天文学中,通过观测天体的角度和时间,可以利用三角函数来计算天体的位置和运动轨迹。
例如,通过测量某颗恒星在不同时刻的高度角和方位角,结合地球的自转和公转,利用三角函数可以确定恒星在天球上的坐标。
2、日食和月食的计算日食和月食的发生可以通过三角函数来预测。
通过计算太阳、地球和月球之间的相对位置和角度关系,能够确定日食和月食的发生时间、类型和区域。
五、三角函数在工程中的应用1、机械振动在机械工程中,机器部件的振动问题经常涉及三角函数。

高中三角函数讲义概述及解释说明1. 引言1.1 概述在高中数学课程中,三角函数是一个重要的内容。
它是研究角度和三角形等几何图形性质的基础工具,并且在实际生活中有广泛的应用。
掌握三角函数的定义、性质以及其在解决实际问题中的应用是每位高中生数学学习的必备知识。
1.2 文章结构本文将围绕高中三角函数展开讲述。
首先,我们将介绍高中三角函数的基本概念,包括角度和弧度的概念以及正弦、余弦和正切的定义。
然后,我们将探讨三角函数之间的关系与公式推导,包括同一角度不同三角函数之间的关系与变化规律,倍角、半角以及相关角公式推导与应用,以及其他三角函数如割、减等的公式与性质说明。
接下来,我们将着重介绍高中三角函数在解决实际问题中的应用,例如测量和测绘领域、机械工程和建筑设计领域,以及物理学和天文学领域。
最后,在结论部分,我们将对主要内容进行总结与回顾,并提出对高中三角函数学习的建议以及进一步研究方向的展望。
1.3 目的本文的目的是为高中生提供一份全面且易懂的三角函数讲义,帮助他们掌握高中三角函数相关知识,并能够将其应用于实际问题解决中。
通过本文的学习,读者将能够理解三角函数在几何图形、物理和工程等领域的重要性,并从中获得启示,拓宽自己在数学领域的思维方式和解决问题的能力。
2. 高中三角函数的基本概念:2.1 角度和弧度的概念:在高中数学中,我们常常用角度来表示一个角的大小。
角度是以度(°)为单位来衡量的,一个圆共有360°。
但在三角函数的研究中,也经常使用弧度来表示角的大小。
弧度是单位圆上与它所对应的弧长相等的一段弧所对应的长度,常用符号“rad”表示。
一周对应的弧长为2π,即一个圆心角为360°或2π弧度。
2.2 正弦、余弦和正切的定义:在三角函数中,最基本的三个函数是正弦(sin)、余弦(cos)和正切(tan)。
这些函数可以通过单位圆上点的坐标来定义。
正弦函数(sin):给定一个角θ,在单位圆上以θ作为终边所对应点(x, y)的y坐标即为该角θ的正弦值。

三角函数讲义任意角的三角函数及同角三角函数的关系知识点知识点一三角函数的概念1.利用单位圆定义任意角的三角函数如图,在平面直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么:(1)y 叫做α的正弦,记作sin α,即sin α=y ;(2)x 叫做α的余弦,记作cos α,即cos α=x ;(3)y x 叫做α的正切,记作tan α,即tan α=y x(x ≠0).2.一般地,设角α终边上任意一点的坐标为(x ,y ),它与原点的距离为r ,则sin α=y r ,cos α=x r ,tan α=y x . 知识点二正弦、余弦、正切函数值在各象限的符号口诀概括为:一全正、二正弦、三正切、四余弦(如图).知识点三诱导公式一终边相同的角的同一三角函数的值相等,即:sin(α+k ·2π)=sin α,cos(α+k ·2π)=cos α,tan(α+k ·2π)=tan α,其中k ∈Z .作用:可把任意角的三角函数值问题转化为0~2π间角的三角函数值问题.体现了三角函数的周期性。
知识点四三角函数的定义域正弦函数y =sin x 的定义域是R ;余弦函数y =cos x 的定义域是R ;正切函数y =tan x 的定义域是{x |x ∈R且x ≠k π+π2,k ∈Z }.知识点五三角函数线如图,设单位圆与x 轴的正半轴交于点A ,与角α的终边交于P 点.过点P 作x 轴的垂线PM ,垂足为M ,过A 作单位圆的切线交OP 的延长线(或反向延长线)于T 点.单位圆中的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线.记作:sin α=MP ,cos α=OM ,tan α=AT .知识点六同角三角函数的基本关系1.同角三角函数的基本关系式(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:tan α=sin αcos α (α≠k π+π2,k ∈Z ). 2.同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形公式:sin 2α=1-cos 2α;cos 2α=1-sin 2α.(2)tan α=sin αcos α的变形公式:sin α=cos αtan α;cos α=sin αtan α.题型一三角函数定义的应用【例1】已知θ终边上一点P (x,3)(x ≠0),且cos θ=1010x ,求sin θ,tan θ.【例2】已知角α的终边经过点P (-4a,3a )(a ≠0),求sin α,cos α,tan α的值;2.角α的终边经过点P (-b,4)且cos α=-35,则b 的值为( ) A .3 B .-3 C .±3 D .5题型二三角函数符号的判断【例1】判断下列三角函数值的符号:(1)sin 3,cos 4,tan 5;(2)sin(cos θ)(θ为第二象限角).【例2】若tan x <0,且sin x -cos x <0,则角x 的终边在() A .第一象限 B .第二象限C .第三象限D .第四象限【过关练习】1.若sin θ<0且tan θ<0,则θ是第象限的角.2.使得lg(cos αtan α)有意义的角α是第象限角.题型三诱导公式一的应用【例1】求下列各式的值:(1)sin(-1 395°)cos 1 110°+cos(-1 020°)sin 750°;(2)sin -11π6+cos 12π5·tan 4π.【过关练习】1.求下列各式的值:(1)cos 25π3+tan -15π4;(2)sin 810°+tan 765°-cos 360°.2.sin(-1 380°)的值为( )A .-12 B.12 C .-32D.323.求下列各式的值.(1)a 2sin(-1 350°)+b 2tan 405°-2ab cos(-1 080°);(2)tan 405°-sin 450°+cos 750°.题型四利用三角函数线求角、解不等式【例1】根据下列三角函数值,作角α的终边,然后求角的取值集合:(1)cos α=12;(2)tan α=-1.【例2】利用单位圆中的三角函数线,分别确定角θ的取值范围.(1) sin θ≥32;(2)-12≤cos θ<32.【例3】当α∈0,π2时,求证:sin α<α<="">【过关练习】1.如果π4<α<π2,那么下列不等式成立的是( ) A .cos α<="" αB .tan α<="" αC .si n α<="" αD .cos α<="" α2.如图在单位圆中角α的正弦线、正切线完全正确的是( )A .正弦线PM ,正切线A ′T ′B .正弦线MP ,正切线A ′T ′C .正弦线MP ,正切线ATD .正弦线PM ,正切线AT3.在[0,2π]上,满足sin x ≥12的x 的取值范围为( ) A.0,π6 B.π6,5π6 C.π6,2π3D.5π6,π题型五求三角函数定义域【例1】求下列函数的定义域.(1)f (x )=sin x ·tan x ;(2)f (x )=lg sin x +9-x 2.【过关练习】1. 求函数f (x )=1-2cos x +lnsin x -22的定义域.2.函数y =tanx -π3的定义域为( ) A.x |x ≠π3,x ∈R B.?x |x ≠k π+π6,k ∈Z C.x |x ≠k π+5π6,k ∈Z D.x |x ≠k π-5π6,k ∈Z题型六三角函数知一求二【例1】已知cos α=-817,求sin α,tan α的值.【例2】已知tan α=2,求下列代数式的值.(1)4sin α-2cos α5cos α+3sin α;(2)14sin 2α+13sin αcos α+12cos 2α.【过关练习】1.已知tan α=43,且α是第三象限角,求sin α,cos α的值.2.已知α是第四象限角,cos α=1213,则sin α等于( ) A.513 B .-513 C.512 D .-5123.已知tan α=3,求下列各式的值. (1)3cos α-sin α3cos α+sin α;(2)2sin 2α-3sin αcos α.4.已知sin α=55,则sin 4α-cos 4α的值为( ) A .-15 B .-35 C.15 D.35题型七三角函数平方关系及其应用【例1】已知sin θ+cos θ=15,θ∈(0,π),求:(1)sin θ-cos θ;(2)sin 3θ+cos 3θ.【例2】已知sin α+cos α=m ,求sin 3α+cos 3α的值.【过关练习】1.已知sin θ、cos θ是关于x 的方程x 2-ax +a =0的两个根(a ∈R ).(1)求sin 3θ+cos 3θ的值;(2)求tan θ+1tan θ的值.2.若sin A =45,且A 是三角形的一个内角,求5sin A +815cosA -7的值.3.已知sin α+cos α=15,α∈(0,π),则tan α的值是( ) A.34 B .-34 C.43 D .-43 题型八三角函数的化简证明【例1】已知α是第三象限角,化简:1+sin α1-sin α-1-sin α1+sin α.【例2】证明三角恒等式cos α1-sin α=1+sin αcos α【例3】已知下列等式成立.(1)a sin θ-b cos θ=a 2+b 2;(2)sin 2θm 2+cos 2θn 2=1a 2+b 2.求证:a 2m 2+b 2n 2=1.【过关练习】1.若α是第三象限角,化简 1+cos α1-cos α+1-cos α1+cos α.2.求证:2sin x cos x -1cos 2x -sin 2x =tan x -1tan x +1.3.已知tan 2α=2tan 2β+1,求证:sin 2β=2sin 2α-1.课后练习【补救练习】1.若sin θcos θ>0,则θ在( )A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限 2.已知α是第四象限角,cos α=1213,则sin α等于( ) A.513 B .-513 C.512 D .-5123.利用三角函数线比较下列各组数的大小(用“>”或“<”连接):(1)sin 23π________sin 45π;(2)cos 23π________cos 45π;(3)tan 23π________tan 45π.4.函数y =lg cos x 的定义域为________________.5.利用三角函数线,写出满足下列条件的角α的集合:(1)sin α≥22;(2)cos α≤12.6.已知角α的终边上有一点P (24k,7k ),k ≠0,求sin α,cos α,tan α的值.【巩固练习】1.已知角α的终边上一点的坐标为?sin 2π3,cos 2π3,则角α的最小正值为( ) A.5π6 B.2π3 C.5π6 D.11π62.如果3π4<θ<π,那么下列各式中正确的是( ) A .co s θ<="" θB .sin θ<="" θC .tan θ<="" θD .cos θ<="" θ3.若0<α<2π,且sin α<32,cos α>12,则角α的取值范围是( ) A .(-π3,π3) B .(0,π3) C .(5π3,2π) D .(0,π3)∪(5π3,2π) 4.已知sin θ+cos θsin θ-cos θ=2,则sin θcos θ的值是( ) A.34 B .±310 C.310 D .-3105.已知α终边经过点(3a -9,a +2),且sin α>0,cos α≤0,则a 的取值范围为.6.函数f (x )=cos 2x -sin 2x 的定义域为________________.7.化简sin 2β+cos 4β+sin 2βcos 2β的结果是.8.已知sin α=15,求cos α,tan α.9.判断下列各式的符号:(1)sin 340°cos 265°;(2)sin 4tan-23π4;(3)sin (cos θ)cos (sin θ)(θ为第二象限角).10.求证:tan θ·sin θtan θ-si n θ=1+cos θsin θ.【拔高练习】1.若sin 2x >cos 2x ,则x 的取值范围是( )A .{x |2k π-34π<="">π,k ∈Z } B .{x |2k π+π4<="">π,k ∈Z } C .{x |k π-π4<="">,k ∈Z } D .{x |k π+π4<="">π,k ∈Z } 2.若角α的终边与直线y =3x 重合且sin α<0,又P (m ,n )是α终边上一点,且|OP |=10,则m -n = .3.函数y =|sin x |sin x +|cos x |cos x -2|sin x cos x |sin x cos x的值域是. 4.若α为第三象限角,则cos α1-sin 2α+2sin α1-cos 2α的值为. 5.在△ABC 中,2sin A = 3cos A ,则角A = .6.已知4sin θ-2cos θ3sin θ+5cos θ=611,求下列各式的值.(1)5cos 2θsin 2θ+2sin θcos θ-3cos 2θ; (2)1-4sin θcos θ+2cos 2θ.7.化简:1cos 2α1+tan 2α-1+sin α1-sin α(α为第二象限角).8.证明:sin α-cos α+1sin α+cos α-1=1+sin αcos α;。

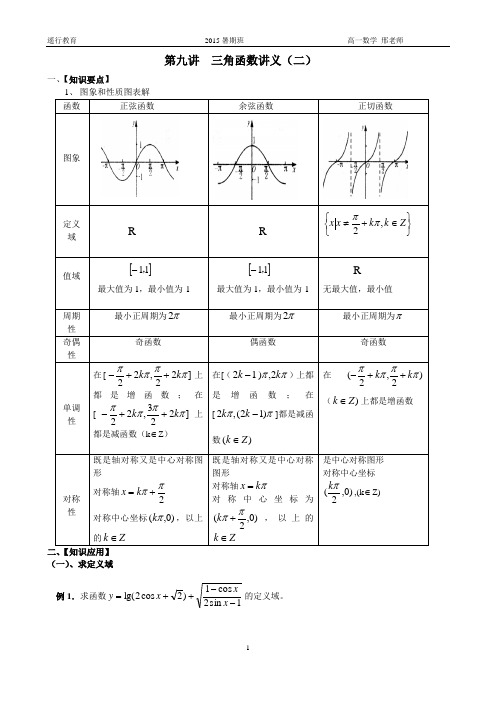
第九讲 三角函数讲义(二)一、【知识要点】R 二、【知识应用】 (一)、求定义域例1.求函数1sin 2cos 1)2cos 2lg(--++=x xx y 的定义域。
(二)、利用三角函数的性质比较大小 例1.设75sin π=a 、72cos π=b 、72tan π=c ,则( ) A .a b c <<B .a c b <<C .b c a <<D .b a c <<(三)、复合型三角函数图像的识别例1.函数x y cos ln = 其中22ππ<<-x 的图象是( )(四)、求值域、最值1、利用三角函数的有界性求值域1、形如y=asinx+bcosx+c 型引入辅助角公式化为22b a +sin(x+φ)+c 再求值域. 例1、求函数f(x)=2sinx+cos(x+3π)的值域2、形如y=asin 2x+bsinxcosx+ccos 2x 型通过降幂转化为Asinx+Bcosx 再求值域. 例2、f(x)=23asinx ·cosx-2asin 2x+1(a>0)的值域2、用换元法化为二次函数求值域1、形如y=sin 2x+bsinx+c 型令sinx=t 转化为二次函数再求值域. 例3、k<-4,求y=cos2x+k(cosx-1)的值域2、形如y=asinx·cosx+b (sinx±cosx )+c ,换元令sinx±cosx=t 转化为二次函数在]2,2[-上的值域问题 例4、求函数y=sinx ·cosx+sinx+cosx 的值域xxA .B .C .D .3、考察结构特征,用分离常数法求值域形如y=d x c bx a ++cos cos 型,可用分离常数法转化为y=a+xb 再求值域.例5、求函数y=1cos 21cos 2-+x x 的值域.4、反函数思想求值域形如y=d x c bx a ++sin cos 可用反函数思想转化为f(y)sin(x+φ)=g(y)求值域.例6、求y=3sin 22cos 3--x x 的值域.5、化为一元二次方程用判别式求值域形如y=dx c bx a ++sin cos 也可用判别式求值域例7、求函数y=xxcos 2sin +的值域6、根据代数函数的单调性求值域形如y=asint+tb sin ,令sint=x ,根据函数y=ax+x b的单调性求值域.例8、θ∈(0,π),则函数y=sin θ+θsin 2的值域为_________.(五)、求三角函数的周期例1.已知函数x x x x y 22cos 3cos sin 2sin +⋅+=,(1)求该函数的最小正周期;(2)求函数的最小值及相应的x 的集合。
三角函数完美讲义
1.引言
三角函数是高中数学的重要知识点之一,也是解决几何和物理
问题的基础。
本讲义旨在提供一个完整且简明易懂的三角函数讲解,帮助学生更好地理解和应用三角函数的概念和性质。
2.基本概念
研究前提:了解直角三角形和基本三角比的概念
三角函数定义:正弦、余弦和正切的定义及图示
三角恒等式:介绍常见的三角恒等式及其证明方法
3.三角函数图像
正弦函数图像:介绍正弦函数的周期、振幅、相位和对称性
余弦函数图像:介绍余弦函数的周期、振幅、相位和对称性
正切函数图像:介绍正切函数的周期、渐近线和对称性
4.三角函数性质
基本性质:介绍正弦、余弦和正切函数的定义域、值域和奇偶性
三角函数的推导:从直角三角形的角度推导三角函数的值
5.三角函数应用
角度的测量单位:介绍弧度制和度制的转换关系
三角函数应用举例:解决实际问题时如何运用三角函数
三角函数的相关性:介绍三角函数之间的关系,如和差公式和倍角公式
6.总结
本讲义通过简明易懂的语言和清晰明了的图示,全面介绍了三角函数的基本知识和应用。
希望学生能够通过本讲义的研究,更加深入地理解和掌握三角函数,为日后的高中数学研究和实际应用打下坚实的基础。
以上是《三角函数完美讲义》的框架概述,具体内容请根据需要进行补充。
希望对您有所帮助!。
《三角函数应用》讲义一、三角函数的基本概念在数学的广阔领域中,三角函数是一类非常重要的函数。
它们包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)等。
正弦函数 sin 是指在一个直角三角形中,某个锐角的对边与斜边的比值。
余弦函数 cos 则是该锐角的邻边与斜边的比值。
正切函数 tan 是对边与邻边的比值。
这些函数的定义域和值域都有特定的范围。
例如,正弦函数和余弦函数的值域都在-1 到 1 之间。
二、三角函数的图像和性质(一)正弦函数图像正弦函数的图像是一个周期为2π 的波浪形曲线。
它在 x = 0 时取值为 0,在 x =π/2 时取值为 1,在 x =π 时取值为 0,在 x =3π/2 时取值为-1,然后在 x =2π 时又回到 0,如此循环。
正弦函数具有奇偶性,是一个奇函数,即 sin(x) = sin(x)。
(二)余弦函数图像余弦函数的图像也是周期为2π 的曲线,不过它在 x = 0 时取值为 1,在 x =π/2 时取值为 0,在 x =π 时取值为-1,在 x =3π/2 时取值为0,在 x =2π 时又回到 1。
余弦函数是偶函数,即 cos(x) = cos(x)。
(三)正切函数图像正切函数的图像是一个周期为π 的波浪形曲线,但它在一些特定的点上没有定义,比如 x =π/2 +kπ(k 为整数)。
三、三角函数的应用实例(一)测量高度在实际生活中,如果我们想要测量一座山或者建筑物的高度,但又无法直接测量时,三角函数就可以派上用场。
假设我们站在离建筑物一段距离的地方,测量出我们与建筑物底部的水平距离,以及我们仰望建筑物顶部的仰角。
通过三角函数的正切关系,就可以计算出建筑物的高度。
例如,我们站在离建筑物 100 米的地方,仰角为 60°。
那么建筑物的高度 h 就可以通过 tan 60°= h / 100 计算得出。
(二)航海中的方向和距离计算在航海中,船只的航行方向和距离的计算经常用到三角函数。
三角函数复习讲义一、基础知识定义1 角,一条射线绕着它的端点旋转得到的图形叫做角。
若旋转方向为逆时针方向,则角为正角,若旋转方向为顺时针方向,则角为负角,若不旋转则为零角。
角的大小是任意的。
定义2 角度制,把一周角360等分,每一等价为一度,弧度制:把等于半径长的圆弧所对的圆心角叫做一弧度。
360度=2π弧度。
若圆心角的弧长为L ,则其弧度数的绝对值|α|=rL,其中r 是圆的半径。
定义3 三角函数,在直角坐标平面内,把角α的顶点放在原点,始边与x 轴的正半轴重合,在角的终边上任意取一个不同于原点的点P ,设它的坐标为(x ,y ),到原点的距离为r,则正弦函数s in α=r y ,余弦函数co s α=r x ,正切函数tan α=xy,余切函数cot α=yx, 定理1 同角三角函数的基本关系式, 倒数关系:tan α=αcot 1,商数关系:tan α=αααααsin cos cot ,cos sin =;乘积关系:tan α×co s α=s in α,cot α×s in α=co s α;平方关系:s in 2α+co s 2α=1 定理2 诱导公式(Ⅰ)s in (α+π)=-s in α, co s(π+α)=-co s α, tan (π+α)=tan α; (Ⅱ)s in (-α)=-s in α, co s(-α)=co s α, tan (-α)=-tan α;(Ⅲ)s in (π-α)=s in α, co s(π-α)=-co s α, tan =(π-α)=-tan α; (Ⅳ)s in ⎪⎭⎫⎝⎛-απ2=co s α, co s ⎪⎭⎫⎝⎛-απ2=s in α(奇变偶不变,符号看象限)。
定理3 正弦函数的性质,根据图象可得y =s inx (x ∈R )的性质如下。
单调区间:在区间⎥⎦⎤⎢⎣⎡+-22,22ππππk k 上为增函数,在区间⎥⎦⎤⎢⎣⎡++ππππ232,22k k 上为减函数,最小正周期为2π. 奇偶数. 有界性:当且仅当x =2kx +2π时,y 取最大值1,当且仅当x =3k π-2π时, y 取最小值-1。
对称性:直线x =k π+2π均为其对称轴,点(k π, 0)均为其对称中心,值域为[-1,1]。
这里k ∈Z .定理4 余弦函数的性质,根据图象可得y =co s x (x ∈R )的性质。
单调区间:在区间[2k π, 2k π+π]上单调递减,在区间[2k π-π, 2k π]上单调递增。
最小正周期为2π。
奇偶性:偶函数。
对称性:直线x =k π均为其对称轴,点⎪⎭⎫⎝⎛+0,2ππk 均为其对称中心。
有界性:当且仅当x =2k π时,y 取最大值1;当且仅当x =2k π-π时,y 取最小值-1。
值域为[-1,1]。
这里k ∈Z . 定理5 正切函数的性质:由图象知奇函数y =tanx (x ≠k π+2π)在开区间(k π-2π, k π+2π)上为增函数, 最小正周期为π,值域为(-∞,+∞),点(k π,0),(k π+2π,0)均为其对称中心。
sin y x =cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =;当22x k ππ=- ()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性2π2ππ函数性质奇偶性奇函数偶函数奇函数单调性在2,222k kππππ⎡⎤-+⎢⎥⎣⎦()k∈Z上是增函数;在32,222k kππππ⎡⎤++⎢⎥⎣⎦()k∈Z上是减函数.在[]()2,2k k kπππ-∈Z上是增函数;在[]2,2k kπππ+()k∈Z上是减函数.在,22k kππππ⎛⎫-+⎪⎝⎭()k∈Z上是增函数.对称性对称中心()(),0k kπ∈Z对称轴()2x k kππ=+∈Z对称中心(),02k kππ⎛⎫+∈Z⎪⎝⎭对称轴()x k kπ=∈Z对称中心(),02kkπ⎛⎫∈Z⎪⎝⎭无对称轴定理6 两角和与差的基本关系式:co s(α±β)=co sαco sβ s inαs inβ,s in(α±β)=s inαco sβ±co sαs inβ;tan(α±β)=.)tantan1()tan(tanβαβα±定理7 和差化积与积化和差公式:s inα+s inβ=2s in⎪⎭⎫⎝⎛+2βαco s⎪⎭⎫⎝⎛-2βα,s inαco sβ=21[s in(α+β)+s in(α-β)],s inα-s inβ=2s in⎪⎭⎫⎝⎛+2βαco s⎪⎭⎫⎝⎛-2βα,co sαs inβ=21[s in(α+β)-s in(α-β)],co sα+co sβ=2co s⎪⎭⎫⎝⎛+2βαco s⎪⎭⎫⎝⎛-2βα,co sαco sβ=21[co s(α+β)+co s(α-β)],co sα-co sβ=-2s in⎪⎭⎫⎝⎛+2βαs in⎪⎭⎫⎝⎛-2βα,s inαs inβ=-21[co s(α+β)-co s(α-β)].定理8 倍角公式:s in 2α=2s in αco s α,co s2α=co s 2α-s in 2α=2co s 2α-1=1-2s in 2α,tan 2α=.)tan 1(tan 22αα- 定理9 半角公式:s in ⎪⎭⎫⎝⎛2α=2)cos 1(α-±,co s ⎪⎭⎫ ⎝⎛2α=2)cos 1(α+±, tan ⎪⎭⎫⎝⎛2α=)cos 1()cos 1(αα+-±=.sin )cos 1()cos 1(sin αααα-=+ 定理10 万能公式: ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2tan 12tan 2sin 2ααα, ⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛-=2tan 12tan 1cos 22ααα,.2tan 12tan 2tan 2⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=ααα定理11 辅助角公式:如果a , b 是实数且a 2+b 2≠0,则取始边在x 轴正半轴,终边经过点(a , b )的一个角为β,则s in β=22ba b +,co s β=22ba a+,对任意的角α.a s in α+bco s α=)(22b a +s in (α+β).定理12 正弦定理:在任意△ABC 中有R CcB b A a 2sin sin sin ===,其中a , b , c 分别是角A ,B ,C 的对边,R 为△ABC 外接圆半径。
定理13 余弦定理:在任意△ABC 中有a 2=b 2+c 2-2bco s A ,其中a ,b ,c 分别是角A ,B ,C 的对边。
定理14 图象之间的关系:y =s inx 的图象经上下平移得y =s inx +k 的图象;经左右平移得y =s in (x +ϕ)的图象(相位变换);纵坐标不变,横坐标变为原来的ω1,得到y =s in x ω(0>ω)的图象(周期变换);横坐标不变,纵坐标变为原来的A 倍,得到y =A s inx 的图象(振幅变换);y =A s in (ωx +ϕ)(ω>0)的图象(周期变换);横坐标不变,纵坐标变为原来的A 倍,得到y =A s inx 的图象(振幅变换);y =A s in (ωx +ϕ)(ω, ϕ>0)(|A |叫作振幅)的图象向右平移ωϕ个单位得到y =A s in ωx 的图象。
定义4 函数y =s inx ⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡-∈2,2ππx 的反函数叫反正弦函数,记作y =a r c s inx (x ∈[-1, 1]),函数y =co s x (x ∈[0, π]) 的反函数叫反余弦函数,记作y =a r cco s x (x ∈[-1, 1]). 函数y =tanx ⎪⎪⎭⎫⎝⎛⎥⎦⎤⎢⎣⎡-∈2,2ππx 的反函数叫反正切函数。
记作y =a r ctanx (x ∈[-∞, +∞]). y =co s x (x ∈[0, π])的反函数称为反余切函数,记作y =a r ccotx (x ∈[-∞, +∞]).定理15 三角方程的解集,如果a ∈(-1,1),方程s inx =a 的解集是{x |x =n π+(-1)n a r c s ina , n ∈Z }。
方程co s x =a 的解集是{x |x =2kx ±a r cco s a , k ∈Z }. 如果a ∈R ,方程tanx =a 的解集是{x |x =k π+a r ctana , k ∈Z }。
恒等式:a r c s ina +a r cco s a =2π;a r ctana +a r ccota =2π. 定理16 若⎪⎭⎫⎝⎛∈2,0πx ,则s inx <x <tanx . 习题1、三角函数线的应用1.已知sinα=31,则tan α=_______.2.满足21sin ≥x 的x 的取值范围是____________________.3.已知π0<x <2, sinx 、tanx 、x 的大小为______________. 4.(2005全国Ⅲ 1)已知α是第三象限的角,则2α是 ( ) A.第一或二象限的角 B.第二或三象限的角 C.第一或三象限的角 D.第二或四象限的角5.(2002全国高考文5)在(0,2π)内,使sinx>cosx 成立的x 的取值范围是( )A.ππ5π()(π)424 ,, B.π(π)4, C.π5π()44, D.π5π3π(π)()442,, 6.(2000全国高考题)已知sinα>sinβ,那么下列命题成立的是 ( )A.若α、β是第一象限角,则cosα>cosβB.若α、β是第二象限角,则tanα>tanβC.若α、β是第三象限角,则cosα>cosβD.若α、β是第四象限角,则tanα>tanβ2、求三角函数值7.(04湖北13) tan2010°的值为 .8. (05北京) 已知tan 22α=,则 (I)πtan(α+)4的值为______; (Ⅱ)6sin α+cos α3sin α2cos α-的值为___________.9.(05福建卷17 )已知πx 02-<<,1sin x cos x 5+=.则(I) sinx -cosx=____; (Ⅱ)22x x x x 3sin 2sin cos cos 2222tan x cot x-+=+_______. 10.(04全国高考题)已知锐角三角形ABC 中,3sin(A +B)=5,1sin(A B)=5-.(Ⅰ)求证:tanA=2tanB ; (Ⅱ)设AB=3,求AB 边上的高. (Ⅰ)证明:∵3sin(A +B)=5,1sin(A B)=5-,3、已知三角函数值求角11.(04全国Ⅱ卷)已知函数y=tan(2x+φ)的图象过点π(0)12,,则φ可以是 ( ) A.π6-B.π6C.π12-D.π1212.(1995全国) sin 220°+cos 250°+sin20°cos50°的值是________.4、三角恒等变换13.(03全国高考1)已知πx (02∈-,),4cos x =5,则tan2x= ( )A.247B.247-C.724 D.724-14.(03全国高考4)函数y=2sinx(sinx+cosx)的最大值为 ( ) A.21+ B.12- C.2 D.215.(04福建2)tan15°+cot15°的值是 ( ) A.2 B.2+3 C.4 D.334 16.(04湖南,理17) ππ1ππsin(+2α)sin(2α)=α()44442-∈,,, 求2sin 2α+tanα-cotα-1的值. 17.(04湖南,文17)已知πtan(+α)=24,求212sin αcos αcos α+的值. 18.(05福建卷17)已知π1<x <0sinx +cosx =25-,.(I)求sinx -cosx 的值;(Ⅱ)求22x x x x 3sin 2sin cos +cos 2222tanx +cotx-的值.19.(1992年)已知π3π312<β<α<cos(αβ)=sin(α+β)=24135--,,,求sin2α的值5、三角函数图像及性质20. (2002全国文,17)如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx +φ)+b.(Ⅰ)求这段时间的最大温差; (Ⅱ)写出这段曲线的函数解析式.21.(2003全国高考题文20)已知函数f(x)=2sinx(sinx+cosx). (Ⅰ)求函数f(x)的最小正周期和最大值;(Ⅱ)在给出的直角坐标系中,画出函数y=f(x)在区间ππ[]22-,上的图像.22.(2000全国高考题 17)已知函数213y =cos x +sinxcosx +1x R 22∈,. (Ⅰ)当函数y 取得最大值时,求自变量x 的集合;(Ⅱ)该函数的图像可由y=sinx(x ∈R)的图像经过怎样的平移和伸缩变换得到? 23.(04重庆17)求函数y=sin 4x+23sinxcosx -cos 4x 的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间.6、三角函数的应用 (1)三角函数的最值问题① 形如y=asinx+bcosx+c 型,转化为22y a b sin(x )k =+++φ型 24. (1996全国高考题)当ππx 22-≤≤时,函数f(x)=sinx+3cosx 的 ( ) A.最大值是1,最小值是-1 B.最大值是1,最小值是-21C.最大值是2,最小值是-2D.最大值是2,最小值是-1 ② 形如y=asin 2x+bsinx·cosx+cos 2x 型,通过降幂转化成Asin2x+Bcos2x 型 例:求y=sin 2x+2sinx·cosx+3cos 2x 的最小值及取得最小值时的x 的集合,并求其最大值.③ 形如y=asin 2x+bsinx+c 或y=acos 2x+bcosx+c 型,令sinx=t 或cosx=t 转化成y=at 2+bt+c 的二次函数型.25.(1997全国高考题)函数y=cos 2x -3cosx+2的最小值为( ) A.2 B.0 C.41- D.6④ 形如y=a(sinx+cosx)+bsinx·cosx+c 型,令sinx+cosx=t (2t 2)-≤≤,则sinx·cosx=2t 12-,转化为2b b y =t +at +c 22-的二次函数型.26.求函数y=1+sinx+cosx+sinx·cosx 的值域. ⑤ 形如a cos x b y ccos x d +=+或 a sin x b(y )csin x d+=+型,可用分离常数法或|cosx|≤1来解决.27.(1999广东高考题)函数2+cosxy =2cosx-的最大值是 ( )A.53B.25C.3D.5 ⑥ 形如cosx +ay =sinx +b型,常使用几何法,转化为斜率问题研究,也可以转化为22y a b sin(x )k =+++φ型.(2)解三角形28.(04全国Ⅳ12)△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边.如果 a 、b 、c 成等差数列,∠B=30°,△ABC 的面积为32,那么b=( ) A.231+ B.31+ C.232+ D.32+ (3)三角函数与向量29.(05江西18)已知向量πx x a =(2cos tan(+))224,,πx b =(2sin(+)24 ,πx tan())24-.令f(x)=a b ⋅ ,求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.(4)三角函数与解析几何30.(04湖南2)设直线 ax+by+c=0的倾斜角为α,且sin α+cos α=0,则a ,b 满足 ( )A.a+b=1B. a -b=1C. a+b=0D. a -b=0 (5)三角函数与方程、不等式 31.求函数12y =2+log x +tanx 的定义域.1.解:已知sinα=31,则tanα=24±. 2.解:满足1sin x 2≥的x 的取值范围是π5π2k π+x 2k π+ k z 66≤≤∈ 3.解:已知π0<x <2,则 sinx 、tanx 、x 的大小为tanx> x>sinx.4.D5.C6.D7.解:2010°=5×3600+2100,tan2010°= tan 2100= tan30033=8.解:(I)∵tan 22α=,∴ 22tan 2242tan 1431tan 2α⨯α===-α--;所以tan tantan 14tan()41tan 1tan tan 4πα+πα+α+==π-α-α41134713-+==-+ (Ⅱ)由(I)得 4tan α3=-, 所以 6sin α+cos α6tan 13sin α2cos α3tan 2α+=-α-46()173463()23-+==--. 9.解法一:(I)由1sin x cos x 5+=,平方得sin 2x+2sinxcosx+cos 2x=125, 即242sinxcosx 25=-,∵(sin x -cosx) 2=1-2sinxcosx=4925.又∵π<x <02-,∴sinx<0,cosx>0,sinx -cosx<0,故7sinx cosx 5-=-.解法二:(I)联立方程221sinx +cosx =5sin +cos x =1⎧⎪⎨⎪⎩, 由①得1sinx =cosx 5-将其代入②,整理得25cos 2x -5cos x -12=0, ∴3cos x 5=-或4cos x 5=,∵π<x <02-,∴3sin x 54cos x 5⎧=-⎪⎪⎨⎪=⎪⎩,故7sinx cosx 5-=-.(Ⅱ)222x x x x x 3sin 2sin cos +cos 2sin sinx +12(cosx sinx)22222tanx +cotx tanx +cotx tanx +cotx---+===[2-(sinx+cosx)]sinxcosx=108125-. 10.由3sin(A +B)=5,1sin(A B)=5-∴32sin A cos B cos Asin B sin A cos B tan A 55 2.11tan B sin A cos B cos Asin B cos Asin B 55⎧⎧+==⎪⎪⎪⎪⇔⇔=⎨⎨⎪⎪-==⎪⎪⎩⎩∴:tanA=2tanB. (Ⅱ)解:∵π<A +B <π2,3sin(A +B)=5,∴3tan(A B)4+=-,即tanA +tanB 31tanAtanB 4=--,将tanA=2tanB 代入上式并整理得,2tan 2B -4tanB -1=0,解得26tanB =2±,舍去负值得2+6tanB =2, ∴tanA=2tanB=2 6.+ 设AB 边上的高为CD.则AB=AD+DB=CD CD 3CD +=tanA tanB 2+6,由AB=3,得CD=26+.所以AB 边上的高等于26+. 11.A12.解:原式=12(1-cos40°)+12(1+cos100°)+sin20°cos50° =1+12(cos100°-cos40°)+12(sin70°-sin30°)=34-sin70°sin30°+12sin70°=3413.D 解: ∵π4x (0cos x =25∈-,),,∴33sin x =tan x =54--,,则 32244tan 2x =97116-⨯=--14.A解: y=2sin 2x+sin2x=sin2x -cos2x +12sin(2x )14π=-+. ∴函数y=2sinx(sinx+cosx)的最大值为12+.故选择A.15.C 解: tan15°+cot15°000124sin15cos15sin 30===.故选择C 16.解: 由ππsin(2α)sin(2α)44+⋅-ππsin(2α)cos(2α)44=+⋅+ 1π111sin(+4α)=cos4α=cos4α=22242=⇒, 又ππα(,)42∈,4α∈(π,2π),5π4α=3,∴5πα=12. 于是2sin 2α+tanα-cotα-122sin αcos α2cos2αcos2α+=cos2αsin αcos αsin2α----=-(2cos2α+2cot2α)=5π5π(cos +2cot )66-=325)3223(=---.17.解:由π1+tan αtan(+α)==241-tan α,得1tan α.3=于是22221sin α+cos α=2sin αcos α+cos α2sin αcos α+cos αα221()+1tan α+123===.12tan α+132+13⨯ 18.本题主要考查三角函数的基本公式、三角恒等变换、各个象限内三角函数符号的特点等基本知识,以及推理和运算能力解法一:(I)由1sin x cos x 5+=,平方得sin 2x+2sinxcosx+cos 2x=125, 即242sinxcosx 25=-,∵(sin x -cosx) 2=1-2sinxcosx=4925.又∵π<x <02-,∴sinx<0,cosx>0,sinx -cosx<0,故7sinx cosx 5-=-.解法二:(I)联立方程221sinx +cosx =5sin +cos x =1⎧⎪⎨⎪⎩, 由①得1sinx =cosx 5-将其代入②,整理得25cos 2x -5cos x -12=0,∴3cos x 5=-或4cos x 5=,∵π<x <02-,∴3sin x 54cos x 5⎧=-⎪⎪⎨⎪=⎪⎩,故7sinx cosx 5-=-. (Ⅱ)222x x x x x 3sin 2sin cos +cos 2sin sinx +12(cosx sinx)22222tanx +cotx tanx +cotx tanx +cotx---+===[2-(sinx+cosx)]sinxcosx=108125-.19.解:由于π3πβ<α24<<,可得到π3πα24π3πβ24⎧<<⎪⎪⇒⎨⎪<<⎪⎩3ππα+β2<<, π3πα243ππβ42βα⎧<<⎪⎪⎪-<-<-⇒⎨⎪<⎪⎪⎩ππαβ44αβ>0⎧-<-<⎪⇒⎨⎪-⎩π0<αβ4-<. ……6分 ∴4cos(αβ)5+=-,5sin(αβ)13-=. ……8分 又2α= (α+β)+(α-β) ……9分∴ sin2α=sin[(α+β)+(α-β)]=sin(α+β)cos(α-β)+cos(α+β)sin(α-β) ……11分3124556()()51351365=-⨯+-⨯=-. ……12分20.解:(Ⅰ)由图示,这段时间的最大温差是30-10=20℃.(Ⅱ)图中从6时到14时的图像是函数y=Asin(ωx +φ)+b.的半个周期,∴12π=1462ω⨯-,解得πω=8. 由图示,1A =(3010)=102-, 1b =(10+30)=202, 0 6 8 10 12 14 20 10 30y 温度/0C 时间/hx这时,y=10sin(π8ωx +φ)+20,将x=6,y=10代入上式,可取3π4=φ. 综上可知,所求的解析式为y=10sin(π8x +3π4)+20 (x ∈[6,14]).21.解:(Ⅰ)f(x)=2sin 2x+2sinxcosx=1-cos2x+sin2xπππ=1+2(sin2xcoscos2xsin )=1+2sin(2x )444-- ∴函数f(x)的最小正周期为π,最大值为21+. (Ⅱ)由(Ⅰ)知 x 3π8-π8-π83π8 5π8y121- 121+1故函数y= f(x)在区间ππ[]22-,上的图像是22.解:(Ⅰ) 213y =cos x +sinxcosx +1222113=(2cos x 1)+(2sinxcosx)+1444-+ 135=cos2x sin2x +444+1ππ5=(sin cos2x sin2xcos )+2664+1π5=sin(2x )+264+. ……6分 y 取得最大值必须且只需ππ2x =+2k πk z 62+∈,即πx =k πk z 6+∈.x y12 O 2.5 π2π2-π8π8-π4π4-3π83π8-3π21.50.5所以当函数y 取得最大值时,自变量x 的集合为π{x |x =k πk z}6+∈……8分 (Ⅱ)将函数y=sinx 依次进行如下变换:① 把函数y=sinx 的图像向左平移π6,得到函数πy =sin(x )6+的图像; ②把得到的图像上各点横坐标缩短到原来的12倍(纵坐标不变),得到函数πy =sin(2x )6+的图像;③把得到的图像上各点纵坐标缩短到原来的12倍(横坐标不变),得到函数1πy =sin(2x )26+的图像;④把得到的图像向上平移54个单位长度,得到函数1π5y =sin(2x )+264+的图像;综上得到函数213y =cos x +sinxcosx +122的图像. ……12分 23.解:y=sin 4x+23sinxcosx -cos 4x=(sin 2x+cos 2x) (sin 2x -cos 2x)+3sin2x =3sin2x -cos 2x=2 sin(2x -6π). ∴函数最小正周期为π;最小值-2;在[0,π]上的单调递增区间为π[0]3,,π[π]3,24.①解: 函数f(x)=sinx+3cosx=2 sin(x+π3),∵ππx 22-≤≤,∴ππ5πx +636-≤≤,∴1πsin(x +)123-≤≤,π12sin(x +)23-≤≤.故选择D.②解: y=sin 2x+2sinx·cosx+3cos 2=1+sin2x+2cos 2x=2+sin2x+cos2x =2+2sin(2x+π4),y 最小值为2-2;当ππ2x 2k πk z 42+=-∈,即取得最小值时的x 的集合为3π{x |x k πk z}8=-∈,其最大值为22+③ 25.解: y=cos 2x -3cosx+2231(cos x )24=--,当cosx=1时,y min =0. 故选择B.④ 26.解: 令sinx+cosx=t (2t 2)-≤≤,则sinx·cosx=2t 12-,22t 11y t 1(t 1)22-=++=+,当t=-1时取得最小值0;当t =2时取得最大值322+.⑤ 27 解: 由2+cosx y =2cosx -得,2y 2|cosx |=||1y 1-≤+,3y 2-10y+3≤0,解得1y 33≤≤.答案.C28.解: 如果a 、b 、c 成等差数列,则2b= a+c ,ΔABC 13S =acsinB 22=,ac=6, 又b 2=a 2+c 2-2accosB=(a+c)2-2ac -2accosB=4b 2-12-63,整理得, 3b 2=4+23,∴b=31+.29.解:x x πx πx πf(x)=a b =22cos sin(+)+tan(+)tan()2242424⋅-x x1tantan 1x 2x 2x 2222cos (sin cos )x x222221tan 1tan 22+-=++⋅-+.2x x x2sincos 2cos 1222=+-π=sinx +cosx =2sin(x +).4当πx =4时,max πf(x)|=f()=24. 最小正周期为T=2π. f(x)在[0]4π,是单调增加,在[]4ππ,是单调减少.30.解: 直线 ax+by+c=0的倾斜角为α,且sin α+cos α=0,则ak ta n α1b==-=-, ∴a -b=0. 故选择D.31.解: 函数的定义域为122+log x 0tanx 0πx k π+k z 2⎧≥⎪⎪⎪≥⎨⎪⎪≠∈⎪⎩1122log x 2log 4πk πx k π+2πx k π+k z 2⎧≥-=⎪⎪⎪⇒≤<⎨⎪⎪≠∈⎪⎩ 0<x 4πk πx k π+k z 2≤⎧⎪⇒⎨≤<∈⎪⎩0<x 4πk πx k π+k z 2≤⎧⎪⇒⎨≤<∈⎪⎩, ∴π0x 2<<或πx 4<≤,即. π{x |0x πx 4}2<<<≤或.。