求AOE网络中的关键路径算法
- 格式:doc
- 大小:33.00 KB
- 文档页数:4

F福建电脑UJIAN COMPUTER福建电脑2017年第11期1引言有向无环图在工程和管理中的应用有两种:AOV 网和AOE 网,前者用顶点表示活动,有向弧表示活动间。
后者用顶点表示事件,弧表示活动,弧上的权值表示活动持续的时间。
AOE 网在工程计划和管理中用于解决两类问题,一类是求解影响工程进度的关键活动,另一类是求解完成整个工程所需要的最少时间。
在AOE 网中唯一一个入度为零的顶点称作源点;唯一一个出度为零的顶点称作汇点。
从源点到汇点的最长路径称作关键路径,关键路径的长度就是完成整个工程任务所需要的最短时间。
关键路径上的活动都是关键活动。
如果这些活动中的任意一项未能按期完成,则整个工程就要延期。
如果某个关键活动的进度能够提前,那么整个工程就可能提前完成。
2算法所用数据结构:设图G =(V ,VR )是一个具有n 个顶点的有向网,其中,V 为顶点集,VR 为两个顶点间的关系的集合。
G 的邻接矩阵定义为如下n 伊n 矩阵A :则定义如下数组和矩阵:top_sort [n ]:存放G 的一个拓扑序列ve [n ]:ve [i ]为事件vi 的最早发生时间vl [i ]:vl [i ]为事件vi 的最晚发生时间e [n ][n ]:e [i ][j ]为活动<vi ,vj>的最早开始时间l [n ][n ]:l [i ][j ]为活动<vi ,vj>的最晚开始时间3基于邻接矩阵的拓扑排序(Topological Sort)的实现在顶点集V 和弧集E 构成的有向图G=(V ,E)中,满足如下条件的顶点序列(v i1,v i2,v i3…,v in )称为拓扑序列:对于序列中的任意两个顶点v i 、v j ,如果在G 中存在一条从v i 到v j 的路径,那么在序列中v i 一定在v j 之前。
如图1所示有向网的一个拓扑序列为:v 0,v 1,v 2,v 3,v 4,v 5,v 6,v 7,v 8。


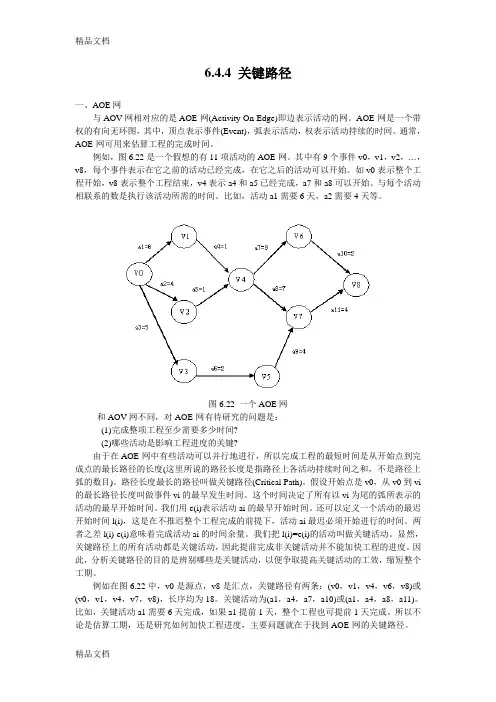

数据结构课程设计报告专业网络工程班级姓名学号指导老师评分计算AOE网的关键路径AOE网即边表示活动的网络。
通常,可用AOE网来估算工程计划的完成时间。
如下所示的AOE网包括11项活动,9个事件,每个事件都有所需的完成时间。
我们现在要解决的是:(1)完成整项工程至少需要多少时间(最短时间);(2)哪些活动是影响工程进度的关键(关键活动)。
用e(i)表示活动最早开始时间,l(i)表示活动的最迟开始时间,则l(i)-e(i)为完成该活动的时间余量。
对于本例列表如下:下图就是上述AOE网的关键路径:请编程完成下列工作:1、输入:(1)顶点的信息和入度;(2)AOE网的边(始点、终点和权值)。
2、输出:(1) AOE网的邻接表(按“顶点入度:—>顶点权值”的格式输出)如a 0:-->4 5-->3 4-->2 6(2)输出关键活动每行所显示的分别为开始事件、结束事件、最早开始时间、最迟开始时间和完成活动的时间余量:当l(i)-e(i)=0时,在该行注明为关键活动。
如:a b 0 0 0 关键活动源程序#include<stdio.h>#include<stdlib.h>#include<iomanip.h>#include <process.h>//#define PROJECTNUMBER 9//10//#define PLANNUMBER 11//13typedef struct node{int adjvex;int dut;struct node *next;}edgenode;typedef struct{int projectname;int id;edgenode *link;}vexnode;//vexnode Graphicmap[PROJECTNUMBER];void CreateGraphic(vexnode* Graphicmap,int projectnumber,int activenumber){int begin,end,duttem;edgenode *p;for(int i=0;i<projectnumber;i++){Graphicmap[i].projectname=i;Graphicmap[i].id =0;Graphicmap[i].link =NULL;}printf("某项目的开始到结束在图中的节点输入<vi,vj,dut>\n");printf("如:3,4,9 回车表示第三节点到第四节点之间的活动用了9个单位时间\n"); for(int k=0;k<activenumber;k++){scanf("%d,%d,%d",&begin,&end,&duttem);p=(edgenode*)malloc(sizeof(edgenode));p->adjvex =end-1;p->dut =duttem;Graphicmap[end-1].id ++;p->next =Graphicmap[begin-1].link ;Graphicmap[begin-1].link =p;}}int SearchMapPath(vexnode* Graphicmap,int projectnumber,int activenumber,int& totaltime){int i,j,k,m=0;int front=-1,rear=-1;int* topologystack=(int*)malloc(projectnumber*sizeof(int));//用来保存拓扑排列int* vl=(int*)malloc(projectnumber*sizeof(int));//用来表示在不推迟整个工程的前提下,VJ允许最迟发生的时间int* ve=(int*)malloc(projectnumber*sizeof(int));//用来表示Vj最早发生时间int* l=(int*)malloc(activenumber*sizeof(int));//用来表示活动Ai最迟完成开始时间 int* e=(int*)malloc(activenumber*sizeof(int));//表示活动最早开始时间edgenode *p;totaltime=0;for(i=0;i<projectnumber;i++) ve[i]=0;for(i=0;i<projectnumber;i++){if(Graphicmap[i].id==0){topologystack[++rear]=i;m++;}}while(front!=rear){front++;j=topologystack[front];m++;p=Graphicmap[j].link ;while(p){k=p->adjvex ;Graphicmap[k].id --;if(ve[j]+p->dut >ve[k])ve[k]=ve[j]+p->dut ;if(Graphicmap[k].id ==0)topologystack[++rear]=k;p=p->next ;}}if(m<projectnumber){printf("\n本程序所建立的图有回路不可计算出关键路径\n");printf("将退出本程序\n");return 0;}totaltime=ve[projectnumber-1];for(i=0;i<projectnumber;i++)vl[i]=totaltime;for(i=projectnumber-2;i>=0;i--){j=topologystack[i];p=Graphicmap[j].link ;while(p){k=p->adjvex ;if((vl[k]-p->dut )<vl[j])vl[j]=vl[k]-p->dut ;p=p->next ;}}i=0;printf("| 起点 | 终点 | 最早开始时间 | 最迟完成时间 | 差值 | 备注 |\n");for(j=0;j<projectnumber;j++){p=Graphicmap[j].link;while(p){k=p->adjvex ;e[++i]=ve[j];l[i]=vl[k]-p->dut;printf("| %4d | %4d | %4d | %4d | %4d |",Graphic map[j].projectname +1,Graphicmap[k].projectname +1,e[i],l[i],l[i]-e[i]);if(l[i]==e[i])printf(" 关键活动 |");printf("\n");p=p->next ;}}return 1;}void seekkeyroot(){int projectnumber,activenumber,totaltime=0;system("cls");printf("请输入这个工程的化成图形的节点数:");scanf("%d",&projectnumber);printf("请输入这个工程的活动个数:");scanf("%d",&activenumber);vexnode* Graphicmap=(vexnode*)malloc(projectnumber*sizeof(vexnode)); CreateGraphic(Graphicmap,projectnumber,activenumber);SearchMapPath(Graphicmap,projectnumber,activenumber,totaltime);printf("整个工程所用的最短时间为:%d个单位时间\n",totaltime);system("pause");}int main(){char ch;for(;;){do{system("cls");printf("| 欢迎进入求关键路径算法程序 |");for(int i=0;i<80;i++)printf("*");printf("%s","(S)tart开始输入工程的节点数据并求出关键路径\n"); printf("%s","(E)xit退出\n");printf("%s","请输入选择:");scanf("%c",&ch);ch=toupper(ch);}while(ch!='S'&&ch!='E');switch(ch){case'S':seekkeyroot(); break; case'E':return 1; }}}。

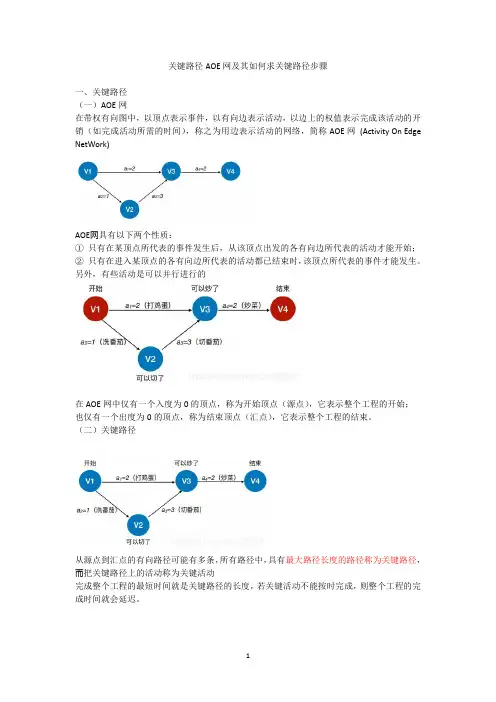
关键路径AOE网及其如何求关键路径步骤一、关键路径(一)AOE网在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称AOE网(Activity On Edge NetWork)AOE⽹具有以下两个性质:①只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始;②只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生。
另外,有些活动是可以并行进行的在AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;也仅有一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
(二)关键路径从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,⽽把关键路径上的活动称为关键活动完成整个工程的最短时间就是关键路径的长度,若关键活动不能按时完成,则整个工程的完成时间就会延迟。
活动ai的时间余量d(i)=l(i)-e(i),表⽰在不增加完成整个工程所需总时间的情况下,活动ai 可以拖延的时间若一个活动的时间余量为零,则说明该活动必须要如期完成,d(i)=0即l(i)=e(i)的活动ai是关键活动由关键活动组成的路径就是关键路径(三)求关键路径的步骤(四)求所有事件的最早发生时间1.求所有事件的最早发生时间ve()(五)求所有事件的最迟发生时间1.求所有事件的最迟发生时间vl()1.求所有活动的最早发生时间e()1.求所有活动的最迟发生时间l()(八)求所有活动的时间余量(九)关键活动、关键路径的特性若关键活动耗时增加,则整个工程的工期将增长缩短关键活动的时间,可以缩短整个工程的工期当缩短到一定程度时,关键活动可能会变成非关键活动可能有多条关键路径,只提高⼀条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。


关键路径的计算从源点到汇点路径长度最长的路径为该project的关键路径,即关键路径可以保证全部路径的活动都可以完毕。
ok,再次进⼊我们的作业题:例如以下图所看到的的AOE⽹(弧上权值代表活动的持续天数)1)完毕此project最少所须要多少天?2)哪些是关键活动,在图中表⽰出关键路径我们先计算最早发⽣时间ve和最迟发⽣时间vl:12345678910Ve05612151616192123Vl09612152116192123⾸先呢,编号1和编号10分别为该project的源点和汇点,我们规定最早发⽣时间ve(源点)=0,最迟发⽣时间vl(汇点)=ve(汇点)。
那么这两个量该怎样计算呢,看图:对于事件i来说,ve(i) = Max{ve(m) + dut(<m, i>)},vl(i) = Min{vl(j) – dut(<i, j>)};当中ve(m)代表i前⼀个事件的最早发⽣时间,dut(<m, i>)表⽰从m到i的持续时间,⼤家能够把它看成⼀个递归算法,⼀直调⽤ve(),直到ve(源点)为⽌,然后取其最⼤值,由于它要保证全部路径上的活动都能完毕;⽽最迟发⽣时间和前者⼀样,⼀直递归调⽤vl(),直到vl(汇点)为⽌,然后取其最⼩值就可以。
回到原题中对⽐例图能够⾮常快地得到表格所看到的内容。
我们再来看两个概念:e(i)和l(i),前者为活动ai 的最早可能開始时间,后者为活动ai的最迟同意開始时间。
差别于前边的ve和vl,e和l为标识的是某活动的时间,⽽前者是某事件的时间。
假如从事件m到事件i的活动为af,则有e(f)=ve(m), l(f)=vl(i)–dut(<m,i>) ,即活动af的最早可能開始时间为其弧尾事件最早可能发⽣时间;最迟同意開始时间为其弧尾事件最迟发⽣时间与两个事件的持续时间之差。
是不是感觉有点别扭,但仅仅要理解了这⼏个关键词也就⾮常easy看懂了。

关键路径算法相关概念: (1)AOE (Activity On Edges)⽹络如果在⽆有向环的带权有向图中⽤有向边表⽰⼀个⼯程中的各项活动(Activity),⽤边上的权值表⽰活动的持续时间(Duration),⽤顶点表⽰事件(Event),则这样的有向图叫做⽤边表⽰活动的⽹络,简称AOE (Activity On Edges)⽹络。
AOE ⽹是⼀个带权的有向⽆环图。
AOE⽹络在某些⼯程估算⽅⾯⾮常有⽤。
例如,可以使⼈们了解: a、完成整个⼯程⾄少需要多少时间(假设⽹络中没有环)? b、为缩短完成⼯程所需的时间, 应当加快哪些活动? (2)关键路径(Critical Path) 在AOE⽹络中, 有些活动顺序进⾏,有些活动并⾏进⾏。
从源点到各个顶点,以⾄从源点到汇点的有向路径可能不⽌⼀条。
这些路径的长度也可能不同。
完成不同路径的活动所需的时间虽然不同,但只有各条路径上所有活动都完成了,整个⼯程才算完成。
因此,完成整个⼯程所需的时间取决于从源点到汇点的最长路径长度,即在这条路径上所有活动的持续时间之和。
这条路径长度最长的路径就叫做关键路径(Critical Path)。
(3)由于实际⼯程只有⼀个开始点和⼀个结束点,因此AOE⽹存在唯⼀的⼊度为0的开始点(⼜称源点)和唯⼀的出度为0的结束点(⼜称汇点)参数定义: (1)事件的最早发⽣时间 etv(earliest time of vertex):即顶点V k的最早发⽣时间。
(2)事件的最晚发⽣时间 ltv(latest time of vertex):即顶点V k的最晚发⽣时间,也就是每个顶点对应的事件最晚需要开始的时间,超出此事件将会延误整个⼯期。
(3)活动的最早开⼯时间 ete(earliest time of edge):即弧ak的最早发⽣时间。
(4)活动的最晚开⼯时间 lte(latest time of edge):即弧ak的最晚发⽣时间,也就是不推迟⼯期的最晚开⼯时间。

AOE网和关键路径AOE网(Activity On Edge Network)是一个带权的有向无环图。
其中用顶点表示事件,弧表示活动,权值表示两个活动持续的时间。
AOE网是以边表示活动的网。
关键路径:AOE网中从起点至终点最长的路径。
关键路径上的活动均为关键活动。
最早开始时间:在关键路径上,从开始到该任务的最早执行的时间,取最大值最晚开始时间:关键路径的总时间-反向得出该任务的时间注意:关键路径不一定只有一条松弛时间:不影响完工前提下可能被推迟完成的最大时间松弛时间=关键路径的总时间-包含该任务的关键路径花的时间松弛时间=最晚开始时间-最早开始时间计算完成项目的最少时间:计算关键路径试题:1、下图所示的AOE网表示一项包含8个活动的工程。
活动d的最早开始时间和最迟开始时间分别是()A、3和7B、12和12C、12和14D、15和15求AOE网的关键路径的步骤如下:解析:选C2、某软件项目的活动图如下图所示,其中顶点表示项目里程碑,链接顶点的边表示包含的活动,变色数字表示活动的持续时间(天)。
完成该项目的最少时间为(17)天。
由于某种原因,现在需要同一个开发人员完成BC和BD,则完成该项目的最少时间为(18)天。
(17) A.11 B.18 C.20 D.21(18) A.11 B.18 C.20 D.21【答案】B D【解析】关键路径为ABCEFJ 和ABDGFJ ,18天。
BC持续时间3天,BD持续时间2天,由一天完成,则可以把BC持续时间作为5天,BD持续时间也为5天,则关键路径为ABDGFJ,21天3、某软件项目的活动图如下图所示,其中顶点表示项目里程碑,连接顶点的边表示包含的活动,边上的数字表示活动的持续时间(天),则完成该项目的最少时间为(17)天。
活动BD 和HK 最早可以从第(18)天开始。
(活动AB、AE 和AC 最早从第1 天开始)(17) A.17 B.18 C.19 D.20(18) A.3 和10 B.4 和11 C.3 和9 D.4 和10【答案】D B【解析】因为网络图是从0开始算的,按题目要求活动AB从第1天开始的话,就是1、2、3,活动BD就是第4天开始,相应的活动HK就是第11天开始。
关键路径的概念和算法AOE⽹:在⼀个表⽰⼯程的带权有向图中,⽤顶点表⽰事件,⽤有向边表⽰活动,边上的权值表⽰活动的持续时间,称这样的有向图叫做边表⽰活动的⽹,简称AOE⽹。
AOE⽹中没有⼊边的顶点称为始点(或源点),没有出边的顶点称为终点(或汇点)。
AOE⽹的性质:⑴只有在某顶点所代表的事件发⽣后,从该顶点出发的各活动才能开始;⑵只有在进⼊某顶点的各活动都结束,该顶点所代表的事件才能发⽣。
关键路径:在AOE⽹中,从始点到终点具有最⼤路径长度(该路径上的各个活动所持续的时间之和)的路径称为关键路径。
关键活动:关键路径上的活动称为关键活动。
关键活动:e[i]=l[i]的活动 由于AOE⽹中的某些活动能够同时进⾏,故完成整个⼯程所必须花费的时间应该为始点到终点的最⼤路径长度。
关键路径长度是整个⼯程所需的最短⼯期。
与关键活动有关的量:⑴事件的最早发⽣时间ve[k] ve[k]是指从始点开始到顶点vk的最⼤路径长度。
这个长度决定了所有从顶点vk发出的活动能够开⼯的最早时间。
⑵事件的最迟发⽣时间vl[k] vl[k]是指在不推迟整个⼯期的前提下,事件vk允许的最晚发⽣时间。
⑶活动的最早开始时间e[i] 若活动ai是由弧<vk , vj>表⽰,则活动ai的最早开始时间应等于事件vk的最早发⽣时间。
因此,有:e[i]=ve[k]⑷活动的最晚开始时间l[i] 活动ai的最晚开始时间是指,在不推迟整个⼯期的前提下,ai必须开始的最晚时间。
若ai由弧<vk,vj>表⽰,则ai的最晚开始时间要保证事件vj的最迟发⽣时间不拖后。
因此,有:l[i]=vl[j]-len<vk,vj>⽰例:所以:代码实现:123456789101112131415161718192021222324252627282930313233Status TopologicalOrder(ALGraph G, Stack &T){// 有向⽹G 采⽤邻接表存储结构,求各顶点事件的最早发⽣时间ve(全局变量)。
关键路径若在带权的有向图中,以顶点表示事件,以有向边表示活动,边上的权值表示活动的开销(如该活动持续时间),则此带权的有向图称为边表示活动的网(Activity on Edge Network) ,简称AOE 网。
【例】图7.21 是一个网。
其中有9 个事件v 1 , v 2 , … , v 9 ;11 项活动 a 1 , a 2 , … , a 11 。
每个事件表示在它之前的活动已经完成,在它之后的活动可以开始。
如v 1 表示整个工程开始,v 9 表示整个工程结束。
V 5 表示活动a 4 和a 5 已经完成,活动a 7 和a 8 可以开始。
与每个活动相联系的权表示完成该活动所需的时间。
如活动 a 1 需要 6 天时间可以完成。
(1)AOV 网具有的性质⒈只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始。
⒉只有在进入某一顶点的各有向边所代表的活动都已经结束,该顶点所代表的事件才能发生。
⒊表示实际工程计划的AOE 网应该是无环的,并且存在唯一的入度过为0 的开始顶点和唯一的出度为0 的完成顶点。
(2)由事件v j 的最早发生时间和最晚发生时间的定义, 可以采取如下步骤求得关键活动:1. 从开始顶点v 1 出发, 令ve(1)=0, 按拓扑有序序列求其余各顶点的可能最早发生时间。
Ve(k)=max{ve(j)+dut(<j,k>)} (7.1 )j ∈T其中T 是以顶点v k 为尾的所有弧的头顶点的集合(2 ≤ k ≤ n) 。
如果得到的拓朴有序序列中顶点的个数小于网中顶点个数n ,则说明网中有环,不能求出关键路径,算法结束。
2. 从完成顶点v n 出发,令vl(n)=ve(n) ,按逆拓朴有序求其余各顶点的允许的最晚发生时间: vl(j)=min{vl(k)-dut(<j,k>)}k ∈S其中S 是以顶点v j 是头的所有弧的尾顶点集合(1 ≤ j ≤ n-1) 。
关键路径算法
关键路径
定义:关键路径是包含AOE图中所有顶点(事件)的最⼤路径长度,其长度代表所有活动完成所需最短时间
涉及概念:AOE图,ve,vl,ee,el
AOE图:
activities on edges
边表⽰活动(具体的⼯程内容),边长度(权值)代表活动所花费的时间
顶点表⽰事件(事件不是⼯程内容,可以理解为⼀个状态,⽤以描述所有活动的完成情况)
ve,vl,ee,el分别代表事件最早开始时间、事件最晚开始时间、活动最早开始时间、活动最晚开始时间
注:AOE图之外还有AOV图,也即顶点表⽰活动,有向边仅代表活动先后顺序⽽没有权值,故AOV图不能⽤来求所有活动完成的最短时间(关键路径)
解释:⾄于为什么最⼤长度代表最短时间,主要是因为在AOE图中,当指向⼀个顶点的所有边所代表的活动都完成后这个事件才能发⽣。
⽽所有边代表的活动的完成才是整个⼯程的完成
注意:AOE⽹是有向⽆环的,也即不能存在事件之间的相互依赖
计算⽅法:
按ve,vl,ee,el的次序计算
ve,ee从起点到终点顺着边的⽅向进⾏计算,vl,el则从终点到起点逆着边的⽅向进⾏计算
ve[x]=max(ve[x1]+e1,ve[x2]+e2,...,ve[xn]+en)其中xi是有边指向x的顶点,ei是从xi指向x的边
vl[x]=min(vl[x1']-e1',vl[x2']-e2',...,vl[xn']-en')
ee[x]=ve[x]
el[x]=vl[xi']-ei'
所有ee[x]=el[x]的边x都是关键路径上的边,它们代表关键活动(关键路径可以不⽌⼀条)。
//求AOE网络中的关键路径算法
#include <cstdio>
#include <cstring>
#define MAXN 100 //顶点个数的最大值
#define MAXM 200 //边数的最大值
struct ArcNode
{
int to, dur, no; //边的另一个顶点,持续时间,活动序号
ArcNode *next;
};
int n, m; //顶点个数、边数
ArcNode* List1[MAXN]; //每个顶点的边链表表头指针(出边表) ArcNode* List2[MAXN]; //每个顶点的边链表表头指针(入边表) int count1[MAXN]; //各顶点的入度
int count2[MAXN]; //各顶点的出度
int Ee[MAXN]; //各事件的最早可能开始时间
int El[MAXN]; //各事件的最迟允许开始时间
int e[MAXM]; //各活动的最早可能开始时间
int L[MAXM]; //各活动的最迟允许开始时间
void CriticalPath( ) //求关键路径
{
//拓扑排序求Ee
int i, j, k;
int top1 = -1;
ArcNode* temp1;
memset( Ee, 0, sizeof(Ee) );
for( i=0; i<n; i++ )
{
if( count1[i]==0 )
count1[i] = top1, top1 = i;
}
for( i=0; i<n; i++ )
{
if( top1==-1 )
{
printf( "Network has a cycle!\n" ); return;
}
else
{
j = top1; top1 = count1[top1];
temp1 = List1[j];
while( temp1!=NULL )
{
k = temp1->to;
if( --count1[k]==0 )
count1[k] = top1, top1 = k;
if( Ee[j] + temp1->dur > Ee[k] ) //有向边<j,k> Ee[k] = Ee[j] + temp1->dur;
temp1 = temp1->next;
}//end of while
}//end of else
}//end of for
//逆拓扑排序求El
int top2 = -1;
ArcNode* temp2;
for( i=0; i<n; i++ )
{
El[i] = Ee[n-1];
if( count2[i]==0 )
count2[i] = top2, top2 = i;
}
for( i=0; i<n; i++ )
{
j = top2; top2 = count2[top2];
temp2 = List2[j];
while( temp2!=NULL )
{
k = temp2->to;
if( --count2[k]==0 )
count2[k] = top2, top2 = k;
if( El[j] - temp2->dur < El[k] ) //有向边<k,j> El[k] = El[j] - temp2->dur;
temp2 = temp2->next;
}//end of while
}//end of for
//求各活动的e[k]和L[k]
memset( e, 0, sizeof(e) ); memset( L, 0, sizeof(L) ); printf( "The critical activities are:\n" );
for( i=0; i<n; i++ ) //释放边链表上各边结点所占用的存储空间{
temp1 = List1[i];;
while( temp1!=NULL )
j = temp1->to; k=temp1->no; //有向边<i,j>
e[k] = Ee[i]; L[k] = El[j] - temp1->dur;
if( e[k]==L[k] )
printf( "A%d : %d->%d\n", k, i, j );
temp1 = temp1->next;
}
}
}
int main( )
{
int i, u, v, w; //循环变量、边的起点和终点
scanf( "%d%d", &n, &m ); //读入顶点个数n,边数
memset( List1, 0, sizeof(List1) ); memset( List2, 0, sizeof(List2) );
memset( count1, 0, sizeof(count1) ); memset( count2, 0, sizeof(count2) );
ArcNode *temp1, *temp2;
for( i=0; i<m; i++ )
{
scanf( "%d%d%d", &u, &v, &w ); //读入边的起点和终点
count1[v]++;
temp1 = new ArcNode; //构造邻接表
temp1->to = v; temp1->dur = w;
temp1->no = i+1; temp1->next = NULL;
if( List1[u]==NULL ) List1[u] = temp1;
else{ temp1->next = List1[u]; List1[u] = temp1; }
count2[u]++;
temp2 = new ArcNode; //构造邻接表
temp2->to = u; temp2->dur = w;
temp2->no = i+1; temp2->next = NULL;
if( List2[v]==NULL ) List2[v] = temp2;
else{ temp2->next = List2[v]; List2[v] = temp2; } }
CriticalPath( );
for( i=0; i<n; i++ ) //释放边链表上各边结点所占用的存储空间
{
temp1 = List1[i]; temp2 = List2[i];
while( temp1!=NULL )
{
List1[i] = temp1->next; delete temp1; temp1 = List1[i];
}
while( temp2!=NULL )
List2[i] = temp2->next; delete temp2; temp2 = List2[i];
}
}
return 0;
}
代码来自。