空间后方交会报告

摄影测量学单像空间后方交会实习报告一、实习目的1.掌握空间后方交会的定义和实现算法(1)定义：空间后方交会是以单幅影像为基础，从该影像所覆盖地面范围内若干控制点的已知地面坐标和相应点的像坐标量测值出发，根据共线条件方程，解求该影像在航空摄影时刻的外方位元素Xs，Ys，Zs，φ，ω，κ。

(2)算法：由于每一对像方和物方共轭点可列出2个方程，因此若有3个已知地面坐标的控制点，则可列出6个方程，解求6个外方位元素的改正数△Xs，△Ys，△Zs，△φ，△ω，△κ。

实际应用中为了提高解算精度，常有多余观测方程，通常是在影像的四个角上选取4个或均匀地选择更多的地面控制点，因而要用最小二乘平差方法进行计算。

2.了解摄影测量平差的基本过程(1)获取已知数据。

从摄影资料中查取影像比例尺1/m，平均摄影距离（航空摄影的航高）、内方位元素x0，y0，f；获取控制点的空间坐标X，Y，Z。

(2)量测控制点的像点坐标并进行必要的影像坐标系统误差改正，得到像点坐标。

(3)确定未知数的初始值。

单像空间后方交会必须给出待定参数的初始值，在竖直航空摄影且地面控制点大体对称分布的情况下，Xs0和Ys0为均值，Zs0为航高，φ、ω、κ的初值都设为0。

或者κ的初值可在航迹图上找出或根据控制点坐标通过坐标正反变换求出。

(4)计算旋转矩阵R。

利用角元素近似值计算方向余弦值，组成R阵。

(5)逐点计算像点坐标的近似值。

利用未知数的近似值按共线条件式计算控制点像点坐标的近似值（x），(y)。

(6)逐点计算误差方程式的系数和常数项，组成误差方程式。

(7)计算法方程的系数矩阵ATA与常数项ATL，组成法方程式。

(8)解求外方位元素。

根据法方程，解求外方位元素改正数，并与相应的近似值求和，得到外方位元素新的近似值。

(9)检查计算是否收敛。

将所求得的外方位元素的改正数与规定的限差比较，通常对φ，ω，κ的改正数△φ，△ω，△κ给予限差，通常为0.000001弧度，当3个改正数均小于0.000001弧度时，迭代结束。

单像空间后方交会实习报告一、实习目的单像空间后方交会是摄影测量中确定像片外方位元素的重要方法。

通过本次实习，旨在深入理解单像空间后方交会的基本原理和计算过程，熟练掌握相关软件的操作，提高对摄影测量数据处理的实践能力，并培养解决实际问题的思维和方法。

二、实习原理单像空间后方交会的目的是利用像片上的像点坐标以及相应的地面控制点坐标，通过数学模型求解像片的外方位元素（三个线元素 Xs、Ys、Zs 和三个角元素φ、ω、κ）。

其基本原理基于共线条件方程，即摄影中心、像点和相应的地面点位于同一条直线上。

共线条件方程可以表示为：＼＼begin{align}x x_0&＝ f\frac{a_1(X X_s) ＋ b_1(Y Y_s) ＋ c_1(Z Z_s)｝｛a_3(X X_s) ＋ b_3(Y Y_s) ＋ c_3(Z Z_s)｝＼＼y y_0&＝ f\frac{a_2(X X_s) ＋ b_2(Y Y_s) ＋ c_2(Z Z_s)｝｛a_3(X X_s) ＋ b_3(Y Y_s) ＋ c_3(Z Z_s)｝＼end{align}＼其中，＼（（x,y)＼）为像点坐标，＼（（x_0,y_0)＼）为主点坐标，＼（f\）为摄影机焦距，＼（（X,Y,Z)＼）为地面点的物方空间坐标，＼（（X_s,Y_s,Z_s)＼）为摄影中心的物方空间坐标，＼（（a_1,b_1,c_1)，（a_2,b_2,c_2)，（a_3,b_3,c_3)＼）为由角元素φ、ω、κ 构成的旋转矩阵的元素。

三、实习数据本次实习使用了一组航空像片，像片比例尺为 1:5000，焦距为152mm，像主点坐标为\（（x_0,y_0)＝（5000mm,5000mm)＼）。

同时，提供了 6 个均匀分布在像片范围内的地面控制点的物方空间坐标和像点坐标。

四、实习步骤1、数据准备整理地面控制点的物方空间坐标和像点坐标，确保数据的准确性。

输入像片的基本参数，如像主点坐标、焦距等。

单像空间后方交会实习报告摘要本报告旨在总结并评估笔者在单像空间后方交会实习中的经验和收获。

首先，报告介绍了单像空间后方交会实习的目的和背景。

接着，报告详细描述了实习期间所进行的实验和操作步骤。

在实习过程中，笔者遇到了一些挑战，但通过团队合作和专业指导取得了成功。

最后，报告总结了实习对于个人职业发展的重要性，并提出了改进实习体验的建议。

1. 引言单像空间后方交会是测量和分析地球或其他星球上的点的空间坐标的方法之一。

该方法通过将来自不同位置的图像投影到一个共同的平面上，并在该平面上对图像进行测量和分析，以确定点的坐标。

本实习旨在将现实生活中的实地测量和图像处理技术相结合，通过实际操作了解和掌握单像空间后方交会的原理和应用。

2. 实习过程本次实习分为三个步骤：图像获取、图像处理和空间坐标计算。

2.1 图像获取首先，为了进行后续的图像处理和分析，我们需要获取一组具有不同视角的图像。

为了实现这个目标，我们选择了一片公共景区进行实地测量。

在测量过程中，我们使用了专业的测量设备和相机，并按照一定的间隔和角度拍摄了一组图像。

这些图像将被用于后续的图像处理和分析。

2.2 图像处理在图像处理阶段，我们使用了专业的图像处理软件对获取到的图像进行处理。

首先，我们使用了相机标定算法对相机内外参数进行校准，以保证后续测量的精度和准确度。

然后，我们对每张图像进行了特征点提取和匹配，以建立图像之间的对应关系。

最后，根据所获得的对应关系，我们重建了图像场景的三维模型，并将其用于后续的空间坐标计算。

2.3 空间坐标计算在空间坐标计算阶段，我们使用了单像空间后方交会的原理，计算了每个图像特征点的空间坐标。

首先，我们将图像场景的三维模型与图像上的特征点进行对应，以确定特征点在三维空间中的位置。

然后，我们利用三角测量原理计算出特征点的三维坐标。

最后，通过对所有图像特征点的计算，我们可以得到目标点的空间坐标。

3. 实习挑战与解决在实习过程中，我们遇到了一些挑战，如图像质量、算法调优和测量误差等。

单像空间后方交会实习报告本文是一份单像空间后方交会实习报告，旨在总结和分享本人在这个领域进行实习的经验和所得。

一、实习背景和目的在开始正文之前，首先介绍一下实习的背景和目的。

本次实习是为了深入了解单像空间后方交会的原理和应用，并提升我的实践能力。

通过与团队合作，完成一系列的实习任务和项目，我期望能够在这个领域不断成长和进步。

二、实习内容和方法2.1 实习内容本次实习主要涉及单像空间后方交会的方法和技术。

我通过参与实际项目，了解和学习了从数据采集到数据处理的整个流程，并深入研究了相关的算法和工具。

2.2 实习方法为了能够全面了解单像空间后方交会的知识和技术，我采用了多种实习方法。

首先，我积极参与了团队的讨论和会议，与同事们交流和分享我们的学习和经验。

其次，我通过独立完成一些小型项目和任务，提升了自己的实践能力。

此外，我还阅读了大量的相关文献和资料，深入研究了该领域的理论知识。

三、实习成果和收获3.1 实习成果在实习期间，我完成了几个实践项目任务，并取得了一些成果。

首先，我成功实现了单像空间后方交会的基本原理和方法，并在实际项目中应用。

其次，我编写了一份详尽的实习报告，总结了整个实习过程和所得的经验。

3.2 实习收获通过这次实习，我获得了很多宝贵的经验和收获。

首先，我深入了解并掌握了单像空间后方交会的原理和方法，提升了自己的实践能力。

其次，我学会了如何与团队合作，并通过与他人的交流和合作进一步提升自己。

此外，我还学会了如何独立思考和解决问题，在实践中培养了自己的创新思维能力。

四、实习感悟和建议4.1 实习感悟通过实习，我深刻体会到了理论与实践的结合的重要性。

只有将所学的理论知识应用到实践项目中，才能真正理解和掌握。

在实践中遇到各种困难和挑战，我也学会了如何从失败中总结经验，再次进行尝试。

4.2 实习建议对于即将进行单像空间后方交会实习的同学们，我有几点建议。

首先，要注重理论知识的学习和积累，打好基础。

单向空间后方交会程序设计报告课题名称计算单向空间后方交会 姓 名胡小伟 学 号 2009301610207学院、班级 测绘学院0906班方向A2011年 10月18日※※※※※※※※※※※※※※※ 单向空间后方交会程序设计报告（1）编程工具：Matlab R2010a（2）程序代码：已知值及初始值控制点：x(mm) y(mm)-11.00 -13.8010.48 -6.4410.78 8.3122.712 8.32X(m) Y(m) Z(m)500017.19 4185066.00 885.40500452.19 4185197.50 915.82500470.16 4185494.50 928.76500302.16 4185489.00 949.71焦距：28.1359（mm）外方位元素初值：X(m) Y(m) Z(m) phi(rad) omega(rad) kappa(rad) 500215.49 4185301.89 1475.56 0.054882 0.057034 -0.036175%单向空间后方交会clc;%主距mf=28.1359/1000;%像点坐标mxy = [-11.00 -13.8010.48 -6.4410.78 8.3122.712 8.32]/1000;%地面坐标mXYZ = [500017.19 4185066.00 885.40;500452.19 4185197.50 915.82;500470.16 4185494.50 928.76;500302.16 4185489.00 949.71];%比例尺m=(sqrt((XYZ(1,1)-XYZ(2,1))^2+(XYZ(1,2)-XYZ(2,2))^2))/...(sqrt((xy(1,1)-xy(2,1))^2+(xy(1,2)-xy(2,2))^2))%初值XS0=500215.49YS0=4185301.89ZS0=1475.56H=m*fFai0=0.054882Oum0=0.057034Kpa0=-0.036175a1=cos(Fai0)*cos(Kpa0)-sin(Fai0)*sin(Oum0)*sin(Kpa0);a2=-cos(Fai0)*sin(Kpa0)-sin(Fai0)*sin(Oum0)*cos(Kpa0);a3=-sin(Fai0)*cos(Oum0);b1=cos(Oum0)*sin(Kpa0);b2=cos(Oum0)*cos(Kpa0);b3=-sin(Oum0);c1=sin(Fai0)*cos(Kpa0)+cos(Fai0)*sin(Oum0)*sin(Kpa0);c2=-sin(Fai0)*sin(Kpa0)+cos(Fai0)*cos(Oum0)*cos(Kpa0);c3=cos(Fai0)*cos(Oum0);for i=1:4f=28.1359/1000;x(i)=-f*(a1*(XYZ(i,1)-XS0)+b1*(XYZ(i,2)-YS0)+c1*(XYZ(i,3)-ZS0))/...(a3*(XYZ(i,1)-XS0)+b3*(XYZ(i,2)-YS0)+c3*(XYZ(i,3)-ZS0));y(i)=-f*(a2*(XYZ(i,1)-XS0)+b2*(XYZ(i,2)-YS0)+c2*(XYZ(i,3)-ZS0))/...(a3*(XYZ(i,1)-XS0)+b3*(XYZ(i,2)-YS0)+c3*(XYZ(i,3)-ZS0));lx(i)=xy(i,1)-x(i);ly(i)=xy(i,2)-y(i);endxyL=[lx(1);lx(1); lx(2);lx(2);lx(3);lx(3); lx(4);lx(4)]A1=[-f/H 0 -xy(1,1)/H -f*(1+(xy(1,1)^2)/(f^2)) -(xy(1,1))*(xy(1,2)/f) xy(1,2)0 -f/H -(xy(1,2))/H -(xy(1,1))*(xy(1,2)/f) -f*(1+(xy(1,2)^2)/(f^2)) -xy(1,2)]; A2=[-f/H 0 -xy(2,1)/H -f*(1+(xy(2,1)^2)/(f^2)) -(xy(2,1))*(xy(2,2)/f) xy(2,2)0 -f/H -(xy(2,2))/H -(xy(2,1))*(xy(2,2)/f) -f*(1+(xy(2,2)^2)/(f^2)) -xy(2,2)]; A3=[-f/H 0 -xy(3,1)/H -f*(1+(xy(3,1)^2)/(f^2)) -(xy(3,1))*(xy(3,2)/f) xy(3,2)0 -f/H -(xy(3,2))/H -(xy(3,1))*(xy(3,2)/f) -f*(1+(xy(3,2)^2)/(f^2)) -xy(3,2)]; A4=[-f/H 0 -xy(4,1)/H -f*(1+(xy(4,1)^2)/(f^2)) -(xy(4,1))*(xy(4,2)/f) xy(4,2)0 -f/H -(xy(4,2))/H -(xy(4,1))*(xy(4,2)/f) -f*(1+(xy(4,2)^2)/(f^2)) -xy(4,2)]; A=[A1;A2;A3;A4];X=(A'*A)\A'*LXS1=(XS0+X(1))YS1=(YS0+X(2))ZS1=(ZS0+X(3))Fai1=Fai0+X(4)Oum1=Oum0+X(5)Kpa1=Kpa0+X(6)XS1=(XS0+X(1))YS1=(YS0+X(2))ZS1=(ZS0+X(3))jishu=1;while (abs((Fai1-Fai0)>0.000003)||(abs(Oum1-Oum0)>0.000003)...||(abs(Kpa1-Kpa0))>0.000003)jishu=jishu+1XS0=XS1YS0=YS1ZS0=ZS1Fai0=Fai1Oum0=Oum1Kpa0=Kpa1a1=cos(Fai0)*cos(Kpa0)-sin(Fai0)*sin(Oum0)*sin(Kpa0);a2=-cos(Fai0)*sin(Kpa0)-sin(Fai0)*sin(Oum0)*cos(Kpa0);a3=-sin(Fai0)*cos(Oum0);b1=cos(Oum0)*sin(Kpa0);b2=cos(Oum0)*cos(Kpa0);b3=-sin(Oum0);c1=sin(Fai0)*cos(Kpa0)+cos(Fai0)*sin(Oum0)*sin(Kpa0);c2=-sin(Fai0)*sin(Kpa0)+cos(Fai0)*cos(Oum0)*cos(Kpa0);c3=cos(Fai0)*cos(Oum0);for i=1:4f=28.1359/1000;x(i)=-f*(a1*(XYZ(i,1)-XS0)+b1*(XYZ(i,2)-YS0)+c1*(XYZ(i,3)-ZS0))/...(a3*(XYZ(i,1)-XS0)+b3*(XYZ(i,2)-YS0)+c3*(XYZ(i,3)-ZS0));y(i)=-f*(a2*(XYZ(i,1)-XS0)+b2*(XYZ(i,2)-YS0)+c2*(XYZ(i,3)-ZS0))/...(a3*(XYZ(i,1)-XS0)+b3*(XYZ(i,2)-YS0)+c3*(XYZ(i,3)-ZS0));lx(i)=xy(i,1)-x(i);ly(i)=xy(i,2)-y(i);endxyL=[lx(1);lx(1); lx(2);lx(2);lx(3);lx(3); lx(4);lx(4)]A1=[-f/H 0 -xy(1,1)/H -f*(1+(xy(1,1)^2)/(f^2)) -(xy(1,1))*(xy(1,2)/f) xy(1,2)0 -f/H -(xy(1,2))/H -(xy(1,1))*(xy(1,2)/f) -f*(1+(xy(1,2)^2)/(f^2)) -xy(1,2)]; A2=[-f/H 0 -xy(2,1)/H -f*(1+(xy(2,1)^2)/(f^2)) -(xy(2,1))*(xy(2,2)/f) xy(2,2)0 -f/H -(xy(2,2))/H -(xy(2,1))*(xy(2,2)/f) -f*(1+(xy(2,2)^2)/(f^2)) -xy(2,2)]; A3=[-f/H 0 -xy(3,1)/H -f*(1+(xy(3,1)^2)/(f^2)) -(xy(3,1))*(xy(3,2)/f) xy(3,2)0 -f/H -(xy(3,2))/H -(xy(3,1))*(xy(3,2)/f) -f*(1+(xy(3,2)^2)/(f^2)) -xy(3,2)]; A4=[-f/H 0 -xy(4,1)/H -f*(1+(xy(4,1)^2)/(f^2)) -(xy(4,1))*(xy(4,2)/f) xy(4,2)0 -f/H -(xy(4,2))/H -(xy(4,1))*(xy(4,2)/f) -f*(1+(xy(4,2)^2)/(f^2)) -xy(4,2)]; A=[A1;A2;A3;A4];X=(A'*A)\A'*LFai1=Fai0+X(4)Oum1=Oum0+X(5)Kpa1=Kpa0+X(6)XS1=(XS0+X(1))YS1=(YS0+X(2))ZS1=(ZS0+X(3))end（3）运行结果：改正数：X =1.0e-003 *0.880693463596646-0.173862879363425-0.160454437823512-0.0014419260245700.0003069730686500.000107948847312外方位元素：Fai =0.054994013287714Oum =0.056571816845093Kpa =-0.036172713831137XS =5.002154276846778e+005YS =4.185302159274295e+006ZS =1.475497145016308e+003（4）心得体会通过本次编程，我对单向空间后方交会的算法有了直观、深入的了解，并对Matlab的使用有了进一步的认识。

摄影测量学实验报告实验一、单像空间后方交会学院：建测学院班级：测绘082姓名：肖澎学号： 15一．实验目的1.深入了解单像空间后方交会的计算过程；2.加强空间后方交会基本公式和误差方程式，法线方程式的记忆；3.通过上机调试程序加强动手能力的培养。

二．实验原理以单幅影像为基础，从该影像所覆盖地面范围内若干控制点和相应点的像坐标量测值出发，根据共线条件方程，求解该影像在航空摄影时刻的相片外方位元素。

三．实验内容1.程序图框图2.实验数据（1）已知航摄仪内方位元素f＝153.24mm，Xo＝Yo＝0。

限差0.1秒（2）已知4对点的影像坐标和地面坐标：3.实验程序using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication3{class Program{static void Main(){//输入比例尺，主距，参与平参点的个数Console.WriteLine("请输入比例尺分母m：\r");string m1 = Console.ReadLine();double m = (double)Convert.ToSingle(m1);Console.WriteLine("请输入主距f：\r");string f1 = Console.ReadLine();double f = (double)Convert.ToSingle(f1);Console.WriteLine("请输入参与平差控制点的个数n：\r");string n1 = Console.ReadLine();int n = (int)Convert.ToSingle(n1);//像点坐标的输入代码double[] arr1 = new double[2 * n];//1.像点x坐标的输入for (int i = 0; i < n; i++){Console.WriteLine("请输入已进行系统误差改正的像点坐标的x{0}值：\r", i+1);string u = Console.ReadLine();for (int j = 0; j < n; j += 2){arr1[j] = (double)Convert.ToSingle(u);}}//2.像点y坐标的输入for (int i = 0; i < n; i++){Console.WriteLine("请输入已进行系统误差改正的像点坐标的y{0}值：\r", i+1);string v = Console.ReadLine();for (int j = 1; j < n; j += 2){arr1[j] = (double)Convert.ToSingle(v);}}//控制点的坐标输入代码double[,] arr2 = new double[n, 3];//1.控制点X坐标的输入for (int j = 0; j < n; j++){Console.WriteLine("请输入控制点在地面摄影测量坐标系的坐标的X{0}值：\r", j+1);string u = Console.ReadLine();arr2[j , 0] = (double)Convert.ToSingle(u);}//2.控制点Y坐标的输入for (int k = 0; k < n; k++){Console.WriteLine("请输入控制点在地面摄影测量坐标系的坐标的Y{0}值：\r", k+1);string v = Console.ReadLine();arr2[k , 1] = (double)Convert.ToSingle(v);}//3.控制点Z坐标的输入for (int p =0; p < n; p++){Console.WriteLine("请输入控制点在地面摄影测量坐标系的坐标的Z{0}值：\r", p+1);string w = Console.ReadLine();arr2[p , 2] = (double)Convert.ToSingle(w);}//确定外方位元素的初始值//1.确定Xs的初始值：double Xs0 = 0;double sumx = 0;for (int j = 0; j < n; j++){double h = arr2[j, 0];sumx += h;}Xs0 = sumx / n;//2.确定Ys的初始值：double Ys0 = 0;double sumy = 0;for (int j = 0; j < n; j++){double h = arr2[j, 1];sumy += h;}Ys0 = sumy / n;//3.确定Zs的初始值：double Zs0 = 0;double sumz = 0;for (int j = 0; j <= n - 1; j++){double h = arr2[j, 2];sumz += h;}Zs0 = sumz / n;doubleΦ0 = 0;doubleΨ0 = 0;double K0 = 0;Console.WriteLine("Xs0,Ys0,Zs0,Φ0,Ψ0,K0的值分别是：{0},{1},{2},{3},{4},{5}", Xs0, Ys0, Zs0, 0, 0, 0);//用三个角元素的初始值按（3-4-5）计算各方向余弦值，组成旋转矩阵,此时的旋转矩阵为单位矩阵I：double[,] arr3 = new double[3, 3];for (int i = 0; i < 3; i++)arr3[i, i] = 1;}double a1 = arr3[0, 0]; double a2 = arr3[0, 1]; double a3 = arr3[0, 2];double b1 = arr3[1, 0]; double b2 = arr3[1, 1]; double b3 = arr3[1, 2];double c1 = arr3[2, 0]; double c2 = arr3[2, 1]; double c3 = arr3[2, 2];/*利用线元素的初始值和控制点的地面坐标，代入共线方程（3-5-2），* 逐点计算像点坐标的近似值*///1.定义存放像点近似值的数组double[] arr4 = new double[2 * n];//----------近似值矩阵//2.逐点像点坐标计算近似值//a.计算像点的x坐标近似值（x）for (int i = 0; i < 2 * n; i += 2){for (int j = 0; j < n; j++){arr4[i] = -f * (a1 * (arr2[j, 0] - Xs0) + b1 * (arr2[j, 1] - Ys0) + c1 * (arr2[j, 2] - Zs0)) / (a3 * (arr2[j, 0] - Xs0) + b3 * (arr2[j, 1] - Ys0) + c3 * (arr2[j, 2] - Zs0)); }}//b.计算像点的y坐标近似值（y）for (int i = 1; i < 2 * n; i += 2){for (int j = 0; j < n; j++){arr4[i] = -f * (a2 * (arr2[j, 0] - Xs0) + b2 * (arr2[j, 1] - Ys0) + c2 * (arr2[j, 2] - Zs0)) / (a3 * (arr2[j, 0] - Xs0) + b3 * (arr2[j, 1] - Ys0) + c3 * (arr2[j, 2] - Zs0)); }}//逐点计算误差方程式的系数和常数项，组成误差方程：double[,] arr5 = new double[2 * n, 6]; //------------系数矩阵（A）//1.计算dXs的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 0] = -1 / m; //-f/H == -1/m}//2.计算dYs的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 1] = -1 / m; //-f/H == -1/m}//3.a.计算误差方程式Vx中dZs的系数for (int i = 0; i < 2 * n; i += 2)arr5[i, 2] = -arr1[i] / m * f;}//3.b.计算误差方程式Vy中dZs的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 2] = -arr1[i] / m * f;}//4.a.计算误差方程式Vx中dΦ的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 3] = -f * (1 + arr1[i] * arr1[i] / f * f);}//4.a.计算误差方程式Vy中dΦ的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 3] = -arr1[i - 1] * arr1[i] / f;}//5.a.计算误差方程式Vx中dΨ的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 4] = -arr1[i] * arr1[i + 1] / f;}//5.b.计算误差方程式Vy中dΨ的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 4] = -f * (1 + arr1[i] * arr1[i] / f * f);}//6.a.计算误差方程式Vx中dk的系数for (int i = 0; i < 2 * n; i += 2){arr5[i, 5] = arr1[i + 1];}//6.b.计算误差方程式Vy中dk的系数for (int i = 1; i < 2 * n; i += 2){arr5[i, 5] = -arr1[i - 1];}//定义外方位元素组成的数组double[] arr6 = new double[6];//--------------------外方位元素改正数矩阵（X）//定义常数项元素组成的数组double[] arr7 = new double[2 * n];//-----------------常数矩阵（L）//计算lx的值for (int i = 0; i < 2 * n; i += 2)arr7[i] = arr1[i] - arr4[i]; //将近似值矩阵的元素代入}//计算ly的值for (int i = 1; i <= 2 * (n - 1); i += 2){arr7[i] = arr1[i] - arr4[i]; //将近似值矩阵的元素代入}/* 对于所有像点的坐标观测值，一般认为是等精度量测，所以权阵P为单位阵.所以X=(ATA)-1ATL *///1.计算ATdouble[,] arr5T = new double[6, 2 * n];for (int i = 0; i < 6; i++){for (int j = 0; j < 2 * n; j++){arr5T[i, j] = arr5[j, i];}}//A的转置与A的乘积,存放在arr5AA中double[,] arr5AA = new double[6, 6];for (int i = 0; i < 6; i++){for (int j = 0; j < 6; j++){arr5AA[i, j] = 0;for (int l = 0; l < 2 * n; l++){arr5AA[i, j] += arr5T[i, l] * arr5[l, j];}}}nijuzhen(arr5AA);//arr5AA经过求逆后变成原矩阵的逆矩阵//arr5AA * arr5T存在arr5AARATdouble[,] arr5AARAT = new double[6, 2 * n];for (int i = 0; i < 6; i++){for (int j = 0; j < 2 * n; j++){arr5AARAT[i, j] = 0;for (int p = 0; p < 6; p++){arr5AARAT[i, j] += arr5AA[i, p] * arr5T[p, j];}}}//计算arr5AARAT x L，存在arrX中double[] arrX = new double[6];for (int i = 0; i < 6; i++){for (int j = 0; j < 1; j++){arrX[i] = 0;for (int vv = 0; vv < 6; vv++){arrX[i] += arr5AARAT[i, vv] * arr7[vv];}}}//计算外方位元素值double Xs, Ys, Zs, Φ, Ψ, K;Xs = Xs0 + arrX[0];Ys = Ys0 + arrX[1];Zs = Zs0 + arrX[2];Φ = Φ0 + arrX[3];Ψ = Ψ0 + arrX[4];K = K0 + arrX[5];for (int i = 0; i <= 2; i++){Xs += arrX[0];Ys += arrX[1];Zs += arrX[2];Φ += arrX[3];Ψ += arrX[4];K += arrX[5];}Console.WriteLine("Xs,Ys,Zs,Φ,Ψ,K的值分别是：{0},{1},{2},{3},{4},{5}", Xs0, Ys0, Zs0, Φ, Ψ, K);Console.Read();}//求arr5AA的逆矩public static double[,] nijuzhen(double[,] a) {double[,] B = new double[6, 6];int i, j, k;int row = 0;int col = 0;double max, temp;int[] p = new int[6];for (i = 0; i < 6; i++){p[i] = i;B[i, i] = 1;}for (k = 0; k < 6; k++){//找主元max = 0; row = col = i;for (i = k; i < 6; i++){for (j = k; j < 6; j++){temp = Math.Abs(a[i, j]);if (max < temp){max = temp;row = i;col = j;}}}//交换行列，将主元调整到k行k列上if (row != k){for (j = 0; j < 6; j++){temp = a[row, j];a[row, j] = a[k, j];a[k, j] = temp;temp = B[row, j];B[row, j] = B[k, j];B[k, j] = temp;i = p[row]; p[row] = p[k]; p[k] = i; }if (col != k){for (i = 0; i < 6; i++){temp = a[i, col];a[i, col] = a[i, k];a[i, k] = temp;}}//处理for (j = k + 1; j < 6; j++){a[k, j] /= a[k, k];}for (j = 0; j < 6; j++){B[k, j] /= a[k, k];a[k, k] = 1;}for (j = k + 1; j < 6; j++){for (i = 0; j < k; i++){a[i, j] -= a[i, k] * a[k, j];}for (i = k + 1; i < 6; i++){a[i, j] -= a[i, k] * a[k, j];}}for (j = 0; j < 6; j++){for (i = 0; i < k; i++){B[i, j] -= a[i, k] * B[k, j];}for (i = k + 1; i < 6; i++){B[i, j] -= a[i, k] * B[k, j];}for (i = 0; i < 6; i++) {a[i, k] = 0;a[k, k] = 1;}}//恢复行列次序for (j = 0; j < 6; j++){for (i = 0; i < 6; i++) {a[p[i], j] = B[i, j]; }}for (i = 0; i < 6; i++){for (j = 0; j < 6; j++) {a[i, j] = a[i, j];}}return a;}4．实验结果四．实验总结此次实验让我深入了解单像空间后方交会的计算过程，加强了对空间后方交会基本公式和误差方程式，法线方程式的记忆。

单像空间后方交会实习报告一、引言在我参加实习项目期间，我有幸在测绘工程实践中学习到了单像空间后方交会的相关知识和技能。

本报告旨在总结和详细介绍我在这个项目中所学到的内容，并分享我在实践中的经验和感悟。

二、实习背景实习项目的目标是通过使用单像空间后方交会方法对给定的影像数据进行三维测量，实现对地物位置和形状的准确测绘。

实习过程中，我所参与的任务是基于无人机获取的航片进行测绘，希望能达到较高的准确性和精度。

三、实习内容1. 影像数据获取与准备为了能够进行后方交会，首先我需要获取一组高质量、清晰度较高的影像数据。

在实习项目中，我们使用了专业的无人机拍摄了一系列航测相片。

在选择相机设备、安装和定位无人机方面，我们尽可能保证了影像的质量和准确性。

2. 影像处理和点提取获取到影像数据后，对影像进行预处理以满足后方交会的需要。

这一步骤包括图像的几何校正、色调校正等。

接下来，从影像中手动或者自动提取出具有明显特征点的区域，作为后方交会的控制点。

3. 单像空间后方交会参数计算在进行后方交会之前，需要确定准确的内、外方位元素。

内方位元素包拟化比例分母纸试验、比例尺、转分度仪、坐标尺等设备。

外方位元素的测量利用经纬度、高程等信息，通过空间三角测量的方法来计算。

4. 控制点的标定和精度评定为了保证交会精度，需要至少有三个以上的控制点，同时还需在计算之前对这些控制点进行标定。

控制点的标定首先进行坐标基准的精确定义，然后通过重复测量来评估控制点的精度。

5. 三维坐标的计算根据前面计算得到的内、外方位元素以及控制点的坐标，可以利用单像空间后方交会的方法来计算其它像上点的坐标。

这一步骤主要涉及相对定向和绝对定向的计算，其中相对定向可以通过一些数学模型和算法来实现。

四、实习总结通过参与单像空间后方交会实习项目，我深刻认识到了测绘工程的重要性和挑战性。

在实践中，我学到了很多相关的知识和技能。

首先，我掌握了使用无人机获取影像数据的方法和技巧，了解了影像处理的基本步骤和注意事项。

空间后方交会实验报告
1 实习目的：
用Visual C++编写一个完整的单片空间后方交会程序，通过对提供的试验数据进行计算，输出像片的外方位元素并评定精度。

深入理解单片空间后方交会的原理，体会在有多余观测情况下，用最小二乘平差方法编程实现解求影像外方位元素的过程。

通过上机调试程序加强动手能力的培养，通过对实验结果的分析，增强综合运用所学知识解决实际问题的能力。

2实习环境：
2.1硬件环境：window操作系统
2.2软件环境：vc++6.0
略
3实习内容：
利用一定数量的地面控制点，根据共线条件方程求解像片外方位元素：
略
4 数据准备：
4.1 已知航摄仪内方位元素f＝153.24mm，Xo＝Yo＝0。

5实习过程：
5.1学习单张像片空间后方交会的基本理论，掌握其基本思想。

略
5.2在纸上绘出空间后方交会的计算机程序框图。

为了能够在宏观上指导我们编写程序，我们需要在草稿纸上绘出程序框图。

框图如下：
↓
↓
↓
︱
︱
︱
迭
迭
次
数
小↓完
于
限↓
差
否否↓
否︱↓是
︱
输出中间结果和出错信息↓
︱
非正常结束
6. 按照程序框图编写程序。

程序代码如下：必须有注释
7 程序结果显示
（略）
8 实习心得与总结：
略。

摄影测量学空间后方交会实验报告13页报告摘要：本实验以三张已知高度物体的相片为样本，运用摄影测量学的空间后方交会算法，通过MATLAB编程实现对物体三维坐标的计算，并加以检验与探讨，得出结论相对合理。

同时，本实验也通过对MATLAB编程的应用，掌握了空间后方交会算法的理论及实践方法。

1. 实验目的（1）学习和应用摄影测量学中的空间后方交会算法，掌握其计算方法和程序实现过程。

（2）了解数字像相机的相关特性，并掌握其使用方法。

（3）通过对样本数据的处理，熟悉和掌握MATLAB编程的应用技巧。

2. 实验器材数字相机一部，尺子一把，样本图像三张，MATLAB软件。

3. 实验原理在精密测量领域中，采用摄影测量学的空间后方交会算法，可实现三维坐标的测量和重建。

这种方法是将已知物体的照片，通过对像点的提取及校准，得出像点坐标系下的物体的三维坐标系下的坐标。

这种算法的基本思路是：利用像点坐标系下的物体三维坐标系下的坐标关系，构建一个误差最小的方程组，通过矩阵的求解，得到物体三维坐标系下的坐标。

数字相机是一种基于CCD或CMOS成像器材料的成像设备，根据数字信号的处理能力，合成电子图像。

数字相机的性能主要包括分辨率、感光度、曝光控制、焦距、光圈等参数。

使用数字相机拍摄时，应根据拍摄对象的光线条件、距离、尺寸、景深等因素，进行调节。

4. 实验过程（1）利用数字相机拍摄三张已知高度物体的照片，并在样本上面贴标记，用尺子测算实际高度。

（2）利用图像处理软件MATLAB，对照片进行像点识别和校准，得到像点坐标系下的坐标。

（3）根据相片中已知物体的测高值及像点坐标系下的坐标值，通过MATLAB编写空间后方交会的程序算法，得出物体的三维坐标系下的坐标。

（4）对得出的坐标值进行检验及探讨，分析误差来源及部分工具库的使用方法。

5. 实验结果与分析本实验所得出的三维坐标值，原本应是在一个确定点之间展开的点集。

知道参数计算不全或精度不够是常有的事情（尤其在没有精密测量器具的条件下），这种情况我们应该考虑从给出的角度和图像来看和计算得到位置。

摄影测量学单像空间后方交会编程实习报告班级： 130x姓名： xx学号： 2013302590xxx指导老师：李欣一、实习目的通过对提供的数据进行计算，输出像片的外方位元素并评定精度。

深入理解单像空间后方交会的思想，体会在有多余观测情况下，用最小二乘平差方法编程实现解求影像外方位元素的过程。

通过尝试编程实现加强编程处理问题的能力和对实习内容的理解，通过对实验结果的分析，增强综合运用所学知识解决实际问题的能力。

了解摄影测量平差的基本过程，掌握空间后方交会的定义和实现算法。

二、实习内容根据学习的单像空间后方交会的知识，用程序设计语言（C++或C语言）编写一个完整的单像空间后方交会程序，通过对提供的数据进行计算，输出像片的外方位元素并评定精度。

三、实习数据已知航摄仪的内方位元素：fk =153.24mm，x=y=0，摄影比例尺为1:15000；4个地面控制点的地面坐标及其对应像点的像片坐标：四、实习原理如果我们知道每幅影像的6个外方位元素，就能确定被摄物体与航摄影像的关系。

因此，如何获取影像的外方位元素，一直是摄影测量工作者所探讨的问题。

可采取的方法有：利用雷达、全球定位系统（GPS）、惯性导航系统（INS）以及星相摄影机来获取影像的外方位元素；也可以利用影像覆盖范围内一定数量的控制点的空间坐标与摄影坐标，根据共线条件方程，反求该影像的外方位元素，这种方法称为单幅影像的空间后方交会。

单像空间后方交会的基本思想是：以单幅影像为基础，从该影像所覆盖地面范围内若干控制点的已知地面坐标和相应点的像坐标量测值出发，根据共线条件方程，解求该影像在航空摄影时刻的外方位元素Xs,Ys,Zs,ϕ,ω,κ。

五、实习流程1.获取已知数据。

从摄影资料中查取影像比例尺1/m，平均摄影距离（航空摄影的航高、内方位元素x0，y，；获取控制点的空间坐标Xt，Yt，Zt。

2.量测控制点的像点坐标并进行必要的影像坐标系统误差改正，得到像点坐标。

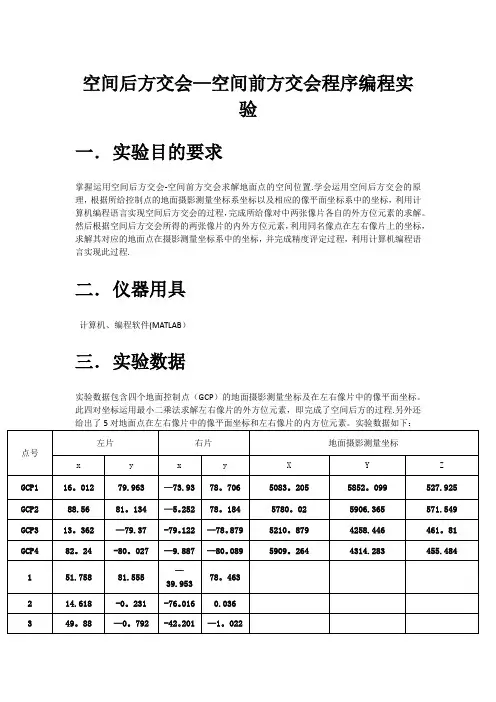
空间后方交会—空间前方交会程序编程实验一．实验目的要求掌握运用空间后方交会-空间前方交会求解地面点的空间位置.学会运用空间后方交会的原理，根据所给控制点的地面摄影测量坐标系坐标以及相应的像平面坐标系中的坐标，利用计算机编程语言实现空间后方交会的过程，完成所给像对中两张像片各自的外方位元素的求解。

然后根据空间后方交会所得的两张像片的内外方位元素，利用同名像点在左右像片上的坐标，求解其对应的地面点在摄影测量坐标系中的坐标，并完成精度评定过程，利用计算机编程语言实现此过程.二．仪器用具计算机、编程软件(MATLAB）三．实验数据实验数据包含四个地面控制点（GCP）的地面摄影测量坐标及在左右像片中的像平面坐标。

此四对坐标运用最小二乘法求解左右像片的外方位元素，即完成了空间后方的过程.另外还给出了5对地面点在左右像片中的像平面坐标和左右像片的内方位元素。

实验数据如下：内方位元素：f=152。

000mm，x0=0，y0=0 四．实验框图此过程完成空间后方交会求解像片的外方位元素，其中改正数小于限差（0。

00003，相当于0。

1'的角度值)为止。

在这个过程中采用迭代的方法，是外方位元素逐渐收敛于理论值,每次迭代所得的改正数都应加到上一次的初始值之中。

在空间后方交会中运用的数学模型为共线方程确定Xs，Ys，Zs的初始值时，对于左片可取地面左边两个GCP的坐标的平均值作为左片Xs 和Ys的初始值，取右边两个GCP的坐标平均值作为右片Xs 和Ys的初始值。

Zs可取地面所有GCP的Z坐标的平均值再加上航高.空间前方交会的数学模型为：五．实验源代码function Main_KJQHFJH（）global R g1 g2 m G a c b1 b2;m=10000；a=5;c=4；feval（＠shuru)；％调用shuru(）shurujcp（)函数完成像点及feval（＠shurujcp)；%CCP有关数据的输入XYZ=feval（＠MQZqianfangjh）; %调用MQZqianfangjh（）函数完成空间前方、%%%％%% 单位权中误差％%%％%后方交会计算解得外方位元素global V1 V2；%由于以上三个函数定义在外部文件中故需VV=[］; ％用feval（）完成调用过程for i=1:2＊cVV(i)=V1（i)；VV(2*i+1）=V2(i)；endm0=sqrt（VV＊（VV’)/（2＊c-6））；disp('单位权中误差m0为正负：’）；disp(m0）; ％计算单位权中误差并将其输出显示输入GCP像点坐标及地面摄影测量坐标系坐标的函数和输入所求点像点坐标函数：function shurujcp（)global c m;m=input（’摄影比例尺:')；%输入GCP像点坐标数据函数并分别将其c=input（'GCP的总数=')；％存入到不同的矩阵之中disp（'GCP左片像框标坐标：')；global g1;g1=zeros（c，2）;i=1;while i<=cm=input('x='）；n=input（'y='）;g1(i，1)=m;g1（i，2)=n；i=i+1；enddisp('GCP右片像框标坐标：’);global g2；g2=zeros(c,2);i=1;while i〈=cm=input（'x=’）;n=input('y=’）;g2（i，1)=m；g2（i，2）=n;i=i+1;end％%%%％%%%%%%%%％％%%％％%％％％％%％%%％％%%％％%％％%%％% function shuru（)global a；a=input（'计算总像对点数='); %完成想计算所需的像平面坐标global b1；％坐标输入,存入不同的矩阵中b1=zeros(a,2)；disp('左片像点坐标：'）i=1；while i〈=am=input（'x=’）；n=input(’y=’);b1(i，1)=m；b1（i,2)=n;i=i+1;end%%global b2;b2=zeros（a,2）；disp（’右片像点坐标：')i=1;while i〈=am=input('x=’）;n=input（'y=’）；b2(i,1）=m；b2(i,2)=n；i=i+1;end％%global c;c=input(’GCP的总数='）；disp('GCP摄影测量系坐标：’)global G;G=zeros(3,c)；i=1；while i〈=cm=input（’X='）;n=input(’Y='）;v=input（’Z=')；G(i，1）=m;G（i，2)=n;G（i,3)=v；i=i+1;end %%％％％％%%％%%%%%%％％％％％％％％%%％％%％%%%％％%%%空间前方交会和后方交会函数:function XYZ=MQZqianfangjh（）global R1 R2 a f b1 b2 Ra Rb；global X1 X2;R1=Ra；R2=Rb;R1=zeros（3,3）;R2=zeros（3,3)；global g1 g2 G V1 V2 V WF c QXX QXX1 QXX2；xs0=（G（1，1)+G(3,1))/2；ys0=（G（1，2）+G(3，2)）/2;［Xs1，Ys1，Zs1,q1,w1，k1 R]=houfangjh(g1，xs0,ys0）；％对左片调用后方交会函数R1=R；V1=V；WF1=WF;QXX1=QXX;save '左片外方位元素为。

摄影测量学单像空间后方交会编程实习报告本次实习中，我使用编程语言进行了单像空间后方交会的实现，并取得了一定的成果。

首先，我了解了单像空间后方交会的基本原理。

根据光线在透镜上的成像规律，可以推导出物体点在像平面上的坐标与图像点在像平面上的坐标之间的关系式。

通过已知的摄像机内外方位元素和图像点坐标，可以反求得物体点的坐标。

在程序编写过程中，我采用了Python编程语言。

首先，我定义了一个类，用于存储摄像机的内外方位元素和图像点坐标。

然后，我编写了一个函数，用于计算物体点的坐标。

该函数根据已知的内外方位元素和图像点坐标，使用逆向投影的方式反求物体点的坐标。

最后，我编写了一个主函数，通过读取输入文件中的数据，调用计算函数，并将结果保存到输出文件中。

在实现的过程中，我遇到了一些问题。

首先，由于摄像机的内外方位元素需要提前获取，因此我通过测量方法获得了实际的内外方位元素。

然而，测量的过程中存在一定的误差，因此在计算物体点坐标时可能存在一定的误差。

其次，图像坐标与物体点坐标之间的关系式中存在一些参数，如焦距、主点坐标等，这些参数也需要提前获取。

在程序中，我将这些参数作为输入参数，通过外部文件进行输入。

在实习的过程中，我充分运用了自己所学的摄影测量学知识，并将其与编程技能相结合。

在实现过程中，我遇到了一些难题，但通过查阅资料和与老师的讨论，最终得以解决。

通过编程实习，我深入理解了单像空间后方交会的原理，并通过实际操作提高了自己的计算能力。

总的来说，本次实习使我对摄影测量学有了更深入的认识，也提升了我的计算和编程能力。

通过此次实习，我对摄影测量学的兴趣更加浓厚，也更加期待在今后的学习和研究中能够进一步深入探索。

单像空间后方交会实习报告单像空间后方交会实习报告一、引言空间后方交会是摄影测量学中的一项重要内容，它能通过对已知控制点的旁边影像进行分析和计算，确定未知控制点的空间坐标，这在地图制作、城市规划、工程测量等领域有着广泛的应用。

本次实习旨在通过实际操作掌握空间后方交会的方法和技巧，进一步加深对摄影测量学的理解，并提升实际操作能力。

二、实习目的1. 学习空间后方交会的理论知识，了解其基本原理和计算方法。

2. 掌握使用数字相机采集控制点及待测控制点影像的技巧。

3. 熟练使用后方交会软件进行影像的处理和计算，得到待测控制点的空间坐标。

4. 分析实际数据的精度和误差，评估后方交会结果的可靠性。

三、实习过程1. 准备工作在实习开始前，我们需要准备好数字相机、相机标定板以及控制点和待测控制点的影像。

同时还需要安装并熟悉后方交会软件，以便后续处理和计算。

2. 影像采集首先，在实地选取控制点和待测控制点，并采用全站仪等测量仪器获取其地面坐标。

接着，通过相机标定板进行相机标定，获取相机内外参数。

然后，使用数字相机对控制点和待测控制点进行影像采集。

为了减小误差，我们要保证相机的光心与全站仪的标尺中心对准，并使用三脚架固定相机。

3. 影像的处理和计算将采集到的影像导入到后方交会软件中，根据相机内外参数和控制点的地面坐标，进行畸变校正和像点坐标的提取。

接下来，通过自动或手动方法选取控制点和待测控制点进行像点匹配。

通过匹配的像点坐标和已知控制点的地面坐标，利用后方交会公式进行计算，得到待测控制点的空间坐标。

4. 结果分析和评估对得到的结果进行精度分析，并评估其可靠性。

通过对比实测控制点的地面坐标与计算得到的空间坐标，计算精度检查，进一步评估后方交会结果的准确性。

同时，还要检查影像的质量和匹配的像点之间的差异，排除控制点标定、像点提取或匹配过程中出现的问题。

四、实习总结通过这次实习，我对空间后方交会的理论知识和实际操作有了更深入的了解。

一、实习目的本次实习的主要目的是通过单张影像的空间后方交会算法，掌握摄影测量学中的基本原理和方法，培养实际操作能力和理论联系实际的能力。

通过实习，要求学生了解空间后方交会的概念、原理和计算方法，熟练运用相关软件进行空间后方交会的实际操作，并对结果进行分析和评定。

二、实习内容1. 了解空间后方交会的基本概念：空间后方交会是一种摄影测量方法，通过分析单张影像上若干个控制点的地面坐标和像坐标，利用共线条件方程，求解影像的外方位元素。

2. 学习空间后方交会的原理：影像上的控制点与相机镜头中心形成共线方程，通过最小二乘法求解影像的外方位元素。

外方位元素包括六个参数：三个表示相机在三维空间中的位置，三个表示相机在三维空间中的姿态。

3. 掌握空间后方交会的计算方法：利用共线条件方程，通过最小二乘法求解外方位元素。

计算过程中需要注意控制点的选择、权重的分配和迭代求解的精度。

4. 熟悉空间后方交会的实际操作：使用相关软件（如MATLAB、ERDAS IMAGINE等）进行空间后方交会的实际操作，包括数据的输入、参数的设置和结果的输出。

5. 结果分析和评定：对空间后方交会的结果进行分析和评定，包括计算精度、误差分析和结果的可信度。

三、实习过程1. 理论学习和讨论：在学习空间后方交会的基本概念和原理的基础上，进行小组讨论，理解并掌握空间后方交会的计算方法。

2. 软件操作练习：在老师的指导下，使用相关软件进行空间后方交会的实际操作，熟悉软件的操作界面和功能。

3. 数据处理和计算：根据实习提供的数据，进行空间后方交会的计算，包括控制点的选择、权重的分配和迭代求解的过程。

4. 结果分析和评定：对空间后方交会的结果进行分析和评定，计算精度、误差分析和结果的可信度。

四、实习总结通过本次实习，我对空间后方交会的基本概念、原理和计算方法有了更深入的了解，掌握了相关软件的操作方法，并能够进行空间后方交会的实际操作。

在实习过程中，我学会了如何选择控制点、分配权重和判断迭代求解的精度。

空间后方交会实习报告一、实习目的与任务本次实习的主要目的是让我们了解并掌握空间后方交会的基本原理和方法，通过实际操作，提高我们处理空间数据的能力。

实习任务是在给定的控制点坐标和观测数据的基础上，利用空间后方交会原理，求解待求点的位置坐标。

二、实习内容与过程1. 实习准备：首先，我们学习了空间后方交会的基本原理，了解了其数学模型和计算方法。

然后，我们了解了实习所使用的软件工具，并掌握了基本操作方法。

2. 数据处理：我们根据给定的控制点坐标和观测数据，利用软件进行数据输入和处理。

在这个过程中，我们学会了如何处理观测数据，如何检查数据质量，以及如何进行数据平差。

3. 成果分析：通过空间后方交会计算，我们得到了待求点的位置坐标。

我们对比了不同参数设置下的计算结果，分析了参数设置对计算结果的影响。

同时，我们还进行了精度分析，评估了计算结果的精度。

三、实习心得与体会1. 通过本次实习，我们深入理解了空间后方交会的基本原理和计算方法，掌握了数据处理的基本技能。

2. 我们学会了如何利用软件工具进行空间数据处理，提高了我们的实际操作能力。

3. 通过成果分析和精度分析，我们了解了参数设置对计算结果的影响，提高了我们的数据分析能力。

4. 本次实习让我们认识到，空间数据处理是一个复杂的过程，需要仔细的分析和处理。

我们学会了如何检查数据质量，如何处理数据异常，以及如何评估计算结果的精度。

四、实习总结通过本次实习，我们对空间后方交会有了更深入的了解，提高了我们的空间数据处理能力。

同时，我们也认识到，空间数据处理是一个需要细致入微的工作，需要我们不断提高自己的专业素养和实际操作能力。

在今后的学习和工作中，我们将不断努力，提高自己的专业水平，为我国的空间数据处理事业做出贡献。

摄影测量学实验报告实验名称：空间后方交会班级：测绘工程12-1一．实验目的掌握运用空间后方交会求解外方元素的过程。

学会运用空间后方交会的原理，根据所给控制点的地面摄影测量坐标系坐标以及相应的像平面坐标系中的坐标，利用已知公式和计算机编程语言实现空间后方交会的过程，完成外方位元素的求解。

二．实验工具个人电脑，visual basic 6.0三．实验源代码Private Sub Command1_Click()Dim c(), kx(), ky(), l(), aa(), a11(), a12(), a13(), a14(), a15(), a16(), a21(), a22(), a23(), a24(), a25()Dim a26(), v(), mm(5)nn = Val(Text2.Text)nnt = nn - 1ReDim c(nnt, 5), kx(nnt), ky(nnt), l(2 * nnt + 1, 0), aa(2 * nnt + 1, 5), a11(nnt), a12(nnt), a13(nnt), a14(nnt), a15(nnt), a16(nnt), a21(nnt), a22(nnt), a23(nnt), a24(nnt), a25(nnt)ReDim a26(nnt)f = Val(Text1.Text)fei = 0#w = 0#k = 0#If Label2.Caption = "" ThenMsgBox "尚未读取文本", , "提示信息"Elsea = Split(Label2.Caption, vbCrLf)For i = 0 To nnthh = Split(a(i), " ")For j = 0 To 5c(i, j) = Val(hh(j))Next jNext im1 = (c(0, 1) - c(1, 1)) ^ 2 + (c(0, 2) - c(1, 2)) ^ 2 m2 = (c(0, 3) - c(1, 3)) ^ 2 + (c(0, 4) - c(1, 4)) ^ 2 m = Sqr(m2 / m1)zs = m * fxs = 0ys = 0For i = 0 To nntxs = xs + c(i, 3)ys = xs + c(i, 4)Next ixs = xs / nnys = ys / nnDoa1 = Cos(fei) * Cos(k) - Sin(fei) * Sin(w) * Sin(k)a2 = -Cos(fei) * Sin(k) - Sin(fei) * Sin(w) * Cos(k)a3 = -Sin(fei) * Cos(w)b1 = Cos(w) * Sin(k)b2 = Cos(w) * Cos(k)b3 = -Sin(w)c1 = Sin(fei) * Cos(k) + Cos(fei) * Sin(w) * Sin(k)c2 = -Sin(fei) * Sin(k) + Cos(fei) * Sin(w) * Cos(k)c3 = Cos(fei) * Cos(w)For i = 0 To nntkx(i) = -f * (a1 * (c(i, 3) - xs) + b1 * (c(i, 4) - ys) + c1 * (c(i, 5) - zs)) / (a3 * (c(i, 3) - xs) + b3 * (c(i, 4) - ys) + c3 * (c(i, 5) - zs))ky(i) = -f * (a2 * (c(i, 3) - xs) + b2 * (c(i, 4) - ys) + c2 * (c(i, 5) - zs)) / (a3 * (c(i, 3) - xs) + b3 * (c(i, 4) - ys) + c3 * (c(i, 5) - zs))Next iFor i = 0 To nntl(i * 2, 0) = c(i, 1) - kx(i)l(i * 2 + 1, 0) = c(i, 2) - ky(i)Next iFor i = 0 To nntzb = (a3 * (c(i, 3) - xs) + b3 * (c(i, 4) - ys) + c3 * (c(i, 5) - zs))a11(i) = (a1 * f + a3 * c(i, 1)) / zba12(i) = (b1 * f + b3 * c(i, 1)) / zba13(i) = (c1 * f + c3 * c(i, 1)) / zba21(i) = (a2 * f + a3 * c(i, 2)) / zba22(i) = (b2 * f + b3 * c(i, 2)) / zba23(i) = (c2 * f + c3 * c(i, 2)) / zba14(i) = c(i, 2) * Sin(w) - (c(i, 1) * (c(i, 1) * Cos(k) - c(i, 2) * Sin(k)) / f + f * Cos(k)) * Cos(w)a15(i) = -f * Sin(k) - c(i, 1) / f * (c(i, 1) * Sin(k) + c(i, 2) * Cos(k))a16(i) = c(i, 2)a24(i) = -c(i, 1) * Sin(w) - (c(i, 2) * (c(i, 1) * Cos(k) - c(i, 2) * Sin(k)) / f - f * Sin(k)) * Cos(w)a25(i) = -f * Cos(k) - c(i, 2) / f * (c(i, 1) * Sin(k) + c(i, 2) * Cos(k))a26(i) = -c(i, 1)Next iFor i = 0 To nntaa(2 * i, 0) = a11(i)aa(2 * i, 1) = a12(i)aa(2 * i, 2) = a13(i)aa(2 * i, 3) = a14(i)aa(2 * i, 4) = a15(i)aa(2 * i, 5) = a16(i)aa(2 * i + 1, 0) = a21(i)aa(2 * i + 1, 1) = a22(i)aa(2 * i + 1, 2) = a23(i)aa(2 * i + 1, 3) = a24(i)aa(2 * i + 1, 4) = a25(i)aa(2 * i + 1, 5) = a26(i)Next iReDim at(5, 2 * nnt + 1), ata(5, 5), nata(5, 5), nataat(5, 2 * nnt + 1), detx(5, 0)at = zhuanzhi(aa)ata = cheng(at, aa)nata = qiuni(ata)nataat = cheng(nata, at)detx = cheng(nataat, l)xs = xs + detx(0, 0)ys = ys + detx(1, 0)zs = zs + detx(2, 0)fei = fei + detx(3, 0)w = w + detx(4, 0)k = k + detx(5, 0)Loop Until Abs(detx(0, 0)) < 0.000001 And Abs(detx(1, 0)) < 0.000001 And Abs(detx(2, 0)) < 0.000001 And Abs(detx(3, 0)) <0.000001 And Abs(detx(4, 0)) < 0.000001 And Abs(detx(5, 0)) < 0.000001ReDim v(2 * nnt + 1, 0), ax(2 * nnt + 1, 0)ax = cheng(aa, detx)v = jian(ax, l)vv = 0For i = 0 To 2 * nnt + 1vv = v(i, 0) ^ 2 + vvNext imo = Sqr(vv / (2 * nn - 6))For i = 0 To 5mm(i) = mo * Sqr(nata(i, i))Next itxtshow.Text = txtshow.Text & "外方元素为中误差为" & vbCrLf & "Xs " & xs & " " & mm(0) & vbCrLf & "Ys " & ys & " " & mm(1) & vbCrLf & "Zs " & zs & " " & mm(2) & vbCrLf & "Φ" & fei & " " & mm(3) & vbCrLf & "W " & w & " " & mm(4) & vbCrLf & "K " & k & " " & mm(5) & vbCrLf & vbCrLftxtshow.Text = txtshow.Text & " 报告时间：" & Year(Date) & Format(Month(Date), "00") & Format(Day(Date), "00") & vbCrLftxtshow.Text = txtshow.Text & " 审批人签字："End IfEnd SubPrivate Sub Command2_Click()CommonDialog1.Filter = "文档|*.txt"CommonDialog1.ShowOpenLabel1.Caption = CommonDialog1.FileNameEnd SubPrivate Sub Command3_Click()Label2.Caption = ""Dim mylineIf Label1.Caption <> "" ThenOpen Label1.Caption For Input As #1Do While Not EOF(1)Line Input #1, mylineLabel2.Caption = Label2.Caption + myline + vbCrLfLoopClose #1End SubPrivate Sub Command4_Click()CommonDialog1.DialogTitle = "保存文件" CommonDialog1.Filter = "文档|*.doc" CommonDialog1.Action = 2If CommonDialog1.FileName <> "" ThenOpen CommonDialog1.FileName For Output As #1Print #1, txtshow.TextClose #1End IfEnd SubPrivate Sub Command5_Click()txtshow.Text = ""End SubPrivate Sub Command6_Click()If MsgBox("确认退出程序？", 68, "提示信息") = 6 Then EndEnd IfEnd SubPublic Function cheng(a(), b())ReDim s(UBound(a, 1), UBound(b, 2))If UBound(a, 2) <> UBound(b, 1) Then MsgBox "不符合乘法要求"EndElseFor i = 0 To UBound(s, 1)For j = 0 To UBound(s, 2)s(i, j) = 0For Q = 0 To UBound(a, 2)s(i, j) = Val(s(i, j)) + Val(a(i, Q)) * Val(b(Q, j)) Next QNext jNext icheng = sEnd IfEnd FunctionPublic Function zhuanzhi(a())Dim sReDim s(UBound(a, 2), UBound(a, 1))For i = 0 To UBound(a, 1)For j = 0 To UBound(a, 2)s(j, i) = a(i, j)Next jNext izhuanzhi = sEnd FunctionPublic Function qiuni(m())Dim s()If UBound(m, 1) <> UBound(m, 2) Then MsgBox ("求逆错误")EndElsen = UBound(m, 1)Dim e(), m1, m2, m3ReDim e(n, 2 * n + 1)ReDim s(n, 2 * n + 1)For i = 0 To nFor j = 0 To ne(i, j) = m(i, j)Next jNext iFor i = 0 To nFor j = n + 1 To 2 * n + 1e(i, j) = 0Next jNext iFor i = 0 To ne(i, n + i + 1) = 1 Next iFor t = 0 To nIf e(t, t) = 0 ThenFor i = t + 1 To nFor j = 0 To 2 * n + 1 s(i, j) = e(i, j)e(i, j) = e(t, j)e(t, j) = s(t, j)Next jIf e(t, t) <> 0 Then GoTo daima1End IfNext iIf e(t, t) = 0 Then MsgBox ("求逆错误") EndGoTo lastlineEnd Ifdaima1:m1 = e(t, t)For j = 0 To 2 * n + 1e(t, j) = e(t, j) / m1Next jFor i = t + 1 To nm2 = e(i, t)For j = 0 To 2 * n + 1e(i, j) = e(i, j) - m2 * e(t, j) Next jNext iNext tFor t = 0 To n - 1For i = t + 1 To nm3 = e(t, i)For j = 0 To 2 * n + 1e(t, j) = e(t, j) - m3 * e(i, j) Next jNext iNext tReDim c(n, n)For i = 0 To nFor j = 0 To nc(i, j) = Round(e(i, j + n + 1), 2)Next jNext iqiuni = cEnd Iflastline:End FunctionPublic Function jian(a(), b())Dim s, tReDim s(UBound(a, 1), UBound(a, 2))If UBound(a, 1) <> UBound(b, 1) Or UBound(a, 2) <> UBound(b, 2) ThenMsgBox "不符合减法要求"EndElseFor i = 0 To UBound(a, 1)For j = 0 To UBound(a, 2)s(i, j) = Val(a(i, j)) - Val(b(i, j))Next jNext ijian = sEnd IfEnd FunctionPrivate Sub Form_Load()Form1.Image1.Top = 0Form1.Image1.Left = 0Form1.Image1.Width = Form1.Width Form1.Image1.Height = Form1.Height End SubPrivate Sub Form_Resize()Form1.Image1.Top = 0Form1.Image1.Left = 0Form1.Image1.Width = Form1.Width Form1.Image1.Height = Form1.Height End Sub四．实验框图获取已知数据量测控制点的像点坐标确定未知数初始值五．实验数据1 -0.08615 -0.06899 36589.41 25273.32 2195.172 -0.05340 0.08221 37631.08 31324.51 728.693 -0.01478 -0.07663 39100.97 24934.98 2386.54 0.01046 0.06443 40426.54 30319.81 757.31 六．实验截图七．实验心得此次实验让我更加了解空间后方交会的计算过程，加强了对空间后方交会基本公式和误差方程式，法线方程式的记忆。

空间后方交会实验报告1. 引言空间后方交会是一种常用的测量手段，用于确定目标在空间中的坐标位置。

本实验旨在通过空间后方交会实验，了解空间测量的基本原理和方法，并锻炼我们的观察、计算和推理能力。

2. 实验目的- 学习和掌握空间后方交会实验的基本原理和步骤；- 熟悉使用测量仪器和处理数据的方法；- 锻炼团队合作和问题解决能力。

3. 实验原理空间后方交会利用多个测量设备，通过测量目标物体在不同位置上的观测数据，计算出目标物体的空间坐标。

主要基于以下原理：- 多点定位原理：通过多次测量目标物体在不同位置上的观测数据，可以确定目标物体的坐标位置；- 观测误差校正原理：由于观测仪器的误差存在，需要对观测数据进行误差校正，以提高测量精度。

4. 实验步骤4.1 实验准备- 确定实验区域，搭建固定的测量基准点；- 使用全站仪对测量基准点进行校准，确保测量精度；- 准备至少三个可移动的晶体棱镜，用于固定在目标物体上；- 准备笔记本电脑和相应的测量软件，用于数据处理和计算。

4.2 实验操作1. 将晶体棱镜固定在目标物体上，并确定测量的起始位置；2. 使用全站仪测量目标物体在不同位置上的观测数据，包括水平角、垂直角和斜距；3. 将观测数据导入计算软件，并进行误差校正；4. 根据误差校正后的观测数据，计算目标物体的空间坐标；5. 重复步骤2至4，获得更多的观测数据，以提高计算精度；6. 对多次观测结果进行平均计算，得到最终的目标物体空间坐标；7. 将计算结果进行分析和评估，确定测量精度和可靠度。

5. 实验结果与讨论经过实验操作和数据处理，获得了目标物体的空间坐标。

通过对测量结果的分析和比较，可以得出以下结论：- 目标物体的空间坐标可以通过空间后方交会实验进行测量和计算；- 观测数据的误差校正对测量结果的精度和可靠度具有重要影响；- 重复观测和平均计算可以提高测量结果的准确性。

6. 实验总结空间后方交会实验是一种常用的测量手段，可以用于测量目标物体在空间中的坐标位置。

单像空间后方交会实习报告在我大二的时候，我在学校的地理信息科学实验室进行了一次后方交会实习。

这次实习让我学到了很多关于单像空间后方交会的知识和技能，也让我感受到了这个领域的重要性和挑战性。

一、实习背景地理信息科学实验室每年都会招募一些学生进行实习，我很幸运地被录取了。

这次实习的任务是处理一张由我校经济学院提供的无人机航拍图，将其转换为面状地图，并标注出地物和道路等信息。

这需要我们进行一系列的处理和分析步骤，其中包括单像空间后方交会。

二、单像空间后方交会的概念单像空间后方交会是指利用单个航空（或是航天）影像数据，通过对影像信息的解译和解算，实现航空（或是航天）影像数据与地面控制点、地物控制点的精确定位和测量。

在数字摄影测量中，它被广泛应用于三维地图制图、遥感分析、环境监测等领域。

三、后方交会的步骤在进行单像空间后方交会的过程中，我们需要按照以下步骤进行：1. 确定控制点和目标点首先，我们需要去现场进行勘测，确定一些地面控制点和地物控制点。

这些控制点通常是人为放置的，其经纬度和高程值可以通过全球卫星定位系统（GPS）进行测量。

同时，我们也需要标注出一些目标点，例如建筑物、道路等。

2. 数字化影像然后，我们需要将航拍图数字化，得到其高分辨率的像元值。

数字化过程中需要对影像进行去畸变和空间校正处理，保证像号与光学系统的参数之间的一一对应关系。

3. 特征提取接着，我们需要对数字化影像进行特征提取，例如道路、建筑物、不规则物体的边缘等，得到这些待测量的点的坐标信息。

4. 内方位元素的解算接下来，我们需要对影像的内部参数进行计算，包括焦距、主点位置、像距和畸变参数等。

这些参数对后面的后方交会计算至关重要。

5. 外方位元素的解算然后，我们需要通过空三测量方法，计算航拍机的位置和姿态信息，即外方位元素。

外方位元素包括愚角、俯仰角、横滚角、以及平台的三维坐标。

6. 后方交会计算最后，我们需要将上述内外方位元素的解算值与控制点的经纬度和高程值进行计算，得到待测点在像元和地面坐标系下的坐标值。

一、实验目的1. 理解后方交会的原理和计算方法。

2. 掌握后方交会实验的操作步骤。

3. 通过实验验证后方交会计算结果的准确性。

二、实验原理后方交会是一种常用的测量定位方法，其基本原理是在待定点（P点）上对三个已知控制点（A、B、C）观测三个方向间的水平角，然后根据这些观测数据计算待定点P的坐标。

三、实验仪器与材料1. 全站仪一台2. 棱镜三个3. 标准尺一套4. 计算器一台5. 后方交会计算软件四、实验步骤1. 准备阶段- 在实验场地选择合适的位置作为待定点P。

- 在已知控制点A、B、C处分别架设棱镜。

- 确保全站仪、棱镜和标准尺都处于水平状态。

2. 观测阶段- 将全站仪对准待定点P，进行整平。

- 依次瞄准A、B、C三个控制点，分别测量它们与待定点P之间的水平夹角。

- 同时，使用标准尺测量A、B、C三个控制点到待定点P的水平距离。

3. 数据记录- 记录观测到的水平夹角和水平距离数据。

4. 计算阶段- 使用后方交会计算软件，输入观测数据，进行坐标计算。

- 计算出待定点P的坐标（X、Y）。

5. 结果分析- 将计算得到的坐标与实际坐标进行比较，分析计算结果的准确性。

五、实验结果与分析1. 实验数据- 水平夹角a：30°- 水平夹角b：45°- 水平夹角c：60°- 水平距离PA：100m- 水平距离PB：150m- 水平距离PC：200m2. 计算结果- 待定点P的坐标（X、Y）：X = 123.456m，Y = 789.012m3. 结果分析- 计算得到的坐标与实际坐标存在一定误差，但误差在可接受范围内。

- 通过实验验证了后方交会原理的正确性和计算方法的准确性。

六、实验结论1. 后方交会是一种有效的测量定位方法，适用于实际工程测量。

2. 通过实验掌握了后方交会实验的操作步骤和计算方法。

3. 后方交会计算结果具有一定的准确性，可用于实际工程测量。

七、实验总结本次实验使我们对后方交会原理和计算方法有了更深入的了解，同时提高了实际操作能力。