多边形裁剪算法

weiler-atherton多边形裁剪算法weileratherton多边形裁剪算法，又称为weiler-atherton算法，是一种用于对多边形进行裁剪的算法。

它可以被用于计算机图形学中的裁剪任务，如可视化、图像处理和计算机辅助设计等领域。

本文将详细介绍weileratherton多边形裁剪算法的原理、步骤和实现方法。

1. 算法原理：weileratherton多边形裁剪算法是基于边界点的引入和处理的。

该算法将两个多边形相互之间进行裁剪，并生成裁剪结果。

算法使用四个边界点集合，分别为输入多边形的边界点集合(输入多边形顶点经过一系列处理得到)，裁剪多边形的外部边界点集合和内部边界点集合，以及裁剪结果的边界点集合。

2. 算法步骤：weileratherton多边形裁剪算法的具体步骤如下：(1) 初始化：创建输入多边形的边界点集合、裁剪多边形的外部边界点集合和内部边界点集合，并将输入多边形的边界点添加至外部边界点集合中。

(2) 遍历输入多边形的每条边：对于输入多边形的每条边，判断其与裁剪多边形的相交情况。

(3) 相交情况处理：若相交情况为内部相交或外部相交，则根据交点生成新的内部边界点，并添加至相应的边界点集合中。

(4) 构造裁剪结果：根据输入多边形的边界点集合和裁剪多边形的内部边界点集合，生成裁剪结果的边界点集合。

(5) 根据边界点集合构造裁剪结果：根据裁剪结果的边界点集合，绘制裁剪结果多边形。

3. 算法实现：weileratherton多边形裁剪算法的实现可以使用编程语言来完成。

一种常用的实现方法是通过遍历输入多边形的每个边，利用线段与裁剪多边形的边界的相交情况判断是否产生交点，并根据交点生成新的边界点。

具体的实现步骤如下：(1) 初始化输入和裁剪多边形的边界点集合。

(2) 遍历输入多边形的每条边，对于每条边，判断其与裁剪多边形的每条边的相交情况。

(3) 根据相交情况，判断是否生成交点，如果有生成交点，则根据交点生成新的边界点，并添加至相应的边界点集合中。

具有拓扑关系的任意多边形裁剪算法拓扑关系是指在空间中，几何对象之间的相对位置和连接关系。

任意多边形裁剪算法是指对于两个多边形A和B，确定A相对于B的位置关系，并将A裁剪成相对于B的部分。

常用的具有拓扑关系的任意多边形裁剪算法有Sutherland-Hodgman算法和Weiler-Atherton算法。

Sutherland-Hodgman算法是一种简单而直观的裁剪算法，它以多边形A为基础，对多边形A的每条边进行裁剪，最终得到所需的裁剪结果。

算法步骤如下：1.对于裁剪窗口的每条边界，确定其相对于多边形A的左侧。

2.对多边形A的每条边进行裁剪处理，生成新的顶点序列。

3.重复步骤2，直到对所有的边界完成处理。

4.返回裁剪结果。

其中，对于多边形A的每条边进行裁剪处理的具体步骤如下：1.对于多边形A的每条边，判断边的起点和终点是否在裁剪窗口内。

2.如果起点和终点都在窗口内，则将边加入新的顶点序列。

3.如果起点在窗口内，而终点在窗口外，则计算边与窗口边界的交点，并将交点加入新的顶点序列。

4.如果起点在窗口外，而终点在窗口内，则计算边与窗口边界的交点，并将交点作为起点加入新的顶点序列。

5.如果起点和终点都在窗口外，则忽略这条边。

Sutherland-Hodgman算法的优点在于简单易懂，对于凸多边形和凹多边形都适用，但由于其每条边都需要进行裁剪处理，效率较低。

Weiler-Atherton算法是一种基于点集的裁剪算法，它将两个多边形视为点的集合，并通过点集之间的拓扑关系进行裁剪操作。

算法步骤如下：1.对于多边形A和多边形B，找到它们的交点。

2.根据交点和各自的顺时针或逆时针顺序，将交点按序列分别加入多边形A和多边形B的顶点序列。

3.对多边形A和多边形B的顶点序列进行裁剪处理，得到裁剪结果。

Weiler-Atherton算法的优点在于避免了对每条边进行裁剪的操作，对于复杂多边形的裁剪效果好，但实现较为复杂。

以上是具有拓扑关系的任意多边形裁剪算法的简要介绍。

weiler-atherton多边形裁剪算法-回复什么是Weiler-Atherton多边形裁剪算法？Weiler-Atherton多边形裁剪算法是一种用于计算两个多边形的相交部分的算法。

该算法可以确定两个多边形之间的交集，并生成裁剪后的多边形。

该算法是由Weiler于1977年提出，并由Atherton稍后改进而得名。

它是一种基于点的算法，通过遍历多边形的顶点和边缘来确定它们之间的交集。

Weiler-Atherton多边形裁剪算法非常适用于计算计算机图形学中的裁剪操作，例如裁剪线段、多边形或曲线。

它可以用于裁剪2D和3D场景中的对象，以提高性能并减少渲染的计算量。

下面将为您详细介绍Weiler-Atherton多边形裁剪算法的具体步骤。

步骤1：确定裁剪区域首先，需要定义一个裁剪区域，它是一个多边形，用于裁剪目标多边形。

裁剪区域可以是任何形状，包括凸多边形和凹多边形。

步骤2：确定多边形边缘与裁剪区域的交点接下来，需要遍历目标多边形的所有边缘，并找出它们与裁剪区域的交点。

对于每个边缘，需要检查它是否与裁剪区域相交，并找出相交点的坐标。

步骤3：确定裁剪区域边缘与多边形的交点然后，需要遍历裁剪区域的所有边缘，并找出它们与目标多边形的交点。

同样地，对于每个边缘，需要检查它是否与目标多边形相交，并找出相交点的坐标。

步骤4：确定裁剪多边形的内、外部点在这一步中，需要根据目标多边形和裁剪区域的交点，确定哪些点位于裁剪多边形的内部，哪些点位于外部。

一种常用的方法是使用奇偶规则，根据交点的数量判断点位于多边形内部还是外部。

步骤5：生成裁剪多边形最后，根据确定的内、外部点，生成裁剪后的多边形。

可以通过连接内部点和交点来生成裁剪后的多边形。

需要注意的是，由于Weiler-Atherton多边形裁剪算法是基于点的，因此在处理封闭多边形时需要考虑交点的顺序。

如果交点的顺序不正确，可能会导致生成的裁剪多边形出现错误。

总结Weiler-Atherton多边形裁剪算法是一种用于计算两个多边形相交部分的算法。

具有拓扑关系的任意多边形裁剪算法中国的地理空间数据处理发展迅速，形状分析技术受到技术界的广泛应用。

多边形裁剪是一种常见的形状分析技术，它可以用来从空间数据集中提取出多边形范围内的空间对象，以便进行深入分析和分类处理，同时也可以用来测量多边形的面积和周长等。

具有拓扑关系的多边形裁剪算法是多边形裁剪的一种，它可以从拓扑关系的多边形中提取出正确的多边形边界，而不用考虑多边形的内部点和边的连接关系。

这种算法的特点是，可以对多边形的边缘点和其他类型的点进行分类，考虑到其它多边形的拓扑关系，分析出能够完整描述多边形的边界，从而为后续空间数据处理提供了一种有效的算法。

具有拓扑关系的多边形裁剪算法的基本原理是：首先通过计算多边形内部点和边缘点之间的拓扑关系，对所有多边形内点进行分类；然后针对每个分类，采用多边形切割算法，将一个多边形分割成多个小的多边形，每个小的多边形的定义由多边形的点和边组成；最后，根据分类后的多边形点和边之间的拓扑关系，对经过分割的多个多边形边界重新进行切割，完成裁剪。

该算法与其他常见的多边形裁剪算法相比，有着明显的优势。

第一，由于该算法采用多边形分割算法和拓扑关系分析算法相结合，它能够有效地处理多边形内部点和边缘点之间的拓扑关系，从而达到较高的准确性和可靠性；第二，该算法的实现不需要大量的预处理，复杂度较低，从而大大减少了算法执行时间；第三，该算法能够有效处理多边形中出现的不闭合、重叠等异常状况，从而得到更加准确的结果。

实际应用中，该算法可以用来自动提取多边形边界，从而检测出满足特定要求的多边形，从而为后续多边形分析和处理提供可靠的基础数据。

此外，该算法也可以用来检测多边形的内部是否存在大量的噪声，以便及时采取措施将其消除，保证多边形的精确性和准确性。

总之，具有拓扑关系的多边形裁剪算法是一种有效而可靠的多边形裁剪算法，可以有效地从复杂的多边形中提取出正确的多边形边界，为地理空间数据处理提供有效的技术支持。

Weiler－Atherton任意多边形裁剪Sutherland－Hodgeman算法解决了裁剪窗口为凸多边形窗口的问题，但一些应用需要涉及任意多边形窗口（含凹多边形窗口）的裁剪。

Weiler-Atherton多边形裁剪算法正是满足这种要求的算法。

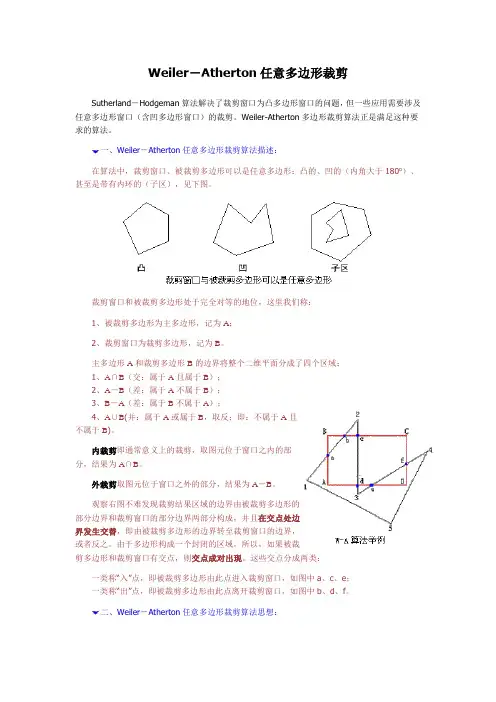
一、Weiler－Atherton任意多边形裁剪算法描述：在算法中，裁剪窗口、被裁剪多边形可以是任意多边形：凸的、凹的（内角大于180o）、甚至是带有内环的（子区），见下图。

裁剪窗口和被裁剪多边形处于完全对等的地位，这里我们称：1、被裁剪多边形为主多边形，记为A；2、裁剪窗口为裁剪多边形，记为B。

主多边形A和裁剪多边形B的边界将整个二维平面分成了四个区域：1、A∩B（交：属于A且属于B）；2、A－B（差：属于A不属于B）；3、B－A（差：属于B不属于A）；4、A∪B(并：属于A或属于B，取反；即：不属于A且不属于B)。

内裁剪即通常意义上的裁剪，取图元位于窗口之内的部分，结果为A∩B。

外裁剪取图元位于窗口之外的部分，结果为A－B。

观察右图不难发现裁剪结果区域的边界由被裁剪多边形的部分边界和裁剪窗口的部分边界两部分构成，并且在交点处边界发生交替，即由被裁剪多边形的边界转至裁剪窗口的边界，或者反之。

由于多边形构成一个封闭的区域，所以，如果被裁剪多边形和裁剪窗口有交点，则交点成对出现。

这些交点分成两类：一类称“入”点，即被裁剪多边形由此点进入裁剪窗口，如图中a、c、e；一类称“出”点，即被裁剪多边形由此点离开裁剪窗口，如图中b、d、f。

二、Weiler－Atherton任意多边形裁剪算法思想：假设被裁剪多边形和裁剪窗口的顶点序列都按顺时针方向排列。

当两个多边形相交时，交点必然成对出现，其中一个是从被裁剪多边形进入裁剪窗口的交点，称为“入点”，另一个是从被裁剪多边形离开裁剪窗口的交点，称为“出点”。

算法从被裁剪多边形的一个入点开始，碰到入点，沿着被裁剪多边形按顺时针方向搜集顶点序列；而当遇到出点时，则沿着裁剪窗口按顺时针方向搜集顶点序列。

多边形裁剪的Sutherland—Hodgman算法1>. Sutherland—Hodgman多边形裁剪算法思想该算法的基本思想是每次用窗口的一条边界及其延长线来裁剪多边形的各边。

多边形通常由它的顶点序列来表示，经过裁剪规则针对某条边界裁剪后，结果形成新的顶点序列，又留待下条边界进行裁剪，…，直到窗口的所有边界都裁剪完毕，算法形成最后的顶点序列，才是结果多边形（它可能构成一个或多个多边形）。

当多边形一个顶点Pi相对于窗口某条边界及其延长线进行剪裁时，不外乎下列四种情况（即裁剪规则）：1、顶点Pi在内侧，前一顶点Pi-1也在内侧，则将Pi纳入新的顶点序列；2、顶点Pi在内侧，前一顶点Pi-1在外侧，则先求交点Q，再将Q、Pi依次纳入新的顶点序列；3、顶点Pi在外侧，前一顶点Pi-1在内侧，则先求交点Q，再将Q纳入新的顶点序列；4、顶点Pi与前一顶点Pi-1均在外侧，则顶点序列中不增加新的顶点。

2>. Sutherland—Hodgman多边形裁剪算法步骤考虑多边形相对于一条边界及其延长线进行裁剪的算法：1．从主函数得到待裁剪多边形的顶点序列P[][2]、顶点序列数n、窗口一条边界参数xl（假如为矩形窗口的左边界）；2．赋初值：将顶点序列中的最后一个顶点赋给前一顶点S；设置初始标志flag：if(S在边界内侧)flag=0;else flag=1；设新的顶点序列数j=0；3．对多边形各顶点进行裁剪规则处理，结果放入新的多边形顶点序列Q[][2]中：for(对第一个顶点直到最后一个顶点，逐一处理）{if(Pi在边界内侧){if(flag!=0){flag=0;求交点并放入新的多边形顶点序列Qj中；j++；}将当前顶点放入新的多边形顶点序列Qj中：Qj=Pi；j++；}else{if(flag==0){flag=1;求交点并放入新的多边形顶点序列Qj中；j++；}}将当前顶点赋给S：S=Pi；}4．做返回准备：将新的多边形顶点序列Q又逐一放回原多边形顶点序列P中：P=Q；将新的多边形顶点数j放回原多边形顶点数n中：n=j；/////////////////////////////////////////////////////////////////////////////// /////////-----多边形裁剪的Sutherland—Hodgman算法---------///////////////////////////////////////////////////////////////////////////////// //////void CMyClip_AView::ClipedgeL(CPoint polypoint[], CPoint clipwindow[], UINT polynum)/*其中参数polypoint[]为多边形顶点,clipwindow[]为裁剪窗口顶点,polynum为多边形顶点数目*/{//找出裁剪窗口边界long xl,xr,yt,yb;UINT i;xl=clipwindow[0].x;xr=clipwindow[0].x;yt=clipwindow[0].y;yb=clipwindow[0].y;for(i=1;i<=4;i++){if(xl>clipwindow[i].x)xl=clipwindow[i].x;if(xr<clipwindow[i].x)xr=clipwindow[i].x;if(yb>clipwindow[i].y)yb=clipwindow[i].y;if(yt<clipwindow[i].y)yt=clipwindow[i].y;}//CPoint B[Polygon_Num],C[Polygon_Num];UINT m_nA,m_nB;int x,y;long tem1,tem2;m_nA=polynum;/*记载原始多边形顶点顶点个数*/m_nB=0;/*记载新生成多边形顶点顶点个数*/for(i=0;i<m_nA;i++){if(polypoint[i].x<xl && polypoint[i+1].x<xl) /*判断的多边形边两个端点都在外部，不做处理*/{continue;/*如果是这种情况，那么就对继续对下一条多边形边作判断，也就是说下面的判断不用做了*/}if(polypoint[i].x>=xl && polypoint[i+1].x>=xl) /*边两个端点都在内部，保留*//*因为每个保留的点在数组中只出现一次，且下一次判断时第二个端点一定会要取到，因此只保留的两个点中的第一个*/{B[m_nB].x =polypoint[i].x ;B[m_nB].y =polypoint[i].y ;m_nB=m_nB+1;continue;}if(polypoint[i].x<xl && polypoint[i+1].x>=xl)/*边两个端点起点在外部，终点在内部，求交点，然后交点，终点都应该送入临时数组*/{/*保留交点*/x=xl;tem1=(xl-polypoint[i].x);//tem2=(xl-x1)*dy/dx+y1;//y/x=dy/dx---->y=x*dy/dxtem2=tem1*(polypoint[i+1].y-polypoint[i].y)/(polypoint[i+1].x-polypoint[i].x)+p olypoint[i].y;y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB=m_nB+1;continue;}if(polypoint[i].x>=xl && polypoint[i+1].x<xl)/*起点在内部，终点在外，求交点，然后起点，交点送入临时数组*/{ /*保留内部点*/B[m_nB].x =polypoint[i].x ;B[m_nB].y =polypoint[i].y ;m_nB=m_nB+1;/*保留交点*/x=xl;tem1=(xl-polypoint[i].x);tem2=tem1*(polypoint[i+1].y-polypoint[i].y)/(polypoint[i+1].x-polypoint[i].x)+p olypoint[i].y;y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB=m_nB+1;continue;}}//把第一个点的数据拷贝到最后//形成裁剪后的多边形if(i==m_nA){B[m_nB]=B[0];}//下------------------m_nA=0;for(i=0;i<m_nB;i++){if(B[i].y<yb && B[i+1].y<yb)//两个点全在下方{continue;//下一条边}if(B[i].y>=yb && B[i+1].y>=yb)//p1,p2都在yb上方{C[m_nA].x =B[i].x;C[m_nA].y =B[i].y;m_nA++;continue;}if(B[i].y<yb && B[i+1].y>=yb)//p1在下，P2在上,留交点，外－＞内y=yb;tem1=yb-B[i].y;//tem2=x1+(yb-y1)*dx/dytem2=tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y) + B[i].x; x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}if(B[i].y>=yb && B[i+1].y<yb)//p1在上方，P2在下方，留P1和交点,内－外{//save p1C[m_nA].x=B[i].x;C[m_nA].y=B[i].y;m_nA++;//留交点y=yb;tem1=yb-B[i].y;//tem2=x1+(yb-y1)*dx/dytem2=tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y)+B[i].x; x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}}//形成第二次裁剪多边形if(i==m_nB){C[m_nA]=C[0];}//右------------------m_nB=0;for(i=0;i<m_nA;i++){if(C[i].x>xr && C[i+1].x>xr)//P1，P2都在右方--go next{continue;if(C[i].x<=xr && C[i+1].x<=xr)//P1，P2都在左方，留P1{B[m_nB].x =C[i].x;B[m_nB].y =C[i].y;m_nB++;continue;}if(C[i].x>xr && C[i+1].x<=xr)//P1在右方，P2在左方，留交点{x=xr;tem1=C[i].x-xr;tem2=C[i].y-tem1*(C[i+1].y-C[i].y)/(C[i+1].x-C[i].x); y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB++;continue;}if(C[i].x<=xr && C[i+1].x>xr)//P1在内，P2在外，留P1和交点{//save p1B[m_nB].x =C[i].x;B[m_nB].y =C[i].y;m_nB++;//save 交点x=xr;tem1=C[i].x-xr;tem2=C[i].y-tem1*(C[i+1].y-C[i].y)/(C[i+1].x-C[i].x); y=tem2;B[m_nB].x =x;B[m_nB].y =y;m_nB++;continue;}}//三次裁剪后的新多边形if(i==m_nA){B[m_nB]=B[0];}//上-------------------m_nA=0;for(i=0;i<m_nB;i++){if(B[i].y>yt && B[i+1].y>yt)//p1,p2都在上方,next{continue;}if(B[i].y<=yt && B[i+1].y<=yt)//p1,p2都在下方,留P1{C[m_nA].x =B[i].x;C[m_nA].y =B[i].y;m_nA++;continue;}if(B[i].y>yt && B[i+1].y<=yt)//P1在上方，P2在下方外－＞内,留交点{y=yt;tem1=B[i].y-yt;//tem2=x1+(yb-y1)*dx/dytem2=B[i].x-tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y); x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}if(B[i].y<=yt && B[i+1].y>yt)//P1在下方，P2在上方，内－＞外，留P1和交点{//save p1,,,C[m_nA].x =B[i].x;C[m_nA].y =B[i].y;m_nA++;//save 交点y=yt;tem1=B[i].y-yt;//tem2=x1+(yb-y1)*dx/dytem2=B[i].x-tem1*(B[i+1].x-B[i].x)/(B[i+1].y-B[i].y);x=tem2;C[m_nA].x =x;C[m_nA].y =y;m_nA++;continue;}}//形成裁剪后的多边形if(i==m_nB){C[m_nA]=C[0];}CClientDC dc(this);CPen tempen;tempen.CreatePen(PS_SOLID,1,RGB(255,0,0));dc.SelectObject(tempen);dc.MoveTo(C[0]);for(i=1;i<=m_nA;i++){dc.LineTo(C[i]);}}//.....（注：可编辑下载，若有不当之处，请指正，谢谢!）。

复杂多边形窗口的多边形裁剪的改进算法复杂多边形窗口的多边形裁剪是计算机图形学领域中的一个重要问题。

这个问题涉及到了两个多边形的相交，求取相交部分的算法。

这个问题在游戏开发、工程制图、计算机辅助设计等领域都有广泛应用。

然而，复杂多边形窗口的多边形裁剪问题不易解决，深入研究之后，发现现行的算法在实际运用中存在一些问题，需要改进。

一、现行的多边形裁剪算法现行的多边形裁剪算法主要有两种，分别是Sutherland-Hodgman算法和Weiler-Atherton算法。

这两种算法在实现方面相对简单，适用面广，被广泛运用。

1. Sutherland-Hodgman算法Sutherland-Hodgman算法是一种逐边裁剪的算法。

该算法将待裁剪多边形沿着裁剪窗口的四个边分别进行裁剪，从而得到最终结果。

该算法基于的思想是将多边形沿着裁剪边拆分成多个三角形，然后对每个三角形进行分类，得到最终的结果。

但是该算法存在一定的问题，比如会向四个方向输出不必要的顶点信息。

2. Weiler-Atherton算法Weiler-Atherton算法是一种基于点和交点的算法。

该算法首先查找所有的交点，并寻找他们之间的连接线段。

这些交点和线段形成了一个新的多边形，然后将这个新多边形剔除窗口外的部分，得到最终结果。

这个算法的主要问题是，当多边形的顶点数量很大时，会产生大量的交点，造成计算时间上的消耗。

二、改进的多边形裁剪算法考虑到现行的两种多边形裁剪算法存在一定的问题，我们提出了一种改进的多边形裁剪算法。

该算法基于分段的概念，分别对多边形和裁剪窗口的各条边进行分段，以减少计算量。

具体而言，我们将多边形和窗口的边按照其坐标值的大小，分为若干个段。

然后，我们逐段进行裁剪。

这个方法最初提出于1984年，但在当时的计算机技术条件下，没有得到推广应用。

如今，我们可以用现代的算力来完成这个算法的运算。

改进算法的主要步骤如下：1. 将多边形和裁剪窗口的各条边按照其坐标值的大小，分为若干个段。

Weiler－Atherton任意多边形裁剪Sutherland－Hodgeman算法解决了裁剪窗口为凸多边形窗口的问题，但一些应用需要涉及任意多边形窗口（含凹多边形窗口）的裁剪。

Weiler-Atherton多边形裁剪算法正是满足这种要求的算法。

一、Weiler－Atherton任意多边形裁剪算法描述：在算法中，裁剪窗口、被裁剪多边形可以是任意多边形：凸的、凹的（内角大于180o）、甚至是带有内环的（子区），见下图。

裁剪窗口和被裁剪多边形处于完全对等的地位，这里我们称：1、被裁剪多边形为主多边形，记为A；2、裁剪窗口为裁剪多边形，记为B。

主多边形A和裁剪多边形B的边界将整个二维平面分成了四个区域：1、A∩B（交：属于A且属于B）；2、A－B（差：属于A不属于B）；3、B－A（差：属于B不属于A）；4、A∪B(并：属于A或属于B，取反；即：不属于A且不属于B)。

内裁剪即通常意义上的裁剪，取图元位于窗口之内的部分，结果为A∩B。

外裁剪取图元位于窗口之外的部分，结果为A－B。

观察右图不难发现裁剪结果区域的边界由被裁剪多边形的部分边界和裁剪窗口的部分边界两部分构成，并且在交点处边界发生交替，即由被裁剪多边形的边界转至裁剪窗口的边界，或者反之。

由于多边形构成一个封闭的区域，所以，如果被裁剪多边形和裁剪窗口有交点，则交点成对出现。

这些交点分成两类：一类称“入”点，即被裁剪多边形由此点进入裁剪窗口，如图中a、c、e；一类称“出”点，即被裁剪多边形由此点离开裁剪窗口，如图中b、d、f。

二、Weiler－Atherton任意多边形裁剪算法思想：假设被裁剪多边形和裁剪窗口的顶点序列都按顺时针方向排列。

当两个多边形相交时，交点必然成对出现，其中一个是从被裁剪多边形进入裁剪窗口的交点，称为“入点”，另一个是从被裁剪多边形离开裁剪窗口的交点，称为“出点”。

算法从被裁剪多边形的一个入点开始，碰到入点，沿着被裁剪多边形按顺时针方向搜集顶点序列；而当遇到出点时，则沿着裁剪窗口按顺时针方向搜集顶点序列。

多边形裁剪算法多边形裁剪算法多边形裁剪是用线段对一些形状进行处理的一种常见算法。

它通常用于地图显示、机械加工以及其他基于图形的计算机图形系统中。

裁剪有一个边界框，其中包含可被裁剪的部分，以及无法被裁剪的区域。

多边形裁剪指的是在边界框内裁剪掉不符合要求的部分，只保留符合边界框的多边形。

下面将介绍一种基本的多边形裁剪算法——贝尔格罗夫多边形裁剪算法。

贝尔格罗夫多边形裁剪算法(Brelgorff Polygon Clipping Algorithm)是一种用于生成裁剪多边形轮廓的算法，由荷兰科学家Berlgorff于1890年发明。

它主要用于多边形裁剪。

贝尔格罗夫多边形裁剪算法的思想是：从一个多边形的起点，每次移动到下一个顶点，v，判断是否在裁剪区域内，若在裁剪区域内，则标记当前顶点v为可视边界，否则为不可视边界；然后，从v移动到下一个顶点，只要发现在裁剪区域外的边界，就必须标记下一个顶点为可视边界；最后，当发现多边形完全不在裁剪区域内时，就会将多边形的所有顶点都标记为不可视边界。

贝尔格罗夫多边形裁剪算法的实现方式如下：第一步：设置多边形的顶点序列。

第二步：从多边形的起点开始遍历顶点，检查每个顶点是否在裁剪区域内，将在裁剪区域内的顶点标记为可视边界，将在裁剪区域外的顶点标记为不可视边界。

第三步：对不可视边界进行处理，若两个不可视边界之间有一个可视边界，则以可视边界为结束位置，将不可视边界之间的边加入到多边形的边界框中；若两个不可视边界之间没有可视边界，则以最后一个不可视边界为结束位置，将不可视边界之间的边加入到多边形的边界框中。

第四步：对可视边界进行处理，遍历可视边界，将可视边界添加到多边形的边界框中。

第五步：根据多边形的边界框计算出裁剪后的多边形轮廓，即裁剪后的多边形。

贝尔格罗夫多边形裁剪算法具有以下特点：实现简单，复杂度较低，多边形裁剪时不要求多边形的顶点按边界框顺序排列，且可以处理任意多边形。

贝尔格罗夫多边形裁剪算法是一种常用的多边形裁剪算法，它对图形的显示、机械加工以及其他基于图形的计算机图形系统有着重要的应用。

多边形裁剪⼀、多边形的裁剪如果按线段的⽅法裁剪，得到的是⼀系列线段。

⽽实际上，应该得到的是下图所⽰的有边界的区域：多边形裁剪算法的输出应该是裁剪后的多边形边界的顶点序列！需要构造能产⽣⼀个或多个封闭区域的多边形裁剪算法⼆、Sutherland-Hodgeman多边形裁剪该算法的基本思想是将多边形边界作为⼀个整体，每次⽤窗⼝的⼀条边对要裁剪的多边形和中间结果多边形进⾏裁剪，体现⼀种分⽽治之的思想把平⾯分为两个区域：包含有窗⼝区域的⼀个域称为可见侧；不包含窗⼝区域的域为不可见侧裁剪得到的结果多边形的顶点有两部分组成：（1）落在可见⼀侧的原多边形顶点（2）多边形的边与裁剪窗⼝边界的交点根据多边形每⼀边与窗⼝边所形成的位置关系，沿着多边形依次处理顶点会遇到四种情况：（1）第⼀点S在不可见侧⾯，⽽第⼆点P在可见侧交点I与点 P均被加⼊到输出顶点表中。

（2）是S和P都在可见侧则P被加⼊到输出顶点表中（3）S在可见侧，⽽P在不可见侧则交点I被加⼊到输出顶点表中（4）如果S和P都在不可见侧输出顶点表中不增加任何顶点在窗⼝的⼀条裁剪边界处理完所有顶点后，其输出顶点表将⽤窗⼝的下⼀条边界继续裁剪while对于每⼀个窗⼝边或⾯ do begin if P1 在窗⼝边的可见⼀侧 then 输出P1 for i=1 to n do begin if P1 在窗⼝边的可见⼀侧 then if P1+1 在窗⼝边的可见⼀侧 then 输出 P1+1 else 计算交点并输出交点 else if Pi+1 在窗⼝可见⼀侧，then 计算交点 并输出交点，同时输出Pi+1 end endendSutherland-Hodgeman算法不⾜之处利⽤Sutherland-Hodgeman裁剪算法对凸多边形进⾏裁剪可以获得正确的裁剪结果，但是凹多边形不⾏。

具有拓扑关系的任意多边形裁剪算法从几何方面来看，多边形是一种复杂的几何形状，由点、线、面或其他复杂几何体组成，具有自身独特的几何特征，它可以用来表达几何图形中点、线、面等形状，多边形裁剪是几何图形处理中重要的一项任务。

例如，当我们打印一幅图片或绘制一幅图像时，多边形裁剪算法非常重要，可以帮助我们将图像准确地输出到打印机或绘图板上。

本文针对几何图形多边形的特点，提出了一种新的任意多边形裁剪算法，具有拓扑关系。

任意多边形裁剪（polygon clipping）是几何图形处理中一个重要的分支，它可以实现图像的裁剪、分块、测量距离等操作，并且在许多应用场景中得到了广泛的应用。

本文提出的算法，是将几何图形的拓扑关系考虑在多边形的裁剪中，可以实现更精确的图像分割。

新的任意多边形裁剪算法的总体步骤如下：第一步，确定图形的拓扑关系。

此处采用的方法是，对图形的边界点进行标号，以表示该边是出边还是入边，构や一个基本拓扑元素表。

第二步，根据外部边界点，检查每个多边形边界点之间的关系，根据拓扑关系将边界点重新排序。

第三步，用给定的边界点构建一个多边形，完成多边形裁剪操作。

本文提出的新算法具有以下几个优点：1.进了传统的多边形裁剪算法，多边形的拓扑关系能够更加准确地反映出多边形的形状和特征，从而使多边形的裁剪更加准确；2.够实现更精确的图像分割，同时可以减少绘图、标记等不必要的操作；3.因为拓扑关系能够有效降低计算复杂度，因此将使算法的运行效率提高。

本文提出的新算法在各种多边形图形处理应用中具有重要意义，例如空间几何建模、三维数据分析等方面。

最后，本文还将提出一些可以改进算法的思路，以提高算法的效率，使得它能够更好地应用到实际的图形处理项目中。

总之，本文提出的新的任意多边形裁剪算法能够有效解决几何图形处理中的拓扑关系问题，极大地提高了图像裁剪、分块、测量距离等操作的精确度，并且可以有效地减少绘图、标记等不必要的操作。

本文提出的拓扑关系多边形裁剪算法在各种多边形图形处理应用中具有重要意义，最终将使得算法应用更广泛，并且能够在更多的图形处理项目中得到应用和改进。

一个有效的多边形裁剪算法摘要:多边形多裁剪与线剪裁相比具有更广泛的实用意义,因此它是目前裁剪研究的主要课题.提出了一个多边形裁剪多边形的有效算法.其中的多边形都可以是一般多边形,既可以是凹多边形,也可以是有内孔的多边形.该算法不仅可以求多边形的“交”(多边形裁剪),而且可以求多边形的“并”和“差”.它是以所提出的一系列新方法和新技术为基础而形成的.首先,该算法使用单线性链表数据结构,与其他使用双链表或树结构的算法相比,具有占用空间少及处理速度快的特点;其次,找到了两个多边形之间进、出点之间的关系.再通过合理的数据结构处理,减少了算法对多边形链表的遍历次数,而且允许多边形既可以按顺时针方向也可以按逆时针方向输入.最后,判断和计算交点是裁剪算法的主要工作.提出了一个具有最少计算量的交点判断和计算方法,进一步加快了算法的运行速度.与其他同类算法进行了比较,结果表明,新算法具有最简单的结构和最快的执行速度.正文:1.基本概念与定义.为了便于下面对算法的讲解,本节首先介绍有关多边形裁剪的一些基本概念及术语.(1) 多边形的边的方向与内外区域的关系.如果多边形的边的方向是顺时针的(即多边形的顶点是以顺时针的顺序输入的),则在沿着多边形的边走时,右侧区域为多边形的内部;相反,如果多边形的边的方向是逆时针的,则在沿着多边形的边走时,左侧区域为多边形的内部.对于具有孔洞的多边形,只要把内孔边界和外边界以相反的方向表示,由上面的规则判断多边形的内部仍然适用.(2) 进点和出点的定义.设I是多边形S和C的一个交点,如果S沿着S的边界的方向在I点从C的外部进入C的内部,则称I为对于C的一个进点.反之,如果S在I点从C的内部出到C的外部,则称I为对于C的一个出点.例如,对于如图1所示的多边形C和S及其交点I,若S的方向为逆时针方向S 1→S2→S3→S4→S5,则I5I1I3是对于C的进点,I4I2I6是对于C的出点.如果S的方向为顺时针方向S5→S4→S3→S2→S1,则对于C来说,I2I4I6是进点,I1I5I3是出点(3) 进点和出点的判定.假设多边形S的一条边Si Si+1与另一多边形C有交点.当点Si是C的外点时,则沿着S的走向,边Si Si+1与C的第一个交点I必是C的进点;而当Si是C的内点时,I必是C的出点.由于沿着S的边界对于C的进点和出点是交替出现的(两多边形的边重合或者两多边形在顶点处相交的情况除外.这类特殊情况的处理将在第5节进行讨论),所以,只需判断第1个交点是进点还是出点,其他交点的进出性则可依次确定.对于一个多边形裁剪另一个多边形的过程,就是求两个多边形的相交区域(我们称其为结果多边形或输出多边形).结果多边形是由实体多边形位于裁剪多边形内的边界和裁剪多边形位于实体多边形内的边界组成的.2.新算法的数据结构多边形裁剪算法需要一个适当的数据结构来存储多边形及交点,并能够在其上进行正确的操作.在Weiler的算法中,输入多边形组成一个树形结构.Greiner-Hormann算法采用双向链表的结构,每个多边形由一个双向链表来表示.每找到一个交点,就将其分别插入到实体多边形和裁剪多边形的两个双向链表中.Greiner-Hormann算法使用了线性链表,与Weiler算法的树形结构相比降低了数据结构的复杂性.本文的算法采用单链表来表示所有的多边形(输入和输出),与Greiner-Hormann算法的双向链表结构相比,不仅由于少用了一个指针域而节省了存储空间,而且还进一步降低了数据结构的复杂性.我们知道,在插入一个交点时,双向链表所需修改的指针数是单链表的2倍,因此,对单链表的操作不仅简单,而且也省时.新算法的每个多边形由一个单链表来表示,单链表的每一个结点按序(多边形顶点输入的顺序)存储着多边形的一个顶点.最后一个结点的指针指向第1个结点(循环单链表).每个链表由一个头指针指向其第1个结点,实体多边形链表的第1个结点由头指针HeadS指示;裁剪多边形链表的第一个结点由头指针HeadC指示.结点的结构定义如下(其中coordinates表示坐标类型,用于存储顶点或交点的坐标值;pointer表示指针类型):Vertex={x, y: coordinates;inters, used: Boolean;next: pointer;}交点的数据结构如下:Intersection={x, y: coordinates;inters, used: Boolean;next1, next2: pointer;}其中的指针域用于将交点分别插入到两个多边形的单链表中,第1指针域next1用于插入实体多边形链表;第2个指针域next2用于插入裁剪多边形链表.这样的数据结构定义使算法在求出一个交点时只需建立1个Intersection(交点)类型的结点,并分别插入到两个多边形的单链表中,而不像Greiner-Hormann算法那样,要建立两个交点类型的结点,然后将每一个插入到一个多边形的链表中,而插入到两个链表中的这两个交点类型的结点之间也要用指针域neighbor彼此相连.应该注意的是,实体多边形链表中的交点的进出性是对裁剪多边形而言的,而裁剪多边形链表中的交点的进出性则是对实体多边形而言的.在这两个数据结构的定义中,布尔类型域inters用于区分该结点是否Intersection(交点)类型的结点;used域用于有多个输出多边形时.所有交点的used域的初值都为0,当一个交点被输出时,其used域被置为1.裁剪结果可能得到多个分立的输出多边形,因此需要设立一个指针链表Out,其每个结点有一个指针域polygon指向一个输出多边形链表的第一个结点.该指针链表的结点结构如下:Out={polygon: pointer;next: pointer;}图2给出了对图1的多边形进行裁剪时,Greiner-Hormann算法和新算法所使用的数据结构.可见,新算法的数据结构要比Greiner-Hormann算法简单得多.3.新算法新算法分为3个阶段.第1个阶段,判断及计算第1个交点,并由其进出性判断两个多边形是否同向.如果不同向,则将裁剪多边形链表反向,然后将该交点插入到两个多边形的链表中.第2阶段,依次以实体多边形的每一个边对裁剪多边形进行直线裁剪操作,判断及计算其余交点,并以正确的顺序插入到两个多边形的链表中.第3阶段,遍历整个链表,输出最终结果.我们以下面的引理开始算法第1阶段的描述.引理1. 如果两个相交多边形的边的取向相同(均为顺时针或逆时针方向),则对一个多边形是进点的交点对另一个多边形必是出点.证明:设分别属于两个相交多边形S和C的两个相交边为Se 和Ce,我们首先考虑两个相交多边形的边的取从下向上穿过S(图3a的情况)),则由图3显然可见,C经过交点从多边形S内走向S外,即该交点是对于多边形S的出点;而另一方面,边S向均为顺时针方向的情况.在这种情况下,多边形边的右侧为多边形内侧(在图3中由阴影表示).考虑两边之间的夹角,由于此夹角是由两边的相对位置决定的,所以我们可以将一个边的方向固定而讨论另一个边方向变化的各种情况.在图3中,设Se 边的方向是从左向右固定不变的,如果Ce的正向与Se的正向的夹角在0o~180o之间(即Ceeee则是经过该交点从多边形C外走向C内,即该交点是对于多边形C的进点如果Ce 的正向与Se的正向的夹角在180o~360o之间(即Ce从上向下穿过Se(如图3(b)所示),则由图显然可见,该交点对于多边形S是进点,而对于多边形C则是出点.这就是我们要证明的结论.对于两个相交多边形的边的取向均为逆时针方向的情况,可用相同的方法证明该引理. □根据该引理,对其中一个多边形求出一个进点或出点以后,在两个多边形方向相同的情况下,其对另一个多边形的进出性也就确定了.这样,如果两个多边形的方向相同,则在求出交点时只需判断和标记它对其中一个多边形是进点还是出点.它对另一个多边形的进出性则相反.而由第1节的讨论可知,由于沿着一个多边形的边界,在其上的进点和出点是交替出现的.所以只需标记第1个交点是进点还是出点,其他交点的进出性则可依次确定.最终我们得出一个结论:如果两个多边形的方向相同,则要标记所有交点对于两个多边形的进出性,只需标记任何一个多边形链表中的第1个交点的进出性即可(在后面的算法描述中,我们用变量Sin来标记实体多边形链表中的第1个交点对于裁剪多边形是否为进点).因此,新算法的第1步就要是判断两个多边形是否同向.如果不同向,则将裁剪多边形链表反向,使两个多边形的方向相同.判断两个多边形是否同向,是通过判断一个交点(如第1个交点)对于两个多边形的进出性来完成的.如果该点对于实体多边形的进出性与对于裁剪多边形的进出性不同,则可知两个多边形取向相同;否则,两个多边形的取向相反.新算法将交点的计算与进出性判断合成一步进行.当一个多边形的一个边对另一个多边形进行直线裁剪操作之后,如果有交点,即可根据交点在这个边上的排序的奇偶性来确定交点对另一个多边形的进出性.这样在计算交点的同时也确定了该交点的进出性.详细的描述见第4节.下面是算法的第1部分的形式描述,其中指针变量PS和PC分别指向实体多边形链表和裁剪多边形链表中正在被处理的当前结点.另外,我们把由结点PS↑和其下一个结点PS↑.next↑定义的边简称为由PS指向的边.PS=HeadS;Repeat以PS指向的边与裁剪多边形进行直线裁剪操作(即求交点的操作,见第4节);if (上述直线裁剪操作有交点) then{如图2所示,将每个交点(可能有多个)按其在该边上的顺序插入到实体多边形链表和裁剪多边形链表的对应相交边的两个结点之间;由Sin标记插入到实体多边形链表中的第1个交点对于裁剪多边形的进出性,Sin=1表示进;令PF指向第1个交点结点,以备算法的第3阶段使用;将PC指向该交点在裁剪多边形上的对应边;以PC指向的边与实体多边形进行直线裁剪操作;求出上述第1个交点对于实体多边形的进出性;if上述第1个交点对于实体多边形和裁剪多边形的进出性相同 then 逆转裁剪多边形的链表;令PS指向实体多边形的下一个边;转到算法的第2阶段;}令PS指向实体多边形的下一个边;until PS=HeadS;两个多边形无交点,算法结束;在第2阶段,算法从第1阶段求出交点的那个实体多边形边的下一个边开始,用每一个实体多边形边与裁剪多边形求交点,并如图2所示,给每个交点建立一个包含该交点坐标的新的交点结点,然后将其插入到实体多边形链表和裁剪多边形链表的对应相交边的两个结点之间.例如,一个交点是由结点PS↑和其下一个结点PS↑.next↑所定义的实体多边形的边与由结点PC↑和其下一个结点PC↑.next↑所定义的裁剪多边形的边相交形成的,那么该交点结点就应该被插入到实体多边形链表的结点PS↑和其下一个结点PS↑.next↑之间,同时被插入到裁剪多边形链表的结点PC↑和其下一个结点PC↑.next↑之间.当一个边上有多个交点时,则以该边的方向为序将这些交点插入其中.例如,如果该边的方向是从左向右的斜线,则可按交点的x坐标的大小顺序插入这些交点.在这个阶段,算法不需要标记交点的进出性,因为如前所述,算法只需在第1阶段用变量Sin来标记实体多边形链表中的第1个交点对于裁剪多边形的进出性,其余交点对于两个多边形的进出性便由如前所述的规律可知.下面是算法的第2部分的形式描述.Repeat以PS指向的边与裁剪多边形进行直线裁剪操作;if (上述直线裁剪操作有交点) then 将每个交点按其在该边上的顺序插入到实体多边形链表和裁剪多边形链表的对应相交边的两个结点之间;令PS指向实体多边形的下一个边;until PS=HeadS;转到算法的第3阶段;在算法的第3阶段,通过遍历已插入交点结点的实体多边形和裁剪多边形链表来跟踪结果多边形的边界,最后产生输出多边形链表.跟踪一个结果多边形的边界是以实体多边形链表中的一个进点(对于裁剪多边形)开始的.从该进点到实体多边形链表中的下一个交点(记为N1)之间的实体多边形的边界全部是结果多边形的边界.N1既是对于裁剪多边形的出点也是对于实体多边形的进点,因此从N1点开始到裁剪多边形链表中的下一个交点之间的裁剪多边形的边界全部是结果多边形的边界(如图1所示).输出这些边界.重复此过程,一直到回到实体多边形链表中的开始进点为止,便跟踪输出了一个结果多边形.在上述过程中,实体多边形链表中的进点(对于裁剪多边形)的used域被标记为1,以表明从它开始的边界已经被输出过.“used域”用于有多个结果多边形的情况.算法第3阶段的遍历是以实体多边形链表的顺序进行的.从实体多边形链表中的第1个进点开始,如果该进点(当前进点)的used域为0(表明它未被输出过),则将其置为1,并执行上一段所述的跟踪过程输出一个结果多边形;如果该进点的used域为1,则走到实体多边形链表的下一个进点,即该进点的下一个交点的下一个交点(如前所述,在多边形链表中交点的进出性是相隔分布的).以下一个进点为当前进点,重复此过程,一直到回到实体多边形链表中的第1个进点为止.所有的进点都被访问过,所有的结果多边形也都被输出.至此,算法结束.下面是算法第3阶段的形式描述.if Sin=0 then 令PF指向实体多边形链表中的下一个交点结点,以确保PF指向第1个进点;PP=PF;repeatif PP所指的交点结点的used域为0 then{PO=PP;建立一个新的输出多边形链表,并将指向该链表的头指针加入到指针链表Out的最后(在polygon域当中);repeat将PO所指的交点结点(一定是进点)的used域置为1;将从PO所指的交点结点开始(用next1指针域)到下一个交点结点(记为N1)之前的实体多边形链表中的结点加入到输出多边形链表的最后,并使PO指向N1;将从PO所指的交点结点开始(用next2指针域)到下一个交点结点(记为N2)之前的裁剪多边形链表中的结点加入到输出多边形链表的最后,并使PO指向N2;until PO=PP}else 使PP指向实体多边形链表中的下一个进点结点(即下一个交点结点的下一个交点结点);until PP=PF;算法结束,输出多边形链表由指针链表Out的polygon域指出.该算法不仅可以求多边形的“交”(多边形裁剪),而且稍加修改就可以求多边形的“并”和“差”.只要输出多边形从出点到入点的边(而不是上述的从入点到出点)即可得到多边形的“并”.要得到多边形的“差”也很简单,只需使两个多边形一个顺时针取向,另一个逆时针取向即可.对于有内孔的多边形,只要把内孔边界和外边界以相反的方向表示,则第1节的多边形的边的方向与内外区域的关系仍然适用.此时,只判断实体多边形和裁剪多边形的外边界方向即可:若方向相同,则不必调整;若方向相反,则把裁剪多边形的链表反向.然后,分别求出实体多边形的内、外边界与裁剪多边形的内、外边界的交点,并把交点插入到相应的数据结构中.最后遍历所有交点求出输出结果多边形.为了使算法能够裁剪有内孔的多边形,只需对上述算法进行少量的修改.用一个链表来表示有内孔的多边形时会多出一条边,如图4中的边C1C9.为了避免出现这种情况,我们采用如下的方法:将多边形链表的第1个结点换成上述交点结点的结构,即具有两个指针域next1和next2.其中next1用于指向多边形的外边界的第2个结点,而next2用于指向多边形的内边界的第1个结点.内边界的第1个结点同样具有两个指针域next1和next2,如果有第2个内孔,则由next2指向;如果没有,其next2指针域为空.这样,对多边形链表(可能包括多个边界链表)遍历的结束条件就不是回到链表的第1个结点了,而是回到其next2指针域为空的第1个结点.在算法中,每个边界的第1个结点都设一个头指针Head指向,自然区别于其他结点。

SutherlandHodgman多边形裁剪算法Sutherland-Hodgman多边形裁剪算法是一种用于裁剪二维多边形的算法，它是由伊恩·萨瑟兰（Ian Sutherland）和威廉·霍德曼（William E. Hodgman）在1962年提出的。

这种算法基于线段裁剪的思想，通过迭代过程逐步减少多边形的顶点数量，直到多边形完全被裁剪为止。

一、算法步骤1.初始化：将待裁剪的多边形P和裁剪多边形Q的边界表示为一系列的顶点。

设P的顶点集合为{p0, p1, , pn}，Q的顶点集合为{q0, q1, , qm}。

2.排序：将P的所有顶点按照逆时针（或顺时针）的顺序排列，将Q的所有顶点也按照逆时针（或顺时针）的顺序排列。

3.初始化裁剪结果：将裁剪结果设为一个空的多边形R。

4.迭代过程：从i=0开始，依次进行以下步骤，直到i=n或j=m：a. 确定P的第i个顶点pi是否在Q的边界内部（即判断pi是否在Q的凸壳上）。

如果pi不在Q的边界内部，则直接将pi添加到裁剪结果R中。

b. 如果pi在Q的边界内部，则找到Q边界上与pi最近的两个点，记为qi1和qi2。

根据这两个点的位置，将P的第i个顶点pi分割成两个部分，分别位于qi1和qi2之间的线段以及线段外的部分。

将这两个部分分别添加到R中。

c. 将i增加1，如果i<n，跳转到步骤4.4开始下一轮迭代；否则结束迭代。

5.返回结果：将R作为裁剪结果输出。

二、算法复杂度Sutherland-Hodgman多边形裁剪算法的时间复杂度为O(n+m)，其中n和m分别为待裁剪多边形P和裁剪多边形Q的顶点数量。

这是因为每次迭代过程中，我们最多只处理n个P的顶点和m个Q的顶点。

空间复杂度为O(n+m)，因为我们需要存储P和Q的顶点以及裁剪结果R的多边形表示。

三、算法应用Sutherland-Hodgman多边形裁剪算法可以用于各种需要裁剪二维多边形的场景，如计算机图形学中的视口裁剪、图像处理中的形状裁剪等。