计算机图形学之裁剪算法

梁友栋裁剪算法
梁友栋裁剪算法是一种常用的计算机图形学算法，用于将线段或多边形裁剪成可见部分。

该算法由梁钰栋和友松教授于1978年提出，因此得名为梁友栋裁剪算法。

在计算机图形学中，裁剪是指将一个图形对象的一部分或全部从视图中删除，以便在屏幕上显示。

裁剪算法是计算机图形学中的一个重要问题，因为它可以提高图形渲染的效率和质量。

梁友栋裁剪算法的基本思想是将线段或多边形与裁剪窗口进行比较，确定它们的可见部分。

裁剪窗口是一个矩形，表示屏幕上显示的区域。

如果线段或多边形完全在裁剪窗口内部，则它们是可见的，否则需要进行裁剪。

梁友栋裁剪算法的具体步骤如下：
1. 将线段或多边形的两个端点坐标表示为(x1,y1)和(x2,y2)。

2. 计算线段或多边形与裁剪窗口的交点，得到交点坐标(x,y)。

3. 判断交点是否在裁剪窗口内部，如果是，则将交点加入可见部分的点集合中。

4. 重复步骤2和3，直到所有交点都被处理完毕。

5. 根据可见部分的点集合，绘制线段或多边形的可见部分。

梁友栋裁剪算法的优点是简单易懂，计算量小，适用于各种类型的线段和多边形。

它可以用于计算机图形学中的各种应用，如计算机辅助设计、计算机游戏、虚拟现实等。

梁友栋裁剪算法是计算机图形学中的一种重要算法，它可以提高图形渲染的效率和质量，是计算机图形学领域不可或缺的一部分。

计算机图形学课程实验报告信息与计算科学（三）上机实验3：裁剪算法班级：姓名：学号：上机实验(3)的题目和要求一、实验目的掌握图形裁剪算法的基本思想，并能上机编程实现相应的算法。

二、实验要求（Direction）1．每个学生单独完成。

2．开发语言规定为C语言。

3．请在自己的实验报告上写明姓名、学号、班级。

4．每次交的实验报告内容包括：试验目的和意义、题目、程序制作步骤、主程序（包括源代码注释）。

三、实验题目实验题1：上机编一程序实现直线的中点裁剪算法。

具体要求如下说明：1 该程序能实现窗口屏幕上任意一条直线的裁剪；2 直线段要求可以随机输入；运行结果图：裁剪之前裁剪之后#define LE 2#define RI 4#define BO 6#define TO 10#define XLEFT 150#define XRIGHT 350#define YBOTTOM 150#define YTOP 300#include "math.h"#include "stdio.h"#include "graphics.h"void main(){int x1,y1,x2,y2,xx,yy,xxx,yyy;int graphdriver=DETECT,graphmode;initgraph(&graphdriver,&graphmode," ");setcolor(6);line(XLEFT,YTOP,XRIGHT,YTOP);line(XLEFT,YBOTTOM,XRIGHT,YBOTTOM);line(XLEFT,YTOP,XLEFT,YBOTTOM);line(XRIGHT,YTOP,XRIGHT,YBOTTOM);x1=50;y1=200;x2=400;y2=300;setcolor(1);line(x1,y1,x2,y2);xx=0;yy=0;xxx=0;yyy=0;draw_ett(x1,y1,x2,y2,&xx,&yy);draw_ett(x2,y2,xx,yy,&xxx,&yyy);setcolor(4);line(xx,yy,xxx,yyy);getch();closegraph();}int encode (int x, int y, int *code){ int c=0;if (x<XLEFT) c=c|LE;else if (x>XRIGHT) c=c|RI;if (y<YBOTTOM) c=c|BO;else if (y>YTOP) c=c|TO;*code=c;return code;}draw_ett(int x1, int y1, int x2, int y2, int *x, int *y) { int code1,code2,code;int xx,yy;float d,d1,d2;encode(x1,y1,&code1);encode(x2,y2,&code2);if (code2==0) { xx=x2;yy=y2; *x=xx; * y=yy;return;}if ((code1&code2)!=0) return;L1: xx=(x1+x2)/2;yy=(y1+y2)/2;encode(xx, yy, &code);d1=(yy-y1)*(yy-y1);d2=(xx-x1)*(xx-x1);d=sqrt(d1+d2);if (d<=1) { *x=xx;*y=yy; return;}if ((code&code1)!=0){ x1=xx; y1=yy; }else { x2=xx; y2=yy;}goto L1;}实验题2：实现Sutherland－Hodgeman多边形裁剪算法。

vatti裁剪算法Vatti裁剪算法是计算机图形学中非常重要的一种算法，它可以对图形进行裁剪以避免渲染过多无用区域，提高图形渲染效率。

下面，我将详细介绍Vatti裁剪算法的原理及其使用方法。

一、概述Vatti裁剪算法最初由Vatti在1984年提出，并在1992年得到了完整的形式化描述。

该算法主要用于多边形裁剪，它将多边形的裁剪视为一系列直线段的计算，从而避免了复杂的多边形运算，减少了计算量。

二、原理Vatti裁剪算法的原理可以简单概括为：将裁剪区域表示为一系列半平面的交集，将多边形表示为一系列线段的并集，然后对这两个集合进行运算，得到裁剪后的多边形。

具体来说，Vatti裁剪算法主要分为两个阶段：首先将裁剪区域表示为n个闭合的凸多边形的交集，然后将多边形分解为线段，并依次对每个线段进行裁剪运算。

1. 裁剪区域的表示a. 输入：在平面上给出n个凸多边形，表示为每个多边形的顶点。

b. 输出：一个表示裁剪区域的半平面集合。

c. 算法步骤：(1) 将每个凸多边形表示为一系列有向线段。

(2) 对每个有向线段Si，计算其左侧半平面：对于多边形中的每个顶点Vj，如果它在Si的左侧，则计算对应的另一个有向线段S'j，使得S'j与Si组成一个包含多边形的半平面。

(3) 重复步骤2，以便得到n个半平面。

(4) 对这n个半平面进行交集运算，得到裁剪区域。

2. 多边形裁剪a. 输入：一个表示多边形的线段集合，以及表示裁剪区域的半平面集合。

b. 输出：裁剪后的多边形。

c. 算法步骤：(1) 将多边形表示为一系列线段的并集。

(2) 对于每条线段Si，计算其与半平面集合的交集。

(3) 将线段的交集组成一个新的集合S'，作为裁剪后的多边形。

三、使用方法1. 准备工作在进行Vatti裁剪算法之前，需要准备好多边形的顶点和裁剪区域的半平面集合。

多边形的顶点可以通过手动或程序计算得到，而裁剪区域的半平面集合则需要根据具体需求进行计算。

计算机图形学的裁剪算法
计算机图形学的裁剪算法是图形学的一种重要算法，它的基本思想是将一个完整的几何图形（如线段、多边形、圆圈等）按照指定的裁剪窗口（矩形）进行裁剪，只保留在窗口内的部分，而把窗口外的部分抛弃掉。

由于裁剪算法的应用非常广泛，像图形显示系统、图形设备接口（GDI）和图形处理器（GPU）等都广泛使用裁剪算法。

计算机图形学的裁剪算法可以分为两种：2D裁剪算法和
3D裁剪算法。

2D裁剪算法是基于二维空间的，它将一个几何
图形投影到一个平面上，然后按照指定的窗口裁剪；而3D裁
剪算法是基于三维空间的，它将一个几何图形投影到一个三维空间，然后按照指定的窗口裁剪。

2D裁剪算法的基本步骤如下：首先，将要裁剪的几何图
形投影到平面上；其次，计算出投影后的几何图形以及裁剪窗口之间的交点；最后，将裁剪窗口内的部分保留，而把窗口外的部分抛弃掉。

3D裁剪算法的基本步骤如下：首先，将要裁剪的几何图
形投影到三维空间；其次，计算出投影后的几何图形以及裁剪窗口之间的交点；最后，将裁剪窗口内的部分保留，而把窗口外的部分抛弃掉。

计算机图形学的裁剪算法在图形处理中有着重要的作用，它不仅能够有效减少图形处理时间，而且还可以节约存储空间。

此外，它还可以有效提高图形处理效率，提高图形显示效果。

但是，它也存在着一定的局限性，比如，当几何图形的运动变得复杂时，它就会变得费时费力，这就对性能产生了一定的影响。

总之，计算机图形学的裁剪算法是图形学的重要算法，它的应用非常广泛，在图形处理中有着重要的作用。

虽然它也存在着一定的局限性，但是它仍然是一种有效的图形处理算法。

梁友栋裁剪算法梁友栋裁剪算法是计算机图形学中的一种裁剪算法，主要用于将一个多边形或直线段与一个矩形框进行裁剪。

该算法由梁友栋提出，因此得名。

该算法的基本思想是：将线段或多边形的端点表示为参数方程式，并通过求解参数方程式与裁剪边界的交点来确定裁剪后的线段或多边形。

具体来说，对于一条线段（或多边形的一条边），假设其起点为P1(x1,y1)，终点为P2(x2,y2)，则可以将其表示为以下参数方程式：x = x1 + t * (x2 - x1)y = y1 + t * (y2 - y1)其中t取值范围为[0,1]。

这个参数方程式描述了从P1到P2之间所有可能的点。

现在需要判断这条线段是否与矩形框相交，如果相交，则需要找到相交部分并输出。

对于矩形框上下左右四条边，可以分别用以下参数方程式表示：左：x = xmin右：x = xmax上：y = ymax下：y = ymin接下来需要求解线段和每条矩形边界的交点。

以左侧矩形边界为例，将其参数方程式代入线段参数方程式中，得到以下两个方程：x1 + t * (x2 - x1) = xminy1 + t * (y2 - y1) = y解这个方程组可以得到t的值，进而可以求出相交点的坐标。

对于其他边界也是类似的求解过程。

求解出所有相交点后，需要判断哪些部分需要被保留。

对于线段而言，如果起点和终点都在矩形框内，则整条线段需要被保留；如果起点和终点都在矩形框外，则整条线段需要被裁剪掉；如果只有一端在矩形框内，则需要根据相交点位置判断哪一部分需要被保留。

对于多边形而言，可以将每条边看作一个线段，然后分别进行裁剪操作。

裁剪后的所有线段再组合成新的多边形。

梁友栋裁剪算法的优势在于其简单易懂、高效快速、适用范围广泛。

它不仅可以用于二维图形的裁剪，还可以扩展到三维图形中去。

此外，在实际应用中，该算法还常常和其他算法结合使用，如多边形填充算法、图像变换算法等。

总之，梁友栋裁剪算法是计算机图形学中一种重要的裁剪算法，具有广泛的应用前景和研究价值。

Cohen-Sutherland 直线段裁剪算法是一种计算机图形学中的算法，用于裁剪二维图形中超出指定矩形区域的线段。

算法步骤如下：
定义四个常量，分别表示矩形区域的四个边界：TOP, BOTTOM, LEFT, RIGHT。

对于每条待裁剪的线段，计算其与矩形区域的交集情况，可以使用一个 4 位的二进制数表示，其中每一位分别表示线段与矩形上、下、左、右边界的交集情况。

例如，如果线段与矩形上边界有交集，则二进制数的第 0 位为 1，否则为 0。

根据线段的端点坐标和矩形区域的边界坐标，判断线段与矩形区域的相对位置关系，可以分为以下三种情况：
a. 线段完全在矩形区域内，不需要裁剪，直接保留。

b. 线段完全在矩形区域外，不需要裁剪，直接舍弃。

c. 线段部分在矩形区域内，部分在矩形区域外，需要进行裁剪。

4. 对于需要裁剪的线段，根据其与矩形边界的交点坐标，将线段裁剪成两部分，分别计算每部分与矩形区域的交集情况，并递归进行裁剪，直到所有线段都被处理完毕。

Cohen-Sutherland 直线段裁剪算法可以快速地裁剪二维图形中超出指定矩形区域的线段，是计算机图形学中的常用算法之一。

第1篇一、实验目的本次实验旨在深入理解并掌握裁剪算法的基本原理，通过编程实现Cohen-Sutherland算法和Liang-Barsky算法，对图形进行窗口裁剪，从而提高图形处理效率，优化显示效果。

二、实验环境1. 开发环境：Visual Studio 20192. 编程语言：C++3. 图形库：OpenGL三、实验内容1. 理解裁剪算法的基本原理；2. 实现Cohen-Sutherland算法；3. 实现Liang-Barsky算法；4. 对图形进行窗口裁剪，并展示裁剪效果。

四、实验过程1. 理解裁剪算法的基本原理裁剪算法是计算机图形学中的一个重要技术，用于将一个图形或图像中不需要的部分去除，只保留需要的部分。

常见的裁剪算法有Cohen-Sutherland算法、Liang-Barsky算法等。

Cohen-Sutherland算法是一种编码线段裁剪算法，通过将线段端点相对于窗口的位置进行编码，判断线段是否与窗口相交，从而实现裁剪。

Liang-Barsky算法是一种参数化线段裁剪算法，通过计算线段参数，判断线段是否与窗口相交，从而实现裁剪。

2. 实现Cohen-Sutherland算法（1）定义窗口边界首先，定义窗口边界，包括左边界、右边界、上边界和下边界。

（2）编码线段端点将线段端点相对于窗口的位置进行编码，编码规则如下：- 如果端点在窗口内，则编码为0；- 如果端点在窗口左侧，则编码为1；- 如果端点在窗口右侧，则编码为2；- 如果端点在窗口上方，则编码为4；- 如果端点在窗口下方，则编码为8。

（3）判断线段是否与窗口相交将线段两端点的编码进行异或运算，如果结果为0，则线段与窗口相交；否则，线段与窗口不相交。

（4）裁剪线段如果线段与窗口相交，则根据端点编码，将线段分为两部分，分别进行裁剪。

3. 实现Liang-Barsky算法（1）定义窗口边界首先，定义窗口边界，包括左边界、右边界、上边界和下边界。

cohensutherland裁剪算法实验报告Cohen-Sutherland裁剪算法是计算机图形学中一种常用的线段裁剪算法，它能够快速地确定一个线段是否在一个给定的窗口内部，以及剪切后的线段如何变化。

该算法的基本思想是将给定的窗口划分为九个区域，其中一种情况是窗口内没有线段，另一种情况是线段完全位于窗口内部，其他情况下需要进行裁剪处理。

具体来说，算法根据线段的起点和终点的位置判断其所处区域，并使用二进制编码进行表示。

Cohen-Sutherland裁剪算法使用四位标记，分别表示线段位于左、右、下、上四个区域。

二进制编码规则如下：左边界：0001右边界：0010下边界：0100上边界：1000当线段的二进制编码全为0时，表示线段完全位于窗口内部；当线段的二进制编码与给定窗口的二进制编码进行与运算时，结果全为0时，表示线段与窗口无交集；其他情况下则需要进行裁剪。

裁剪的具体过程如下：1. 首先计算线段起点和终点的编码，并确定是否需要裁剪；2. 若线段的编码全为0，则直接绘制该线段；3. 若线段与窗口的编码进行与运算结果全为0，则表明线段与窗口无交集，不进行绘制；4. 若线段需要进行裁剪，则计算线段与窗口的交点，并更新线段的起点和终点；5. 重复步骤2-4，直到线段裁剪完成。

Cohen-Sutherland裁剪算法的优点在于能够快速地判断线段是否与窗口有交集，并进行有效的裁剪处理。

它只需要对线段起点和终点进行编码，并进行一系列的与运算和位运算即可完成整个裁剪过程。

此外，该算法也适用于三维空间中的线段裁剪。

然而，Cohen-Sutherland裁剪算法也存在一些局限性。

当线段与窗口有交集时，该算法只能找到线段与窗口的交点，而无法找到线段与窗口的所有交点。

此外，在处理多边形的裁剪时，该算法效果不佳。

总结起来，Cohen-Sutherland裁剪算法是一种简单且高效的线段裁剪算法，适用于二维和三维空间中的线段裁剪。

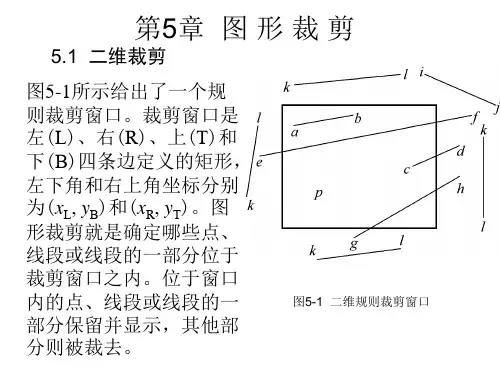
计算机图形学裁剪算法详解裁剪算法详解在使⽤计算机处理图形信息时，计算机内部存储的图形往往⽐较⼤，⽽屏幕显⽰的只是图的⼀部分。

因此需要确定图形中哪些部分落在显⽰区之内，哪些落在显⽰区之外，以便只显⽰落在显⽰区内的那部分图形。

这个选择过程称为裁剪。

最简单的裁剪⽅法是把各种图形扫描转换为点之后，再判断各点是否在窗内。

但那样太费时，⼀般不可取。

这是因为有些图形组成部分全部在窗⼝外，可以完全排除，不必进⾏扫描转换。

所以⼀般采⽤先裁剪再扫描转换的⽅法。

(a)裁剪前 (b) 裁剪后图1.1 多边形裁剪1直线段裁剪直线段裁剪算法⽐较简单，但⾮常重要，是复杂图元裁剪的基础。

因为复杂的曲线可以通过折线段来近似，从⽽裁剪问题也可以化为直线段的裁剪问题。

常⽤的线段裁剪⽅法有三种：Cohen-Sutherland,中点分割算法和梁友栋－barskey 算法。

1.1 Cohen-Sutherland裁剪该算法的思想是：对于每条线段P1P2分为三种情况处理。

（1）若P1P2完全在窗⼝内，则显⽰该线段P1P2简称“取”之。

（2）若P1P2明显在窗⼝外，则丢弃该线段，简称“弃”之。

（3）若线段既不满⾜“取”的条件，也不满⾜“弃”的条件，则在交点处把线段分为两段。

其中⼀段完全在窗⼝外，可弃之。

然后对另⼀段重复上述处理。

为使计算机能够快速判断⼀条直线段与窗⼝属何种关系，采⽤如下编码⽅法。

延长窗⼝的边，将⼆维平⾯分成九个区域。

每个区域赋予4位编码CtCbCrCl.其中各位编码的定义如下：图1.2 多边形裁剪区域编码图5.3线段裁剪裁剪⼀条线段时，先求出P1P2所在的区号code1,code2。

若code1=0,且code2=0，则线段P1P2在窗⼝内，应取之。

若按位与运算code1&code2≠0，则说明两个端点同在窗⼝的上⽅、下⽅、左⽅或右⽅。

可判断线段完全在窗⼝外，可弃之。

否则，按第三种情况处理。

求出线段与窗⼝某边的交点，在交点处把线段⼀分为⼆，其中必有⼀段在窗⼝外，可弃之。

cohensutherland裁剪算法实验报告Cohen-Sutherland裁剪算法是一种用于计算机图形学中线段裁剪的算法。

该算法用于确定一个给定的线段是否跨越了一个裁剪窗口，并且在必要的情况下将该线段裁剪到窗口内。

Cohen-Sutherland算法是一种基于二进制编码的线框裁剪算法，其运算速度很快，广泛应用于计算机图形学中。

实验内容：本次实验主要内容是使用Cohen-Sutherland裁剪算法对线段图形进行裁剪。

具体实验过程如下：1. 对于给定的线段和裁剪窗口，首先需要对线段进行编码。

2. 判断线段是否在裁剪窗口内。

如果线段的两个端点都在裁剪窗口内，则该线段完全位于裁剪窗口内，不需要进行裁剪。

3. 如果线段的两个端点都在裁剪窗口外，则该线段完全位于裁剪窗口外，在此情况下可以直接将该线段丢弃。

4. 如果线段的一个端点在裁剪窗口内，而另一个端点在裁剪窗口外，则需要对该线段进行裁剪。

5. 根据线段的编码，在裁剪窗口的不同区域内确定该线段与裁剪窗口的相交点。

6. 在裁剪窗口内，将线段裁剪到与裁剪窗口相交的部分，并输出裁剪后的线段。

实验步骤：本次实验使用Python语言编写程序，具体代码实现如下：# 定义裁剪窗口的左，下，右，上位置LEFT = 100BOTTOM = 100RIGHT = 500TOP = 400# 定义编码区域INSIDE = 0LEFT_EDGE = 1RIGHT_EDGE = 2BOTTOM_EDGE = 4TOP_EDGE = 8# 定义裁剪函数def cohen_sutherland(x1, y1, x2, y2):# 对线段进行编码code1 = encode(x1, y1)code2 = encode(x2, y2)accept = Falsewhile True:# 如果两端点都在裁剪窗口内if code1 == INSIDE and code2 == INSIDE:accept = Truebreak# 如果两端点都不在裁剪窗口内elif (code1 & code2) != 0:break# 如果有一个端点在裁剪窗口内，但另一个端点不在else:x = 0y = 0if code1 != INSIDE:code_out = code1else:code_out = code2if code_out & TOP_EDGE:x = x1 + (x2 - x1) * (TOP - y1) / (y2 - y1)y = TOPelif code_out & BOTTOM_EDGE:x = x1 + (x2 - x1) * (BOTTOM - y1) / (y2 - y1) y = BOTTOMelif code_out & RIGHT_EDGE:y = y1 + (y2 - y1) * (RIGHT - x1) / (x2 - x1)x = RIGHTelif code_out & LEFT_EDGE:y = y1 + (y2 - y1) * (LEFT - x1) / (x2 - x1)x = LEFTif code_out == code1:x1 = xy1 = ycode1 = encode(x1, y1)else:x2 = xy2 = ycode2 = encode(x2, y2)if accept:print("Line accepted from %.2f, %.2f to %.2f, %.2f." %(x1, y1, x2, y2))# 实现点编码函数def encode(x, y):code = INSIDEif x < LEFT:code = LEFT_EDGEelif x > RIGHT:code = RIGHT_EDGEif y < BOTTOM:code = BOTTOM_EDGEelif y > TOP:code = TOP_EDGEreturn code# 输入线段坐标并进行裁剪cohen_sutherland(50, 200, 600, 300)实验结果：输入线段坐标(50, 200)和(600, 300)，运行裁剪函数，输出结果为：Line accepted from 100.00, 240.00 to 500.00, 300.00.结果说明，经过裁剪后，线段(50, 200)和(600, 300)被裁剪到了裁剪窗口内，从(100, 240)到(500, 300)。

大学实验报告学院：计算机科学与信息学院专业：软件工程班级：102班** 实验组实验时间指导教师成绩实验工程名称实验五直线和多边形的裁剪实验目的掌握直线段的裁剪算法以及多边形的裁剪算法实验要求熟练掌握直线段的裁剪算法以及多边形的裁剪算法的根本原理，并编写测试代码进展实验。

实验原理Cohen-Sutherland直线剪裁算法以区域编码为根底，将窗口及其周围的，8个方向以4 bit的二进制数进展编码。

右图所示的编码方法将窗口及其邻域分为5个区域：⑴域：区域(0000)。

⑵上域：区域(1001, 1000, 1010)。

⑶下域：区域(0101, 0100, 0110)。

⑷左域：区域(1001, 0001, 0101)。

⑸右域：区域(1010, 0010, 0110)。

当线段的两个端点的编码的逻辑"与〞非零时，线段为显然不可见的，对*线段的两个端点的区号进展位与运算，可知这两个端点是否同在视区的上、下、左、右；Cohen-Sutherland直线剪裁算法的算法思想是：对于每条线段P1P2分为三种情况处理。

〔1〕假设P1P2完全在窗口，则显示该线段P1P2简称"取〞之。

〔2〕假设P1P2明显在窗口外，则丢弃该线段，简称"弃〞之。

〔3〕假设线段既不满足"取〞的条件，也不满足"弃〞的条件，则在交点处把线段分为两段。

其while (code1 != 0 || code2 != 0) {if ((code1 & code2) != 0) {// 两端点的编码相与不为0，表示直线在窗口外return;}if (code1 != 0) {code = code1;} else {code = code2;}if ((LEFT & code) != 0) {// 直线的端点与矩形窗口的左边编码相与！=0* = *L;y = y1 + (y2 - y1) * (*L - *1) / (*2 - *1);// 求直线与矩形窗口的左边界的交点} elseif ((RIGHT & code) != 0) {// 直线的端点与矩形窗口的右边编码相与！=0* = *R;y = y1 + (y2 - y1) * (*R - *1) / (*2 - *1);// 求直线与矩形窗口的右边界的交点} elseif ((BOTTOM & code) != 0) {// 直线的端点与矩形窗口的下边编码相与！=0y = YB;* = *1 + (*2 - *1) * (YB - y1) / (y2 - y1);// 求直线与矩形窗口的下边界的交点} elseif ((TOP & code) != 0) {// 直线的端点与矩形窗口的上边编码相与！=0y = YT;* = *1 + (*2 - *1) * (YT - y1) / (y2 - y1);// 直线的端点与矩形窗口的上// 边编码相与！=0}if (code == code1) {*1 = *;y1 = y;code1 = encode(*, y);} else {*2 = *;y2 = y;code2 = encode(*, y);}}g.drawLine((int) (*1 + 0.5), (int) (y1 + 0.5), (int) (*2 + 0.5),(int) (y2 +0.5));}二、多边形裁剪的核心代码为：通过点集画直线或者多边形：privatevoid draw() {//通过点集画直线或者多边形for (int i = 1; i < points.size(); i++) {Point p1 = new Point();p1 = points.get(i);int *1 = (int) p1.get*();int y1 = (int) p1.getY();Point p2 = new Point();p2 = points.get(i - 1);int *2 = (int) p2.get*();int y2 = (int) p2.getY();g.drawLine(*1, y1, *2, y2);}}多边形的裁剪函数：private Point[] cutPicture(Point[] point, Point[] edge) {// 剪裁函数，参数为〔点集，边〕Point[] intersectPoint = new Point[20];//存放交点的集合for (int j = 0; j < 20; j++) {intersectPoint[j] = new Point();}Point s = new Point();Point p = new Point();Point t = new Point();int i = 0;int length = point.length;s = point[length - 1];for (int j = 0; j < length; j++) {p = point[j];if (inside(p, edge)) {// sp在窗口，情况1if (inside(s, edge)) {intersectPoint[i] = p;i += 1;} else {// s在窗口外，情况4t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;intersectPoint[i] = p;i += 1;}} elseif (inside(s, edge)) {// s在窗口，p在窗口外，情况3t = intersect(s, p, edge);intersectPoint[i] = t;i += 1;}// 情况2没有输出s = p;}List<Point> tempList = new ArrayList<Point>();for (int k = 0; k < i; k++) {if (intersectPoint[k] != null) {Point pt = intersectPoint[k];tempList.add(pt);}}Point[] temp = new Point[tempList.size()];for (int j = 0; j < tempList.size(); j++) {temp[j] = new Point();temp[j] = tempList.get(j);}intersectPoint = temp;return intersectPoint;}判断点是否在裁剪边的可见侧：privateboolean inside(Point point, Point[] edge) {//判断点是否在裁剪边的可见侧// 裁剪边为窗口下边if ((edge[0].y == edge[1].y) && (edge[0].* < edge[1].*)) {if (point.y >= edge[0].y) {returntrue;}}// 裁剪边为窗口上边if ((edge[0].y == edge[1].y) && (edge[0].* > edge[1].*)) {if (point.y <= edge[0].y) {returntrue;}}// 裁剪边为窗口右边if ((edge[0].* == edge[1].*) && (edge[0].y < edge[1].y)) {if (point.* <= edge[0].*) {returntrue;}}// 裁剪边为窗口左边if ((edge[0].* == edge[1].*) && (edge[0].y > edge[1].y)) {if (point.* >= edge[0].*) {returntrue;}}returnfalse;}直线段与窗口边界求交：private Point intersect(Point s, Point p, Point[] edge) {//直线段与窗口边界求交，并返回交点Point t = new Point();if (edge[0].y == edge[1].y) {// 水平裁剪边t.y = edge[0].y;t.* = s.* + (edge[0].y - s.y) * (p.* - s.*) / (p.y - s.y);} elseif (edge[0].* == edge[1].*) {// 垂直裁剪边t.* = edge[0].*;t.y = s.y + (edge[0].* - s.*) * (p.y - s.y) / (p.* - s.*);}return t;}鼠标的监听类〔部类〕：class MouseMonitor e*tends MouseAdapter {//通过鼠标的单击获取点，并画出直线或者多边形publicvoid mouseClicked(MouseEvent e) {points.add(e.getPoint());if (points.size() > 1) {draw();}}}键盘的监听类〔部类〕：class KeyMonitor e*tends KeyAdapter {// 键盘控制publicvoid keyPressed(KeyEvent e) {switch (e.getKeyCode()) {case KeyEvent.VK_R:// 清空画布和点集panel.repaint();points.removeAll(points);break;case KeyEvent.VK_W://对裁剪窗口的处理g.setColor(Color.RED);g.drawRect(*L, YB, *R - *L, YT - YB);//存放裁剪窗口的边top = new Point[2];// 存放裁剪窗口的上边top[0] = new Point(*L, YB);top[1] = new Point(*R, YB);right = new Point[2];//存放裁剪窗口的右边right[0] = new Point(*R, YB);right[1] = new Point(*R, YT);bottom = new Point[2];//存放裁剪窗口的下边bottom[0] = new Point(*R, YT);bottom[1] = new Point(*L, YT);left = new Point[2];//存放裁剪窗口的左边left[0] = new Point(*L, YT);left[1] = new Point(*L, YB);break;case KeyEvent.VK_A://对直线段进展裁剪g.setColor(Color.GREEN);Point p1 = points.get(0);Point p2 = points.get(1);lineCut(p1.get*(), p1.getY(), p2.get*(), p2.getY()); break;case KeyEvent.VK_B://对多边形进展裁剪source = new Point[points.size()];//得到多边形的点for (int i = 0; i < points.size(); i++) {source[i] = points.get(i);}g.setColor(Color.GREEN);wT = cutPicture(source, top);//得到多边形与裁剪窗口上边的交点wR = cutPicture(wT, right);//得到多边形与裁剪窗口右边的交点wB = cutPicture(wR, bottom);//得到多边形与裁剪窗口下边的交点wL = cutPicture(wB, left);//得到多边形与裁剪窗口左边的交点第二种情况：线段在裁剪窗口的部，线段完全可见。

中点裁剪算法中点裁剪算法（Midpoint Clipping Algorithm）是计算机图形学中常用的裁剪算法之一。

它主要用于将超出视窗范围的线段进行裁剪，使其仅展示在视窗内部的部分，从而提高图形渲染的效率，减少不必要的计算和显示。

生动起来，我们可以将视窗比喻成日常生活中的窗户。

当我们通过窗户观察外面的风景时，有时候可能会看到一段超过窗户边界的景象，这时我们会用窗户的框架来“裁剪”这段景象，只显示窗户内部的景象。

同样，中点裁剪算法就是模拟这个过程，在计算机图形中，通过剔除超出视窗的线段部分，加速图形显示的过程。

中点裁剪算法的核心思想是利用直线的斜率来判断线段与视窗边界的交点，并判断线段是否位于视窗内。

它的基本步骤如下：1. 首先确定视窗的边界，可以是矩形、圆形或其他形状。

2. 对于每条线段，判断其两个端点是否位于视窗内，如果都在视窗内，则直接显示该线段。

3. 如果线段的一个端点在视窗内，另一个端点在视窗外，则根据线段的斜率确定其与视窗边界的交点。

4. 根据交点的位置和斜率，确定裁剪的起点和终点，从而得到位于视窗内的线段。

5. 重复以上步骤，对所有需要裁剪的线段进行处理。

中点裁剪算法的优点是简单、高效、易于实现。

它避免了对线段上的每个像素进行判断，而是通过斜率的变化快速确定起点和终点。

同时，由于其采用了从线段起点到终点的扫描方式，可以保证裁剪结果的准确性和连贯性。

除了在计算机图形学中的应用外，中点裁剪算法还可以应用于计算机辅助设计、机器人运动控制等领域。

它为我们展示了如何通过简单的几何计算方法，提高图形处理和计算效率的思路和方法。

总而言之，中点裁剪算法是一种有效的裁剪算法，具有广泛的应用场景。

通过合理利用线段的斜率和裁剪边界的交点，它可以快速准确地裁剪线段，提高图形渲染效率，使得图形显示更加符合人眼观察的要求。

在实际应用中，我们可以根据具体需求进行改进和扩展，以满足不同场景下的裁剪需求。