计算机图形学二维图形的裁剪
- 格式:pptx
- 大小:109.40 KB
- 文档页数:7




计算机图形学中的二维裁剪算法研究计算机图形学研究的是如何在计算机上制图,根据研究对象的不同又分为二维图形学和三维图形学。
二维图形学研究的范畴是点,线,面。
本文就是介绍计算机图形学中的众多基本算法之一的二维剪裁算法。
在二维剪裁算法中,椭圆形窗口线剪裁算法又是应用最为广泛的算法之一,所以将是本文重点论述的对象。
标签:计算机图形学;二维剪裁算法;椭圆形窗口线剪裁算法计算机图形学中的基本算法对于计算机图形学应用于实践有着重要的作用,而且算法需要时时更新才能够发挥出计算机图形学在实践中的作用。
本文对计算机二维剪裁算法进行介绍,并对其中的椭圆窗口线剪裁算法进行着重的研究分析,探讨如何使该算法更加的稳定高效,方便易行。
算法可以指导人们的工作与生活,所以笔者在本文通过坐标分析设计出一个算法以供读者参考。
1 二维剪裁算法的基本介绍剪裁算法是计算机图形学中的基础算法之一。
剪裁在日常生活和工作中的应用十分广泛,最典型的一个应用就是对整体场景中的局部目的物进行剪裁。
剪裁的过程其实就是将场景中的目的物标记圈出来,一般为矩形窗口框圈出。
矩形窗口框为闪动的虚线框,可以根据剪裁的目的物大小随意变换矩形框的大小。
此外具体说来,剪裁算法还有其他的形式。
如:点剪裁,线段剪裁,多边形剪裁,曲线及文字剪裁等。
现在笔者再详细介绍二维剪裁算法。
二维剪裁算法分为两种,一种是对线段的剪裁,一种是对多边形的剪裁。
因为线段和多边形往往是二维平面中的图形,故而使用二维剪裁算法对其进行剪裁。
目前对该领域的研究已经取得了很丰硕的成果,已经有很多成熟也高效实用的二维剪裁算法。
详细地来说,这些经典的算法有Cyrus—berk二维剪裁算法,Cohen—Sutherland二维多边形剪裁算法等等。
2 椭圆形窗口线剪裁算法的简介在计算机图形学中,椭圆形窗口线剪裁算法是十分重要的一种基础算法。
该算法之所以十分重要,笔者总结为两点原因:首先椭圆形是几何图形中最基础的图形之一,其次在我们的日常生活和工作当中有很多地方的剪裁工作是更适合椭圆形的(我们生活与工作之中,很少有标准的圆形目的物去剪裁,更多情况下是不规则的图像剪裁,而椭圆形可以更好的,更多的剪裁出合适的目的物)。



计算机图形学的裁剪算法
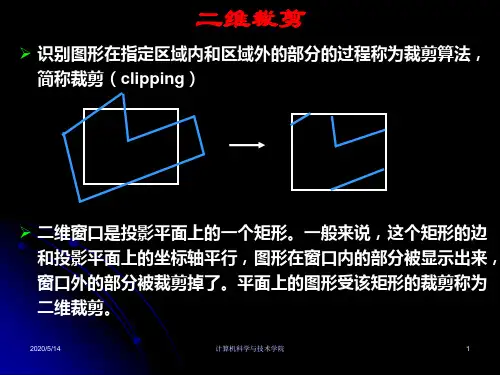
计算机图形学的裁剪算法是图形学的一种重要算法,它的基本思想是将一个完整的几何图形(如线段、多边形、圆圈等)按照指定的裁剪窗口(矩形)进行裁剪,只保留在窗口内的部分,而把窗口外的部分抛弃掉。
由于裁剪算法的应用非常广泛,像图形显示系统、图形设备接口(GDI)和图形处理器(GPU)等都广泛使用裁剪算法。
计算机图形学的裁剪算法可以分为两种:2D裁剪算法和
3D裁剪算法。
2D裁剪算法是基于二维空间的,它将一个几何
图形投影到一个平面上,然后按照指定的窗口裁剪;而3D裁
剪算法是基于三维空间的,它将一个几何图形投影到一个三维空间,然后按照指定的窗口裁剪。
2D裁剪算法的基本步骤如下:首先,将要裁剪的几何图
形投影到平面上;其次,计算出投影后的几何图形以及裁剪窗口之间的交点;最后,将裁剪窗口内的部分保留,而把窗口外的部分抛弃掉。
3D裁剪算法的基本步骤如下:首先,将要裁剪的几何图
形投影到三维空间;其次,计算出投影后的几何图形以及裁剪窗口之间的交点;最后,将裁剪窗口内的部分保留,而把窗口外的部分抛弃掉。
计算机图形学的裁剪算法在图形处理中有着重要的作用,它不仅能够有效减少图形处理时间,而且还可以节约存储空间。
此外,它还可以有效提高图形处理效率,提高图形显示效果。
但是,它也存在着一定的局限性,比如,当几何图形的运动变得复杂时,它就会变得费时费力,这就对性能产生了一定的影响。
总之,计算机图形学的裁剪算法是图形学的重要算法,它的应用非常广泛,在图形处理中有着重要的作用。
虽然它也存在着一定的局限性,但是它仍然是一种有效的图形处理算法。


西北农林科技大学实习报告学院名称:理学院专业班级:姓名:学号:课程:计算机图形学实验报告日期:第十五周实验四二维图形的裁剪一、实验目的1)加深直线段的剪裁算法的理解。
2)熟练掌握一种裁剪算法的编程方法。
二、实验步骤1)分析直线段和矩形窗口的位置关系,选定比较合理算法流程。
2)画出程序流程图。
3)编写程序的源程序。
4)编辑源程序并进行调试。
5)进行特殊模式的运行测试,并结合情况进行调整。
三、实验内容1)在编码算法、中点分割算法、Liang-Barsky算法三种中任选一种作为编程模型。
2)编写直线段裁剪的源程序。
3)建议有能力的学生编写多边形裁剪程序。
4)在计算机上编辑编译运行,实现直线段的裁剪。
原理1.直线和窗口的关系:直线和窗口的关系可以分为如下3类:(1)整条直线在窗口内。
此时,不需剪裁,显示整条直线。
(2)整条直线在窗口外,此时,不需剪裁,不显示整条直线。
(3)部分直线在窗口内,部分直线在窗口外。
此时,需要求出直线与窗框的交点,并将窗口外的直线部分剪裁掉,显示窗口内的直线部分。
直线剪裁算法有两个主要步骤。
首先将不需剪裁的直线挑出,即删去在窗外的直线。
然后,对其余直线,逐条与窗框求交点,并将窗口外的部分删去。
2.Cohen-Sutherland直线剪裁算法:(1)输入直线段的两端点坐标p1(x1,y1),p2(x2,y2),以及窗口的4条边界坐标,y wt ,y wb,y wl,y wr.(2)对p1,p2进行编码,点p1的编码为code1,点p2的编码为code2.(3)若code1| code2=0,对直线p1p2“简取”之,转(6);否则,若code1& code2≠0,对直线段“简弃”之,转(7);当上述两条均不满足时,进行步骤(4)。
(4)确保p1在窗口外部。
若p1在窗口内,则交换p1和p2的坐标值和编码。
(5)根据p1编码从低位开始寻找值为1的地方,从而确定p1在窗口外的哪一侧,然后求出直线段与相应窗口边界的交点S,并用交点S的坐标值替换p1的坐标值,即在交点S处把线段一分为二,因此可以去掉p1S。