当前位置：文档之家 › § 10-5 直齿圆柱齿轮传动的承载能力计算

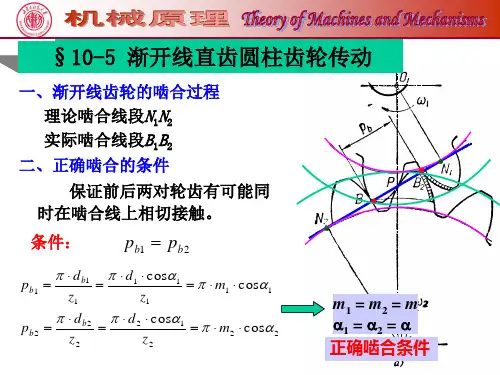
§ 10-5 直齿圆柱齿轮传动的承载能力计算

  • 格式：ppt
  • 大小：3.32 MB
  • 文档页数：44

下载文档原格式

  / 44

合集下载

齿轮传动的受力分析

齿轮传动的受力分析

轮齿的受力分析
10-8 标准锥齿轮传动 的强度计算
§10-8 标准锥齿轮传动的强度计算
二、轮齿的受力分析
2
Fa2
Fr2
Ft2 × ⊙
Fa1
Fn α
直齿圆柱齿轮强度计算1
F' Fr1
Ft1 Fa1 P
Ft1
n1 Fr1
T1
1
δ1
Fn
Ft －圆周力， ★主反从同 Fr －径向力， ★指向各自的轮心
Ft
1
Fr1
ω1
Ft1
Ft2
Fωr22
Ft1 × Fr1 Fr2 ⊙ Ft2
2
10-7 标准斜齿 圆柱齿轮传动的 强度计算
轮齿的受力分析
§10-7 标准斜齿圆柱齿轮传动的强度计算
一、轮齿的受力分析
圆周力Ft—主反从同
Ft
2T1 d1
径向力Fr—指向各自的轮心
F' Ft 2T1
cos d1cos
Fr F'tann2d T1 1ctao nsn
Fn
T1
N2
αt
d21
t
N1
O2
α
Fr
c
Fn N2 αt
Ft
d21
★方向： 圆周力Ft—主反从同 径向力Fr—指向各自的轮心
α ω1
O（1主动）
α ω1
O1（主动）
§10-5 标准直齿圆柱齿轮传动的强度计算
图示直齿圆柱齿轮，轮1主动，转向直如齿圆图柱齿轮，强度试计算1在图中标出Ft1 Ft2 Fr1 Fr2的方向。
轴向力Fa—主动轮左右手螺旋法则
d
2 n2
P
Ft
Fa2

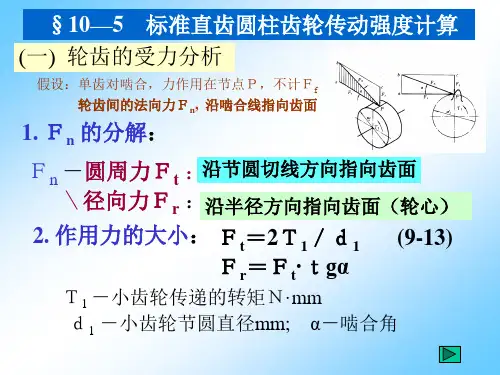
齿轮传动系数计算方法

齿轮传动系数计算方法

齿宽系数φ 的选择： ⒊ 齿宽系数 d 的选择： φd ↑→ b ↑ →承载能力↑ 表10—7 但载荷分布不 均匀↑→应取得适当 计算（实用）齿宽 ： b= φd d1 B1=b+5~8 B2=b
㈡ 齿轮传动的许用应力
齿轮的许用应力： 齿轮的许用应力：
K N σ lim [σ ] = S
弯曲: 弯曲 S=SF=1.25~1.5
2
2 KT1 u ± 1 Z E d1 ≥ 2.32 3 ⋅ φd u [σ H ]
（四）齿轮传动强度计算说明
因配对齿轮σ ⒈ 因配对齿轮 H1 =σH2，按接触设计时取 [σH] 1 与[σH] 2的较小者代入设计公式 较小者代入设计公式 2. 硬齿面齿轮传动，材料、硬度一样，设计时 硬齿面齿轮传动，材料、硬度一样， 分别按两种强度设计，取较大者为计算结果 分别按两种强度设计，
d 1 = d 1t 3 K K t
或 m n = m nt 3 K K t
齿轮传动的设计参数、 §10—6 齿轮传动的设计参数、许用应力与精度选择 ㈠齿轮传动的设计参数选择 压力角α的选择 的选择: ⒈ 压力角 的选择 一般齿轮 α=20°； 航空用齿轮α=25° 齿数的选择： ⒉ 齿数的选择： d1一定，齿数Ｚ1 ↑→重合度 平稳性好 一定，齿数Ｚ 重合度↑平稳性好 重合度 →m小→加工量 ，但齿轮弯曲强度差 小 加工量 加工量↓， 闭式软齿面 闭式软齿面 ：Ｚ1宜取多→提高平稳性，Ｚ1 =20~40 Ｚ 开式或闭式硬齿面 齿面：Ｚ1宜取少→保证轮齿弯曲强度 开式或闭式硬齿面 Ｚ1 ≥17 (ha*=1,C*=0.25)
p ca cos γ ⋅ h 6 p ca cos γ ⋅ h M σ F0 = = = 2 W 1× S S2 6 KFt 取 h = K h m ， S = K s m ， p ca = 代入得： b cos α 6 KFt cos γ ⋅ K h m KFt 6 K h cos γ = ⋅ σ F0 = 2 bm K s 2 cos α b cos α ⋅ (K s m )

直齿圆柱齿轮传动的受力分析和载荷计算

直齿圆柱齿轮传动的受力分析和载荷计算

齿轮的受力方向： 根据齿轮的工作 状态，确定受力 方向是垂直于齿 轮轴线还是平行 于齿轮轴线。
齿轮的受力大小： 根据齿轮的工作 条件、材料、转 速等因素，计算 齿轮的受力大小。
齿轮的受力分析： 分析齿轮在传动 过程中所受到的 力，包括主动轮 上的驱动力和从 动轮上的阻力。
齿轮的受力计算： 根据齿轮的几何 尺寸、转速、材 料等因素，计算 齿轮的受力，为 齿轮的强度校核 和设计提供依据。
齿轮热效应：齿轮传动过程中的摩擦和发热，导致齿轮变形和热不平衡，引起齿轮振动和噪 声
齿轮制造误差：如齿形误差、齿距 误差等
齿轮动态特性：如固有频率、阻尼 比等
添加标题
添加标题
添加标题
添加标题
装配误差：如中心距误差、轴线平 行度误差等
工作条件：如负载大小、转速高低、 润滑条件等
振动频率：分析齿轮的振动频率，判断是否符合设计要求。 振动幅度：测量齿轮的振动幅度，判断是否在允许范围内。 噪声等级：根据齿轮的噪声等级，评估其对环境的影响程度。 动态响应：分析齿轮的动态响应特性，评估其抗干扰能力和稳定性。
单击此处添加标题
齿轮的效率对于齿轮传动系统的性能和可靠性具有重要影响，是评估齿轮传动系 统性能的重要指标之一。
单击此处添加标题
在直齿圆柱齿轮传动中，其效率计算公式为：η=1-(d/D)，其中η为齿轮的效率， d为齿轮的分度圆直径，D为齿轮的齿传递的功率与输入功率之比 计算公式：效率=输出功率/输入功率 影响因素：齿轮的制造精度、润滑条件、传动装置的装配精度等 提高效率的方法：优化设计、提高制造和装配精度、改善润滑条件等
XX,a click to unlimited possibilities
汇报人：XX
CONTENTS

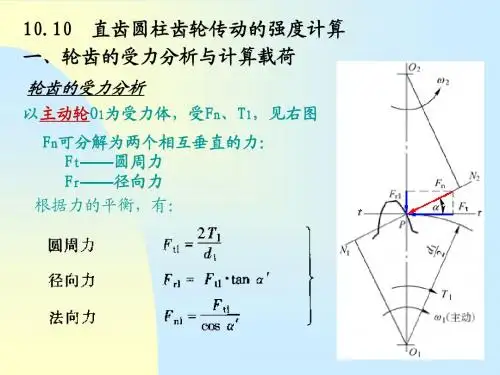
15直齿圆柱齿轮传动的强度计算

15直齿圆柱齿轮传动的强度计算

二、齿轮传动的强度计算
齿轮传动的强度计算是根据轮齿可能出现的失效形式和 设计准则来进行的，由于轮齿的主要失效形式是齿面疲劳点 蚀和轮齿疲劳折断，因此只讨论齿面接触疲劳强度和齿根弯 曲疲劳强度的计算
1.齿面接触疲劳强度计算 1.齿面接触疲劳强度计算
针对齿面点蚀失效进行的 齿面点蚀是因为接触应力过大引起的。 接触应力过大引起的 齿面点蚀是因为接触应力过大引起的。齿轮啮合可看 作是分别以接触处的曲率半径ρ 作是分别以接触处的曲率半径ρl、ρ2为半径的两个圆柱 赫兹应力公式计算 体的接触，其最大接触应力可由赫兹应力公式计算， 体的接触，其最大接触应力可由赫兹应力公式计算，即
10.10 直齿圆柱齿轮传动的强度计算 一、轮齿的受力分析与计算载荷
轮齿的受力分析
以主动轮O1为受力体，受Fn、T1，见右图 主动轮O 为受力体， 可分解为两个相互垂直的力： Fn可分解为两个相互垂直的力： Ft——圆周力 圆周力 Fr——径向力 径向力 根据力的平衡，有：
其中： 其中： 主动轮传递的转矩Ｎ mm Ｔ1 －主动轮传递的转矩Ｎ·mm 主动轮分度圆直径mm; mm;非标准时用节圆直径代替 ｄ1 －主动轮分度圆直径mm;非标准时用节圆直径代替
对于斜齿圆柱齿轮传动从前端面进入啮合到后端面脱离啮合其在啮合线上的长度比直齿圆柱齿轮增加了btg斜齿圆柱齿轮的啮合面斜齿圆柱齿轮传动的重合度端面重合度附加重合度附加重合度是由于齿的倾斜而产生它随齿宽b和的增大而增大这是斜齿轮传动平稳承载能力较高的原因之一当量齿轮及当量齿数在研究斜齿轮法面齿形时可以虚拟一个与斜齿轮的法面齿形相当的直齿轮称这个虚拟的直齿轮为该斜齿的当量齿轮其齿数则称四斜齿圆柱齿轮的当量齿数和最小齿数在进行强度计算和用成形法加工齿轮选择铣刀时必须知道斜齿轮的法面齿形通常用近似的方法来分析做法如图所示过斜齿轮分度圆柱上齿廓的任一点c作齿的法面nn该法面与分度圆柱面的交线为一椭圆椭圆的长半轴为

第10章_齿轮传动

第10章_齿轮传动
2KTYFaYsa 1 校核公式： 校核公式： σF = ≤ [σF ] 3 2 φd m z1
2KT YFaYsa 1 m≥ 3 ⋅ 设计公式： 设计公式： 2 φdz1 [σF ]
三、齿面接触疲劳强度计算 基本公式──赫兹应力计算公式， 基本公式 赫兹应力计算公式，即: 赫兹应力计算公式
F ×( ± ) ca 小齿轮单对齿啮合的 ρ1 ρ2 σH = 最低点综合曲率最大。 最低点综合曲率最大。 2 1− µ2 1− µ1 2 π( + )L E E 1 1 为方便计算， 为方便计算， 1 1 1 以节点为接触应力计算点。 以节点为接触应力计算点。 为综合曲率 令 = ± 1 1
二、齿轮的设计准则 轮齿折断 齿面点蚀 齿面磨损 齿面胶合 塑性变形 设计准则： 设计准则： 保证足够的齿根弯曲疲劳强度，以免发生齿根折断。 保证足够的齿根弯曲疲劳强度，以免发生齿根折断。 保证足够的齿面接触疲劳强度，以免发生齿面点蚀。 保证足够的齿面接触疲劳强度，以免发生齿面点蚀。 闭式软齿面齿轮传动， 闭式软齿面齿轮传动，以保证齿面接触疲劳强度为主 闭式硬齿面或开式传动，以保证齿根弯曲疲劳强度为主。 闭式硬齿面或开式传动，以保证齿根弯曲疲劳强度为主。
再去查图（ 再去查图（KFN， KHN ）
—— σlim为齿轮的疲劳极限
弯曲强度计算时： 弯曲强度计算时： σlim＝σFE 接触强度计算时： 接触强度计算时： σlim＝σHlim
—— S为安全系数 为安全系数
弯曲强度计算时： 弯曲强度计算时： S= S F=1.25~1.50 接触强度计算时： 接触强度计算时： S= S H=1.0
三、齿轮材料选用的基本原则 齿轮材料必须满足工作条件的要求，如强度、 齿轮材料必须满足工作条件的要求，如强度、 寿命、可靠性、经济性等； 寿命、可靠性、经济性等； 应考虑齿轮尺寸大小，毛坯成型方法及热处理 应考虑齿轮尺寸大小， 和制造工艺； 和制造工艺； 钢制软齿面齿轮， 钢制软齿面齿轮，其配对两轮齿面的硬度差应 保持在30~50HBS或更多。 或更多。 保持在 或更多

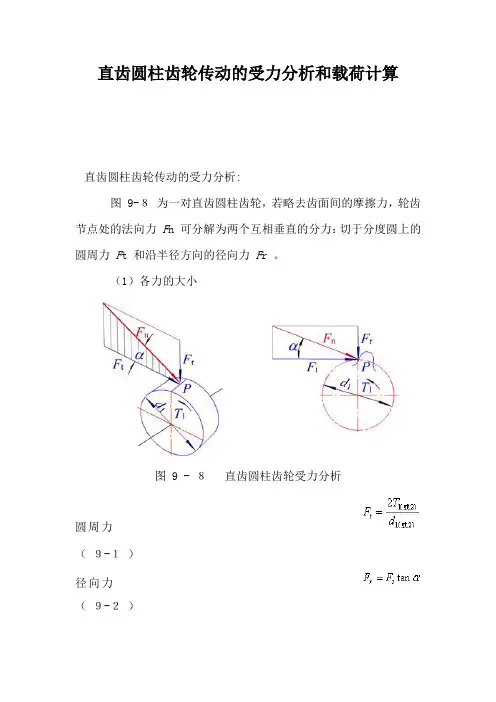
直齿圆柱齿轮传动的受力分析和载荷计算

直齿圆柱齿轮传动的受力分析和载荷计算

直齿圆柱齿轮传动的受力分析和载荷计算直齿圆柱齿轮传动的受力分析:图 9-８为一对直齿圆柱齿轮，若略去齿面间的摩擦力，轮齿节点处的法向力F n 可分解为两个互相垂直的分力：切于分度圆上的圆周力F t 和沿半径方向的径向力F r 。

（1）各力的大小图 9 - ８直齿圆柱齿轮受力分析圆周力（９-１）径向力（９-２）法向力（９-３）其中转矩（９-４）式中：T1 ，T2 是主、从动齿轮传递的名义转矩，N.mm ；d1 ，d2 是主、从动齿轮分度圆直径， mm ；为分度圆压力角；P是额定功率， kW ；n1 ，n2 是主动齿轮、从动轮的转速， r/min 。

作用在主动轮和从动轮上的各对应力大小相等，方向相反。

即：，，（2）各力的方向主动轮圆周力的方向与转动方向相反；从动轮圆周力的方向与转动方向相同；径向力F r 分别指向各自轮心 ( 外啮合齿轮传动 ) 。

9.4.2 计算载荷前面齿轮力分析中的F n 、F t 和F r 及F a 均是作用在轮齿上的名义载荷。

原动机和工作机性能的不同有可能产生振动和冲击；轮齿在啮合过程中会产生动载荷；制造安装误差或受载后轮齿的弹性变形以及轴、轴承、箱体的变形，会使载荷沿接触线分布不均，而同时啮合的各轮齿间载荷分配不均等，因此接触线单位长度的载荷会比由名义载荷计算的大。

所以须将名义载荷修正为计算载荷。

进行齿轮的强度计算时，按计算载荷进行计算。

（９－４）计算载荷(９ - ５)载荷系数(９- ６)式中：K是载荷系数；K A 是使用系数；K v 是动载系数；是齿向载荷分布系数；是齿间载荷分配系数。

1 ．使用系数K A使用系数K A 是考虑由于齿轮外部因素引起附加动载荷影响的系数。

其取决于原动机和工作机的工作特性、轴和联轴器系统的质量和刚度以及运行状态。

其值可按表 9 - ３选取。

表 9-３使用系数K A工作机的工作特性工作机器原动机的工作特性及其示例电动机、均匀运转的蒸气机、燃气轮机蒸气机、燃气轮机液压装置电动机（经多缸内燃机单缸内燃机（小的，启动转矩大）常启动启动转矩大）均匀平稳发电机、均匀传送的带式或板式运输机、螺旋输送机、轻型升降机、机床进给机构、通风机、轻型离心机、均匀密度材料搅拌机等1.00 1.101.251.50轻微冲击不均匀传送的带式输送机、机床的主传动机构、重型升降机、工业与矿用风机、重型离心机、变密度材料搅拌机、给水泵、转炉、轧机、1.25 1.351.51.75中等冲击橡木工机械、胶积压机、橡胶和塑料作间断工作的搅拌机、轻型球磨机、木工机械、钢坯初轧机、提升装置、单缸活塞泵等1.50 1.601.752.00严重挖掘机、重型球磨机、橡 1.75 1.85 2.0 2.25冲击胶揉合机、落沙机、破碎机、重型给水泵、旋转式钻探装置、压砖机、带材冷轧机、压坯机等0或更大注： 1. 对于增速传动，根据经验建议取表中值的 1.1 倍。

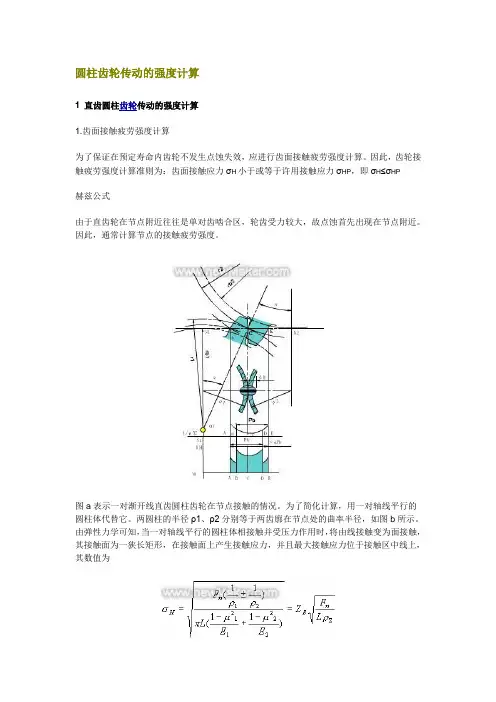
圆柱齿轮传动强度的计算

圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。

上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。

齿轮传动

齿轮传动

Kα取决于轮齿刚度、pb误差、修缘量等。
KHα——用于σH KFα ——用于σF
10-4 齿轮传动的计算载荷
26
4、齿向载荷分配系数Kβ 考虑使轮齿沿接触线产生载荷分布不均匀现象。 制造方面：齿向误差 影响因素 安装方面：轴线不平行等 使用方面：轴变形、轮齿变形、支承变形等
讨论：
a）轴承作非对称布置时， 弯曲变形对Kβ的影响。
10-2 齿轮传动的失效形式及设计准则 6
失效形式
齿轮的失效发生在轮齿，其它部分很少失效。
失效形式
轮齿折断 齿面损伤
齿面接触疲劳磨损（齿面点蚀） 齿面胶合 齿面磨粒磨损
齿面塑性流动 一、轮齿折断
常发生于闭式硬齿面或开式传动中。
现象：①局部折断 ②整体折断
10-2 齿轮传动的失效形式及设计准则 7
3、有良好的加工工艺性，便于齿轮加工。 1）大直径d＞400 用ZG 2）大直径齿轮：齿面硬度不宜太高，HB＜200，以免中途换刀
4、材料易得、价格合理。 举例：起重机减速器：小齿轮45钢调质 HB230~260 大齿轮45钢正火 HB180~210 机床主轴箱：小齿轮40Cr或40MnB 表淬 HRC50~55 大齿轮40Cr或40MnB 表淬 HRC45~50
第十章 齿 轮 传 动
§10-1 齿轮传动概述 §10-2 齿轮传动的失效形式及设计准则 §10-3 齿轮的材料及其选择原则 §10-4 齿轮传动的计算载荷 §10-5 标准直齿圆柱齿轮传动的强度计算 §10-6 齿轮传动设计参数、许用应力与精度选择 §10-7 标准斜齿圆柱齿轮传动的强度计算 §10-8 标准锥齿轮传动的强度计算 §10-9 齿轮的结构设计 §10-10 齿轮传动的润滑
动载系数

齿轮2

齿轮2

齿轮滚刀
二、根切现象、不根切的最少齿数和变位修正法
1.根切现象 用范成法切削标准齿轮时,如果齿轮 的齿数过少，刀具的齿顶就会切去轮齿根 部的一部分，这种现象称为根切。 2.根切原因
.
3. 不产生根切的最少齿数 不根切条件 PN1≥ PB2
ha rsin≥ sin h* m a mZ sin≥ sin 2 a 2 h* 得: Z≥ sin2
（1）无侧隙啮合方程式：
inv 2 tan ( x1 x2 ) /( z1 z2 ) inv
用此公式，已知（ x1+x2 ）时，求出啮合角， 再根据 acos = acos ，进一步求出变位齿轮
1
O1

传动满足无侧隙条件的中心距 a 。
中心距变动系数 y: ym= a- acos ，求出啮合 已知 a ）时，根据 acos = a
每把刀的刀刃形状,按它加工范围的最少齿数齿轮的齿形 来设计。
2.范成法
切削 （沿轮坯轴向） 进刀和让刀 （沿轮坯径向） 范成运动 （模拟齿轮啮合传动） 刀具与轮坯以i12=1/2=Z2 /Z1回转
用同一把刀具,通过 调节i12 ,就可以加工相 同模数、相同压力角 , 不同齿数的齿轮。
齿轮插刀
齿条插刀
ym (r1 r2 ) cos / cos (r1 r2 ) 角， 再根据无侧隙啮合方程式，进一步求出 y ( z1 z )(cos ） 。 变位系数和（2 x1+x2 / cos 1) / 2

2
O2
z z a a ym 1 2 y m 2
重合度与Z1、Z2及有关 齿数愈多 重合度愈大 啮合角愈大 重合度愈小
§10-6 渐开线齿廓的切制原理、根切和最少齿数

10-05 标准直齿圆柱齿轮传动的强度计算

10-05 标准直齿圆柱齿轮传动的强度计算

受载分析及应力计算公式
当齿顶受载时，轮齿根部
的应力如图。载荷 pca 对危险 截面产生的应力有弯曲应力和 压应力。 注意：在齿根危险截面处
的压应力仅为弯曲应力的百分
之几，故可忽略。计算时仅考 虑水平分力产生的弯曲应力。
受载分析及应力计算公式
取h = Khm，S = KSm，并将
代入，得：
齿形系数YFa及应力校正系数YFs
YFa是一个无量纲系数，它只与轮齿的齿廓形状有关，而与 齿的大小（模数m）无关。 在实际计算时，还应计入齿根危险截面处的过渡圆角所引 起的应力集中作用以及弯曲应力以外对齿根应力的影响，因此， 引入应力校正系数YSa。 齿根弯曲疲劳强度校核计算公式 ：
齿形系数YFa及应力校正系数YSa 表
齿根弯曲疲劳强度公式
10-5 标准直齿圆柱齿轮传动的强度计算
（1）轮齿的受力分析
（2）齿根弯曲疲劳强度计算
（3）齿面接触疲劳强度计算
（4）齿轮传动的强度计算说明
轮齿的受力分析
• 法向载荷Fn • 圆周力Ft • 径向力Fr
T1——小齿轮传递的转矩，N.mm； d1——小齿轮的节圆直径，对标准齿轮即为分 度圆直径，mm； α——啮合角，对标准齿轮，α=20°。
齿根弯曲疲劳强度校核计算公式 ：
按齿根弯曲疲劳强度设计齿轮的计算公式：
按齿根弯曲疲劳强度设计时，[σ]F1/(YFa1YSa1)或 [σ]F2/(YFa2YSa2)中较小的数值代入设计公式进行计算。
齿宽系数
装置 状况 φd 两支承相对小 齿轮对称布置 0.9-1.4 (1.2-1.9) 两支承相对小齿 轮不对称布置 0.7-1.15 (1.1-1.65) 小齿轮作 悬臂布置 0.4-0.6

§10—5渐开线直齿圆柱齿轮的啮合传动

§10—5渐开线直齿圆柱齿轮的啮合传动

△=e2′-s1′= e1′-s2′ 但为了使齿轮在正转和反转 时避免轮齿间的冲击，这种齿侧 间隙一般都很小，通常是由制造 公差来保证的。而在设计、计算 齿轮的公称尺寸时，都按无侧隙 来考虑，即△=0。 由图10-13可见，侧隙的大小 与中心距的大小有关。
2）保证两轮的顶隙c为标准值，即c=c*m。 在一轮的齿顶圆 与另一轮的齿根圆之 间应留有一定的间隙， 称为顶隙。顶隙的标 准值为c=c*m。 由图可见，顶隙 的大小也与中心距大 小有关。
图10-17
2、重合度(Contact 、
Ratio)
通常把B1B2与pb的比值εα称为齿轮传动的重合度 重合度。其 重合度 大小反映了齿轮连续传动的程度。则： εα= B1B2 / pb≥1——连续传动条件 在实际的工程中，应要求εα≥[εα]（许用重合度 许用重合度）。 [εα] 许用重合度 随齿轮机构的使用要求和制造精度而定，常用的推荐值见 P184表10-3。
∵ a= r1 +r2= r1′+r2′ 且i12= r2′/ r1′= r2 / r1 ∴ r1= r1′， r2= r2′即分度圆 与节圆重合，两个分度圆 相切。 这种按标准中心距 （即分度圆与节圆重合） 的安装，称为标准安装 标准安装。 标准安装
在标准安装时： ∵ 标准齿轮分度圆上：s1= e1= s2=e2=πm/2，且分度圆与 节圆重合 ∴ s1′= e1′= s2′=e2′=πm/2 ∴ △=e2′-s1′= e1′-s2′=0 ——无侧隙条件 ∴ 标准齿轮在标准安装时，能满足无侧隙啮合的要求。
图10-13 a
2、标准中心距和标准安装 、 当顶隙为标准值c=c*m 时，设中心距为a，则 a = ra1+ c + rf2 =r1+ha*m+c*m+r2-( ha*+c*)m = r1 +r2 = m ( z1 + z2 ) / 2 即两轮的中心距a等 于两轮的分度圆半径之和。 我们把这种中心距称为标 标 准中心距。 准中心距

直齿圆柱齿轮传动的齿面接触强度计算赫兹公式

直齿圆柱齿轮传动的齿面接触强度计算赫兹公式

受力变形
载荷集中
制造误差 安装误差
计算齿轮强度时，采用
附加动载荷
(
Fn b
)max
(
Fn b
)min
用计算载荷KFn代替名义载荷Fn以考虑载荷集中和附
加动载荷的影响，K----载荷系数
表11-3 载荷系数K
原动机
工作机械的载荷特性
均匀
中等冲击
大的冲击
电动机
1.1~1.2
1.2~1.6
1.6~1.8
多缸内燃机
第11章 齿轮传动
§11-1 §11-2 §11-3 §11-4 §11-5 §11-6 §11-7 §11-8 §11-9 §11-10
轮齿的失效形式 齿轮材料及热处理 齿轮传动的精度 直齿圆柱齿轮传动的作用力及计算载荷 直齿圆柱齿轮传动的齿面接触强度计算 直齿圆柱齿轮传动的弯曲强度计算 斜齿圆柱齿轮传动 直齿圆锥齿轮传动 齿轮的构造 齿轮传动的润滑和效率

u 1 2
u d1 sin

(u 1)2
ua sin
在节点处，载荷由一对轮齿来承担：Fn

Ft
cos

2T1
d1 cos
一对钢制齿轮：
弹性模量：E1=E2=2.06×105 MPA 泊松比：μ1=μ2= 0.3, α=20˚ 代入赫兹公式得： HH2385335035(u(uu1bu)1ab3)a2K32KTT11 [ H ]
模数m不能成为衡量齿轮接触强度的依据。当配对齿轮的材料不同时，公 式中的系数也不同。
钢----铸铁 取：285 ，铸铁----铸铁 取： 250
许用接触应力：[
H
]

H lim

机械设计习题集答案第十章 齿轮传动(100323修改)

机械设计习题集答案第十章 齿轮传动(100323修改)

题10-5 在图示的直齿圆柱齿轮传动中,齿轮1为主动齿轮,齿轮2为中间齿轮,齿轮 3为从动齿轮。

已知齿轮3所受的扭矩m N 983⋅=T ,其转速n 3=180r/min,Z 3=45,Z 2=25, Z 1=22,m=4mm 。

假设齿轮啮合效率及轴承效率均为1,试求:（1） 啮合传动时,作用在各齿轮上的圆周力F t 和径向力F r ,并将各力及齿轮转向标于图上；（2）说明中间齿轮2在啮合时的应力性质和强度计算时应注意的问题；（3）若把齿轮2作为主动齿轮,则在啮合传动时其应力性质有何变化,其强度计算与前面有何不同解答: 1．m N 444.54m N 4525983233232⋅=⋅⨯=⨯==z zT d d T T ；m N 911.47m N 2522444.542122121⋅=⋅⨯=⨯==z zT d d T TN9.1088N 224911.47200020002000111112=⨯⨯====mz T d T F F t t N3.39620tan tan 01112====t t r r F F F F αN 8.1158N 20cos 9.1088cos 0112====αt n n F F F ； 由齿轮2受力平衡条件得：N 9.1088,N 3.3962'22'2====t t r r F F F F ；3r F 与'2r F ,3t F 与'2t F 是作用力与反作用力的关系, ∴3r F ='2r F ,3t F ='2t F2．齿轮2在啮合传动时,齿轮根部弯曲应力:对称循环,双向受载。

齿面接触应力:脉动循环。

在校核弯曲强度时，应将齿根弯曲疲劳极限值乘以。

3．若齿轮2为主动,则其弯曲应力和接触应力都为脉动循环,但2轮每转一周时，轮齿同侧齿面啮合次数为2，则其应力循环次数增加2倍。

题10-5图 题解10-5图题10-6 图示为二级斜齿圆柱齿轮减速器,第一级斜齿轮的螺旋角1β的旋向已给出。

齿轮传动概述

齿轮传动概述

P n1
N mm
P为传递的功率（KW）
n1----小齿轮上的转速
d ----小齿轮上的分度圆直径，
力的方向
d1
α Fn
Ft
Fr
C
ω1
Fn
Fr
α
Ft
C
d1
ω1
n1
Fr1
Ft1
Ft2
Fr2
n2
Ft1⊙○×FFrrF12 t2n1 n2
方向：
Ft1与ω1反向（阻力）
圆周力Ft Ft2与ω2同向（动力）
调质
650
360
1100
900
217~255 310~360
35SiMn
750
450
217~269
38SiMnMo
700 550
217~269
40Cr
700 500
241~286
20Cr
650 400
300
20CrMnTi
1100 850 300
渗碳后淬火
12Cr2Ni4
1100 850 320 58~62HRC
Kv 1.8
动 1.6 载 系 1.4 数 Kv 1.2
1.0 0
10 9
8 7 6
十分精密的齿轮装置
10 20
30 40
50 m/s
3.齿间载荷分配系数Ka：
产生原因：
双对齿 啮合
轮齿弹性变形和 齿距误差
两对齿上载荷分配不 均
采取措施：提高制造精度
表10-3 齿间载荷分配系数Kα
KAFl/b 精度等级II组
Kv ─动载系数 Kβ─齿向载荷分布系数
2.动载系数Kv：
产生原因： 1)由制造、安装误差及轮齿受载后变形所引起的基节不等 ——瞬时传动比不是定值—— 产生冲击和动载荷

齿轮传动的计算载荷

齿轮传动的计算载荷

恰好相切；受载后，轴产生弯曲变形（图<轮齿所受的载荷分布不均>）,轴上的齿轮也就随之偏斜，这就使作用在齿面的载荷沿接触线分布不均匀（图<轮齿所受的载荷分布不均>）。

图<轮齿所受的载荷分布不均>当然，轴的扭转变形，轴承、支座的变形以及制造，装配的误差也是使齿面上载荷分布不均的因素。

计算轮齿强度时，为了计及齿面上载荷沿接触线分布不均的现象，通常以系数Kβ来表示齿面上分布不均的程度对轮齿强度的影响。

为了改善载荷沿接触线分布不均的程度，可以采用增大轴、轴承及支座的刚度，对称的配置轴承，以及适当的限制轮齿的宽度等措施。

同时应尽可能避免齿轮作悬臂布置（即两个支承皆在齿轮的一边）。

对高速、重载（如航空发动机）的齿轮传动应更加重视。

除上述一般措施外，也可把一个齿轮的轮齿做成鼓形（右图）。

当轴产生弯曲变形而导致齿轮偏斜时，鼓形齿齿面上载=1.11+0.18+0.15×=1.11+0.18(1+0.6)+0.15× =1.11+0.18(1+6.7)+0.15× =1.12+0.18+0.23×=1.12+0.18(1+0.6)+0.23× =1.12+0.18(1+6.7)+0.23× =1.15+0.18+0.31×=1.15+0.18(1+0.6)+0.31× =1.15+0.18(1+6.7)+0.31×=1.05+0.26+0.10×=1.05+0.26(1+0.6) +0.10×=1.05+0.26(1+6.7) +0.10×=0.99+0.31+0.12×=0.99+0.31(1+0.6) +0.12×=0.99+0.31(1+6.7) +0.12×=1.05+0.26+0.16×=1.05+0.26(1+0.6) +0.16×=1.05+0.26(1+6.7) +0.16×=1.0+0.31+0.19×=1.0+0.31(1+0.6) +0.19×=1.0+0.31(1+6.7) +0.19×。

变位内啮合直齿圆柱齿轮传动的计算公式

变位内啮合直齿圆柱齿轮传动的计算公式

变位内啮合直齿圆柱齿轮传动的计算公式1. 引言1.1 概述变位内啮合直齿圆柱齿轮传动是一种常见的机械传动方式，广泛应用于各种机械装置中。

在设计和分析变位内啮合直齿圆柱齿轮传动时，需要准确计算相关参数和力学特性，以确保传动系统的可靠性和高效性。

本文旨在介绍变位内啮合直齿圆柱齿轮传动的计算公式，帮助读者理解和应用这些公式。

1.2 文章结构本文主要分为四个部分：引言、变位内啮合直齿圆柱齿轮传动的计算公式、计算公式应用实例以及结论与展望。

下面将对每个部分进行详细说明。

1.3 目的本文的目的是介绍变位内啮合直齿圆柱齿轮传动的计算公式，并通过实际应用案例来说明其具体使用方法。

通过阅读本文，读者可以了解到如何根据给定的齿轮参数来计算接触比力和压力角，并学会分析结果和验证计算公式的准确性。

此外，本文还将展望后续研究方向和拓展，包括其他齿轮传动类型的计算公式研究。

通过本文的阅读，读者可以深入了解变位内啮合直齿圆柱齿轮传动，并在实际应用中灵活运用相关的计算公式。

2. 变位内啮合直齿圆柱齿轮传动的计算公式2.1 齿轮参数定义在变位内啮合直齿圆柱齿轮传动中，我们首先需要定义一些关键的齿轮参数。

这些参数包括：- 齿数：分别表示驱动轮和从动轮上的齿数，分别记为Z1和Z2。

- 模数：表示齿轮的常规参数，记为m。

- 压力角：表示啮合点处切线与轴线间的夹角，记为α。

- 分度圆直径：分别表示驱动轴和从动轴上的分度圆直径，分别记为D1和D2。

2.2 接触比力分析接触比力是变位内啮合直齿圆柱齿轮传动中一个重要的参数。

它可以用来评估传动过程中发生的载荷情况。

接触比力的计算公式如下所示：Ft = (P*D1*cosα)/Z1其中，Ft表示接触比力，P表示传递功率。

2.3 压力角计算方法压力角是变位内啮合直齿圆柱齿轮传动中另一个重要参数。

它影响着齿轮传动的性能和效率。

压力角的计算方法如下所示：cosα= cos(atan(tanα) - (1/m)*((Z2*sin(atan(tan α)))/sqrt(Z1^2-(Z2*cos(atan(tanα)))^2)))其中，cosα表示压力角，tanα表示压力角切线，Z1表示驱动轮的齿数，Z2表示从动轮的齿数。

直齿圆柱齿轮传动的强度计算

直齿圆柱齿轮传动的强度计算

2.14
YS 1.44 1.47 1.51 1.53 1.54 1.55 1.56 1.58 1.59 1.61 1.63 1.65 1.67 1.69 1.71 1.73 1.77 1.80
1.88
返回
机械设计基础
Machine Design Foundation
直齿圆柱齿轮传动的强度计算
对于一对齿轮啮合传动而言，因为两齿轮的齿数一般不相同，所
越小，轮齿的弯曲强度越低。因此，应当在满足轮齿弯曲强度的前提
下，尽可能选取较多的齿数。对于闭式硬齿面齿轮传动或开式齿轮传
动，通常取z1=17~20；对于闭式软齿面齿轮传动，通常取z1=20~30。 当z1确定后，即可按传动比i=z2/z1，求出z2。为使两个齿轮的轮齿磨 损均匀，应尽可能使z1和z2互为质数。
按式（10-21）计算所得各力均为作用在轮齿上的名义载荷。进 行齿轮的强度计算时，要考虑由于原动机和工作机的工作特性所引起 的动力过载、齿轮副的啮合误差所引起的附加动载荷、轴的变形和齿 轮制造误差所引起的载荷沿齿宽分布不均匀、同时啮合的各对轮齿间 载荷分配不均匀等因素对轮齿受载的影响，应将名义载荷Fn修正为计 算载荷FnC，即
面，由工程力学可推得齿根弯曲疲劳强度的校核公式为
F
2FT1 bm2 z1
YFYS
[ F ]
（10-25）
σF——齿根处产生的最大弯曲应力，MPa ；
YF——反映轮齿形状对齿根弯曲应力影响的齿形系数，见表10-5；
YS——反映齿根圆角引起的应力集中和危险截面压应力等其他应力
影响的应力修正系数，见表10-5；
向转动，故[σH] 1= [σH] 2=0.9σHlim=0.9×1450=1305MPa。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
◆主动轮上与啮合 2 T 1 圆周力： F 点速度方向相反 t d1 ◆从动轮上与啮合 点速度方向相同
P
径向力：Fr = Ft tan
指向各自的轮心
Ft 总作用力： Fn cos
指向齿体
2、 斜齿圆柱齿轮受力分析
★力的大小：
圆周力： F 2T1 t
d1
径向力：
Fr Ft tan t Ft tan n cos
第十章 齿轮传动
齿轮传动概述 齿轮传动的失效形式及设计准则 齿轮的材料及其选择原则 齿轮传动的计算载荷 标准直齿圆柱齿轮传动的强度计算 齿轮传动设计参数、许用应力与精度选择 标准斜齿圆柱齿轮传动的强度计算
标准锥齿轮传动的强度计算 齿轮的结构设计
齿轮传动的润滑
第十章 齿轮传动
§1
★齿轮传动的特点和分类 1、齿轮传动的特点
∴按齿根弯曲疲劳强度设计→按齿面接触疲劳强度校核；
2. 开式齿轮传动 ∵磨损失效（为条件性计算）为主→折断失效∴只按齿根弯 曲疲劳强度设计，求出 m →将 m 增大 5∼15% ，以补偿磨 损的影响。
§3
齿轮材料、热处理及其选择原则
1. 对齿轮材料的基本要求是 ：齿面要硬、齿芯要韧※ 2. 常用齿轮材料和热处理 见表 ⑴钢
Fr2 Fa2 Ft1 Ft2 n1 T1 Fr1 Fa1
★力的大小： 圆周力：
★力的方向： 圆周力： ◆主动轮上与啮合 点速度方向相反 ◆从动轮上与啮合 点速度方向相同 径向力：
T2
2T1 Ft1 Fa2 d1
径向力：
Fr1 = Ft2 tan t= Fr2 ◆指向各自的轮心 轴向力： 轴向力：
3、 齿面胶合
高速、重载、高温条件下→压力↑、温度↑ 、 油粘 度↓→ 金属直接接触→熔焊→撕裂→胶合。
措施： ↑齿面硬度、 ↓表面粗糙度 、采用抗胶合能 力强的油（如硫化油）、在润滑油中加入极压添加 剂等。
4、 齿面磨粒磨损
→ 是开式齿轮传动主要失效形式。 相对滑动+“磨粒”（金属微粒、杂质、灰尘） → 磨损→平稳性↓、冲击、噪声，齿厚↓ →失真 、折断 。 措施：开式→闭式。
2、动载系数Kv ① 物理意义 考虑齿轮副在啮合过程中因啮合误差和运转速度而 引起的内部附加动载荷的影响； ② 动载荷产生的原因及影响因素 齿轮传动的制造、安装误差及 受载后轮齿的变形→基圆齿距不相等→i瞬≠常数→动载荷 ③ 减小动载荷的措 施 采用修缘齿，即 将轮齿的齿顶的一小 部分齿廓曲线修成压 力角>20°的渐开线 ；但应特别注意的是 ，修缘量不可过大， 否则会因重合度减小 过多，致使动载荷不 一定就相应减小，因 此修缘量的选择应适 ④动载系数取值方法 一般齿轮传动可根据 当。 齿轮精度等级进行选择。
⑴优点 与带、链等传动比较，具有传递 功率范围大、允许工作转速高、传动效率 高、传动比准确、使用寿命长、工作可靠、 结构紧凑等。 ⑵缺点 工作中有振动、冲击和噪声，并 有动载荷产生；无过载保护性能；制造与 安装精度高，成本高；须用专门设备制造 等。
概述
2、齿轮传动的分类
⑴按工作条件分类
①闭式齿轮 传动 齿轮 传动封闭在 箱体内，具 有良好的润 滑条件，能 防尘。 ③半开式齿轮传动 齿轮在护罩内，但 不密封，可以设置 油池润滑，润滑条 件较好；亦有的仅 把齿轮罩上，只起 防尘作用，润滑条 件较差。 ⑵按齿轮齿面 硬度分类
②开式齿轮 传动 齿轮 外露，润滑 条件差，不 能防尘。
①软齿面齿轮 ①硬齿面齿轮 齿面硬度 齿面硬度＞ ≤350HBS的齿轮。 350HBS的齿 轮。
★圆柱齿轮的基本参数
1. 模数 m 对于一般动力传动，要求：m＞1.5～2。 2. 传动比 i和齿数比 u
n主 z从 d从 i n从 z主 d主
（一）齿轮传动的失效形式 1、轮齿折断
①疲劳折断
初始裂纹→应力重复作 用→裂纹扩展→折断 ②过载折断 意外过载（或磨损→ 齿厚↓、冲击载荷） →突然折断 措施： ↑过渡圆角半径； ↓表面粗糙度；对齿根进行强化处理；选用韧性 好的材料；采用合理的变位等。
2、齿面点蚀
→ 是闭式软齿面齿轮传动主要失效形式。 ◆H →变应力、N ↑ →细微裂纹 →扩展 → 剥落； ◆主要发生在节线附近齿根一侧。 措施：↑齿面硬度；↓表面粗糙度；采用粘度高的 油；采用较大的变位系数等
4、齿向载荷分布系数K ① 物理意义考虑工作载荷沿轮齿接触线方向分布不均匀性的影响；
②产生原因及影响因素 齿轮传动工作时，由于轴的弯曲和扭转变形、轴承的弹 性位移以及传动装置的制造和安装误差等原因，导致齿轮副相互倾斜及轮齿扭曲 ，最终造成轮齿沿接触线产生载荷分布的不均匀。其影响因素主要有齿轮在轴上 位置的安排、轴承及支座的刚度等因素。
b
B1
单对齿啮合 的上界点
单对齿啮合 的下界点
（二）
★思路：
直齿圆柱齿轮齿根弯曲疲劳强度计算
问题：①载荷在齿上的作用点和载荷数值？ ②如何确定齿根危险剖面的位置？ ③最大应力应包括哪些应力？ 第①个问题：假定全部载荷Fn由一对轮齿 承受且作用于 齿顶→并用重合度系数Yε来修正误差； 第②个问题：30°切线法确定危险剖面位置→ 危险 截面：a1a2 → s 第③个问题：在轮齿的危险剖面上存在三种应力 由Fn cos γ→ F 、 B2
1）锻钢 ①软齿面齿轮：（HBS≤350 ） 工艺过程：轮坯→正火或调质处理→切齿，切制后精度→ 7、8 级； ②硬齿面齿轮：（ HBS > 350 ）
工艺过程：轮坯→切削加工→表面硬化处理→磨齿等精加工。 2）铸钢 形状复杂、尺寸较大的齿轮（要求耐磨、强度高）。
⑵铸铁
用于大直径、低速、小功率、工作平稳及开式传动中。
径向力：
◆指向各自的轮心
Ft2
轴向力：
◆主动轮Fa1用左、 右手定则 ◆从动轮用对应关 系求：Fa2=-Fa1 ★左、右手定则： 左旋左手（右旋右手） ，四指顺转向，拇 指为Fa1的方向 。
例题1：
Ft1
Fr1 Fr2 Ft2 Fa2
n1 Fa1
n2
例题2：
有一两级斜齿圆柱齿轮传动，其布置方式如图所示，今欲使轴Ⅱ所受 的轴向力大小相等、方向相反，设β1=19°，试确定第二对齿轮的螺旋角 β2和轮齿的旋向。已知：z1 =12，z2=30，mn=10mm；z1 ′ =12，z2′=45， mn ′ =14mm。
3. 中心距a
z大 u 1 z小
减速传动→ u=i 增速传动→ u=1/i
最好为计算整数。
4.齿宽和齿宽系数 ψd
b d d1
b , a a
b d d1 , b a a
一般取：b2=b（圆整值）， b1=b2 +（5～10）mm 大齿轮宽度
两齿轮接触宽度
小齿轮宽度
§2 齿轮传动的失效方式及设计准则
Ft2 F t2 F F r2 ω2
y x z F F r1 r1
Ft1 F t1 ω1
r2
F a1 F a1 FF a2 a2
◆指向各自的大端；
★对应关系：
Ft1 Ft 2 Fr1 Fa 2 Fx1 Fr 2
4、蜗杆传动的受力分析
★旋向（蜗杆蜗轮啮合时） ： ※ 蜗杆右旋——蜗轮也是右旋 蜗杆左旋——蜗轮也是左旋 n2
3、齿间载荷分配系数K ① 物理意义 考虑同时啮合的各齿对间载荷分配不均匀性的影响； ② 产生原因及 ∵ 1 ＜εα＜2，当双对齿啮合时，在理想状态下，载荷应 平均分配在两对齿上。但实际上，由于齿轮制造的误差和轮齿受力后变形，造 成载荷在各齿对之间的分配时不均匀的。 ③主要影响因素 1）受载后轮齿变形； 2）轮齿制造误差（特别是 基节偏差）； 3）齿廓修形（修缘量）； 4）磨合效果。 ④取值方法 一般不需要 精确计算的齿轮和 ≤30°的斜齿圆柱齿轮 传动可根据其精度等级 由表查取;

轴向力：
Fa Ft tan
法向力：
Fn
F cos n
Fa
Ft cos cos n
★力的方向：
◆力要画在啮合点上 （齿宽中点的分度圆 处）且与相应的坐标 轴平行。
y
Ft1
Fa2 Fr1
圆周力：
◆主动轮上与啮合 点速度方向相反
◆从动轮上与啮合 点速度方向相同 x Fa1 z
Fr2
⑶非金属材料
主要用于低速、轻载、要求噪声小的齿轮传动中。
◇齿轮材料的选择
基本原则： （1）必须满足工作条件的要求；（2）综合考虑工艺性和经济性的要求。 参考原则：
◆选择适当的热处理方法： 正火碳钢——只能用于制作在载荷平稳或轻度冲击下工作的齿轮。 调质碳钢——可用于制作在中等冲击载荷下工作的齿轮。 合金钢——常用于制作高速、重载并在冲击载荷下工作的齿轮。 ◆一对齿轮的材料搭配： ① 小齿轮的材料和热处理方法比大齿轮的强；
5、 齿面塑性变形
→ 是低速、重载的软齿面齿轮传动的主要失效形式。 软齿面在低速、重载条件下→齿面压力↑ 及摩 擦力的作用→表层局部塑性流动 。 措施： ↑齿面硬度、 ↑润滑油粘度。
（二）齿轮传动设计准则※
1. 闭式齿轮传动 ⑴闭式软齿面齿轮传动： （接触疲劳磨损即点蚀失效为主） ∴按齿面接触疲劳强度设计→按齿根弯曲疲劳强度校核； ⑵闭式硬齿面齿轮传动： （弯曲疲劳折断失效为主）
③ 减小载荷分布不均的措施 a) 增大轴、轴承及支座的刚度；b) 合理布置齿 轮在轴上的位置；c)选择合理的齿轮宽度；d)提高齿轮传动的制造和安装精度； e)在一对齿轮中把一个齿轮的轮齿制作成鼓形齿等。
④ 取值方法
§5
标准直齿圆柱齿轮传动的强度计算
（一）轮齿受力分析
★力的作用点： ——齿宽中点的分度圆处 ★力的大小： ★力的方向：
F’ Fn F’
Fa
2T1 Ft d m1