第十讲 圆的面积培优提高练习

2022-2023学年六年级数学上册典型例题系列之第一单元圆的面积提高篇（解析版）编者的话：《2022-2023学年六年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题、专项练习、分层试卷三大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

分层试卷部分是根据试题难度和掌握水平，主要分为基础卷、提高卷、拓展卷三大部分，其优点在于考点广泛，分层明显，适应性广。

本专题是第一单元圆的面积提高篇。

本部分内容考察与圆有关的阴影部分图形面积，包括八种常见求阴影部分面积的方法，题目综合性强，难度非常大，建议根据学生掌握情况选择性进行讲解，一共划分为九个考点，欢迎使用。

【考点一】圆的面积与羊吃草问题。

【方法点拨】该题型关键是画出羊吃草的范围图，较复杂的问题是由多个不同部分的图形组成，需要分开计算面积。

【典型例题1】在一块草坪地的木桩上拴着一只羊，绳长2米．这只羊最多能吃着草地的面积是多少平方米？解析：3.14×22＝3.14×4＝12.56（平方米）答：这只羊最多可以吃到的草地的面积是12.56平方米。

【典型例题2】草场上有一个长20m，宽10m 的关闭着的羊圈，在羊圈的一角用长30m的绳子拴着一只羊（见右图），这只羊能够活动的范围有多大？解析：羊活动的范围受到绳长的影响，从图中可以分析得到，羊活动的范围由四分之三个半径为30米的圆的面积、四分之一个半径为20米的圆、四分之一个半径为10米的圆的面积组成。

【对应练习1】一只狗被拴在底座为边长3m 的等边三角形建筑物的墙角上（如图），绳长是4m ，求狗所能到的地方的总面积。

解析：狗不能走到三角形里面去，如示意图，狗所到达的面积由300°圆心角，半径为4m 的扇形和两个半径为4-3=1米，圆心角为120°的扇形组合而成的。

圆的周长与面积(典型问题)培优专项50练(含解析)完美打印版圆的周长与面积培优专项50练（含解析）一、选择题（共15小题）1.如果 c = 28.26 米，圆的面积是多少？A。

20.25 平方米B。

14.13 平方米C。

63.585 平方米D。

64.85 平方米2.用一根长 6.28 米的绳子刚好能围一棵树的树干 2 圈。

如果树干的横截面为圆形，那么它的面积是多少？A。

12.56 平方米B。

3.14 平方米C。

1.57 平方米D。

0.785 平方米3.一个圆的半径扩大 2 倍，那么面积和周长会发生什么变化？A。

面积和周长扩大 2 倍B。

面积扩大 4 倍，周长扩大 2 倍C。

周长扩大 4 倍，面积扩大 2 倍4.把一张圆形纸片沿半径平均分成若干份，拼成一个近似的长方形。

这个长方形的周长与圆的周长相比会怎么样？A。

等于圆的周长B。

大于圆的周长C。

小于圆的周长D。

无法比较5.一个长方形和一个圆的周长相等。

已知长方形的长是 9 分米，宽是6.7 分米，圆的面积是多少？A。

31.4 平方分米B。

78.5 平方分米C。

314 平方分米D。

68.8 平方分米6.如果把圆的半径按 1:3 缩小，那么新的圆与原来的圆的面积比是多少？A。

3:1B。

1:3C。

1:9D。

9:17.一个环形的玉环，外直径为 8 厘米，内直径为 6 厘米，这个玉环的面积是多少？A。

12.56 平方厘米B。

18.84 平方厘米C。

21.98 平方厘米D。

31.4 平方厘米8.用 2019 厘米长的铁丝先围成一个圆，再用这根铁丝围成了一个正方形。

圆和正方形周长相比会怎么样？A。

一样长B。

圆的周长更长C。

正方形的周长更长9.如图，把圆分成若干等份，拼成近似的长方形后，周长增加了 8 dm。

原来的这个圆的面积是多少？A。

12.56 平方分米B。

25.12 平方分米C。

50.24 平方分米10.两个圆的周长相等，那么它们的面积会怎么样？A。

也相等B。

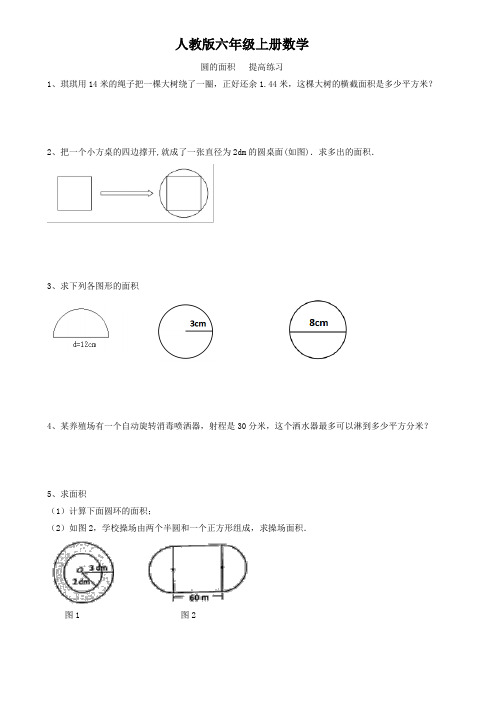
人教版六年级上册数学圆的面积提高练习1、琪琪用14米的绳子把一棵大树绕了一圈，正好还余1.44米，这棵大树的横截面积是多少平方米？2、把一个小方桌的四边撑开,就成了一张直径为2dm的圆桌面(如图)．求多出的面积．3、求下列各图形的面积4、某养殖场有一个自动旋转消毒喷洒器，射程是30分米，这个洒水器最多可以淋到多少平方分米？5、求面积（1）计算下面圆环的面积；（2）如图2，学校操场由两个半圆和一个正方形组成，求操场面积．图1 图26、一个圆与一个长方形面积相等，圆周长是18.84厘米，长方形长6厘米，宽是多少厘米？7、一个长方形和一个圆形的水池，周长相等，长方形的长是6.42米，宽是3米，圆形水池的占地面积是多少平方米？8、戴老师画出一个面积与长方形面积相等的圆，如下图。

已知圆的周长是25.12cm，那么这个长方形的长是多少？9、下图中阴影部分的面积是小圆面积的1，大圆面积与小圆面积的比是5∶3。

已知阴影部分的面积是412 cm2，大圆的面积是多少？10、希望小学的操场如下图所示。

现在要给操场铺上一层煤渣，米师傅为了测量出操场周长，绕操场跑了2圈，米师傅跑了多少米？若每平方米需要煤渣16千克，那么全部铺完需要煤渣多少吨？11、在下边的长方形中画一个最大的圆，并求出余下的面积。

12、要给一个直径是20m的圆形花坛铺满草皮，每平方米草皮15元，购买这些草皮需要多少元？13、石英钟的时针长6厘米，一昼夜，时针扫过的面积是多少平方厘米？14、用一根铁丝刚好围成一个边长是6.28米的正方形，那么用它能围成一个最大面积是多少的圆形？15、一个圆形花坛直径是16米，花坛周围是一条小路，小路面宽3米，这条环形小路占地面积多少平方米？16、儿童乐园有一个圆形花坛，量得它的周长是50.24米。

（1）这个花坛的占地面积是多少平方米？（2）如果要在花坛周围修一条1米宽的小路，这条小路的面积是多少平方米？（3）如果要给这条小路铺上地砖，每平方米需要85元，这样一共需要多少元？17、一只闹钟，它的分针长4㎝，这根分针的尖端转动一昼夜所走的路程是多少厘米？18、一个钟表的分针长8厘米，半小时后，分针扫过的面积是多少平方厘米？19、在一张长4厘米，宽3厘米的长方形纸片上，剪去一个最大的半圆。

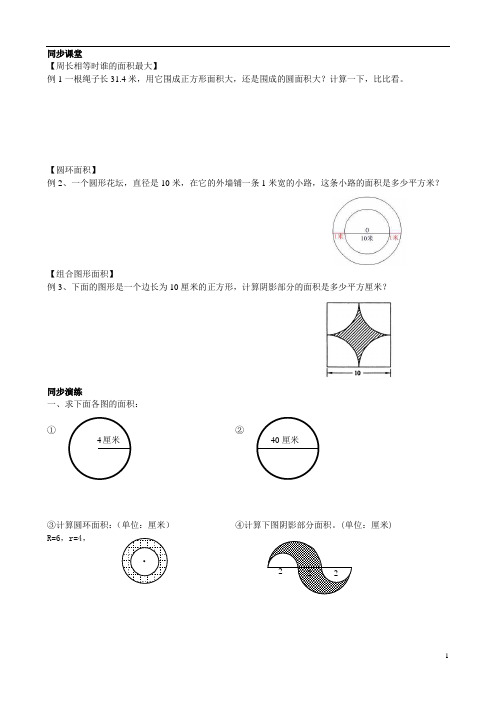
同步课堂【周长相等时谁的面积最大】例1一根绳子长31.4米，用它围成正方形面积大，还是围成的圆面积大？计算一下，比比看。

【圆环面积】例2、一个圆形花坛，直径是10米，在它的外墙铺一条1米宽的小路，这条小路的面积是多少平方米？【组合图形面积】例3、下面的图形是一个边长为10厘米的正方形，计算阴影部分的面积是多少平方厘米？同步演练一、求下面各图的面积：①②③计算圆环面积：（单位：厘米）④计算下图阴影部分面积。

(单位：厘米) R=6，r=4，二、填空题：（1）一个圆的周长从9.42厘米,增加到12.56厘米，直径增加了（）厘米，面积增加了（）平方厘米。

（2）在一张长为8厘米，宽为5厘米的长方形纸中剪下一个最大的圆，这个圆的直径是（）厘米，周长是（）厘米，面积是（）平方厘米。

（3）大圆直径比小圆直径长6厘米，小圆与大圆半径的比是1：4，大圆面积比小圆面积大（）平方厘米。

（4）公园里自动旋转喷灌装置半径是10米，它的最大喷灌面积是（）平方米。

（5）一根铁丝可以围成一个长40厘米，宽22.8厘米的长方形，如果用这根铁丝围成一个圆，面积是（）平方厘米？（6）把一个圆剪拼成一个和它面积相等的长方形，周长增加了6厘米，原来这个圆的面积是（）平方厘米。

（7）在一个半径为6厘米的圆内画一个最大的正方形，这个正方形的面积是（）平方厘米。

（8）一根铁丝长62.8厘米，用它围成两个相等的圆，则两个圆的面积之和是（）平方厘米。

三、选择题：（1）一个圆的直径扩大3倍，它的面积扩大（）A、3倍B、6倍C、9倍（2）如果一个圆的直径与正方形边长相等，那么圆的面积（）正方形的面积。

A、大于B、等于C、小于（3）一张长方形纸长15厘米，宽8厘米，在这张纸上剪下一个最大的圆，剩余面积是（）平方厘米A、69.76B、50.24C、64四、应用题：（1）一块草坪周长是50.24米，这块草坪占地多少平方米？（2）从一个长5分米，宽4分米的长方形木板上锯下一个最大的圆，剩下的木板是多少平方分米？（3）一个圆形桌面的周长是3.768米。

《圆的面积》拔高练习、填空1.圆的半径是6厘米，它的周长是（），面积是（）。

2.圆的直径是10厘米，它的周长是（），面积是（）。

3.一个半圆形，半径是3厘米，周长是（），面积是（）。

4.一个圆的周长是12.56厘米，它的直径是（），面积是（）。

5.一张圆桌面的周长是376.8厘米，要在它上面配一块圆形玻璃，这块圆形玻璃的面积是（）。

6.用一根长10.28米绳子，围成一个半圆形，这个半圆的半径是（）米，面积是（）平方米。

7.在长5厘米、宽4厘米的长方形中画一个最大的圆，这个圆的周长是（），面积是（）。

8.一个圆的半径扩大3倍，直径扩大（）倍，周长扩大（）倍，面积扩大（）倍。

9.两个圆的直径比是3:2,则它们的半径比是（），周长比是（），面积比是（）。

10.一个挂钟，分针长50厘米，时针长40厘米，分针的尖端转一圈的长度是（），时针转一周扫过的面积是（）。

11.甲、乙两圆的周长之比是3: 5,则甲圆面积比乙圆面积小（--）。

二、填表三、判断。

1.周长相等的两个圆，面积也一定相等。

（）2.周长相等的正方形和圆，圆的面积大。

（）3.半径是2厘米的圆，它的面积和周长一样大。

（）4.圆与正方形面积相等，则圆的周长比正方形短。

（）5.两个圆比较，周长较小的那个圆面积也一定小。

（）四、应用题。

1.一个圆形茶盘的直径是40厘米，它的周长和面积各是多少？2.一个圆形观赏鱼池，周长是251.2米，这个鱼池的占地面积是多少平方米？3.一个圆形花坛的周长是50.24米，在里面种两种花，种菊花的面积与茶花的面积比是2：5,这两种花的面积分别是多少？4.从一张正方形纸上剪下一个周长是18.84厘米的最大圆，求被剪掉的纸屑的面积。

5.在一张周长为24厘米的正方形硬纸板上，剪一个最大的圆，这个圆的周长和面积各是多少？6.把一个圆平均分成若干等份后，能拼成一个周长为20.7分米的长方形,这个圆形的面积是多少平方分米？7.小圆直径是大圆的3，大圆周长是25.12厘米，小圆面积是多少平方厘4米？8.一个圆与一个长方形面积相等，圆周长是18.84厘米，长方形长6厘米, 宽是多少厘米？9.两个大小不等的圆形粮仓，小粮仓的底面周长是12.56米，它的占地面积是大粮仓的-，大粮仓占地面积是多少平方米？310.一个正方形面积是20平方厘米，在这个正方形中所作的最大的圆的面积是多少平方厘米？。

六年级上册数学专项培优提升训练圆的面积1．如图，直角三角形（阴影部分）的面积是15平方厘米，求圆的面积。

2．三角形的底是18分米，计算涂色部分的面积。

3．计算图中阴影部分的面积。

（单位：cm）4．如图，圆的面积等于长方形的面积，圆的周长是25.12cm，求阴影部分的面积。

5．求图中形阴影部分的面积。

6．求下面各图形中阴影部分的面积．（单位：cm）7．求如图阴影部分面积。

（单位：厘米）8．如图，刘大爷靠墙围了一个直径是8米的半圆形菜园，在它的外围铺了一条1米宽的小路。

这条小路的面积是多少平方米？9.儿童公园有一个半径3米的半圆形鱼池，在鱼池四周铺了1米宽的小路。

小路的面积是多少平方米？10．如图，大圆的直径是6厘米，小圆的直径是4厘米。

大圆涂色部分的面积比小圆涂色部分的面积大多少平方厘米？11．已知图中阴影部分的面积是25平方厘米，求圆环的面积。

12．用一张圆形纸片剪下一个最大的正方形，如图，圆的直径是8cm，剪下正方形后，剩下部分的面积是多少？13．欢庆“六一”军事体验主题爱国主义教育活动，其中有一项射击项目如图，教官用9.42米长的彩绳靠墙角围了一个最大的靶场（如图所示），便于同学们射击，这个靶场的面积是多少平方米？14．已知涂色部分的面积是12cm2，求圆环的面积。

15．如下图，正方形的面积是10平方厘米，求圆的面积。

16．如图，大圆面积与小圆面积的比是5：3。

已知阴影部分的面积是12cm2，占小圆面积的。

大圆的面积是多少cm2？17．折扇又名“撒扇”、“纸扇”等，是一种用竹木或象牙做扇骨、韧纸或绫绢做扇面的能折叠的扇子。

如图是一把绫绢折扇，做这样一把折扇扇面至少需要绫绢面料多少平方分米？18．美美妈妈在淘宝上买了一个三层角柜（如图），正好可以摆放在客厅的90°墙角处，这个角柜可以放置物品的面积是多少平方厘米？参考答案及解析1．如图，直角三角形（阴影部分）的面积是15平方厘米，求圆的面积。

（ 圆的面积提高练习一、 填空1、 叫做圆的周长。

叫做圆的面积。

2、我们把一个圆平均分成若干等份，再拼成一个近似的长方形，这个近似的长方形的长相当于，宽相当于 ，因为长方形的面积等于 ，所以圆的面积 = = 。

3、已知一个圆的周长是 18.84 分米，这个圆的面积是 。

4、一辆汽车通过长 2826 米的大桥，汽车车轮直径是 1.5 米，每分钟转动 120 周，这辆汽车通过大桥要用 分。

5、在一个边长是 6 厘米的正方形中，画一个最大的圆，这个圆的周长是 ，面积是 。

6、圆的半径扩大 3 倍，它的直径 ，周长 ，面积 。

7、在一张长 6 分米、宽 4 分米的长方形纸上，剪下一个最大的圆，剩下的面积是 。

8、小圆的半径是 3 厘米，大圆的半径是 5 厘米，小圆和大圆的直径的比是 ，周长的比是，面积的比是 。

9、一根铁丝长 31.4 厘米，围成一个正方形，面积是 ；围成一个圆形，面积是 。

10、三根同样长的铁丝，一根围成长方形，一根围成正方形，一根围成圆形，面积最大的是。

二、 判断题1、 半径是 2 分米的圆，它的周长与面积相等。

（ ）2、 用圆规画一个周长 9.42 厘米的圆，圆规两脚间的距离是 3 厘米。

（ ）3、 两个圆的周长相等，它们的面积也相等。

（ ）4、 大、小两个圆，它们的直径的比是 2：5，周长的比也是 2：5，面积的比也是 2：5。

（ ）5、 半圆的面积是整个圆面积的一半，半圆的周长也是整个圆周长的一半。

）6、 面积相等的正方形和圆形，圆形的周长大。

（ ）三、 应用题1、 一种圆形钟表面，它的周长是 25.12 厘米，它的面积是多少平方厘米？③ 已知这个长方形的长比宽多 10.7 厘米。

2、 一个圆形花坛，它的直径是 8 米，在花坛周围铺了一条宽 1 米的环形小路，这条小路的面积是多少平方米？④这个长方形的周长是 51.4 厘米。

3、 一个圆形纸片，把它平均等分成若干个小扇形，再拼成一个近似的长方形。

圆的面积例1：把一个圆形纸片分成若干等份，拼成以半径为宽的近似长方形，已知长方形的周长为24.84cm。

圆形纸片的面积是多少？练习1：（1）一个圆形蓄水池的周长是25.12m，这个蓄水池的占地面积是多少？（2）一种压路机的前轮直径1.5米，宽2米。

如果每分钟滚动5圈，它每分钟前进多少米？每分钟压路面多少平方米？例2：如图，已知圆的面积是125.6平方厘米，求正方形的面积？练习2：（1）如下图：已知正方形的面积是120平方厘米，求圆的面积？（2）周长相等的长方形、正方形和圆，（）面积最大。

A 长方形B 正方形C 圆D 无法确定例3：正方形的面积是20平方厘米，求阴影部分的面积。

练习3：（1）在一个面积是80平方厘米的正方形中剪下一个最大的圆，求余下的面积.（2）如图所示，图形中正方形的面积是50平方厘米，求图中阴影部分的面积。

例4：在下图的扇形中，正方形的面积是30平方厘米。

求阴影部分的面积。

练习4：（1）如图所示，图形中正方形的面积是50平方厘米，求图中阴影部分的面积。

（2）在正方形ABCD中，AC＝6厘米。

求阴影部分的面积。

例5：求图中阴影部分的面积（单位：厘米）。

练习5：（1）求下面图形中阴影部分的面积（单位：厘米）。

（2）求下面图形中阴影部分的面积（单位：厘米）例6：下图中三个圆的面积都是200平方分米，求阴影部分的面积。

练习6：（1）下图中每个圆的半径都是6分米，求阴影部分的面积。

（2）图中每个圆的面积都是9.42平方厘米，求阴影部分的面积。

例7：下图中阴影部分的面积是25平方厘米。

求圆环的面积是多少？练习7：（1）下图中阴影部分的面积是5平方厘米。

求圆环的面积是多少？例8：下图中阴影甲的面积比阴影乙的面积多28平方厘米，AB=40厘米，CB垂直于AB，求BC的长。

练习8：（1）下图三角形ABC是直角三角形，阴影(Ⅰ)比阴影(Ⅱ)的面积小23平方米，BC的长度是多少米？（2）三角形ABC是直角三角形，AB是圆的半径,AB= 20厘米，如果甲比乙大64平方厘米，求CD的长。

3．圆的面积(教材30～34页)能力提升激活巧思维，送你金钥匙!【能力点一】运用推理法解决计算圆的面积问题例1右图中，三角形的面积是6 m2，圆的面积是多少平方米?分析三角形的两条直角边都是圆的半径，三角形的面积等于两条直角边乘积的一半，也就是等于圆的半径的平方的一半。

因此，由三角形的面积是6 m2推理得出圆的半径的平方等于6×2＝12(m2)，即r2＝12 m2。

求出圆的半径的平方的值，再乘π就可以求出圆的面积。

解答3．14×(6×2)＝37．68(m2)答：圆的面积是37．68 m2。

提示在计算圆的面积时，如果已知半径平方的值，可直接乘π求出圆的面积。

【能力点二】用割补法求阴影部分的面积例2如下图，OA，OB分别是小半圆的直径，且OA＝OB＝6 cm，∠BOA＝90°，阴影部分的面积是多少平方厘米?分析图中阴影部分的形状不规则，将椭圆形阴影通过切割分成相等的两部分，然后分别补到另一部分的阴影上，使不规则图形变成规则图形。

如下图所示：由此得出：阴影部分的面积＝14大圆的面积－三角形AOB的面积。

解答3．14×62×14－6×6×12＝28．26－18＝10．26(cm2)答：阴影部分的面积是10．26 cm2。

提示用割补法把阴影部分转化成14大圆的面积与直角三角形面积的差是解题的关键。

赛点题库勇敢来探索，风采尽展现！1．探究题下图中，正方形的面积是8 m2，求阴影部分的面积。

2．探究题如下图，阴影①的面积比阴影②的面积少6 dm2。

求BC的长是多少分米。

3．潜能开发题下面是由4个半径为5 cm的等圆围成的图形，求阴影部分的面积。

4．竞赛题手工课上，小红用一张直径为20 cm的圆形纸片剪出如图所示的风车图案(空白部分)，则被剪掉的纸片(阴影部分)的面积是cm2。

(π取3．14)(2011·第九届希望杯)1．分析：由正方形的面积是8 m2可知,r2＝8 m2。