程序18数据分析双因素方差分析

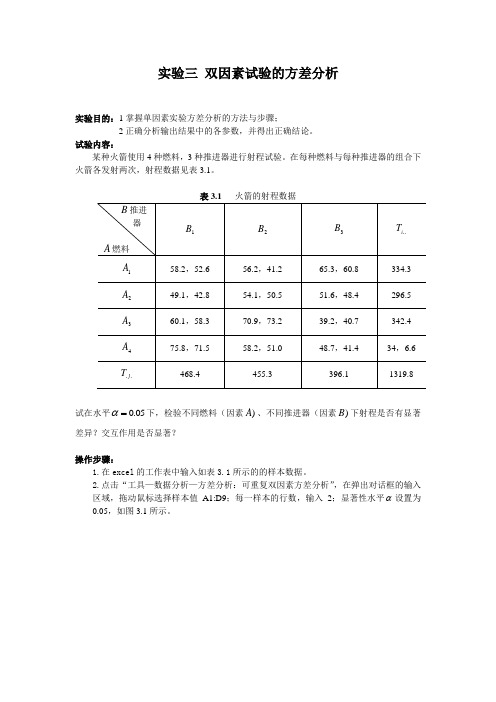
实验三 双因素试验的方差分析实验目的：1掌握单因素实验方差分析的方法与步骤；2正确分析输出结果中的各参数，并得出正确结论。

试验内容：某种火箭使用4种燃料，3种推进器进行射程试验。

在每种燃料与每种推进器的组合下火箭各发射两次，射程数据见表3.1。

表3.1 火箭的射程数据试在水平05.0=α下，检验不同燃料（因素)A 、不同推进器（因素)B 下射程是否有显著差异？交互作用是否显著？操作步骤：1.在excel 的工作表中输入如表3.1所示的的样本数据。

2.点击“工具—数据分析—方差分析：可重复双因素方差分析”，在弹出对话框的输入区域，拖动鼠标选择样本值A1:D9；每一样本的行数，输入2；显著性水平α设置为0.05，如图3.1所示。

图3.1 应用excel“数据分析”功能求双因素等重复方差分析的有关参数3．点击确定，输出参数的窗口如图3.2所示。

图3.2 应用excel“数据分析”功能求双因素等重复方差分析的有关参数结果分析：图3.2 中仅列示了输出结果中的方差分析表。

“样本”即燃料因子，“列”即推进器因子，“交互”为燃料和推进器因子的交互作用，SS 为平方和；df 是自由度；P-value 为P 值，即所达到的临界显著水平；F crit 是Fα（t-1，N-t）的值。

由方差分析表可知，因子A （燃料）的作用是一般显著的（P-value的值为0.025969<0.05）;因子B（推进器）的作用是高度显著的（P-value的值为0.003506<0.01）；而交互作用是极其显著的（P-value的值为6.15E-05<<0.01）,这说明燃料的作用于与推进器之间有着密切的关系，也即每种推进器都有各自最合自得最佳燃料。

双因素方差分析结果解读双因素方差分析（Two-wayANOVA）是一种分析数据的统计方法，它可以检验同一总体的两个或多个变量之间的差异。

双因素方差分析的一个重要特点是它可以检验基于不同组别、不同资源或者不同情况下同一个总体上的差异。

它可以检验在多个组别之间存在差异、或者在不同组别之间存在偏差的情况。

本文将通过介绍双因素方差分析的原理、分析方法、结果解读方法，帮助读者更好地解读双因素方差分析的结果。

首先，双因素方差分析的原理是涉及两个不同的自变量，即因变量和一个或多个自变量。

因变量是一个连续的响应变量，而自变量则分为定类的自变量和定序的自变量，根据不同的实验需求采用不同的变量。

例如，定类的自变量可以用于比较基于性别或不同药物治疗后被试者的反应，定序的自变量则可用于比较基于疗程的不同反应。

其次，双因素方差分析需要构建一个双因素的实验单元，即一个自变量和一个因变量的实验设计，它可以确定每个组别之间的比较，比如在不同性别和不同处方药物治疗下被试者的反应。

双因素方差分析可以检验两个或多个因变量是否相对独立，以及独立或不独立的因变量是否存在差异。

最后，双因素方差分析的结果解读是比较重要的一步，它可以有效地解释出双因素实验单元下的差异或偏差，帮助研究者更好地做出他们的决策。

通常，根据双因素方差分析的结果可以检测出两个或多个自变量的差异，以及基于性别、时间、处方药物治疗等不同情况下的被试者的反应等。

只有当双因素方差分析的F值超过某一显著性水平的时候（通常为0.05或0.01），双因素方差分析的结果才被认为是显著的，可以通过结果解释和决策。

综上所述，双因素方差分析是一种非常有用的统计方法，可以检验同一总体的两个或多个变量之间的差异。

其中双因素方差分析原理，分析方法，以及结果解读方法都非常重要，有助于我们在解决实际问题时更好地解读双因素方差分析的结果，识别出不同组别，或者在不同组别之间存在的差异，从而发现新的实验结果，增加研究的学术价值。

双因素方差分析一、双因素方差分析的含义和类型（一）双因素方差分析的含义和内容在实际问题的研究中，有时需要考虑两个因素对实验结果的影响。

例如上一节中饮料销售量的例子，除了关心饮料颜色之外，我们还想了解销售地区是否影响销售量，如果在不同的地区，销售量存在显著的差异，就需要分析原因，采用不同的推销策略，使该饮料品牌在市场占有率高的地区继续深入人心，保持领先地位，在市场占有率低的地区，进一步扩大宣传，让更多的消费者了解，接受该产品。

在方差分析中，若把饮料的颜色看作影响销售量的因素A，饮料的销售地区看作影响因素B。

同时对因素A和因素B进行分析，就称为双因素方差分析。

双因素方差分析的内容包括：对影响因素进行检验，究竟一个因素在起作用，还是两个因素都起作用，或是两个因素的影响都不显著。

双因素方差分析的前提假定：采样地随机性，样本的独立性，分布的正态性，残差方差的一致性。

（二）双因素方差分析的类型双因素方差分析有两种类型：一个是无交互作用的双因素方差分析，它假定因素A 和因素B的效应之间是相互独立的，不存在相互关系；另一个是有交互作用的双因素方差分析，它假定因素A和因素B的结合会产生出一种新的效应。

例如，若假定不同地区的消费者对某种品牌有与其他地区消费者不同的特殊偏爱，这就是两个因素结合后产生的新效应，属于有交互作用的背景；否则，就是无交互作用的背景。

有交互作用的双因素方差分析已超出本书的范围，这里介绍无交互作用的双因素方差分析。

1.无交互作用的双因素方差分析。

无交互作用的双因素方差分析是假定因素A和因素B的效应之间是相互独立的，不存在相互关系；2.有交互作用的双因素方差分析。

有交互作用的双因素方差分析是假定因素A和因素B的结合会产生出一种新的效应。

例如，若假定不同地区的消费者对某种颜色有与其他地区消费者不同的特殊偏爱，这就是两个因素结合后产生的新效应，属于有交互作用的背景，否则，就是无交互作用的背景。

二、数据结构方差分析的基本思想：通过分析研究中不同来源的变异对总变异的贡献大小，从而确定可控因素对研究结果影响力的大小。

双因素方差分析剖析在双因素方差分析中，有两个主要的因素被研究。

这些因素可以是两个不同的处理条件、两个不同的处理时间、两个不同的处理剂量等。

同时，每个因素都可以有两个或多个水平（即取值范围）。

为了进行双因素方差分析，研究人员首先需要确定研究对象和目标变量。

然后他们需要确定每个因素的水平和变量的测量方法。

例如，如果他们想要研究两种不同的药物对于治疗一种疾病的效果，他们需要确定每种药物的剂量以及测量疾病症状的方法。

接下来，研究人员需要收集数据，并进行统计分析。

在双因素方差分析中，主要的统计指标是方差和F值。

方差用来衡量不同因素和不同水平之间的差异。

F值是方差之比，用来判断不同因素之间是否存在显著差异。

进行双因素方差分析之后，研究人员可以得出结论。

如果F值大于临界值，那么可以得出不同因素之间存在显著差异的结论。

如果F值小于临界值，那么就可以得出不同因素之间没有显著差异的结论。

此外，研究人员还可以通过进行后续的多重比较来进一步分析不同因素之间的差异。

常用的多重比较方法包括Tukey方法和Bonferroni方法。

然而，双因素方差分析也存在一些限制。

首先，它只能处理两个或多个因素对于一个或多个变量的影响。

如果有更多的因素需要考虑，就需要进行更复杂的分析方法。

其次，双因素方差分析假设变量的分布是正态分布的，并且各组之间的方差是相等的。

如果数据不符合这些假设，就需要采用其他的非参数方法进行分析。

总之，双因素方差分析是一种常用的统计方法，可以帮助研究人员研究两个或更多因素对于一个或多个变量的影响。

它可以帮助确定不同因素之间的重要性，并且可以探索不同因素之间的相互作用。

然而，研究人员需要在收集数据和进行分析时注意假设的前提条件，并且需要根据具体情况选择合适的统计方法。

双因素方差分析流程双因素方差分析呀，可有趣啦。

方差分析大家可能都有点耳闻，双因素方差分析呢，就是在有两个影响因素的情况下进行的分析哦。

比如说我们想研究不同的教学方法和不同的学习时间对学生成绩的影响，教学方法和学习时间就是这两个因素啦。

那我们开始这个分析流程吧。

一、数据收集。

这可是很重要的一步呢。

我们得先确定好要研究的两个因素，然后针对这两个因素的不同水平组合去收集数据。

就像刚刚说的教学方法和学习时间，教学方法可能有传统教学、多媒体教学、小组合作教学这几种水平，学习时间可能有每天2小时、3小时、4小时这些水平。

然后找一群学生，把他们分别分到这些不同水平组合的组里，最后记录下他们的成绩，这就收集好数据啦。

二、计算平均值。

把收集来的数据按照不同的因素水平组合进行分组，然后计算每组的平均值。

这就像是把同学们按照不同的教学方法和学习时间分好组后，算出每个组的平均成绩。

这个平均值能让我们大概了解每个组的整体情况呢。

三、计算离差平方和。

这一步有点小复杂，但是别怕哦。

我们要计算总的离差平方和、因素A的离差平方和、因素B的离差平方和以及误差的离差平方和。

总的离差平方和就是所有数据与总平均值的差的平方和，它反映了所有数据的离散程度。

因素A的离差平方和呢，是在只考虑因素A的情况下，各水平均值与总均值的差的平方和，它体现了因素A对结果的影响程度。

同理，因素B的离差平方和是考虑因素B时的情况。

误差的离差平方和就是用总的离差平方和减去因素A和因素B的离差平方和得到的，它表示除了这两个因素之外其他随机因素的影响。

四、计算自由度。

自由度这个概念也很有趣呢。

总的自由度等于数据的总数减1。

因素A的自由度等于因素A的水平数减1，因素B的自由度等于因素B的水平数减1，误差的自由度就等于总的自由度减去因素A和因素B的自由度。

自由度就像是给每个部分一个活动的空间，不同的部分有不同的自由度哦。

五、计算均方。

均方就是离差平方和除以自由度啦。

我们要计算因素A的均方、因素B的均方和误差的均方。