空间解析几何与向量微分

习题7-1 空间直角坐标系1.填空题（1）下列各点所在象限分别是：a .（1，-2，3）在________________；b .（2，3，-4）在________________；c .（2，-3，-4）在________________；d .（-2，-3，1）在________________。

（2）点P(-3,2,-1)关于平面XOY 的对称点是_______，关于平面YOZ 的对称点是_________，关于平面ZOX 的对称点是__________，关于X 轴的对称点是__________，关于Y 轴的对称点是____________，关于Z 轴的对称点是____________。

（3）点A(-4,3,5)在XOY 平面上的射影点是_________，在YOZ 平面上的射影点是_________，在ZOX 面上的射影点是__________，在X 轴上的射影点是_________，在Y 轴上的射影点是__________，在Z 轴上的射影点是__________。

（4）已知空间直角坐标系下，立方体的4个顶点为A(,,a a a ---)，B(,,a a a --)，C(,,a a a --)和D （,,a a a ），则其余顶点分别为___________，_____________，___________， ___________。

2.已知三角形的三个顶点A（2，-1，4)，B(3，2，-6)，C(-5，0，2)，求过A、B、C 三点的中线的长度。

3.已知平行四边形ABCD的两个顶点A（2，-3，-5），B（-1，3，2）及它的对角线的交点E（4，-1，7），求顶点C、D的坐标。

4.已知某直线线段AB被点C（2，0，2）及点D(5，-2，0)内分为3等分，求端点A、B的坐标。

5.求点M（-4，3，-5）到各坐标轴的距离。

6.在YOZ面上，求与三个已知点A(3，1，2)，B（4，-2，-2）和C(0，5，1)等距离的点。

第六章.向量代数与空间解析几何本章内容在本课程当中是单独的一个部分，应该说是属于几何的内容，之所以需要在微积分的课程里进行单独的讨论，是因为我们在后面学习多元函数的微积分时，必须和这些几何知识发生关系，所谓多元的函数，从几何意义方面来理解，就是定义域在平面乃至更高维度的空间区域上，这样如果要想得到对于多元函数的直观几何理解，就必须对于平面乃至更高维度的空间中的几何现象具有一定的知识。

向量。

向量可以说是几何的最为基本的概念。

因为几何对象的两个基本要素：方向和长度，用一个向量就可以完全表达，从向量的概念出发，可以构造出整个的几何世界。

由于本课程的限制，我们不从一般的观念出发来展开向量的理论，而是基于直观的，运用向量来表示的几何当中的有向直线段，来说明我们需要涉及的有限的向量知识。

我们完全可以把一个向量理解为一根有向直线段，而不会出现任何理论上的错误。

基于向量的这种直观图象，可以定义向量的基本属性。

首先，我们定义两个向量相等的意思，就是两个向量的大小与方向都相同，对于这里的具体的一种向量—有向直线段，就是必须长度相等，而方向相同，所谓方向相同，按照几何的意义，就是两根直线段相互平行，而且指向相同。

注意，这里初学者常常产生误解的地方，就是认为要求两个有向直线段方向一样，就一定是要求它们在同一个直线上，或者是相互重合，这是因为还不习惯在一般的空间当中考虑问题，特别是要养成在三维空间当中考虑几何对象的习惯，记住方向相同，是与这两个向量的空间位置无关的，只要它们所在的直线相互平行，而指向一致即可。

在两个向量之间定义加法与减法，就是我们在力学当中以及很熟悉的力的合成的平行四边形法则，当然这是一种直接的基于几何图象的定义方式，下面我们通过在空间引入坐标，来得到更一般的定义。

空间直角坐标系以及向量代数。

在空间当中引入坐标的目的，和物理学当中引入单位制一样，是提供一个度量几何对象的方法，首先一个坐标系必须能够提供方向的定义，使得任意的方向都能够由于坐标系而得到确定与唯一的描述；然后必须能够提供长度的单位，基于这个单位能够度量空间长度。

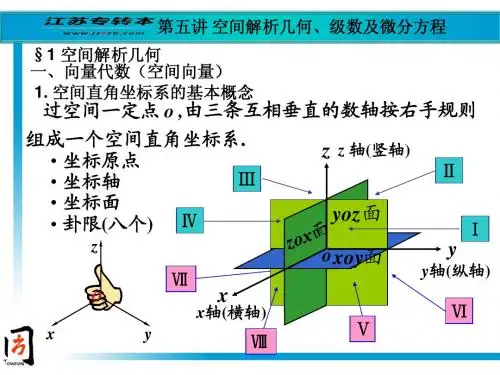
第七章 空间解析几何与向量代数 为了学习多元函数微积分的需要，本章首先建立空间直角坐标系，并引进在工程技术 上有着广泛应用的向量，介绍向量的一些运算．然后以向量为工具来讨论空间的平面与直线 方程，最后介绍空间曲面与空间曲线及二次曲面.第一节 空间直角坐标系一、 空间直角坐标系众所周知，实数x 与数轴上的点是一一对应的，二元数组(x ,y )与坐标平面上的点是一一对应的，从而可以用代数的方法讨论几何问题．类似地，通过建立空间直角坐标系，把空间中的点与一个三元有序数组(x ,y ,z )建立一一对应关系，用代数的方法研究空间问题.1.空间直角坐标系的建立过空间定点O 作三条互相垂直的数轴，它们都以O 为原点，并且通常取相同的长度单位．这三条数轴分别称为x 轴、y 轴、z 轴．各轴正向之间的顺序通常按下述法则确定：以右手握住z 轴，让右手的四指从x 轴的正向以π/2的角度转向y 轴的正向，这时大拇指所指的方向就是z 轴的正向．这个法则叫做右手法则(图7-1)．这样就组成了空间直角坐标系．O 称为坐标原点，每两条坐标轴确定的平面称为坐标平面，简称为坐标面．x 轴与y 轴所确定的坐标面称为xOy 坐标面．类似地有yOz 坐标面、zOx 坐标面．这些坐标面把空间分成八个部分，每一部分称为一个卦限(图7-2)．x 、y 、z 轴的正半轴的卦限称为第Ⅰ卦限，从第Ⅰ卦限开始，从z 轴的正向向下看，按逆时针方向，先后出现的卦限依次称为第Ⅱ、Ⅲ、Ⅳ卦限，第Ⅰ、Ⅱ、Ⅲ、Ⅳ卦限下方的空间部分依次称为第Ⅴ、Ⅵ、Ⅶ、Ⅷ卦限。

图7-1 图7-22.空间中点的直角坐标设M 为空间的一点，若过点M 分别作垂直于三坐标轴的平面，与三坐标轴分别相交于P ，Q ，R 三点，且这三点在x 轴、y 轴、z 轴上的坐标依次为x ，y ，z ，则点M 唯一地确定了一个有序数组(x ，y ，z )．反之，设给定一个有序数组(x ，y ，z )，且它们分别在x 轴、y 轴和z 轴上依次对应于P ，Q 和R 点，若过P ，Q 和R 点分别作平面垂直于所在坐标轴，则这三个平面确定了唯一的交点M ．这样，空间的点就与一个有序数组(x ，y ，z )之间建立了一一对应关系(图7-3)．有序数组(x ，y ，z )就称为点M 的坐标，记为M (x ，y ，z )，它们分别称为横坐标、纵坐标和竖坐标．显然，原点O的坐标为(0，0，0)，坐标轴上的点至少有两个坐标为0，坐标面上的点至少有一个坐标为0．例如，在x轴上的点，均有y＝z＝０；在xOy坐标面上的点，均有z ＝０．图7-3 图7-4二、空间两点间的距离公式设空间两点M１（x1, y1, z1)、M2 (x2, y2, z2),求它们之间的距离d=12M M．过点M 1,M2各作三个平面分别垂直于三个坐标轴，形成如图7-4所示的长方体．易知 2222121212()d M M M Q QM M QM==+∆是直角三角形222121()M P PQ QM M PQ=++∆是直角三角形222122M P P M QM''''=++()()()222212121x x y y z z=-+-+-所以d=（7-1-1 ）特别地，点M(x，y，z)与原点O(0，0，0)的距离(图7-3)d OM==例1在z轴上求与两点A(-4，1，7)和B(3，5，-2)等距离的点．解因所求的点M在z轴上，故设该点坐标为M(0，0，z)，依题意MA MB=，即=解得z＝149，所求点为M ( 0，0，149)．习题7-11．在空间直角坐标系中，定出下列各点的位置：A (1，3，2)，B (1，2，-1)，C (-1，-2，3)，D(0，-2，0)，E (-3，0，1)．2． 求点(a ,b ,c )关于(1) 各坐标面；(2) 各坐标轴；(3) 坐标原点的对称点的坐标．3． 自点P 0(x 0, y 0, z 0)分别作各坐标面和坐标轴的垂线，写出各垂足的坐标．4． 求点M (4，-3，5)到各坐标轴间的距离．5． 在y Ｏz 面上，求与三个已知点A (3，1，2)，B (4，-2，2)和C (0，5，1)等距离的点．6． 试证明以三点A (4，1，9)，B (10，-1，6)，C (2，4，3)为顶点的三角形是等腰直角三角形．第二节 向量及其运算一、 向量的概念在物理学和工程技术中经常会碰到一些既有大小又有方向的量，如力、速度等，我们把这类量称为向量(或矢量)．空间中的向量常用具有一定长度且标有方向的线段(称为有向线段)来表示。

第七章向量与空间解析几何空间解析几何是多元函数微积分学必备的基础知识.本章首先建立空间直角坐标系；然后引进有广泛应用的向量及其运算，以它为工具，讨论空间的平面和直线；最后介绍空间曲面和空间曲线的部分内容.第一节空间直角坐标系平面解析几何是我们已经熟悉的，所谓解析几何就是用解析的，或者说是代数的方法来研究几何问题.引起这场数学史上伟大革命的正是坐标系的建立.代数运算的基本对象是数，几何图形的基本元素是点.正如我们在平面解析几何中所见到的那样，通过建立平面直角坐标系使几何中的点与代数的有序数之间建立一一对应关系.在此基础上，引入运动的观点，使平面曲线和方程对应，从而使我们能够运用代数方法去研究几何问题.同样，要运用代数的方法去研究空间的图形——曲面和空间曲线，就必须建立空间内点与数组之间的对应关系.一、空间直角坐标系空间直角坐标系是平面直角坐标系的推广.过空间一定点O，作三条两两互相垂直的数轴，它们都以O为原点.这三条数轴分别叫做x轴(横轴)、y轴(纵轴)、z轴(竖轴)，统称坐标轴.它们的正方向按右手法则确定，即角度转向以右手握住z轴，右手的四个手指指向x轴的正向以π2y轴的正向时，大拇指的指向就是z轴的正向(见图7-1)，这样的三条坐标轴就组成了一空间直角坐标系O x y z，点O叫做坐标原点.图7-1三条坐标轴两两分别确定一个平面，这样定出的三个相互垂直的平面:x O y，y O z，z O x，统称为坐标面.三个坐标面把空间分成八个部分，称为八个卦限，上半空间(0)z>中，从含有x轴、y轴、z轴正半轴的那个卦限数起，按逆时针方向分别叫做Ⅰ，Ⅱ，Ⅲ，Ⅳ卦限；下半空间(0)z<中，与Ⅰ，Ⅱ，Ⅲ，Ⅳ四个卦限依次对应的叫做Ⅴ，Ⅵ，Ⅶ，Ⅷ卦限(见图7-2).图7-2确定了空间直角坐标系后，就可以建立起空间点与数组之间的对应关系.设M 为空间的一点，过点M 作三个平面分别垂直于三条坐标轴，它们与x 轴、y 轴、z 轴的交点依次为,,P Q R (见图7-3).这三点在x 轴、y 轴、z 轴上的坐标依次为x ，y ，z .这样，空间的一点M 就唯一地确定了一个有序数组(,,)x y z ，它称为点M 的直角坐标，并依次把x ， y 和z 叫做点M 的横坐标、纵坐标和竖坐标.坐标为(,,)x y z 的点M ，通常记为(,,)M x y z .图7-3反过来，给定了一有序数组(,,)x y z ，我们可以在x 轴上取坐标为x 的点P ，在y 轴上取坐标为y 的点Q ，在z 轴上取坐标为z 的点R ，然后通过P ，Q 与R 分别作x 轴、y 轴与z 轴的垂直平面，这三个平面的交点M 就是具有坐标(,,)x y z 的点(见图7-3).从而对应于一有序数组(,,)x y z ，必有空间的一个确定的点M .这样，就建立了空间的点M 和有序数组(,,)x y z 之间的一一对应关系.如图7-3所示. x 轴、y 轴和z 轴上的点的坐标，分别为(,0,0)P x ，(0,,0)Q y ，(0,0,)R z ；x O y 面、y O z 面和z O x 面上的点的坐标，分别为(,,0)A x y ，(0,,)B y z ，(,0,)C x z ；坐标原点O 的坐标为(0,0,0)O .它们各具有一定的特征，应注意区分.二、 空间两点间的距离设11112222(,,),(,,)M x y z M x y z 为空间两点，为了用两点的坐标来表达它们间的距离d ，我们过12M M 各作三个分别垂直于三条坐标轴的平面.这六个平面围成一个以12,M M 为对角线的长方体(见图7-4).根据勾股定理，有图7-42221212M MM NN M=+222111.M P M Q M R +=+因为11221M P P P xx ==-， 11221M Q Q Q y y ==－， 11221M R R R z z ==－，所以12d M M =.特别地，点(,,)M x y z 与坐标原点(0,0,0)O 的距离为d O M =第二节 向量及其运算一、 向量及其线性运算1. 向量概念我们曾经遇到的物理量有两种：一种是只有大小的量，叫做数量，如时间、温度、距离、质量等；另一种是不仅有大小，而且还有方向的量，叫做向量或矢量，如速度、加速度、力等.在数学上，往往用一条有向线段来表示向量，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向.如图7-5所示，以1M 为始点、2M 为终点的有向线段所表示的向量，用记号12M M表示.有时也用一个黑体字母或上面加箭头的字母来表示向量，如向量，，，a b i u 或 ,,,a b i u等.图7-5向量的大小叫做向量的模，向量12M M或a 的模分别记为12M M或a . 在研究向量的运算时，将会用到以下几个特殊向量与向量相等的概念： 单位向量 模等于1的向量称为单位向量.逆向量(或负向量) 与向量a 的模相等而方向相反的向量称为a 的逆向量，记为-a . 零向量 模等于0的向量称为零向量，记作0，零向量没有确定的方向，也可以说它的方向是任意的.向量相等 两个向量a 与b ，如果它们方向相同，且模相等，就说这两个向量相等，记作=a b .自由向量 与始点位置无关的向量称为自由向量(即向量可以在空间平行移动，所得向量与原向量相等).我们研究的向量均为自由向量，今后，必要时可以把一个向量平行移动到空间任一位置2. 向量的线性运算 （1） 向量的加(减)法.仿照物理学中力的合成，我们可如下规定向量的加(减)法. 定义1 设a ，b 为两个(非零)向量，把a ，b 平行移动使它们的始点重合于M ，并以a ，b 为邻边作平行四边形，把以点M 为一端的对角线向量1M N定义为a ，b 的和，记为+a b(见图7-6).这样用平行四边形的对角线来定义两个向量的和的方法，叫做平行四边形法则.由于平行四边形的对边平行且相等，所以从图7-6可以看出，+a b 也可以按下列方法得出：把b 平行移动，使它的始点与a 的终点重合，这时，从a 的始点到b 的终点的有向线段1M N就表示向量a 与b 的和+a b (见图7-7).这个方法叫做三角形法则.图7-6 图7-7定义2 设a ，b 为两个（非零）向量，b 的逆向量为－b .称向量a 与向量－b 的和向量为向量a 与向量b 的差向量，简称为向量a 与向量b 的差.即-=+a b a b.按定义容易用作图法得到向量a 与b 的差.把向量a 与b 的始点放在一起，则由b 的终点到a 的终点的向量就是a 与b 的差-a b (见图7-8).图7-8在定义1与定义2中，我们都假设a ，b 为非零向量.其实这只是为了几何直观的需要，事实上a ，b 都可以是零向量.根据零向量的定义，我们可以将零向量看成一个没有方向的点.这样我们就可以约定：任何向量与零向量的和与差都等于该向量自己. 向量的加法满足下列性质：+=+a b b a； (交换律)()()++=++a b c a b c ； (结合律)+=a 0a ； ()0+-=a a (2) 向量与数量的乘法.定义3 设λ是一实数，向量a 与λ的乘积λa 是一个这样的向量：当>0λ时，λa 的方向与a 的方向相同，它的模等于a 的λ倍，即λλ=a a ； 当<0λ时，λa 的方向与a 的方向相反，它的模等于a 的λ倍，即λλ=a a ； 当0λ=时，λa 是零向量，即0λ=a .向量与数量的乘法满足下列性质(λ，μ为实数)： ()()λμλμ=a a ； (结合律) ()λμλμ+=+a a a ； (分配律) ()λλλ+=+a b a b . (分配律)设a e 是方向与a 相同的单位向量，则根据向量与数量乘法的定义，可以将a 写成a =a a e这样就把一个向量的大小和方向都明显地表示出来.由此若a 为非零向量，也有a =a e a就是说把一个非零向量除以它的模就得到与它同方向的单位向量.二、 向量的坐标表示1. 向量在轴上的投影为了用分析方法来研究向量，需要引进向量在轴上的投影的概念. （1) 两向量的夹角.设a ，b 为两个非零向量，任取空间一点O ，作O A =a ， O B =b，则称这两向量正向间的夹角θ为两向量a 与b 的夹角(见图7-9)，记作(,)θ=ab 或 π(,),0θθ=≤≤b a . 当a 与b 同向时，0θ=；当a 与b 反向时，πθ=.图7-9(2) 点A 在x 轴上的投影.过点A 作与x 轴垂直的平面，交x 轴于点A '，则点A '称为点A 在x 轴上的投影(见图7-10).图7-10 图7-11(3) 向量AB 在x 轴上的投影.首先我们引进轴上的有向线段的值的概念设 AB 是x 轴上的有向线段.如果数λ满足λA B = ，且当AB 与x 轴同向时λ是正的，当 AB 与x 轴反向时λ是负的，那么数λ叫做x 轴上有向线段AB 的值，记作A B ，即λA B =.设,A B 两点在x 轴上的投影分别为A '，B '(见图7-11)，则有向线段''A B 的值A B ''称为向量AB 在x 轴上的投影，记作j P r x A B A B ''= ，它是一个数量. x 轴叫做投影轴.这里应特别指出的是：投影不是向量，也不是长度，而是数量，它可正，可负，也可以是零.关于向量的投影，有下面两个定理.定理1 向量 AB 在x 轴上的投影等于向量 AB 的模乘以x 轴与向量AB 的夹角α的余弦，即j P r cos x A B A B a =.证 过A 作与x 轴平行，且有相同正向的x '轴，则x 轴与向量AB 间的夹角α等于x '轴与向量AB 间的夹角(见图7-12).从而有j j P r P r cos x x A B A B A B A B a '''==.图7-12显然，当α是锐角时，投影为正值；当α是钝角时，投影为负值；当α是直角时，投影为0定理2 两个向量的和在某轴上的投影等于这两个向量在该轴上投影的和，即j j j 1212P r ()P r P r x x x a a a a +=+图7-13证 设有两个向量12,a a 及某x 轴，由图7-13可以看到j j j 12P r ()P r ()P r x x x A B B C A C A C ''+=+==a a，而j j j j 12P r P r P r P r x x x x A B B C A B B C A C ''''''+=+=+=a a，所以j j j 1212P r ()P r P r x x x +=+a a a a显然，定理2可推广到有限个向量的情形，即j j j j 1212P r ()P r P r P r x n x x x n +++=+++a a a a a a2. 向量的坐标表示 (1) 向量的分解.设空间直角坐标系O x y z ，以,,i j k 表示沿x 轴、y 轴、z 轴正向的单位向量，并称它们为这一坐标系的基本单位向量.始点固定在原点O 、终点为M 的向量O M =r，称为点M的向径.图7-14设向径O M终点M 的坐标为(,,)x y z .过点M 分别作与三条坐标轴垂直的平面，依次交坐标轴于,,P Q R (见图7-14)，根据向量的加法，有O M O P P M M M ''==++r，但 ,P M O P M M O Q ''==， 所以 O P O Q O R=++r. 向量,,O P O Q O R ，分别称为向量O M =r在,,x y z 轴上的分向量.根据数与向量的乘法，得,O P x =i ,O Q y =j O R z =k .因此，有O M x y z ==++r i j k.这就是向量r 在坐标系中的分解式，其中,,x y z 三个数是向量O M =r在三条坐标轴上的投影.一般地，设向量12,=aM M 12,M M 的坐标分别为1111(,,)M x y z 及2222(,,)M x y z ，如图7-15所示.由于图7-15122121M M O M O M =-=-r r，而 2222x y z =++r i j k ，1111x y z =++r i j k ，所以()()=++-++a i j k i j k x y z x y z 222111 ()()()-+-+-i j k =x x y y z z 212121.这个式子称为向量12M M按基本单位向量的分解式，其中三个数量212121,,x y z a x x a y y a z z =-=-=-是向量12M M =a在三个坐标轴上的投影.我们也可以将向量a 的分解式写成.x y z a a a =++a i j k(2) 向量的坐标表示.向量a 在三个坐标轴上的投影,,x y z a a a 叫做向量a 的坐标，并将a 表示为(),,x y za a a =a ，上式叫做向量a 的坐标表示式.从而基本单位向量的坐标表示式是()()()1,0,0,0,1,0,0,0,1===i j k .零向量的坐标表示式为0,0,00=（）.起点为(),,M x y z 1111、终点为(),,M x y z 2222的向量的坐标表示式为()21212112,,M M x x y y z z ---=，特别地，向径的坐标就是终点的坐标，即(),,=O M x y z(3) 向量的模与方向余弦的坐标表示式.向量可以用它的模和方向来表示，也可以用它的坐标来表示.为了找出向量的坐标与向量的模、方向之间的联系，我们先介绍一种表达空间方向的方法.与平面解析几何里用倾角表示直线对坐标轴的倾斜程度相类似，我们可以用向量12M M =a 与三条坐标轴(正向)的夹角,,αβγ来表示此向量的方向，并规定π0α≤≤、π0β≤≤、π0γ≤≤ (见图7-16)，,,αβγ叫做向量a 的方向角.过点12,M M 各作垂直于三条坐标轴的平面，如图7-16所示.可以看出，由于12,P M Mα∠=又21M P M P ⊥，所以1cos cos 12x a M P M M ααa＝＝＝，1c o s c o s 12y a M Q M M ββ===a， （7-2-1）1cos=cos 12.z a M R M M γ==aa z ＝M 1R ＝｜｜cos γ＝｜a ｜cos γ.图7-16公式(7-2-1)中出现的不是方向角αβγ，，本身而是它们的余弦，因而，通常也用数组cos cos cos αβγ、、来表示向量a 的方向，叫做向量a 的方向余弦.把公式(7-2-1)代入向量的坐标表示式，就可以用向量的模及方向余弦来表示向量()cos cos cos αβγ=++a a i j k ， （7-2-2）而向量a 的模为12M M ==a由此得向量a 的模的坐标表示式=a （7-2-3）再把(7-2-3)式代入(7-2-1)式，可得向量a 的方向余弦的坐标表示式cos cos ,cos a αa βa γ⎧⎪=⎪⎪⎪=⎨⎪⎪⎪=⎪⎩（7-2-4）把公式(7-2-4)的三个等式两边分别平方后相加，便得到222cos cos cos 1αβγ++=，即任一向量的方向余弦的平方和等于1.由此可见，由任一向量a 的方向余弦所组成的向量()cos cos cos ,,αβγ是单位向量，即cos cos cos =αβγ++a e i j k .例1 已知两点()1225,,P －及()2167,P -，，试求：(1) 12P P 在三条坐标轴上的投影及分解表达式； (2) 12P P 的模；(3) 12P P的方向余弦；(4)12P P 上的单位向量12e PP .解 (1)设12(,,)x y z P P a a a =，则12P P在三条坐标轴上的投影分别为：3,8,2x y z a a a =-==于是12P P的分解表达式为38212P P i j k++=-.(2)12P P ==(3)12cos x a α==P P12cos ya β==p p ，12cos za γ==p p .(4))e 38212i j k =++-PP .(4) 用坐标进行向量的线性运算.利用向量的分解式，向量的线性运算可以化为代数运算. 设λ是一数量，,x y z x y z a a a b b b b =++=++a i j k i j k ，则()()x y z x y z a a a b b b ±=±a b i j k i j k ＋＋＋＋()()()x x y y z z a b a b a b =±+±+±i j k ；()x y z x y z λλa a a λa λa λa =++=++a i j k i j k或()()(),,,,,,xy z x y z x x y y z zaa ab b b a b a b a b ±±±±=，()(),,,,x y z x y z λa a a λa λa λa =.这就是说，两向量之和(差)的坐标等于两向量同名坐标之和(差)；数与向量之积，等于此数乘上向量的每一个坐标.例2 从点()217,A -，沿向量8912=+-a i j k 的方向取线段A B ，使AB 34=，求点B 的坐标.解 设点B 的坐标为(,,)x y z ，则()()()217A B x y z -+++-i j k=.按题意可知AB上的单位向量与a 上的单位向量相等，即＝A B a e e .而34A B =，17a ==，所以127343434A By x z +--==++e i j kAB AB， 8912171717a ==++a e i j k a比较以上两式，得283417x -=， 193417y +=， 7123417z -=-. 解得 181717,,x y z ===-.所以，点B 的坐标为1817,17()-，.例3 22345 ,,=-+=+-a i j k b i j k 求3-a b 方向的单位向量.解 因为()()3322345=-=-+-+-c a b i j k i j k3711=-+i j k.于是c ==，所以371133c c a b i j k c a b-===-+-e ）.三、 向量的数量积与向量积1. 两向量的数量积在物理学中，我们知道当物体在力F 的作用下(见图7-17)，产生位移s 时，力F 所做的功图7-17()cos ,W =F s Fs .这样，由两个向量F 和s 决定了一个数量 ()cos ,F s Fs .根据这一实际背景，我们把由两个向量F 和s 所确定的数量 ()cos ,F s Fs 定义为两向量F 与s 的数量积. 定义4 a 与b 的模与它们的夹角余弦的乘积，叫做a 与b 的数量积，记为a·b ，即()cos ,⋅=a b a b ab .因其中的 ()cos ,b ab 是向量b 在向量a 的方向上的投影，故数量积又可表示为 Prj ⋅=a a b a b，同样 Prj⋅=b a b b a . 数量积满足下列运算性质：（1）⋅=⋅a b b a ； （交换律）（2）()++⋅⋅⋅a b c =a b a c ； （分配律） （3）()()()λλλ⋅=⋅=⋅a b a b a b .（结合律）由数量积的定义，容易得出下面的结论： （1）2⋅=a a a ；（2）两个非零向量a 与b 互相垂直的充要条件是0⋅=a b . 数量积的坐标表示式设,x y z x y z a a a a b b b b =++=++i j k i j k ，由于基本单位向量，，i j k 两两互相垂直，从而，⋅=⋅=⋅=⋅=⋅=⋅=i j j k k i j i k j i k .又因为，，i j k 的模都是1，所以1⋅=⋅=⋅=i i j j k k ，因此，根据数量积的运算性质可得x x y y z z a b a b a b ⋅=++a b ，即两向量的数量积等于它们同名坐标的乘积之和.由于 ()co s ,⋅=a b a b ab ，当a ,b 都是非零向量时，有 ()cos ,a b a b a b ++⋅==a b ab a b.这就是两向量夹角余弦的坐标表示式.从这个公式可以看出，两非零向量互相垂直的充要条件为0x x y y z z a b a b a b ++=. (7-2-5)例4 求向量()322,,=-a 和()3,0,0=b 的夹角.解 因为 ()3320209⋅=⋅+-⋅+⋅=a b ，5==a ，=3b ，所以()93cos ,535⋅===⨯a b a b a b.故其夹角()arccos 5383,5=≈︒'a b .例5 求向量()412,,=-a 在()31,,0=b 上的投影. 解 因为 ()43112011⋅=⋅+-⋅+⋅=a b ，==b ，所以Prj ⋅===b a b a b.例6 在x O y 平面上，求一单位向量与437(,,)=-p 垂直. 解 设所求向量为(),,a b c ，因为它在x O y 平面上，所以0c =.又(),,0a b 与()437,,=-p 垂直，且是单位向量，故有22-43=10a b a b +=+，.由此求得34,55a b =±=±， 因此所求向量为34,,055⎛⎫±± ⎪⎝⎭.2. 两向量的向量积在研究物体转动问题时，不但要考虑此物体所受的力，还要分析这些力所产生的力矩.下面举例说明表示力矩的方法.图7-18设O 为杠杆L 的支点，有一个力F 作用于这杠杆上P 点处，F 与OP 的夹角为θ(见图7-18).由物理学知道，力F 对支点O 的力矩是一向量M ，它的模sin M O Q O P θ=F F=.而M 的方向垂直于 OP 与F 所确定的平面（即M 既垂直于OP ，又垂直于F ），M 的指向按右手规则，即当右手的四个手指从OP 以不超过π的角转向F 握拳时，大拇指的指向就是M 的指向.由两个已知向量按上述规则来确定另一向量，在其他物理问题中也会遇到，抽象出来，就是两个向量的向量积的概念.定义5 设a ，b 为两个向量，若向量c 满足(1) sin (,)=c a b ab ，即等于以,a b 为邻边的平行四边行的面积； (2)c 的方向垂直于,a b 所确定的平面，并且按顺序,,a b c 符合右手法则.则称向量c 为向量a 与向量b 的向量积，记为⨯a b （如图7-19），即=⨯c a b.图7-19向量积满足下列规律：（1）⨯=-⨯a b b a （向量积不满足交换律）； （2）()+⨯=⨯+⨯a b c a c b c ；（3）()()()λλλ⨯=⨯=⨯a b a b a b .由向量积的定义，容易得出下面的结论： （1）⨯=a a 0；（2） 两个非零向量a 与b 互相平行的充要条件是⨯=a b 0. 3. 向量积的坐标表示式设,x y z x y z a a a b b b =++=++a i j k b i j k .则()()x y z x y z a a a b b b ⨯=⨯a b i j k i j k ＋＋＋＋()()()x x x y x z a b a b a b =⨯⨯⨯+i i i j i k ++ y x y y y za b a b a b ⨯⨯⨯+j i j j j k （）+（）+（）z x z y z za b a b a b ⨯⨯⨯k i k j k k （）＋（）＋（）. 由于⨯=⨯=⨯=i i j j k k 0， ⨯=i j k ， ,⨯=j k i⨯=k i j ，⨯=j i k -， ⨯=k ji -， ⨯=i k j -.因此()()().y z z y z x x z x y y x a b a b a b a b a b a b ⨯=-+-+a b i j k －这就是向量积的坐标表示式.这个公式可以用行列式(行列式的定义及简单运算见本书后附录)写成下列便于记忆的形式，即⨯=ij k a b xy z xyza a ab b b从这个公式可以看出，两非零向量a 和b 互相平行的条件为0,0,0y z z y z x x z x y y x a b a b a b a b a b a b -=-=-=，或y x z xyza a ab b b ==. (7-2-6)例7 设2=+-ai j k，2=-+bi j k.计算⨯a b .解 211112i j k a b ⨯=--()()()212111222111⎡⎤⎡⎤⎡⎤=⋅--+-⋅-⋅+⋅--⋅⎣⎦⎣⎦⎣⎦i j k53=--i j k.例8 求以()123A ，，，()345B ，，，()247,,C 为顶点的三角形的面积S . 解 根据向量积的定义，可知所求三角形的面积S 等于12A B A C ⨯ . 因为=222A B ++i j k ， 24A C +i j k＝＋，222124A B A C ⨯=ij k=462-+i j k ，所以12S A B A C =⨯==.例9 已知()211,,=a ，()111,,=-b ，求与a 和b 都垂直的单位向量. 解 设=⨯c a b ，则c 同时垂直于a 和b .于是，c 上的单位向量是所求的单位向量.因为23=⨯=--c a b i j k ，==c ，所以==c e c c⎛⎫-=-⎝c e 都是所求的单位向量.第三节 空间直线与平面本节将以向量为工具，在空间直角坐标系中建立最简单的空间图形——平面和直线的代数方程.一、 曲面方程的概念平面解析几何把曲线看作动点的轨迹，类似地，空间解析几何可把曲面当作是一个动点或一条动曲线按一定规律而运动产生的轨迹.一般地，如果曲面S 与三元方程(),,0F x y z =之间存在如下关系： （1） 曲面S 上任一点的坐标都满足方程(),,0F x y z =；（2） 不在曲面S 上的点的坐标都不满足这个方程，满足方程的点都在曲面上. 那末称(),,0F x y z =为曲面S 的方程，而曲面S 称为方程的图形.二、 空间直线的方程在平面解析几何中，我们知道，x O y 平面上的一定点和一非零向量就确定了一条直线.在三维空间的情形也是一样.设空间直线L 过定点0000(,,)M x y z ，且平行于非零向量m n p =++s i j k这时直线的位置就完全确定了（如图7-20），下面我们来求这条直线的直线方程.图7-20设(,,)M x y z 是直线L 上任意一点，因为L 平行于向量s ，所以0000()()()M M x x y y z z =-+-+-i j k0M M平行于向量s ，由两向量平行的充要条件式（7-2-6）有x x y y z z mnp---== （7-3-1）（7-3-1）称为直线L 的对称式方程，也叫做直线L 的标准式方程. 在建立直线L 的标准式方程（7-3-1）时，我们用到了向量0M M平行于向量s 的充要条件，即这两个向量的对应坐标成比例.如果我们设这个比列系数为t ，则有x x y y z z tmnp---===，那么000,,x x m t y y n t z z p t =+=+=+ （7-3-2）当t 从-∞变到+∞时，方程（7-3-2）就是过点0000(,,)M x y z 的直线L 的参数方程，其中t 是参数，向量s 称为直线L 的方向向量.向量s 的坐标,,m n p 叫做直线的方向数.例1 求过两点()1111,,M x y z ，()2222,,M x y z 的直线的方程 解 可以取方向向量()21212112,,M M x x y y z z =---s=.由直线的标准式方程可知，过两点12,M M 的直线方程为111212121x x y y z z x x y y z z ---==---.上式称为直线的两点式方程.例2 用标准式方程及参数式方程表示直线10,2340.x y z x y z +++=⎧⎨+++=⎩解 为寻找直线的方向向量s ，在直线上找出两个点即可，令=10x ，代入题中方程组，得 000,2y z ==- 同理，令1=0x ，代入题中方程组，得1113,22y z ==-即点(0)-，，A 12与点13(0)2，，B 2在直线上. 取()111,,22AB ==-s .因此，所给直线标准式方程为12211y x z -+==- 参数方程为12,,2.x t y t z t =-⎧⎪=⎨⎪=-+⎩， 注意 本例提供了化直线的一般方程为标准方程和参数方程的方法.三、 平面及其方程垂直于平面的非零向量叫做该平面的法向量.容易看出，平面上的任一向量都与该平面的法向量垂直.我们知道，过空间一点可以作，而且只能作一平面垂直于一已知直线，所以当平面Π上的一点0000(,,)M x y z 和它的法向量(,,)A B C =n 为已知时，平面Π的位置就完全确定了.图7-21设0000(,,)M x y z 是平面Π上一已知点，(,,)A B C =n 是它的法向量(见图7-21)，(,,)M x y z 是平面Π上的任一点，那么向量0M M必与平面Π的法向量n 垂直，即它们的数量积等于零：00M M ⋅=n . 由于(,,)A B C =n ，0000(,,)M M x x y y z z =---，所以有000()()()0A x x B y y C z z -+-+-= (7-3-3)因为所给的条件是已知一定点0000(,,)M x y z 和一个法向量(,,)A B C =n ，方程(7-3-3)叫做平面的点法式方程.例3 求过点23(0)-,,及法向量(1,2,3)=-n 的平面方程.解 根据平面的点法式方程(7-3-3)，得所求平面的方程为(2)2(3)30x y z --++= 或2380x y z =+-=.将方程(7-3-3)化简，得A xB yC zD +++=， (7-3-4)其中000D A x B y C z =---.由于方程(7-3-3)是,,x y z 的一次方程，因此任何平面都可以用三元一次方程来表示.反过来，对于任给的一个形如(7-3-4)的三元一次方程，我们取满足该方程的一组解000,,x y z ，则0000A x B y C z D +++= (7-3-5)由方程(7-3-4)减去方程(7-3-5)，得000()()()0A x x B y y C z z -+-+-= (7-3-6)把它与方程(7-3-3)相比较，便知方程 (7-3-6)是通过点0000(,,)M x y z ，且以(,,)A B C =n 为法向量的平面方程.因为方程(7-3-4)与(7-3-6)同解，所以任意一个三元一次方程(7-3-4)的图形是一个平面.方程(7-3-4)称为平面的一般式方程，其中,,x y z 的系数就是该平面的法向量n 的坐标，即(,,)A B C =n .例4 如图7-22所示，平面Π在三个坐标轴上的截距分别为,,a b c ，求此平面的方程(设0,0,0a b c ≠≠≠).图7-22解 因为,,a b c 分别表示平面Π在x 轴、y 轴、z 轴上的截距，所以平面Π通过三点(,0,0),(0,,0),(0,0,)A a B b C c ，且这三点不在一直线上.先找出平面Π的法向量n ，由于法向量n 与向量A B ，A C都垂直，可取A B A C =⨯n ，而(,,0),(,0,)A B a b A C a c =-=-，所以得00A B A C ab ac=⨯=--ij k nb c a c a b =++i j k.再根据平面的点法式方程(7-3-3)，得此平面的方程为()(0)(0)0bc x a ac y ab z -+-+-=. 由于0,0,0ab c ≠≠≠，上式可改写成1y xz a b c++=. (7-3-7) 式(7-3-7)叫做平面的截距式方程.下面我们讨论一下特殊位置的平面方程.(1) 过原点的平面方程. 因为平面通过原点，所以将0x y z ===代入方程(7-3-4)，得0D =.故过原点的平面方程为0A x B y C z ++=， (7-3-8)其特点是常数项0D =.(2) 平行于坐标轴的平面方程.如果平面平行于x 轴，则平面的法向量(,,)A B C =n 与x 轴的单位向量(1,0,0)=i 垂直，故0⋅=n i ，即1000A B C ⋅+⋅+⋅=由此，有A =从而得到平行于x 轴的平面方程为B yC zD ++=，其方程中不含x .类似地，平行于y 轴的平面方程为0A x C z D ++=；平行于z 轴的平面方程为A xB y D ++=.(3) 过坐标轴的平面方程.因为过坐标轴的平面必过原点，且与该坐标轴平行.根据上面讨论的结果，可得过x 轴的平面方程为B yC z +=；过y 轴的平面方程为0A x C z +=；过z 轴的平面方程为0Ax B y +=.(4) 垂直于坐标轴的平面方程. 如果平面垂直于z 轴，则该平面的法向量n 可取与z 轴平行的任一非零向量(0,0,)C ，故平面方程为0C z D +=.类似地，垂直于x 轴的平面方程为0A x D +=，垂直于y 轴的平面方程为0B y D +=；而z =表示x O y 坐标面，0x =表示y O z 坐标面，0y =表示z O x 坐标面. 例5 指出下列平面位置的特点，并作出其图形： (1) 4x y +=； (2) 2z =.解 (1) 4x y +=，由于方程中不含z 的项，因此平面平行于z 轴(见图7-23). (2) 2z =，表示过点2(00)，，且垂直于z 轴的平面(见图7-24).图7-23 图7-24四、 有关平面与直线的位置关系1. 两平面的夹角及平行、垂直的条件设平面1Π与2Π的法向量分别为1111(,,)A B C =n 和2222(,,)A B C =n .如果这两个平面相交，它们之间有两个互补的二面角(见图7-25)，其中一个二面角与向量1n 与2n 的夹角相等.所以我们把这两平面的法向量的夹角中的锐角称为两平面的夹角.根据两向量夹角余弦的公式，有12cos cos(,)θ==n n (7-3-9)图7-25从两非零向量垂直、平行的条件，立即推得两平面垂直、平行的条件. 两平面12,ΠΠ互相垂直的充要条件是1212120A A B B C C ++=； (7-3-10)两平面12,ΠΠ互相平行的充要条件是111222A B C A B C ==. (7-3-11)例6 设平面1Π与2Π的方程分别为260x y z -+-=及250xy z ++-=，求它们的夹角.解 根据公式(7-3-9)得1cos 2θ==，所以平面1Π与2Π的夹角为π3θ=. 例7 一平面通过点1(1,1,1)P 和2(0,1,1)P -，且垂直于平面0x y z ++=，求这平面的方程.解平面0x y z ++=的法向量为1(1,1,1)=n ，又向量12(1,0,2)P P =--在所求平面上，设所求平面的法向量为n ，则n 同时垂直于向量12P P及1n ，所以可取112(1,1,1)(1,0,2)(2,1,1)P P =⨯=⨯--=-n n，故所求平面方程为2(1)(1)(1)0x y z --+-+-=，或20x y z --=.2. 两直线的夹角及平行、垂直的条件 设两直线1L 和2L 的标准式方程分别为111111x x y y z z m n p ---==和222222x x y y z z m n p ---==，两直线的方向向量()111,,m n p 1s =与()222,,m n p 2s =的夹角（这里指锐角或直角）称为两直线的夹角，记为θ，则cos θ=. (7-3-12)由此推出，两直线互相垂直的充要条件是121212 0m m n n p p ++=； (7-3-13)两直线互相平行的充要条件是111222m n p m n p == . (7-3-14)例8 求直线113:141y x z L -+==-和直线22:221y x zL +==--的夹角. 解 直线1L 的方向向量()1,41-1s =，，直线2L 的方向向量为()221--2s =，，，故直线1L 与2L 的夹角θ的余弦为cos θ===. 所以 π4θ=. 例9 求经过点()2,0,1-且与直线2360,42390x y z x y z -+-=⎧⎨-++=⎩平行的直线方程.解 所求直线与已知直线平行，其方向向量可取为()()()231423728,,,,,,=⨯-⨯-=--12s n n =.根据直线的标准式方程，得所求直线的方程为21728y x z -+==--. 例10 求过点213()，，，且与直线11321y x z-+==-垂直相交的直线方程. 解 先作一平面过点213()，，，且垂直于已知直线，那么这平面的方程应为()()()32+2130.x y z ----=再求已知直线与这平面的交点.把已知直线的参数方程13,12,x t y t z t =-+⎧⎪=+⎨⎪=-⎩代入平面方程，解之得37t =.再将求得的t 值代入直线参数方程中，即得 2133,,777x y z ===-. 所以，交点的坐标是2133,,777⎛⎫- ⎪⎝⎭. 于是，向量2132133,,777⎛⎫---- ⎪⎝⎭是所求直线的一个方向向量，故所求直线的方程为1232133213777y x z --==-----， 即123214y x z ---==-. 3. 直线与平面的夹角及平行、垂直的条件直线L 与它在平面Π上的投影所成的角称为直线L 与平面Π的夹角，一般取锐角(见图7-26).图7-26设直线L 的方程为ox x y y z z mnp---==，其方向向量(),,m n p =s ；平面Π的方程为0Ax B y C z D +++=，其法向量(),,A B C =n ，则πcos 2θ⎛⎫-=⎪⎝⎭n s n s ， 即sin θ=. (7-3-15)从而，直线L 与平面Π平行的充要条件是m B n C p ++=； (7-3-16)直线L 与平面Π垂直的充要条件是A B Cm n p==. (7-3-17) 例11 设平面Π的方程为0Ax B y C z D +++=，()1111,,M x y z 是平面外的一点，试求1M 到平面Π的距离.图7-27解 在平面Π上取一点()0000,,M x y z (见图7-27)，则点M 1到平面Π的距离Prj 0101n M M d M M ⋅==n n，而()()()11101000·M M A x x B y y C z z -+-+-n ＝由于点()000,,x y z 在平面Π上，有0000A x B y C z D +++=，即 000A x B y C z D ++=-，由此可得11101M M A x B y C z D ⋅=+++n，所以d =(7-3-18)公式（7-3-18）称为点到平面的距离公式.第四节 空间曲面与曲线一、 曲面及其方程在上一节中，我们考察了最简单的曲面——平面，以及最简单的空间曲线——直线，建立了它们的一些常见形式的方程.在这一节里，我们将介绍几种类型的常见曲面.1. 球面方程到空间一定点0M 之间的距离恒定的动点的轨迹为球面. 例1 建立球心在点()0000,,M x y z ，半径为R 的球面的方程.解 将球面看作空间中与定点等距离的点的轨迹.设(),,M x y z 是球面上的任一点，则0.M M R =由于0M M =所以R =.两边平方，得2222000x x y y z z R ---=（）+（）+（）(7-4-1) 显然，球面上的点的坐标满足这个方程，而不在球面上的点的坐标不满足这个方程.所以，方程(7-4-1)就是以()0000,,M x y z 为球心，以R 为半径的球面方程.如果0M 为原点，即0000x y z ===，这时球面方程为2222x y z R ++= (7-4-2)若记20A x =-，20B y =-，20C z =-， D 222200x y z R =++-，则式(7-4-1)可化为2220x y z A x B y C z D ++++++=（7-4-3） （7-4-3）式称为球面的一般方程由(7-4-3)式可以看出，球面的方程是关于,,x y z 的二次方程，它的222x y z ，，三项系数相等，并且方程中没有,,x y y z z x 的项.对于形如式（7-4-3）的一般方程，我们有下面几个结论：(1) 当22240A B C D ++->时，上式为一球面方程； (2) 当22240A B C D ++-=时，上式只表示一个点；(3) 当22240A B C D ++-<时，上式表示一个虚球，或者说它不代表任何图形. 例2 方程222240x y z x y ++-+=表示怎样的曲面? 解 通过配方，原方程可以改写为()()22212=5x y z -+++.与式(7-4-1)比较，可知原方程表示球心在点120,,0M -（）、半径R =的球面. 2. 柱面设给定一条曲线C 及直线l ，则平行于直线l ，且沿曲线C 移动的直线L 所形成的曲面叫做柱面.定曲线C 叫做柱面的准线，动直线L 叫做柱面的母线(见图7-28).图7-28如果柱面的准线是x O y 面上的曲线C ，其方程为() ,0f x y =， (7-4-4)柱面的母线平行于z 轴，则方程(),0f x y =就是这柱面的方程(见图7-29).因为在此柱面上任取一点(),,M x y z ，过点M 作直线平行于z 轴，此直线与x O y 面相交于点()0,,0M x y ，点0M 就是点M 在x O y 面上的投影.于是点0M 必落在准线上，它在x O y 面上的坐标(),x y 必满足方程(),0f x y =，这个方程不含z 的项，所以点M 的坐标(),,x y z 也满足方程(),0fx y =.。

学高数的顺序
学习高等数学（高数）的顺序通常遵循数学学科的自然发展逻辑和学生的学习能力。

以下是一个常见的高数学习顺序：
1. 微积分基础：首先学习函数的极限、连续性、导数和微分等基本概念和方法。

这是高数的基础，为后续内容打下基础。

2. 积分学：接下来学习不定积分、定积分以及积分的应用，如求解面积、体积等。

3. 多元函数微积分：在掌握了一元函数微积分的基础上，进一步学习多元函数的极限、偏导数、全微分、二重积分、三重积分等内容。

4. 微分方程：学习一阶、二阶以及高阶微分方程的解法，了解微分方程在实际问题中的应用。

5. 向量代数与空间解析几何：学习向量的概念、运算以及空间解析几何的基本知识，为后续的高级课程做准备。

6. 级数理论：学习无穷级数的概念和性质，掌握级数的收敛性判别方法以及级数求和的方法。

7. 线性代数：学习矩阵的基本概念和运算，了解线性方程组、线性变换、特征值与特征向量等内容。

8. 概率论与数理统计：学习随机事件、概率、随机变量、概率分布、参数估计、假设检验等统计学的基本概念和方法。

在实际学习过程中，学生可以根据自己的兴趣、专业需求以及教学安排等因素，适当调整学习顺序。

同时，建议在每个阶段都进行充分的练习和复习，以加深对知识点的理解和记忆。

机器学习数学知识积累之线性代数解析⼏何，微积分解析⼏何解析⼏何的基本思想是⽤代数的⽅法来研究⼏何，把空间的⼏何结构系统地代数化，数量化向量的定义⼀个有长度和⽅向的⽮量，和标量(scalar)相对应向量的⼤⼩（有向线段的长度）称为向量的模 $|\vec{a}|$长度为1的向量称为单位向量向量的平⾏(共线)，共⾯和垂直向量共线平⾏的充分必要条件是：存在⼀个标量$ \lambda $ 使得以下成⽴: $$\vec{a} = \lambda \vec{b}$$向量共⾯的充分必要条件是：a,b,c之间存在线性变换关系使得以下成⽴：$$\vec{c} = \lambda \vec{b}+ \eta \vec{a}$$向量垂直的充分必要条件是：$$\vec{a} \cdot \vec{b} = 0$$向量的线性运算加法：三⾓形法则，平⾏四边形法则,多边形法则(多个向量尾⾸相连，最终A的起点到Z的终点连接起来即为所有这些向量的和)减法数乘：只改变向量长度，⽅向⼀致或相反（随这个数据正负⽽定）向量加减法⼏何⽰意图向量的代数表⽰把空间中所有的向量的尾部都拉到坐标原点，这样N维点空间可以与N维向量空间建⽴⼀⼀对应关系：N维点空间中点(0，0，0…0)取作原点，那么每⼀个点都可以让⼀个向量和它对应，这个向量就是从坐标原点出发到这个点为⽌的向量。

向量在轴上的投影$C'和D‘$分别称为点$C,D$在轴u上的投影，向量$\vec{CD}$在轴u上的投影为C,D两点在u轴上的投影点$C',D'$组成的有向线段$\vec{C'D'}$的值，其绝对值等于向量$|\vec{C'D'}|$，其正负的符号由$\vec{C'D'}$的⽅向决定，当$\vec{C'D'}和u$轴同⽅向时值为正，反⽅向时值为负。

记为$Prj_u\vec{CD}$投影定理:向量$\vec{CD}$在轴u上的投影等于向量的模乘以轴与向量的夹⾓的余弦:$$Prj_u\vec{CD}=|\vec{CD}|cos(\varphi )$$性质定理:n个向量的和在轴上的投影等于两个向量在该轴上的投影之和.$$Prj_u(a_1+a_2+..+a_n) = Prj_ua_1+Prj_ua_2+...+Prj_ua_n$$向量的内积(数量积，点乘)和外积内积:两个向量的内积或者叫点乘结果是⼀个标量，其值等于a,b的模乘以其夹⾓的cos值。

(6) a , b , c 共面 [a , b , c ] 0 a x a y az
bx cx by cy
a x bx a y by az bz 0.
bz 0. cz
二、空间解析几何
1、空间曲面方程 (1) 空间曲面一般方程
F ( x , y , z ) 0 或 z f ( x , y ) 等。
向量代数
向量的 线性运算
向量概念
向量的 表示法
向量的积
数量积 混合积 向量积
空间解析几何 空间直角坐标系
一般方程 旋转曲面
曲线
参数方程 一般方程 参数方程
曲面
平 面
柱
面
直 线
二次曲面
一般方程
对称式方程 点法式方程
向 向量的坐标表达式、模、方向余弦、 量 单位向量、在另一向量上的投影; 空间两 代 点间的距离; 向量的垂直与平行、数量积 数 与向量积及其运算规律与性质意义 空 间 解 析 柱面、旋转曲面、二次曲面方程；空 几 何 间直线在坐标面上的投影
它满足交换律、结合律、分配律。
0 向量积 a b a b sin ( a ,^ b ) n , 0 a , b 所在平面的 n : 按“右手法则”垂直于 单位向量。 i j k a b a x a y az S a b . bx b y bz
a x a y az 0 与a 平行的单位向量为 a { , , } |a | |a | |a | 2 2 2 其中| a | a x a y az
的投影。
一、向量代数
ay ax a 的方向余弦为 cos , cos , |a | |a | az cos , 方向余弦满足 |a | cos2 cos2 cos2 1.

则 AB = ( x2 x1 )2 ( y2 y1 )2 ( z2 z1 )2
第五讲 空间解析几何、级数及微分方程 2. 空间向量的概念
向量: 既有大小, 又有方向的量称为向量 (又称矢量). 表示法: 向量的模 : 有向线段 M1 M2 , 或 a； 向量的长度,
向径 (矢径): 起点为原点的向量； 自由向量: 与起点无关的向量； 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量,
ax a y az a b 即 = = bx by bz
第五讲 空间解析几何、级数及微分方程
向量积的行列式计算法
(a y bz a z by ) i (a z bx a x bz ) j (a x by a y bx ) k
i j = ax a y k az
a = ax i a y j az k b = bx i by j bz k
平面椭圆柱面双曲柱面抛物柱面第五讲空间解析几何级数及微分方程一般地在三维空间柱面柱面平行于准线xoz面上的曲线母线柱面准线xoy面上的曲线母线准线yoz面上的曲线母线表示方程表示方程表示方程第五讲空间解析几何级数及微分方程斜率为1的直线平面解析几何中空间解析几何中轴的直线平行于yoz面的平面圆心在00半径为轴为中心轴的圆柱面平行于轴的平面平面解析几何和空间解析几何的一些比较第五讲空间解析几何级数及微分方程级数一常数项级数1
注：以后我们判定空间中 的直线与直线、平面与平 面，以及直线与平面的位 置关系，归根到底都是判 定两个向量的位置关系， 因此要牢记这些结论！
②两个向量平行的判定
a b
a b = 0 ax a y az = = bx by bz
第五讲 空间解析几何、级数及微分方程 例1. 解：

微积分下册知识点第一章 空间解析几何与向量代数 （一） 向量及其线性运算1、 向量,向量相等,单位向量,零向量,向量平行、共线、共面；2、 线性运算：加减法、数乘；3、 空间直角坐标系：坐标轴、坐标面、卦限,向量的坐标分解式；4、 利用坐标做向量的运算：设),,(z y x a a a a =,),,(z y x b b b b = ,则),,(z z y y x x b a b a b a b a ±±±=±,),,(z y x a a a a λλλλ=；5、 向量的模、方向角、投影：1） 向量的模：222z y x r ++= ；2） 两点间的距离公式：212212212)()()(z z y y x x B A -+-+-=3） 方向角：非零向量与三个坐标轴的正向的夹角γβα,,4） 方向余弦：rzr y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα5） 投影：ϕcos Pr a a j u =,其中ϕ为向量a 与u 的夹角;（二） 数量积,向量积1、 数量积：θcos b a b a=⋅12a a a =⋅2⇔⊥b a 0=⋅b az z y y x x b a b a b a b a ++=⋅2、 向量积：b a c⨯=大小：θsin b a ,方向：c b a,,符合右手规则10 =⨯a a 2b a //⇔0 =⨯b azy x zy x b b b a a a kj i b a=⨯运算律：反交换律 b a a b⨯-=⨯（三） 曲面及其方程 1、 曲面方程的概念：0),,(:=z y x f S2、 旋转曲面：yoz 面上曲线0),(:=z y f C ,绕y 轴旋转一周：0),(22=+±z x y f 绕z 轴旋转一周：0),(22=+±z y x f3、 柱面：),(=y x F 表示母线平行于z轴,准线为⎪⎩⎪⎨⎧==0),(z y x F 的柱面 4、 二次曲面不考1） 椭圆锥面：22222z by a x =+ 2） 椭球面：1222222=++c z b y a x旋转椭球面：1222222=++cz a y a x3） 单叶双曲面：1222222=-+czb y a x4） 双叶双曲面：1222222=--cz b y a x5） 椭圆抛物面：z by a x =+22226） 双曲抛物面马鞍面：z b y a x =-22227） 椭圆柱面：12222=+b y a x 8） 双曲柱面：12222=-b y a x9） 抛物柱面：ay x =2（四） 空间曲线及其方程1、 一般方程：⎪⎩⎪⎨⎧==0),,(0),,(z y x G z y x F2、 参数方程：⎪⎪⎩⎪⎪⎨⎧===)()()(t z z t y y t x x ,如螺旋线：⎪⎪⎩⎪⎪⎨⎧===bt z t a y t a x sin cos3、 空间曲线在坐标面上的投影⎪⎩⎪⎨⎧==0),,(0),,(z y x G z y x F ,消去z ,得到曲线在面xoy 上的投影⎪⎩⎪⎨⎧==00),(z y x H（五） 平面及其方程 1、 点法式方程：0)()()(000=-+-+-z z C y y B x x A法向量：),,(C B A n =,过点),,(000z y x2、 一般式方程：0=+++D Cz By Ax截距式方程：1=++czb y a x 3、 两平面的夹角：),,(1111C B A n = ,),,(2222C B A n = ,222222212121212121cos CB AC B A C C B B A A ++⋅++++=θ⇔∏⊥∏21 0212121=++C C B B A A⇔∏∏21// 212121C C B B A A ==4、 点),,(0000z y x P 到平面0=+++D Cz By Ax 的距离：222000C B A DCz By Ax d +++++=（六） 空间直线及其方程1、 一般式方程：⎪⎩⎪⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A2、 对称式点向式方程：p z z n y y m x x 000-=-=-方向向量：),,(p n m s =,过点),,(000z y x3、 参数式方程：⎪⎪⎩⎪⎪⎨⎧+=+=+=pt z z nty y mt x x 0004、 两直线的夹角：),,(1111p n m s = ,),,(2222p n m s =,222222212121212121cos pn m p n m p p n n m m ++⋅++++=ϕ⇔⊥21L L 0212121=++p p n n m m⇔21//L L212121p p n n m m ==5、 直线与平面的夹角：直线与它在平面上的投影的夹角,222222sin p n m C B A CpBn Am ++⋅++++=ϕ⇔∏//L 0=++Cp Bn Am⇔∏⊥L pCn B m A ==第二章 多元函数微分法及其应用 （一） 基本概念1、 距离,邻域,内点,外点,边界点,聚点,开集,闭集,连通集,区域,闭区域,有界集,无界集;2、 多元函数：),(y x f z =,图形：3、 极限：A y x f y x y x =→),(lim ),(),(00 4、 连续：),(),(lim 00),(),(00y x f y x f y x y x =→5、 偏导数：xy x f y x x f y x f x x ∆-∆+=→∆), (), (lim ),(0000000yy x f y y x f y x f y y ∆-∆+=→∆),(),(lim ),(0000000 6、 方向导数：βαcos cos y fx f l f ∂∂+∂∂=∂∂其中βα,为l的方向角; 7、 梯度：),(y x f z =,则j y x f i y x f y x gradf y x),(),(),(000000+=;8、 全微分：设),(y x f z =,则d d d z z z x y x y∂∂=+∂∂ （二） 性质1、 函数可微,偏导连续,偏导存在,函数连续等概念之间的关系：2、 闭区域上连续函数的性质有界性定理,最大最小值定理,介值定理3、 微分法 1） 定义：u x2） 复合函数求导：链式法则 z若(,),(,),(,)z f u v u u x y v v x y ===,则v yz z u z v x u x v x ∂∂∂∂∂=⋅+⋅∂∂∂∂∂,z z u z vy u y v y∂∂∂∂∂=⋅+⋅∂∂∂∂∂ 充分条件3） 隐函数求导：两边求偏导,然后解方程组 （三） 应用 1、 极值1） 无条件极值：求函数),(y x f z =的极值解方程组 ⎪⎩⎪⎨⎧==00yx f f 求出所有驻点,对于每一个驻点),(00y x ,令),(00y x f A xx =,),(00y x f B xy =,),(00y x f C yy =,① 若02>-B AC ,0>A ,函数有极小值, 若02>-B AC ,0<A ,函数有极大值；② 若02<-B AC ,函数没有极值； ③ 若02=-B AC ,不定;2） 条件极值：求函数),(y x f z =在条件0),(=y x ϕ下的极值 令：),(),(),(y x y x f y x L λϕ+= ———Lagrange 函数解方程组 ⎪⎪⎩⎪⎪⎨⎧===0),(0y x L L y x ϕ2、 几何应用1） 曲线的切线与法平面曲线⎪⎪⎩⎪⎪⎨⎧===Γ)()()(:t z z t y y t x x ,则Γ上一点),,(000z y x M 对应参数为0t 处的切线方程为：)()()(00000t z z z t y y y t x x x '-='-='- 法平面方程为：))(())(())((000000=-'+-'+-'z z t z y y t y x x t x2） 曲面的切平面与法线曲面0),,(:=∑z y x F ,则∑上一点),,(000z y x M 处的切平面方程为：))(,,())(,,())(,,(0=-+-+-z z z y x F y y z y x F x x z y x F zyx法线方程为：),,(),,(),,(000000000000z y x F z z z y x F y y z y x F x x z y x -=-=-第三章 重积分（一） 二重积分一般换元法不考1、 定义：∑⎰⎰=→∆=nk k k k Df y x f 1),(lim d ),(σηξσλ2、 性质：6条3、 几何意义：曲顶柱体的体积;4、 计算：1） 直角坐标⎭⎬⎫⎩⎨⎧≤≤≤≤=b x a x y x y x D )()(),(21ϕϕ,21()()(,)d d d (,)d bx ax Df x y x y x f x y y φφ=⎰⎰⎰⎰⎭⎬⎫⎩⎨⎧≤≤≤≤=d y c y x y y x D )()(),(21φφ,21()()(,)d d d (,)d dy cy Df x y x y y f x y x ϕϕ=⎰⎰⎰⎰2） 极坐标⎭⎬⎫⎩⎨⎧≤≤≤≤=βθαθρρθρθρ)()(),(21D21()()(,)d d (cos ,sin )d Df x y x y d f βρθαρθθρθρθρρ=⎰⎰⎰⎰（二） 三重积分 1、 定义： ∑⎰⎰⎰=→Ω∆=nk k k k kv f v z y x f 1),,(limd ),,(ζηξλ2、 性质：3、 计算：1） 直角坐标⎰⎰⎰⎰⎰⎰=ΩDy x z y x z zz y x f y x v z y x f ),(),(21d ),,(d d d ),,(-------------“先一后二”⎰⎰⎰⎰⎰⎰=ΩZD bayx z y x f z v z y x f d d ),,(d d ),,(-------------“先二后一”2） 柱面坐标⎪⎪⎩⎪⎪⎨⎧===zz y x θρθρsin cos ,(,,)d (cos ,sin ,)d d d f x y z v f z z ρθρθρρθΩΩ=⎰⎰⎰⎰⎰⎰3） 球面坐标⎪⎪⎩⎪⎪⎨⎧===ϕθϕθϕcos sin sin cos sin r z r y r x 2(,,)d (sin cos ,sin sin ,cos )sin d d d f x y z v f r r r rr φθφθφφφθΩΩ=⎰⎰⎰⎰⎰⎰（三） 应用 曲面D y x y x f zS ∈=),(,),(:的面积：y x yz x z A Dd d )()(122⎰⎰∂∂+∂∂+=第五章 曲线积分与曲面积分 （一） 对弧长的曲线积分 1、 定义：1(,)d lim (,)ni i i Li f x y s f s λξη→==⋅∆∑⎰2、 性质： 1[(,)(,)]d (,)d (,)d .LLLf x y x y s f x y sg x y s αβαβ+=+⎰⎰⎰ 212(,)d (,)d (,)d .LL L f x y s f x y s f x y s =+⎰⎰⎰).(21L L L +=3在L上,若),(),(y x g y x f ≤,则(,)d (,)d .LLf x y sg x y s ≤⎰⎰4l s L=⎰d l 为曲线弧 L 的长度3、 计算：设),(y x f 在曲线弧L 上有定义且连续,L 的参数方程为)(),(),(βαψϕ≤≤⎪⎩⎪⎨⎧==t t y t x ,其中)(),(t t ψϕ在],[βα上具有一阶连续导数,且0)()(22≠'+'t t ψϕ,则(,)d [(),( ,()Lf x y s f t t t βαφψαβ=<⎰⎰（二） 对坐标的曲线积分1、 定义：设 L 为xoy 面内从 A 到B 的一条有向光滑弧,函数),(y x P ,),(y x Q 在 L 上有界,定义∑⎰=→∆=nk k k k Lx P x y x P 1),(lim d ),(ηξλ,∑⎰=→∆=nk k k kLy Q y y x Q 1),(lim d ),(ηξλ.向量形式：⎰⎰+=⋅LLy y x Q x y x P r F d ),(d ),(d2、 性质：用-L 表示L 的反向弧 , 则⎰⎰⋅-=⋅-LL r y x F r y x F d ),(d ),( 3、 计算： 设),(,),(y x Q y x P 在有向光滑弧L 上有定义且连续,L 的参数方程为):(),(),(βαψϕ→⎪⎩⎪⎨⎧==t t y t x ,其中)(),(t t ψϕ在],[βα上具有一阶连续导数,且0)()(22≠'+'t t ψϕ,则(,)d (,)d {[(),()]()[(),()LP x y x Q x y y P t t t Q t t βαφψφφψ'+=+⎰⎰4、 两类曲线积分之间的关系：设平面有向曲线弧为⎪⎩⎪⎨⎧==)()( t y t x L ψϕ：,L 上点),(y x 处的切向量的方向角为：βα,,)()()(cos 22t t t ψϕϕα'+''=,)()()(cos 22t t t ψϕψβ'+''=, 则d d (cos cos )d LLP x Q y P Q s αβ+=+⎰⎰.（三） 格林公式1、格林公式：设区域 D 是由分段光滑正向曲线 L 围成,函数),(,),(y x Q y x P 在D 上具有连续一阶偏导数, 则有⎰⎰⎰+=⎪⎪⎭⎫⎝⎛∂∂-∂∂LD y Q x P y x y P x Q d d d d2、G 为一个单连通区域,函数),(,),(y x Q y x P 在G 上具有连续一阶偏导数,则y Px Q ∂∂=∂∂ ⇔曲线积分 d d LP x Q y +⎰在G 内与路径无关 ⇔曲线积分d d 0LP x Q y +=⎰⇔ y y x Q x y x P d ),(d ),(+在G 内为某一个函数),(y x u 的全微分 （四） 对面积的曲面积分1、 定义：设∑为光滑曲面,函数),,(z y x f 是定义在∑上的一个有界函数,定义 i i i i ni S f S z y x f ∆=∑⎰⎰=→∑),,(lim d ),,(10ζηξλ 2、 计算：———“一投二换三代入”),(:y x z z =∑,xy D y x ∈),(,则x z y x z y x z y x f S z y x f y x D yx ,(),(1)],(,,[d ),,(22++=⎰⎰⎰⎰∑（五） 对坐标的曲面积分1、 预备知识：曲面的侧,曲面在平面上的投影,流量2、 定义：设∑为有向光滑曲面,函数),,(),,,(),,,(z y x R z y x Q z y x P 是定义在∑上的有界函数,定义1(,,)d d lim (,,)()ni i i i xy i R x y z x y R S λξηζ∑→==∆∑⎰⎰同理,1(,,)d d lim (,,)()ni i i i yz i P x y z y z P S λξηζ∑→==∆∑⎰⎰1(,,)d d lim (,,)()ni i i i zx i Q x y z z x R S λξηζ∑→==∆∑⎰⎰3、 性质： 121∑+∑=∑,则12d d d d d d d d d d d d d d d d d d P y z Q z x R x yP y z Q z x R x y P y z Q z x R x y ∑∑∑++=+++++⎰⎰⎰⎰⎰⎰2-∑表示与∑取相反侧的有向曲面 , 则d d d d R x y R x y -∑∑=-⎰⎰⎰⎰4、 计算：——“一投二代三定号”),(:y x z z =∑,xy D y x ∈),(,),(y x z z =在xy D 上具有一阶连续偏导数,),,(z y x R 在∑上连续,则(,,)d d [,,(,)]d d x yD R x y z x y R x y z x y x y ∑=±⎰⎰⎰⎰,∑为上侧取“ + ”, ∑为下侧取“ - ”. 5、 两类曲面积分之间的关系：()R Q P y x R x z Q z y P dcos cos cos d d d d d d ⎰⎰⎰⎰∑∑++=++γβα其中γβα,,为有向曲面∑在点),,(z y x 处的法向量的方向角;（六） 高斯公式1、 高斯公式：设空间闭区域Ω由分片光滑的闭曲面∑所围成, ∑的方向取外侧, 函数,,P Q R 在Ω上有连续的一阶偏导数,则有⎰⎰⎰⎰⎰∑Ω++=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂yx R x z Q z y P z y x z R y Q x P d d d d d d d d d或()⎰⎰⎰⎰⎰∑Ω++=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂S R Q P z y x z R y Q x P d cos cos cos d d d γβα（七） 斯托克斯公式1、 斯托克斯公式：设光滑曲面 ∑ 的边界 Γ是分段光滑曲线, ∑ 的侧与 Γ 的正向符合右手法则,),,(),,,(),,,(z y x R z y x Q z y x P 在包含∑ 在内的一个空间域内具有连续一阶偏导数,则有⎰⎰⎰Γ∑++=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂z R y Q x P y x y P x Q x z x R z P z y z Q y R d d d d d d d d d为便于记忆, 斯托克斯公式还可写作:⎰⎰⎰Γ∑++=∂∂∂∂∂∂z R y Q x P RQ P zy x y x x z z y d d d d d d d d d 第六章 常微分方程1、微分方程的基本概念含未知函数的导数或微分的方程称为微分方程； 未知函数是一元函数的微分方程,称为常微分方程;未知函数是多元函数的微分方程,称为偏微分方程；微分方程中未知函数的导数的最高阶数,称为微分方程的阶.能使微分方程成为恒等式的函数,称为微分方程的解. 如果微分方程的解中含任意常数,且独立的即不可合并而使个数减少的任意常数的个数与微分方程的阶数相同,这样的解为微分方程的通解. 不包含任意常数的解为微分方程特解.2、典型的一阶微分方程可分离变量的微分方程： 对于第1种形式,运用积分方法即可求得变量可分离方程的通解：)()(d )(d )(y g x h dxdyx x f y y g ==或2、 齐次微分方程：代入微分方程即可;3、 一阶线性微分方程型如称为一阶线性微分方程; 其对应的齐次线性微分方程的解为利用常数变异法可得到非齐次的线性微分方程的通解4、 伯努利方程： 于是U 的通解为：5、 全微分方程：7、可降阶的高阶常微分方程 12型的微分方程),(6.4.2 )1()(-=n n y x f y 3型的微分方程),(6.4.3 y y f y '='' 8、线性微分方程解的结构 1函数组的线性无关和线性相关 2线性微分方程的性质和解的结构叠加原理：二个齐次的特解的线性组合仍是其特解；二个线性无关齐次的特解的线性组合是其通解 3刘维尔公式4二阶非齐线性微分方程解的结构特解的求解过程主要是通过常数变异法,求解联立方程的解：⎰⎰=xx f y y g d )(d )( )( )( yxx x y y ψϕ='='或者 ,)( 可将其化为可分离方程中，令在齐次方程xy u x y y =='ϕ , xu y x y u ==，则令,u dx du x dx dy +=.)()1(的方程形如c by ax f y ++=',y b a u '+=').(u f bau =-'原方程可化为)()(x q y x p y =+' d )(。

数学强化班（武忠祥）-⾼数第⼋章向量代数与解析⼏何及多元微分在⼏何上应⽤第⼋章向量代数与空间解析⼏何及多元微分学在⼏何上的应⽤第⼀节向量1．数量积1）⼏何表⽰：αcos ||||b a b a =?. 2) 代数表⽰: z z y y x x b a b a b a ++=?b a . 3) 运算规律:i) 交换律: a b b a ?=?ii) 分配律: .)(c a b a c b a ?+?=+? 4) ⼏何应⽤:i) 求模: a a a ?=||ii) 求夹⾓: ||||cos b a ba ?=α iii) 判定两向量垂直: 0=??⊥b a b a 2.向量积1) ⼏何表⽰ b a ?是⼀向量. 模: αsin ||||||b a b a =?. ⽅向: 右⼿法则.2) 代数表⽰: zyx z y xb b b a a a k j ib a =?. 3) 运算规律 i) b a ?= )(a b ?-ii) 分配律: ?a (c b +)=b a ?+c a ?. 4)⼏何应⽤:i) 求同时垂直于a 和b 的向量: b a ?.ii) 求以a 和b 为邻边的平⾏四边形⾯积:=S |b a ?|.iii)判定两向量平⾏: ?b a //0=?b a . 3.混合积: c b a abc ??=)()( 1) 代数表⽰:zyxz y xz y xc c c b b b a a a =)(abc . 2) 运算规律:i) 轮换对称性: )()()(cab bca abc ==. ii) 交换变号: )()(acb abc -=. 3) ⼏何应⽤i) 平⾏六⾯体V =|)(|abc .ii)判定三向量共⾯: c b a ,,共⾯?(abc )=0.题型⼀向量运算例8.1 设,2)(=??c b a 则=+?+?+)()]()[(a c c b b a .解 )()]()[(a c c b b a +?+?+)(][a c c b b b c a b a +??+?+?+?=a cbc c b a c a c c a a b a c b a ??+??+??+??+??+??=)()()()()()( a c b c b a ??+??=)()( 4)(2=??=c b a .例8.2 已知3||,2||==b a ,则=??+))(()()(b a b a b a b a .解 22)())(()()(b a b a b a b a b a b a ?+?=??+ ),(c o s ),(s i n 222222∧∧+=b a b a b a b a 3622==b a .例8.3 已知2||,2||==b a ,且2=?b a ,则=?||b a.A)2 B)22 C)22D)1 解由于2),cos(==?∧b a b a b a ，⽽2,2==b a ，则21),cos(=∧b a ，从⽽4),(π=∧b a .故 22122),s i n (=?==?∧b a b a b a题型⼆向量运算的应⽤及向量的位置关系例8.4 已知}4,4,2{-=a ,}2,2,1{--=b ,求a 与b 的⾓平分线向量且使其模为32。

绕 z 轴旋转所成的旋转曲面的方程为 f ± 绕 y 轴旋转所成的旋转曲面的方程为 设 C : f ( x , y ) = 0 ⊂ xoy
( x + y , z) = 0 f (y ,± x + z ) = 0
2 2
2 2
2 2 绕 x 轴旋转所成的旋转曲面的方程为 f x ,± y + z = 0
绕 y 轴旋转所成的旋转曲面的方程为 设 C : f ( x , z ) = 0 ⊂ zox
( f (±
x2 + z2
) , y) = 0
) , z) = 0
2 2 绕 x 轴旋转所成的旋转曲面的方程为 f x ,± y + z = 0
绕 z 轴旋转所成的旋转曲面的方程为
( f (±
x2 + y2
记忆法：轴不变，其余两元团团转。 记忆法：轴不变，其余两元团团转。
x2 y2 z2 用截痕法研究曲面的形状。 例1 已知方程 2 + 2 − 2 = 1 用截痕法研究曲面的形状。 a b c 2 2
解 （1）用 z = 0 截此曲面，得 截此曲面， ） 截此曲面， 用 z = h 截此曲面，得
x y + 2 =1 2 a b
z=0
x2 y2 h2 + 2 =1+ 2 2 a b c z=h
第九章 空间解析几何
用代数的方法研究几何问题称为解析几何 平面解析几何 空间解析几何
P ↔ ( x, y)
一元微积分 多元微积分
P ↔ ( x, y, z)
本章的主要内容 : §9.1 空间直角坐标系 向量概念和运算; §9.2 向量概念和运算; 曲面方程和空间曲线方程 和空间曲线方程; §9.3 曲面方程和空间曲线方程; §9.4 平面方程 §9.5 空间直线方程; 空间直线方程; 二次曲面. 常见二次曲面 §9.6 常见二次曲面.

-。

b与a的差b a．向量加法的性质〔运算律〕②结合律+的模一般地不等于a的模加b的模，而有a b a ba b+≤+，即三角形两边之和大于等于第三向量与数的乘法Array、向量的定义：向量a与数m的乘积是一个向量，它的模等于m a，方向与a相同〔假设反〔假设m<0〕。

、向量与数量乘法的性质(运算律)②分配律≠，则向量b平行于a得充分必要条件是：存在唯一实数λ，使b=λa。

a0在实际问题中，有些向量与其起点有关，有些向量与其起点无关。

由于一切向量的共性是它们都有大小和方向，所以在数学上我们研究与起点无关的向量，并称这种向量为自由向量〔以后简称向量〕，即只考虑向量的大小和方向，而不管它的起点在什么地方。

当遇到与起点有关的向量时〔例如，谈到某一质点的运动速度时，这速度就是与所考虑的那一质点的位置有关的向量〕，可在一般原则下作特别处理。

上的射影。

投影向量的定义：AB 的始点A B ''就定义AB 在轴u 上的投影向量。

向量在轴上的投影：向量A B ''在轴AB 在轴u 上的投影，记为投影AB 。

向量在轴上的投影性质：性质1〔投影定理〕AB =cos AB ϕ与向量AB 的夹角。

推论：相等矢量在同一轴上的射影相等。

性质2：Prj(12a a +)=Prj 1a +Prj 2a 。

性质2可推广到有限个向量的情形。

性质3：Prj u λa =λPrj u a 。

向量在坐标轴上的分向量与向量的坐标：向量a 在坐标轴上的投影向量,,y z i a j a k 称为向量在坐标轴上的分向量。

向量a 在三条坐标轴上的投影,y z a a 叫做向量的坐标，记为：a ={,,x y a a 由向量在轴上的投影定义，a 在直角坐标系Oxyz 中的坐标{,,x y z a a a a ，由此可知，向量的投影具有与坐标相同的性质。

利用向量的坐标，可得向量的加法、减法以及向量与数的乘法的运算如下：a ={,x y a a ，{,,}x y zb b b b =利用向量加法的交换律与结合律，以及向量与数乘法的结合律与分配律，有{,x y z z a b a b b a b +=+++{x a b a b -=-{,}x y a a a λλλ=由此可见，对向量进行加、减及与数相乘，只须对向量的各个坐标分别进行相应的数量运算就行了。

bx by bz 2.垂直: a ⊥ b ⇔ axbx + ayby + azbz = 0 .
ax ay az 3. a,b,c 共面 ⇔ bx by bz = 0 .
cx cy cz 【例 4】已知=a {1, 2, −3}，=b {2, −3, k} ， c = {−2, k, 6} ，
（1）若 a ⊥ b ，求 k ;（2）若 a c ，求 k ;（3）若 a,b,c 共面，求 k .
x − x1 x2 − x1 x3 − x1
y − y1 y2 − y1 y3 − y1
z − z1 z2 − z1 = 0 ． z3 − z1
【评注】（1）.法向量是不唯一的.
（2）. Ax + By + Cz = 0 表示通过原点的平面， Ax + By + D =0 表示平行于 z 轴的平面，
A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 .
2.一般式：空间 O − xyz 中平面方程为三元一次方程
Ax + By + Cz + D = 0
3. 截距式：在 x 轴、 y 轴、 z 轴上的截距分别为 a, b, c (abc ≠ 0) 的平面方程为
x + y + z =1 abc 4.三点式：过空间不共线的三点{x1, y1, z1}，{x2, y2, z2}，{x3, y3, z3} 的平面方程为
二.直线方程 平行于直线的非零向量称为该直线的方向向量，记为 s = {m, n, p}，方向向量不唯一.
1.对称式（点向式）:过点 ( x0 , y0 , z0 ) 且方向向量为 s = {m, n, p}的直线方程为

高数每周疑难问题总结
以下是一些常见的高数疑难问题：
1. 极限概念与性质：理解极限的概念和性质是高数的基础，但学生经常对极限的运算、无穷小、有界量等概念感到困惑。

2. 连续性与可导性：连续性和可导性是微积分的重要概念，但学生经常混淆它们之间的关系和区别。

3. 微分法则与运算：微分法则和运算也是高数的重点，学生在应用这些法则时经常出错。

4. 积分的应用与计算：积分在高数中占有重要地位，但学生经常对积分的概念、性质和应用感到困惑。

5. 多元函数的微分与偏导数：多元函数的微分和偏导数是高数的难点，学生经常对它们的概念和计算感到困惑。

6. 级数的收敛与发散：级数是高数的一个重要部分，但学生经常对级数的收敛和发散的概念和性质感到困惑。

7. 空间解析几何与向量：空间解析几何与向量在高数中也有重要地位，但学生经常对向量的运算、向量的模、向量的数量积等概念感到困惑。

8. 微积分的应用题：微积分的应用题是高数的重点，但学生经常对如何应用微积分解决实际问题感到困惑。

以上只是部分高数疑难问题，具体问题可能因学生的学习进度和理解程度而异。

建议定期进行总结和回顾，以加深对高数知识的理解。

第五篇 向量代数与空间解析几何第八章 向量代数与空间解析几何解析几何的基本思想是用代数的方法来研究几何的问题，为了把代数运算引入几何中来，最根本的做法就是设法把空间的几何结构有系统的代数化，数量化. 平面解析几何使一元函数微积分有了直观的几何意义，所以为了更好的学习多元函数微积分，空间解析几何的知识就有着非常重要的地位.本章首先给出空间直角坐标系，然后介绍向量的基础知识，以向量为工具讨论空间的平面和直线，最后介绍空间曲面和空间曲线的部分容.第1节 空间直角坐标系1.1 空间直角坐标系用代数的方法来研究几何的问题，我们需要建立空间的点与有序数组之间的联系，为此我们通过引进空间直角坐标系来实现.1.1.1 空间直角坐标系过定点O ，作三条互相垂直的数轴，这三条数轴分别叫做x 轴(横轴）、y 轴(纵轴)、z 轴(竖轴)，它们都以O 为原点且具有相同的长度单位. 通常把x 轴和y 轴配置在水平面上，而z 轴则是铅垂线；它们的正方向要符合右手规则：右手握住z 轴，当右手的四指从x 轴的正向转过2角度指向y 轴正向时，大拇指的指向就是z 轴的正向，这样就建立了一个空间直角坐标系（图8-1），称为Oxyz 直角坐标系，点O 叫做坐标原点.图8-1在Oxyz 直角坐标系下，数轴Ox ,Oy ,Oz 统称为坐标轴，三条坐标轴中每两条可以确定一个平面，称为坐标面，分别为xOy ，yOz ，zOx ，三个坐标平面将空间分为八个部分，每一部分叫做一个卦限（图8-2），分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ表示.yxzO图8-21.1.2 空间点的直角坐标设M 为空间中的任一点，过点M 分别作垂直于三个坐标轴的三个平面，与x 轴、y 轴和z 轴依次交于A 、B 、C 三点，若这三点在x 轴、y 轴、z 轴上的坐标分别为x ，y ，z ，于是点M 就唯一确定了一个有序数组(, , )x y z ，则称该数组(, , )x y z 为点M 在空间直角坐标系Oxyz 中的坐标，如图8-3．x ，y ，z 分别称为点M 的横坐标、纵坐标和竖坐标．图8-3反之，若任意给定一个有序数组(, , )x y z ，在x 轴、y 轴、z 轴上分别取坐标为x ，y ，z 的三个点A 、B 、C ，过这三个点分别作垂直于三个坐标轴的平面，这三个平面只有一个交点M ，该点就是以有序数组(, , )x y z 为坐标的点，因此空间中的点M 就与有序数组(, , )x y z 之间建立了一一对应的关系．注：A 、B 、C 这三点正好是过M 点作三个坐标轴的垂线的垂足．yxzOyxzAB C(,,)M x y z1.2 空间中两点之间的距离设两点111(, , )M x y z ，222(, , )N x y z ，则M 与N 之间的距离为212212212)()()(z z y y x x d -+-+-= （8-1-1）事实上，过点M 和N 作垂直于xOy 平面的直线，分别交xOy 平面于点1M 和1N ，则1MM ∥1NN ，显然，点1M 的坐标为11(, , 0)x y ，点1N 的坐标为22(, , 0)x y （如图8-4）．图8-4由平面解析几何的两点间距离公式知，1M 和1N 的距离为：21221211)()(||y y x x N M -+-=．过点M 作平行于xOy 平面的平面，交直线1NN 于2N ，则11M N ∥2MN ，因此2N 的坐标为221(, , )x y z ，且212212112)()(||||y y x x N M MN -+-==，在直角三角形N MN 2中，||||122z z N N -=，所以点M 与N 间的距离为2122122122222)()()(||||z z y y x x N N MN d -+-+-=+=．例1 设(1, 2, 0)A -与(1, 0, 2)B --为空间两点，求A 与B 两点间的距离． 解 由公式（8-1-1）可得，A 与B 两点间的距离为d ==例2 在z 轴上求与点(3, 5, 2)A -和(4, 1, 5)B -等距的点M ．解 由于所求的点M 在z 轴上，因而M 点的坐标可设为(0, 0, )z ，又由于MA MB =，由公式（8-1-1），得222222)5(1)4()2(53z z -++-=--++．从而解得72=z ，即所求的点为2(0, 0, )7M ．习题8-11．讨论空间直角坐标系的八个卦限中的点的坐标的符号． 2．在坐标轴上的点和在坐标平面上的点的坐标各有何特点？ 3．在空间直角坐标系中，画出以下各点：(2, 0, 0)A ；(0, 3, 0)B -；(3, 0, 1)C ；(3, 2, 1)D -．4．求点(1, 2, 3)-关于各坐标平面对称的点的坐标． 5．求点(1, 2, 3)关于各坐标轴对称的点的坐标． 6．求以下各对点间的距离： (1) (0, 1, 3)A -与(2, 1, 4)B ；(2) (1, 4, 2)C -与D(2, 7, 3)．7．在坐标平面yOz 上求与三点(3, 1, 2)A 、(4, 2, 2)B --和(0, 5, 1)C 等距的点． 8．求点(12, 3, 4)A -与原点、各坐标平面和各坐标轴的距离．9. 证明以()()()A 4,3,1,B 7,1,2,C 5,2,3为顶点的三角形△ABC 是一等腰三角形.第2节 空间向量的代数运算2.1 空间向量的概念在日常生活中，我们经常会遇到一些量，如质量、时间、面积、温度等，它们在取定一个度量单位后，就可以用一个数来表示．这种只有大小没有方向的量，叫做数量（或标量）．但有一些量，如力、位移、速度、电场强度等，仅仅用一个实数是无法将它们确切表示出来，因为它们不仅有大小，而且还有方向，这种既有大小又有方向的量，叫做向量（或矢量）．在数学上，我们用有向线段AB 来表示向量，A 称为向量的起点，B 称为向量的终点，有向线段的长度就表示向量的大小，有向线段的方向就表示向量的方向．通常在印刷时用黑体小写字母a ，b ，c ，…来表示向量，手写时用带箭头的小写字母, ,,a b c来记向量.向量的长度称为向量的模，记作a 或AB ，模为1的向量叫做单位向量，模为0的向量叫做零向量，记作0，规定：零向量的方向可以是任意的．本章我们讨论的是自由向量，即只考虑向量的大小和方向，而不考虑向量的起点，因此，我们把大小相等，方向相同的向量叫做相等向量，记作a =b .规定：所有的零向量都相等.与向量a 大小相等，方向相反的向量叫做a 的负向量(或反向量)，记作 a ． 平行于同一直线的一组向量称为平行向量（或共线向量）．平行于同一平面的一组向量，叫做共面向量，零向量与任何共面的向量组共面.2.2 向量的线性运算2.2.1 向量的加法我们在物理学中知道力与位移都是向量，求两个力的合力用的是平行四边形法则，我们可以类似地定义两个向量的加法．定义1 对向量a ，b ，从同一起点A 作有向线段AB 、AD 分别表示a 与b ，然后以AB 、AD 为邻边作平行四边形ABCD ，则我们把从起点A 到顶点C 的向量AC 称为向量a 与b 的和（图8-5），记作a +b ．这种求和方法称为平行四边形法则．图8-5 图8-6若将向量b 平移，使其起点与向量a 的终点重合，则以a 的起点为起点，b 的终点为终ab Cabc =a +b点的向量c 就是a 与b 的和(图8-6），该法则称为三角形法则．多个向量，如a 、b 、c 、d 首尾相接，则从第一个向量的起点到最后一个向量的终点的向量就是它们的和a +b +c +d （图8-7）．图8-7对于任意向量a ，b ，c ，满足以下运算法则： (1)a +b =b +a (交换律)．(2)()()a +b +c =a +b +c (结合律)． (3)0a +=a ．2.2.2 向量的减法定义2 向量a 与b 的负向量-b 的和，称为向量a 与b 的差，即()--a b =a +b ．特别地，当b =a 时，有()-0a +a =.由向量减法的定义，我们从同一起点O 作有向线段OA ，OB 分别表示a ，b ，则()OA OB OA OB --=+-a b =OA BO BA =+=．也就是说，若向量a 与b 的起点放在一起，则a ，b 的差向量就是以b 的终点为起点，以a 的终点为终点的向量（图8-8）．图8-82.2.3数乘向量定义3 实数λ与向量a 的乘积是一个向量，记作λa ，λa 的模是λa ，方向： 当0λ>时，λa 与a 同向；当0λ<时，λa 与a 反向；当0λ=时，λ0a =．abcda +b +c +daabb -a bBAC对于任意向量a ，b 以与任意实数λ，μ，有运算法则： (1) ()()λμλμa =a ． (2) ()+λμλμ+a =a a ．(3) ()+λλλ+a b =a b ．向量的加法、减法与数乘向量运算统称为向量的线性运算，λμa +b 称为a ，b 的一个线性组合(, )R λμ∈．特别地，与 a 同方向的单位向量叫做a 的单位向量，记做a e ，即aa e a=.上式说明：一个非零向量除以它的模的结果是一个与原向量同方向的单位向量.例1 如图8-9，在平行六面体///ABCD B C D /—A 中，设/=AA ,a AD =b AB =c ,试用,,a b c 来表示对角线向量//,.AC A C图8-9解 ''AC AB BC CC =++'AB BC AA =++a b c =++；'''AC A A AB BC AA AB AD =++=-++a b c =++.由于向量λa 与a 平行，所以我们通常用数与向量的乘积来说明两个向量的平行关系.即有,定理1 向量a 与非零向量b 平行的充分必要条件是存在一个实数λ，使得λa =b .2.3 向量的坐标表示2.3.1向量在坐标轴上的投影设A 为空间中一点，过点A 作轴u 的垂线，垂足为'A ，则'A 称为点A 在轴u 上的投影(图8-10)．图8-10若M 为空间直角坐标系中的一点，则M 在x 轴、y 轴、z 轴上的投影为A 、B 、C ，如图8-11所示．图8-11设向量AB 的始点与终点B 在轴u 的投影分别为A '、B '，那么轴u 上的有向线段A B ''的值A B ''叫做向量AB 在轴u 上的投影，记作u prj AB A B ''=，轴u 称为投影轴.图8-12当A B ''与轴u 同向时，投影取正号，当A B ''与轴u 反向时，投影取负号． 注 (1) 向量在轴上投影是标量．(2) 设MN 为空间直角坐标系中的一个向量，点M 的坐标为111(, , )x y z ，点N 的坐标为222(, , )x y z ，显然，向量MN 在三个坐标轴上的投影分别为12x x -，12y y -，12z z -． 2.3.2向量的坐标表示yxzOA B CM取空间直角坐标系Oxyz ，在x 轴、y 轴、z 轴上各取一个与坐标轴同向的单位向量，依次记作, , i j k ，它们称为坐标向量．空间中任一向量a ，它都可以唯一地表示为, , i j k 数乘之和． 事实上，设MN a =，过M 、N 作坐标轴的投影，如图8-13所示．MN =MA+AP +PN =MA+MB +MC a =．由于MA 与i 平行，MB 与j 平行，MC 与k 平行，所以，存在唯一的实数, , x y z ，使得MA x =i ，MB y =j ，MC z =k ，即x y z a =i +j +k ． (8-2-1)图 8-13我们把(8-2-1)式中, , i j k 系数组成的有序数组(, , )x y z 叫做向量a 的直角坐标，记为{, , }x y z a =，向量的坐标确定了，向量也就确定了．显然，(8-2-1)中的, , x y z 是向量a 分别在x 轴、y 轴、z 轴上的投影．因此，在空间直角坐标系中的向量a 的坐标就是该向量在三个坐标轴上的投影组成的有序数组．例2 在空间直角坐标系中设点(3, 1, 5)M -，(2, 3, 1)N -，求向量MN 与NM 的直角坐标．解 由于向量的坐标即为向量在坐标轴上的投影组成的有序数组，而向量的各投影即为终点坐标与起点坐标对应分量的差．所以向量MN 的坐标为{5, 4, 4}--，向量NM 的坐标为{5, 4, 4}-． 例3(定比分点公式) 设111(,,)A x y z 和222(,,)B x y z 为两已知点，有向线段AB 上的点M 将它分为两条有向线段AM 和MB ，使它们的值的比等于数(1)λλ≠-，即AMMBλ=，求分点(,,)M x y z 的坐标.图8-14 解 如图8-14，因为AM 与MB 在同一直线上，且同方向，故AM MB λ=⋅，而122{,,}AM x x y y z z =---， 222{,,}MB x x y y z z =---222{(),(),()}MB x x y y z z λλλλ=---所以 12()x x x x λ-=-，12()y y y y λ-=-，12()z z z z λ-=- 解得121212,,.111x x y y z z x y z λλλλλλ+⋅+⋅+⋅===+++当λ=1, 点M 的有向线段→AB x 2.3.3向量可以用它的模与方向来表示，设空间向量12a M M =分别为,,αβγ，规定： 0,0απ≤≤≤称,,αβγ为向量a 的方向角因为向量a 12cos cos x a M M a αα=⋅=⋅12cos cos y a M M a ββ=⋅=⋅(8-2-2)12cos cos z a M M a γγ=⋅=⋅公式(8.2.2)中出现的cos ,cos ,cos αβγ称为向量a 的方向余弦.而{,,}{cos ,cos ,cos }x y z a a a a a a a αβγ==⋅⋅⋅{cos ,cos ,cos }a a a e αβγ=⋅=⋅{cos ,cos ,cos }a e αβγ=是与向量a 同方向的单位向量.而 a =M M =12,,x y z M P a M Q a M R a ===111，故向量a 的模为 x a a a =+2(8-2-3)从而向量a 的方向余弦为cos a αβγ===(8-2-4)并且 222cos cos cos 1αβγ++=.例4 已知两点1M 和()21,3,0M ,求向量12M M 的模、方向余弦和方向角.解12(12,32,0(1,1,M M =--=-2)2(1)1(222=-++-=；11cos ,cos ,cos 22αβγ=-==； 23,,334πππαβγ===. 例5 已知两点(4,0,5)A 和(7,1,3)B ，求与AB 同方向的单位向量e . 解 因为{74,10,35}{3,1,2},AB =---=-所以23AB == 于是 {}.e =2.4 向量的数量积在物理中我们知道，一质点在恒力F 的作用下，由A 点沿直线移到B 点，若力F 与位移向量AB 的夹角为θ，则力F 所作的功为||||cos W F AB θ=⋅⋅．类似的情况在其他问题中也经常遇到．由此，我们引入两向量的数量积的概念． 定义1 设a ，b 为空间中的两个向量，则数cos ,a b a b叫做向量a 与b 的数量积(也称积或点积)，记作⋅a b ，读作“a 点乘b ”．即cos ,⋅a b =a b a b （8-2-5）其中,a b 表示向量a 与b 的夹角，并且规定0, π≤≤a b ．两向量的数量积是一个数量而不是向量，特别地当两向量中一个为零向量时，就有0⋅a b =.由向量数量积的定义易知：(1)2⋅a a =a ，因此=a(2) 对于两个非零向量a ，b ，a 与b 垂直的充要条件是它们的数量积为零，即⊥a b ⇔0⋅a b =．注 数量积在解决有关长度、角度、垂直等度量问题上起着重要作用． 数量积的运算满足如下运算性质： 对于任意向量a ，b 与任意实数λ，有 (1) 交换律：⋅⋅a b =b a ．(2) 分配律：()⋅⋅⋅a b +c =a b +a c ．(3) 与数乘结合律：()()()λλλ⋅⋅=⋅a b =a b a b ． (4)0⋅≥a a 当且仅当0a =时，等号成立．例6 对坐标向量i ，j ，k ，求⋅i i ，⋅j j ，⋅k k ，⋅i j ，⋅j k ，⋅k i ． 解 由坐标向量的特点与向量积的定义得1⋅⋅⋅i i =j j =k k =， 0⋅⋅⋅i j =j k =k i =．例7 已知2=a ，3=b ，2, 3π=a b ，求a b ⋅，(2)()-+a b a b ⋅，+a b ． 解 由两向量的数量积定义有2cos , 23cos 3π⋅=⨯⨯a b =a b a b 123()=32=⨯⨯--．(2)()=22-⋅+⋅⋅-⋅-⋅a b a b a a +a b b a b b22=2-⋅-a a b b 222(3)23=11=---⨯-．2()()+=⋅+a b a +b a b =⋅⋅+⋅+⋅a a +a b b a b b222=+⋅+a a b b 2222(3)3=7=+⨯-+，因此+=a b ．在空间直角坐标系下，设向量111{,,}x y z a =，向量222{,,}x y z b =，即111x y z ++a =i j k , 222x y z ++b =i j k ．则111222()()x y z x y z ⋅++⋅++a b =i j k i j k121212()()+()x x x y x z ⋅+⋅⋅=i i i j i k 121212()()+()y x y y y z ⋅+⋅⋅+j i j j j k 121212()()+()z x z y z z ⋅+⋅⋅+k i k j k k ．由于1⋅⋅⋅i i =j j =k k =， 0⋅⋅⋅i j =j k =k i =，所以121212x x y y z z ⋅++a b =．(8-2-6)也就是说，在直角坐标系下，两向量的数量积等于它们对应坐标分量的乘积之和．同样，利用向量的直角坐标也可以求出向量的模、两向量的夹角公式以与两向量垂直的充要条件，即设非零向量111{,,}x y z a =，向量222{,,}x y z b =，则=a (8-2-7)cos ||||⋅=a ba,b a b=． (8-2-8)⊥a b ⇔1212120x x y y z z ++=． (8-2-9)例8 在空间直角坐标系中，设三点(5, 4, 1)A -，(3, 2, 1)B ，(2, 5, 0)C -．证明:ABC ∆是直角三角形．证明 由题意可知{2, 6, 0}AB =-，={3, 1, 1}AC ---，则(2)(3)6(1)0(1)0AB AC ⋅=-⨯-+⨯-+⨯-=，所以AB AC ⊥．即ABC ∆是直角三角形．2.5向量的向量积在物理学中我们知道，要表示一外力对物体的转动所产生的影响，我们用力矩的概念来描述．设一杠杆的一端O 固定，力F 作用于杠杆上的点A 处，F 与OA 的夹角为θ，则杠杆在F 的作用下绕O 点转动，这时，可用力矩M 来描述．力F 对O 的力矩M 是个向量，M 的大小为||||||sin OA OA =M F ,F ．M 的方向与OA 与F 都垂直，且OA ，F ，M 成右手系，如图8-16所示．图8-162.5.1向量积的定义在实际生活中，我们会经常遇到象这样由两个向量所决定的另一个向量，由此，我们引入两向量的向量积的概念．定义2 设a ，b 为空间中的两个向量，若由a ，b 所决定的向量c ，其模为sin , c =a b a b ． (8-2-10)其方向与a ，b 均垂直且a ，b ，c 成右手系（如图8-17），则向量c 叫做向量a 与b 的向量积(也称外积或叉积)．记作⨯a b ，读作“a 叉乘b ”．注 (1) 两向量a 与b 的向量积⨯a b 是一个向量，其模⨯a b 的几何意义是以a ，b 为邻边的平行四边形的面积． (2)⨯0a a =这是因为夹角θ=0，所以⨯0a a = 图8-17(3)对两个非零向量a 与b ，a 与b 平行(即平行)的充要条件是它们的向量积为零向量．a ∥b ⇔⨯0a b =．向量积的运算满足如下性质：对任意向量a ，b 与任意实数λ，有 (1) 反交换律：⨯-⨯a b =b a ． (2) 分配律:()⨯⨯⨯a b +c =a b +a c ，()⨯⨯⨯a +b c =a c +b c ．(3) 与数乘的结合律：()()()λλλ⨯⨯⨯a b =a b =a b ．例9 对坐标向量i ，j ，k ，求⨯i i ，⨯j j ，⨯k k ，⨯i j ，⨯j k ，⨯k i ． 解⨯⨯⨯0i i =j j =k k =．⨯i j =k ，⨯j k =i ，⨯k i =j ．2.5.2向量积的直角坐标运算在空间直角坐标系下，设向量111{, , }x y z a =，向量222{, , }x y z b =，即111x y z ++a =i j k ，222x y z ++b =i j k ，因为⨯⨯⨯0i i =j j =k k =． ⨯i j =k ，⨯j k =i ，⨯k i =j ， ⨯-j i =k ，⨯-k j =i ，⨯-i k =j ．则111222()()x y z x y z ⨯++⨯++a b =i j k i j k121212()()+()x x x y x z ⨯+⨯⨯=i i i j i k 121212()()+()y x y y y z ⨯+⨯⨯+j i j j j k 121212()()+()z x z y z z ⨯+⨯⨯+k i k j k k121212121212()()+()()()()x y y x y z z y x z z x -⨯-⨯--⨯=i j j k k i 121212121212()()+()y z z y x z z x x y y x ----=i j k ．为了便于记忆，借助于线性代数中的二阶行列式与三阶行列式有111111222222y z x z x y y z x z x y ⨯-a b =i j +k 111222x y z x y z =i j k ． 注 设两个非零向量111{, , }x y z a =，222{, , }x y z b =，则a ∥b ⇔⨯0a b =，⇔212121z z y y x x ==． 若某个分母为零，则规定相应的分子为零．例10 设向量{1,2,1}--a =，{2,0,1}b =，求⨯a b 的坐标．解211112121012120201----⨯--=-i j ka b =i j +k 234=--i j +k ．因此⨯a b 的直角坐标为{2, 3, 4}--．例11 在空间直角坐标系中，设向量{3, 0, 2}a =，{1, 1, 1}--b =，求同时垂直于向量a 与b 的单位向量．解 设向量⨯c =a b ，则c 同时与a ，b 垂直．而302111⨯--i j kc =a b =23=-+i j +k ，所以向量c 的坐标为{2, 1, 3}-．再将c 单位化，得02,1,3}={=-c ，即{与-- 为所求的向量． 例12 在空间直角坐标系中，设点(4, 1, 2)A -，(1, 2, 2)B -，(2, 0, 1)C ，求ABC ∆的面积．解 由两向量积的模的几何意义知：以AB 、AC 为邻边的平行四边形的面积为AB AC ⨯，由于{3, 3, 4}AB =--，{2, 1, 1}AC =--，因此33453211AB AC ⨯=--=++--i j ki j k ，所以21AB AC ⨯=故ABC ∆的面积为235=∆ABC S ．2.6向量的混合积定义3 给定空间三个向量,,a b c ，如果先作前两个向量a 与b 的向量积，再作所得的向量与第三个向量c 的数量积，最后得到的这个数叫做三向量,,a b c 的混合积，记做()a b c ⨯⋅或abc ⎡⎤⎣⎦.说明：三个不共面向量,,a b c 的混合积的绝对值等于以,,a b c 为棱的平行六面体的体积V .定理如果111a X i Y j Z k =++，222b X i Y j Z k =++，333c X i Y j Z k =++，那么 111222333.X Y Z abc X Y Z X Y Z ⎡⎤=⎣⎦习题8-21.,,,,,().ABCD AB AD AC DB MA M ==设为一平行四边形试用表示为平行四边形对角线的交点a b.a b12.,().2M AB O OM OA OB =+设为线段的中点,为空间中的任意一点证明 2223.?(1)()();(2)();(3)()().==⨯=⨯对于任意三个向量与判断下列各式是否成立a,b c,a b c b c a a b a b a b c c a b4.:(1);(2)(3).利用向量证明三角形的余弦定理正弦定理；勾股定理5.设,,a b c 为单位向量,且满足0a b c ++=,求.a b b c c a ++6.1(3,2,2),(1,3,2),(8,6,2),322a b c a b + c.求=-==--7.已知三点(3,0,2),A B AB ==求的坐标、模、方向余弦和方向角.8.一向量的终点在点B(2,-1,7),它在x 轴、y 轴和z 轴上的投影依次为4，-4和7.求这向量的起点A 的坐标.9．设2=a ，4=b ，3πa,b =，求⋅a b ，(2)-⋅a b b ，-a b ． 10．设向量a ，b ，c 两两垂直，且1=a ，2=b ，3=c ，求向量d =a +b +c 的模与d,a ．11．在空间直角坐标系中，已知{1,2,3}-a = ，{2,2,1}-b = ，求： (1)⋅a b ；(2) 25⋅a b ；(3) a ；(4)cos a,b ．12.已知向量2332和,,a i j k b i j k c i j =-+=-+=-，计算 （1）()();a b c a c b -（2）()();a b b c +⨯+（3）()a b c ⨯.13．设向量a ，b 的直角坐标分别为{1, 3, 2}--和{2, 4, }k -，若a b ⊥，求k 的值．14．设向量{2, 1, 1}-a =，{1, 3, 0}-b =，求以、a b 为邻边构造的平行四边形面积． 15．求同时垂直于向量{3, 2, 4}-a =和纵轴的单位向量．16．已知三角形三个顶点(4, 1, 2)A -，(3, 0, 1)B -，(5, 1, 2)C ，求ABC ∆的面积．第3节 空间中的平面与直线方程在本节我们以向量为工具，在空间直角坐标系中讨论最简单的曲面和曲线——平面和直线.3.1平面与其方程首先利用向量的概念，在空间直角坐标系中建立平面的方程，下面我们将给出几种由不同条件所确定的平面的方程．3.1.1平面的点法式方程若一个非零向量n 垂直于平面π，则称向量n 为平面π的一个法向量．显然，若n 是平面π的一个法向量，则λn (λ为任意非零实数)都是π的法向量，即平面上的任一向量均与该平面的法向量垂直．由立体几何知识知道，过一个定点0000(, , )M x y z 且垂直于一个非零向量{, , }A B C n =有且只有一个平面π．设(, , )M x y z 为平面π上的任一点，由于π⊥n ，因此0M M ⊥n ．由两向量垂直的充要条件，得00M M =⋅n ,而0000{, , }M M x x y y z z =---，{, , }A B C n =，所以可得0)()()(000=-+-+-z z C y y B x x A ． (8-3-1)由于平面π上任意一点(, , )M x y z 都满足方程(8-3-1)，而不在平面π上的点都不满足方程(8-3-1)，因此方程(8-3-1)就是平面π的方程．由于方程(8-3-1)是给定点0000(, , )M x y z 和法向量{, , }A B C n =所确定的，因而称式(8-3-1)叫做平面π的点法式方程．图8-18例1 求通过点0(1, 2, 4)M -且垂直于向量{3, 2, 1}-n =的平面方程．解 由于{3, 2, 1}-n =为所求平面的一个法向量，平面又过点0(1, 2, 4)M -，所以，由平面的点法式方程(6-14)可得所求平面的方程为3(1)2(2)1(4)=0x y z --⋅++⋅-，整理，得32110x y z -+-=．例2 求过三点()12,1,4M -，()2M 1,3,2--，()3M 0,2,3 的平面π的方程． 解 所求平面π的法向量必定同时垂直于12M M 与13M M ．因此可取12M M 与13M M 的向量积1213M M M M ⨯为该平面的一个法向量n ．即1213n =M M M M ⨯．由于12{3, 4, 6}M M =--，13{2, 3, 1}M M =--，因此1213-631i j kn =M M M M =342⨯---149i j k,=+-,因此所求平面π的方程为0419214=--++-)()()(z y x ，化简得.015914=--+z y x一般地，过三点(,,)(1,2,3)k k k k M x y z k =的平面方程为1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 称为平面的三点式方程。

向量在解析几何中的发展及应用摘要：向量又称为矢量，最初被应用于物理学．很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量．在现代数学中向量是一个重要概念，向量在解析几何整个知识体系中占有非常重要的地位, 它可以使图形量化,使图形间关系代数化.向量是研究图形问题的有力工具.本文主要介绍向量在解析几何中的一些简单应用。

关键词：向量解析几何定理前言向量在整个解析几何中占有非常重要的地位,因此它的应用在解决几何问题时是最基础最普遍的方法,尤其是在几何的证明问题中,使用向量的分解定理和向量的基础知识以及向量的一些定理可以起到事半功倍的效果.除此之外,用向量可以将一些代数问题几何化,这样借助向量的性质可以快速明了的解决一些难题。

另外,向量在推导一些几何公式时,使得问题简化了很多。

第一章研究背景第一节向量的起源向量又称为矢量，最初被应用于物理学．很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量．大约公元前350年前，古希腊著名学者亚里士多德就知道了力可以表示成向量，两个力的组合作用可用著名的平行四边形法则来得到．“向量”一词来自力学、解析几何中的有向线段．最先使用有向线段表示向量的是英国大科学家牛顿．课本上讨论的向量是一种带几何性质的量，除零向量外，总可以画出箭头表示方向．但是在高等数学中还有更广泛的向量．例如，把所有实系数多项式的全体看成一个多项式空间，这里的多项式都可看成一个向量．在这种情况下，要找出起点和终点甚至画出箭头表示方向是办不到的．这种空间中的向量比几何中的向量要广泛得多，可以是任意数学对象或物理对象．这样，就可以指导线性代数方法应用到广阔的自然科学领域中去了．因此，向量空间的概念，已成了数学中最基本的概念和线性代数的中心内容，它的理论和方法在自然科学的各领域中得到了广泛的应用．而向量及其线性运算也为“向量空间”这一抽象的概念提供出了一个具体的模型．从数学发展史来看，历史上很长一段时间，空间的向量结构并未被数学家们所认识，直到19世纪末20世纪初，人们才把空间的性质与向量运算联系起来，使向量成为具有一套优良运算通性的数学体系．向量能够进入数学并得到发展，首先应从复数的几何表示谈起．18世纪末期，挪威测量学家威塞尔首次利用坐标平面上的点来表示复数a＋bi，并利用具有几何意义的复数运算来定义向量的运算．把坐标平面上的点用向量表示出来，并把向量的几何表示用于研究几何问题与三角问题．人们逐步接受了复数，也学会了利用复数来表示和研究平面中的向量，向量就这样平静地进入了数学．但复数的利用是受限制的，因为它仅能用于表示平面，若有不在同一平面上的力作用于同一物体，则需要寻找所谓三维“复数”以及相应的运算体系．19世纪中期，英国数学家哈密尔顿发明了四元数（包括数量部分和向量部分），以代表空间的向量．他的工作为向量代数和向量分析的建立奠定了基础．随后，电磁理论的发现者，英国的数学物理学家麦克思韦尔把四元数的数量部分和向量部分分开处理，从而创造了大量的向量分析．三维向量分析的开创，以及同四元数的正式分裂，是英国的居伯斯和海维塞德于19世纪80年代各自独立完成的．他们提出，一个向量不过是四元数的向量部分，但不独立于任何四元数．他们引进了两种类型的乘法，即数量积和向量积．并把向量代数推广到变向量的向量微积分．从此，向量的方法被引进到分析和解析几何中来，并逐步完善，成为了一套优良的数学工具。

第七章 向量代数与空间解析几何§7.2 平面与直线一、 空间解析几何1 空间解析几何研究的基本问题。

（1）已知曲面（线）作为点的几何轨迹，建立这曲面（线）的方程， （2）已知坐标x ，y 和z 间的一个方程（组），研究这方程（组）所表示的曲面（线）。

2 距离公式 空间两点()111,,A x y z 与()222,,B x y z 间的距离d 为d =3 定比分点公式(),,M x y z 是AB 的分点：AMMBλ=,点A,B 的坐标为()111,,A x y z ，()222,,B x y z ，则 121x x x λλ+=+，121y y y λλ+=+，121z z z λλ+=+ 当M 为中点时， 122x x x +=，122y y y +=，122z zz += 二、平面及其方程。

1 法向量： 与平面π垂直的非零向量，称为平面π的法向量，通常记成n 。

对于给定的平面π，它的法向量有无穷多个，但它所指的方向只有两个。

2 点法式方程： 已知平面π过()000,,M x y z 点，其法向量n ＝{A,B,C},则平面π的方程为 ()()()0000A x x B y y C z z -+-+-= 或()00n r r ⋅-=其中 {}{}0000,,,,,r x y z r x y z ==3 一般式方程：0Ax By Cz D +++=其中A, B, C 不全为零. x, y, z 前的系数表示π的法线方向数，n ＝{A,B,C}是π的法向量 特别情形： 0Ax By Cz ++=，表示通过原点的平面。

0Ax By D ++=，平行于z 轴的平面。

0Ax D +=，平行yOz 平面的平面。

x ＝0表示yOz 平面。

4 三点式方程：设()111,,A x y z ,()222,,B x y z ,()333,,C x y z 三点不在一条直线上。

则通过A,B,C 的平面方程为： 1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 5 平面束：设直线L 的一般式方程为1111222200A x B y C z D A x B y C z D +++=⎧⎨+++=⎩，则通过L的所有平面方程为1K ()1111A xB yC zD ++++2K ()22220A x B y C z D +++=，其中()()12,0,0k k ≠6 有关平面的问题两平面为 1π：11110A x B y C z D +++= 2π：22220A x B y C z D +++=7 设平面π的方程为0Ax By Cz D +++=，而点()111,,M x y z 为平面π外的一点，则M 到平面π的距离d ： d =三 直线及其方程1 方向向量：与直线平行的非零向量S ，称为直线L 的方向向量。