总传热速率方程

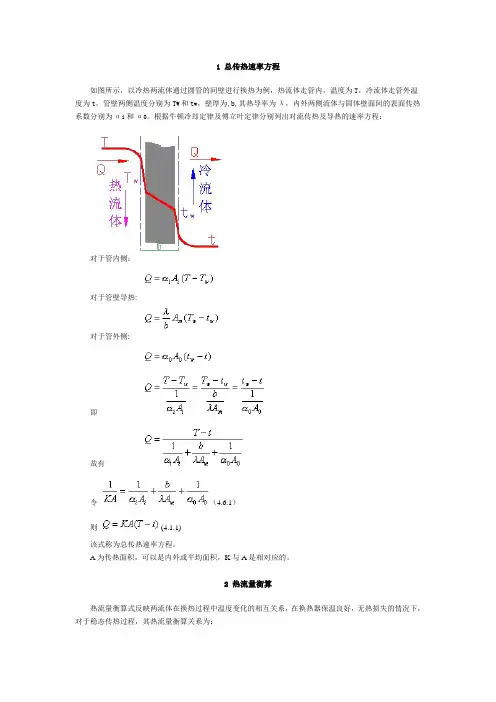
1 总传热速率方程如图所示，以冷热两流体通过圆管的间壁进行换热为例，热流体走管内，温度为T，冷流体走管外温度为t，管壁两侧温度分别为T W和t w，壁厚为,b,其热导率为λ，内外两侧流体与固体壁面间的表面传热系数分别为αi和α0。

根据牛顿冷却定律及傅立叶定律分别列出对流传热及导热的速率方程：对于管内侧：对于管壁导热:对于管外侧:即故有令（4.6.1）则(4.1.1)该式称为总传热速率方程。

A为传热面积，可以是内外或平均面积，K与A是相对应的。

2 热流量衡算热流量衡算式反映两流体在换热过程中温度变化的相互关系，在换热器保温良好，无热损失的情况下，对于稳态传热过程，其热流量衡算关系为：（热流体放出的热流量）=（冷流体吸收的热流量）在进行热衡算时，对有、无相变化的传热过程其表达式又有所区别。

（1）无相变化传热过程式中Q----冷流体吸收或热流体放出的热流量，W；m h,m c-----热、冷流体的质量流量，kg/s；C ph,C pc------热、冷流体的比定压热容，kJ/(kg·K)；T1,t1 ------热、冷流体的进口温度，K；T2,t2------热、冷流体的出口温度，K。

（2）有相变化传热过程两物流在换热过程中，其中一侧物流发生相变化，如蒸汽冷凝或液体沸腾，其热流量衡算式为：一侧有相变化两侧物流均发生相变化，如一侧冷凝另一侧沸腾的传热过程式中r,r1,r2--------物流相变热，J/kg；D,D1,D2--------相变物流量，kg/s。

对于过冷或过热物流发生相变时的热流量衡算，则应按以上方法分段进行加和计算。

3 传热系数和传热面积（1）传热系数K和传热面积A的计算传热系数K是表示换热设备性能的极为重要的参数，是进行传热计算的依据。

K的大小取决于流体的物性、传热过程的操作条件及换热器的类型等，K值通常可以由实验测定，或取生产实际的经验数据，也可以通过分析计算求得。

传热系数K可利用式（4.6.1）进行计算。

传热速率q的方程表达式热传导传热速率方程式Q=KA\Delta t_m=\frac{\Deltat_m}{\frac1{KA}}=\frac{推动力}{热阻}\\ Q：传热速率，W \\ K：总传热系数，W/(m^2\cdot K)\\ A：传热面积，即垂直于热流方向的截面积，m^2\\ \Delta t：两流体的平均温度差，^{\circ}C \\傅里叶定律Q=-\lambda A\frac{dt}{dx}\\ \lambda：热导率或导热系数，W/m\cdot K\\ \frac{dt}{dx}：沿x方向的温度梯度，K/m \\•x方向为热流方向，即温度降低的方向，故\frac{dt}{dx}为负值•因传热速率Q为正值，故式中加上符号热导率\lambda=-\frac{Q}{A\frac{dt}{dx}} \\热导率：数值上等于温度梯度为1^{\circ}C/m,单位时间通过单位传热面积的热量平壁的稳态热传导单层平壁的稳态热传导Q=\frac{\lambda}{b}A(t_1-t_2) =\frac{t_1-t_2}{\frac{b}{\lambda A}} =\frac{\Delta t}{R}=\frac{传热推动力}{热阻}\\ \Delta t:传热推动力\\R=\frac{b}{\lambda A}:热阻 \\热流密度q=\frac{Q}{A}=\frac{\lambda}{b}(t_1-t_2)\\ q：单位面积的传热速率，称为热流密度，W/m^2\\ b:壁厚，m \\多层平壁的稳态热传导Q=\frac{\Delta t}{\frac{b_1}{\lambda_1A}+\frac{b_2}{\lambda_2 A}+\frac{b_3}{\lambda_3 A}}=\frac{\Delta t}{\sum_{i=1}^mR_i}=\frac{总推动力}{总热阻} \\•多层平壁稳态热传导的总推动力等于各层推动力之和,总热阻等于各层热阻之和•并且,因各层的传热速率相等,所以各层的传热推动力与其热阻之比值都相等,也等于总推动力与总热阻之比值•在多层平壁中,热阻大的壁层,其温度差也大圆筒壁的稳态热传导单层圆筒壁的稳态热传导Q=2\pi l\lambda\frac{t_1-t_2}{\ln{\frac{r_2}{r_1}}}=\frac{\Delta t}{R} \\单层平壁类似形式计算式Q=\frac{\lambda}{b}A_m(t_1-t_2)=\frac{t_1-t_2}{\frac{b}{\lambda A_m}}\\ A_m=\frac{A_2-A_1}{\ln\frac{A_2}{A_1}}：对数平均面积 \\A_m的计算近似计算：if\quad A_2/A_1<2,A_m=\frac{A_2+A_1}{2}\\ 或使用对数平均半径r_m=\frac{r_2-r_1}{\ln\frac{r_2}{r_1}}计算A_m=2\pi r_m l\\ 对数平均半径的近似计算：if\quad r_2/r_1<2,r_m=\frac{r_1+r_2}{2} \\热流密度q_l=\frac{Q}{l}=2\pi \lambda\frac{t_1-t_2}{\ln{\frac{r_2}{r_1}}} \\多层圆筒壁的稳态热传导Q=2\pi l\frac{t_1-t_4}{\frac{b_1}{\lambda_1A_{m1}}+\frac{b_2}{\lambda_2A_{m2}}+\frac{b_3}{\lambda_3 A_{m3}}}(三层) \\对流传热对流传热速率方程Q=\alpha A \Delta t=\Delta t/(\frac{1}{\alpha A})\\ \Delta t=\frac{Q}{\alpha A}\\ Q：对流传热速率，W\\ A：传热面积，m^2\\ \Delta t：对流传热温度差，^{\circ}C\\ \alpha：对流传热系数/膜系数，W/(m^2\cdot K)或W/(m^2\cdot ^{\circ}C) \\影响对流传热系数的因素•流体的物理性质•流体对流起因•流体流动状态•流体的相态变化•传热面的形状对流传热的特征数关系式特征数的名称、符号及意义特征数关系式Nu=KRe^aPr^bGr^c \\流体无相变时对流传热系数的经验关系式(管内)•圆形直管==强制湍流==时的对流传热系数\alpha=0.023\frac{\lambda}{d}Re^{0.8}Pr^{n}\\n=\begin{cases} 0.4，流体被加热\\ 0.3，流体被冷却\end{cases} \\ 应用范围：o Re>10^4o$0.7o管长与管径之比l/d\ge 60o流体黏度\mu<2mPa\cdot s•圆形直管内==过渡区==时的对流传热系数\alpha=0.023\frac{\lambda}{d}Re^{0.8}Pr^{n}f\\f=1-\frac{6\times 10^5}{Re^{1.8}}：校正系数 \\ 应用范围：$2300•圆形直管内强制层流时的对流传热系数\alpha=1.86\frac{\lambda}{d}(RePr\frac{d}{l})^{\f rac13}(\frac{\mu}{\mu_w})^{0.14} \\ 应用范围：o Re<2300o RePr\frac{d}{l}>10o Ge<2.5\times 10^4特征尺寸：管内径定性温度：除\mu_w取壁温外，均取流体进、出口温度的算术平均值当Gr>2.5\times 10^4时，需乘以校正系数 f=0.8(1+0.015Gr^{1/3}) \\•在非圆形管内强制对流传热系数特征尺寸改为当量直径d_ed_e=4\times \frac{流体流动截面积}{润湿周边} \\流体有相变时的对流传热•冷凝方式：==膜状冷凝==和==滴状冷凝== 仅介绍饱和蒸汽膜状冷凝时对流传热系数的计算方法•流体在水平管外膜状冷凝时的对流传热系数\alpha=0.725(\frac{\rho^2g\lambda^3r}{n^{2/3}\mu d_0 \Delta t})^{1/4}\\ r：比汽化热，取饱和温度t_s 下的数值，J/kg\\ \rho：冷凝液的密度，kg/m^3\\\lambda：冷凝液的热导率，W/(m\cdot K)\\ \mu：冷凝液的黏度，Pa\cdot s\\ \Delta t：饱和温度t_s与壁面温度t_w之差,\Delta t=t_s-t_w\\ n：水平管束在垂直列上的管子数 \\ 定性温度：取膜温t=\frac{t_s+t_w}{2} 特征尺寸：管外径d_0两流体间传热过程的计算热量衡算•若保温良好，无热损失时，单位时间内热流体放出的热量等于冷流体吸收的热量，即热量衡算式为Q=q_{m1}(H_1-H_2)=q_{m2}(h_1-h_2)\\ Q：热负荷，W\\ q_{m1}、q_{m2}：热、冷流体的质量流量，kg/s\\H_1、H_2：热流体进、出口的比焓，J/kg\\ h_1、h_2：冷流体进、出口的比焓，J/kg \\•若换热器内两流体均无相变化，且流体的比热容c_p可视为Q=q_{m1}c_{p1}(T_1-T_2)=q_{m2}c_{p2}(t_1-t_2)\\c_{p1}、c_{p2}：冷、热流体的平均定压比热容，J/(kg\cdot ^{\circ}C)\\ T_1、T_2：热流体的进、出口温度，^{\circ}C\\ t_1、t_2：冷流体的进、出口温度，^{\circ}C \\•若换热器中一侧有相变 Q=q_{m1}r=q_{m2}c_{p2}(t_2-t_1)\\ r：饱和蒸汽的比汽化热，J/kg \\•若冷凝液出口温度T_2低于饱和温度T_sQ=q_{m1}[r+c_{p1}(T_s-T_2)]=q_{m2}c_{p2}(t_2-t_1) \\变温传热平均温度差\Delta t_m=\frac{\Delta t_1-\Deltat_2}{\ln{\frac{\Delta t_1}{\Delta t_2}}}\\if~~~\frac{\Delta t_1}{\Delta t_2}<2,\Deltat_m=\frac{\Delta t_1+\Delta t_2}{2} \\传热面积A=\frac{Q}{K\Delta t_m} \\总传热系数平壁与薄壁管的总传热系数计算\frac{1}{K}=\frac{1}{\alpha_1}+R_{d1}+\frac{b}{\lam bda}+R_{d2}+\frac{1}{\alpha_2} \\当传热壁热阻很小可忽略，且流体清洁，污垢热阻也可忽略时\frac{1}{K}=\frac{1}{\alpha_1}+\frac{1}{\alpha_2}\\ K=\frac{\alpha_1\alpha_2}{\alpha_1+\alpha_2} \\由此式可知，K必趋近且小于\alpha_1与\alpha_2中较小的值热辐射热辐射的基本概念•凡是热力学温度在零度以上的物体,由于物体内部原子复杂的激烈运动能以电磁波的形式对外发射热辐射线,并向周围空间作直线传播。

传热物理量与传热基本方程一、传热中的一些物理量和单位：1.热量：是能量的一种形式。

用Q表示，[J]；2.传热速率：单位时间内传递的热量q=Q/t,J/s即[w ]；3.热强度（热通量、热流密度）：Q/QS单位时间、单位传热面积所传递的热量。

[ w/m2]；4.焓:单位质量的物质所具有的热量称为焓。

[J/㎏]或[J/mol]5.潜热：单位质量的物体在一定的温度下发生相变时所吸收或放出的热量；6.恒压比热：压强恒定时（常指一个绝对大气压）单位质量的物体温度升高1[K]时所需要的热量。

[J/㎏-1.K-1 ]或[J/mol-1.K-1]；7.显热：物体的质量与比热及温度变化值的乘积。

[Q B=m.C F.△T]。

二.稳态传热与非稳态传热当与热流方向垂直的任一截面上、某点的温度和传热速率随位置变化而不随时间而变化时，称为稳态传热。

当与热流方向垂直的任一截面上、某点的温度和传热速率既随位置变化又随时间而变化时，称为非稳态传热。

三、工业上的换热方法1.直接换热（混合式换热）冷热两种流体在换热中直接混合而交换。

例如:硫酸工业中，对高温的炉气进行降温，就是用冷水与直接接触进行换热。

2.间壁换热：冷热流体处于固体壁面的两侧，热流体将热量传给壁面，通过间壁由另一壁面将热量传给冷流体。

3.蓄热式换热：热流体通过炉内，放出热量使炉温升高，然后将需要加热的冷流体通过炉内，吸收热量炉温下降，然后使热流体再次入炉，如此交替使冷、热流体换热。

四，热量传递的基本方式1.导热（热传导）：物体分子振动或物体内部自由电子的转移而引起的传热过程。

（可以发生在固、液、气三相中。

）2.热对流（给热）：流体各部分之间发生相对位移所引起的热传递过程。

（仅发生在流体中，如气体、液体。

）3.热辐射：因热的原因而产生的电磁波在空间的传递。

（固、液、气都可以进行热辐射，一般以上才考虑热辐射影响。

）五.总传热速率方程a=KS△t m q∝s△t m q=△t m/(1/KS）=传热推动力/传热阻力—传热速率[w ]；—总传热系速[w/m2℃ ]；—传热面积[ m2]；—平均温度差[ ℃ ]。

第四节总传热方程一、间壁两侧流体的传热化工生产中最常用到的传热操作是热流体经管壁向冷流体传热的过程。

该过程称为热交换或换热，这种间壁两侧流体的传热如图3-13所示。

图3-13 间壁传热当冷、热流体分别从间壁（管壁或平面壁）两侧流过的时候热流体一边流动温度逐渐降低，而冷流体则一边流动温度逐渐升高。

很显然，热流体将热量从热流体主体以对流传热的方式传递给间壁，而后热量以导热的方式从间壁的一侧传向另一侧，最后热量从冷流体一侧的间壁以对流传热的方式传递到冷流体的主体，这就是热交换的总的过程。

整个传热过程由对流---导热---对流三个部分串联组成，因而整个过程也称总传热。

二、总传热方式图3-14 流体通过间壁换热示意图图3-14表示一块固体间壁，它的左边是热流体，温度为T，右边是冷流体，温度为t，此间壁垂直于热流方向的传热面积为A。

实验证明，单位时间热流体传给冷流体热量Q与传热面积A 及两流体的温度差△t(=T-t)成正比，即：Q∝A△t写成等式为: Q=KA△t (3-18)或（3-19）式中Q----传热速率，W；K----传热总系数，W/（m2·K）；A----传热面积，m2；△t----温度差，K。

在实际计算中，由于热流体在传热过程中温度是逐渐降低的，冷流体则是逐渐升高的，热流体主体与冷流体主体的温度差△t在不断变化，因而计算中多使用平均温度差△t m,故（3-18）可写成：Q=KA△t m (3-20)三、传热总系数K传热总系数的物理意义可由式（3-20）导出，即：它表示当传热平均温度差为1K时，单位时间内通过单位传热面积所传递的热量。

K值越大，传热热阻就越小，单位面积传递的热量就越多，因此，K值是衡量热交换器性能的一个重要指标。

图3-15 对流传热的温度分布K值可以通过实验测定，也可以从理论上进行计算。

理论计算就是通过间壁两侧流体的对流传热和通过固体壁的导热来进行计算。

传热总系数的计算式可以用两流体通过管壁的恒温传热的例子进行推导。

传热计算传热计算分为两种：设计计算——据任务给定热负荷，确定换热器面积；校核计算——对已有换热器，计算其热负荷、或流体流量、或流体出口温度。

计算基础：热量衡算（即能量衡算）传热速率方程（多用无壁温的总方程）4-4-1能量衡算与推导柏式的能量衡算相比较，在换热器中，①器内无“外功”加入；②位能较小（∵换热器多横置，竖置时△Zmax≤6m），动能变化也较小（∵只有管程流体在分配头处才有些变化），∴一般忽略；③∵流阻转换的热量与热负荷相比很小，∴忽略。

换热器的能量衡算只考虑间壁两侧流体的“焓衡算”。

设换热器绝热，Q L=0；则单位时间内热流体放出的热量等于冷流体吸收的热量：W h(H h1-H h2)=W c(H c2-H c1)=Q(4-30)或(W△H)h=(W△H)c=Q其中的△H不外有下列三种基本形式：①无相变，c p=常数；△H h=c ph（t2-t1）或△H c=c pc（T1-T2）②有相变：△H=r③相变加温变：△H=r+c p△T（/△t）根据实际情况可能组合出许多热量衡算公式。

4-2-2总传热速率微分方程和总传热系数一、总传热速率微分方程∵稳定的间壁传热，流体的对流传热速率Q=间壁的导热速率Q。

∴计算时可任取某侧流体或间壁作为计算对象。

但是，计算式中都涉及壁温，它既难侧又难求取（试差）仿多层平壁，将同一横截面上的两侧流体分别“绝热混合”，它们的差值做为截面传热的中推力，即：式也可以写成：dQ=k(T-t)dS=k△tdS(3-34)对应不同的传热面有：dQ=K i(T-t)dS i=K m(T-t)dS m=K o(T-t)dS o注意①K与α相同处：“局部中传热系数”，计算时取均值②K与dS--对应。

Ki～Km～Ko：二、总传热系数K由和（3--34）：基于不同的传热面：即：换热器在实际进行中，∵流体中结晶等的沉淀、结垢、结焦、聚合或冷却水中的藻类、细菌或流体对管才的腐蚀等原因，都会在管壁上形成污垢层。