对流传热基本方程——牛顿冷却定律

牛顿冷却定律牛顿冷却定律牛顿冷却定律（Newton's law of cooling)：温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。

当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数。

牛顿冷却定律是牛顿在1701年用实验确定的，在强制对流时与实际符合较好，在自然对流时只在温度差不太大时才成立。

是传热学的基本定律之一，用于计算对流热量的多少。

如图所示：温差Δt＝|tw-tf|q＝hΔtΦ＝qA＝AhΔt＝Δt/(1/hA)其中的1/hA 称为对流传热热阻字母代码：q为热流密度h为物质的对流传热系数Φ为传热量A为传热面积冷却定律对于同一物体温度下降的速率,牛顿做过研究,并发现同一物体在外部介质性质及温度相同,本身性质及表面积相同时,物体冷却的速率只与外部与物体的温差有关.一个较周围热的物体温度为T,忽略表面积以及外部介质性质和温度的变化.它的冷却速率(dT/dt)与该物体的温度与周围环境的温度C的差(T-C)成正比.即dT/dt=-k(T-C).其中,t为时间,k为一个常数.计算方法是:对 dT/dt=-k(T-C) 进行积分,得ln(T-C)=-kt+B(B为积分常数)(T-C)=e^(-kt+B) (1)设t=0,也就是物体的初温,(1)变成(T0-C)=e^B然后代入 (1) 得T=C+(T0-C)^(-kt)算出B与k,代入t的值,就可以算出某个时间物体的温度.冷却定律推导出来,在忽略表面积以及外部介质性质和温度的变化,物体温度变化是越来越慢的.一、对权威的牛顿冷却定律提出挑战中学生姆潘巴的精心观察对权威的牛顿冷却定律提出挑战我（姆潘巴）在坦桑尼亚的马干巴中学读三年级时，校中的孩子们做冰淇淋总是先煮沸牛奶，待到冷却后再倒入冰盘，放进电冰箱。

为了争得电冰箱的最后一只冰盘，我决心冒着弄坏电冰箱的风险而把热牛奶放进去了。

一个多小时以后，我们打开电冰箱，里面出现了惊人的奇迹：我的冰盘里的热牛奶已结成坚硬的冰块，而他们的冰里还是稠稠的液体。

对流传热公式
对于对流传热公式，其本质是牛顿冷却定律，即对流传热率与温
度差成正比，与传热面积、传热系数成正比。

其数学表达式为：Q = hAΔT
其中，Q为传热速率，单位为W或J/s；h为对流传热系数，单位
为W/(m²·K)；A为传热面积，单位为m²；ΔT为传热的温度差，单位
为K或℃。

需要注意的是，对流传热系数是由传热流体的性质、流速、传热
面的特性等因素决定的，而其解析式一般是无法给出的，需要通过实
验测定或经验公式来获得。

同时，在实际应用中，涉及较复杂的情况时，如自然对流、强迫对流、辐射对流等，对流传热公式需要结合其
他传热模型和理论来计算。

此外，对流传热过程中还会出现边界层效应、湍流效应等，这些
都需要进行特殊考虑。

还有一些特殊技术和装置，如换热器、冷却塔、空气调节装置等，则需要运用更为复杂的传热理论和模型。

综上所述，对流传热公式是传热学中最常见且基础的一种模型，但在实际应用中需要注意各种特殊因素，并采用合适的传热模型和理论进行分析和计算。

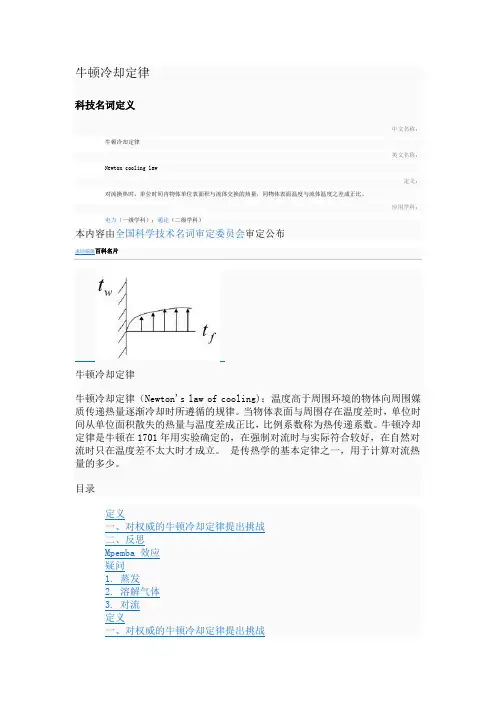
牛顿冷却定律科技名词定义中文名称：牛顿冷却定律英文名称：Newton cooling law定义：对流换热时，单位时间内物体单位表面积与流体交换的热量，同物体表面温度与流体温度之差成正比。

应用学科：电力（一级学科）；通论（二级学科）本内容由全国科学技术名词审定委员会审定公布牛顿冷却定律牛顿冷却定律（Newton's law of cooling)：温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。

当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数。

牛顿冷却定律是牛顿在1701年用实验确定的，在强制对流时与实际符合较好，在自然对流时只在温度差不太大时才成立。

是传热学的基本定律之一，用于计算对流热量的多少。

目录展开编辑本段定义如图所示：温差Δt＝|tw-tf|q＝hΔtΦ＝qA＝AhΔt＝Δt/(1/hA)其中的1/hA 称为对流传热热阻字母代码：q为热流密度h为物质的对流传热系数Φ为传热量A为传热面积一个热的物体的冷却速度与该物体和周围环境的温度差成正比。

分析即 -dT/dt=(T-Tc)/τ式中，-dT/dt——物体的温度随时间下降的速度，负号表示物体的温度是下降的τ——物体的温度从T 下降到环境温度Tc实际所需要的弛豫时间在微分条件下，-dT/dt和(T-Tc)/τ是微线性关系。

这是微线性思维的典范之一。

牛顿冷却定律的这个微分方程没有考虑物体的性质，所以这不是物性方程式。

它只是关于一个假想物体，其温度随时间单纯下降的一个数学微分方程。

与其叫“牛顿冷却定律”，毋宁叫“牛顿冷却定理”更准确。

不过，这个明显的缺点，反而是最大的优点。

它的无比抽象性在宣告：“这是任何物体冷却的共同遵守的数学规律！”。

实验表明物体的温度随时间下降的速度和物体的结构以及理化性质并非完全无关。

尤其是急速冷却的条件下，我们可以修改线性“牛顿冷却定理”，给它添加若干个非线性的项就可以了解决实际问题了。

第八讲对流换热convection heat transfer§8-1 对流换热基本概念一、对流换热过程：对流：是指物体各部分之间发生相对位移，冷热流体相互掺混所引起的能量传递方式，必有导热。

对流换热：流体流过一物体表面时对流与导热联合作用的热量传递过程。

牛顿冷却定律Newton’s law of coolingwt ft 如：f w t t t -=∆th q ∆=hAtt Ah qA Φ1∆=∆==为对流传热热阻hA R 1=二、流动边界层1. 流动(速度)边界层：靠近壁面处流体速度发生显著变化的薄层边界层的厚度(boundary layer thickness):达到主流速度的99%处至固体壁面的垂直距离边界层的特点(1) 有层流(laminar flow),紊流(turbulent flow)之分.•分界点Re c=3X105~3X106,一般可取Re c=5X105•在湍流区,贴壁面还有一极薄的层流底层（粘性底层）(2) δ=δ(x) x↑δ(x)↑(3) δ(x) << x δ(L) << L(4) 流场分为: 主流区(undisturbed flow regime)(potential)边界层区(boundary regime)三、换热微分方程无滑移边界条件（傅里叶定律）0=∂∂-=y yt A λΦ变化率贴壁处流体的法向温度式中：→∂∂=0y y t 联立，得与牛顿冷却公式t hA ∆=Φ0=∂∂-=y y t t h ∆λ四、影响对流换热的因素⏹流动产生的原因：受迫流动，自然对流⏹流体流动情况：层流（Re<2300），紊流（Re>10000）⏹流体的物性：ρ、λ、η等⏹换热面的形状和位臵⏹流体集态的改变§8-2 对流换热基本方程组1.连续性方程(continuity equation)0=∂∂+∂∂yv x u •2.动量方程(momentum equation)⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂22222222y v x v y p F y v v x v u v y u x u x p F y u v x u u u y x ητρητρ惯性力(inertial force)体积力(body force)压力梯度(pressuregradient)粘性力(viscous force)3.能量守恒方程（energy equation)⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂+∂∂2222y t x t a y t v x t u t τ能量变化对流项导热项以此五个量为分析基础。

对流传热第一题：知识点总结（一）对流传热概述1、对流传热：流体流过固体壁时的热量传递。

传热机理：热对流和热传导的联合作用热流量用牛顿冷却公式表示：Φ=hA△t其中对流传热面积A，温差△t，对流传热系数h2、影响对流传热系数的因素（1）流动的起因：>由于流动起因的不同，对流换热分为强迫对流传热与自然对流传热两大类。

（2）流动速度：>根据粘性流体流动存在着层流和湍流两种状态，对流传热分为层流对流传热与湍流对流传热两大类。

（3）流体有无相变：同种流体发生相变的换热强度比无相变时大得多。

（4）壁面的几何形状、大小和位置：对流体在壁面上的运动状态、速度分布和温度分布有很大影响。

（5）流体的热物理性质：影响对流传热系数有热导率λ，密度，比定压热容，流体粘度，体积膨胀系数。

综上所述，影响对流传热系数h的主要因素，可定性地用函数形式表示为h=f（v，l，λ，，，或，，）（二）流动边界层和热边界层1、流动边界层特性：（1）流体雷诺数较大时，流动边界层厚度与物体的几何尺寸相比很小；（2）流体流速变化几乎完全在流动边界层内，而边界层外的主流区流速几乎不变化；（3）在边界层内，粘性力和惯性力具有相同的量级，他们均不可忽略；（4）在垂直于壁面方向上，流体压力实际上可视为不变，即=0；（5）当雷诺数大到一定数值时，边界层内的流动状态可分为层流和湍流。

2、热边界层定义：当流体流过物体，而平物体表面的温度与来流流体的温度不相等时，在壁面上方形成的温度发生显著变化的薄层，称为热边界层。

热边界层厚度：当壁面与流体之间的温差达到壁面与来流流体之间的温差的0.99倍时，即=0.99，此位置就是边界层的外边缘，而该点到壁面之间的距离则是热边界层的厚度记为。

与δ一般不相等。

3、普朗特数流动边界层厚度δ反应流体分子动量扩散能力，与运动粘度有关；而热边界层厚度反应流体分子热量扩散的能力，与热扩散率a有关。

==它的大小表征流体动量扩散率与热量扩散率之比（三）边界层对流传热微分方程组1、连续性方程+=02、动量微分方程根据动量定理可导出流体边界层动量微分方程流体纵掠平壁时3、能量微分方程热扩散率a=边界层能量微分方程式：+=4、对流传热微分方程-------x处的对流传热温差------流体的热导率-------x处壁面上流体的温度变化率（四）、管内强迫对流传热1、全管长平均温度可取管的进、出口断面平均温度的算术平均值作为全管长温度的平均，即=（）2、层流和湍流的判别由雷诺数Re大小来判别针对管内流动，当Re<2200时为层流；Re>1×时为湍流；2200<Re<1×时则为不稳定的过渡段（1）管内流动：（2）板内流动：湍流强迫对流传热管内强迫对流平均对流传热系数特征数关联式为：=0.023R P:考虑边界层内温度分布对对流传热系数影响的温度修正系数；:考虑短管管长对对流传热系数影响的短管修正系数；:考虑管道弯曲对对流传热系数影响的弯管修正系数。

牛顿的冷却定理
牛顿冷却定理，也称为牛顿冷却定律，是由牛顿提出的经验理论，用于描述物体冷却速率与物体和环境温差之间的关系。

该定理指出，当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数。

这一规律适用于温度高于周围环境的物体向周围媒质传递热量并逐渐冷却的过程。

牛顿冷却定律的公式为：
q = hΔt
其中，q 为单位时间从单位面积散失的热量*，h* 为物质的对流传热系数，Δt 为物体与环境的温度差。

这个公式反映了物体冷却速度与环境温度差之间的关系。

此外，牛顿冷却定律还可以表达为微分形式：
-dT/dt = (T - Tc)/τ
其中，T 表示物体的温度*，Tc* 表示环境温度*，t* 表示时间*，τ* 是弛豫时间，表示物体的温度从T 下降到Tc 实际所需要的时间。

这个公式描述了物体温度随时间下降的速度与物体和环境温度差之间的关系。

值得注意的是，牛顿冷却定律在强制对流时与实际符合较好，但在自然对流时只在温度差不太大时才成立。

此外，该定律的适用条件是物体和介质的温度分布都是均匀的，且物体和介质既可以是固体也可以是液体和气体。

总之，牛顿冷却定理是传热学的基本定律之一，用于计算对流热量的多少，对于理解和控制物体的冷却过程具有重要意义。

如需更多与牛顿冷却定理相关的信息，建议查阅物理学专业书籍或咨询物理学专家。

概念一、传热的三种基本方式1．传导又称为热传导，简称导热。

其机理是当物体的内部或两个直接接触的物体之间存在着温度差异时，物体中温度较高部分的分子因振动而与相邻分子碰撞，并将能量的一部分传给后者，为此，热能就从物体温度较高的部分传递到温度较低的部分或从一个温度较高的物体传递给直接接触的温度较低的物体。

其特点是物体中的分子或质点不发生宏观的相对位移。

导热是固体中热传递的主要方式。

2．对流对流又称热对流。

对流仅发生在流体中，其机理是由于流体中质点发生相对位移和混合，而将热能由一处传递到另一处。

对流分为自然对流和强制对流两种。

若流体质点的相对位移是因流体内部各处温度不同而引起的局部密度差异所致，则称为自然对流。

由机械（如搅拌流体）使流体发生对流运动的称为强制对流。

3．辐射辐射又称为热辐射，是一种以电磁波传递热能的方式。

任何物体只要在绝对零度以上，都能发射辐射能。

二、工业换热方式1．间壁式换热：其特点是冷热两种载热体被一固体间壁所隔开，在换热过程中，两种载热体互不接触，热量由热流体通过间壁传给冷流体。

2．混合式换热：其特点是两流体间的热交换，是依靠热流体和冷流体直接接触和混合过程实现的。

3．蓄热式换热器：其特点是冷热两流体间的热量交换是通过壁面周期性的加热和冷却来实现的。

三、稳定传热和不稳定传热稳定传热：若传热系统中各点的温度仅随位置变而不随时间变，则此传热过程为稳定传热。

包括恒温传热和变温传热两种。

不稳定传热：若传热过程中各点温度不仅随位置不同而不同，且随时间而发生变化，这种传热过程称为不稳定传热。

四、导热系数：是衡量物质导热能力的一个物理量。

用λ表示，单位是W/m.℃。

五、对流传热系数：是度量对流传热过程强烈程度的数值。

用α表示，单位为W/m2.℃。

六、影响对流传热系数的因素：1．流体流动产生的原因是自然对流还是强制对流2．流体的流动状况是层流还是湍流。

湍流时的α值比层流时大好几倍甚至更多。

3．流体有无相变化有相变化时的对流传热系数较大。

第三章 传 热－基本概念和基本理论传热是由于温度差引起的能量转移，又称热传递。

由热力学第二定律可知，凡是有温度差存在时，就必然发生热从高温处传递到低温处。

根据传热机理的不同，热传递有三种基本方式：热传导（导热）、热对流（对流）和热辐射。

热传导是物体各部分之间不发生相对位移，仅借分子、原子和自由电子等微观粒子的热运动而引起的热量传递；热对流是流体各部分之间发生相对位移所引起的热传递过程（包括由流体中各处的温度不同引起的自然对流和由外力所致的质点的强制运动引起的强制对流），流体流过固体表面时发生的对流和热传导联合作用的传热过程称为对流传热（给热）；热辐射是因热的原因而产生的电磁波在空间的传递。

任何物体只要在绝对零度以上，都能发射辐射能，只是在高温时，热辐射才能成为主要的传热方式。

传热可依靠其中的一种方式或几种方式同时进行。

传热速率Q 是指单位时间通过传热面的热量（W ）；热通量q 是指每单位面积的传热速率（W/m 2）。

一、 热传导1. 导热基本方程––––傅立叶定律nt dS dQ ∂∂-=λ λ––––导热系数，表征物质导热能力的大小，是物质的物理性质之一，单位为W/（m·℃）。

纯金属的导热系数一般随温度升高而降低，气体的导热系数随温度升高而增大。

式中负号表示热流方向总是和温度剃度的方向相反。

2．平壁的稳定热传导单层平壁：Rt S t t Q ∆=-=λ21多层（n 层）平壁：∑∑∑==+∆=-=ni n i i i n R t S b t t Q 1111λ 公式表明导热速率与导热推动力（温度差）成正比，与导热热阻（R ）成反比。

由多层等厚平壁构成的导热壁面中所用材料的导热系数愈大，则该壁面的热阻愈小，其两侧的温差愈小，但导热速率相同。

3. 圆筒壁的稳定热传导单层圆筒壁：R t S b t t Q m ∆=-=λ21 或 1221ln )(2r r t t l Q -=λπ 当S 2/S 1>2时，用对数平均值，即：1212ln S S S S S m -= 当S 2/S 1≤2时，用算术平均值，即：S m =（S 1+S 2）/2多层（n 层）圆筒壁：∑=+-=n i mii i n S b t t Q 111λ 或∑++-=ii i n r r t t l Q 111ln 1)(2λπ 一包有石棉泥保温层的蒸汽管道，当石棉泥受潮后，其保温效果应降低，主要原因是因水的导热系数大于保温材料的导热系数，受潮后，使保温层材料导热系数增大，保温效果降低。

第十讲一、管内对流传热概述5. 5 管内层流对流换热当流体流过管内，其温度与管壁温度不同时，流体与管壁之间产生的热量传递过程。

第十讲二、光滑圆管内的层流流动1、管内层流流动第十讲2、管内层流流动的特点•当均匀来流进入圆管后，速度分布不断变化，由于粘性作用，壁面处速度为零，流体被排挤到中间，中心速度不断增大;•若流体为不可压，则变化到一定程度后，由于质量守恒，速度剖面不再变化，达到所谓充分发展状态。

第十讲讨论的英文写法，都用frictional coefficient, •f 和cf请注意其区别；•充分发展的概念；•微尺度气体流动的特点：层流；速度剖面随马赫数变化；无充分发展；阻力增加。

第十讲三、圆管内充分发展层流对流换热第十讲讨论•表面传热系数为常数，与定义时所取的传热温差有关。

如果以壁温与流体进口温度之差定义表面传热系数，则由于温差始终逐渐增加，当热流一定时，表面传热系数一定逐渐减小，不再是常数。

•Nu的定义式与Bi相同，但其物理意义不同。

Nu描述的是实际的对流换热量与导热传递的热量的比值，或称为无因次换热量。

第十讲问题等热流边界与等壁温边界相比，Nu要高出16%，为什么？第十讲第十讲讨论•流动进口段的速度梯度、摩擦系数比充分发展段要大，若以两者相差2%定义进口段长度，则有：x = 0.05dRe•热进口段的温度梯度也比充分发展段要大，进口段的换热比充分发展段强。

若以二者相差2%定义热进口段长度，则有：x = 0.05dRePr第十讲小结•管内对流换热的一般求解方法；•圆管内充分发展层流流动与阻力系数；•圆管内充分发展层流换热与努谢尔数；•流体截面能量平均温度的概念。

第十讲作业1、写出等热流和等壁温两种条件下热充分发展能量方程的定解条件；2、直接通过壁面热流定解条件推导热充分发展段的温度分布第十讲。

流体流动–––基本概念与基本原理一、流体静力学基本方程式)(2112z z g p p -+=ρ或 gh p p ρ+=0注意：1、应用条件：静止的连通着的同一种连续的流体。

2、压强的表示方法：绝压—大气压=表压 表压常由压强表来测量；大气压—绝压=真空度 真空度常由真空表来测量。

3、压强单位的换算：1atm=760mmHg=10.33mH 2O=101.33kPa=1.033kgf/cm 2=1.033at4、应用：水平管路上两点间压强差与U 型管压差计读数R 的关系：gR p p A )(21ρρ-=-处于同一水平面的液体，维持等压面的条件必须时静止、连续和同一种液体。

二、定态流动系统的连续性方程式––––物料衡算式常数常数=====≠ρρρρuA A u A u w s A 222111,常数常数======uA A u A u V s A 2211,ρ 21221221///,d d A A u u A ===圆形管中流动常数ρ三、定态流动的柏努利方程式––––能量衡算式1kg 流体：2211221222f p u p u gZ We gZ h ρρ+++=+++∑ [J/kg] 讨论点：1、流体的流动满足连续性假设。

2、理想流体，无外功输入时，机械能守恒式：3、可压缩流体,当Δp /p 1<20%,仍可用上式，且ρ=ρm 。

4、注意运用柏努利方程式解题时的一般步骤，截面与基准面选取的原则。

5、流体密度ρ的计算：理想气体ρ=p M/R T 混合气体 vn n v v m x x x ρρρρ+++= 2211混合液体 n wn w m w m x x x ρρρρ+++= 2211上式中：vi x ––––体积分率；wi x ––––质量分率。

6、g z ，u 2/2，p /ρ三项表示流体本身具有的能量，即位能、动能和静压能。

∑h f 为流经系统的能量损失。

W e 为流体在两截面间所获得的有效功，是决定流体输送设备重要参数。