数字信号习题作业

==============================绪论==============================1. A/D 8bit 5V00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的， 确定其周期。

（1）A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= （2）)81(j e )(π-=n n x 解： （1） 因为ω=73π, 所以314π2=ω, 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π, 这是无理数， 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法乘法序列{2，3，2，1}与序列{2，3，5，2，1}相加为__{4，6，7，3，1}__，相乘为___{4，9，10，2} 。

移位翻转：①已知x(n)波形，画出x(-n)的波形图。

②尺度变换：已知x(n)波形，画出x(2n)及x(n/2)波形图。

卷积和：①h(n)*求x(n)，其他02n 0n 3，h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5}，则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4. 如果输入信号为，求下述系统的输出信号。

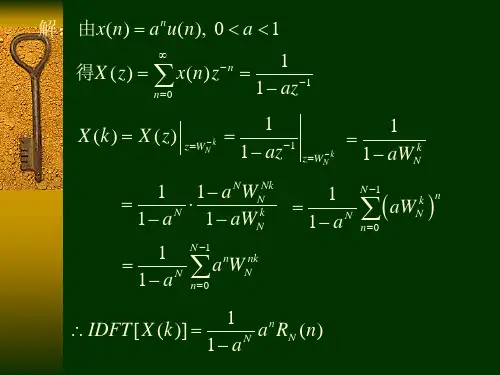
第二章1.判断是否周期序列（2）3()cos()74x n n ππ=-（3）)n 81(j e)n (x π-=（5）7()cos(2)8x n n π=+（6）21()sin ()8x n n π=（7）11()cossin44x n n n ππ=⋅解：若为周期序列，则有)n (x )T n (x =+ N T ∈(2)令 )4n 73cos(]4)T n (73cos[ππππ-=-+则ππm 2T 73= N m ∈得：m 314T =当m=3时，T 可取最小正整数14，所以该序列是周期序列(3)令 )n 81(j ])T n (81[j e e )n (x ππ--+==得πm 2T 81= N m ∈πm 16T =找不到使T 为正整数的m 值∴)n 81(j e)n (x π-=不是周期序列(5)令)2n 87cos(]2)T n (87cos[+=++ππ得 πm 2T 87= N m ∈m 716T =若m=7, T 可取最小正整数16∴)2n 87cos()n (x +=π是周期为16的周期序列。

(6)21()sin ()8x n n π=11cos()42n π-=令)]T n (41cos[2121)T n (x +-=+π111c o s ()224n π=-得 124T m ππ= N m ∈T=8m令m=1,则T 可取最小正整数8∴)n 81(sin )n (x 2π=是周期为8的周期序列(7) 令11()cossin44x n n n ππ=⋅1sin22n π=于是11sin[()]sin 22()22n T n x n T ππ++== 得 ππm 2T 21=T=4m令m=1,T 取最小正整数4∴11()cossin44x n n n ππ=⋅是周期为4的周期序列3.确定系统稳定、因果、线性、非时变性。

(2)∑==nn k 0x(k)T[x(n)](4))n n (x T[x(n)]0-=b n ax n x T +=)()]([)6( )()]([)8(2n x n x T = )632sin()()]([)10(ππ+=n n x n x T)()]([)12(n nx n x T =(2)解：①线性：设∑===nn k k xn x T n y 0)()]([)(111，∑===nn k k xn x T n y 0)()]([)(222)()()(21n bx n ax n x +=)]()([)]([)(21n bx n ax T n x T n y +==∑=+=nn k n ax n ax)()(21∑∑==+=nn k nn k n x b n xa)()(21)()(21n by n ay +=∴该系统是线性系统② 时变性：∑∑--===-=-mn mn t nn k t x m k x m n x T 00)()()]([)]([)()(0m n x T k x m n y mn n k -≠=-∑-=∴该系统是时变系统③ 稳定性：若(),()()x n x n M M ∀∃<均为有界常数∑===nn k k x n x T n y 0)()]([)(∑=≤nn k k x 0)(M n n )(0-≤找不到一个常数，使得p n y <)(，故系统不稳定。

==============================绪论==============================1。

A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1。

①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用（n ） 表示y （n )=｛2，7,19，28,29，15｝2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的； 若是周期的， 确定其周期。

（1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2）)81(j e )(π-=n n x 解: （1） 因为ω=73π， 所以314π2=ω， 这是有理数， 因此是周期序列， 周期T =14。

（2） 因为ω=81, 所以ωπ2=16π， 这是无理数, 因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法 乘法序列｛2，3，2，1}与序列｛2，3，5，2，1}相加为__｛4，6，7,3，1}__，相乘为___｛4，9，10，2｝ 。

移位翻转：①已知x(n)波形，画出x(—n ）的波形图。

②尺度变换:已知x(n)波形，画出x （2n ）及x(n/2）波形图.卷积和:①h(n)*求x(n)，其他2n 0n 3，h(n)其他3n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤=}23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )=｛1,2，4,3},h （n ）={2，3，5}， 求y （n ）=x （n ）＊h （n ）x (m ）={1，2，4,3},h （m ）=｛2,3,5｝，则h (—m ）={5，3,2｝(Step1：翻转)解得y （n )=｛2，7，19,28,29，15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4. 如果输入信号为,求下述系统的输出信号。

冀教版数字同步练习册答案【练习一：基础概念题】1. 什么是数字信号？答案：数字信号是一种用数字形式表示的信号，它由离散的数值组成，通常用二进制形式表示。

2. 模拟信号与数字信号的区别是什么？答案：模拟信号是连续变化的信号，可以是电压、电流等物理量的变化；而数字信号是离散的，通常用二进制形式表示，具有更高的抗干扰能力和易于存储和传输的特点。

3. 数字信号处理的基本步骤是什么？答案：数字信号处理的基本步骤包括采样、量化、编码和解码。

【练习二：应用题】1. 如何将模拟信号转换为数字信号？答案：将模拟信号转换为数字信号的过程称为模数转换（ADC）。

首先对模拟信号进行采样，然后进行量化，将采样值转换为有限数量的数值，最后进行编码，将量化后的数值转换为数字形式。

2. 数字信号的优点有哪些？答案：数字信号的优点包括抗干扰能力强、易于存储和传输、可以进行数字信号处理、便于实现信号的放大和滤波等。

3. 请简述数字滤波器的工作原理。

答案：数字滤波器通过数学算法对数字信号进行处理，以实现滤除噪声或特定频率成分的目的。

常见的数字滤波器有低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。

【练习三：计算题】1. 已知一个模拟信号的采样频率为1000Hz，信号的带宽为500Hz，请计算奈奎斯特采样频率。

答案：奈奎斯特采样频率是信号带宽的两倍，即1000Hz。

2. 如果一个数字信号的量化位数为8位，计算其可能的量化级别。

答案：量化位数为8位，意味着有 \( 2^8 = 256 \) 个可能的量化级别。

3. 假设一个数字信号的编码采用非归零编码方式，请简述其特点。

答案：非归零编码（NRZ）是一种数字信号编码方式，其特点是信号的高电平或低电平代表二进制的“1”或“0”，并且电平在两个码元之间不返回零电平。

【结束语】通过本练习册的练习，相信同学们对数字信号的基本概念、应用以及处理方法有了更深入的理解。

希望同学们能够将所学知识运用到实际中，不断提高自己的数字信号处理能力。

数字信号试题及答案一、选择题1. 数字信号的特点是：A. 连续变化B. 离散变化C. 随机变化D. 周期变化答案：B. 离散变化2. 奈奎斯特定理适用于什么类型的信号？A. 模拟信号B. 数字信号C. 脉冲信号D. 正弦信号答案：A. 模拟信号3. 数字信号的采样率是指：A. 信号的持续时间B. 信号的幅度范围C. 信号的采样点数量D. 信号的频率范围答案：C. 信号的采样点数量4. 在数字信号处理中，量化是指：A. 将模拟信号转换为数字信号B. 将数字信号转换为模拟信号C. 对信号进行编码D. 对信号进行解码答案：A. 将模拟信号转换为数字信号5. 数字信号的传输速率由以下因素决定：A. 采样率和量化位数B. 频率和幅度C. 信噪比和误码率D. 传输介质和距离答案：A. 采样率和量化位数二、填空题1. 数字信号的采样定理由_______和_______提出。

答案：奈奎斯特、香农2. 数字信号的量化位数越大，表示精度越_______。

答案：高3. 数字信号的编码方式常用的有_______和_______编码。

答案：二进制、格雷4. 数字信号的传输速率单位是_______。

答案：比特/秒5. 数字信号的解码是指将_______信号还原为模拟信号。

答案：数字三、简答题1. 请解释奈奎斯特定理的原理及应用。

答：奈奎斯特定理是指在进行信号的采样时，采样频率要大于等于信号频率的两倍，以确保信号能够完全恢复。

它的原理是由于数字信号是离散的，采样过程中可能会出现信息的损失。

奈奎斯特定理的应用主要用于计算信号的最佳采样率，以保证在数字信号处理中不会出现信息丢失。

2. 请说明数字信号的编码方式有哪些，并分别解释其原理。

答：数字信号的编码方式主要有二进制编码和格雷编码。

二进制编码是将信号的每个样本通过二进制数进行表示，利用0和1的排列来表示不同的信号状态。

格雷编码则是改进版的二进制编码，它通过仅仅改变一个位的数值，来表示相邻的两个信号状态，以减少数字信号在编码过程中的误差。

数字信号系统考试试题一、选择题（每题 5 分，共 30 分）1、下列信号中，属于数字信号的是（）A 正弦波信号B 锯齿波信号C 脉冲信号D 模拟音频信号2、数字信号的特点不包括（）A 抗干扰能力强B 便于加密处理C 占用带宽小D 精度高3、在数字系统中，量化误差产生的原因是（）A 编码过程B 采样过程C 保持过程D 量化过程4、对于一个有限长序列 x(n)，其离散傅里叶变换（DFT）的点数为 N，若要使 DFT 结果能准确反映 x(n)的频谱特性，N 应满足（）A N 小于序列长度B N 等于序列长度C N 大于序列长度D N 与序列长度无关5、以下哪种数字滤波器的实现结构可以节省乘法器数量（）A 直接型B 级联型C 并联型D 频率采样型6、若一个数字系统的输入为x(n)，输出为y(n)，系统函数为H(z)，则系统稳定的充要条件是（）A 单位圆内的极点个数为零B 单位圆外的极点个数为零C 单位圆内的零点个数为零 D 单位圆外的零点个数为零二、填空题（每题 5 分，共 30 分）1、数字信号处理的三个主要步骤是：＿_______、＿_______和________。

2、对模拟信号进行采样时，采样频率必须大于信号最高频率的________倍，才能保证采样后的信号能够无失真地恢复原信号。

3、快速傅里叶变换（FFT）算法的基本思想是________。

4、数字滤波器根据其冲激响应的长度可分为________滤波器和________滤波器。

5、在数字通信系统中，常用的差错控制编码方式有________、＿_______和________。

6、数字信号系统中，A/D 转换器的主要性能指标包括________、＿_______和________。

三、简答题（每题 10 分，共 20 分）1、简述数字信号处理与模拟信号处理相比的优点。

答：数字信号处理相比模拟信号处理具有诸多优点。

首先，数字信号具有更高的精度和稳定性。

第一章习题一. 判断题1. 周期分别为N1,N2的两离散序列，在进行周期卷积后，其结果也是周期序列。

对2. FFT可用来计算IIR滤波器，以减少运算量。

错3. 相同的Z变换表达式一定对应相同的时间序列。

正确答案是: 错4. 频率采样法设计FIR滤波器，增加过渡带采样点可增加过渡带衰减。

正确答案是: 对二、选择题1. 采样率过低时，______。

A 量化误差增加 b. 必须增加信号频率c. 产生混叠2. 滤波器的单位脉冲响应的DTFT给出了滤波器的_____。

a. 频率响应b. 幅度c. 相位3. 滤波器的单位脉冲响应的DTFT给出了滤波器的_____。

a. 频率响应b. 幅度c. 相位4. ____序列的收敛域在Ｚ平面上是一环状的。

a. 右边序列b. 双边序列c. 有限长序列5. 稳定系统的收敛域应当_______。

a. 包含单位圆b. 不包含单位圆c. 可以包含单位圆6. A/D 是_____的缩写a. asynchronous digitalb. analog to digitac. analog to discrete7. 连续信号的理想采样值是_____。

a. 连续的b. 离散的c. 时间上连续的8. 一个离散系统，a. 若因果必稳定b. 若稳定必因果c. 稳定与因果无关9. 下列哪一个不是信号的实例a. 语音b. 音乐c. 调制解调器10. 若输出不超前于输入，该系统称为______。

a. 线性b. 非线性c. 因果11. 抗混叠滤波器的目的是a. 去掉模拟信号混叠b. 等效一个高通滤波器c. 将高于采样率一半的频率分量去掉12. 抽样可以表述为______。

a. 将数字信号转化为模拟信号b. 将模拟信号转化为数字信号c. 获得模拟信号的幅度值13. 下面哪个表达式是将x(n)左移三位得到_______a. 3x(n)b. x(3n)c. x(n+3)14. 下面哪个表达式是将x(n)右移三位得到_______a. 3x(n)b. x(3+n)c. x(n-3)15. 关于线性系统的描述正确的是_____a. 遵从叠加原理b. 非时变c. 因果16. D/A变换的第一步是a. 零阶保持 b . 低通抗混叠滤波 c. 将数字代码转换为相应的模拟电平级三、计算题1. 和表示一个序列及其傅氏变换,并且为实因果序列,利用求下列各序列的傅氏变换:解:注意：当t为偶数时[ .] =2x(2n)，当t为奇数时[ .] =0分析：以频率为400Hz的正弦信号为例，分别以2000Hz和1000Hz进行采样，序列长分别为2048点和1024点，对应的频谱如图1、图2所示。

数字信号处理习题集数字信号处理习题集第⼀章习题1、已知⼀个5点有限长序列，如图所⽰，h (n )=R 5(n )。

（1）⽤写出的()n δ()x n 函数表达式；（2）求线性卷积*。

()y n =()x n ()hn 2、已知x (n )=(2n +1)[u (n +2)-u (n -4)],画出x (n )的波形，并画出x (-n )和x (2n )的波形。

3、判断信号是否为周期信号，若是求它的周期。

3()sin 73x n n ππ??=+4、判断下列系统是否为线性的，时不变的，因果的，稳定的？（1），（2）2()(3)y n x n =-0()()cos()y n x n n ω=5、已知连续信号。

()2sin(2),3002a x t ft f Hz ππ=+=（1）求信号的周期。

()a x t （2）⽤采样间隔T=0.001s 对进⾏采样，写出采样信号的表达式。

()a x t ?()a xt （3）写出对应于的时域离散信号的表达式，并求周期。

?()a xt ()x n 6、画出模拟信号数字处理的框图，并说明其中滤波器的作⽤。

第⼆章习题1、求下列序列的傅⽴叶变换。

（1），（2）11()333nx n n ??=-≤ ?[]2()()()n x n a u n u n N =--2、已知理想低通滤波器的频率响应函数为：为整数，000(),0j n j e H e n ωωωωωωπ-?≤≤?=? <≤??cc 求所对应的单位脉冲响应h (n )。

3、已知理想⾼通滤波器的频率响应函数为：，求所对应0()1j H e ωωωωωπ≤≤=<≤??cc 的单位脉冲响应h (n )。

4、已知周期信号的周期为5,主值区间的函数值=,求该周期信号的()(1)n n δδ+-离散傅⾥叶级数和傅⾥叶变换.5、已知信号的傅⽴叶变换为，求下列信号的傅⽴叶变换。

()x n ()j X e ω（1）（2）(3)x n -*()x n -6、已知实因果信号如图所⽰，求和。

数字信号处理练习题一、填空题1）离散时间系统是指系统输入、输出都是___________的系统。

2）在对连续信号均匀采样时，要从离散采样值不失真恢复原信号，则采样周期T与信号最高截止频率fm应满足关系3）因果系统的H(z)z，则H(z)的收敛域为2zz64）因果稳定离散系统的系统函数H(z)的全部极点都落在Z平面的__________________。

5）如果序列某[k]的长度为M，则只有当时，才可由频域采样某[m]恢复原序列，否则产生现象。

6）设序列某[k]长度N＝16，按DIT－FFT做基2FFT运算，则其运算流图有级碟形，每一级由个碟形运算构成。

7）实现数字滤波器的基本运算单元是：_______、________、________。

8）线性相位FIR数字滤波器的第一类线性相位表达式为，满足第一类线性相位的充分必要条件是：h[k]是且9）判断y[k]=k某[k]+b 所代表的系统的线性和时不变性。

.10）有限长序列某[k]的离散傅立叶变换某[m]与其离散时间傅立叶变换某(ej)的关系是二、判断题(正确的在题后括号内打“√”，错的打“某”。

)1）常系数线性差分方程描述的系统一定是线性时不变系统。

()2）两序列的z变换形式相同则这两序列也必相同。

()3）离散傅里叶变换的特点是离散时间、离散频率。

()4）双线性变换法是非线性变换，所以用它设计IIR滤波器不能克服频率响应混叠效应。

()5）当且仅当单位冲击响应满足：h(n)0,n0时，那么线性时不变系统将是一个因果性的系统。

（）6）任意序列某[k]都存在傅立叶变换。

（）7）有限长序列某[k],n1nn2;如果n10，那么z=0不在收敛域内。

（）8）长度为N点的序列某[k]，它的DFT也是一个长度为N的序列。

（）9）FIR滤波器过渡带的宽度与窗函数旁瓣的宽度密切相关。

（）10）III型线性相位滤波器能用于高通滤波的设计。

（）三、选择题(注：Z指Z变换)n1.Z[(1)u(n)]______________________。

第一章数字信号处理概述简答题：1．在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器，它们分别起什么作用？答：在A/D变化之前为了限制信号的最高频率，使其满足当采样频率一定时，采样频率应大于等于信号最高频率2倍的条件。

此滤波器亦称为“抗混叠”滤波器。

在D/A变换之后为了滤除高频延拓谱，以便把抽样保持的阶梯形输出波平滑化，故又称之为“平滑”滤波器。

判断说明题：2．模拟信号也可以与数字信号一样在计算机上进行数字信号处理，自己要增加一道采样的工序就可以了。

（）答：错。

需要增加采样和量化两道工序。

3．一个模拟信号处理系统总可以转换成功能相同的数字系统，然后基于数字信号处理理论，对信号进行等效的数字处理。

（）答：受采样频率、有限字长效应的约束，与模拟信号处理系统完全等效的数字系统未必一定能找到。

因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析，再考虑幅度量化及实现过程中有限字长所造成的影响。

故离散时间信号和系统理论是数字信号处理的理论基础。

第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题：1．过滤限带的模拟数据时，常采用数字滤波器，如图所示，图中T 表示采样周期（假设T 足够小，足以防止混叠效应），把从)()(t y t x 到的整个系统等效为一个模拟滤波器。

（a ） 如果kHz rad n h 101,8)(=π截止于，求整个系统的截止频率。

（b ） 对于kHz T 201=，重复（a ）的计算。

解 （a ）因为当0)(8=≥ωπωj e H rad 时，在数 — 模变换中)(1)(1)(Tj X Tj X Te Y a a j ωω=Ω=所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ，因此对T8π没有影响，故整个系统的截止频率由)(ωj e H 决定，是625Hz 。