概率统计实验报告
- 格式:docx
- 大小:268.46 KB
- 文档页数:20



《概率统计》实验报告
专业 班级 姓名 学号 实验地点 实验时间
一、实验目的
1.学会用matlab 计算常见分布的概率。
2.熟悉matlab 中用于描述性统计的基本操作与命令
3.学会matlab 进行参数估计与假设检验的基本命令与操作
二、实验内容:(给出实验程序与运行结果)
实验一:
1、 设随机变量()23,2X N ,求()25P X <<;()2P X >
2、 一批产品的不合格率为0.02,现从中任取40件进行检查,若发现两件或两件以上不合格品就拒收这批产品,求拒收的概率。
实验二:根据调查,某集团公司的中层管理人员的年薪(单位:万元)数据如下:
40.6 39.6 37.8 36.2 38.8 38.6 39.6 40.0 34.7 41.7
38.9 37.9 37.0 35.1 36.7 37.1 37.7 39.2 36.9 38.3
求其公司中层管理人员年薪的样本均值、样本方差、样本修正方差,画出经验分布函数图、直方图。
实验三:
1、 假设轮胎的寿命服从正态分布,现随机抽取12只轮胎试用,测得它们的寿命(单位:万千米)如下:4.68 4.85 4.32 4.85 4.61 5.02 5.20 4.60 4.58 4.72 4.38 4.70 求平均寿命的最大似然估计值,以及置信度为0.95的置信区间。
2、 已知维尼纤度在正常条件下服从正态分布,方差为2
0.048,从某天产品中抽取5根纤维,测得纤度为1.32 1.55 1.36 1.40 1.44 问这一天纤度的总体方差是否正常? 三、 实验总结与体会
实验分析:。
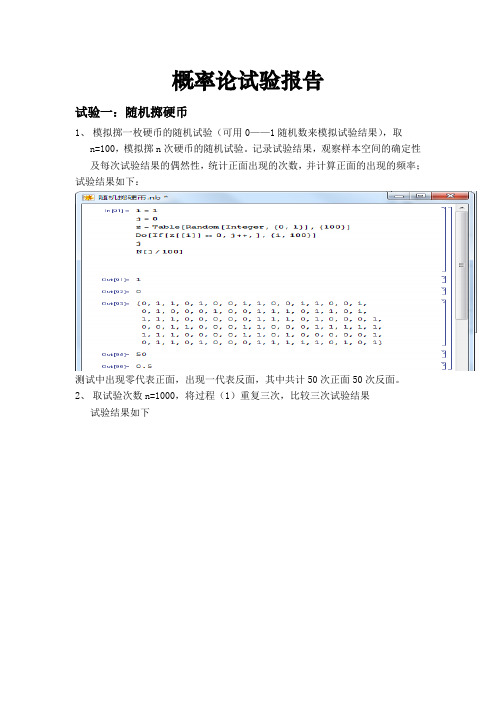
概率论试验报告试验一:随机掷硬币1、模拟掷一枚硬币的随机试验(可用0——1随机数来模拟试验结果),取n=100,模拟掷n次硬币的随机试验。
记录试验结果,观察样本空间的确定性及每次试验结果的偶然性,统计正面出现的次数,并计算正面的出现的频率;试验结果如下:测试中出现零代表正面,出现一代表反面,其中共计50次正面50次反面。
2、取试验次数n=1000,将过程(1)重复三次,比较三次试验结果试验结果如下3、三次结果分别是0.501,0.503,0.521 。
这充分说明模拟情况接近真实情况,频率接近概率0.5。
试验二:高尔顿钉板试验1、自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中,当小球碰到钉子时从左边落下的概率为p , 从右边落下的概率为,1p -碰到下一排钉子又是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20=m 排钉子, 下面进行模拟实验:(1) 取,5.0=p 自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观察5次实验结果的共性及每次实验结果的偶然性;(2) 分别取,85.0,5.0,15.0=p 自板上端放入n 个小球, 取,5000=n 观察n 个小球落下后呈现的曲线我们分析可知,这是一个经典的古典概型试验问题2、具体程序:3、我们分析实验结果可知,若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0p曲线峰值的格子位置向右偏; 当><p曲线峰值的格子位置向左偏。
,5.0试验三:抽签试验1、我们做模拟实验,用1-10的随机整数来模拟实验结果。
在1-10十个随机数中,假设10代表抽到大王,将这十个数进行全排,10出现在哪个位置,就代表该位置上的人摸到大王。
每次随机排列1-10共10个数,10所在的位置随机变化,分别输出模拟实验10次, 100次,1000次的结果, 将实验结果进行统计分析, 给出分析结果。

《概率统计》实验报告实验人员:系(班):矿业工程系机械设计制造及其自动化1404班 学号:20141804408 姓名:李君阳 实验地点:电教楼四层三号机房实验名称:《概率统计》实验时间:2016.5.10,2016.5.17 16:30——18:30.实验目的:1.加强学生的动手能力,让学生掌握对MATLAB 软件的应用。
2.为以后的数学计算节省时间,提高精确度,准确度,合理的利用科学技术。
实验内容:(给出实验程序与运行结果)一、古典概型2、在50个产品中有18个一级品,32个二级品,从中任意抽取30个,求其中恰有20个二级品的概率.解:p=C 3220C 1810c 5030=0.2096>> p=nchoosek(32,20)*nchoosek(18,10)/nchoosek(50,30)p =0.2096二、计算概率1、某人进行射击,设每次射击的命中率为0.02,独立射击200次,试求至少击中两次的概率.2、一铸件的砂眼(缺陷)数服从参数为0.5的泊松分布,求此铸件上至多有1个砂眼的概率和至少有2个砂眼的概率. 解:1.p=1-c 2000∗0.98400-c 2001*0.98199*0.02=0.1458>> p=binopdf(2,200,0.02)p =0.1458 2.P(ζ=0)= 5.00*!05.0-e P(ζ=1)= 5.01*!15.0-e P(ζ1)=0.9098P(ζ)=0.09024、设随机变量()23,2X N ,求()25P X <<;()2P X >解:P(2<X<5)=F(5)-F(2)= )5(1,0σa F -=)235(1,0-F -)232(1,0-F = -=0.08413-(1-0.6915)=0.5328P(|X |>2)=P(X<-2)+P(X>2)=P(X<-2)+1-P(X<2)=0.6977normcdf(5,3,2)-normcdf(2,3,2) ≤2≥吕梁学院《概率统计》实验报告ans =0.5328>> normcdf(-2,3,2)-normcdf(2,3,2)+1ans =0.6977三、作图1、画出N(2,9),N(4,9),N(6,9)的图像进行比较;(图1)画出N(0,1),N(0,4),N(0,9)的图像进行比较.解:y1=normpdf(x,2,3);y2=normpdf(x,4,3);y3=normpdf(x,6,3);plot(x,y1,x,y2,x,y3)>> x=-40:0.01:40;y1=normpdf(x,0,1);y2=normpdf(x,0,2);y3=normpdf(x,0,3);plot(x,y1,x,y2,x,y3)(图2)四、常见统计量的计算1、根据调查,某集团公司的中层管理人员的年薪(单位:万元)数据如下:42 41 39.2 37.6 40.2 40 41 41.4 36.1 43.140.3 39.3 38.4 36.5 38.1 38.5 39.1 40.6 38.3 39.7求其公司中层管理人员年薪的样本均值、样本方差、样本标准差,绘制直方图。

本科实验报告实验名称:《概率与统计》随机模拟实验随机模拟实验实验一设随机变量X 的分布律为-i P{X=i}=2,i=1,2,3......试产生该分部的随机数1000个,并作出频率直方图。
一、实验原理采用直接抽样法:定理:设U 是服从[0,1]上的均匀分布的随机变量,则随机变量-1()Y F U =与X 有相同的分布函数-1()Y F U =(为F(x)的逆函数),即-1()Y F U =的分部函数为()F x .二、题目分析易得题中X 的分布函数为1()1- ,1,0,1,2,3, (2i)F x i x i i =≤≤+=若用ceil 表示对小数向正无穷方向取整,则F(x)的反函数为产生服从[0,1]上的均匀分布的随机变量a ,则m=F -1(a)则为题中需要产生的随 机数。
三、MATLAB 实现f=[]; i=1;while i<=1000a=unifrnd(0,1); %产生随机数a ,服从【0,1】上的均匀分布 m=log(1-a)/log(1/2);b=ceil(m); %对m 向正无穷取整 f=[f,b]; i=i+1; enddisplay(f);[n,xout]=hist(f); bar(xout,n/1000,1)产生的随机数(取1000个中的20个)如下:-1ln(1-)()1ln()2a F a ceil ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦频率分布直方图实验二设随机变量X 的密度函数为24,0,()0,0x xe x f x x -⎧>=⎨≤⎩试产生该分布的随机数1000个,并作出频率直方图 一、实验原理取舍抽样方法,当分布函数的逆函数难以求出时,可采用此方法。
取舍抽样算法的流程为:(1) 选取一个参考分布,其选取原则,一是该分布的随机样本容易产生;二是存在常数C ,使得()()f x Cg x ≤。
(2) 产生参考分布()g x 的随机样本0x ; (3) 独立产生[0,1]上的均匀分布随机数0u ;(4) 若000()()u Cg x f x ≤,则保留x 0,作为所需的随机样本;否则舍弃。
2.(1)BINOMDIST(2,15,0.05,FALSE)=0.13475BINOMDIST(2,15,0.05,TRUE)=0.9638(2)EXPONDIST(1,0.1,FALSE)=0.09048EXPONDIST(4,0.1,TRUE)=0.32968(3)NORMDIST(2,0,1, TRUE)=0.97725NORMSDIST(2)-- NORMSDIST(--2)=0.9545=NORMINV(0.98,0,1)=2.05NORMSDIST(0.1)-- NORMSDIST(--1)=0.3812=NORMINV(0.05,5,100)=--159.49(4)POISSON(4,2,FALSE)=0.090POISSON(4,2,TRUE)=0.9473(5) BINOMDIST(2,15,0.05,FALSE)=0.13475营业税金与社会商品总额关系(1)打开EXCEL,建立数据文件如下图:税收Y 销售X3.93 142.085.96 177.307.85 204.689.82 242.6812.50 316.2415.55 341.9915.79 332.6916.39 389.2918.45 453.40调用线性回归分析程序:单击工具/数据分析/回归/确定,填写对话框,确定后输出结果,分析结果知回归方程为:Y=-2.258+0.0487X(2)对数据调用相关分析程序:依次单击工具/数据分析/相关系数/确定,填写对话框后,单击确定得到下面表格:所以,Y与X的皮尔逊相关系数为: 0.981069(3)建立假设H0:b=0 ,H1:b=/0,统计检验量F=(SSR/k)/(SSE/n-k-1)有数据分析结果知:F=179.6507P(F(1,7)>179.6507)=3.02E-06<<0.05所以认为回归方程是显著有效的。
(4)在(1)中表的B11中补充数据X=320在A11中输入公式=-2.258+0.0487X320运行课的到X=320的点预测值y=13.326。
《概率论与数理统计》MATLAB上机实验实验报告一、实验目的1、熟悉matlab的操作。
了解用matlab解决概率相关问题的方法。
2、增强动手能力,通过完成实验内容增强自己动手能力。
二、实验内容1、列出常见分布的概率密度及分布函数的命令,并操作。
概率密度函数分布函数(累积分布函数) 正态分布normpdf(x,mu,sigma) cd f(‘Normal’,x, mu,sigma);均匀分布(连续)unifpdf(x,a,b) cdf(‘Uniform’,x,a,b);均匀分布(离散)unidpdf(x,n) cdf(‘Discrete Uniform’,x,n);指数分布exppdf(x,a) cdf(‘Exponential’,x,a);几何分布geopdf(x,p) cdf(‘Geometric’,x,p);二项分布binopdf(x,n,p) cdf(‘Binomial’,x,n,p);泊松分布poisspdf(x,n) cdf(‘Poisson’,x,n);2、掷硬币150次,其中正面出现的概率为0.5,这150次中正面出现的次数记为X(1) 试计算X=45的概率和X≤45 的概率;(2) 绘制分布函数图形和概率分布律图形。
答:(1)P(x=45)=pd =3.0945e-07P(x<=45)=cd =5.2943e-07(2)3、用Matlab软件生成服从二项分布的随机数,并验证泊松定理。
用matlab依次生成(n=300,p=0.5),(n=3000,p=0.05),(n=30000,p=0.005)的二项分布随机数,以及参数λ=150的泊松分布,并作出图线如下。
由此可以见得,随着n的增大,二项分布与泊松分布的概率密度函数几乎重合。
因此当n足够大时,可以认为泊松分布与二项分布一致。
4、 设22221),(y x e y x f +−=π是一个二维随机变量的联合概率密度函数,画出这一函数的联合概率密度图像。
概率统计实验报告结论引言概率统计是数学中非常重要的一个分支,它利用统计方法对一定的随机现象进行描述、分析和预测。
本次实验中我们通过模拟实验的方式,利用概率统计的方法对一些实际问题进行了研究和分析。
实验一:骰子实验我们进行了一系列的骰子实验,通过投掷骰子并记录点数的方式来研究骰子的概率分布。
实验结果表明,投掷骰子时,每个面出现的概率是均等的,即每个面的概率是1/6。
这符合理论预期,也验证了概率统计中的等概率原理。
实验二:扑克牌实验通过抽取一副扑克牌中的若干张牌,并记录其点数和花色,我们研究了扑克牌中各个点数和花色的概率分布情况。
实验结果表明,52张扑克牌中各个点数和花色的概率分布近似均等,并且点数和花色之间是相互独立的。
这进一步验证了概率统计中的等概率原理和独立事件的性质。
实验三:掷硬币实验通过进行大量的抛硬币实验,我们研究了硬币正反面出现的概率分布情况。
实验结果表明,掷硬币时正面和反面出现的概率非常接近,都是1/2。
这也符合理论预期,并且进一步验证了概率统计中的等概率原理。
实验四:随机数生成器实验通过计算机程序生成随机数,并对其进行统计分析,我们研究了随机数生成器的质量问题。
实验结果表明,一个好的随机数生成器应该具备均匀分布、独立性和不可预测性等特征。
我们的实验结果显示,所使用的随机数生成器满足这些条件,从而可以被广泛应用于概率统计领域。
实验五:二项分布实验通过进行大量的二项分布实验,我们研究了二项分布的特性。
实验结果表明,二项分布在一定条件下可以近似成正态分布,这是概率统计中的重要定理之一。
实验结果还显示,二项分布的均值和方差与试验的次数和成功的概率有关,进一步验证了概率统计中与二项分布相关的理论。
总结通过本次概率统计实验,我们对骰子、扑克牌、硬币、随机数和二项分布等与概率统计相关的问题进行了研究和分析。
实验结果与理论预期基本一致,验证了概率统计中的一些重要原理和定理。
这些实验结果对我们的概率统计学习和应用有着重要的意义,同时也为我们在探索更深层次的概率统计问题提供了一定的启示和思路。
一、实验目的1. 理解概率统计的基本概念和原理;2. 掌握运用概率统计方法解决实际问题的能力;3. 提高数据分析和处理能力。
二、实验内容1. 随机数生成实验2. 抽样实验3. 假设检验实验4. 估计与预测实验三、实验方法1. 随机数生成实验:使用计算机生成随机数,并分析其分布情况;2. 抽样实验:通过随机抽样,分析样本数据与总体数据的关系;3. 假设检验实验:根据样本数据,对总体参数进行假设检验;4. 估计与预测实验:根据历史数据,建立预测模型,对未来的数据进行预测。
四、实验步骤1. 随机数生成实验(1)设置随机数生成器的参数,如范围、种子等;(2)生成一定数量的随机数;(3)分析随机数的分布情况,如频率分布、直方图等。
2. 抽样实验(1)确定抽样方法,如简单随机抽样、分层抽样等;(2)抽取一定数量的样本数据;(3)分析样本数据与总体数据的关系,如样本均值、标准差等。
3. 假设检验实验(1)根据实际需求,设定原假设和备择假设;(2)计算检验统计量,如t统计量、卡方统计量等;(3)根据临界值表,判断是否拒绝原假设。
4. 估计与预测实验(1)收集历史数据,进行数据预处理;(2)选择合适的预测模型,如线性回归、时间序列分析等;(3)利用历史数据训练模型,并对未来数据进行预测。
五、实验结果与分析1. 随机数生成实验(1)随机数分布呈现均匀分布,符合概率统计的基本原理;(2)随机数的频率分布与理论分布相符。
2. 抽样实验(1)样本均值与总体均值接近,说明抽样效果较好;(2)样本标准差略大于总体标准差,可能受到抽样误差的影响。
3. 假设检验实验(1)根据检验统计量,拒绝原假设,说明总体参数存在显著差异;(2)根据临界值表,确定显著性水平,进一步分析差异的显著性。
4. 估计与预测实验(1)预测模型具有较高的准确率,说明模型能够较好地拟合历史数据;(2)对未来数据进行预测,结果符合实际情况。
六、实验结论1. 概率统计方法在解决实际问题中具有重要作用,能够提高数据分析和处理能力;2. 随机数生成实验、抽样实验、假设检验实验和估计与预测实验均取得了较好的效果;3. 通过本次实验,加深了对概率统计基本概念和原理的理解,提高了运用概率统计方法解决实际问题的能力。
xxxxxx大学实验报告实验题目:熟悉SPSS基本操作环境;掌握SPSS下数据预处理的多种方法。
学生姓名:xxx学院:经济管理专业:工商管理班级:xxxxxxxx学号:xxxxx实验日期:xxxx一、实验目的:熟悉SPSS主要的三类窗口,三种运行方式,掌握数据文件中变量的结构及定义,数据的录入、编辑与保存,读取其他格式的数据文件等;掌握数据文件的合并、数据选取、分组、分类汇总与数据拆分等复杂操作。
二、实验要求:1,横向合并2,纵向合并3 计数4 分类汇总5 拆分6 数据分组三、实验内容:1,横向合并实验步骤:打开数据加工(职工数据).sav→按[data]→[mergefile]→[add variables]→按[Browse]找到数据加工(横向合并职工数据).sav→在[an external SPSS statistics data file]的框中录入数据加工(横向合并职工数据).sav→continue→选match cases on key variables yn sorted files→再选bonus(+)\zgh(+)到[key variable]→OK2 纵向合并实验步骤:打开数据加工(职工数据).sav→[data]→[merge file]→[add cases]→按[Browse]找到数据加工(纵向合并职工数据).sav→在[an external SPSS statistics data file]的框中录入数据加工(横向合并职工数据).sav→continue→将[unpairied variable]中带(+)的变量任意选到[variables yn new active dataset]→ok实验结果:zgh xb zc1 income001 1002 1003 1004 1005 1006 2007 2008 2009 2010 1011 1012 1013 1014 1015 1016 1017 2 1.00 570.00018 1 1.00 400.34019 2 2.00 690.00020 1 2.00 1,003.00015 1 3.00 520.003 计数打开居民储蓄调查数据.sav→[transform]→[count values within cases]→[target variable]中输入一个变量名→把左侧的收入情况和未来收入情况转到[numeric variables]→[definevalues]→[values]中输入1→按[add]→[continue] →ok实验结果:a1 a2 a3 a7_2 a7_3 a91 2 1 3 4 22 0 23 10 12 0 2 8 11 21 1 1 7 10 21 02 4 7 21 02 10 11 21 02 4 11 22 1 2 10 11 21 02 7 8 12 0 2 5 8 24 分类汇总打开居民储蓄调查数据.sav→[data]→[aggregate]→将分类变量户口放入[bresk variable]→将汇总变量(可以随便选取)放入[aggregate variable]→[function]→均值mean→continue→number of cases→ok实验结果:a1 a2 a3 a7_2 a7_3 a9 a11 a13 a9_mean N_BREAK1 1 1 3 42 2 1 1.75 42 2 23 10 1 1 1 1.75 42 2 2 8 11 2 1 1 1.75 41 2 1 7 10 2 2 1 1.75 41 2 2 4 7 2 1 2 1.83 61 2 2 10 11 2 1 2 1.83 61 2 2 4 11 2 1 2 1.83 62 1 2 10 11 2 1 2 1.83 61 32 7 8 1 2 2 1.83 62 2 2 5 8 2 1 2 1.83 65 拆分打开居民储蓄调查数据.sav→data→split file→compare groups→将左侧户口变量转到groups based on→sort the fileby grouping variables→ok实验结果:a1 a2 a3 a7_2 a7_31 1 1 3 41 2 1 7 102 2 23 102 2 2 8 111 2 2 4 71 2 2 10 111 2 2 4 112 1 2 10 111 32 7 82 2 2 5 86 数据分组打开居民储蓄调查数据.sav→transform→recode into different variables→选存取款金额到numeric variable-output variable→在name中输入分组结果的变量名→change→old and new values→range,lowest through value输入1000→new value的value中输入0→按add →range中输入1001→through中输入10000→new value的value中输入1→按add→range,value through highest中输入10001→new value 的value中输入2→按add→continue→oka2 a3 a4 a5 a7_3 a8 a9 a10 a11 a1 2 3 10,000 10 3 2 2 3 1.002 2 2 1,000 11 23 3 3 0.002 3 3 1,000 8 3 2 2 2 0.002 23 700 1 1 1 1 1 0.002 2 2 2,000 9 2 2 1 1 1.003 3 2 200 10 3 2 1 2 0.002 13 15,000 9 3 3 2 1 2.003 3 1 500 9 2 2 2 3 0.002 3 3 700 11 3 3 3 3 0.001 3 1 500 10 3 3 3 1 0.00 质疑或讨论:xxxxxxx大学实验报告实验题目:统计图绘制与基本的统计分析学生姓名:xxxx学院:经济管理专业:工商管理班级:xxxxx学号:xxxxx实验日期:一、实验目的:1,了解刻画集中趋势、离散程度和分布形态的描述统计量的概念2,掌握计算基本描述统计量的基本操作,能正确运用频数分析(交叉分组下的频数分析)及比率分析进行简单的数据分析。
3、熟悉graph菜单下的项目,掌握常见统计图的绘制方法;二、实验要求:1、在数据集anxiety.sav中分不同的subject对变量score值(之和)绘制条图。
2、在数据“cars.sav”中,绘制变量horse和weight的散点图,用orgion的大小来做marks在数据集anxiety.sav中分不同的subject对变量score值(之和)绘制条图,并且按变量trial的不同取值堆积(分段)。
三、实验内容:1、在数据集anxiety.sav中分不同的subject对变量score值(之和)绘制条图1),实验步骤:把Anxiety.sav的数据导入软件中→Graph→legacy dialogs→bar→simple→define→other statistic→把左侧score放入variable→changestatistic→把左侧的subject放入category axis→ok实验结果:2)实验步骤:把Anxiety.sav的数据导入软件中→Graph→legacy dialogs→bar→stacked→define→把左侧score放入variable→change statistic→把左侧的subject放入category axis→把左侧的trail放入define stacksby→ok实验结果:orgion 的大小来做marks实验步骤;把cars.sav的数据导入软件中→Graph→legacy dialogs→scatter\dot→simple scatter→define→把左侧的horse放入Y Axis中→把左侧的weight 放入X Axis中→把左侧的origin放入set markers by 中→ok实验结果:质疑或讨论:xxxxx大学实验报告实验题目:参数检验学生姓名:xxxxx学院:经济管理专业:工商管理班级:xxxxxx学号:xxxx实验日期:一、实验目的:熟悉假设检验的方法和步骤。
2、掌握单样本T检验(one samples T test),两独立样本T检验(independent samples T test),两配对样本(paired samples T test)。
二、实验要求:1、利用住房状况问卷调查数据,推断家庭人均住房面积的平均值是否为20平方米。
2、利用住房状况问卷调查数据,推断本市户口总体和外地户口总体的家庭人均住房面积的平均值是否有显著差异。
三、实验内容:1,实验步骤:实验步骤:选择菜单:Analyze→Compare Means→One-Samples TTest选择待检验的变量到Test Variables,在Test Value 框中输入检验值。
按Option按钮定义其他选项,默认95%的置信区间。
至此,SPSS将自动计算t统计量和对应的概率P值。
2,实验步骤:选择菜单Analyze→Compare Means→Independent-Samples T Test选择检验变量到Test Variable(s)框选择总体标识变量到Grouping Variables框中。
按Define Groups(即为汉语的定义组)按钮定义两总体的标识值两独立样本t检验的Option选项含义与单样本t检验的相同至此,SPSS会首先自动计算F统计量,并计算在两总体相等和不相等下的方差和t 统计量的观测值以及各自对应的双尾概率P值。
实验结果:质疑或讨论:xxxxxx大学实验报告实验题目:方差分析学生姓名:xxxx学院:经济管理专业:工商管理班级:xxxxx学号:xxx实验日期:一、实验目的:1、理解方差分析的前提、原理与意义;2、掌握单因素方差分析与多因素方差分析的方法和步骤,包括方差齐性检验、残差分析等方法;二、实验要求:某企业在制定某商品的广告策略时,收集了该商品在不同地区采用不同广告形式促销后的销售额数据,希望对广告形式和地区是否对商品销售额产生影响进行分析。
三、实验内容:实验步骤:1、选择菜单“Analyze→Compare means→One-Way ANONA2、选择观测变量到Dependent List框3、选择控制变量到Factor框。