中北大学概率论实验报告四

概率论与数理统计应用实验报告
概率论与数理统计是中国大学MOOC《数据科学导论》课程中的一门关键科目，为了加深熟悉概率论与数理统计的过程，我完成了在R语言环境下的相关实验并撰写了这份报告。

实验过程以R Studio为平台。

R studio是一款跨平台，开源的编程环境，可以天然
地支持R语言，为我们提供卓越的实验环境。

所有的实验操作都是在R Studio上进行的。

实验分两步，第一步是正态分布的实验，第二步是对多项式分布的实验。

正态分布的实验
首先，我们构造了1000000以内随机整数，范围为-500000到500000。

将这些整数绘
制灰度图，来查看各项数据的分布情况，数据在中心出现了最多，并且随着两端逐渐减少，绘出的图像符合正态分布的分布曲线，即右尾巴更长。

此外，我们还对构造出的数据进行
正态性分析，使用R语言中的hist函数来绘制正态分布的柱状图，根据结果可以清楚地
看出，数据的分布也是符合正态分布的，由此也证明了构造数据的正确性。

多项式分布的实验
我们首先运用随机数生成器在R语言环境下，构造出多项式分布的数据，将生成的数
据进行灰度图展示，发现随着两端的和逐渐增加，形成非对称的多项式分布的曲线。

同时，我们运用R语言中的hist函数来检验再次检验多项式分布，结果也确实符合多项式分布，从而证明以上步骤是正确的。

经过上述实验，我加深了对概率论与数理统计的熟悉。

构建统计数据，运用R Studio 画出统计图来检验和证明数据是否符合正态分布和多项式分布使我对概率论和数理知识有
了更为深刻的认识，也为今后解决数据科学相关的科学问题奠定基础。

实验四方差分析和回归分析四、实验结果1、用5种不同的施肥方案分别得到某种农作物的收获量（kg）如右：α0.05下，检验施肥方案对农作物的收获量是否有显著影响．在显著性水平=>> X=[67 67 55 42 98 96 91 66 60 69 50 35 79 64 81 70 90 70 79 88];group=[ones(1,4),2*ones(1,4),3*ones(1,4),4*ones(1,4),5*ones(1,4)];[p,table,stats] = anova1(X,group,'on')p =0.0039table ='Source' 'SS' 'df' 'MS' 'F' 'Prob>F''Groups' [3.5363e+03] [ 4] [884.0750] [6.1330] [0.0039]'Error' [2.1622e+03] [15] [144.1500] [] []'Total' [5.6985e+03] [19] [] [] [] stats =gnames: {5x1 cell}n: [4 4 4 4 4]source: 'anova1'means: [57.7500 87.7500 53.5000 73.5000 81.7500] df: 15s: 12.0062因为p=0.0039<0.05，所以施肥方案对农作物的收获量有显著影响。

且由箱型图可知：第2种施肥方案对对农作物的收获量的影响最好，即产量最高。

2、某粮食加工产试验三种储藏方法对粮食含水率有无显著影响，现取一批粮食分成若干份，分别用三种不同的方法储藏，过段时间后测得的含水率如右表：在显著性水平=α0.05下，i x 检验储藏方法对含水率有无显著的影响．>> X=[7.3 8.3 7.6 8.4 8.3 5.4 7.4 7.1 6.8 5.3 7.9 9.5 10 9.8 8.4];group=[ones(1,5),2*ones(1,5),3*ones(1,5)];[p,table,stats] = anova1(X,group,'on')p =8.2495e-004table ='Source' 'SS' 'df' 'MS' 'F' 'Prob>F''Groups' [18.6573] [ 2] [9.3287] [13.5920] [8.2495e-004] 'Error' [ 8.2360] [12] [0.6863] [] []'Total' [26.8933] [14] [] [] []stats =gnames: {3x1 cell}n: [5 5 5]source: 'anova1'means: [7.9800 6.4000 9.1200]df: 12s: 0.8285因为p=8.2495e-004<0.05，所以储藏方法对含水率有显著的影响。

概率论实践与分析研究报告概率论实践与分析研究报告一、研究背景概率论是数学的一个分支，研究随机现象的规律，以及通过具体数据和实验得出结论的方法和工具。

在实际应用中，概率论被广泛应用于风险评估、统计分析、金融模型等领域。

二、研究目的本研究旨在通过实践与分析，探讨概率论在实际问题中的应用，验证其有效性和可行性，并对结果进行分析和解释。

三、研究方法1. 数据收集：收集相关领域的实际数据，并进行整理和清理。

2. 概率分析：根据数据进行概率分析，包括计算概率、期望值、方差等统计指标。

3. 模型建立：基于概率分析结果，建立相应的概率模型，如随机变量模型、概率分布模型等。

4. 实证分析：根据模型进行实证分析，对实际问题进行预测、评估和解释。

四、研究内容与结果根据实际问题的特点和数据可用性，选择了以下几个典型案例进行研究：1. 金融市场风险评估：通过概率分析，计算了不同金融产品的收益率分布和风险指标（如价值-at-风险），并建立了相应的风险模型。

实证分析结果表明，风险模型能够较好地描述金融市场的波动性，并对投资决策提供了参考依据。

2. 生产质量控制：收集了一家制造企业的产品质量数据，进行了概率分析和模型建立。

通过模型预测，企业能够根据不同的质量目标和控制措施，评估不良品率和良品率的概率，并制定相应的质量控制策略。

3. 疾病患病风险评估：通过大样本调查和统计分析，计算了某种疾病的患病率，并建立了相关的概率模型。

根据模型结果，能够对患病风险进行评估，并根据个体的特征进行个性化的风险提示和干预。

五、研究结论通过实践与分析，本研究验证了概率论在实际问题中的应用价值。

概率分析和模型建立能够提供科学的评估和预测方法，为决策提供了理论和实证支持。

此外，研究还发现，在实际应用中，概率论需要结合统计学、数据科学等相关领域的方法和技术，才能更好地应对复杂的实际问题。

六、研究展望虽然本研究初步探索了概率论在实践与分析中的应用，但仍存在一些问题和挑战，如数据的可靠性和可用性、模型的精确性和适用性等。

大学概率统计实验报告引言在概率统计学中，实验是一种重要的数据收集方法。

通过实验，我们可以收集到一系列随机变量的观测值，然后利用统计方法对这些观测值进行分析和推断。

本实验旨在通过一个简单的骰子实验来介绍概率统计的基本理论和方法。

实验目标本实验的目标是通过投掷骰子的实验，验证骰子的随机性，并研究骰子的概率分布。

实验步骤1.准备一个六面骰子和一张记录表格。

2.将骰子投掷20次，并记录每次投掷的结果。

将结果按照出现的次数填入表格中。

3.统计记录表格中每个数字出现的频数，并计算频率。

4.绘制柱状图展示各个数字的频率分布情况。

实验结果与分析根据实验记录表格，我们统计得到了每个数字出现的频数如下：数字 1 2 3 4 5 6频数 4 3 6 2 4 1根据频数，我们可以计算出每个数字的频率。

频率是指某个数字出现的次数与总次数的比值。

通过计算，我们得到了每个数字的频率如下：数字 1 2 3 4 5 6频率0.2 0.15 0.3 0.1 0.2 0.05通过绘制柱状图，我们可以更直观地观察到各个数字的频率分布情况。

柱状图如下所示：0.3 | █| █| █| █0.25 | █| █| █| █0.2 | █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.15 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.1 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.05 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █----------------1 2 3 4 5 6根据实验结果，我们可以观察到以下现象和结论： - 各个数字的频率接近于理论概率，表明骰子的结果具有一定的随机性。

- 数字3的频率最高，约为0.3，而数字6的频率最低，约为0.05。

这说明骰子的结果并不完全均匀，存在一定的偏差。

结论与讨论通过本次实验，我们了解了概率统计的基本理论和方法，并通过投掷骰子的实验验证了骰子的随机性。

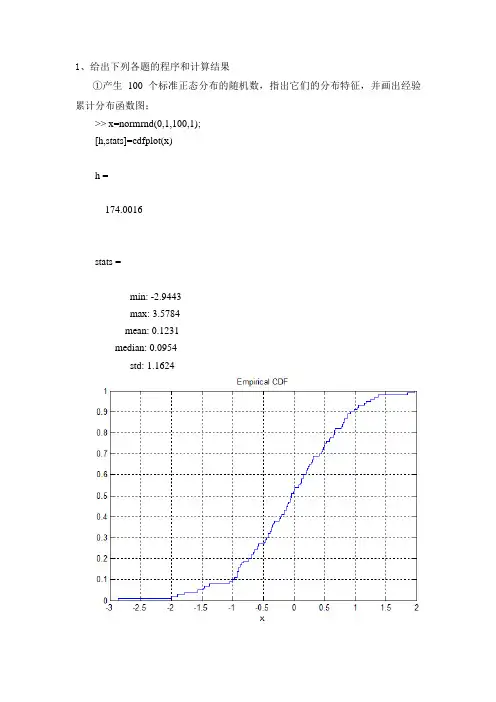
1、给出下列各题的程序和计算结果①产生100 个标准正态分布的随机数，指出它们的分布特征，并画出经验累计分布函数图；>> x=normrnd(0,1,100,1);[h,stats]=cdfplot(x)h =174.0016stats =min: -2.9443max: 3.5784mean: 0.1231median: 0.0954std: 1.1624②产生100 个均值为1，标准差为1的正态分布的随机数，画出它们的直方图并附加正态密度曲线，观察它们之间的拟合程度；x=normrnd(1,1,100,1);h=histfit(x);set(h(1),'FaceColor','c','EdgeColor','b')set(h(2),'color','g')③产生100 个均匀分布的随机数，对这100 个数据的列向量，用加号“*”标注其数据位置，作最小二乘拟合直线；x=1:1:100;y=unifrnd(0,1,1,100);n=1;a=polyfit(x,y,n);y1=polyval(a,x);plot(x,y,'g*',x,y1,'r-')④产生100个参数为5的指数分布的随机数，再产生100个参数为1的指数分布的随机数，用箱形图比较它们均值不确定性的稳健性。

x1=exprnd(5,100,1);x2=exprnd(1,100,1);x=[x1 x2];boxplot(x,1,'m+',0,0)课后题：P261、1题：以下是某工厂通过抽样调查得到的10名工人一周内生产的产品数：149 156 160 138 149 153 153 169 156 156试由这批数据构造经验分布函数并作图。

>> x=[149;156;160;138;149;153;153;169;156;156];[h,stats]=cdfplot(x)h =174.0023stats =min: 138max: 169mean: 153.9000median: 154.5000std: 8.0340P261、3题：假若某地区30名2000年某专业毕业生实习期满后的月薪数据如下：909 1086 1120 999 1320 10911071 1081 1130 1336 967 1572825 914 992 1232 950 7751203 1025 1096 808 1224 1044871 1164 971 950 866 738（1）构造该批数居的频率分布表；（2）画出直方图。

概率论与数理统计实验报告实验名称： 区间估计姓名 学号 班级 实验日期一、实验名称：区间估计二、实验目的：1. 会用MATLAB 对一个正态总体的参数进行区间估计；2. 会对两个正态总体的均值差和方差比进行区间估计。

三、实验要求：1. 用MATLAB 查正态分布表、χ2分布表、t 分布表和F 分布表。

2. 利用MATLAB 进行区间估计。

四、实验内容：1. 计算α=0.1, 0.05, 0.025时，标准正态分布的上侧α分位数。

2. 计算α=0.1, 0.05, 0.025，n =5, 10, 15时，χ2(n )的上侧α分位数（注：α与n相应配对，即只需计算2220.10.050.025(5),(10),(15)χχχ的值，下同）。

3. 计算α=0.1, 0.05, 0.025，n =5, 10, 15时， t (n )的上侧α分位数。

4. 计算α=0.1, 0.05, 0.025时， F (8,15)的上侧α分位数； 验证：0.050.95(8,15)1(15,8)F F =；计算概率{}312P X ≤≤。

5. 验证例题6.28、例题6.29、例题6.30、习题6.27、习题6.30。

五、实验任务及结果：任务一：计算α=0.1, 0.05, 0.025时，标准正态分布的上侧α分位数。

源程序：%1-1x = norminv([0.05 0.95],0,1)%1-2y = norminv([0.025 0.975],0,1)%1-3z = norminv([0.0125 0.9875],0,1)结果：x =-1.6449 1.6449y =-1.9600 1.9600z =-2.2414 2.2414结论：α=0.1时的置信区间为[-1.6449，1.6449]，上侧α分位数为1.6449.α=0.05时的置信区间为[-1.9600，1.9600]，上侧α分位数为1.9600.α=0.025时的置信区间为[-2.2414，2.2414]，上侧α分位数为2.2414.任务二：计算α=0.1, 0.05, 0.025，n=5, 10, 15时，χ2(n)的上侧α分位数（注：α与n 相应配对，即只需计算2220.10.050.025(5),(10),(15)χχχ的值，下同）。

课程实习报告课程名称：概率论与数理统计实习题目：概率论与数理统计姓名：系：专业：年级：学号：指导教师：职称：年月日课程实习报告结果评定目录1.实习的目的和任务............................................. - 1 -2.实习要求..................................................... - 1 -3.实习地点..................................................... - 1 -4.主要仪器设备................................................. - 1 -5.实习内容..................................................... - 1 -5.1 MATLAB基础与统计工具箱初步............................. - 1 -5.2 概率分布及应用实例..................................... - 5 -5.3 统计描述及应用实例..................................... - 7 -5.4 区间估计及应用实例..................................... - 9 -5.5 假设检验及应用实例.................................... - 11 -5.6 方差分析及应用实例.................................... - 15 -5.7 回归分析及应用实例.................................... - 17 -5.8 数理统计综合应用实例.................................. - 22 -6.结束语...................................................... - 29 - 参考文献 ...................................................... - 29 -概率论与数理统计1.实习的目的和任务目的：通过课程实习达到让我们能够应用软件解决实际问题。

概率论上机实验报告《概率论上机实验报告》在概率论的学习中，实验是非常重要的一部分。

通过实验，我们可以验证概率论的理论，加深对概率的理解，同时也可以提高我们的实验能力和数据处理能力。

本次实验报告将详细介绍一次概率论的上机实验，包括实验目的、实验方法、实验结果和实验分析。

实验目的：本次实验的目的是通过随机抽样的方法，验证概率论中的一些基本概念和定理，包括概率的计算、事件的独立性、事件的互斥性等。

通过实际操作，加深对这些概念的理解，同时也提高我们的实验技能和数据处理能力。

实验方法：本次实验采用计算机模拟的方法进行。

首先，我们选择了几个经典的概率问题作为实验对象，包括掷骰子、抽球问题等。

然后，通过编写程序，模拟进行大量的随机实验，得到实验数据。

最后，通过对实验数据的统计分析，验证概率论中的一些基本概念和定理。

实验结果：通过实验，我们得到了大量的实验数据。

通过对这些数据的统计分析，我们验证了概率的计算方法，验证了事件的独立性和互斥性等基本概念和定理。

实验结果表明，概率论中的一些基本概念和定理在实际中是成立的，这也进一步加深了我们对概率论的理解。

实验分析：通过本次实验，我们不仅验证了概率论中的一些基本概念和定理，同时也提高了我们的实验能力和数据处理能力。

通过实验，我们深刻理解了概率论的一些基本概念和定理，并且也掌握了一些实验技能和数据处理技能。

这对我们今后的学习和工作都将有很大的帮助。

总结：通过本次实验，我们深刻理解了概率论的一些基本概念和定理，同时也提高了我们的实验能力和数据处理能力。

这对我们今后的学习和工作都将有很大的帮助。

希望通过这次实验，我们能更加深入地理解概率论，并且提高我们的实验技能和数据处理技能。

概率论实验报告班级：电气211姓名：***学号：**********第一次实验实验一1、实验目的熟练掌握MATLAB软件关于概率分布作图的基本操作会进行常用的概率密度函数和分布函数的作图绘画出分布律图形2、实验要求掌握MATLAB的画图命令plot掌握常见分布的概率密度图像和分布函数图像的画法3、实验内容1、设X~b(20,0,25)(1)生成X的概率密度；(2)产生18个随机数（3行6列）(3)又已知分布函数F(x)=0.45，求x(4)画出X的分布律和分布函数图形4、实验方案了解到MATLAB在二项分布中有计算概率密度函数binopdf，产生随机数的函数binornd，计算确定分布函数值对应的自变量x的函数binoinv，可以直接生成X的概率密度和产生18个随机数（3行6列），求已知分布函数F(x)=0.45对应的x的值。

最后用binopdf函数、binocdf函数和plot函数画出X的分布律和分布函数图形5、实验过程(1)生成X的概率密度binopdf(0:20,20,0.25)ans =Columns 1 through 120.0032 0.0211 0.0669 0.1339 0.1897 0.2023 0.16860.1124 0.0609 0.0271 0.0099 0.0030Columns 13 through 210.0008 0.0002 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000(2)产生18个随机数（3行6列）binornd(20,0.25,3,6)ans =6 4 1 2 6 44 3 6 2 6 24 5 6 6 5 6(3)已知分布函数F(x)的值，求xbinoinv(0.45,20,0.25)ans =5(4) 画出X的分布律和分布函数图形x=0:20;y=binopdf(x,20,0.25);subplot(1,2,1);plot(x,y,'*');x=0:0.01:20;y=binocdf(x,20,0.25);subplot(1,2,2);plot(x,y)6、 小结1.上机时对于matlab 的命令应该灵活使用，明白命令中每个参数的意义及输出内容的意义，对于matlab 命令的理解也应该联系概率论的理论基础2.学习matlab 的命令注意学会总结各个命令的用处与差异，不至于对相似的命令混淆。