湖南省株洲市2018届高三数学第三次11月月考试题 精
- 格式:doc
- 大小:273.51 KB
- 文档页数:7

株洲市十七中2018届高三第三次月考数学试卷(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,考试时间120分钟,共150分第I 卷(选择题)一:选择题(本大题共10小题,每小题5分,共50分,在每小题的四个选项中,只有一项符合题目要求)1. 设实数集R 为全集,集合P ={x |f (x )=0},Q ={x |g (x )=0},H ={x |h (x )=0},则方程0)()()(22=+x h x g x f 的解集是( ) A Q P ∁R HB Q P ∁R HC H Q P DQ P2. 在等差数列{a n }中,若a 4+a 6+a 8+a 10+a 12=120,则2 a 10-a 12的值为 ( )A 20B 22C 24D 283. 如果)()(x f x f -=+π且)()(x f x f =-,则)(x f 可以是( )A x 2s i nB x c o sC x s i nD x s i n 4 已知f (x )=⎩⎨⎧<+≥-)6( )2()6(5x x f x x (x ∈N ),则f (3)的值为( )A 5B 4C 3D 25.已知函数)(x f 为奇函数,且当0>x 时,x x x f 2)(2-=,则当0<x 时)(x f 的递增区间为 ( )A (-∞,-1)B (-1,0)C (-∞,0)D )21,(--∞6 为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象( )A 向右平移6π个单位 B 向右平移3π个单位 C 向左平移6π个单位 D 向左平移3π个单位7 等差数列{}n a 中,n S 是前n 项和,且k S S S S ==783,,则k 的值为 ( )A. 4 B 11 C 2 D 128.设)(x f '是函数)(x f 的导函数,)(x f y '=的图象如右图所示,则)(x f y =的图象最有可能的是( )9 函数y =x +cos x 的大致图象是 ( )AB C D10 已知线段PQ=1,A a 是线段PQ 的中点,2A 是1QA 的中点,3A 是21A A 的中点,4A 是23A A 的中点,……,n A 是12--n n A A 的中点,则n PA 长为 ( )A ⎥⎦⎤⎢⎣⎡-+⋅+12)1(1n n a B ⎥⎦⎤⎢⎣⎡-+⋅+12)1(132n n a C ⎥⎦⎤⎢⎣⎡-+⋅n n a 2)1(1 D⎥⎦⎤⎢⎣⎡-+⋅n n a 2)1(132'(x)姓名__________ 班级______ 计分_______一 选择题 (每小题5分,共50分)把正确答案序号填入下表中第II 卷(非选择题)二:填空题:(本大题共5小题,每小题4分,共20分,请将答案写在题后的横线上)11.i 为虚数单位,则2)1(2i i-+=_________________12 求值()20cos 120sin 5cot 5tan +⋅-=13. 设数列}{n a 的前n 项和为n S ,令nS S S T nn +⋅⋅⋅++=21,称n T 为数列n a a a ,,,21⋅⋅⋅的“理想数” 已知数列50021,,,a a a ⋅⋅⋅的“理想数”为2018,那么,数列50021,,,,5a a a ⋅⋅⋅的“理想数”为_____________________ ;14 设)(1x f -是函数)1(log )(2+=x x f 的反函数,若8)](1)][(1[11=++--b f a f ,则f (a +b )的值为 . 15设⎥⎦⎤⎢⎣⎡-∈4,4,ππy x ,R a ∈且0cos sin 4,02sin 33=++=-+a y y y a x x ,则=+)2c o s (y x ____________三:解答题(本大题有6小题,共80分 解答应写出文字说明,证明过程或演算步骤)16 (本小题满分12分)已知πθπθ22,222tan <<-=求:⑴θtan 的值; ⑵求⎪⎭⎫⎝⎛+--4sin 21sin 2cos 22πθθθ的值17.(本小题满分12分)已知函数]31[,1tan 2)(2,-∈-+=x x x x f θ,其中),(22ππθ-∈(1)当6πθ-=时,求函数)(x f 的最大值与最小值;(2)求θ的取值范围,使)(x f y =在区间]31[,-上是单调函数18.(本小题满分14分) 甲 乙两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时甲赢得乙一张卡片,否则乙赢得甲一张卡片,现定掷硬币次数达9次时,或在此之前某人已赢得所有卡片时游戏中止,设ξ表示游戏中止时掷硬币的次数(1)求ξ的取值范围;(2)求ξ的数学期望E ξ19 (本小题满分14分)已知等比数列{}n a ,22a =,5128a =;(1)求通项n a(2)若2log n n b a =,数列{}n b 的前n 项的和为n S ,且360n S =,求n 的值20.(本小题满分14分)设平面上的动向量),,1(),,(2k t b t s a --==其中t s ,是不同时为0的两个实数,0≥k ,且⊥ (1)求函数关系式)(t f s =;(2)若函数)(t f s =在),1(+∞上是单调增函数,求实数k 的取值范围;(3)对上述)(t f ,当0=k 时,存在正项数列}{n a 满足)()()(21n a f a f a f +++ 2n S =其中)(*21N n a a a S n n ∈+++= , 试求}{n a 的通项公式n a ,并证明32122221<+++na n a a21.(本小题满分14分)已知R m ∈,设命题P :1x 和2x 是方程220x ax --=的两个实根,不等式||3521x x m -≥+对任意实数a ]1,1[-∈恒成立;:Q 函数++=23)(mx x x f+m (6)34+x 在区间(-∞,+∞)上有极值 求使P 正确且Q 也正确的m 的取值范围参考答案一 选择题 (每小题5分,共50分)把正确答案序号填入下表中二:填空题:(本大题共5小题,每小题4分,共20分,请将答案写在题后的横线上)11 i +-2112 2- 13 2018 14 2 15 1三:解答题(本大题有6小题,共80分 解答应写出文字说明,证明过程或演算步骤 )16.解:⑴由222tan -=θ,解得22tan -=θ或θtan =2 ∵πθππθπ<<∴<<2,22 ∴22tan -=θ ⑵原式=θθθθθθπθθθtan 1tan 1cos sin sin cos 4sin 21sin cos 1+-=+-=⎪⎭⎫ ⎝⎛+--+ ∴原式=223221221+=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛--17.解:(1)当6πθ-=时,34)33(1332)(22--=--=x x x x f ∵[]3,1-∈x ∴当33=x 时 34)(min -=x f当1-=x 时 332)(max =x f(2)∵θθ22tan 1)tan ()(--+=x x f 的图象关于θtan =x 对称 ∴由)(x f 在区间[]3,1-上单调知:1tan -≤-θ或3tan ≥-θ又∵⎪⎭⎫⎝⎛-∈2,2ππθ ∴ ⎪⎭⎫⎢⎣⎡⋃⎥⎦⎤ ⎝⎛-∈2,43,2ππππθ18.解:(1)设正面出现的次数为m ,反面出现的次数为n则||519m n m n -=⎧⎪+=ξ⎨⎪≤ξ≤⎩可得 当m =5,n =0或m =0,n =5时,ξ=5; 当m =6,n =1或m =1,n =6时,ξ=7; 当m =7,n =2或m =2,n =7时,ξ=9; 所以ξ的所有可能值为:5,7,9;(2)P (ξ=5)=51212()23216⨯== , P (ξ=7)=175152()264C =P (ξ=9)=1-1555166464-= , 所以E ξ=155527557916646432⨯+⨯+⨯= 19解:212a a q == ,451128a a q ==31164,4,2q q a ∴=∴==,112311422n n n n a a q ---∴==⋅=2322log log 223n n n b a n -===- 1[2(1)3](23)2n n b b nn +-=+---= {}n b ∴是以11b =-为首项,2为公差的等差数列,(123)3602n n nS -+-∴==223600n n ∴--=,20n ∴=或18n =-(舍去) 20n ∴=20.解:(1)由kt t t f s k t t s b a -==⇒=-+-=⋅32)(0)()0,(≥∈k R t (2)恒成立(对),103)(2+∞∈≥-='t k t t f故0,332≥≤≤k k t k 又得;所以]3,0[∈t(3)由332312n n a a a S +++= ,又2323121n n a a a S +++=- )2(≥n 两式相减得:313212)(,n n n n n n n a S S a a S S =+=---即,因为21,0n n n n a S S a =+∴>-,于是2121---=+n n n a S S ,两式相减得: 1,,1,0,131********===->+-=+----a a S a a a a a a a a n n n n n n n n 得又得所以n a n =,由)2)(111(22≥--<n nn nn ,由累加法可得3)11(212122221<-+<+++na n a a n21.解:(1)由题设1x 和2x 是方程220x ax --=的两个实根,得1x +2x =a 且1x 2x =-2, 所以 84)(||22122121+=-+=-a x x x x x x当a ∈[-1,1]时,28a +的最大值为9,即12||x x -≤3由题意,不等式2135x x m -≥+对任意实数a ∈[ 1,1]恒成立求实数m 的取值范围⇔求不等式335≥+m 的解集≥⇔m 所以命题P 真的充要条件为0≥m(2)对函数6)34()(23++++=x m mx x x f 求导,3423)('2+++=m mx x x f 令0)('=x f ,即34232=+++m mx x 此一元二次不等式的判别式16124)34(12422--=+-=∆m m m m若∆=0,则0)('=x f 有两个相等的实根0x ,且)x ('f 的符号如下:因为,f (0x )不是函数f (x )的极值若∆>0,则0)('=x f 有两个不相等的实根1x 和2x (1x <2x ),且)('x f 的符号如下:因此函数f (x )在x =1x 处取得极大值,在x =2x 处取得极小值综上所述,当且仅当∆>0时,函数f (x )在(-∞,+∞)上有极值0161242>--=∆m m 得1-<m ,或4m >,所以命题Q 真的充要条件为1-<m 或4m >综上,使P 正确且Q 正确时,实数m 的取值范围为,4(+∞。

株洲县一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 在△ABC 中,∠A 、∠B 、∠C 所对的边长分别是a 、b 、c .若sinC+sin (B ﹣A )=sin2A ,则△ABC 的形状为()A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形2. 已知f (x )是R 上的偶函数,且在(﹣∞,0)上是增函数,设,b=f (log 43),c=f (0.4﹣1.2)则a ,b ,c 的大小关系为()A .a <c <bB .b <a <cC .c <a <bD .c <b <a3. 已知集合{}ln(12)A x y x ==-,{}2B x x x =≤,全集,则( )U A B =U ()U C A B =I (A )( B ) (C )(D ) (),0-∞1,12⎛⎤-⎥⎝⎦()1,0,12⎡⎤-∞⋃⎢⎥⎣⎦1,02⎛⎤-⎥⎝⎦4. 函数,的值域为( )2-21y x x =-[0,3]x ∈ A. B. C. D.5. 在△ABC 中,已知,则∠C=( )A .30°B .150°C .45°D .135°6. 已知正方体的不在同一表面的两个顶点A (﹣1,2,﹣1),B (3,﹣2,3),则正方体的棱长等于()A .4B .2C .D .27. 执行如图所示的一个程序框图,若f (x )在[﹣1,a]上的值域为[0,2],则实数a 的取值范围是()A .(0,1]B .[1,]C .[1,2]D .[,2] 8. 特称命题“∃x ∈R ,使x 2+1<0”的否定可以写成( )A .若x ∉R ,则x 2+1≥0B .∃x ∉R ,x 2+1≥0C .∀x ∈R ,x 2+1<0D .∀x ∈R ,x 2+1≥09. 两圆C 1:x 2+y 2﹣4x+3=0和C 2:的位置关系是( )A .相离B .相交C .内切D .外切10.某几何体的三视图如图所示,则该几何体的体积为( )A .B .C .D .16163π-32163π-1683π-3283π-班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________【命题意图】本题考查三视图、圆柱与棱锥的体积计算,意在考查识图能力、转化能力、空间想象能力.11.复数z 为纯虚数,若(3﹣i )•z=a+i (i 为虚数单位),则实数a 的值为( )A .﹣B .3C .﹣3D .12.如图,在正方体中,是侧面内一动点,若到直线与直线的距离1111ABCD A B C D -P 11BB C C P BC 11C D 相等,则动点的轨迹所在的曲线是()PA 1 CA.直线B.圆C.双曲线D.抛物线【命题意图】本题考查立体几何中的动态问题等基础知识知识,意在考查空间想象能力.二、填空题13.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对弧长为 .14.在直角梯形分别为的中点,,,DC//AB,AD DC 1,AB 2,E,F ABCD AB AD ⊥===,AB AC 点在以为圆心,为半径的圆弧上变动(如图所示).若,其中,P A AD DE AP ED AF λμ=+u u u v u u u v u u u v,R λμ∈则的取值范围是___________.2λμ-15.已知z ,ω为复数,i 为虚数单位,(1+3i )z 为纯虚数,ω=,且|ω|=5,则复数ω= .16.已知函数,,则 ,的值域21,0()1,0x x f x x x ⎧-≤=⎨->⎩()21xg x =-((2))f g =[()]f g x 为.【命题意图】本题考查分段函数的函数值与值域等基础知识,意在考查分类讨论的数学思想与运算求解能力.17.长方体ABCD ﹣A 1B 1C 1D 1的棱AB=AD=4cm ,AA 1=2cm ,则点A 1到平面AB 1D 1的距离等于 cm . 18.已知函数f (x )=有3个零点,则实数a 的取值范围是 .三、解答题19.已知函数f (x )=log 2(m+)(m ∈R ,且m >0).(1)求函数f (x )的定义域;(2)若函数f (x )在(4,+∞)上单调递增,求m 的取值范围.20.(本小题满分12分)在等比数列中,.{}n a 3339,22a S ==(1)求数列的通项公式;{}n a (2)设,且为递增数列,若,求证:.2216log n n b a +={}n b 11n n n c b b +=g 12314n c c c c ++++<L 21.(本小题满分12分)设椭圆的离心率,圆与直线相切,为坐标原2222:1(0)x y C a b a b +=>>12e =22127x y +=1x y a b+=O点.(1)求椭圆的方程;C (2)过点任作一直线交椭圆于两点,记,若在线段上取一点,使(4,0)Q -C ,M N MQ QN λ=u u u u r u u u rMN R 得,试判断当直线运动时,点是否在某一定直一上运动?若是,请求出该定直线的方MR RN λ=-u u u r u u u rR 程;若不是,请说明理由.22.已知A 、B 、C 为△ABC 的三个内角,他们的对边分别为a 、b 、c ,且.(1)求A ;(2)若,求bc 的值,并求△ABC 的面积.23.已知:函数f (x )=log 2,g (x )=2ax+1﹣a ,又h (x )=f (x )+g (x ).(1)当a=1时,求证:h (x )在x ∈(1,+∞)上单调递增,并证明函数h (x )有两个零点;(2)若关于x 的方程f (x )=log 2g (x )有两个不相等实数根,求a 的取值范围.24.已知f (x )=x 2﹣3ax+2a 2.(1)若实数a=1时,求不等式f (x )≤0的解集;(2)求不等式f (x )<0的解集.株洲县一中2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题题号12345678910答案D C CACABDDD题号1112答案DD.第Ⅱ卷(共110二、填空题13. .14.[]1,1-15. ±(7﹣i ) .16.,. 2[1,)-+∞17. 18. (,1) .三、解答题19.20.(1);(2)证明见解析.131622n n n a a -⎛⎫==- ⎪⎝⎭g 或21.(1);(2)点在定直线上.22143x y +=R 1x =-22.23. 24.。

湖南省三湘名校教育联盟2024-2025学年高三上学期第二次大联考(11月)数学试题(答案在最后)本试卷共4页.全卷满分150分,考试时间120分钟.注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在本式卷和答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应的答案标号涂黑,如有改动,用橡皮擦干净后,再选涂其他答案;回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本式卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{40},{31}A xx B x x =-=-∣∣ ,则集合A B 中所含整数的个数为A.2 B.3C.4D.52.已知3i12iz -=+,则z 的虚部为A.75B.75-C.15-D.153.“202520251ab>”是“33a b >”的A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.已知()1sin 104θ︒+=-,则()sin 2110θ︒+=A.78B.18C.18-D.78-5.经研究表明:光源发射出来的粒子在没有被捕获之前属于光子,光子在离开光源后会与各种粒子撞击,其动量可能会改变,导致其速度降低,最终可能改变身份成为其他范围的粒子(如红外线粒子),不再能被人类的感光设备捕获.已知在某次光学实验中,实验组相关人员用人类感光设备捕获了从同一光源发射出来的两个光子A ,B ,通过数学建模与数据分析得知,此时刻在平面直角坐标系中它们的位移所对应的向量分别为(4,3),(2,10)A B s s == ,设光子B 相对光子A 的位移为s ,则s 在A s上的投影向量的坐标为A.43,55⎛⎫⎪⎝⎭B.(2,7)- C.5239,2525⎛⎫⎪⎝⎭ D.43,2525⎛⎫⎪⎝⎭6.已知等差数列{}n a 的前n 项和为n S ,公差为1,2d a =也为等差数列,则d 的值为A.2B.3C.4D.87.已知函数1()ln 2(1)x f x x m x m+=+≠+关于点(,4)n 中心对称,则曲线()y f x =在点(n m -,())f n m -处的切线斜率为A.14 B.74C.38D.1388.ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且πcos cos 2,3b Cc B A +==,则ABC 的内切圆半径的最大值为A.2B.3C.2D.1二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知正数x ,y 满足21x y +=,则A.81xy B.1412x y+ C.22142x y +D.1(1)4x y +10.三棱台111ABC A B C -中,112AB A B =,设AB 的中点为1,E AA 的中点为1,F A E 与BF 交于点1,G A C 与1C F 交于点H ,则A.直线GH 与直线1BB 异面B.1//GH BC C.线段AE 上存在点P ,使得1//BC 平面1A PCD.线段BE 上存在点P ,使得1//BC 平面1A PC11.设函数2()e ,x f x nx n n +=-+∈N ,记()f x 的最小值为n a ,则A.122a a >- B.1n a n +C.()()n f a f n > D.n m n ma a a +>+三.填空题:本题共3小题,每小题5分,共15分.12.已知命题:“2,20x ax ax ∀∈--<R ”为真命题,则a 的取值范围是______.13.已知P 为边长为4的正六边形ABCDEF 内部及其边界上的一点,则AP AB ⋅的取值范围是______.14.三棱锥P ABC -中,AB AC AB AC ==⊥,平面PBC ⊥平面ABC ,且PB PC =.记P ABC -的体积为V ,内切球半径为r ,则21r V-的最小值为______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)已知函数()2cos 2,(0,π)f x x x x =+∈.(1)求()f x 的单调递减区间;(2)若()f x 在π,12m ⎡⎤⎢⎥⎣⎦上的最小值为-2,求m 的取值范围.16.(本小题满分15分)记首项为1的数列{}n a 的前n 项和为n S ,且2(1)n n S n a =+.(1)探究数列n a n ⎧⎫⎨⎬⎩⎭是否为单调数列;(2)求数列{}2na n a ⋅的前n 项和nT .17.(本小题满分15分)如图,四棱柱1111ABCD A B C D -中,四边形ABCD 是菱形,四面体11A BC D 的体积与四面体111A B BC 的体积之差为12,A BD 的面积为(1)求点A 到平面1A BD 的距离;(2)若11111,,2A B A D A B A C BD =⊥=,求锐二面角11A BD C --的余弦值.18.(本小题满分17分)已知函数2()ln 2x f x ax ax x =+-在(0,)+∞上有两个极值点12,x x ,且21x x <.(1)求a 的取值范围;(2)当21(1,e)x x ∈时,证明:122eln ln e 1x x <+<+.19.(本小题满分17分)对于(2,3,)m m = 项数列{}n a ,若满足111m miii i a am ==-=-∑∑,则称它为一个满足“绝对值关联”的m 阶数列.(1)对于一个满足“绝对值关联”的m 阶数列{}n a .证明:存在,{1,2,,}i j m ∈ ,满足0i j a a <;(2)若“绝对值关联”的m 阶数列{}n a 还满足(1,2,,)i a i m λ=,则称{}n a 为“绝对值λ关联”的m 阶数列.①请分别写出一个满足“绝对值34关联”的4阶数列和满足“绝对值1关联”的5阶数列(不必论证,符合要求即可);②若存在“绝对值λ关联”的n 阶数列(2)n ,求λ的最小值(最终结果用常数或含n 的式子表示).三湘名校教育联盟•2025届高三第二次大联考•数学参考答案、提示及评分细则1.【答案】C 【解析】由题意可得{40},{31}A xx B x x =-=-∣∣ ,可得{30}A B x x =- ∣ ,故集合A B 中所含整数有3,2,1,0---,共4个,故选C.2.【答案】A 【解析】由题意可得3i (3i)(12i)32i 6i 17i 12i (12i)(12i)555z ------====++-,故17i 55z =+,其虚部为75,故选A.3.【答案】A 【解析】由202520251ab> 及指数函数的单调性可得0a b > ,令函数3()f x x =,易得()f x 单调递增,故当0a b > 时,一定有33a b >,故充分性成立,但由33a b >只能推出a b >,即必要性不成立,故“20252025a b >1 ”是“33a b >”的充分不必要条件,故选A.4.【答案】A 【解析】由题意可得()1sin 104θ︒+=-,故()()()()2sin 2110sin 90220cos 22012sin 10θθθθ︒︒︒︒︒+=++=+=-+2171248⎛⎫=--= ⎪⎝⎭,故选A.5.【答案】C 【解析】由向量(4,3),(2,10)A B s s == ,可得(2,10)(4,3)(2,7)B A s AB s s ==-=-=-,所以s 在A s 上的投影向量为218135239(4,3),55252525A A A A As s s s s s ⋅-⎛⎫⋅=⨯=⋅= ⎪⎝⎭ ,故选C.6.【答案】C 【解析】易知232222n n d S a n d n d ⎛⎫-=+-+- ⎪⎝⎭也为等差数列,则232222d n d n d ⎛⎫+-+- ⎪⎝⎭为完全平方,则2322(2)02d d d ⎛⎫---= ⎪⎝⎭,解得4d =,故选C.7.【答案】D 【解析】因为()f x 关于点(,4)n 中心对称,所以函数1()()4ln224x n g x f x n x n x m n ++=+-=++-++为奇函数,则240n -=,即2n =,且3ln 2x y x m +=++为奇函数,所以23m +=-,解得5m =-,故1()ln 5x f x x +=+-2,7x n m -=,且6()2(1)(5)f x x x '=-+-,故切线斜率为13(7)8f '=,故选D.8.【答案】B 【解析】设ABC 的内切圆半径为r ,由题意可得cos cos 2b C c B +=,由余弦定理可得2222a b c b ab +-⋅+2222222222222a c b a b c a c b c a ac a a +-+-+-⋅=+==,而11sin ()22ABC S bc A a b c r ==++ ,故2r =⋅2bcb c ++,由余弦定理可得2222cos a b c bc A =+-,则224b c bc bc =+- ,当且仅当b c =时等号成立,而4=2()3b c bc +-,则b c +=,其中4bc ,故33222bc r b c =⋅=++=(24)t t < ,故24(2)6263t r t t -=⋅=-+ .故选B.9.【答案】AC 【解析】对于A :因为21x y +=18xy ,当且仅当2x y =,即11,42x y ==时取等号,故A 正确;对于B :1424(2)8666x y x y x y x y x y y x +++=+=+++=+,当且仅当8x yy x =,即x =1,22y =时取等号,故B 错误;对于C :因为22x y +,则22142x y + ,当且仅当2x y =,即11,42x y ==时取等号,故C 正确;对于D :因为2112(1)1(1)2(1)2222x y x y x y ++⎡⎤+=⨯+⨯=⎢⎥⎣⎦,当且仅当21x y =+,即1,02x y ==时取等号,这与x ,y 均为正数矛盾,故1(1)2x y +<,故D 错误,故选AC.10.【答案】AD 【解析】如图所示,对于A ,因为1BB ⊂/平面11,BC F BB 平面1BC F B =,故1BB 与平面1BC F 的交点为B ,且是唯一的.又因为B ,G ,H 三点不共线,所以GH 不经过点B ,又GH ⊂平面1BC F ,所以直线GH 与直线1BB 没有交点,即直线GH 与直线1BB 异面,故A 正确;对于B ,因为AB 的中点为1,E AA 的中点为F ,所以点G 是1A AB 的重心,:1:2FG GB =,若1//GH BC ,则1:1:2FH HC =,事实上:()()1111111222A H A C A A AC A F A C A F λλλλ==+=+=+112AC λ ,所以H 是1FC 的中点,1:1:2FH HC =不成立,故B 错误;对于CD 选项,如图,取线段BF 的中点Q ,连接1AQ 并延长,交BE于点P ,下证1//BC 平面1A PC :由H 为1C F 的中点可知1//HQ BC ,又1BC ⊂/平面1,A PC HQ ⊂平面1A PC ,所以1//BC 平面1A PC ,故D 正确,C 错误;故选AD.11.【答案】BCD 【解析】由题意可得()e xf x n '=-,当(,ln )x n ∈-∞时,()0,()f x f x '<单调递减,当(ln ,)x n ∈+∞时,()0,()f x f x '>单调递增,故2(ln )ln n a f n n n n n ==+-.对于A :12212,62ln 2,22a a a a ==---=-2ln 20>,即122a a <-,故A 错误;对于B :设函数2()1ln ,,()2ln 1F x x x x x F x x x '+=--∈=--N ,设函数1()2ln 1,()2,1g x x x g x x x '=--=- 时,则()0()g x g x '>⇒单调递增,故()(1)10g x g =>⇒ ()0()F x F x '>⇒单调递增,故22()(1)01ln 0ln 11n F x F n n n n n n n n a n =⇒--⇒+-+⇒+ ,故B 正确;对于C :易知ln n n >,又因为()f x 在(ln ,)x n ∈+∞上单调递增,故(ln )()(1)f n f n f n <<+ ()n f a ,故()()n f a f n >,故C 正确;对于D :[ln ln()][ln n m m n a a a m n m n m n m n +--=+-+++-ln()]n m +,只需证明ln ln()0n m n m +-+>即可,而ln ln e n n m m +=,由e 1(1)x x x >+易得e n m >(1)m n m mn m n +=++,故ln ln()0n m n m +-+>,同理可得ln ln()0m n n m +-+>,故n m n a a +>+m a ,故D 正确,故选BCD .12.【答案】(8,0-]【解析】因为命题“2,20x ax ax ∀∈--<R ”为真命题,当0a =时,20-<成立,当0a ≠时,则280a a a <⎧⎨∆=+<⎩,解得80a -<<,故a 的取值范围是(8,0]-,故答案为(8,0]-.13.【答案】[-8,24]【解析】由题意可得AB 的模为4,根据正六边形的特征及投影的定义可以得到AP 在AB方向上的投影长度的取值范围是[2,6]-,由数量积定义可知AP AB ⋅ 等于AB 的模与AP 在AB 方向上的投影长度的乘积,所以AP AB ⋅的取值范围是[8,24]-,故答案为[8,24]-.14.62+【解析】设三棱锥P ABC -的高为h ,依题意,可取BC 中点O ,连接OA ,OP ,则OA =1,OB OC OP h ===,则PBC 的面积为1,2h BC h ABC ⋅= 的面积112OA BC ⋅=,由21PA PB h ==+可得PBA 的面积为2212h +,于是三棱锥P ABC -2211h h +++,由等体积可知)2211133r hh h +++=⨯,所以2222222122122h h h r h h ++++==+,故21r V-=2222123221122h h h h h ++-+-=+.设函数22211()2x f x x +=+,且0x >,则()f x '=()2222222212121212x x x x x x +=++++,当3,()0,()2x f x f x '<<单调递减,3()02x f x '>>,()f x 单调递增,所以3()622f x f =+ ,所以62h =时,21r V -取得最小值62+62.15.【解析】(1)由题意可得π()32cos 22sin 2,(0,)6f x x x x x π⎛⎫=+=+∈ ⎪⎝⎭,………………2分令π2,(0,π)6z x x =+∈,则π13π,66z ⎛⎫∈ ⎪⎝⎭,因为π13πsin ,,66y z z ⎛⎫=∈ ⎪⎝⎭的单调递减区间是π3π,22⎡⎤⎢⎥⎣⎦,…………………………………………5分且由π3π22z ,得π2π63x ,所以()f x 的单调递减区间是π2π,63⎡⎤⎢⎥⎣⎦.………………………………7分(2)当π,12x m ⎡⎤∈⎢⎥⎣⎦,则πππ2,2636x m ⎡⎤+∈+⎢⎥⎣⎦,因为()f x 在区间π,12m ⎡⎤⎢⎥⎣⎦上的最小值为-2,……9分即sin y z =在ππ,236m ⎡⎤+⎢⎥⎣⎦上的最小值为-1,又因为π13π,66z ⎛⎫∈ ⎪⎝⎭,所以3ππ13π2,266m +< ……12分即2ππ3m < ,故m 的取值范围为2π,π3⎡⎫⎪⎢⎣⎭.……………………………………………………………13分16.【解析】(1)由题意得2(1)n n S n a =+,当2n 时,112n n S na --=,………………………………1分两式作差得112(1),(1)n n n n n a n a na n a na --=+--=,……………………………………………………3分所以11n n a a n n -=-,则数列n a n ⎧⎫⎨⎬⎩⎭为常数数列,………………………………………………………………5分无单调性,故数列n a n ⎧⎫⎨⎬⎩⎭不是单调数列.……………………………………………………………………6分(2)由(1)可得111n a a n ==,所以n a n =,故22an n n a n ⋅=⋅.……………………………………8分所以231222322n n T n =⋅+⋅+⋅++⋅ ,①……………………………………………………………10分23412122232(1)22n n n T n n +=⋅+⋅+⋅++-⋅+⋅ ,②………………………………………………12分①-②得()231112122222222(1)2,12n nn n n n T n n n +++--=++++-⋅=-⋅=---⋅- ……………14分所以1(1)2 2.n n T n +=-⋅+…………………………………………………………………………………15分17.【解析】(1)如图,连接AC 交BD 于点O ,设四棱柱1111ABCD A B C D -的体积为V Sh =(其中S 为菱形ABCD 的面积,h 为四棱柱ABCD -1111A B C D 的高),…………………………………………1分所以1ABDA 的体积为111236S h V ⋅=,同理四面体111A B BC 的体积为111236S h V ⋅=……………2分又因为四边形ABCD 是菱形,所以111122AO OC AC A C ===,所以点A 到平面1A BD 的距离为点1C 到平面1A BD 距离的一半,所以四面体11A BC D 的体积是四面体1ABDA 的体积的两倍,即13V .……4分设点A 到平面1A BD 的距离为d ,则1111233663V V V d =-==⋅………………………………5分解得3d =分(2)如图,连接1OA ,由111A B A C ⊥得1A B AC ⊥,又四边形ABCD 是菱形,所以AC BD ⊥,又11,,A B BD B A B BD =⊂ 平面1A BD ,所以AC ⊥平面1A BD ,又1AO ⊂平面1A BD ,所以1A O AC ⊥,………………………………………………………………………………………………8分又11,A B A D BO BD ==,所以1A O BD ⊥,…………………………………………………………9分又,,BD AC O BD AC =⊂ 平面ABCD ,所以1A O ⊥平面ABCD ,以点O 为原点,OA 为x 轴,OB 为y 轴,1OA 为z 轴,建立如图所示空间直角坐标系,由(1)知12V =,且菱形ABCD的面积为S =,所以h ==………………………………11分依题意,1(0,0,0),((0,1,0),(O C B C -,易得平面1A BD的一个法向量为(0,0)OC =,…………………………………………………12分设平面1BC D 的一个法向量为(,,)n a b c =,又1(0,1,0),(OB OC ==- ,所以100OB n OC n ⎧⋅=⎪⎨⋅=⎪⎩,即00b a c =⎧⎨-=⎩,取(1,0,1)n = ,…………………………………………………13分故111cos ,2||n OC n OC n OC ⋅<>===⋅ ,……………………………………………………14分故锐二面角11A BD C --的余弦值为2.…………………………………………………………………15分【评分细则】本题第二问若考生通过利用几何法来求解二面角11A BD C --的平面角为11π4A OC ∠=,或者利用余弦定理等来直接求解二面角的余弦值,只要过程合理,最终答案正确均给满分,若过程有误或证明过程不严谨酌情扣一定的分数.18【解析】(1)易得()f x 定义域为(0,),()ln f x x a x '+∞=-,显然0a ≠.…………………………1分①当0a <时,()f x '单调递增,不可能有两零点,不合题意.…………………………………………2分②当0a >时,令函数()()g x f x '=,易得()x a g x x'-=,故(0,)x a ∈时,()0,()g x g x '<单调递减(,)x a ∈+∞时,()0,()g x g x '>单调递增,……………………………………………………………4分当e a 时,有()()(1ln )0g x g a a a =- ,不可能有两零点;当e a >时,有()0,(1)10g a g <=>,由零点存在性定理可得()g x 在区间(1,)a 必有一个零点1x .……………………………………………6分()2(2ln )g a a a a =-,令函数()2ln a a a ϕ=-,则2()10a aϕ'=->,即()a ϕ单调递增,故()(e)a ϕϕ>=e 20->,即()20g a >,故()g x 在(,)a +∞上有零点2x ,综上(e,)a ∈+∞.…8分(2)依题意有()()120g x g x ==,即1122ln ln 0x a x x a x -=-=,故得12211221ln ln ln ln x x x x a x x x x -====-2121ln x x x x -,…………………………………………………………10分因此2121122111ln ln ln 1x x x x x x x x x x ==--,令21(1,e)x t x =∈.则1ln ln 1t x t =-,同理2ln ln 1t t x t =-,故12eln ln x x +=e ln 1t t t +-,欲证122eln ln e 1x x <+<+,即证112ln (e 1)e e t t t t t --<<+++,……12分令函数1()ln 2e t m t t t -=-+,函数1()(e 1)ln ,(1,e)e t n t t t t -=+-∈+,只需证明()0,()0m t n t >>即可,又22222(e)2(e 1)(1)e 1()0(e)(e)t t t m t t t t t '+-+-+-==>++,……………………………………………………14分故()m t 是增函数,故()(1)0m t m >=,又222222(e 1)(e)1e ()e 1(e)(e)t t n t t t t t t '⎛⎫+-+==+-- ⎪++⎝⎭,令函数22e ()e 1h t t t =+--,则22e ()10h t t '=->,故()h t 单调递增,故()(1)0h t h >=,………………16分因此21()()0(e)n t h t t '=>+,故()n t 单调递增,故()(1)0n t n >=,故122eln ln e 1x x <+<+得证.17分【评分细则】第一问若考生求完导后用参变分离的方法来求参数范围,只要最终答案正确均给分,第二问也可用其他方法来证明,逻辑正确,严谨可酌情给分.19.【解析】(1)因为{}n a 为满足“绝对值关联”的m 阶数列,假设0i a ,则11110m m m m i i i i i i i i a a a a====-=-=≠∑∑∑∑1(2)m m - ,不满足题意,同理若0i a ,则111101(2)m m m mi i i i i i i i a aa a m m ====-=-+=≠-∑∑∑∑ ,也不满足题意,………………………………4分所以12,,,m a a a 中必有一些数小于0,也必有一些数大于0,不妨设121,,,0,,,,0l k k m a a a a a a +>< (其中1l k m << ),故存在{1,2,,},{,1,,}i l j k k m ∈∈+ ,满足0i j a a <.………………6分(2)①一个满足“绝对值34关联”的4阶数列为:3333,,,4444--;(答案不唯一,符合要求即可)8分一个满足“绝对值1关联”的5阶数列为:222,,,1,1333--;(答案不唯一,符合要求即可)……10分②设(1,2,,)i a i n λ= ,且111n n i i i i a an ==-=-∑∑.不妨设1212,,,0,,,,0k k k n a a a a a a ++< ,其中1k n < ,并记11,k n i i i i k a x a y ==+==∑∑,为方便起见不妨设x y (否则用i a -代替i a 即可),于是得11,n n i i i i ax y a x y ===+=-∑∑,因为111n n i i i i a a n ==-=-∑∑,即()()1x y x y n +--=-,所以11,22n n y x --=,一方面有1()2n y n k λ-=- ,另一方面12n x k λ- .所以1()n n k k n λλλ--+= ,即1n n λ- ,当且仅当n k k -=,即2n k =时等号成立.………13分(i )当n 为偶数时,设*2,n s s =∈N ,则有前s 项为正数,后s 项为负数的数列111,,,n n n n n n --- ,111,,,n n n n n n ------ 是“绝对值1n n -关联”的n 阶数列,又1n n λ- ,所以λ的最小值为1n n -;……………………………………………………………………14分(ii )当n 为奇数时,设*21,n s s =+∈N ,则11(),22n n y n k x k λλ--=- 等价于21s s k λ+- 且s k λ ,即λ不小于21s s k +-与s k中的最大者.……………………………………………………15分当k s =或1s +时,两者中的最大者均为1,有1λ ,当k s <或1k s >+时,有1s k >或121s s k>+-,则有1λ>,所以取k s =或1s +时,λ可能取得最小值1,且有前s 项为正数,后1s +项为负数数列1111,1,,1,,,,111n n n n n n ------+++ 符合题意,所以λ可以取得最小值1.…………………………………………………………………………………………16分综上所述λ的最小值为()*1,21,21n n s s n n s -⎧=⎪∈⎨⎪=+⎩N .……………………………………………………17分。

湖南省株洲市十三中学2018届高三12月月考试题理科数学★请将答案填写在答题卡的相应位置上★一、选择题:本次题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合2{|,}M y x y x R ==∈,集合{|0,}N y x y x R =+=∈,则MN 等于 ( )A .{|}y y R ∈B .{(1,1),(0,0)}-C .{(0,0)}D .{|0}x x ≥ 2.函数sin 2y x =的一个增区间是 ( ) A .,22ππ⎡⎤-⎢⎥⎣⎦ B .,44ππ⎡⎤-⎢⎥⎣⎦ C .0,2π⎡⎤⎢⎥⎣⎦ D .,02π⎡⎤-⎢⎥⎣⎦3.已知向量)3,2(=,)2,1(-=,若b n a m +与b a 2-共线,则nm等于 ( ) A .2-; B .2 C .21-D .214.设1tan10,1tan10a b +==- ( )A .222a b a b +<<B .222a b b a +<<C .222a b a b +<<D .222a b b a +<< 5.把函数)6sin(π+=x A y 的图象按向量)0,(m a =平移,所得的图象恰好关于原点对称,则m的最小正值是 ( ) A .6π B .3π C .65π D.67π 6.已知(3,1),(2,1)AB =-=n ,且7AC ⋅=n ,则BC ⋅=n ( ) A .2- B .0 C .2-或2 D . 27.函数y = ︳x 21log ︱的定义域为〔a,b 〕,值域为〔0,2〕,则区间〔a,b 〕长度b-a 的最小值为 ( ) A .3 B .43 C .4 D .418.由下列条件解ABC ∆,其中有两解的是 ( )A .20,45,80b A C ===B .30,28,60a c B === C .14,16,45a c A === D .12,15,120a c A ===9.将自然数0,1,2,…按照如下形式进行排列,根据以下规律判定,从2018到2018的箭头方向是 (),10.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y =f (x ),一种是平均价格曲线y =g (x )(如f (2)=3表示开始交易后第2小时的即时价格为3元;g (2)=4表示开始交易后两个小时内所有成交股票的平均价格为4元).下面所给出的四个图象中,实线表示y =f (x ),虚线表示y =g (x ),其中可能正确的是 ( )二、填空题:本大题共5小题,每小题5分,共25分. 11.若角22,πβαπβα<<<-满足,则βα-2的取值范围是____________.12.函数11()sin()cos 633f x x x π=-+图象的相邻的两个对称中心的距离是__________. 13.等差数列{}n a 中,351024a a a ++=,则此数列的前13项的和等于___________. 14.如图,半圆的直径6AB =,O 为圆心,C 为半圆 上不同于A B 、的任意一点,若P 为半径OC 上的动点, 则()PA PB PC +⋅的最小值是__________.15.若函数()f x 是定义在实数集上的奇函数,且(2)()f x f x -=-,给出下列结论: ①()20f =;②()f x 以4为周期;③()f x 的图象关于y 轴对称;④(2)()f x f x +=-. 这些结论中正确的有____________(必须填写序号)。

湖南省株洲市南方中学2024-2025学年高三上学期11月月考数学试卷数学一、单选题1.若集合{}234,,,A i i i i =(i 是虚数单位),{}1,1B =-,则A B ⋂等于()A .{}1-B .{}1C .{}1,1-D .φ2.已知一组数据1x ,2x ,3x ,4x ,5x 的平均数为2,方差为12,则另一组数据132x -,232x -,332x -,432x -,532x -的平均数、标准差分别为()A .2,12B .2,1C .4,2D .4,923.已知奇函数()()22cos x xf x m x -=+⋅,则m =()A .1-B .0C .1D .124.若正四棱锥的高为8,且所有顶点都在半径为5的球面上,则该正四棱锥的侧面积为()A .24B .32C .96D .1285.图1是蜂房正对着蜜蜂巢穴开口的截面图,它是由许多个正六边形互相紧挨在一起构成.可以看出蜂房的底部是由三个大小相同的菱形组成,且这三个菱形不在一个平面上.研究表明蜂房底部的菱形相似于菱形十二面体的表面菱形,图2是一个菱形十二面体,它是由十二个相同的菱形围成的几何体,也可以看作正方体的各个正方形面上扣上一个正四棱锥(如图3),且平面ABCD 与平面ATBS 的夹角为45°,则cos ASB ∠=()A .13B C D 6.在ABC V 中,角A 为π3,角A 的平分线AD 交BC 于点D ,已知AD =()1R 3AB AD AC λλ=-∈ ,则AB AD ⋅= ()A .1B .32C .9D7.设椭圆C :22221x y a b+=(0)a b >>的左、右焦点分别为1F ,2F ,直线l 过点1F .若点2F 关于l 的对称点P 恰好在椭圆C 上,且211212F F F P a =⋅ ,则C 的离心率为()A .13B .23C .12D .258.在锐角ΔA 中,2A B =,则ABAC的取值范围是A .()1,3-B .()1,3C.D .()1,2二、多选题9.已知随机变量()2~1,X N σ,记(1),(13)>-=<<=P X a P X b ,则()A .(3)<=P X aB .12a b -=C .(21)2()-=E X E XD .(21)4()D X D X -=10.已知当π()0,x ∈时,()cos f x x =,并且满足(2π)(2π),(π)(π)0f x f x f x f x +=-++-=,则下列关于函数()f x 说法正确的是()A .3π02f ⎛⎫= ⎪⎝⎭B .周期2πT =C .()f x 的图象关于πx =对称D .()f x 的图象关于(π0)-,对称11.已知等比数列{}n a 的公比为q ,其前n 项的积为n T ,且满足11a >,9910010a a ->,99100101a a -<-,则()A .01q <<B .9910110a a -<C .100T 的值是n T 中最大的D .使1n T >成立的最大正整数数n 的值为198三、填空题12.若52345012345(1)x a a x a x a x a x a x -=+++++,则2a =.13.若直线20(0,0)ax by a b -+=>>被圆222410x y x y ++-+=所截得的弦长为4,则23ab+的最小值为.14.已知函数()e ln 1ax f x x x ax =---,若函数()f x 的最小值恰好为0,则实数a 的最小值是.四、解答题15.如图,在四棱锥P ABCD -中,//BC AD ,1AB BC ==,3AD =,点E 在AD 上,且PE AD ⊥,2PE DE ==.(1)若F 为线段PE 中点,求证://BF 平面PCD .(2)若AB ⊥平面PAD ,求平面PAB 与平面PCD 夹角的余弦值.16.人工智能(AI )是一门极富挑战性的科学,自诞生以来,理论和技术日益成熟.某公司研究了一款答题机器人,参与一场答题挑战.若开始基础分值为m (*m ∈N )分,每轮答2题,都答对得1分,仅答对1题得0分,都答错得1-分.若该答题机器人答对每道题的概率均为12,每轮答题相互独立,每轮结束后机器人累计得分为X ,当2X m =时,答题结束,机器人挑战成功,当X 0=时,答题也结束,机器人挑战失败.(1)当3m =时,求机器人第一轮答题后累计得分X 的分布列与数学期望;(2)当4m =时,求机器人在第6轮答题结束且挑战成功的概率.17.正数数列{}{},n n a b 满足118,16a b ==,且1,,n n n a b a +成等差数列,11,,n n n b a b ++成等比数列.(1)求{}{},n n a b 的通项公式;(2)求证:1211111113n a a a ++⋅⋅⋅⋅<---.18.已知双曲线2222:1(0,0)x y C a b a b-=>>的右顶点()1,0E ,它的一条渐近线的倾斜角为120︒.(1)过点(2,0)-作直线l 交双曲线C 于,M N 两点(不与点E 重合),求证:EM EN ⊥;(2)若过双曲线C 上一点P 作直线与两条渐近线相交,交点为,A B ,且分别在第一象限和第四象限,若1,,23AP PB λλ⎡⎤=∈⎢⎥⎣⎦uu u r uu r ,求AOB V 面积的取值范围.19.已知函数()sin xf x x=.(1)判断函数()f x 在区间()0,3π上极值点的个数并证明;(2)函数()f x 在区间(0,)+∞上的极值点从小到大分别为123,,,,,n x x x x ,设(),n n n a f x S =为数列{}n a 的前n 项和.①证明:120a a +<;②问是否存在*n ∈N 使得0n S ≥?若存在,求出n 的取值范围;若不存在,请说明理由.。
湖南省株洲市2018届高三数学第三次(11月)月考试题(无答案)时量:120 分钟分值:150 分第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知全集 U={2,3,4,5,6,7},集合 A={4,5,7},B={4,6},则 A ∩(U B ) =( )A. {5}B. {2}C. {2, 5}D. {5, 7}(2)复数 z 与复数 i (2 i ) 互为共轭复数(其中 i 为虚数单位),则 z ( )A. 1 2iB. 1 2iC. 1 2iD. 1 2i y ≤5 x(3)已知直线 x y 5 0 与两坐标轴围成的区域为 M ,不等式组 x ≥0 所形成的区域为 N ,现在区域M 中随机放置一点,则该点落在区域N 的概率是( )y ≥3x 开始 S =1,a =2A. 3 4B. 1 2C. 14D. 23 (4)如图所示的程序框图中,输出的 S 的值是( ) A. 80 B. 100 C. 120 D. 140 a = a +1(5)已知ΔABC 的面积为5 3 , A , AB = 5 ,则 BC = ( )6 S=S ×a 是A. 2 3B. 13C. 3 2D. 2 6 S 100?(6)已知等差数列a n 的前 n 项和为 S n ,且 S 105 , a 71 ,则 a 1( )否A . 12B .-1C . 1 2D . 14 输出 S (7)已知一个几何体的三视图如图所示,则该几何体的体积为( )结束A. 60 12B. 60 6C. 72 12πD. 726第 4 题图(8)设 p : x 2x1 , q : log ( x 2x ) 0 ,则 p 是 q 的()A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件(9)已知函数 f (x ) 2 x x 1, g (x ) log 2x x 1,h (x ) log 2 x 1 的零点依次为a , b , c 则()A. a < b <cB. a < c <bC. b< c< aD. b< a<c(10)在正三棱锥内有一半球,其底面与正三棱锥的底面在同一平面内,正三棱锥的三个侧面都和半球相切.如果半球的半径等于1,正三棱锥的底面边长为,则正三棱锥的高等于()A B. C. D.⎣ ⎦(11)已知双曲线x 2 y 21(a 0, b 0) 与抛物线 y 2 = 2 px ( p > 0) 有相同的焦点 F ,且双曲线的一条a 2b 2渐近线与抛物线的准线交于点 M (-3,t ),若 MF153 ,则双曲线的离心率为()2235A.B. C.2 3 2D. 5( 12 ) 已知函数 f x在定义域 R 上的导函数为 fx ,若方程 f x 0无解 , 且ff ( x ) 2017x2017, 当 g x sin x cos x kx 在, 上与 fx 在 R 上的单调性相同时,则实数 k 的取值范围是 () 2 2A., 1B.,2C.1,2D.2,第 II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22) 题~第(23)题为选考题,考生根据要求作答. 二、填空题:本大题共 4 小题,每小题 5 分. (13)设ln 2 a , ln 3 b ,则 e a e b .(其中 e 为自然对数的底数)(14) 设直线l 1 : mx (m 1) y 1 0(m R ) ,若直线 l 1 为圆 x m . 2 y 22 y3 0 的一条对称轴,则实数(15)在 ABC 中,过中线 AD 的中点 E 任作一直线分别交边 AB 、 AC 于 M 、 N 两点,设 AM x AB , AN y AC x , y 0 , 则4x y 的最小值是.(16)已知函数 fx x m e x(其中e 为自然对数的底数),曲线 y线在这两点处的切线都与 y 轴垂直,则实数 m 的取值范围是 . 三、解答题:解答应写出文字说明,证明过程或演算步骤. f x 上存在不同的两点,使得曲(17) (本小题满分 12 分)若a3 sin x , cos x , b cos x , cos x , 0, x R ,f x a b 1, 2且 f x 的最小正周期是 ,设 ABC 三个角 A , B , C 的对边分别为 a , b , c .(Ⅰ)求 的值; (Ⅱ)若 c7 , f C 1 , sin B3sin A ,求2a,b 的值.P (... k2.3.7.(18)(本小题满分12 分)传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。
株洲县高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. f ()=,则f (2)=( )A .3B .1C .2D .2. 计算log 25log 53log 32的值为( )A .1B .2C .4D .83. 奇函数f (x )在区间[3,6]上是增函数,在区间[3,6]上的最大值为8,最小值为﹣1,则f (6)+f (﹣3)的值为( )A .10B .﹣10C .9D .154. 若某几何体的三视图 (单位:cm ) 如图所示,则此几何体的体积是()cm3A .πB .2πC .3πD .4π5. 复数z 满足z (l ﹣i )=﹣1﹣i ,则|z+1|=( )A .0B .1C .D .26. △ABC 的外接圆圆心为O ,半径为2,++=,且||=||,在方向上的投影为()A .﹣3B .﹣C .D .37. 已知△ABC 是锐角三角形,则点P (cosC ﹣sinA ,sinA ﹣cosB )在( )A .第一象限B .第二象限C .第三象限D .第四象限8. 如图,棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中,M 为线段A 1B 上的动点,则下列结论正确的有()①三棱锥M ﹣DCC 1的体积为定值②DC 1⊥D 1M③∠AMD 1的最大值为90° ④AM+MD 1的最小值为2.A .①②B .①②③C .③④D .②③④9. 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为()班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A.B.C.D.610.设向量,满足:||=3,||=4,=0.以,,﹣的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为()A.3B.4C.5D.611.冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示.杂质高杂质低旧设备37121新设备22202根据以上数据,则()A.含杂质的高低与设备改造有关B.含杂质的高低与设备改造无关C.设备是否改造决定含杂质的高低D.以上答案都不对12.S n是等差数列{a n}的前n项和,若3a8-2a7=4,则下列结论正确的是()A.S18=72 B.S19=76C.S20=80 D.S21=84二、填空题13.椭圆的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为 .14.已知三棱柱ABC﹣A1B1C1的侧棱和底面垂直,且所有棱长都相等,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为7π,则此三棱柱的体积为 .15.已知函数y=f(x),x∈I,若存在x0∈I,使得f(x0)=x0,则称x0为函数y=f(x)的不动点;若存在x0∈I ,使得f(f(x0))=x0,则称x0为函数y=f(x)的稳定点.则下列结论中正确的是 .(填上所有正确结论的序号)①﹣,1是函数g(x)=2x2﹣1有两个不动点;②若x0为函数y=f(x)的不动点,则x0必为函数y=f(x)的稳定点;③若x0为函数y=f(x)的稳定点,则x0必为函数y=f(x)的不动点;④函数g(x)=2x2﹣1共有三个稳定点;⑤若函数y=f(x)在定义域I上单调递增,则它的不动点与稳定点是完全相同.16.命题p :∀x ∈R ,函数的否定为 .17.直线l 过原点且平分平行四边形ABCD 的面积,若平行四边形的两个顶点为B (1,4),D (5,0),则直线l 的方程为 .18.棱长为2的正方体的顶点都在同一球面上,则该球的表面积为. 三、解答题19.(本小题满分12分)在等比数列中,.{}n a 3339,22a S ==(1)求数列的通项公式;{}n a (2)设,且为递增数列,若,求证:.2216log n n b a +={}n b 11n n n c b b +=g 12314n c c c c ++++<L 20.已知曲线C 1:ρ=1,曲线C 2:(t 为参数)(1)求C 1与C 2交点的坐标;(2)若把C 1,C 2上各点的纵坐标都压缩为原来的一半,分别得到曲线C 1′与C 2′,写出C 1′与C 2′的参数方程,C 1与C 2公共点的个数和C 1′与C 2′公共点的个数是否相同,说明你的理由. 2015-2016学年安徽省合肥168中学高三(上)10月月考数学试卷(理科)21.如图,在多面体ABCDEF 中,底面ABCD 是边长为2的正方形,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,BF=3,G 和H 分别是CE 和CF 的中点.(Ⅰ)求证:AC ⊥平面BDEF ;(Ⅱ)求证:平面BDGH ∥平面AEF ;(Ⅲ)求多面体ABCDEF 的体积.22.一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图1的矩形,俯视图为两个边长为1的正方形拼成的矩形.V(1)求该几何体的体积;111]S(2)求该几何体的表面积.23.已知函数f(x)=和直线l:y=m(x﹣1).(1)当曲线y=f(x)在点(1,f(1))处的切线与直线l垂直时,求原点O到直线l的距离;(2)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围;(3)求证:ln<(n∈N+)24.已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,且过点D(2,0).(1)求该椭圆的标准方程;(2)设点,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.株洲县高级中学2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题题号12345678910答案A A CBCCBABB题号1112答案A二、填空题13. 20 .14. .15. ①②⑤ 16. ∃x 0∈R ,函数f (x 0)=2cos 2x 0+sin2x 0>3 .17. .18.12π三、解答题19.(1);(2)证明见解析.131622n n n a a -⎛⎫==- ⎪⎝⎭g 或20.21.22.(12).6+23. 24.。
湖南省长沙市2018届高三数学第三次月考试题理(扫描版,无答案) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(湖南省长沙市2018届高三数学第三次月考试题理(扫描版,无答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为湖南省长沙市2018届高三数学第三次月考试题理(扫描版,无答案)的全部内容。
湖南省长沙市2018届高三数学第三次月考试题理(扫描版,无答案)以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The above is the whole content of this article, Gorky said:"th e book istheladder ofhuman progress." I hope youcan make progress with the help of this ladder.Material life is extremely rich,science and technology are developing ra pidly, all of which gradually change the way of people's st udy and leisure. Many people are no longer eager topursue a document, but as long as you still have such a small persistence, youwill continue to grow and progress. When the complex world leads us to chase out, reading an article or doing a problem makes us calm down and return toourselves. With learning, we can activate our imagination and thinking, establish our belief, keep our pure spiritual world and resist the attack of the external world.。
株洲市十七中2018届高三第三次月考数学试卷(理科)说明:1、本套试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,共6页.考试时间为120分钟.2、本卷考试内容:高三选修(II)、集合与简易逻辑、函数、数列、三角函数 第Ⅰ卷(选择题,共50分)一、选择题:(每小题5分,共50分.每小题只有一项是符合题目要求的.请把答案写在答题卷上) 1.=+-ii i 1)1( i i A -B. .. C. 1 D. –12.映射f :A→B,如果满足集合B 中的任意一个元素在A中都有原象,则称为“满射”。
已知集合A 中有4个元素,集合B 中有3个元素,那么从A 到B 的不同满射的个数为( ) A .24 B .6 C . 36 D .723.命题p :若1||1||||,,>+>+∈b a b a R b a 是则的充分而不必要条件. 命题q :函数2|1|--=x y 的定义域是),3[]1,(+∞--∞ 则( )A .“p 或q”为假B .“p 且q”为真C .p 真q 假D .p 假q 真4.设偶函数||log )(b x x f a -=在)0,(-∞上递增,则)1(+a f 与)2(+b f 的大小关系是( )A .)2()1(+=+b f a fB .)2()1(+>+b f a f C.)2()1(+<+b f a f D.不能确定 5.如果数列}{n a 的前n 项和)23(21nn n n S -=,则这个数列 ( ) A .是等差数列但不是等比数列, B .是等比数列但不是等差数列,C.既是等差数列又是等比数列, D.既不是等差数列又不是等比数列, 6.已知θ是锐角,则θθcos sin +可能取得的值是( ) A .34 B .43 C.35 D. 537.)10()(<<=a a x f x,那么)1()(1-=-x fx g 的图象是A B C D8.设)(1x f -是函数)1)((21)(>-=-a a a x f x x 的反函数,则使1)(1>-x f 成立的 x 的取值范围为 ( )A .),21(2+∞-a aB . )21,(2a a --∞C . ),21(2a a a - D . ),[+∞a9.已知βα,为锐角,y x ==βαcos ,sin ,53)cos(-=+βα,则y x 与的函数关系式为( ) A .)153(541532<<+--=x x x y B .)10(541532<<+--=x x x y C .)530(541532<<---=x x x y D .)10(541532<<---=x x x y 10.在x y x y x y y x 2cos ,,log ,222====这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数的个数是( )A .0B .1C .2D .3第Ⅱ卷 (非选择题,共100分)二、填空题:(每小题4分,共20分. 把答案写在答题卷上.)11.在等差数列{}n a 中,12031581=++a a a ,则1193a a -的值为. 12.设)(x f 是一次函数,)4(),5(),2(,15)8(f f f f =成等比数列,则∞→n lim=+++2)()2()1(n n f f f ___________;13. 函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达式为_________________________;14. 设函数)(x f 的定义域为R ,若存在与x 无关的正常数M ,使|||)(|x M x f ≤对一切实数x 都成立,则称函数)(x f 为有界泛函,在函数x x h x x g x x f 2)(,)(,2)(2===,x x x v sin )(=中,属于有界泛函的有_________________;15.设函数f (x )的图象与直线a x =,b x =及x 轴所围成图形的面积称为函数f (x )在[a ,b]上的面积,已知函数y =sin n x 在[0,n π]上的面积为n2(n ∈N *),(i )y =sin3x 在[0,32π]上的面积为 ;(ii )y =sin (3x -π)+1在[3π,34π]上的面积为 .姓名_____________ 班级________ 计分_______一、选择题 (每小题5分,共50分)把正确答案序号填入下表中二、填空题 (每小题4分,共20分)把正确答案填在横线上 11. ______________; 12.____________;:13.___________________ ;14. ______________; 15. _______________; __________________;三:解答题(本大题有6小题,共80分.解答应写出文字说明,证明过程或演算步骤.) 16.(本小题满分12分)设函数)(cos sin 322cos )(R x x x x x f ∈+=的最大值为M ,最小正周期为T.(1)求M 、T 及单调增区间;(2)10个互不相等的正数i x 满足),10,,2,1(10,)( =<=i x M x f i i π且求 1021x x x +++ 的值.(3) 指出该函数图象经过怎样的平移与伸缩变换可得到x y sin =的图象。
2025届高三上学期月考(三)(11月)数学试卷一、单选题(本大题共8小题)1.若复数满足,则( )z 1i34i z +=-z =A .B .C .D .252.已知数列的前项和,则等于( ){}n a n 22n S n n =-345a a a ++A .12B .15C .18D .213.抛物线的焦点坐标为( )24y x =A .B .(1,0)(1,0)-C .D .1(0,)16-1(0,164.如图是函数的部分图象,则函数的解析式可为( )()sin y x ωϕ=+A .B .πsin 23y x ⎛⎫=- ⎪⎝⎭πsin 3y x ⎛⎫=+ ⎪⎝⎭C .D .πsin 26y x ⎛⎫=+ ⎪⎝⎭5πcos 26y x ⎛⎫=- ⎪⎝⎭5.1903年,火箭专家、航天之父康斯坦丁・齐奥尔科夫斯基就提出单级火箭在不考虑空气阻力和地球引力的理想情况下的最大速度满足公式:,其中v 1201lnm m v v m +=分别为火箭结构质量和推进剂的质量,是发动机的喷气速度.已知某单级火12,m m 0v 箭结构质量是推进剂质量的2倍,火箭的最大速度为,则火箭发动机的喷气8km /s 速度为( )(参考数据:,)ln20.7≈ln3 1.1,ln4 1.4≈≈A .B .C .D .10km /s 20km /s80km /s 340km /s6.若,,则的值为( )83cos 5αβ=63sin 5αβ=()cos αβ+A .B .C .D .7.如图,一个质点从原点O 出发,每隔一秒随机向左或向右移动一个单位长度,向左的概率为,向右的概率为,共移动4次,则该质点共两次到达1的位置的概2313率为( )A .B .C .D .42782729498.设为数列的前n 项和,若,且存在,,n S {}n a 121++=+n n a a n *N k ∈1210k k S S +==则的取值集合为( )1a A .B .{}20,21-{}20,20-C .D .{}29,11-{}20,19-二、多选题(本大题共3小题)9.如图,在正方体中,点,分别为,的中点,则下列说1111ABCD A B C D -E F 1AD DB 法正确的是( )A .直线与为异面直线B .直线与所成的角为EF 11D B 1D E1DC 60C .D .平面1D F AD⊥//EF 11CDD C 10.已知是圆上的动点,直线与P 22:4O x y +=1:cos sin 4l x y θθ+=交于点,则( )2:sin cos 1l x y θθ-=Q A .B .直线与圆相切12l l ⊥1l OC .直线与圆截得弦长为D .的值为2l O OQ11.已知三次函数有三个不同的零点,,,()32f x ax bx cx d=+++1x 2x ()3123x x x x <<函数也有三个零点,,,则( )()()1g x f x =-1t 2t()3123t t t t <<A .23b ac>B .若,,成等差数列,则1x 2x 3x 23b x a=-C .1313x x t t +<+D .222222123123x x x t t t ++=++三、填空题(本大题共3小题)12.已知随机变量服从二项分布,若,,则 .X (),B n p ()3E X =()2D X =n =13.已知平面向量,满足,,且在上的投影向量为,则a b 2a = 1= b b a 14a - 为 .a b+ 14.如图,已知四面体的体积为32,,分别为,的中点,,ABCD E F AB BC G 分别在,上,且,是靠近点的四等分点,则多面体的体积H CD AD G H D EFGHBD 为 .四、解答题(本大题共5小题)15.设的内角,,的对边分别为,,,已知.ABC A B C a b c sin cos 0a B A =(1)求;A(2)若,且的面积为的值.sin sin 2sin B C A +=ABC a 16.设,.()()221ln 2f x x ax x x=++a ∈R (1)若,求在处的切线方程;0a =()f x 1x =(2)若,试讨论的单调性.a ∈R ()f x 17.已知四棱锥,底面为菱形,为上的点,过的P ABCD -ABCD ,PD PB H =PC AH 平面分别交于点,且∥平面.,PB PD ,M N BD AMHN(1)证明:;MN PC ⊥(2)当为的中点,与平面所成的角为,求平面H PC ,PA PC PA ==ABCD 60︒与平面所成的锐二面角的余弦值.PAM AMN18.已知双曲线的左、右焦点为,,过的直线与双曲线交于,22:13y x Γ-=1F 2F 2F l ΓA 两点.B (1)若轴,求线段的长;AB x ⊥AB (2)若直线与双曲线的左、右两支相交,且直线交轴于点,直线交轴l 1AF y M 1BF y 于点.N (i )若,求直线的方程;11F AB F MNS S = l (ii )若,恒在以为直径的圆内部,求直线的斜率的取值范围.1F 2F MN l 19.已知是各项均为正整数的无穷递增数列,对于,设集合{}n a *k ∈N ,设为集合中的元素个数,当时,规定.{}*k i B i a k=∈<N ∣kb kB k B =∅0k b =(1)若,求,,的值;2n a n =1b 2b 17b (2)若,设的前项和为,求;2n n a =n b n n S 12n S +(3)若数列是等差数列,求数列的通项公式.{}n b {}n a参考答案1.【答案】C【详解】由可得,1i 34i z +=-()()()()1i 34i 1i 17i 34i 34i 34i 25z +++-+===--+故选:C 2.【答案】B 【详解】因为数列的前项和,{}n a n 22n S n n =-所以.34552=a a a S S ++-()2252522215=-⨯--⨯=故选:B.3.【答案】D【详解】解:由,得,24y x =214x y =所以抛物线的焦点在轴的正半轴上,且,y 124p =所以,,18p =1216p =所以焦点坐标为,1(0,16故选:D 4.【答案】A【详解】观察图象可得函数的最小正周期为,()sin y x ωϕ=+2ππ2π36T ⎛⎫=-= ⎪⎝⎭所以,故或,排除B ;2ππω=2ω=2ω=-观察图象可得当时,函数取最小值,π2π5π63212x +==当时,可得,,2ω=5π3π22π+122k ϕ⨯+=Z k ∈所以,,排除C ;2π2π+3k ϕ=Z k ∈当时,可得,,2ω=-5ππ22π122k ϕ-⨯+=-Z k ∈所以,,π2π+3k ϕ=Z k ∈取可得,,0k =π3ϕ=故函数的解析式可能为,A 正确;πsin 23y x ⎛⎫=- ⎪⎝⎭,D 错误5ππππcos 2cos 2sin 26233y x x x ⎛⎫⎛⎫⎛⎫=-=+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故选:A.5.【答案】B 【详解】由题意,,122m m =122200122lnln 82m m m m v v v m m ++===得,故,03ln82v =0888203ln3ln 2 1.10.7ln 2v ==≈=--故选:B 6.【答案】C 【详解】因为,,83cos 5αβ=63sin 5αβ=所以,,25(3cos 4)62αβ=2(3sin)2536αβ=即所以,2259cos co 6s 1042cos ααββ++=,229sin sin +10sin2536ααββ-=两式相加得,9)104αβ+++=所以cos()αβ+=故选:C .7.【答案】A【详解】共移动4次,该质点共两次到达1的位置的方式有和0101→→→,且两种方式第次移动向左向右均可以,0121→→→4所以该质点共两次到达1的位置的概率为.211124333332713⨯⨯+⨯⨯=故选:A.8.【答案】A 【详解】因为,121++=+n n a a n 所以,()()()()()()212342123+41=++++++37+41=212n n n n n S a a a a a a n nn --⋅⋅⋅=++⋅⋅⋅-=+假设,解得或(舍去),()2=21=210n S n n +=10n 21=2n -由存在,,所以有或,*N k ∈1210kk S S +==19k =20k =由可得,,两式相减得:,121++=+n n a a n +1223n n a a n ++=+22n n a a +-=当时,有,即,20k =2021210S S ==210a =根据可知:数列奇数项是等差数列,公差为2,22n n a a +-=所以,解得,()211+11120a a =-⨯=120a =-当时,有,即,19k =1920210S S ==200a =根据可知:数列偶数项也是等差数列,公差为2,22n n a a +-=所以,解得,()202+10120a a =-⨯=218a =-由已知得,所以.123a a +=121a =故选:A.9.【答案】ABD【详解】如图所示,连接,,,AC 1CD EF 由于,分别为,的中点,即为的中点,E F 1AD DB F AC 所以,面,面,1//EF CD EF ⊄11CDD C 1CD ⊆11CDD C 所以平面,即D 正确;//EF 11CDD C 所以与共面,而,所以直线与为异面直线,即A 正确;EF 1CD 1B ∉1CD EF 11D B 连接,易得,1BC 11//D E BC 所以即为直线与所成的角或其补角,1DC B ∠1D E 1DC 由于为等边三角形,即,所以B 正确;1BDC 160DC B ∠=假设,由于,,所以面,1D F AD ⊥1AD DD ⊥1DF DD D = AD ⊥1D DF 而面显然不成立,故C 错误;AD ⊥1D DF 故选:ABD.10.【答案】ACD 【详解】选项A :因,故,A 正确;()cos sin sin cos 0θθθθ+-=12l l ⊥选项B :圆的圆心的坐标为,半径为,O O ()0,02r =圆心到的距离为,故直线与圆相离,故B 错误;O 1l 14d r==>1l O 选项C :圆心到的距离为,O 1l21d ==故弦长为,故C正确;l ==选项D :由得,cos sin 4sin cos 1x y x y θθθθ+=⎧⎨-=⎩4cos sin 4sin cos x y θθθθ=+⎧⎨=-⎩故,()4cos sin ,4sin cos Q θθθθ+-故,故D 正确OQ ==故选:ACD 11.【答案】ABD 【详解】因为,()32f x ax bx cx d=+++则,,对称中心为,()232f x ax bx c '=++0a ≠,33bb f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对于A ,因为有三个不同零点,所以必有两个极值点,()f x ()f x 即有两个不同的实根,()2320f x ax bx c '=++=所以,即,故A 正确;2Δ4120b ac =->23b ac >对于B ,由成等差数列,及三次函数的中心对称性,123,,x x x 可知为的对称中心,所以,故B 正确;()()22,x f x ()f x 23b x a =-对于C ,函数,当时,,()()1g x f x =-()0g x =()1f x =则与的交点的横坐标即为,,,1y =()y f x =1t 2t 3t 当时,画出与的图象,0a >()f x 1y =由图可知,,,则,11x t <33x t <1313x x t t +<+当时,则,故C 错误;0a <1313x x t t +>+对D ,由题意,得,()()()()()()32123321231a x x x x x x ax bx cx d a x t x t x t ax bx cx d ⎧---=+++⎪⎨---=+++-⎪⎩整理,得,123123122331122331b x x x t t t ac x x x x x x t t t t t t a ⎧++=++=-⎪⎪⎨⎪++=++=⎪⎩得,()()()()2212312233112312233122x x x x x x x x x t t t t t t t t t ++-++=++-++即,故D 正确.222222123123x x x t t t ++=++故选:ABD.12.【答案】9【详解】由题意知随机变量服从二项分布,,,X (),B n p ()3E X =()2D X =则,即得,()3,12np np p =-=1,93p n ==故答案为:913.【答案】【详解】因为在上的投影向量为,b a14a -所以,又,14b a a a aa ⋅⋅=-2a =所以,又,1a b ⋅=-1= b 所以a b+==== 故答案为:14.【答案】11【详解】如图,连接,则多面体被分成三棱锥和四棱锥.,EG ED EFGHBD G EDH -E BFGD -因是上靠近点的四等分点,则,H AD D 14DHE AED S S =又是的中点,故,E AB 11114428DHE AED ABD ABD S S S S ==⨯= 因是上靠近点的四等分点,则点到平面的距离是点到平面的G CD D G ABD C ABD 距离的,14故三棱锥的体积;G EDH -1113218432G EDH C ABD V V --=⨯=⨯=又因点是的中点,则,故,F BC 133248CFG BCD BCD S S S =⨯= 58BFGD BCD S S =又由是的中点知,点到平面的距离是点到平面的距离的,E AB E BCD A BCD 12故四棱锥的体积,E BFGD -51532108216E BFGD A BCD V V --=⨯=⨯=故多面体的体积为EFGHBD 11011.G EDH E BFGD V V --+=+=故答案为:11.15.【答案】(1)π3A =(2)2a =【详解】(1)因为,即,sin cos 0a B A =sin cos a B A =由正弦定理得,sin sin cos A B B A ⋅=⋅因为,所以,则,sin 0B ≠sin A A =tan A =又,所以.()0,πA ∈π3A =(2)因为,由正弦定理得,sin sin 2sin B C A +=2b c a +=因为,所以,π3A =11sin 22ABC S bc A bc === 4bc =由余弦定理,得,2222cos a b c bc A =+-⋅224b c bc +-=所以,则,解得.()234b c bc +-=()22344a -⨯=2a =16.【答案】(1)4230--=x y (2)答案见解析【详解】(1)当时,,,因0a =()221ln 2f x x x x=+()2(ln 1)f x x x =+',1(1),(1)22f f '==故在处的切线方程为,即;()f x 1x =12(1)2y x -=-4230--=x y (2)因函数的定义域为,()()221ln 2f x x ax x x=++(0,)+∞,()(2)ln 2(2)(ln 1)f x x a x x a x a x =+++=++'① 当时,若,则,故,即函数在2a e ≤-10e x <<ln 10,20x x a +<+<()0f x '>()f x 上单调递增;1(0,e 若,由可得.1e x >20x a +=2a x =-则当时,,,故,即函数在上单调1e 2a x <<-20x a +<ln 10x +>()0f x '<()f x 1(,e 2a-递减;当时,,故,即函数在上单调递增;2a x >-ln 10,20x x a +>+>()0f x '>()f x (,)2a-+∞② 当时,若,则,故,即函数在2e a >-1e x >ln 10,20x x a +>+>()0f x '>()f x 上单调递增;1(,)e +∞若,则,故,即函数在上单调递减;12e a x -<<ln 10,20x x a +<+>()0f x '<()f x 1(,)2e a -若,则,故,即函数在上单调递增,02a x <<-ln 10,20x x a +<+<()0f x '>()f x (0,2a-当时,恒成立,函数在上单调递增,2e a =-()0f x '≥()f x ()0,+∞综上,当时,函数在上单调递增,在上单调递减,在2e a <-()f x 1(0,)e 1(,)e 2a -上单调递增;(,)2a-+∞当时,函数在上单调递增;2e a =-()f x ()0,+∞当时,函数在上单调递增,在上单调递减,在上2e a >-()f x (0,2a -1(,2e a -1(,)e +∞单调递增.17.【答案】(1)证明见详解【详解】(1)设,则为的中点,连接,AC BD O = O ,AC BD PO 因为为菱形,则,ABCD AC BD ⊥又因为,且为的中点,则,PD PB =O BD PO BD ⊥,平面,所以平面,AC PO O = ,AC PO ⊂PAC BD ⊥PAC 且平面,则,PC ⊂PAC BD PC ⊥又因为∥平面,平面,平面平面,BD AMHN BD ⊂PBD AMHN PBD MN =可得∥,所以.BD MN MN PC ⊥(2)因为,且为的中点,则,PA PC =O AC PO AC ⊥且,,平面,所以平面,PO BD ⊥AC BD O = ,AC BD ⊂ABCD ⊥PO ABCD 可知与平面所成的角为,即为等边三角形,PA ABCD 60PAC ∠=︒PAC 设,则,且平面,平面,AH PO G = ,G AH G PO ∈∈AH ⊂AMHN PO ⊂PBD 可得平面,平面,∈G AMHN ∈G PBD 且平面平面,所以,即交于一点,AMHN PBD MN =G MN ∈,,AH PO MN G 因为为的中点,则为的重心,H PC G PAC 且∥,则,BD MN 23PM PN PG PB PD PO ===设,则,2AB=11,32PA PC OA OC AC OB OD OP ========如图,以分别为轴,建立空间直角坐标系,,,OA OB OP ,,x y z 则,)()22,0,0,3,0,,1,0,,133AP M N ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭可得,()24,1,0,,0,33AM NM AP ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭设平面的法向量,则,AMN ()111,,x n y z =1111203403n AM y z n NM y ⎧⋅=++=⎪⎪⎨⎪⋅==⎪⎩ 令,则,可得,11x=110,y z ==(n = 设平面的法向量,则,PAM ()222,,m x y z =2222220330m AM y z m AP z ⎧⋅=++=⎪⎨⎪⋅=+=⎩ 令,则,可得,2x =123,1y z ==)m = 可得,cos ,n m =所以平面与平面所成的锐二面角的余弦值PAMAMN18.【答案】(1)线段的长为;AB 6(2)(i)直线的方程为;l 2x y =+(ii )直线的斜率的取值范围为.l 33()(44- 【详解】(1)由双曲线的方程,可得,所以22:13y x Γ-=221,3a b ==,1,2a b c ====所以,,若轴,则直线的方程为,1(2,0)F -2(2,0)F AB x ⊥AB 2x =代入双曲线方程可得,所以线段的长为;(2,3),(2,3)A B -AB 6(2)(i)如图所示,若直线的斜率为0,此时为轴,为左右顶点,此时不构成三角形,矛l l x ,A B 1,,F A B 盾,所以直线的斜率不为0,设,,l :2l x ty =+1122()A x y B x y ,,(,)联立,消去得,应满足,22132y x x ty ⎧-=⎪⎨⎪=+⎩x 22(31)1290t y ty -++=t 222310Δ14436(31)0t t t ⎧-≠⎨=-->⎩由根与系数关系可得,121222129,3131t y y y y t t +=-=--直线的方程为,令,得,点,1AF 110(2)2y y x x -=++0x =1122y y x =+112(0,)2y M x +直线的方程为,令,得,点,1BF 220(2)2y y x x -=++0x =2222y y x =+222(0,)2y N x +,121122221111|||||2||2|F F F B A A F B F S y F S S F y y y -=⨯-==- 111212221||||||222F M N M F MN N S y y x y y y y x x =-=-=-++ ,12122112212121212222(4)2(4)8()||||||44(4)(4)4()16y y y ty y ty y y ty ty ty ty t y y t y y +-+-=-==+++++++由,可得,11F AB F MN S S = 1212212128()||2||4()16y y y y t y y t y y -=-+++所以,所以,21212|4()16|4t y y t y y +++=222912|4()16|43131tt t t t ⨯+-+=--解得,,解得,22229484816||431t t t t -+-=-22916||431t t -=-22021t =经检验,满足,所以222310Δ14436(31)0t t t ⎧-≠⎨=-->⎩t =所以直线的方程为;l 2x y =+(ii )由,恒在以为直径的圆内部,可得,1F 2F MN 2190F MF >︒∠所以,又,110F F N M < 112211,22(2,)(2,22F y y N x x M F =+=+所以,所以,1212224022y y x x +⨯<++121210(2)(2)y y x x +<++所以,所以,1221212104()16y y t y y t y y +<+++2222931109124()163131t t t t t t -+<⨯+-+--所以,解得,解得或,22970916t t -<-271699t <<43t <<43t -<<经检验,满足,222310Δ14436(31)0t t t ⎧-≠⎨=-->⎩所以直线的斜率的取值范围为.l 33()(44- 19.【答案】(1)12170,1,4b b b ===(2)1(1)22n n +-⨯+(3)n a n=【详解】(1)因为,则,2n a n =123451,4,9,16,25a a a a a =====所以,,{}*11i B i a =∈<=∅N ∣{}*22{1}i B i a =∈<=N ∣,{}*1717{1,2,3,4}i B i a =∈<=N ∣故.12170,1,4b b b ===(2)因为,所以,2nn a =123452,4,8,16,32a a a a a =====则,所以,,**12{|1},{|2}i i B i a B i a =∈<=∅=∈<=∅N N 10b =20b =当时,则满足的元素个数为,122i i k +<≤ia k <i 故,121222i i i b b b i+++==== 所以()()()1112345672122822n n n n S b b b b b b b b b b b ++++=++++++++++++ ,1212222n n =⨯+⨯++⨯ 注意到,12(1)2(2)2n n nn n n +⨯=-⨯--⨯所以121321202(1)21202(1)2(2)2n n nS n n ++=⨯--⨯+⨯-⨯++-⨯--⨯ .1(1)22n n +=-⨯+(3)由题可知,所以,所以,11a ≥1B =∅10b =若,则,,12a m =≥2B =∅1{1}m B +=所以,,与是等差数列矛盾,20b =11m b +={}n b 所以,设,11a =()*1n n n d a a n +=-∈N 因为是各项均为正整数的递增数列,所以,{}n a *n d ∈N 假设存在使得,设,由得,*k ∈N 2k d ≥k a t =12k k a a +-≥12k a t ++≥由得,,与是等差数列矛盾,112k k a t t t a +=<+<+≤t b k <21t t b b k ++=={}n b 所以对任意都有,*n ∈N 1nd =所以数列是等差数列,.{}n a 1(1)n a n n =+-=。
湖南省株洲市2018届高三数学第三次(11月)月考试题(无答案)
时量:120 分钟分值:150 分
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知全集U={2,3,4,5,6,7},集合A={4,5,7},B={4,6},则A ∩(U B)=()
A. {5}
B. {2}
C. {2, 5}
D. {5, 7}
(2)复数z 与复数i(2 i) 互为共轭复数(其中i 为虚数单位),则z ()
A. 1
2i
B. 1
2i
C. 1
2i
D. 1 2i
y≤5 x
(3)已知直线x y 5 0 与两坐标轴围成的区域为M ,不等式
组 x≥0
所形成的区域为N,现在区域M 中随机放置一点,则该点落在区域N 的概率是()
y≥
3x
A.
3
4
B.
1
2
C.
1
4
D.
2
3
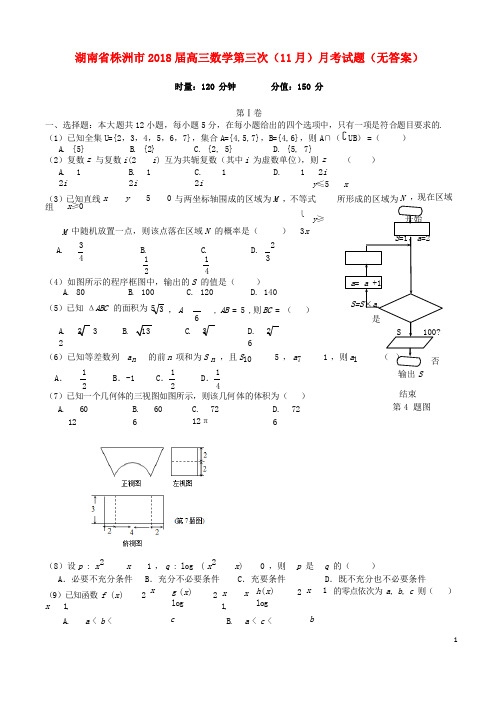
(4)如图所示的程序框图中,输出的S 的值是()
A. 80
B. 100
C. 120
D. 140
(5)已知ΔABC 的面积为53 ,A , AB = 5 ,则BC = ()
6
A. 3 C. 3
2
D. 2
6
(6)已知等差数列 a n 的前n 项和为S n ,且S10 5 ,a7 1
A.
1
2
B.-1 C.
1
2
D.
1
4
输出S
(7)已知一个几何体的三视图如图所示,则该几何体的体积为()结束
A. 60
12
B. 60
6
C. 72
12π
D. 72
6
第4 题图
(8)设p : x2 x 1,q :log (x2 x) 0 ,则 p 是 q 的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件
(9)已知函数f (x) 2
x
x 1,
g(x)
log
2 x x
1,
h(x)
log
2 x 1 的零点依次为a, b, c 则()
A. a< b< c
B. a< c< b
C. b< c< a
D. b< a<
c
(10)在正三棱锥内有一半球,其底面与正三棱锥的底面在同一平面内,正三棱锥的三个侧面都和半球相
切.如果半球的半径等于1,正三棱锥的底面边长为,则正三棱锥的高等于()
A B. C. D.
⎣ (11)已知双曲线 x 2 y 2
1(a 0, b 0) 与抛物线 y 2 = 2 px ( p > 0) 有相同的焦点 F ,且双曲
线的一条 a 2 b 2
渐近线与抛物线的准线交于点 M (-3,t ),若 MF ,则双曲线的离心率为( ) 2 2 3 5
A. B. C. 2 3 2
D. 5
( 12 ) 已知函数 f x 在定义域 R 上的导函数为 f x
,若方程 f x 0
无解 , 且
f f ( x ) 2017x
2017, 当 g x sin x cos x kx 在
, 上与 f x 在 R 上的单调性相同时,则 实数 k 的取值范围是 (
) 2 2 A. , 1 B. 2
C. 1, 2
D.
第 II 卷
本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22) 题~第(23)题为选考题,考生根据要求作答. 二、填空题:本大题共 4 小题,每小题 5 分. (13)设ln 2 a , ln 3 b ,则 e a e b .(其中 e 为自然对数的底数)
(14) 设直线l 1 : mx (m 1) y 1 0(m R ) ,若
直线 l 1 为圆 x m . 2 y 2
2 y
3 0 的一条对称轴,则实数
(15)在 ABC 中,过中线 AD E 任作一直线分别交边 AB 、 AC 于 M 、 N 两点,设 AM x AB , AN y AC x , y 0 , 则4x y 的最小值是
.
(16)已知函数 f
x x m e x
(其中
e 为自然对数的底数),曲线 y
线在这两点处的切线都与 y 轴垂直,则实数 m 的取值范围是 . 三、解答题:解答应写出文字说明,证明过程或演算步骤. f x 上存在不同的两点,使得
曲
(17) (本小题满分 12 分)若a
3 sin x , cos x , b cos x , cos x , 0, x R , f x a b 1
,
2
且 f x 的最小正周期是 ,设 ABC 三个角 A , B , C 的对边分别为 a , b , c .
(Ⅰ)求
(Ⅱ)若 c
7 , f C 1 , sin B
3sin A ,求
2
a,b 的值.
(18)(本小题满分 12 分)传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火 爆荧屏。
将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了 100 名选 手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的 2×2 列联表,并据此资料你是
否有
95
注:K 2
( bc )2 ,其中 n a b c d . (a b )(c d )(a c )(b d )
(Ⅱ)若参赛选手共 6 万人,用频率估计概率,试估计其中优秀等级的选手人数; (Ⅲ)在优秀等级的选手中取 6 名,依次编号为 1,2,3,4,5,6,在良好等级的选手中取 6 名,依次编号 为 1,2,3,4,5,6,在选 出的 6 名优秀等级的选手中任取一名,记其编号为a , 在选出的 6 名良好等级的
ax by 3
选手中任取一名,记其编号为 b ,求使得方程组
x 2 y 2
有唯一一组实数解 ( x , y ) 的概率.
(19)(本小题满分 12 分)如图,在三棱锥 A -BCD 中, AD DC 2, 平面 ADC 平面 ABC , M 为 AB 的中点. (Ⅰ)求证: BC 平面 ADC ; (Ⅱ)求直线 AD 与平面 DMC 所成角的正弦值.
AD DC , AC CB , AB 4 ,
第 19 题图
(20)(本小题满分 12 分)已知 E (1, 0) , K ( 1, 0) , P 是平面上一动点,且满足| PE | • | KE | PK • EK .
(Ⅰ)求点 P 的轨迹 C 对应的方程;
(Ⅱ)过点K 的直线l 与C 相交于A、B 两点(A 点在x 轴上方),点A 关于x 轴的对称点为D ,且EA•EB 8 ,求 ABD 的外接圆的方程.
(21)(本小题满分 12 分) 已知函数 f ( x ) a x x 2 x ln a (a 0, a 1) . (Ⅰ)当 a e 时,判断函数 f (x ) 的单调性;
(Ⅱ)若存在 x 1 , x 2 [ 1,1] ,使得| f ( x 1 ) f ( x 2 ) | e 1 ( e 是自然对数的底数),求实数 a 的取值范围.
请考生在 22、23 两题中任选一题作答,如果多做,则按所做的第一题计分. (22)(本小题满分 10 分)[选修 4-4:坐标系与参数方程选讲]
x 已知过点 P (a , 0) 的直线 l 的参数方程是
3
t 2
( t 为参数),以平面直角坐标系的原点为极点,x 轴 y 1 t 2
的正半轴为极轴,建立极坐标系,曲线 C 的极坐标方 程为 4 cos . (Ⅰ)求直线 l 的普通方程和曲线 C 的直角坐标方程;
(Ⅱ)若直线 l 与曲线 C 交于
A ,
B 两点,试问是否存在实数 a ,使得 求出实数
a 的值;若不存在,说明理由.
(23)(本小题满分 10 分)[选修 4-5:不等式选讲]
x , 0 x
1
PA PB 6 且 AB 4 ?若存在, 已知函数 f ( x )
1
, x 1 x
, g ( x ) af ( x ) x 1 . (Ⅰ)当 a 0 时,若 g ( x ) x 2 b 对任意 x 0, 恒成立,求实数b 的取值范围;
(Ⅱ)当 a 1时,求 g ( x ) 的最大值.。