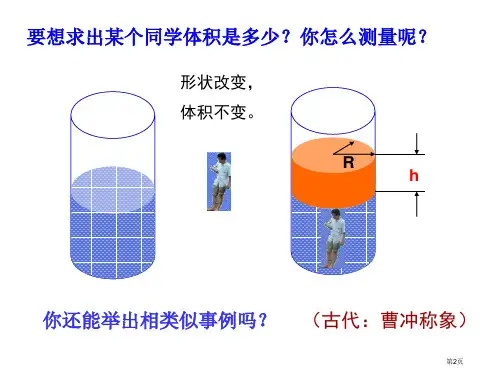
要想求出某个同学体积是多少?你怎么测量呢?
形状改变, 体积不变。
Rபைடு நூலகம்h
你还能举出相类似事例吗? (古代:曹冲称象)
第2页
想一想:
请指出以下过程中,哪些量发生了改变,哪 些量保持不变? 1、把一小杯水倒入另一只大杯中;
解:水底面积、高度发生了改变,水体积和质量都保持不变
2、用一根15cm长铁丝围成一个三角形,然后把 它围成长方形;
在处理实际问题时,我们普通能够经过分析实 际问题, 抽象出数学问题, 然后利用数学思想方法 处理问题.用列表分析数量关系是惯用方法.
第11页
例3、学校组织初三年级100名团员去参加植树活动, 假如挖坑,一天每人能挖树坑3个;假如植树,一天每 人能植树7棵,要使每个树坑恰好能种上一棵树,问应 安排几个人去挖坑,几个人去种树?
方案四
23(x 6) 23x
第5页
一纪念碑建筑底面呈正方形,其四面铺 上花岗岩,形成一个宽为3米正方形边框 (如图中阴影部分),已知铺这个边框恰 好用了192块边长为0.75米正方形花岗岩, 问纪念碑建筑底面边长是多少米?
3x
3 阴影部分面积= 192块边长为0.75正方形花岗岩面积 阴影部分面积= 4个长为(x+3)米、宽为3米长方形
第13页
4.按图示方法搭1个三角形需要3根火柴棒,搭2个三角 形需要5根火柴棒.设共搭成n 个三角形,你怎样用关 于是 n 代数式表示n 个三角形需要火柴棒根数? 现 有根火柴棒,能搭几个这么三角形? 2100根呢?
第14页
1、善于利用图形面积、体积、周长及质量等 捕捉等量关系,从而列出方程。 2、善于用列表分析数量关系。
3、对于等积变形问题,它基本数量关系是相关面积公式,相 等关系特征是存在不变量,也就是用不一样方法来计算阴影 部分面积,面积不变。