下载文档原格式
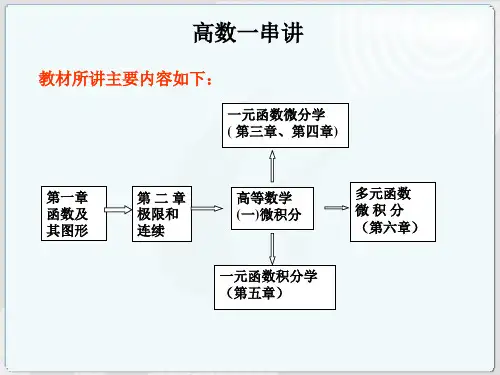
高等数学1：一元函数微积分学
一元函数微积分学是一门具有普遍价值的数学课程，它是描述数学中一元函数的变化趋势以及求解相关问题的一种数学方法。
一元函数微积分学的基础是微积分学，它是由法国数学家库仑发明的一种数学方法，主要是研究函数的微小变化。
微积分学的结果就是一元函数微积分学，它是一种研究函数变化趋势的方法，可以描述函数在各个点的变化状态，也可以用来求解函数的极值和极限，从而获得函数的全局特征。
研究一元函数微积分学需要掌握一些基本概念，如函数极限、微分、导数、极值等，这些概念可以帮助我们更好地理解函数的变化趋势，有助于求解函数的极值、极限等问题。
在研究一元函数微积分学时，除了要掌握一些基本概念外，还要掌握一些解决问题的方法，如泰勒公式、换元法和求积分等。
这些方法可以帮助我们研究函数的变化趋势，从而更好地理解函数的特征。
总之，一元函数微积分学是一门十分重要的数学课程，它能够帮助我们更好地理解函数的变化趋势，有助于求解函数的极值和极限，从而获得函数的全局特征。
研究一元函数微积分学时，除了要掌握一些基本概念外，还要掌握一些解决问题的
方法，如泰勒公式、换元法和求积分等。
只有掌握了这些方法，才能更好地理解函数的特征，并能够解决函数相关的问题。
第二章 一元函数微分学§2、1 导数与微分(甲)内容要点一、导数与微分概念 1、导数的定义设函数)(x f y =在点0x 的某领域内有定义,自变量x 在0x 处有增量x ∆,相应地函数增量)()(00x f x x f y -∆+=∆。
如果极限x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim0000存在,则称此极限值为函数)(x f 在0x 处的导数(也称微商),记作0()f x ',或x x y =',x x dxdy=,)(x x dxx df =等,并称函数)(x f y =在点0x 处可导。
如果上面的极限不存在,则称函数)(x f y =在点0x 处不可导。
导数定义的另一等价形式,令x x x ∆+=0,0x x x -=∆,则0000()()()lim x x f x f x f x x x →-'=-我们也引进单侧导数概念。
右导数:0000000()()()()()lim lim x x x f x f x f x x f x f x x x x +++→∆→-+∆-'==-∆ 左导数:0000000()()()()()lim lim x x x f x f x f x x f x f x x x x---→∆→-+∆-'==-∆ 则有)(x f 在点0x 处可导)(x f ⇔在点0x 处左、右导数皆存在且相等。
2.导数的几何意义与物理意义如果函数)(x f y =在点0x 处导数0()f x '存在,则在几何上0()f x '表示曲线)(x f y =在点()(,00x f x )处的切线的斜率。
切线方程:000()()()y f x f x x x '-=- 法线方程:00001()()(()0)()y f x x x f x f x '-=--≠'设物体作直线运动时路程S 与时间t 的函数关系为)(t f S =,如果0()f t '存在,则0()f t '表示物体在时刻0t 时的瞬时速度。
