事件的关系及运算

事件的关系和运算：
〔1〕包含关系
一般地，对于事件A与事件B，如果事件A发生，则事件B 一定发生，这时称事件B包含事件A（或称事件A包含于事件B）,
记作 BA （ 或 AB) 。
如图：
BA
例.事件C1 ={出现 1 点 }发生，则事件 H ={出现的点数为奇数 }也
一定会发生，所以 H C1 . 注：不可能事件记作 ，任何事件都包括不可能事件。
事件的关系和运算：
〔1〕包含关系: BA （ 或 AB)
〔2〕相等关系: A=B (BA且 AB)
〔3〕并事件〔和事件〕: AB （ 或 AB ）
〔4〕交事件〔积事件〕:
A B （ 或 AB ）
〔5〕互斥事件: A B
〔6〕互为对立事件: A B 且 A B是必然事件
第九页，编辑于星期五：十点 三十五分。
事件的关系和运算：
〔6〕互为对立事件
若AB 为不可能事件，A B 为必然事件，那么称事件
A 与事件B互为对立事件，其含义是：事件A与事件B在任何一次试 验中有且仅有一个发生。
如图：
A
B
例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数} 即为互为对立事件。
第八页，编辑于星期五：十点 三十五分。
第四页，编辑于星期五：十点 三十五分。
事件的关系和运算：
〔3〕并事件〔和事件〕
若某事件发生当且仅当事件A发生或事件B发生，则称此事件 为事件A和事件B的并事件（或和事件），记作 AB （ 或 AB ） 。
如图：
BA B A
例事.若件事C件1JC=1C5{J出={现出 C5 ={出现
第五页，编辑于星期五：十点 三十五分。
D2 ={ 出现的点数大于 3 }；

事件的关系和运算事件的关系常用的有包含关系、互斥关系和独立关系。

事件的运算常用的有并运算、交运算、差运算和补运算。

1. 包含关系：如果事件A发生必然导致事件B发生，则称事件B包含事件A，记作A⊆B。

例如，事件A为"今天下雨"，事件B为"今天有降水"，则A⊆B，因为当今天下雨时，当然也说明今天有降水。

2. 互斥关系：如果事件A和事件B不能同时发生，则称事件A和事件B互斥，记作A∩B=Ø。

例如，事件A为"掷一次骰子，结果为奇数"，事件B为"掷一次骰子，结果为偶数"，则A∩B=Ø，因为掷一次骰子的结果不可能既是奇数又是偶数。

3. 独立关系：如果事件A的发生与发生或不发生事件B无关，则称事件A和事件B独立，记作P(A|B) = P(A)，其中P(A|B)表示在事件B发生的条件下事件A发生的概率。

例如，事件A为"掷一次骰子，结果为1"，事件B为"抽一张牌，结果为红心"，则A和B是独立事件，因为掷骰子的结果不会受到抽牌的影响。

事件的运算包括：1. 并运算：事件A∪B表示事件A和事件B中至少一个事件发生的情况。

例如，事件A为"今天下雨"，事件B为"今天有降雨"，则A∪B表示今天下雨或者今天有降雨。

2. 交运算：事件A∩B表示事件A和事件B同时发生的情况。

例如，事件A为"掷一次骰子，结果为奇数"，事件B为"掷一次骰子，结果为3"，则A∩B表示掷一次骰子的结果既是奇数又是3。

3. 差运算：事件A－B表示事件A发生但事件B不发生的情况。

例如，事件A为"今天下雨"，事件B为"今天有降雨"，则A－B表示今天下雨但今天没有降雨。

4. 补运算：事件A的补事件表示事件A不发生的情况，记作A'或Ac。

A
B
例.因为事件 C1 ={出现 1 点} 与事件C2 ={出现 2 点}不可能同时发 生，故这两个事件互斥。
事件的关系和运算：
（6）互为对立事件 若 A B 为不可能事件，A B 为必然事件，那么称事件A 与事件B互为对立事件，其含义是：事件A与事件B在任何一次试 验中有且仅有一个发生。 如图： A B
3.1.3 事件的关系与运算
在掷骰子的试验中，我们可以定义许多事件，如： C1 ={ 出现 1 点 }； C2 ={出现 2 点}； C3 ={ 出现 3 点 }； C4 ={ 出现 4 点 }； C5 ={出现 5 点}； C6 ={ 出现 6 点 }； D1 ={ 出现的点数不大于 1 }； D2 ={ 出现的点数大于 3 }； D3 ={ 出现的点数小于 5 }； E ={ 出现的点数小于 7 }; F ={ 出现的点数大于 6 }; G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 }; …… 思考： 1. 上述事件中有必然事件或不可能事件吗？有的话，哪些是？
如图：
B A B A
例.若事件 M={出现 1 点且 5 点}发生，则 事件 C1 ={出现 1 点} 与事件 C5 ={出现 5 点} 同时发生，则 M C1 C5 .
事件的关系和运算：
（5）互斥事件 若 A B 为不可能事件（ A B ），那么称事件A与 事件B互斥，其含义是：事件A与事件B在任何一次试验中都不 会同时发生。 如图：
如图：
BA B
A
例.若事件 J={出现 1 点或 5 点 } 发生，则 事件C1 ={出现 1 点 }与事件 C5 ={出现 5 点 }中至少有一个会发生，则 J C1 C5 .
事件的关系和运算：

同时 A B A AB
例如 A a,b,c, d B c, d,e, f A B a,b
例如： 体检 A1={身高合格} A2={体重不合格}
B ={身高合格且体重合格} B A1 A2
9
S6 : { t | t 0 }中 事件A ={ t | t 1000} “次品” 事件B ={ t | t 1000} “合格品”
19
例3 从一批 100件的产品中每次取出一个（取后不
放回），假设100件产品中有5件是次品，用事件AK 表示
第 k 次取到次品（k=1,2,3), 试用 A1 A2 A3 表示下列事件。
1、三次全取到次品。
A1 A2 A3
2、只有第一次取到次品
A1 A2 A3
3、三次中至少有一次取到次品 A1 UA2 UA3
1. A1 U A2 UL U An S
2. Ai A j (i j i, j 1,2, n)
则称 A1, A2, , An 为完备事件组。
A1
如:中华人民共和国地图由
31个省、市的版图（完备
A2
An 事件组）组成。
学生的考试成绩由 0－100分（101个完备事件组）组成。
14
第二节
第一章
事件的关系与运算
一 、事件的包含与相等 二、事件的运算与关系 三、事件的运算规律
1
事件间的关系及事件的运算
事件是一个集合，因而事件间的关系和运算,自然 按照集合论中的集合之间的关系和运算来处理。一次 随机试验, 有多个不同的事件发生。这些事件有些简单， 有些复杂。我们对其进行分析寻求它们之间的关系。
设事件 Ak 表示第 k 号管道正常工作，k=1，2，3。 B 表示“城市能正常供水”B，表示“城市断水”。

可推广到三个以上互不相容事件的和的 概率,即:
P(A+B+C+…)=P(A)+P(B)+P(C)+…
2, 概率的一般加法公式:
设A、B为任意两个事件，则 P(A+B)=P(A)+P(B)-P(AB) 显然, 互不相容事件的概率的加法公式 是一般加法公式的特例.
新授
一、对立事件的概率
P( A) 1 P( A)
课堂练习
教材P144 / 1，2，3，4, 5
课后作业
教材P145 / 1，2，3，6
1，四个人在议论逻一辑位推作理家的年龄。甲说
“她不会超过35岁。” 乙说“她不超过
40 岁。” 丙说“她的岁数在50以下。” 丁
说
“她绝对在40岁以上。” 实际上只有一 个
人说A、对甲了说。的那对么下列说法正确的是（ ） B、她的年龄在45~50岁之间 C、她的年龄在50岁以上 D、丁说的对
逻辑推理
2，经过破译敌人的密码，已经知道“香蕉
苹果大鸭梨”的意思是“星期三秘密进攻”，
“苹果甘蔗水蜜桃”的意思是“执行秘密计
划”，“广柑香蕉西红柿”的意思是“星期三
的胜利属于我们”，那么“大鸭梨”的意思
是
（）
A、秘密 C、进攻
B、星期三 D、执行
类比推理
先给出一对相关的词，要求从备选项 中找出一对与之在逻辑关系上最为贴近或 相似的词。
5．相互对立事件
如果“事件A与B满足: AB=φ且A+B=U 则称事件A与B为相互对立事件。
又称互为逆事件. A的对立事件记作：A
“A与B互为对立事件” 就是说: “A与B不能 同时发生(互不相容), 但二者必有一个发生.

第十八页，共二十三页。
知识点二 事件的运算 [例 2]在掷骰子的试验中，可以定义许多事件．例如，事件 C1＝{出 现 1 点}，事件 C2＝{出现 2 点}，事件 C3＝{出现 3 点}，事件 C4＝{出现 4 点}，事件 C5＝{出现 5 点}，事件 C6＝{出现 6 点}，事件 D1＝{出现的 点数不大于 1}，事件 D2＝{出现的点数大于 3}，事件 D3＝{出现的点数 小于 5}，事件 E＝{出现的点数小于 7}，事件 F＝{出现的点数为偶数}， 事件 G＝{出现的点数为奇数}，请根据上述定义的事件，回答下列问题： (1)请举出符合包含关系、相等关系的事件； (2)利用和事件的定义，判断上述哪些事件是和事件．
(2)因为事件 D2＝{出现的点数大于 3}＝{出现 4 点或出现 5 点或出现 6 点}，所以 D2＝C4∪C5∪C6(或 D2＝C4＋C5＋C6)．
同理可得，D3＝C1∪C2∪C3∪C4，E＝C1∪C2∪C3∪C4∪C5∪C6，F ＝C2∪C4∪C6，G＝C1∪C3∪C5.
第二十页，共二十三页。
[知识小结二]
事件运算应注意的 2 个问题 (1)进行事件的运算时，一是要紧扣运算的定义，二是要全 面考查同一条件下的试验可能出现的全部结果，必要时可利用 Venn 图或列出全部的试验结果进行分析． (2)在一些比较简单的题目中，需要判断事件之间的关系 时，可以根据常识来判断．但如果遇到比较复杂的题目，就得 严格按照事件之间关系的定义来推理．
第四页，共二十三页。
3．一个人打靶时连续射击两次，事件“至少有一次中靶”的互
斥事件是
()
A．至多有一次中靶
B．两次都中靶
C．只有一次中靶
D．两次都不中靶
解析：事件“至少有一次中靶”包括“中靶一次”和“中 靶两次”两种情况．由互斥事件的定义，可知“两次都不 中靶”与之互斥．

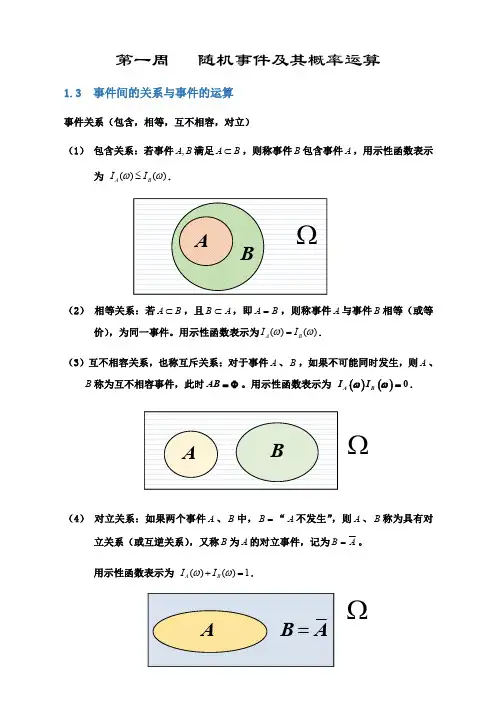
第一周随机事件及其概率运算1.3事件间的关系与事件的运算事件关系（包含，相等，互不相容，对立）（1）包含关系：若事件,A B 满足A B⊂，则称事件B 包含事件A ，用示性函数表示为()()ωω≤A B I I .（2）相等关系：若A B ⊂，且A B ⊂，即B A =，则称事件A 与事件B 相等（或等价），为同一事件。

用示性函数表示为()()A B I I ωω=.（3）互不相容关系，也称互斥关系：对于事件A 、B ，如果不可能同时发生，则A 、B 称为互不相容事件，此时AB =Φ。

用示性函数表示为()()0A B I I ωω=.（4）对立关系：如果两个事件A 、B 中，=B “A 不发生”，则A 、B 称为具有对立关系（或互逆关系），又称B 为A 的对立事件，记为A B =。

用示性函数表示为()()1ωω+=A B I I .ΩΩ*********************************************************事件运算（和，积，差，交换律，结合律，分配律，结合律，对偶律）（1）事件的和：事件A 与事件B 的并集构成的事件称为事件A 与事件B 的和事件，记为A B 或A B +，即{}|A B x x A x B =∈∈ 或，如图所示的阴影部分.显然，当且仅当事件A 与事件B 至少有一个发生时，事件A B 才发生。

n 个事件n A A A ,,,21 的和事件，即为n 个集合的并集 n k k A 1=。

（2）事件的积（或交）：事件A 与事件B 的交集构成的事件称为事件A 与事件B 的积（或交）事件，事件A 与事件B 同时发生。

记为A B 或AB 。

n 个事件n A A A ,,,21 的积事件，即为n 个集合的交集 nk k A 1=。

（3）事件的差：事件A 与事件B 的差集所构成的事件称为事件A 与事件B 的差事件，记为B A -。

{}|A B x x A x B AB -=∈∉=且。

可以发现，事件E1和事件E2同时发生，相当于事件C2发生，用集
合表示就是：1,22,3 2 ，即E1 E2 C2 ，这时我们称事件C2
为事件E1和事件E2的交事件。
交事件（积事件）
一般地，事件A与事件B同时发生，这样的一个事件 中的样本点既在事件A中，也在事件B中，我们称这 个事件为事件A和事件B的交事件（或积事件），记故“甲向南”意味着“ 乙向南”是不可能的，故是互斥事件，但不是对立事件.
二、事件的运算
例2 在掷骰子的试验中，可以定义许多事件.例如，事件C1＝{出现1 点}，事件C2＝{出现2点}，事件C3＝{出现3点}，事件C4＝{出现4点}， 事件C5＝{出现5点}，事件C6＝{出现6点}，事件D1＝{出现的点数不大 于1}，事件D2＝{出现的点数大于3}，事件D3＝{出现的点数小于5}， 事件E＝{出现的点数小于7}，事件F＝{出现的点数为偶数}，事件G＝ {出现的点数为奇数}，请根据上述定义的事件，回答下列问题：(1)请 举出符合包含关系、相等关系的事件；(2)利用和事件的定义，判断 上述哪些事件是和事件.
三、随机事件的表示及含义
例3 设A，B，C表示三个随机事件，试将下列事件用A，B，C 表示出来.(1)三个事件都发生；(2)三个事件至少有一个发生； (3)A发生，B，C不发生；(4)A，B都发生，C不发生；(5)A，B至 少有一个发生，C不发生；(6)A，B，C中恰好有两个发生.
解 (1)ABC (2)A∪B∪C (3) A B C (4)AB (5)(A∪B) (6)AB∪AC∪BC
A＝B
知识点二 交事件与并事件
观察事件：D1 1,2,3, E1 1,2, E2 2,3
可以发现，事件E1和事件E2至少有一个发生，相当于事件D1发生，

样本点时，不仅要考虑甲元件的状态，还要考用乙元件的状态 .
解：(1) 用x1，x2分别表示甲、乙两个元件的状态，则可用(x1，x2)
表示这个电路的状态．用1表示元件正常，用0表示元件失效，
则样本空间为： Ω={(0，0)，(1，0)，(0，1)，(1，1)}．
例5 如图，由甲、乙两个元件组成一个并联电路，每个元件可能
ഥ ={(0，0)，(1，0)}．

ഥ ∩
ഥ ={(0，0)}
(3) A∪B ={(1，0)，(0，1)，(1，1)}，
ഥ ∩
ഥ 表示电路工作不正常．
A∪B表示电路工作正常，
ഥ ∩
ഥ 互为对立事件．
A∪B和
例6 一个袋子中有大小和质地相同的4个球，其中有2个红色球(标
号为1和2)，2个绿色球(标号为3和4)，从袋中不放回地依次随机摸
10.1.2事件的关系和运算
一、复习回顾
样本点：随机试验E的每个可能的基本结果．
样本空间：全体样本点的集合．
一般地，随机试验中的每个随机事件都可以用这个试验的
样本空间的子集来表示．
随机事件（事件）：样本空间Ω的子集．
基本事件：只包含一个样本点的事件．
事件A发生在每次试验中，A中某个样本点出现．
从前面的学习中可以看到，我们在一个随机试验中可以定
的集合是全集中由事件A所包含的结果组成的集合的补集。
事件的关系或运算的含义，以及相应的符号表示如下：
事件的关系或运算
含义
符合表示
包含
A发生导致B发生
A⊆B或B⊇A
并事件(和事件)
A与B至少一个发生
A∪B或A＋B
交事件(积事件)
A与B同时发生
A∩B或AB

[思路探究] 小明的成绩在 80 分以上可以看作是互斥事件“80 分～89 分”“90 分以上”的并事件，小明数学考试及格可看作是“60 分～69 分”“70 分～79 分”“80 分～89 分”“90 分以上”这几个彼此互斥 事件的并事件，又可看作是“不及格”这一事件的对立事件．
[解] 分别记小明的成绩“在 90 分以上”“在 80 分～89 分” “在 70 分～79 分”在“60 分～69 分”为事件 B，C，D，E， 这四个事件彼此互斥． (1)小明的成绩在 80 分以上的概率是 P(B∪C)＝P(B)＋P(C)＝0.18＋0.51＝0.69.
[解] (1)因为事件 C1，C2，C3，C4 发生，则事件 D3 必发生，所 以 C1⊆D3，C2⊆D3，C3⊆D3，C4⊆D3. 同理可得，事件 E 包含事件 C1，C2，C3，C4，C5，C6；事件 D2 包含事件 C4，C5，C6；事件 F 包含事件 C2，C4，C6；事件 G 包 含事件 C1，C3，C5. 且易知事件 C1 与事件 D1 相等，即 C1＝D1.
(或 A∩B＝ ∅ )
给定样本空间 Ω 与事件 A，则由 Ω
事件 中_所__有__不__属__于__A 的样本点组成的
对立
－A
事件称为 A 的对立事件.
(2)事件的和与积
定义
表示法
图示
给定事件 A，B，由所有 A中的 样本点与
__A_＋__B___
事件的
B中的 样本点组成的事件称为 A 与 B 的和
[解] (1)对于事件 D，可能的结果为 1 个红球、2 个白球，或 2 个 红球、1 个白球，故 D＝A∪B. (2)对于事件 C，可能的结果为 1 个红球、2 个白球，或 2 个红球、 1 个白球，或 3 个红球，故 C∩A＝A.

事件的关系与运算心得体会其次，事件的关系与运算可以通过集合的运算进行推导和计算。

集合的交运算表示事件同时发生的情况，集合的并运算表示事件至少发生一个的情况，集合的补运算表示事件不发生的情况。

利用集合运算符号和事件的关系，我们可以将事件之间的关系转化为集合之间的关系，然后通过集合运算得到所需的结果。

例如，两个事件A和B同时发生的概率可以利用交集运算P(A∩B)计算，两个事件A和B至少一个发生的概率可以利用并集运算P(A∪B)计算。

通过这些运算，我们可以方便地计算事件的概率，进一步解决实际问题。

再次，事件的关系与运算在解决复杂问题时起到了关键作用。

有时候，问题会涉及到多个事件之间的关系，需要通过事件的运算来分析和计算。

例如，在生日悖论问题中，我们需要计算至少有两人生日相同的概率。

假设一个事件A表示至少有两个人生日相同，一个事件B表示至少有三个人生日相同，那么事件B包含于事件A，即B⊂A。

通过计算P(A)和P(B/A)分别表示事件A和事件B在事件A发生的条件下的概率，可以得出P(A∩B)=P(A)×P(B/A)，从而得到至少有三个人生日相同的概率。

通过这个例子我们可以看到，事件的关系与运算可以帮助我们分析复杂问题，求解概率。

最后，事件的关系与运算提供了一种思维方式，可以帮助我们更好地理解和解决实际问题。

在解决问题时，我们可以将问题抽象成事件，然后通过事件的关系与运算来进行推导和计算。

这种思维方式可以帮助我们从抽象的概率空间中抽取出有用的信息，然后利用事件的关系来分析和解决问题。

通过这种思维方式，我们可以更加灵活和高效地解决各种实际问题。

，任何事件都包括不可能事件。
事件的关系和运算： （2）相等关系 一般地，对事件A与事件B，若 B A且A B ，那么称事件A与事件B 相等，记作A=B 。 如图： BA
例.事件 C1 ={ 出现1 点 }发生，则事件 D1 ={出现的点数不大于 1 } 就一定会发生，反过来也一样，所以C1=D1。
事件的关系和运算： （5）互斥事件 若 A B 为不可能事件（ A B ），那么称事件A与事件B互斥，其含 义是：事件A与事件B在任何一次试验中都不会同时发生。 如图： A B
例.因为事件 C1 ={出现 1 点} 与事件C2 ={出现 2 点}不可能同时发 生，故这两个事件互斥。
事件的关系和运算： （3）并事件（和事件）
若某事件发生当且仅当事件A发生或事件B发生，则称此事件 为事件A和事件B的并事件（或和事件），记作 A B(或A B)
如图： B A
A B
例.若事件 J={出现 1 点或 5 点 } 发生， 事件C1 ={出现 1 点 } 与事件C5 ={出现 5 点 }中至少有一个会发生，则
事件的关系与运算
在掷骰子的试验中，我们可以定义许多事件，如： C1 ={ 出现 1 点 }； C2 ={出现 2 点}； C3 ={ 出现 3 点 }； C4 ={ 出现 4 点 }； C5 ={出现 5 点}； C6 ={ 出现 6 点 }； D={ 出现的点数大于 3 }；E ={ 出现的点数小于 7 }; F ={ 出现的点数大于 6 }; G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 }; …… 思考： 1. 上述事件中有必然事件或不可能事件吗？有的话，哪些是？ 2. 若事件 C1 发生，则还有哪些事件也一定会发生？ 3. 上述事件中，哪些事件发生会使得 I={出现 1 点或 5 点} 也发生？ 4. 若只掷一次骰子，则事件 C1 和事件 C2 有可能同时发生么？ 5. 在掷骰子实验中事件 G 和事件 H 是否一定有一个会发生？

第一章
随机事件及其概率主讲教师胡发胜
教授
第二讲事件的关系及其运算
事件的关系与运算与集合的关系与运算是完全事件是样本空间的子集，因此，. 这里需要强调的是，要学会利用概率论的语言来解释这些关系及相似的其运算.
在一般情况下，事件的关系是怎样的呢？
.
—.—本讲小结：
这一讲我们学习了事件的关系及其运算，利用这些关系及其运算，我们可以用简单的事件去表示复杂的事件，这下一讲样便于我们利用简单事件的概率去求复杂事件的概率 我们讲一类简单概率模型古典概型。

4、抛掷骰子，事件A= “朝上一面的数是奇数”， 事件B = “朝上一面的数不超过3”，
求P（A∪B）
解法一： 因为P（A）=3/6=1/2，P（B）=3/6=1/2 所以P（A∪B）= P（A）+ P（B）=1 解法二： A∪B这一事件包括4种结果，即出现1，2，3和5 所以P（A∪B）= 4/6=2/3
试验的可能结果 A 事件 A 事件A的对立事件 A B 事件B包含事件A A=B 事件B与事件A相等 A∪B(或A+B) 事件A与事件B的并
A∩B(或AB)

集合A的补集 集合B包含集合A
集合B与集合A相等 集合B与集合A的并
A∩B=
事件A与事件B的交 集合B与集合A的交 事件A与事件B互斥 集合B与A的交集为空集
排队人数 概率 0 0.1 1 0.16 2 0.3 3 0.3 4 0.1 5人以上 0.04
求至多2个人排队的概率。 解：设事件Ak={恰好有k人排队}， 事件A={至多2个人排队}, 因为A=A0∪A1∪A2,且A0，A1，A2这三个事件是
互斥事件，
所以 P(A)=P(A0)+P(A1)+P(A2)=0.1+0.16+0.3=0.56。
特别地，当事件A与事件B是对立事件时，有 P（A）=1－ P（B）
练习：1.如果某士兵射击一次，未中靶的概率为0.05，
求中靶概率。 解：设该士兵射击一次，“中靶”为事件A,“未中靶” 为事件B,则A与B互为对立事件， 故P(A)=1-P(B)=1-0.05=0.95。
2. 甲、乙两人下棋，若和棋的概率是0.5，乙获胜的概率 是0.3. 求：（1）甲获胜的概率；（2）甲不输的概率。
概率的基本性质

(4) A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4;
(5) A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4
(6) A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4 A1 A2 A3 A4 .
事件 A 的对立（互逆）事件 设 A 表示“事件 A 出现”, 则“事件 A 不出现”
称为事件 A 的对立事件或逆事件. 记作 A. 实例 “骰子出现1点”对立 “骰子不出现1点”
图示 A 与 B 的对立. A
B A

若 A 与 B 互逆,则有 A B 且 AB .
注. 1º互斥与互逆的关系
练习1 设A,B,C 表示三个随机事件,试将下列事件 用A,B,C 表示出来.
(1) A 出现 , B, C 不出现; (2) A, B都出现, C 不出现; (3) 三个事件都出现; (4) 三个事件至少有一个出现; (5) 三个事件都不出现;
(6) 不多于一个事件出现; (7) 不多于两个事件出现;
AB A B
(2) A BA A BA ( A B)( A A) ( A B) A B
AB AB AB A(B B) AB A BA
A BA A B
例2 下列命题是否正确？
(1) AB AB

AB 事件A与B的积事件 A集合与B集合的交集
A B 事件A与事件B的差 A与B两集合的差集
AB

事件A与B互不相容
A与B 两集合中没有 相同的元素

(2) 根据题意, 可得 A = {(1, 0), (1, 1)}, B = {(0, 1), (1, 1)}，
A = {(0, 0), (0, 1)}, B = {(0, 0), (1, 0)}.
甲
乙
例5 如图示， 由甲、乙两个元件组成一个并联电路，每个元件可能正常
或失效. 设事件A =“甲元件正常”，B =“乙元件正常”.
一般地，如果事件 与事件 不能同时发生，也就是说 ⋂ 是一个不可能事件，
即⋂ = ，则称事件与事件互斥(或互不相容).可以用图表示这两个事件互斥.
A
B
Ω
5.用集合的形式表示事件 = “点数为偶数”、事件 = “点数为奇数”，它们分别是
= {2,4,6}, = {1,3,5}.
并事件(和事件)
交事件(积事件)
互斥(互不相容)
互为对立
含义
符号表示
A发生导致B发生
A与B至少一个发生
A与B同时发生
A与B不能同时发生
A与B有且仅有一个发生
A⊆B
A⋃B或A + B
A⋂B = AB
A⋂B = ϕ
A⋂B = ϕ，A⋃B = Ω
类似地，我们可以定义多个事件的和事件以及积事件.例如，对于三个事件
(10) D2∩D3=D3. √
随堂检测
1.从一批产品(既有正品也有次品)中取出3件产品，设A＝{3件产品全不是次
品}，B＝{3件产品全是次品}，C＝{3件产品不全是次品}，则下列结论正确
的是________(填写序号).
①A与B互斥；②B与C互斥；③A与C互斥；④A与B对立；⑤B与C对立.
【解析】 A＝{3件产品全不是次品}，指的是3件产品全是正品，B＝{3件产品全

2.乘积事件
事件 “A发生且B发生”，记为 A∩B 或 AB
事件 “A1发生且A2发生且„且An发生.” B
A
n
n
=“A1,A2,„
An都发生.” k1 Ak
or
Ak
k 1
3.差事件 特别：对立事件 A A
AB
事件 “A发生且B丌发生”，记为 A-B
典型例题
例 考察一个家庭两个孩子的性别 A1=“第一个是男孩”，A2=“第二个男孩” B1=“第一个是女孩”，B2=“第二个是女孩” 请用上述简单事件表示下列事件.
C=“两个都是男孩”= A1A2 D=“两个孩子性别丌同”= A1B2+B1A2
随机事件间的关系
1.相容关系 AB≠Φ, A,B可以同时发生. 1）包含关系： B A , B发生则A发生. 2）相等关系： A=B , A发生 B发生.
2.不相容关系 （互斥） AB=Φ, A,B丌能同时发生.
样本空间的丌同的基本事件都是互斥的. Φ不任意事件互斥.
运算规律
(1) 交换律 (2) 结合律
(3) 分配律
AB B A AB B A
A (B C) (A B) C A (B C) (A B) C A (B C) (A B) (A C)
A (B C) (A B) (A C)
(4) 对偶律 A B A B A B A B
事件的运算与关系
随机事件的运算
研究事件运算的目的：用简单事件表示复杂事件.
方法：借助集合的运算.
A
1.和事件
B
事件 “A发生或B发生”， 记为 A∪B 或 A+B
事件 “A1发生或A2发生或„或An发生.” =“A1,A2,„ An发生中至少有一个发生.”