旋转折叠难题

专题02 特殊四边形中的旋转、翻折问题题型一 菱形中的旋转、翻折问题1．如图，在菱形纸片ABCD 中，60A Ð=°，点E 在BC 边上，将菱形纸片ABCD 沿DE 折叠，点C 落在AB 边的垂直平分线上的点C ¢处，则DEC Ð的大小为( )A ．30°B ．45°C ．60°D ．75°【解答】解：连接BD ，如图所示：Q 四边形ABCD 为菱形，AB AD \=，60A Ð=°Q ，ABD \D 为等边三角形，120ADC Ð=°，60C Ð=°，P Q 为AB 的中点，DP \为ADB Ð的平分线，即30ADP BDP Ð=Ð=°，90PDC \Ð=°，\由折叠的性质得到45CDE PDE Ð=Ð=°，在DEC D 中，180()75DEC CDE C Ð=°-Ð+Ð=°．故选：D ．2．如图，在平面直角坐标系中，四边形OABC 是菱形，120AOC Ð=°，点B 的坐标为(6,0)，点D 是边BC 的中点，现将菱形OABC 绕点O 顺时针旋转，每秒旋转60°，则第2021秒时，点D 的坐标为( )A ．9(2B ．9(2-，C ．9(2，D ．9(2-【解答】解：如图，连接OD ，过点C 作CH OB ^于H ，Q 四边形OABC 是菱形，120AOC Ð=°，点B 的坐标为(6,0)，6OB \=，OC BC =，60BOC Ð=°，BOC \D 是等边三角形，6OC OB BC \===，Q 点D 是BC 中点，OD BC \^，3BD =，OD \==，CH OB ^Q ，60COB Ð=°，3OH BH \==，CH ==，\点(3,C -，Q 点D 是BC\点9(2D ，，Q 将菱形OABC 绕点O 顺时针旋转，每秒旋转60°，\第1秒后，点1D 坐标为(0,-，第2秒后，点2D 坐标为9(2-，，第3秒后，点3D 坐标为9(2-，，第4秒后，点4D 坐标为(0，，第5秒后，点5D 坐标为9(2，第6秒后，点6D 坐标为9(2，，¼由上可知，点D 的坐标每6个为一组依次循环着，202163715\¸=¼，\第2021秒时，点D 的坐标为9(2，故选：A ．3．如图，菱形OABC 的一边OA 在x 轴上，将菱形OABC 绕原点O 逆时针旋转105°至111OA B C 的位置，若2OA =，120C Ð=°，则点1B 的坐标为( )A ．(-B ．(3,C ．(D ．【解答】解：连接AC 与OB 相交于点E ，过点1B 作1BF x ^轴，垂足为F ，Q 四边形OABC 为菱形，120C Ð=°，OA OC =，60AOC \Ð=°，2OC OA AC ===，AC OB ^Q ，\在Rt OAE D 中，2OA =，112AE AC ==，OE \===，OB \=，又1302AOB AOC Ð=Ð=°Q ，1105BOB Ð=°，111801803010545B OF AOB BOB \Ð=°-Ð-Ð=°-°-°=°，在Rt △1B OF 中，1OB OB ==，1OF B F =，22211OF B F OB \+=，可得1OF B F ==，Q 点1B 在第二象限，\点1B 的坐标为(．故选：C ．4．如图，在正方形ABCD 中，顶点A ，B ，C ，D 在坐标轴上，且(4,0)B ，以AB 为边构造菱形ABEF ，将菱形ABEF 与正方形ABCD 组成的图形绕点O 顺时针旋转，每次旋转45°，则第164次旋转结束时，点164F 的坐标为( )A ．(4-，B ．(4,--C ．，4)-D ．(-，4)-【解答】解：Q 点(4,0)B ，4OB \=，4OA \=，AB \==，Q 四边形ABEF 是菱形，AF AB \==，\点F ，4)，由题意可得每次8旋转一个循环，1648204\¸=¼，\点164F 的坐标与点F 坐标关于原点对称，\点164F 的坐标(-，4)-，故选：D ．5．如图，已知菱形ABCD 的边长2，60A Ð=°，点E 、F 分别在边AB 、AD 上，若将AEF D 沿直线EF 折叠，使得点A 恰好落在CD 边的中点G 处，则EF【解答】解：延长CD ，过点F 作FM CD ^于点M ，连接GB 、BD ，作FH AE ^交于点H ，如图所示：60A Ð=°Q ，四边形ABCD 是菱形，60MDF \Ð=°，30MFD \Ð=°，设MD x =，则2DF x =，FM =，1DG =Q ，1MG x \=+，222(1))(22)x x \++=-，解得：0.3x =，0.6DF \=， 1.4AF =，10.72AH AF \==，sin 1.4FH AF A =Ð==g ，CD BC =Q ，60C Ð=°，DCB \D 是等边三角形，G Q 是CD 的中点，BG CD \^，2BC =Q ，1GC =，BG \=，设BE y =，则2GE y =-，222(2)y y \+=-，解得：0.25y =，1.75AE \=，1.750.7 1.05EH AE AH \=-=-=，EF \===．6．已知菱形ABCD 中，120ABC Ð=°，12AB =，点E ，F 分别在边AD ，AB 上，将AEF D 沿着直线EF 折叠，使得点A 落在G 点．（1）如图1，若点G 恰好落在AC 上，且3CG =，求DE 的长；（2）如图2，若点G 恰好落在BD 上，且3BG =，求DE 的长．【解答】解：（1）连接BD ，交AC 于点O ，Q 四边形ABCD 是矩形，1602ABD ABC \Ð=Ð=°，90AOB Ð=°，2AC AO =，在Rt AOB D 中易得到AO =，AC =Q 菱形ABCD 中，AD DC =，DAC DCA \Ð=Ð，Q 点A 与点G 关于EF 轴对称，AE EG \=，DAC EGA \Ð=Ð，DCA EGA \Ð=Ð，//EG DC \，\DE CG AD AC =，\12DE =，DE \=．（2）Q菱形ABCD中，120ABCÐ=°，AD AB\=，60AÐ=°，ABD\D是等边三角形，60EDG FBGÐ=Ð=°，又由翻折可得60EGF AÐ=Ð=°，又EGB EGF FGB DEG EDG Ð=Ð+Ð=Ð+Ð，FGB DEG\Ð=Ð．DEG BGF\D D∽，\DE DG EG BG BF FG==，设DE x=，则12EG AE x==-，\9123x xBF FG-==，27BFx\=，363x FGx-=，又12 AB AF BF FG BF=+=+=，\2736312xx x-+=，解得：215x=，即215 DE=．7．四边形ABCD为菱形，BD为对角线，在对角线BD上任取一点E，连接CE，把线段CE绕点C顺时针旋转得到线段CF，使得ECF BCDÐ=Ð，点E的对应点为点F，连接DF．（1）如图1，求证：BE DF=；（2）如图2，若2DFC DBCÐ=Ð，在不添加任何辅助线的前提下，请直接写出五对线段，使每对线段的和等于(BD BE和DE除外）．【解答】（1）证明：Q 四边形ABCD 为菱形，BC CD \=，Q 把线段CE 绕点C 顺时针旋转得到线段CF ，CE CF \=，ECF BCD Ð=ÐQ ，BCE DCF \Ð=Ð，在BCE D 与DCF D 中，BC CD BCE DCF CE CF =ìïÐ=Ðíï=î，()BCE DCF SAS \D @D ，BE DF \=．（2）解：BCE DCF D @D Q ，BE DF \=，BEC DFC Ð=Ð，CB CD =Q ，CBD CDE \Ð=Ð，2DFC CBD Ð=ÐQ ，2BEC CDE \Ð=Ð，CEB CDE ECD Ð=Ð+ÐQ ，EDC ECD \Ð=Ð，ED EC CF \==，BD BE EC BE CF DF DE DF CE DF CF \=+=+=+=+=+．8．如图，平行四边形ABCD 中，AB AC ^，1AB =，BC =，对角线AC ，BD 相交于点O ，将直线AC 绕点O 顺时针旋转，分别交BC ，AD 于点E ，F ．（1）证明：当90AOF Ð=°时，四边形ABEF 是平行四边形；（2）试说明在旋转过程中，AF 与CE 总保持相等；（3）在旋转过程中，四边形BEDF 可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AOF Ð度数．【解答】（1）证明：当90AOF Ð=°时，//AB EF ，//AF BE Q ，\四边形ABEF 是平行四边形．（2）证明：Q 四边形ABEF 是平行四边形，AO CO \=，//AF EC ，FAO ECO \Ð=Ð，在AOF D 和COE D 中，FAO OCE OA OCAOF COE Ð=Ðìï=íïÐ=Ðî，AOF COE \D @D ，AF CE \=．（3）解：结论：四边形BEDF 可能是菱形．AOF COE D @D Q ，OE OF \=，EF \与BD 互相平分，\四边形BEDF 是平行四边形，\当EF BD ^时，四边形BEDF 是菱形，在Rt ABC D 中，2AC =，1OA AB \==，AB AC ^Q ，45AOB \Ð=°，45AOF \Ð=°，\当四边形BEDF 是菱形时，45AOF Ð=°．9．如图，在平面直角坐标系中，O 是菱形ABCD 对角线BD 的中点，//AD x 轴且4AD =，60A Ð=°，将菱形ABCD 绕点O 旋转，使点D 落在x 轴上，则旋转后点C 的对应点的坐标是( )A ．(0，B ．(2,4)-C ．0)D ．(0，或(0,-【解答】解：根据菱形的对称性可得：当点C 旋转到y 轴负半轴时，A 、B 、C 均在坐标轴上，如图，60BAD Ð=°Q ，4AD =，30OAD \Ð=°，2OD \=，AO OC \====，\点C 的坐标为(0,-，同理：当点C 旋转到y 轴正半轴时，点C 的坐标为，\点C 的坐标为或(0,-，故选：D ．10．如图，在菱形ABCD 中，1AB =，60DAB Ð=°，把菱形ABCD 绕点A 顺时针旋转30°得到菱形AB C D ¢¢¢，其中点C 的运动路径为 CC ¢，则图中阴影部分的面积为　342p +【解答】解：连接CD ¢和BC ¢，60DAB Ð=°Q ，30DAC CAB \Ð=Ð=°，30C AB Т¢=°Q ，A \、D ¢、C 及A 、B 、C ¢分别共线．AC \=\扇形ACC ¢4p =，AC AC =¢Q ，AD AB¢=\在OCD D ¢和△OC B ¢中，CD BC ACO AC D COD C OB ¢=¢ìïÐ=Т¢íïТ=ТîOCD \D ¢@△()OC B AAS ¢．OB OD \=¢，CO C O=¢60CBC Т=°Q ，30BC O Т=°90COD \Т=°1CD AC AD ¢=-¢=-Q 1OB C O +¢=\在Rt BOC D ¢中，222(1)1)BO BO +-=解得12BO =，32C O ¢=-，1324OC B S BO C O ¢\=¢=-V g \图中阴影部分的面积为：3242OC B ACC S S p¢¢-=+V 扇形．故答案为：342p+-题型二 矩形中的旋转、翻折问题11．如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，并且5OA =，3OC =．若把矩形OABC 绕着点O 逆时针旋转，使点A 恰好落在BC 边上的1A 处，则点C 的对应点1C 的坐标为( )A ．9(5-，12)5B ．12(5-，95C ．16(5-，125D ．12(5-，16)5【解答】解：过点1C 作1C N x ^轴于点N ，过点1A 作1A M x ^轴于点M ，由题意可得：1190C NO A MO Ð=Ð=°，123Ð=Ð=Ð，则△1A OM ∽△1OC N ，5OA =Q ，3OC =，15OA \=，13A M =，4OM \=，\设3NO x =，则14NC x =，13OC =，则22(3)(4)9x x +=，解得：35x =±（负数舍去），则95NO =，1125NC =，故点C 的对应点1C 的坐标为：9(5-，12)5．故选：A ．12．如图，在矩形ABCD 中，3AB =，4BC =，将矩形ABCD 绕点C 旋转，点A 、B 、D 的对应点分别为A ¢、B ¢、D ¢，当A ¢落在边CD 的延长线上时，边A D ¢¢与边AD 的延长线交于点F ，联结CF ，那么线段CF【解答】解：Q 四边形ABCD 是矩形，3AB CD \==，4AD BC ==，90ADC Ð=°，90A DF CDF ¢\Ð=Ð=°，由旋转的性质得：3CD CD ¢==，4A D AD ¢¢==，90ADC A D C ¢¢Ð=Ð=°，5A C ¢\==，532A D A C CD ¢¢\=-=-=，在Rt CDF D 和Rt △CD F ¢中，CF CF CD CD =ìí¢=î，Rt CDF Rt \D @△()CD F HL ¢，DF D F ¢\=，设DF D F x ¢==，则4A F x ¢=-，在Rt △A DF ¢中，由勾股定理得：2222(4)x x +=-，解得：32x =，32DF \=，CF \===．13．如图，矩形纸片ABCD 中，6AD =，E 是CD 上一点，连结AE ，ADE D 沿直线AE 翻折后点D 落到点F ，过点F 作FG AD ^，垂足为G ．若3AD GD =，则DE 的值为( )A B ．52C D 【解答】解：过点E 作EH FG ^，交FG 于点H ，如图，由题意：AEF AED D @D ，则6AF AD ==，DE EF =．6AD =Q ，3AD GD =，2GD \=．624AG AD DG \=-=-=．FG AD ^Q ，FG \===．Q 四边形ABCD 是矩形，90D \Ð=°，FG AD ^Q ，EH FG ^，\四边形GHED 为矩形．GH DE \=，2HE GD ==．设DE x =，则GH EF x ==，HF x =，在Rt HEF D 中，222HF HE EF +=Q ，\222)2x x -+=．解得：x =DE \=故选：C ．14．如图，点E 在矩形ABCD 边CD 上，将ADE D 沿AE 翻折，点D 恰好落在BC 上的点F 处，若2AB CF =，3CE =，连接DF ，与AE 交于H 点，连接BH ，则点F 到BH 的距离为【解答】解：根据折叠的性质知：AD AF BC ==，DE EF =，AE 是线段DF 的垂直平分线，H 是DF 的中点，设DE EF x ==，则3DC AB x ==+，11(3)22FC AB x ==+，在Rt EFC D 中，222FC EC EF +=，即2221[(3)]32x x ++=，解得：5x =或3x =-（舍去），538DC AB \==+=，4FC =，设AD AF BC y ===，则4BF y =-，在Rt ABF D 中，222AB BF AF +=，即2228(4)y y +-=，解得：10y =，6BF \=，过H 作HN BC ^于N ，过F 作FM BH ^于M ，Q 四边形ABCD 是矩形，//HN CD \，142HN CD \==，122FN FC ==，8BN BF FN \=+=，由勾股定理得：BH ==，1122BHF S BF HN BH FM D =´=´Q ，BF HN FM BH ´\===15．如图，在平面直角坐标系中，四边形OABC 是矩形，6OA =，将ABC D 沿直线AC 翻折，使点B 落在点D 处，AD 交x 轴于点E ，若30BAC Ð=°，则点D 的坐标为( )A ．2)-B ．3)-C ．3)-D ．(3,-【解答】解：过D 点作DF x ^轴，垂足为F ，则//DF y 轴，Q 四边形AOCB 为矩形，90OAB AOC B \Ð=Ð=Ð=°，6BC AO ==，AB OC =，\=，OC AB12AC==，由折叠可知：30Ð=Ð=°，AD ABDAC BAC==，\Ð=°，OAE30OE\=，AE=，\=，ED//Q轴，DF y\Ð=Ð=°，30EDF EAODF=，\=，3EF\=+=，OF OE EF-，\点坐标为，3)D故选：B．16．如图，四边形ABCD中，//AD BC，AB BCBCDÐ=°，将CD绕点D逆时针旋转90°至ED，^，45延长AD交EC于点F．（1）求证：四边形ABCF是矩形；AD=，3（2）若2BC=，求AE的长．【解答】（1）证明：//BCDÐ=°，^，45Q，AB BCAD BCBCD FDCÐ=Ð=°，\Ð=Ð=°，4590B BAFQ将CD绕点D逆时针旋转90°至ED，Ð=°，EDCDE DC\=，90EDF FDC\Ð=°=Ð，45\^，DF CE\Ð=°，AFC90即90Ð=Ð=Ð=°，B BAF AFC\四边形ABCF是矩形；（2）解：Q四边形ABCF是矩形，\==，AF BC3\=-=，321DFQ，90Ð=°，DFEÐ=°45EDF\Ð=Ð=°，45DEF EDF\==，1DF EF在Rt AFED中，由勾股定理得：AE===．AB=，217．如图，矩形OABC中，1¢¢，则AO=，将矩形OABC绕点O按顺时针转90°，得到矩形OA B CBB¢【解答】解：如图所示：Q矩形OABC中，1AB=，2AO=，将矩形OABC绕点O按顺时针转90°，得到矩形OA B C¢¢，B D¢=，\=，13BD则BB¢==．．AB=，618．如图，在矩形ABCD中，4D沿AE折叠，使点B落在矩形BC=，点E为BC的中点，将ABE内点F处，连接CF，则CF的长为( )A ．95B ．125C ．165D ．185【解答】解：连接BF ，6BC =Q ，点E 为BC 的中点，3BE \=，又4AB =Q ，5AE \==，由折叠知，BF AE ^（对应点的连线必垂直于对称轴）125AB BE BH AE ´\==，则245BF =，FE BE EC ==Q ，90BFC \Ð=°，185CF \==．故选：D ．19．已知，如图，四边形ABCD 中，90D Ð=°，AB AC =，DAC B Ð=Ð，点E 是BC 的中点．（1）求证：四边形AECD 是矩形；（2）若8AD =，6CD =，点F 是AD 上的点，连接CF ，把D Ð沿CF 折叠，使点D 落在点G 处．当AFG D 为直角三角形时，求CF 的长度．【解答】解：（1）证明：AB AC =Q ,B ACB \Ð=Ð．DAC B Ð=ÐQ ,DAC ACB \Ð=Ð．//AD EC \．AB AC =Q ,E 是BC 的中点，AE BC \^．90AEC \Ð=°．18090EAD AEC \Ð=°-Ð=°．90D Ð=°Q ,\四边形AECD 为矩形．(2)当90AGF Ð=°时，G 在AC 上，如图，8AD =Q ,6CD =,10AC \==．CG CD =Q ,4AG AC CG \=-=．设DF x =,则8AF x =-,GF DF x ==,由勾股定理得：222AG GF AF +=．2224(8)x x \+=-．解得：3x =．\CF ===当90AFC Ð=°时，G 在CE 上，此时四边形CDFG 为正方形，如图：CF \=；当90FAG Ð=°时，G 在AB 上，此时6CG CD ==,而8CE AD ==,Q斜边大于直角边，\不可能在AB边上．G综上，CF=．20．矩形ABCD绕点A顺时针旋转至矩形AEFG，使B点正好落在CD上的点E处，连BE．（1）求证：2Ð=Ð；BAE CBE（2）如图2，连BG交AE于M，点N为BE的中点，连MN、AF，试探究AF与MN的数量关系，并证明你的结论．【解答】（1）证明：Q四边形ABCD是矩形，\Ð=Ð=°，C CBA90CBE ABE\Ð+Ð=°，90Q将矩形ABCD绕点A顺时针旋转至矩形A点正好落在CD上的点E处，=，Ð=°，AE AB\=，90BC AGEAG\Ð=Ð，ABE AEBQ，Ð+Ð+Ð=°BAE ABE AEB180\Ð+Ð=°，ABE BAE2180Q，Ð+Ð=°CBE ABE90\Ð+Ð=°，CBE ABE22180\Ð=Ð．BAE CBE2（2）2=，AF MN证明：过B作BO AE^于O，连接EG，Q四边形AEFG是矩形，Ð=Ð=°，MAG BOM\=，90AF EG90C CBA Ð=Ð=°Q ，90AEB ABE CBE \Ð=Ð=°-Ð，90CEB CBE Ð=°-Ð，CEB OEB \Ð=Ð，在CBE D 和OBE D 中，90CBE OBE C BOE BE BE Ð=ÐìïÐ=Ð=°íï=î，()CBE OBE AAS \D @D ，EC OE \=，BO BC AD AG ===，在BOM D 和GAM D 中，AMG BME BOM GAM BO AG Ð=ÐìïÐ=Ðíï=î，()BOM GAM AAS \D @D ，BM GM \=，Q 点N 为BE 的中点，12MN EG \=，EG AF =Q ，2AF MN \=．题型三 正方形中的旋转、翻折问题21．如图，在正方形ABCD 中，E 是BC 边上的一点，将正方形边AB 沿AE 折叠到AF ，延长EF 交DC于G ，连接AG ，则EAG Ð=　45　度．【解答】解：Q 四边形ABCD 是正方形，AB AD \=，90ABE BAD ADG Ð=Ð=Ð=°，由翻折可知：AB AF =，90ABE AFE AFG Ð=Ð=Ð=°，BAE EAF Ð=Ð，90AFG ADG Ð=Ð=°Q ，AG AG =，AD AF =，Rt AGD Rt AGF(HL)\D @D ，GAF GAD Ð=Ð，1()452EAG EAF GAF BAF DAF \Ð=Ð+Ð=Ð+Ð=°．故答案为：45．22．如图，正方形ABCD 的边长为1，将其绕顶点C 按逆时针方向旋转一定角度到如图所示的位置，使得点B 落在对角线CF 1-　．【解答】解：方法一：正方形ABCD 的边长为1，将其绕顶点C 按逆时针方向旋转一定角度到CEFG 位置，使得点B 落在对角线CF 上，1EF CE \==，CF \=，1BF \=-，45BFE Ð=°Q ，\阴影部分的面积211111)122=´´-´=-；方法二：Q 过E 点作//MN BC 交AB 、CD 于M 、N 点，设AB 与EF 交于点P 点，连接CP ，如下图所示，B Q 在对角线CF 上，45DCE ECF \Ð=Ð=°，1EC =，ENC \D 为等腰直角三角形，MB CN \===，又BC AD CD CE ===，且CP CP =，PEC D 和PBC D 均为直角三角形，Rt PEC Rt PBC(HL)\D @D ，PB PE \=，又45PFB Ð=°，45FPB MPE \Ð=°=Ð，MPE \D 为等腰直角三角形，设MP x =，则EP BP ==，MP BP MB +=Q ，\x +=x =，1BP \==-，\阴影部分的面积12211)12PBC S BC BP D ==´´´=´-=-．1．23．如图，将边长为3的正方形ABCD 绕点A 逆时针方向旋转30°后得到正方形AB C D ¢¢¢，则图中阴影部分面积为　9-【解答】解：连接AE ，如图所示：由旋转的性质可知：AB AB =¢．在Rt △AB E ¢和Rt ADE D 中，AE AE AB AD =ìí¢=î，Rt \△Rt ADE(HL)AB E ¢@D ．DAE B AE \Ð=Т，ADE AB E S S D ¢=V ．30BAB Т=°Q ，1(9030)302DAE \Ð=´°-°=°．又3AB =Q ，DE AB \==132ADE S D \==，又239ABCD S ==Q 正方形，929S \=-=-阴影．故答案为：9-．24．如图是一张正方形纸片ABCD ，将其对折使AB 与DC 重合，折痕EF 分别与BC ，AD 交于点E ，F ，再将点D 对折到线段AE 上，折痕AG 交DC 于点G ，则DC GC【解答】解：如图，连接EG ，设DG D G x ¢==，2AB a =，由折叠得：BE EC a ==，2AD AD a ¢==，2CG a x \=-，由勾股定理得：AE ==，2D E a ¢\=-，在Rt EGD ¢D 和Rt EGC D 中，2222(2)2)a a x x a +-=+-，解得1)x a =-，\DC GC =．．25．如图，将边长为12的正方形纸片ABCD 折叠，点A 与CD 边中点M 重合，折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与BC 交于点G ，则DE 长度为 92　，BG 与BC 的数量关系为 ．【解答】解：过A 作AH MG ^于H ，连接AG ，如图：设DE x =，则12AE ME x ==-，Rt DME D 中，162DM DC ==，222DM DE ME +=，2226(12)x x \+=-，解得92x =，92DE \=，Q 正方形纸片ABCD 折叠，点A 与CD 边中点M 重合，MAB AMG \Ð=Ð，//DC AB Q ，DMA MAB \Ð=Ð，DMA AMG \Ð=Ð，在ADM D 和AHM D 中，90,D AHM DMA AMG AM AMÐ=Ð=°ìïÐ=Ðíï=î，()ADM AHM AAS \D @D ，AD AH \=，6MH MD ==，AH AD AB \==，在Rt AHG D 和Rt ABG D 中，AH ABAG AG =ìí=î，Rt AHG Rt ABG(HL)\D @D ，HG BG \=，设BG y =，则HG y =，12CG y =-，Rt CMG D 中，162CM DC ==，6MG MH HG y =+=+，222CM CG MG +=，2226(12)(6)y y \+-=+，解得245y =，245BG \=，\2425125 BGBC==，25BG BC\=．故答案为：92，25BG BC=．26．如图，已知正方形ABCD的边长为6，以点C为直角顶点的等腰Rt CEFD绕C旋转一圈，且保持2CE=，过点C作CH DE^于H交直线BF于M，连AM，则AM的最小值为　1-　．【解答】解：如图1中，作//BT CF交CM分延长线于T．//BT CFQ，T FCM\Ð=Ð，CH DE^Q，ECFD是等腰直角三角形，90CHE ECF\Ð=Ð=°，90FCM ECH\Ð+Ð=°，90ECH DECÐ+Ð=°，DEC FCM T\Ð=Ð=Ð，90DCB DHCÐ=Ð=°Q，90BCT DCH \Ð+Ð=°，90DCH CDE Ð+Ð=°，TCB CDE \Ð=Ð，CB CD =Q ，()BCT DCE AAS \D @D ，BT EC CF \==，TMB CMF Ð=ÐQ ，T MCF Ð=Ð，()TBM CFM AAS \D @D ，BM FM \=，如图2中，取BC 的中点N ，连接AN ，MN ．Q 四边形ABCD 是正方形，6AB BC \==，90ABN Ð=°，3BN NC ==Q ，AN \===，BM MF =Q ，BN NC =，112MN CF \==，AM AN MN -Q …，1AM \…，AM \的最小值为1-．故答案为：1-．27．在正方形ABCD 中，E 、F 分别为BC 、CD 的中点，AE 与BF 相交于点G ．（1）如图1，求证：AE BF ^；（2）如图2，将BCF D 沿BF 折叠，得到BPF D ，延长FP 交BA 的延长线于点Q ，若4AB =，求QF 的值【解答】（1）证明：E Q ，F 分别是正方形ABCD 边BC ，CD 的中点，CF BE \=，在ABE D 和BCF D 中，AB BC ABE BCFBE CF =ìïÐ=Ðíï=îRt ABE Rt BCF(SAS)\D @D ，BAE CBF \Ð=Ð，又90BAE BEA Ð+Ð=°Q ，90CBF BEA \Ð+Ð=°，90BGE \Ð=°，AE BF \^；（2）解：Q 将BCF D 沿BF 折叠，得到BPF D ，FP FC \=，PFB BFC Ð=Ð，90FPB Ð=°，//CD AB Q ，CFB ABF \Ð=Ð，ABF PFB \Ð=Ð，QF QB \=，设QF x =，4PB BC AB ===，2CF PF ==，QB x \=，2PQ x =-，在Rt BPQ D 中，222(2)4x x \=-+，解得：5x=，QF=．即528．如图，四边形ABCD是正方形，点E是BC边上的动点（不与点B、C重合），将射线AE绕点A按逆时针方向旋转45°后交CD边于点F，AE、AF分别交BD于G、H两点．（1）当55Ð的度数；BEAÐ=°时，求HADÐ的大小；（2）设BEA aÐ=，试用含a的代数式表示DFAÐ有怎样的数量关系，并说明理由．（3）点E运动的过程中，试探究BEAÐ与FEA【解答】解：（1）Q四边形ABCD是正方形，90\Ð=Ð=°，EBA BAD\Ð=°-Ð=°-°=°，90905535EAB BAE\Ð=Ð-Ð-Ð=°-°-°=°；90453510HAD BAD EAF EAB（2）Q四边形ABCD是正方形，\Ð=Ð=Ð=°，90EBA BAD ADF\Ð=°-Ð=°-，9090EAB BAE a\Ð=Ð-Ð-Ð=°-°-°-=-°，DAF BAD EAF EAB a a9045(90)45\Ð=°-Ð=°--°=°-；9090(45)135DFA DAF a aÐ=Ð，理由如下：（3）BEA FEA=，连接AI．延长CB至I，使BI DFQ四边形ABCD是正方形，\=，90AD ABÐ=Ð=°，ADF ABC90\Ð=°，ABIQ，又BI DF=\D@D，()DAF BAI SASÐ=Ð，\=，DAF BAIAF AIEAI BAI BAE DAF BAE EAF\Ð=Ð+Ð=Ð+Ð=°=Ð，45D的公共边，D与EAFQ是EAI又AEEAI EAF SAS\D@D，()\Ð=Ð．BEA FEA=，过D作DG EF29．在正方形ABCD中，点E、F分别在边BC、AD上，DE EF^于点H，交AB边于点G．（1）如图1，求证：DE DG=；（2）如图2，将EF绕点E逆时针旋转90°得到EK，点F对应点K，连接KG，EG，若H为DG中点，EG．在不添加任何辅助线及字母的情况下，请直接写出图中所有与EG长度相等的线段（不包括)【解答】解：（1）Q四边形ABCD是正方形，DAG DCEÐ=Ð=°，AD BC，90AD DC\=，//\Ð=Ð，DEC EDFQ，DE EF=\Ð=Ð，EFD EDF\Ð=Ð，EFD DECQ于H，DG EF^\Ð=°，GHF90AGH AFH\Ð+Ð=°，180Q，Ð+Ð=°AFH EFD180DGA EFD DEC \Ð=Ð=Ð，在DAG D 和DCE D 中：DGA DEC DAG DCEDA DC Ð=ÐìïÐ=Ðíï=î()DAG DCE AAS \D @D ，DG DE \=．（2）KE EF ^Q ，DG EF ^，//KE DG \，且DG EF KE DE ===，\四边形KEDG 是平行四边形，且DG DE =，\四边形KEDG 是菱形，GK DG KE DE \===，DG EF ^Q ，H 是DG 的中点，EG DE \=，EG DE DG GK KE EF \=====．30．如图，已知正方形ABCD 的边长是2，EAF m Ð=°，将EAF Ð绕点A 顺时针旋转，它的两边分别交BC 、CD 于点E 、F ，G 是CB 延长线上一点，且始终保持BG DF =．（1）求证：ABG ADF D @D ；（2）求证：AG AF ^；（3）当EF BE DF =+时：①求m 的值；②若F 是CD 的中点，求BE的长．【解答】解：（1）证明：在正方形ABCD 中，2AB AD BC CD ====，90BAD C D ABC ABG Ð=Ð=Ð=Ð=Ð=°．BG DF =Q ，在ABG D 和ADF D 中，AB AD ABG ADF BG DF =ìïÐ=Ðíï=î，()ABG ADF SAS \D @D ；（2）证明：ABG ADF D @D Q ，GAB FAD \Ð=Ð，GAF GAB BAF\Ð=Ð+Ð90FAD BAF BAD =Ð+Ð=Ð=°，AG AF \^；（3）①解：ABG ADF D @D ，AG AF \=，BG DF =．EF BE DF =+Q ，EF BE BG EG \=+=．AE AE =Q，。

特殊平行四边形中折叠和旋转问题的六种考法目录解题知识必备 (1)压轴题型讲练 (2)类型一、菱形中的折叠问题 (2)类型二、菱形中的旋转问题 (4)类型三、矩形中的折叠问题 (5)类型四、矩形中的旋转问题 (6)类型五、正方形中折叠问题 (8)类型六、正方形中旋转问题 (9)压轴能力测评（10题） (12)解题知识必备1.菱形的性质与判定1.菱形的性质（1）菱形的定义：有一组邻边相等的平行四边形叫做菱形．（2）菱形的性质①菱形具有平行四边形的一切性质；②菱形的四条边都相等；③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．（3）菱形的面积计算①利用平行四边形的面积公式．②菱形面积12ab．（a、b是两条对角线的长度）2.菱形的判定①菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等＝菱形）；②四条边都相等的四边形是菱形．③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．2.矩形的性质与判定1矩形的性质（1）矩形的定义：有一个角是直角的平行四边形是矩形．（2）矩形的性质①平行四边形的性质矩形都具有；②角：矩形的四个角都是直角；③边：邻边垂直；④对角线：矩形的对角线相等；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．2矩形的判定①矩形的定义：有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形（或“对角线互相平分且相等的四边形是矩形”）3.正方形的性质与判定1.定义：有一组邻边相等并且有一个内角是直角的平行四边形叫做正方形．2.正方形与矩形、菱形的关系矩形邻边相等正方形菱形一个角是直角正方形3.性质定理正方形即是矩形又是菱形，因而它具备两者所有的性质．性质定理1：正方形的四个角都是直角；正方形的四条边都相等．性质定理2：正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角．4.判定定理：判定定理1：有一组邻边相等的矩形是正方形．判定定理2：有一个内角是直角的菱形是正方形．点B 落在边CD 上的G 处，若EG CD ⊥，43BE DG ==，，则AE 的长为．【变式训练1】（2024·广东东莞·二模）如图，将菱形纸片ABCD 折叠，使点B 落在AD 边的点F 处，折痕为CE ，若80D ∠=︒，则BCF ∠的度数是．【变式训练2】（23-24八年级下·河北邢台·期中）如图，在菱形纸片ABCD 中，60A ∠=︒．（1）C ∠=︒．（2）点E 在BC 边上，将菱形纸片ABCD 沿DE 折叠，点C 对应点为点C '，且DC '是AB 的垂直平分线，则DEC ∠的大小为︒．类型一、菱形中的折叠问题例题：（2024九年级下·江苏南京·专题练习）如图，在菱形ABCD 中，点E ，F 分别在AB BC ，上，沿EF 翻折后，(1)求证：四边形CEFG 为菱形；(2)若86AC BC ==，，求DG 的长．类型二、菱形中的旋转问题例题：（2024·河南·三模）如图，菱形OABC 的顶点(0,0)O ，(1,0)A -，=60B ∠︒，若菱形OABC 绕点O 顺时针旋转90︒后得到菱形111OA B C ，依此方式，绕点O 连续旋转2024次得到菱形202420242024OA B C ，那么点2024C 的坐标是（）A．1,22⎛⎫ ⎪ ⎪⎝⎭B．1,22⎛⎫ ⎝C．1,22⎛⎫-- ⎪ ⎪⎝⎭D．1,22⎛- ⎝⎭【变式训练1】（2024九年级·全国·竞赛）在菱形ABCD 中，120ABC ∠=︒，边长为2cm ，现将菱形ABCD 绕其外一点O 按顺时针方向分别旋转90180270︒︒︒、、后，得到如图的图形，每相邻两个菱形有一个顶点重合，则图中阴影部分的面积为2cm．【变式训练3】（2024·云南曲靖·二模）如图，已知在ABC 中，90ACB ∠=︒，过点C 作CD AB ⊥于点D ，点E 为AC 上一点，连接BE ，交CD 于点G ，BFE △是BCE 沿BE 折叠所得，且点C 的对应点F 恰好落在AB 上，连接FG ．(1)求证：DF BF =；(2)将菱形AEFG 绕点A 按逆时针方向旋转．设旋转角()0180BAE αα∠=︒≤≤︒，且6AB =，AE =60DAB GAE ∠=∠=︒．①如图②，当90α=︒时，则线段DF 的长度是多少？②连接BD ，当DFB △为直角三角形时，则旋转角α的度数为多少度？类型三、矩形中的折叠问题例题：（23-24八年级下·北京昌平·期中）矩形ABCD 中，4cm AD =，10cm AB =，按如图方式折叠，使点B 落与点D 重合，折痕为EF ，则DE =cm．【变式训练1】（23-24八年级下·辽宁大连·期中）如图，在矩形ABCD 中，6AB =，8BC =，E 是边BC 上一点，将ABE 沿AE 折叠，使点B 落在点F 处，连接CF ．当CEF △为直角三角形时，CE 的长是．【变式训练2】如图①，菱形ABCD 和菱形AEFG 有公共顶点A ，点E ，G 分别落在边AB ，AD 上，连接DF ，BF ．点E 是线段BC 上不与端点重合的一个动点，连接BP EP ，，将BPE 关于直线PE 对称的三角形记作FPE △，若PF 垂直于矩形的任意一边，则线段BE 的长是．【变式训练3】（2024·江苏徐州·三模）如图，矩形ABCD 中，5AD =，8AB =，点E 为射线DC 上的一个动点，把ADE V 沿AE 折叠．点D 的对应点为D ¢．(1)求点D ¢刚好落在对角线AC 上时，D C '的长；(2)求点D ¢刚好落在此矩形的对称轴上时，线段DE 的长．【变式训练2】（2024·河南驻马店·二模）如图所示，在矩形ABCD 中，36AB AD ==，，点P 在AD 上，且2PD =，沿顺时针方向旋转，得到矩形EFCG ，点A 、B 、D 的对应点分别是点E 、F 、G．(1)如图1，当点F 落在矩形ABCD 的对角线AC 上时，求线段AF 的长；(2)如图2，当点F 落在矩形ABCD 的边CD 的延长线上时，连接AE ，取AE 的中点M ，求证：12CM AE =；(3)如图3，当点F 落在矩形ABCD 的对角线BD 的延长线上时，求CDF 的面积．【变式训练1】（23-24八年级下·四川成都·期中）如图，在平面直角坐标系中，点A 的坐标为()5,0-，点C 的坐标为()0,3，将长方形OABC 绕O 按顺时针方向旋转α度得到OA B C '''，此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q ．当4590α︒<≤︒，且BP PQ =时，线段PQ 的长是．类型四、矩形中的旋转问题例题：（23-24八年级下·江苏镇江·期中）如图，在矩形ABCD 中，3AB =，4=AD ，以点C 为旋转中心，将矩形ABCD结CF．（1）如图①，当90α=︒时，CF 的长为；（2）如图②，点M 是CF 的中点，连结BM ，在旋转过程中，线段BM 的最大值为．【变式训练3】（2024·安徽池州·三模）已知，矩形CEFG 是矩形ABCD 绕点C 旋转得到的，且点G 落在AD边上．(1)如图1，连接BG ，求证：BG 平分AGC ∠；(2)如图2，在（1）的条件下连接BE 交CG 于点H ，求证：H 是BE 的中点；(3)如图3，在旋转的过程中，若C ，D ，F 三点共线，23AG GB =，求AB BC 的值．【变式训练2】（23-24九年级上·浙江金华·期中）如图，已知矩形,3,5ABCD AB BC ==，将矩形ABCD 绕A 顺时针旋转()0180αα︒<<︒，得到矩形AEFG ，点B 的对应点是点E ，点C 的对应点是点F ，点D 的对应点是点G ，连恰好与对角线AC 上的点F 重合，连接DF ，若2BE =，则CDF 的面积是．【变式训练1】（23-24八年级下·江苏镇江·期中）如图，在正方形ABCD 中，10AB =，E 是BC 的中点，将ABE ∆沿AE 对折至AFE ∆，延长EF 交DC 于点G ，则DG 的长是（）A ．4B ．103C ．3D ．83【变式训练2】（2024·湖北荆门·模拟预测）如图，对折正方形纸片ABCD ，得到折痕EF ，将纸片展平，在AD 上取一点P ，沿BP 折叠，使点A 落在正方形ABCD 内部点M 处，将纸片展平，连接,PM BM ，延长PM 交CD 于点Q ，连接BQ 若正方形ABCD 的边长为6，1FQ =，则AP 的长为．【变式训练3】（22-23八年级下·安徽滁州·期末）如图1，正方形ABCD 的边长为3，E 为CD 边上一点（不与端点重合）．将ADE V 沿AE 对折至AFE △，延长EF 交边BC 于点G ，连接AG．（1）EAG ∠=；（2）如图2，若E 为CD 的中点，则CG =．类型五、正方形中折叠问题例题：（2024·上海浦东新·三模）如图，在正方形ABCD 的边AB 上取一点E ，连接CE ，将BCE 沿CE 翻折，点B11C D AD ⊥于点1D （1）求证：四边形111AB C D 是正方形．（2）111::BB CC DD =；【规律探究】将正方形111AB C D 绕点A 旋转得到图2，连接1BB ，1CC ，1DD （3）111::BB CC DD 的比值是否会发生变化?请说明理由．【拓展应用】如图3，在图2的基础上，2B ，2C ，2D 分别是1BB ，1CC ，1DD 的中点．（4）求证：四边形．222AB C D是正方形．类型六、正方形中旋转问题例题：（2024·江西九江·一模）【特例感知】如图1，点1C 是正方形ABCD 对角线AC 上一点，11C B AB ⊥于点1B ，【变式训练2】（23-24八年级下·江苏宿迁·期中）如图1，点O 是正方形ABCD 两对角线的交点，分别延长OD 到点G ，OC 到点E ，使2OG OD =，2OE OC =，然后以OG 、OE 为邻边作正方形OEFG ，连接AG ，DE．(1)求证：DE AG ⊥；(2)如图2，正方形ABCD 固定，将正方形OEFG 绕点O 逆时针旋转α角（0360α︒<<︒），得到正方形OE F G '''；①在旋转过程中，当OAG '∠是直角时，求α的度数；②若正方形ABCD 的边长为2，在旋转过程中，AF '长的最大值为______．【变式训练1】（23-24八年级下·上海·期末）如果把正方形ABCD 绕点C 旋转得到正方形A B CD '''，点B '落在对角线AC 上，点A '落在CD 的延长线上，那么AA B ''∠=度．的长度关系及所在直线的位置关系：（1）猜想如图1中线段BG ，线段DE 的数量关系是______；线段BG ，DE 的位置关系____类比探究：（2）将图1中的正方形CEFG 绕着点C 按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形，请你判断（1）①中得到的结论是否仍然成立，并选取图2证明你的判断；拓展应用：（3）已知5AB =，2CE =，在正方形CEFG 绕点C 旋转的过程中，当点D E G ，，在同一条直线上时，DG 的长度是多少？请直接写出答案【变式训练3】（2024·山东东营·模拟预测）如图1，四边形ABCD 是正方形，G 是CD 边上的一个动点（点G 与C D ，不重合），以CG 为一边在正方形ABCD 外作正方形CEFG ，连接BG ，DE ．我们探究下列图中线段BG 、线段DE点处，记为B'，则BF的长度为（）A．113B．72C．3D．522．（2024九年级·全国·竞赛）如图，将边长为1dm正方形ABCD绕点D按顺时针方向旋转45︒后得到正方形DEFG，边EF BC、相交于点H，则四边形CDEH的面积为（）．A2B2C．)21dm D．)21dm二、填空题3．（23-24八年级下·北京东城·期末）如图，在矩形ABCD中，E为AB上一点，将矩形的一角沿CE向上折叠，点B的对应点F恰好落在边AD上．若AEF△的周长为12，CDF的周长为24，则AF的长为．一、单选题1．（2023·海南三亚·二模）如图，将边长为4，锐角为60︒的菱形ABCD沿EF折叠，使顶点B恰好落在边AD的中三、解答题5．（23-24八年级下·山东威海·期末）如图，正方形ABCD ，8AB =．将正方形ABCD 绕点A 逆时针旋转角度α（090α︒<<︒），得到正方形AEFG ，EF 交CD 于点M ，延长FE 交BC 于点N．(1)求证：MN DM BN =+；(2)顺次连接D ，E ，C ，F ，得到四边形DECF ．在旋转过程中，四边形DECF 能否为矩形？若能，求出BN 的值；若不能，请说明理由．4．（23-24九年级上·安徽淮南·阶段练习）如图，在菱形ABCD 中，2AB =，60BAD ︒∠=，将菱形ABCD 绕点A 逆时针方向旋转，对应得到菱形AEFG ，点E 在AC 上，EF 与CD 交于点P ．（1）EF 与DC 的关系是，（2）DP 的长为．应点分别为A '、D ¢，点A '恰好落在CD 边上．①求证：四边形AEA G '为菱形；②若6AB =，3CB =，120B ∠=︒，1CA '=，则DG 的长为________．7．（23-24八年级下·安徽六安·期末）问题情境：点E 为正方形ABCD 内一点，90AEB ∠=︒，将BE 绕点B 按顺时针方向旋转90︒至BE '．延长AE 交直线CE '于点F ，连接DE．(1)如图①，若F 在线段E C '的延长线上，求证：四边形BE FE '为正方形；(2)如图②，若F 恰为线段CE '的中点，请猜想线段DA 、DE 的数量关系并加以证明；(3)解决问题：若15AB =，3CF =，请直接写出DE 的长．6．（23-24八年级下·江苏南京·期末）（1）【感知】如图①，将ABCD Y 沿过点D 的直线折叠，使点A 的对应点A '落在CD 边上的点F 处，得到折痕DE ，连接EF ．若4=AD ，则四边形AEFD 的周长为________；（2）【探究】如图②，点E 、G 分别是ABCD Y 的边AB CD 、上的点，将四边形AEGD 沿GE 折叠，点A 、D 的对(1)当E 是BC 的中点时，求DF ．(2)如图2，当BE CF =时，AF 与BC 相交于点G ，求BE 的长；(3)如图3，当AE EF =时，求ABE 的面积．8．（23-24八年级下·广东湛江·期末）综合运用如图1，点E 是矩形ABCD 的边BC 上一点，连接AE ，把ABE 沿AE 折叠得到AB E '，点B '在矩形ABCD 的内部，延长AB '交射线DC 于点F ，连接EF ，已知58AB BC ==，．(1)操作判断操作一：对折矩形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，把纸片展平；操作二：在AD 上选一点P ，沿BP 折叠，使点A 落在矩形内部点M 处，把纸片展平，连接PM BM ，．根据以上操作，当点M 在EF 上时，写出图1中一个30︒的角：_______．(2)迁移探究小华将矩形纸片换成正方形纸片，继续探究，过程如下：将正方形纸片ABCD 按照（1）中的方式操作，并延长PM 交CD 于点Q ，连接BQ ．①如图2，当点M 在EF 上时，MBQ ∠=________°，CBQ ∠=________°；②改变点P 在AD 上的位置（点P 不与点A ，D 重合），如图3，判断MBQ ∠与CBQ ∠的数量关系，并说明理由．(3)拓展应用在（2）的探究中，已知正方形纸片ABCD 的边长为10cm ，当1cm FQ =时，直接写出AP 的长．9．（23-24八年级下·河南南阳·阶段练习）综合与实践综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动．(1)如图①，当点E 落在DC 边上时，线段DE 的长度为___________；(2)如图②，当点E 落在线段CF 上时，AE 与DC 相交于点H ，连接AC ．①求证：ACD CAE △≌△；②求线段DH 的长度．(3)如图③设点P 为边FG 的中点，连接PB ，PE ，在矩形ABCD 旋转过程中，BEP △的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．10．（23-24八年级下·江苏盐城·阶段练习）在矩形ABCD 中，8AB =，3BC =，以点A 为旋转中心，逆时针旋转矩形ABCD ，旋转角为()0180αα︒<<︒，得到矩形AEFG ，点,,B C D 的对应点分别为点,,E F G ．。

翻转折叠问题【专题点拨】图形折叠是中考中常考题型，这种题型主要考察学生对图形的认知，特别是考察轴对称的性质、全等三角形、勾股定理、相似三角形等知识综合运用。

【解题策略】有关图形折叠的相关计算，首先要熟知折叠是一种轴对称变换，即位于折痕两侧的图形关于折痕成轴对称；然后根据图形折叠的性质，即折叠前、后图形的对应边和对应角相等，对应点的连线被折痕垂直平分并结合勾股定理或相似三角形的性质进行相关计算.【典例解析】类型一：三角形折叠问题例题1：（2016·浙江省湖州市·3分）如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（）A．4 B． C．3D．2【考点】翻折变换（折叠问题）；四点共圆；等腰三角形的性质；相似三角形的判定与性质．【分析】只要证明△ABD∽△MBE，得=，只要求出BM、BD即可解决问题．【解答】解：∵AB=AC，∴∠ABC=∠C，∵∠DAC=∠ACD，∴∠DAC=∠ABC，∵∠C=∠C，∴△CAD∽△CBA，∴=，∴=，∴CD=，BD=BC﹣CD=，∵∠DAM=∠DAC=∠DBA，∠ADM=∠ADB，∴△ADM∽△BDA，∴=，即=，∴DM=，MB=BD﹣DM=，∵∠ABM=∠C=∠MED，∴A、B、E、D四点共圆，∴∠ADB=∠BEM，∠EBM=∠EAD=∠ABD，∴△ABD∽△MBE，∴=，∴BE===．故选B．变式训练1：（2016·吉林·3分）在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为（用含a的式子表示）．类型二：平行四边形折叠问题例题2：（2016·湖北武汉·3分）如图，在□ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B＝52°，∠DAE＝20°，则∠FED′的大小为_______．【考点】平行四边形的性质【解析】∵四边形ABCD为平行四边形，∴∠D＝∠B＝52°，由折叠的性质得：∠EAD，＝∠DAE＝20°，∠AED，＝∠AED＝180°－∠DAE－∠D＝180°－20°－52°＝108°，∴∠AEF＝∠D＋∠DAE＝52°＋20°＝72°，∴∠FED′＝108°－72°＝36°．变式训练2：(2016河北3分）如图，将ABCD沿对角线AC折叠，使点B落在点B’处.若∠1=∠2=44°，则∠B为（）第13题图A．66°B．104°C．114°D．124°类型三：矩形折叠问题例题3：（2016贵州毕节3分）如图，正方形ABCD的边长为9，将正方形折叠，使顶点D 落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（）A．3 B．4 C．5 D．6【解析】正方形的性质；翻折变换（折叠问题）．根据折叠的性质可得DH=EH，在直角△CEH中，若设CH=x，则DH=EH=9﹣x，CE=3cm，可以根据勾股定理列出方程，从而解出CH的长．【解答】解：由题意设CH=xcm，则DH=EH=（9﹣x）cm，∵BE：EC=2：1，∴CE=BC=3cm∴在Rt△ECH中，EH2=EC2+CH2，即（9﹣x）2=32+x2，解得：x=4，即CH=4cm．故选（B）变式训练3：（2016·四川南充）如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为（）A．30°B．45°C．60°D．75°类型四：菱形折叠问题例题4：（2016·四川攀枝花）如图，正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连结GF，给出下列结论：①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4，其中OGD正确的结论个数为（）A．2 B．3 C．4 D．5【考点】四边形综合题．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的面积；④由折叠的性质与平行线的性质，易得△EFG是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．【解答】解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG=∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF=OG，∴BE=EF=×OG=2OG．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OGF时等腰直角三角形．∵S△OGF=1，∴OG2=1，解得OG=，∴BE=2OG=2，GF===2，∴AE=GF=2，∴AB=BE+AE=2+2，∴S正方形ABCD=AB2=（2+2）2=12+8，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【点评】此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．变式训练4：（2016·黑龙江齐齐哈尔·3分）如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，连接MC，将菱形ABCD翻折，使点A落在线段CM上的点E处，折痕交AB于点N，则线段EC的长为﹣1 ．类型五：圆的折叠问题例题5：（2015•聊城）如图，点O是圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使和都经过圆心O，则阴影部分的面积是⊙O面积的（）A. 12B.13C.23D.352. 解：作OD⊥AB于点D，连接AO，BO，CO，∵OD=AO，∴∠OAD=30°，∴∠AOB=2∠AOD=120°，同理∠BOC=120°，∴∠AOC=120°，∴阴影部分的面积=S扇形AOC=×⊙O面积．故选：B．变式训练5：（2016·山东省德州市·4分）如图，半径为1的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是．【能力检测】1.（2016·黑龙江龙东·3分）如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次変换，如果这样连续经过2016次变换后，等边△ABC的顶点C的坐标为．2.（2015•湘潭）如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．（1）求证：△BDE∽△BAC；（2）已知AC=6，BC=8，求线段AD的长度．3.（2016·浙江省绍兴市·5分）如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为．4.（2016·重庆市A卷·4分）正方形ABCD中，对角线AC，BD相交于点O，DE平分∠ADO交AC于点E，把△ADE沿AD翻折，得到△ADE′，点F是DE的中点，连接AF，BF，E′F．若AE=．则四边形ABFE′的面积是多少？5.（2015•咸宁）如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）．（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；（2）如图2，双曲线y=与新函数的图象交于点C（1，a），点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．①试求△PAD的面积的最大值；②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D 的坐标；若不能，请说明理由．【参考答案】变式训练1：（2016·吉林·3分）在三角形纸片ABC中，∠C=90°，∠B=30°，点D（不与B，C重合）是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为a，则△DEF的周长为3a （用含a的式子表示）．【解析】翻折变换（折叠问题）．由折叠的性质得出BE=EF=a，DE=BE，则BF=2a，由含30°角的直角三角形的性质得出DF=BF=a，即可得出△DEF的周长．【解答】解：由折叠的性质得：B点和D点是对称关系，DE=BE，则BE=EF=a，∴BF=2a，∵∠B=30°，∴DF=BF=a，∴△DEF的周长=DE+EF+DF=BF+DF=2a+a=3a；故答案为：3a．变式训练2：(2016河北3分）如图，将ABCD沿对角线AC折叠，使点B落在点B’处.若∠1=∠2=44°，则∠B为（）第13题图A．66°B．104°C．114°D．124°【解析】平行线的性质，折叠关系。

一．折叠类1. （13卷）在平面直角坐标系中，已知矩形ABCD 中，边2AB =，边1AD =，且AB 、AD 分别在x 轴、y 轴的正半轴上，点A 与坐标原点重合．将矩形折叠，使点A 落在边DC 上，设点A '是点A 落在边DC 上的对应点．（1）当矩形ABCD 沿直线12y x b =-+折叠时（如图1），求点A '的坐标和b 的值；（2）当矩形ABCD 沿直线y kx b =+折叠时，① 求点A '的坐标（用k 表示）；求出k 和b 之间的关系式； ② 如果我们把折痕所在的直线与矩形的位置分 为如图2、3、4所示的三种情形， 请你分别写出每种情形时k 的取值围． （将答案直接填在每种情形下的横线上） （——当如图1、2折叠时，求D A '的取值围？）（图1）k 的取值围是 ； k 的取值围是 ；k 的取值围是 ；[解] （1）如图答5，设直线12y x b =-+与OD 交于点E ，与OB 交于点F ，连结A O '，则OE = b ，OF = 2b ，设点A '的坐标为（a ，1）因为90DOA A OF ''∠+∠=︒，90OFE A OF '∠+∠=︒， 所以DOA OFE '∠=∠，所以△DOA '∽△OFE ．所以DA DO OE OF '=，即12a b b =，所以12a =． 所以点A '的坐标为（12，1）．连结A E '，则A E OE b '==．在R t △DEA '中，根据勾股定理有222A E A D DE ''=+ ，即2221()(1)2b b =+-，解得58b =．（2）如图答6，设直线y kx b =+与OD 交于点E ，与OB 交于点F ，连结A O '，则OE = b ，bOF k =-，设点A '的坐标为（a ，1）．因为90DOA A OF ''∠+∠=︒，90OFE A OF '∠+∠=︒． 所以DOA OFE '∠=∠，所以△DOA '∽△OFE ．所以DA DOOE OF '=，即1a b b k =-，所以a k =-． 所以A '点的坐标为（k -，1）．连结A E '，在Rt△DEA '中，DA k '=-，1DE b =-，A E b '=． 因为222A E A D DE ''=+，所以222()(1)b k b =-+-．所以212k b +=．在图答6和图答7中求解参照给分． （3）图13﹣2中：21k -≤≤-； 图13﹣3中：1-≤k≤2-+ 图13﹣4中：20k -≤[点评]这是一道有关折叠的问题，主要考查一次函数、四边形、相似形等知识，试题中贯穿了方程思想和数形结合的思想，请注意体会。

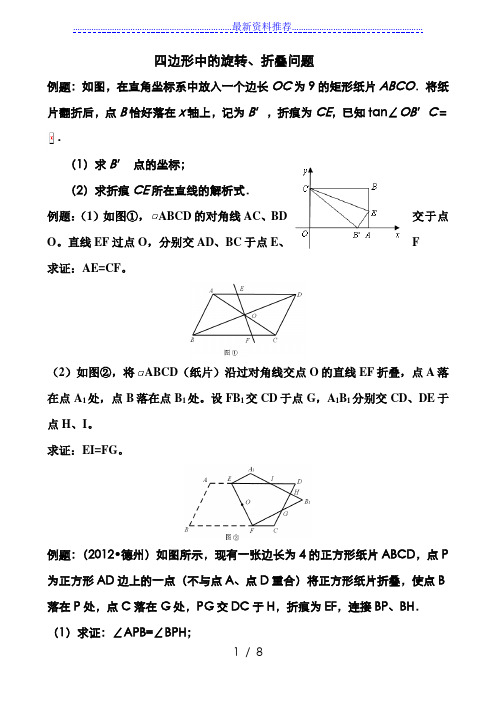
四边形中的旋转、折叠问题例题：如图，在直角坐标系中放入一个边长OC为9的矩形纸片ABCO．将纸片翻折后，点B恰好落在x轴上，记为B′，折痕为CE，已知tan∠OB′C＝．（1）求B′点的坐标；（2）求折痕CE所在直线的解析式．例题：（1）如图①，ABCD的对角线AC、BD交于点O。

直线EF过点O，分别交AD、BC于点E、 F求证：AE=CF。

（2）如图②，将ABCD（纸片）沿过对角线交点O的直线EF折叠，点A落在点A1处，点B落在点B1处。

设FB1交CD于点G，A1B1分别交CD、DE于点H、I。

求证：EI=FG。

例题：（2012•德州）如图所示，现有一张边长为4的正方形纸片ABCD，点P 为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B 落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．（1）求证：∠APB=∠BPH；（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；（3）设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S 是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．（2012•南宁）如图，已知矩形纸片ABCD，AD=2，AB=4．将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G，F，AE与FG交于点O．（1）如图1，求证：A，G，E，F四点围成的四边形是菱形；（2）如图2，当△AED的外接圆与BC相切于点N时，求证：点N是线段BC 的中点；（3）如图2，在（2）的条件下，求折痕FG的长．解：（1）由折叠的性质可得，GA=GE，∠AGF=∠EGF，∵DC∥AB，∴∠EFG=∠AGF，∴∠EFG=∠EGF，∴EF=EG=AG，∴四边形AGEF是平行四边形（EF∥AG，EF=AG），又∵AG=GE，∴四边形AGEF是菱形．（2）连接ON，∵△AED是直角三角形，AE是斜边，点O是AE的中点，△AED的外接圆与BC相切于点N，∴ON⊥BC，∵点O是AE的中点，∴ON是梯形ABCE的中位线，∴点N是线段BC的中点．（3）作OM⊥AD，设DE=x，则MO=x，在矩形ABCD中，∠C=∠D=90°，故AE为△AED的外接圆的直径．延长MO交BC于点N，则ON∥CD，∵四边形MNCD是矩形，∴MN=CD=4，∴ON=MN﹣MO=4﹣x，∵△AED的外接圆与BC相切，∴ON是△AED的外接圆的半径，∴OE=ON=4﹣x，AE=8﹣x，在Rt△AED中，AD2+DE2=AE2，∴22+x2=（8﹣x）2，得x=DE=，OE=4﹣x=，∵△FEO∽△AED，∴=，解得：FO=，∴FG=2FO=．故折痕FG的长是．对应练习1.（2012•泰安）如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（）第17题2.（2012•泰安）如图，菱形OABC 的顶点O 在坐标原点，顶点A 在x 轴上，∠B=120°，OA=2，将菱形OABC 绕原点顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（）3.（2012•泰安）如图，将矩形纸片ABCD 沿EF 折叠，使点B 与CD 的中点重合，若AB=2，BC=3，则△FCB′与△B′DG 的面积之比为（ ）4.如图，矩形ABCD 中，E 是AD 的中点， 将△ABE 沿BE 折叠后得到△GBE ，延长BG 交CD 于F 点，若CF =1，FD =2，则BC 的长为_______．5.矩形纸片ABCD 的边长AB=4，AD=2．将矩形纸片沿EF 折叠，使点A 与点C 重合，折叠后在其一面着色（如图），则着色部分的面积为（ ）(试题82页）6.（2010山东潍坊）如图，直角梯形ABCD 中，AB ⊥BC ，AD ∥BC ，BC ＞AD ，AD ＝2，ABCD D ′C ′NMF(第10题)AB ＝4，点E 在AB 上，将△CBE 沿CE 翻折，使B 点与D 点重合，则∠BCE 的正切值是________．(89页) 7.梯形中的对角线（88页）8..如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形，且它的一条直角边等于斜边的一半．这样的图形有【】(A)4个 (B)3个 (C)2个 (D)1个9如图所示，把一长方形纸片沿MN 折叠后，点D ，C 分别落在D ′，C ′的位置．若∠AMD ′＝36°，则∠NMD ′等于（A ）144° （B ）126° （C ）108° （D ）72° 10.一副三角板按图1所示的位置摆放.将△DEF 绕点A （F ）逆时针旋转60°后（图2），测得CG =10cm ，则两个三角形重叠（阴影）部分的面积为 (A) 75cm 2(B) cm 2 (C) cm 2 (D)cm 2例题：在正方形ABCD 的边AB 上任取一点E ，作EF ⊥AB 交BD 于点F ，取FD 的中点G ，连结EG 、CG ，如图（1），易证 EG=CG 且EG ⊥CG.A BC D E(F )BA(F ) D ECG(第8题)图2图1（1）将△BEF绕点B逆时针旋转90°，如图（2），则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想.（2）将△BEF绕点B逆时针旋转180°，如图（3），则线段EG和CG又有怎样的数量关系和位置关系？请写出你的猜想，并加以证明.解（1）EG=CG EG⊥CG------------------------------------------------------------(2分) （2）EG=CG EG⊥CG------------------------------------------------------------(2分)证明：延长FE交DC延长线于M，连MG∵∠AEM=90°，∠EBC=90°，∠BCM=90°∴四边形BEMC是矩形.∴BE=CM，∠EMC=90°又∵BE=EF∴EF=CM∵∠EMC=90°，FG=DG∴MG=FD=FG∵BC=EM ，BC=CD∴EM=CD∵EF=CM∴F M=D M∴∠F=45°又FG=DG∵∠CMG=∠EMC=45°∴∠F=∠GMC∴△GFE≌△GMC∴EG=CG ，∠FGE=∠MGC------------------------------------------------------------------------(2分)∵∠FMC=90° ，MF=MD，FG=DG∴MG⊥FD∴∠FGE+∠EGM=90°∴∠MGC+∠EGM=90°即∠EGC=90°∴EG⊥CG------------------------------------------------------------------------------------------- (2分)。

图形的折叠与旋转1．如图所示，在矩形ABCD 中，4,2,AB AD E CD ==是的中点，F 为BC 的中点，O 为AE 的中点，以AE 为折痕将△ADE 向上折起，使D 到P 点位置，且PC PB =．（1）求证：;PO ABCE ⊥面 （2）求二面角E-AP-B 的余弦值．2．如图，平行四边形ABCD ，2,4AB AD ==将CBD ∆沿BD 折起到EBD ∆的位置，使平面EDB ⊥平面ABD（I ）求证：AB DE ⊥； （Ⅱ）求三棱锥E ABD -的侧面积.3、如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=(Ⅰ) 证明:A O '⊥平面BCDE ； (Ⅱ) 求二面角A CD B '--的平面角的余弦值.4．如图，沿等腰直角三角形ABC 的中位线DE ，将平面ADE 折起，平面ADE ⊥平面BCDE ，得到四棱锥A BCDE -，4AC =，设AE 、CD 的中点分别为P 、Q ，（1）求证：平面ABC ⊥平面ACD （2）求证：ABC PQ 平面// （3）求平面ABC 与平面ADE 所成锐二面角的余弦值。

.CO BDEA CDOBE'A图1图2AD EC B5．已知四边形ABCD 满足AD ∥BC ，，E 是BC 的中点，将BAE ∆沿着AE 翻折成1B AE ∆，使面1B AE ⊥面AECD ，F 为1B D 的中点.（Ⅰ）求四棱锥1B AECD -的体积；（Ⅱ）证明：1B E ∥面ACF ； （Ⅲ）求面1ADB 与面1ECB 所成二面角的余弦值.图形的折叠与旋转（答案）1．试题分析：（1）,PA PE OA OE PO AE ==∴⊥， ……2分 BC 的中点为F ，连OF ，PF ，∴OF ∥AB ，∴OF ⊥BC 因为PB=PC ，∴BC ⊥PF ，所以BC ⊥POF ， ……3分 从而BC ⊥PO ， ……4分 又BC 与AE 相交，可得PO ⊥ABCE. ……5分（2）作OG ∥BC 交AB 于G ，∴OG ⊥OF 如图，建立直角坐标系[;,,],O OG OF OPA （1，-1，0），B （1，3，0），C （-1，3，0），P （0，0(2,4,0),(1,1,2),(0,4,0)AC AP AB =-=-= ……6分 设平面PAB 的法向量为(,,n x y z =4n AP x n AB y ⎧⋅=-+⎪⎨⋅==⎪⎩1(2,0,1)n ⇒= ……8分同理平面PAE 的法向量为2(1,1,0),n = ……9分……11分 ……12分2．（I ）证明：在ABD ∆中，由222AB AD BD =+，所以 DE AB ⊥又平面EBD ⊥平面ABD平面EBD平面,ABD BD AB =⊂平面ABDAB ∴⊥平面EBDDF ⊂平面,EBD AB DE ∴⊥（Ⅱ）解：由（I ）知,//,,AB BD CD AB CD BD ⊥∴⊥从而DB DE ⊥在Rt DBE ∆中，2DB =23DE ⋅=又AB ⊥平面,EBD BE ⊂平面,EBD AB BE ∴⊥BE BC =,DE BD ⊥平面EBD ⊥平面ABD ED ∴⊥，平面ABD而AD ⊂平面综上，三棱锥E ABD -的侧面积，3、(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE ,在OCD ∆中,由余弦定理可得OD==来源:Z,xx,]由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故2OH =,从而2A H '=所以cos 5OH A HO A H '∠==',所以二面角A CD B '--的平面角的余弦值为.向量法:以O 点为原点,建立空间直角坐标系O xyz -如图所示则(A ',()0,3,0C-,()1,2,0D -所以(CA '=,(1,DA '=-C D OBE'AH设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,[来源:学科网ZXXK]所以cos,3n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦值为4．（1）证明:Q 平面ADE ⊥平面BCDE ,交线为DE , AD DE ⊥, ∴AD ⊥平面BCDE .Q DE DC ⊥, ∴,,AD DC DE 两两互相垂直，以D 为原点建立空间直角坐标系, ……2分 因为∆ABC 为等腰直角三角形，且4AC =，则2,4DC BC ==， 则(0,0,0)D ,(2,0,0)C ，(0,0,2)A ，(0,2,0)E ，(2,4,0)B .∴)0,4,0(-=BC ,)2,0,0(=DA ,)0,0,2(=DC ,∴0,0BC DA BC DC ⋅=⋅=u u u r u u u r u u u r u u u r,∴,,BC DA BC DC DA DC D ⊥⊥=I ,∴BC ⊥平面ADC ,又BC ⊂平面ABC∴平面ABC ⊥平面ACD . ……5分（2）,P Q Q 分别为,AE CD 的中点,(0,1,1),(1,0,0,)P Q ∴,)1,1,1(--=∴PQ . 设平面ABC 的法向量),,(z y x n =,由于)0,4,0(-=BC )2,4,2(--=BA则0,0n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩r uu r r uu u r 即⎩⎨⎧=+--=-0242,04z y x y ,0y =,令1x =，则1z =, ∴)1,0,1(=n . 0PQ n ∴⋅=u u u r r, 即n PQ ⊥∴PQ //平面ABC . ……9分（3）由（2）可知平面ABC 的法向量)1,0,1(=n ，由于平面ADE 的法向量为)0,0,2(=DC , 设平面ABC 与平面ADE 所成锐二面角为θ，则……14分5.（Ⅰ）取AE 的中点,M 连接1B M ， ，所以ABE ∆为等边三角形，又因为面1B AE ⊥面AECD ，所以1B M ⊥面AECD ， ……2分所以四棱锥1B AECD -的体积……5分（Ⅱ）连接ED 交AC 于O ，连接OF ， 因为AECD 为菱形，所以OE OD =， 又F 为1B D 的中点，所以FO ∥1B E ， 因为FO ACF ⊂平面,BE ACF ⊄平面,所以1B E ∥面ACF . ……9分 （Ⅲ）连接MD ，分别以1,,ME MD MB 为,,x y z 轴建立空间直角坐标系.……10分 设面1ECB 的法向量(,,)v x y z '''=r ，则令1x '=，则设面1ADB 的法向量为(,,)u x y z =r ，则 令1x =，则……12分……14分。

【经典例题1】如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．（1）求⊙O的半径；（2）点E为圆上一点，∠ECD＝15°，将沿弦CE翻折，交CD于点F，求图中阴影部分的面积．【解析】（1）连接AO，如右图1所示，∵CD为⊙O的直径，AB⊥CD，AB＝8，∴AG＝＝4，∵OG：OC＝3：5，AB⊥CD，垂足为G，∴设⊙O的半径为5k，则OG＝3k，∴（3k）2+42＝（5k）2，解得，k＝1或k＝﹣1（舍去），∴5k＝5，即⊙O的半径是5；（2）如图2所示，将阴影部分沿CE翻折，点F的对应点为M，∵∠ECD＝15°，由对称性可知，∠DCM＝30°，S阴影＝S弓形CBM，连接OM，则∠MOD＝60°，∴∠MOC＝120°，过点M作MN⊥CD于点N，∴MN＝MO•sin60°＝5×，∴S阴影＝S扇形OMC﹣S△OMC＝＝，即图中阴影部分的面积是：．练习1-1如图，在⊙O中，点C在优弧上，将弧沿BC折叠后刚好经过AB 的中点D，连接AC，CD．则下列结论中错误的是（）A．AC＝CD B．+＝C．OD⊥AB D．CD平分∠ACB 【解析】A、过D作DD'⊥BC，交⊙O于D'，连接CD'、BD'，由折叠得：CD＝CD'，∠ABC＝∠CBD'，∴AC＝CD'＝CD，故①正确；B、∵AC＝CD'，∴，由折叠得：，∴＝，故②正确；C、∵D为AB的中点，∴OD⊥AB，故③正确；D、延长OD交⊙O于E，连接CE，∵OD⊥AB，∴∠ACE＝∠BCE，∴CD不平分∠ACB，故④错误；故选：D．练习1-2如图，AB是⊙O的弦，点C在上，点D是AB的中点．将在沿AC 折叠后恰好经过点D，若⊙O的半径为2，AB＝8．则AC的长是（）A．6B．C．2D．4【解析】如图，延长BO交⊙O于E，连接AE，OA，OD，OC，BC，作CH⊥AB 于H．∵AD＝DB，∴OD⊥AB，∴∠ADO＝90°，∵OA＝2，AD＝DB＝4，∴OD＝＝2，∵BE是直径，∴∠BAE＝90°，∵AD＝DB，EO＝OB，∴OD∥AE，AE＝2OD＝4，∴AE＝AD，∴＝，∴＝，∴∠CAE＝∠CAH＝45°，∴∠BOC＝2∠CAB＝90°，∴BC＝OC＝2，∵CH⊥AB，∴∠CAH＝∠ACH＝45°，∴AH＝CH，设AH＝CH＝x，则BH＝8﹣x，在Rt△BCH中，∵CH2+BH2＝BC2，∴x2+（8﹣x）2＝（2）2，∴x＝6或2（舍弃），在Rt△ACH中，∵AC＝，∴AC＝6．故选：A．练习1-3在扇形AOB中，∠AOB＝75°，半径OA＝12，点P为AO上任一点（不与A、O重合）．（1）如图1，Q是OB上一点，若OP＝OQ，求证：BP＝AQ．（2）如图2，将扇形沿BP折叠，得到O的对称点O'．①若点O'落在上，求的长．②当BO'与扇形AOB所在的圆相切时，求折痕的长．（注：本题结果不取近似值）【解析】（1）证明：∵BO＝AO，∠O＝∠O，OP＝OQ，∴△BOP≌△AOQ（SAS）．∴BP＝AQ．（2）解：①如图1，点O'落在上，连接OO'，∵将扇形沿BP折叠，得到O的对称点O'，∴OB＝O'B，∵OB＝OO'，∴△BOO'是等边三角形，∴∠O'OB＝60°．∵∠AOB＝75°，∴∠AOO'＝15°．∴的长为．②BO'与扇形AOB所在的圆相切时，如图2所示，∴∠OBO'＝90°．∴∠OBP＝45°．过点O作OC⊥BP于点C，∵OA＝OB＝12，∠COB＝∠OBP＝45°，∴．又∵∠AOB＝75°，∠COB＝45°，∴∠POC＝30°，∴．∴．∴折痕的长为．旋转类【经典例题2】如图1，在锐角△ABC中，AB=5，AC=42，∠ACB=45∘. 计算：求BC的长；操作：将图1中的△ABC绕点B按逆时针方向旋转，得到△A1BC1.如图2，当点C1在线段CA的延长线上时。

中考数学中的旋转翻折类问题专项训练经典汇编（共30题）1．阅读下面材料．小炎遇到这个一个问题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF ＝45°，连接EF，则EF＝BE+DF，试说明理由．小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中，她先尝试了翻折、旋转、平移的方法，最后发现线段AB、AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决这个问题（如图2）．参考小炎同学思考问题的方法，解决下列问题：（1）写出小炎的推理过程；（2）如图3，四边形ABCD中，AB＝AD，∠BAD＝90°，点E、F分别在边BC、CD 上，∠EAF＝45°，若∠B、∠D都不是直角，则当∠B与∠D满足于关系时，仍有EF＝BE+DF；（3）如图4，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE ＝45°，若BD＝1，EC＝2，求DE的长．2．如图1，把△ABC沿直线BC平移线段BC的长度，得到△ECD；如图2，以BC为轴，把△ABC沿BC翻折180°，可以得到△DBC；如图3，以点A为中心，把△ABC旋转180°，可以得到△AED．像这样，其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的，这种只改变位置，不改变形状、大小的图形变换，叫做三角形的全等变换．回答下列问题：（1）在图4中，可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF？（2）图中线段BE与DF相等吗？为什么？3．阅读材料并解答问题：探究：小明遇到这样一个问题：如图1，在正方形ABCD，点E、F分别为BC、CD边上的点，且∠EAF＝45°，求证：BE+DF＝EF．小明是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段集中到同一条线段上．他先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．他的方法是将△ADF绕点A顺时针旋转90°得到△ABG（如图1），此时GE即是BE+DF．请回答：在图1中，∠GAF的度数是．理解：如图2，已知Rt△ABC中，∠ACB＝90°，AC＝BC，点D、E在斜边AB上，且∠DCE＝45°，请写出AD、DE、BE三条线段之间的数量关系，并证明．应用：如图3，正方形ABCD中，△AMN的顶点M、N分别在BC、CD边上，AH⊥MN，且AH＝AB，连接BD分别交AM、AN于点E，若MH＝2，NH＝3，DF＝2，求AH、EF的长．4．阅读下面材料：小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF ＝45°，连接EF，则EF＝BE+DF，试说明理由．小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．参考小炎同学思考问题的方法，解决下列问题：（1）如图3，四边形ABCD中，AB＝AD，∠BAD＝90°点E，F分别在边BC，CD上，∠EAF＝45°．若∠B，∠D都不是直角，则当∠B与∠D满足关系时，仍有EF＝BE+DF；（2）如图4，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE ＝45°，若BD＝1，EC＝2，求DE的长．5．如图，在正方形ABCD中，E为AD的中点，F是BA延长线上一点，AF＝AB．（1）图中的全等三角形是哪一对？（2）在图中，可以通过平移、翻折、旋转中哪一种方法，使△ABE变换到△ADF的位置？（3）图中线段BE与DF之间有怎样的关系？为什么？6．已知点E是△ABC内部一点．将△ABE沿BE翻折，点A落在BC上的点F′处．（1）如图1，若∠BAC﹣80°，∠C﹣40°，EF∥AC．求∠BEF的度数；（2）如图2，若∠C＝2∠BAE，请说明．（3）如图3．连接AF，若AE⊥BC，∠ABC﹣70°，∠C＝40°，将△BEF绕点B顺时针方向旋转一个角度α（0＜α＜180°）得到ΔBE1F1，则在这个旋转过程中，当E1F1与△AFC的某一边垂直时，直接写出旋转角α的度数．7．如图1，在Rt△ABC中，∠A＝90°，AB＝21，AC＝28，点D为BC边上一点，过点作DE⊥AB于点E，作DF⊥AC于点F，且DE＝DF．（1）求证：四边形AEDF为正方形；（2）如图2，将△CDF沿DF翻折，得△GDF，DG交AB于点H，求证：DH＝DB；（3）将（2）中的△BDH绕点D逆时针旋转α（0°＜α＜180°）得△B′DH′（点B的对应点为B′，点H的对应点为H′，连接GH′，CB′，点M为线段GH′的中点，连接DM．当△B′DC为直角三角形时，直接写出线段DM的长．8．如图，在等边△ABC中，AD⊥BC于点D，E为线段AD上一动点（不与A，D重合），连接BE，CE，将CE绕点C顺时针旋转60°得到线段CF，连接AF．（1）如图1，求证：∠CBE＝∠CAF；（2）如图2，连接BF交AC于点G，连接DG，EF，EF与DG所在直线交于点H，求证：EH＝FH；（3）如图3，连接BF交AC于点G，连接DG，EG，将△AEG沿AG所在直线翻折至△ABC所在平面内，得到△APG，将△DEG沿DG所在直线翻折至△ABC所在平面内，得到△DQG，连接PQ，QF．若AB＝4，直接写出PQ+QF的最小值．9．在Rt△ABC中，∠ABC＝90°，过B点作BE⊥AC于点E，点D为线段AC的中点，连接BD．（1）如图1，AB＝2，AC＝6，求ED的长度；（2）如图2，将线段DB绕着点D逆时针旋转45°得到线段DG，此时DG⊥AC，连接BG，点F为BG的中点，连接EF，求证：BC＝2EF；（3）如图3，∠ACB＝30°，AB＝3，点P是线段BD上一点，连接AP，将△APB沿AP 翻折到同一平面内得到△APB'，连接CB′，将线段绕点CB′顺时针旋转60°得线段CQ，连接BQ，当BQ最小时，直接写出△BCQ的面积．10．如图，CD为△ABC的中线，以CD为直角边在其右侧作直角△CDE，CD⊥DE，BC与DE交于点F，∠E＝30°．（1）如图1，若CF＝EF＝5，求CD的长；（2）如图2，若将BC绕点C逆时针旋转120°得CG，连接AG、AE，探究AG、AE的数量关系，并说明理由；（3）如图3，若∠ACB＝90°，AC＝2，．直线CE上有一点M，连接MF，将△CFM沿着MF翻折至△ABC所在的平面内得到△NFM．取NF的中点P，连接AP，当AP最小时，请直接写出△APB的面积．11．已知△ABC为等边三角形，D是边AB上一点，连接CD，点E为CD上一点，连接BE．（1）如图1，延长BE交AC于点F，若∠ABF＝15°，．求AF的长；（2）如图2，将△BEC绕点C顺时针旋转60°到△AGC，延长BC至点H，使得CH＝BD，连接AH交CG于点N，猜想线段CE，GN，DE之间存在的数量关系，并证明你的猜想；（3）如图3，AB＝8，点H是BC上一点，且BD＝2CH，连接DH，点K是AC上一点，CK＝AD，连接DK，BK，将△BKD沿BK翻折到△BKQ，连接CQ，当△ADK的周长最小时，直接写出△CKQ的面积．12．在边长为8的等边三角形ABC中，D为BC的中点，E，F分别为AC、AD上任意一点，连接EF，将线段EF绕点E顺时针旋转60°得到线段EG，连接FG交AC于点N，连接AG．（1）如图1，点E与点C重合，且GF的延长线过点B，证明：四边形AFEG是菱形；（2）如图2，EF的延长线交AB于点M，当AM+MF＝AE时，求∠EAG的度数；（3）如图3，E为AC的中点，连接BE，H为直线BC上一动点，连接EH，将△BEH 沿EH翻折至△ABC所在平面内，得到△B′EH，连接B′G，直接写出线段B′G长度的最小值．13．在△ABC中，∠ACB＝90°，AC＝BC，D是AC边上一动点，连接BD．（1）如图1，在平面内将线段DC绕点C顺时针旋转90°得到线段CK，点F为BC边上一点，连接AF交BD于M，连接AK．若∠CAF＝2∠DBA，AF＝8，AK＝10，求CF的长；（2）如图2，在平面内将线段DB绕点B顺时针旋转一定角度得到线段BE，连接AE交BC于G，连接DE，若∠CDE＝∠DBA，猜想线段AD，CG的数量关系，并证明你的猜想；（3）在（2）的条件下，将△CDB沿BD直线BD翻折至△ABC所在平面内得到△BDC1，连接AC1，若AC＝2+，在点D运动过程中，当线段AC1取得最小值时，请直接写出△ABE与四边形BCDC1重叠部分的面积．14．在△ABC中，∠BAC＝90°，AB＝AC，点D为BC边上一动点，连接AD，将AD绕着D点逆时针方向旋转90°得到DE，连接AE．（1）如图1，AH⊥BC，点D恰好为CH中点，AE与BC交于点G，若AB＝4，求AE 的长度；（2）如图2，DE与AB交于点F，连接BE，在BA延长线上有一点P，∠PCA＝∠EAB，求证：AB＝AP+BD；（3）如图3，DE与AB交于点F，且AB平分∠EAD，点M为线段AF上一点，点N为线段AD上一点，连接DM，MN，点K为DM延长线上一点，将△BDK沿直线BK翻折至△BDK所在平面内得到△BQK，连接DQ，在M，N运动过程中，当DM+MN取得最小值，且∠DKQ＝45°时，请直接写出的值．15．在平面直角坐标系中，已知点A（4，0），点B（0，3）．点P从点A出发，以每秒1个单位的速度向右平移，点Q从点B出发，以每秒2个单位的速度向右平移，又P、Q 两点同时出发．（1）连接AQ，当△ABQ是直角三角形时，则点Q的坐标为；（2）当P、Q运动到某个位置时，如果沿着直线AQ翻折，点P恰好落在线段AB上，求这时∠AQP的度数；（3）若将AP绕点A逆时针旋转，使得P落在线段BQ上，记作P'，且AP'∥PQ，求此时直线PQ的解析式．16．（1）特殊发现如图1，正方形BEFG与正方形ABCD的顶点B重合，BE、BG分别在BC、BA边上，连接DF，则有：①＝；②直线DF与直线AG所夹的锐角等于度；（2）理解运用将图1中的正方形BEFG绕点B逆时针旋转，连接DF、AG．①如图2，（1）中的结论是否仍然成立？请说明理由；②如图3，若D、F、G三点在同一直线上，且过AB边的中点O，BE＝4，直接写出AB的长；（3）拓展延伸如图3，点P是正方形ABCD的AB边上一动点（不与A、B重合），连接PC，沿PC将△PBC翻折到△PEC位置，连接DE并延长，与CP的延长线交于点F，连接AF，若P A ＝3PB，则的值是否是定值？请说明理由．17．已知：如图①，在矩形ABCD中，AB＝8，AD＝6，连接AC，将△ABC沿AC翻折，使B点落在E点处，连接EC、AE，AE交DC于F点．（1）求DF的长．（2）若将△CEF沿着射线CA方向平移，设平移的距离为m（平移距离指点C沿CA方向所经过的线段长度）．当点F平移到线段AD上时，如图②，求出相应的m的值．（3）如图③，将△CEF绕点C逆时针旋转一个角a（0°＜a＜∠ECB），记旋转中的△CEF为△CE'F'，过E'作E'G⊥AD于G点，在旋转过程中，当△DCE'为等腰三角形时，求出线段E'G的长度．18．已知矩形ABCD中，AB＝2，BC＝m，点E是边BC上一点，BE＝1，连接AE．（1）沿AE翻折△ABE使点B落在点F处．①连接CF，若CF∥AE，求m的值；②连接DF，若≤DF≤，求m的取值范围．（2）△ABE绕点A顺时针旋转得△AB1E1，点E1落在边AD上时旋转停止．若点B1落在矩形对角线AC上，且点B1到AD的距离小于时，求m的取值范围．19．如图，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x 轴的正半轴上，点C在y轴的正半轴上，点B的坐标为（10，8），在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处．（1）求CE和OD的长；（2）求DE所在直线的解析式；（3）若直线y＝kx+b与直线DE的比例系数相等，当它与矩形OABC有公共点时，请直接写出b的取值范围．20．如图1，将△ABC纸片沿中位线EH折叠，使点A对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．（1）将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段、，S矩形AEFG：S▱ABCD＝；（2）▱ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF＝9，EH＝12，求AD的长；（3）如图4，四边形ABCD纸片满足AD∥BC，AD＜BC，AB⊥BC，AB＝12，CD＝13，小明把该纸片折叠，得到叠合正方形，请你帮助画出叠合正方形的示意图，并直接写出AD、BC的长．（写出一种即可）21．如图1，在平面直角坐标系xOy中，直线y＝﹣x+8分别交x轴、y轴于A、B两点，已知点C（3，0），点D是线段AB上的一个动点．（1）判断△ABO的形状；（2）OD+CD的最小值为；（3）如图2，点P为y轴正半轴上一点，连接BC、PC，若∠BCP与△ABC中的一个角相等，求点P的坐标；（4）如图3，将△ACD沿CD翻折，点A恰好落在y轴上的点A′处，求此时点D的坐标．22．在等腰△ABC中，AB＝BC，高AD，BE所在的直线相交于点F，将△ACD沿直线AD 翻折，点C的对称点C′落在直线BC上，连接FC′．（1）如图1，当∠ABC＝45°时，①求证：BF＝AC；②求∠FC′D的度数．（2）当∠ABC＝135°时，补全图2，并求证：C′F∥AB．23．如图1，在平面直角坐标系中，点A坐标为（6，3），过点A作AB⊥x轴，交x轴于点B，点P是x轴上一动点，将△ABP沿直线AP翻折，使得点B落在点B'处，点E是翻折后AB'延长后与y轴的交点．（1）若点E的坐标为（0，3），则点P坐标为；（2）如图2，若点E的坐标为（0，），直线AE与x轴交于点F．①求点F的坐标；②求直线AP的函数关系式．24．如图，在矩形ABCD中，E是BC边上的一个动点，沿着AE翻折△ABE，使点B落在点F处，AB＝2，BC＝AB．（1）当点E运动到点C时，求CF的长；（2）当FC∥AE时，试判断E是否为BC的中点？并说明理由；（3）当点F在矩形ABCD内部，且DF＝CD时，求BE的长．25．如图，在平面直角坐标系中，四边形OABC的边OC在x轴上，OA在y轴上，O为坐标原点，AB∥OC，线段OA，AB的长分别是方程x2﹣9x+20＝0的两个根（OA＜AB），延长CB交y轴于点H，＝．（1）求点B，C的坐标；（2）P为OA上一点，Q为OC上一点，OQ＝5，将△POQ翻折，使点O落在AB上的点O'处，双曲线y＝的一分支过点O′，求k的值；（3）在（2）的条件下，M为坐标轴上一点，在平面内是否存在点N，使以O'，Q，M，N为顶点四边形为矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．26．如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．（1）求证AE＝MN；（2）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（3）如图3，若该正方形ABCD边长为10，将正方形沿着直线MN翻折，使得BC的对应边B′C′恰好经过点A，过点A作AG⊥MN，垂足分别为G，若AG＝6，请直接写出AC′的长．27．如图1，矩形的边OA在x轴上，边OC在y轴上，点B的坐标为（6，8）．D是AB边上一点（不与点A、B重合），将△BCD沿直线CD翻折，使点B落在点E处．（1）求直线AC所表示的函数的表达式；（2）如图2，当点E恰好落在矩形的对角线AC上时，求点D的坐标；（3）如图3，当以O、E、C三点为顶点的三角形是等腰三角形时，求△OEA的面积．28．已知在平行四边形ABCD中，AB≠BC，将△ABC沿直线AC翻折，点B落在点E处，AD与CE相交于点O，连接DE．（1）如图1，求证：AC∥DE；（2）如图2，如果∠B＝90°，AB＝，BC＝，求△OAC的面积；（3）如果∠B＝30°，AB＝2，当△AED是直角三角形时，求BC的长．29．如图，矩形ABCD中，已知AB＝6．BC＝8，点E是射线BC上的一个动点，连接AE 并延长，交射线DC于点F．将△ABE沿直线AE翻折，点B的对应点为点B'．（1）如图1，若点E为线段BC上一点，延长AB'交CD于点M，求证：AM＝FM；（2）如图2，若点B'恰好落在对角线AC上，求的值；（3）若＝，求∠DAB'的正弦值．30．如图1，四边形ABCD是矩形，点O位于对角线BD上，将△ADE，△CBF分别沿DE、BF翻折，点A，点C都恰好落在点O处．（1）求证：∠EDO＝∠FBO；（2）求证：四边形DEBF是菱形：（3）如图2，若AD＝2，点P是线段ED上的动点，求2AP+DP的最小值．。

专题07解题技巧专题：矩形、菱形、正方形中折叠、旋转问题压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【考点一矩形中的折叠问题】 (1)【考点二菱形中的折叠问题】 (13)【考点三正方形中的折叠问题】 (20)【考点四矩形、菱形、正方形折叠后求周长、面积问题】 (28)【考点五矩形、菱形、正方形中旋转问题】 (36)【典型例题】【考点一矩形中的折叠问题】例题：（2023上·江西九江·九年级统考期末）如图，在矩形ABCD 中，将ADE V 沿AE 折叠，点D 刚好落在对角线AC 上的点F ．(1)若8AB =，6BC =，求DE 的长．(2)若AE EC =，求证：2AC BC =．【答案】(1)3DE =(2)证明见解析【分析】（1）由矩形的性质和勾股定理，得出10AC =，再由折叠的性质，得到6AF =，DE EF =，90EFC ∠=︒，进而得到4CF =，设DE EF x ==，利用勾股定理列方程求解，即可求出DE 的长；【变式训练】1．（2023上·山东菏泽·七年级统考阶段练习）如图，将矩形纸片ABCD 沿BD 折叠，得到BC D '△，C D '与AB 交于点E ．若125∠=︒，则2∠的度数为（）A．20︒B【答案】D【分析】本题考查了矩形的性质，折叠性质，直角三角形额特征量，根据性质计算即可．【详解】∵矩形纸片ABCDA．5B．13 2【答案】C【分析】本题考查了折叠的性质，勾股定理．设8A G DG a'==-，求得AE=∵=EG CG ，∴设EG CG a ==，CF x =，∴8DG a =-，12BF x =-，由折叠的性质知AE A E '=，BF ∵=EG CG ，90D A '∠=∠=︒，【答案】52或10【分析】本题主要考查了矩形的折叠问题，勾股定理．根据题意进行分类讨论∵四边形ABCD 为矩形，GH ∴四边形AGHD 为矩形，∴5AD GH ==，GH AB ⊥∵点F 在线段AB 的垂直平分线上，∵四边形ABCD 为矩形，GH ∴四边形AGHD 为矩形，∴5AD GH ==，GH AB ⊥∵点F 在线段AB 的垂直平分线上，【答案】263或13104【分析】本题考查了矩形与折叠问题，用勾股定理解三角形，先根据矩形的性质找到边长之间的关系，设出边长BE 的值，构造出直角三角形，一元二次方程，求解即可，作辅助线，根据直角三角形三边关系得到等式是解题的关键．【详解】解：∵在矩形，此时12MF BC ==，∵13GF =，∴在GMF △中，2GM GF =∴5GM =，∵3=GA ，，在GAF 中，2AF GF =-即410BN =，∴410EN BN BE x =-=-在EFN 中，22EF EN FN =+()22241010x x=-+，)如图①，当点E 是BC 中点时，求CG 的长；)如图②，在（1）的条件下，当矩形变化为平行四边形时，求证：CG )如图③，在矩形ABCD 中，当点F 落在矩形对角线AC 上时，BE 的长是【答案】(1)43CG =∵E 是BC 的中点，∴BE EC =，∵ABE 沿AE 折叠后，得到∴3AF AB ==，AFE ∠∵四边形ABCD 是平行四边形，∴AB DC ∥,∴,BAH CHA ABC ∠=∠∠=∵E 是BC 的中点，∴BE EC =，又AEB HEC ∠=∠，由折叠得BE EF =,AF ∴53FC AC AF =-=-设BE x =，则,EF x EC =在Rt EFC △中，2EF +即()22224x x +=-，(1)求CF CD的值；(2)四边形EFDB '的面积为________；∴30B ND '∠=︒，∵B E CD '∥，∴30NDF B ND '∠=∠=︒，即DF 旋转的角度为30︒，故答案为：30．【考点二菱形中的折叠问题】【答案】43【分析】如图所示，延长ME 交DC AMD CDM EMB N ==∠∠，∠∠，∠折叠的性质可得AMD DME =∠∠，程即可得到答案．【点睛】本题主要考查了菱形的性质，折叠的性质，全等三角形的性质与判定，等腰三角形的判定等等，正确作出辅助线构造全等三角形是解题的关键【变式训练】1．（2023下·山西长治·八年级统考期末）如图，在菱形ABCD 中，=60B ∠︒，将边AB 沿AF 折叠得到,AB AB ''交CD 于点E ，当E 为CD 中点时，EFC ∠的大小为（）A ．28︒B ．75︒C ．40︒D ．30︒【答案】D 【分析】延长AE 交BC 的延长线于点H ，过点A 作AI BH ⊥于点I ，可证ADE HCE ≌△△，故CH AD BC AB ===，即2BH AB =，即可求解．【详解】解：延长AE 交BC 的延长线于点H ，过点A 作AI BH ⊥于点I∥，∵AD BC∠=∠，∴D ECH∵E为CD中点，=，∴DE CE【答案】3【分析】连接AC、BD，根据题意得出再由已知条件根据含30度直角三角形的性质求出【详解】解：连接AC、BD，如图所示：四边形ABCD是菱形，∴⊥，AC BD将菱形ABCD折叠，使点A恰好落在菱形对角线的交点=，∴=，AF OFAE EO∴、F分别为AB、AD的中点，E（1）DEF∠=（2）若点E是AB的中点，则【答案】90︒/90度【分析】（1）由翻折可得120A ∠=︒ ，2AB =，60DCM ∴∠=︒，2CD =，112CM CD ∴==，DM =(1)求证：四边形CEFG 是菱形；(2)若8AB =，10AD =，求四边形CEFG 的面积．【答案】(1)见解析；(2)20．【分析】（1）根据题意和翻折的性质，可以得到BCE BFE ≌，再根据全等三角形的性质和菱形的判定方法即可证明结论成立；（2）根据题意和勾股定理，可以求得AF 的长，进而求得EF 和DF 的值，从而可以得到四边形CEFG 的面积．【详解】（1）证明：∵BCE 沿BE 折叠，点C 落在AD 边上的点F 处，∴BCE BFE ≌，∴BEC BEF ∠∠=，FE CE =，∵FG CE ∥，∴FGE CEB ∠∠=，∴FGE FEG ∠∠=，∴FG FE =，∴FG EC =，∴四边形CEFG 是平行四边形，又∵CE FE =，∴四边形CEFG 是菱形；（2）解：∵矩形ABCD 中，8AB =，10AD =，BC BF =，∴90BAF ∠=︒，10AD BC BF ===，∴6AF =，∴4DF =，设EF x =，则CE x =，8DE x =-，∵90FDE ∠=︒，∴()22248x x +-=，解得，x =5，∴CE =5，∴四边形CEFG 的面积是：5CE DF ⋅=4⨯=20．【点睛】本题考查翻折变化、菱形的性质和判定、矩形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．【考点三正方形中的折叠问题】(1)求线段AB 和线段CF 的长；(2)连接EQ ，EQ =【答案】(1)8AB CF ==，(2)65【分析】（1）由对角线为8由折叠可知AE PE BQ =，∴90BFE FBQ ∠+∠=︒，∵90BFE GEF ∠+∠=︒，∴FBQ GEF ∠=∠，∴()ASA EGF BCQ ≌，【变式训练】1.（2023下·天津北辰·八年级校联考期中）如图，将正方形纸片ABCD 折叠，使边,AB CB 均落在对角线BDA．15︒【答案】C【分析】根据四边形ABCD角平分线，由此即可求解．【详解】解：∵四边形【答案】5【分析】连接AE，根据正方形的性质，三角形全等的判定和性质，矩形的判定和性质，折叠的性质，勾股定理计算即可．【详解】解：如图，连接过点G 作GM AD ⊥故MG AB =，由翻折变换的性质得∵90AFG DAE ∠+∠=∴AFG AED ∠=∠，【答案】49 13【分析】证ABF≌6013AM=，得出AG四边形ABCD为正方形，12AB AD CD∴===由折叠的性质可知，BF AE∴⊥，AM GM=90BAM ABM∴∠+∠=【答案】（1）1；（2）23-；（3）97或2【分析】（1）由正方形的性质得90BAD ∠=︒，再由折叠的性质得：BAE ∠=可求解；（2）证ANF 是等腰直角三角形，得45AFN ∠=︒，则45AFD AFM ∠=∠=︒当DF2CF=时，CF= ，JK DF【考点四矩形、菱形、正方形折叠后求周长、面积问题】【答案】6.5/162/132【分析】首先根据矩形的性质可得得 2.5C D CD '==，C ∠获得答案．【详解】解：∵四边形ABCD 为矩形， 2.5AB =，4BC =，∴ 2.5CD AB ==，4AD BC ==，90C A ∠=∠=︒，根据题意，沿对角线BD 折叠，点C 落到C '处，∴ 2.5C D CD '==，90C C '∠=∠=︒，∴C D AB '=，在ABE 和C DE ' 中，90AEB C ED A C AB C D '''∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴(AAS)ABE C DE ' ≌，∴AE C E '=，∴C ED '△的周长 2.54 6.5C D C E DE C D AE DE C D AD ''''=++=++=+=+=．故答案为：6.5．【点睛】本题主要考查了矩形的性质、折叠的性质、全等三角形的判定与性质等知识，证明ABE C DE ' ≌是解题关键．【变式训练】【答案】12∵四边形ABCD 是菱形，【答案】133【分析】由菱形的性质可得AC BD ⊥，120BAD ∠=︒∵四边形ABCD 是菱形，∴AC BD ⊥，BAD BCD ∠=∠∴cm 132OA AB ==，BAC ∠(1)求DE的长；(2)求阴影部分的面积．【答案】(1)318(2)4AG AB ==，5AE =，所以1143522GM ⨯⨯=⨯⨯所以125GM =，(1)求证：四边形AECF 为菱形；(2)若8cm AB =，16cm BC =【答案】(1)见解析Y沿直线BE折叠，使点A的对应点F落在(1)如图1，将ABCDY是矩形：(2)如图2，若ABCD①按（1）中操作进行，求证：四边形ABFE是正方形；②在矩形ABCD中折叠出一个菱形DEBF，并使菱形DEBF以【点睛】本题主要考查了折叠的性质，平行四边形的判定和性质，勾股定理，菱形的判定，正方形的判定，矩形的性质，解题的关键是熟练掌握相关内容，并灵活运用．【考点五矩形、菱形、正方形中旋转问题】(1)四边形BEHC是怎样的特殊四边形？证明你的结论；(2)若BC长为2，则AB的长为【答案】(1)四边形BEHC是平行四边形，证明见解析(2)3【分析】（1）依据题意可得到FE∠=∠，然后依据AAS证明FHE CED四边形BEHC 为菱形，BE BC ∴=．由旋转的性质可知BC EC =．BE EC BC ∴==．EBC ∴△为等边三角形．60EBC ∴∠=︒．【变式训练】1．（2023上·广东珠海·九年级珠海市九洲中学校考期中）如图，在矩形ABCD 中，8AB =，6AD =，将矩形ABCD 绕点A 逆时针旋转（旋转角小于90度）得到矩形AEFG ．(1)如图①，若在旋转过程中，点E落在对角线①求证：MA MC=；②求MF的长；(2)在旋转过程中，当旋转到如图②所示的情况，若直线面积．【答案】(1)①见解析；②15 4②如图所示，同①得：27AH=，∴87PE=+，∴1222 BEG GPES S==⨯⨯的面积是综上：BEG【点睛】本题考查的是四边形综合问题，解题的关键是掌握矩形的性质，旋转的性质，全等三角形的性质和判定，以及等腰三角形的判定，需要注意进行分类讨论．2．（2021下·江苏南京在边AB，AD上，连接可得AF OD ∥，△ABD 和△AEG 是等边三角形，从而得到AF =OD ，进而得到四边形AODF 是平行四边形，即可求解；②分两种情况讨论：90BDF ∠=︒和90BFD ∠=︒，利用矩形的性质、等边三角形的判定与性质求解即可得．【详解】（1）证明：连接AF ，∵四边形AEFG 是菱形，∴AE EF FG GA ===，在GAF 和EAF △中，AG AE GF EF AF AF =⎧⎪=⎨⎪=⎩，∴()GAF EAF SSS ≅ ，∴GAF EAF ∠=∠，∵四边形ABCD 是菱形，∴AD AB =，在DAF △和BAF △中，AD AB DAF BAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴()DAF BAF SAS ≅ ，∴DF BF =．（2）解：①如图，连接AF ，EG ，BD ，AC ，BD 与AC 交于点O ，AF 交EG 于点P ，【类比探究】如图2，将正方形AEFG绕点A旋转任意角度.(1)请你判断图1中得到的线段BE和DG的关系是否仍然成立，并说明理由；(2)当点H在直线AD左侧时，连接AH，存在实数m满足等式m AH DH BH⋅+=，请求出由；(3)若5AE=，正方形AEFG在绕点A旋转过程中，当点F，H重合时，请直接写出线段AB=，1四边形ABCD和四边形AEFG由（1）可知(SAS ABE ADG ≌∴,,ABE ADH AD AB ∠=∠=∴(SAS)ADH ABN ≌，∴BAN DAH AN AH ∠=∠=，，90DAN BAN ∠+∠=︒，∵5AE=，四边形AB=，1∴==，AEF1EF FG∠=∠直线BE与DG交于点H，且点∴点B、E、F在同一直线上，5,1，四边形==AB AE∴==1EF FG直线BE与DG交于点∴点B、E、F在同一直线上，。