人工智能A星算法解决八数码难题程序代码

基于A星算法解决8数码问题的编程实现一、问题描述8数码问题又称9宫问题。

在给定的33⨯棋格的9个格子内分别放从1到8互不相等的八个数，剩下的一格即为空格，此程序中空格我们用0来表示。

通常把8个符号在棋格上的排列顺序称作8数码的状态。

开始时，规则给定一个初始状态和一个目标状态，并要求被试者对棋格内的数字经过若干次移动由初始状态达到目标状态，这个过程中只有空格向附近的棋格移动，且每次只能移动一次。

如我们给定8数码的初始状态和目标状态分别如图1、2所示。

图1 初始状态图2 目标状态则要求以图1为初始状态，通过交换0和0的上、下、左、右四个方位的数字（每次只能和其中一个交换），达到图2所示目标状态。

二、算法说明根据任务要求，本文采用A*搜索算法。

1. 状态的表示在A*算法中，需要用到open表和closed表，在open表中，待扩展节点间有很严格的扩展顺序。

因此在表示当前状态的变量中，必须要有能指向下一个扩展节点的指针，以完成对open表中元素的索引。

从这一点上看，open表中的元素相互间即构成了一个线性表，因此初步选定使用结构体表示问题的状态。

如图3所示，表示问题的结构体包括表示当前节点状态的DATA和指向open 表中下一个待扩展节点的指针NEXT。

图3 结构体现在进一步考虑DATA中包括的内容：如图1、2所示，8数码问题的提出是以一个33⨯数表表示的，因此本文中采用一个33⨯的二维数组s[3][3]表示当前状态的具体信息。

另一方面，A*搜索算法是通过考察节点的代价值来决定open表的排序的，因此在表示当前状态的DATA中还应该有对当前节点代价值的描述。

根据A*算法的定义，当前节点的代价值由估价函数给出，即：=+f n d n h n()()()其中：()d n表示当前节点n在搜索树中的深度；h n是启发函数。

()本例h(n)=p(n)+w(n)其中：p(n)表示每个将牌与其目标位置之间最短距离的总和；w(n)表示不在位的将牌个数。

一、实验内容和要求八数码问题：在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

例如：图1 八数码问题示意图请任选一种盲目搜索算法（广度优先搜索或深度优先搜索）或任选一种启发式搜索方法（全局择优搜索，加权状态图搜索，A 算法或A* 算法）编程求解八数码问题（初始状态任选）。

选择一个初始状态，画出搜索树，填写相应的OPEN 表和CLOSED表，给出解路径，对实验结果进行分析总结，得出结论。

二、实验目的1. 熟悉人工智能系统中的问题求解过程；2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用；3. 熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验算法A*算法是一种常用的启发式搜索算法。

在A*算法中，一个结点位置的好坏用估价函数来对它进行评估。

A*算法的估价函数可表示为：f'(n) = g'(n) + h'(n)这里，f'(n)是估价函数，g'(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h'(n)是n到目标的最短路经的启发值。

由于这个f'(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点的最佳路径的估计代价。

在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。

用f(n)作为f'(n)的近似，也就是用g(n)代替g'(n)，h(n)代替h'(n)。

这样必须满足两个条件：（1）g(n)>=g'(n)（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增。

（2）h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。

a星算法求解八数码问题python一、介绍八数码问题是一种经典的智力游戏，也是人工智能领域中的经典问题之一。

在这个问题中，有一个3×3的棋盘，上面摆着1至8这8个数字和一个空格，初始状态和目标状态都已知。

要求通过移动数字，将初始状态变换成目标状态。

其中空格可以和相邻的数字交换位置。

为了解决这个问题，我们可以使用A*算法。

本文将详细介绍如何用Python实现A*算法来求解八数码问题。

二、A*算法简介A*算法是一种启发式搜索算法，常用于寻找最短路径或最优解等问题。

它基于Dijkstra算法，并加入了启发式函数来加速搜索过程。

在A*算法中，每个节点都有两个估价值：g值和h值。

g值表示从起点到该节点的实际代价，h值表示从该节点到目标节点的估计代价。

启发式函数f(n) = g(n) + h(n) 表示从起点到目标节点的估计总代价。

A*算法采用优先队列来保存待扩展的节点，并按照f(n)值从小到大排序。

每次取出队头元素进行扩展，并将扩展出来的新节点按照f(n)值插入队列中。

当扩展出目标节点时，算法结束。

三、八数码问题的状态表示在八数码问题中，每个状态都可以表示为一个3×3的矩阵。

我们可以用一个一维数组来表示这个矩阵，其中0表示空格。

例如，初始状态可以表示为[2, 8, 3, 1, 6, 4, 7, 0, 5]，目标状态可以表示为[1, 2, 3, 8, 0, 4, 7, 6, 5]。

四、A*算法求解八数码问题的步骤1.将初始状态加入优先队列中，并设置g值和h值为0。

2.从队头取出一个节点进行扩展。

如果该节点是目标节点，则搜索结束；否则，将扩展出来的新节点加入优先队列中。

3.对于每个新节点，计算g值和h值，并更新f(n)值。

如果该节点已经在优先队列中，则更新其估价值；否则，将其加入优先队列中。

4.重复第2步至第3步直到搜索结束。

五、Python实现以下是用Python实现A*算法求解八数码问题的代码：```import heapqimport copy# 目标状态goal_state = [1,2,3,8,0,4,7,6,5]# 启发式函数：曼哈顿距离def h(state):distance = 0for i in range(9):if state[i] == 0:continuerow = i // 3col = i % 3goal_row = (state[i]-1) // 3goal_col = (state[i]-1) % 3distance += abs(row - goal_row) + abs(col - goal_col)return distance# A*算法def A_star(start_state):# 初始化优先队列和已访问集合queue = []visited = set()# 将初始状态加入优先队列中，并设置g值和h值为0heapq.heappush(queue, (h(start_state), start_state, 0))while queue:# 取出队头元素进行扩展f, state, g = heapq.heappop(queue)# 如果该节点是目标节点，则搜索结束；否则，将扩展出来的新节点加入优先队列中。

二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。

距离的定义为：“某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。

距离越小，该节点的效果越好。

某个状态所有将牌到目标位置的距离之和用“h值”表示。

2.主要函数2.1countH（state & st）;countH函数功能是计算st状态的h值。

计算过程中将会用到rightPos数组，数组里记录的是目标状态下，0~9每个将牌在九宫格里的位置（位置 = 行下标 * 3 + 列下标）。

2.2f（state * p）;f()=h()+level2.3look_up_dup(vector<state*> & vec, state * p);在open表或close表中，是否存在指定状态p，当找到与p完全相等的节点时，退出函数。

2.4search(state & start)；在open表不为空时，按f值由小到大对open表中元素进行排序。

调用findZero()函数找到0值元素的位置。

空格可以向上下左右四个方向移动，前提是移动后不能越过九宫格的边界线。

确定某方向可走后，空格移动一步，生成状态p’。

此时，检查open表中是否已有p’，若有，更新p’数据；检查close表中是否已有p’，若有，将p’从close表中删除，添加到open表中。

重复的执行这个过程，直到某状态的h值为零。

2.5dump_solution(state * q)；在终端输出解路径。

// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数)，这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时，若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等（对应位置元素相等），完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值，对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st，计算它的h值。

#include<iostream>#include<time.h>#include<windows.h>#include<vector>#include<cmath>using namespace std;struct node{int a[3][3]; //存放矩阵int father; //父节点的位置int gone; //是否遍历过,1为是,0为否int fn; //评价函数的值int x,y; //空格的坐标int deep; //节点深度};vector<node> store; //存放路径节点int mx[4]={-1,0,1,0};int my[4]={0,-1,0,1}; //上下左右移动数组int top; //当前节点在store中的位置bool check(int num) //判断store[num]节点与目标节点是否相同,目标节点储存在store[0]中{for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(store[num].a[i][j]!=store[0].a[i][j])return false;}}return true;}bool search(int num) //判断store[num]节点是否已经扩展过 ,没有扩展返回true{int pre=store[num].father; //pre指向store[num]的父节点位置bool test=true;while(!pre){ //循环直到pre为0,既初始节点for(int i=0;i<3;i++){for (int j=0;j<3;j++){if(store[pre].a[i][j]!=store[num].a[i][j]){test=false;break;}}if(test==false) break;}if(test==true) return false;pre=store[pre].father; //pre继续指向store[pre]父节点位置}return true;}void print(int num) //打印路径,store[num]为目标节点{vector<int> temp; //存放路径int pre=store[num].father;temp.push_back(num);while(pre!=0){ //从目标节点回溯到初始节点temp.push_back(pre);pre=store[pre].father;}cout<<endl;cout<<"*********数码移动步骤*********"<<endl;int mm=1; //步数for(int m=temp.size()-1;m>=0;m--){cout<<"---第"<<mm<<"步---："<<endl;for(int i=0;i<3;i++){for(int j=0;j<3;j++){cout<<store[temp[m]].a[i][j]<<" ";}cout<<endl;}mm++;cout<<endl;}cout<<"所需步数为: "<<store[num].deep<<endl;return;}int get_fn(int num) //返回store[num]的评价函数值{int fn_temp=0; //评价函数值bool test=true;for(int i=0;i<3;i++){ //当找到一个值后,计算这个值位置与目标位置的距离差,test置为false后继续寻找下一个值for(int j=0;j<3;j++){test=true;for(int k=0;k<3;k++){for(int l=0;l<3;l++){if((store[num].x!=i||store[num].y!=j)&&store[num].a[i][j]==store[0].a[k][l]){ //寻值时排除空格位fn_temp=fn_temp+abs(i-k)+abs(j-l);test=false;}if(test==false) break;}if(test==false) break;}}}fn_temp=fn_temp+store[num].deep; //加上节点深度return fn_temp;}void kongxy(int num) //获得空格坐标{for(int i=0;i<3;i++){for(int j=0;j<3;j++){if(store[num].a[i][j]==0){store[num].x=i;store[num].y=j;}}}return;}int main(){cout<<"-----------A*算法解决8数码问题------------"<<endl;while(true){store.clear(); //清空storevector<int> open; //建立open表int i,j,m,n,f;int min; //store[min]储存fn值最小的节点int temp;bool test;top=1; //当前节点在store的位置,初始节点在store[1]int target[9];int begin[9]; //储存初始状态和目标状态,用于判断奇偶int t1=0,t2=0; //初始状态和目标状态的奇偶序数node node_temp;store.push_back(node_temp);store.push_back(node_temp); //用于创建store[0]和store[1],以便下面使用cout<<"请输入初始数码棋盘状态,0代表空格："<<endl; //输入初始状态,储存在store[1]中test=false;while(test==false){f=0;for(i=0;i<3;i++){for(j=0;j<3;j++){cin>>temp;store[1].a[i][j]=temp;begin[f++]=temp;}}test=true;for(i=0;i<8;i++){ //检查是否有重复输入,若有则重新输入for(j=i+1;j<9;j++){if(begin[i]==begin[j]){test=false;break;}}if(test==false) break;}if(test==false) cout<<"输入重复,请重新输入:"<<endl;}kongxy(1); //找出空格的坐标cout<<"请输入目标数码棋盘状态,0代表空格： "<<endl; //输入目标状态,储存在store[0]中test=false;while(test==false){f=0;for(i=0;i<3;i++){for(j=0;j<3;j++){cin>>temp;store[0].a[i][j]=temp;target[f++]=temp;}}test=true;for(i=0;i<8;i++){ //检查是否有重复输入,若有则重新输入for(j=i+1;j<9;j++){if(target[i]==target[j]){test=false;break;}}if(test==false) break;}if(test==false){cout<<"输入重复,请重新输入:"<<endl;continue; //若重复,重新输入}for(i=0;i<9;i++){ //检查目标状态与初始状态是否匹配test=false;for(j=0;j<9;j++){if(begin[i]==target[j]){test=true;break;}}if(test==false) break;}if(test==false) cout<<"输入与初始状态不匹配,请重新输入:"<<endl;}for(i=1;i<9;i++){ //判断奇偶序数是否相同,若不相同则无法找到路径for(j=1;i-j>=0;j++){if(begin[i]>begin[i-j]){if(begin[i-j]!=0) t1++;}}}for(i=1;i<9;i++){for(j=1;i-j>=0;j++){if(target[i]>target[i-j]){if(target[i-j]!=0) t2++;}}}if(!(t1%2==t2%2)){cout<<"无法找到路径."<<endl;cout<<endl;//system("pause");//return 0;continue;}LARGE_INTEGER Freg;LARGE_INTEGER Count1,Count2;QueryPerformanceFrequency(&Freg);QueryPerformanceCounter(&Count1);//获取时间Count1double d;store[1].father=0; //初始化参数store[1].gone=0;store[1].deep=0; //初始节点的父节点为0store[1].fn=get_fn(1);if(check(1)){ //判断初始状态与目标状态是否相同print(1);//system("pause");//return 0;cout<<endl;continue;}open.push_back(1); //把初始状态在store中的位置数压入open表中while(!open.empty()){ //当open表不为空时,开始寻找路径if(check(top)) break;min=top;int i_min=0;for(i=0;i<open.size();i++){ //遍历open表中元素,找出store中fn值最小的节点if(store[open[i]].fn<=store[min].fn&&store[open[i]].gone==0){min=open[i];i_min=i;}}store[min].gone=1;open.erase(open.begin()+i_min); //把最小节点标记遍历过,并从open表中删除m=store[min].x;n=store[min].y; //空格坐标for(f=0;f<4;f++){ //上下左右移动空格i=m+mx[f];j=n+my[f];if(i>=0&&i<=2&&j>=0&&j<=2){ //当变换后的空格坐标在矩阵中时,开始移动top++;store.push_back(store[min]); //把store[min]压入store中成为新增节点,位置为store[top]store[top].father=min; //新增节点的父节点为minstore[top].gone=0; //新增节点未被访问store[top].deep=store[min].deep+1; //新增节点的深度为父节点深度+1temp=store[top].a[m][n]; //交换空格与相邻数字store[top].a[m][n]=store[top].a[i][j];store[top].a[i][j]=temp;store[top].x=i; //移动后的空格坐标store[top].y=j;store[top].fn=get_fn(top); //移动后的fn值open.push_back(top); //把top压入open表中if(check(top)){ //检查是否到达目标print(top);//system("pause");//return 0;break;}if(search(top)==false){ //检查新增节点是否被访问过,若访问过,则删除此节点top--;store.pop_back();open.pop_back();}}}}QueryPerformanceCounter(&Count2);//获取时间Count2d=(double)(Count2.QuadPart-Count1.QuadPart)/(double)Freg.QuadPart*1000.0;//计算时间差，d的单位为ms.cout<<"算法时间为为"<<d<<" ms."<<endl;cout<<endl;}return 0;system("pause");}。

用A算法实现的八数码问题C++源码用A*算法实现的八数码问题C++源码#include <iomanip>#include <stdlib.h>#include <iostream.h>#include <time.h>#include <stdio.h>#include <conio.h>//using namespace std;//定义默认目标状态static int target[9]={1,2,3,8,0,4,7,6,5};//八数码类class EightNum{private:int num[9];int diffnum;//与目标状态位置不同的数的个数. int deapth;//派生的深度.int evalfun;//状态的估价值public:EightNum *parent;//生成当前状态的父状态. EightNum *state_pre;//当前状态前生成状态. EightNum *state_next;//当前状态后生成状态.//成员函数声明EightNum(void);EightNum(int initnum[9]);int get_evalfun();void eval_func();void getnum(int num1[9]);void setnum(int num1[9]);void show(void);void show_spec(int i);int null_position(void);EightNum& operator =(EightNum& NewEightN);EightNum& operator =(int num2[9]);int operator ==(EightNum& NewEightN);int operator ==(int num2[9]);};//八数码类定义//八数码类成员函数定义EightNum::EightNum(void){//初始化数组num[]for(int i=0;i<9;i++)num[i]=i;}EightNum::EightNum(int initnum[9]){//用输入的数组初始化num[]for(int i=0;i<9;i++)num[i]=initnum[i];}int EightNum::get_evalfun(){//返回估价值return evalfun;}void EightNum::eval_func(){//估价函数int i,temp;temp=0;for(i=0;i<9;i++){if(num[i]!=target[i])temp++;}diffnum=temp;if(this->parent==NULL) deapth=0;else deapth=this->parent->deapth+1;evalfun=deapth+temp;}void EightNum::getnum(int num1[9]){//取出八数码数值for(int i=0;i<9;i++)num1[i]=num[i];}void EightNum::setnum(int num1[9]){//写入八数码数值for(int i=0;i<9;i++)num[i]=num1[i];}void EightNum::show(){//八数码输出函数for(int i=0;i<9;i++){cout<<num[i]<<" ";if((i+1)%3==0)cout<<"\n";}}void EightNum::show_spec(int i){//结果步骤输出函数cout<<num[i];cout<<"<--";}int EightNum::null_position(){//查找空格位置int i,j;for(i=0;i<9;i++){if(num[i]==0)j=i;}return j;}EightNum& EightNum::operator =(EightNum& NewEightN){//"="重载,针对八数码类的引用for(int i=0;i<9;i++)num[i]=NewEightN.num[i];diffnum=NewEightN.diffnum;deapth=NewEightN.deapth+1;evalfun=diffnum+deapth;return *this;}EightNum& EightNum::operator =(int num2[9]){//"="重载,用于数组赋值for(int i=0;i<9;i++)num[i]=num2[i];return *this;}int EightNum::operator ==(EightNum& NewEightN){//"=="重载,用于八数码类中状态的比较int compere=1;for(int i=0;i<9;i++)if(num[i]!=NewEightN.num[i]){compere=0;break;}if(compere==0) return 0;else return 1;}int EightNum::operator ==(int num2[9]){//"=="重载,用于数组的比较int compere=1;for(int i=0;i<9;i++)if(num[i]!=num2[i]){compere=0;break;}if(compere==0) return 0;else return 1;}//八数码类函数定义结束int solve(int num[9],int target[9]){//判断是否有解的函数,利用逆序数的奇偶性来判断int i,j;int num_con=0,tar_con=0;for(i=0;i<9;i++)for(j=0;j<i;j++){if(num[j]<num[i] && num[j]!=0)num_con++;if(target[j]<target[i] && target[j]!=0)tar_con++;}num_con=num_con%2;tar_con=tar_con%2;if((num_con==0 && tar_con==0)||(num_con==1 && tar_con==1))return 1;elsereturn 0;}//空格移动函数int moveup(int num[9]){//空格上移for(int i=0;i<9;i++)if(num[i]==0) break;if(i<3) return 0;else {num[i]=num[i-3];num[i-3]=0;return 1;}}int movedown(int num[9]){//空格下移for(int i=0;i<9;i++)if(num[i]==0) break;if(i>5) return 0;else {num[i]=num[i+3];num[i+3]=0;return 1;}}int moveleft(int num[9]){//空格左移for(int i=0;i<9;i++)if(num[i]==0) break;if(i==0||i==3||i==6) return 0;else {num[i]=num[i-1];num[i-1]=0;return 1;}}int moveright(int num[9]){//空格右移for(int i=0;i<9;i++)if(num[i]==0) break;if(i==2||i==5||i==8) return 0;else {num[i]=num[i+1];num[i+1]=0;return 1;}}int exist(int num[9],EightNum *a){//判断是否重复搜索函数EightNum *t;for(t=a;t!=NULL;t=t->parent)if(*t==num) return 1;//调用"=="进行数组比较else return 0;}EightNum* find(EightNum *s){//寻找估价函数值最小的节点EightNum *m,*n;int min=s->get_evalfun();m=n=s;for(m=s;m!=NULL;m=m->state_next){if(min>m->get_evalfun()){n=m;min=m->get_evalfun();}return n;}}int main(void)//主函数{int i,j;int flag;int num[9];int error;do{//输入判断error=0;cout<<"请输入八数码问题的初始状态(用0代表空格,中间用空格隔开):"<<endl;for(i=0;i<9;i++){flag=0;cin>>num[i];for(j=0;j<i;j++)if(num[j]==num[i])flag=1;if(num[i]<0||num[i]>8||flag==1){error++;}}if(error!=0)cout<<"输入数据错误!请重新输入!"<<endl;}while(error!=0);cout<<"是否改变默认的目标状态?(y/n)";char input;cin>>input;int error1;if(input=='y'||input=='Y'){do{error1=0;cout<<"请输入新的目标状态(用0代表空格):"<<endl;for(i=0;i<9;i++){flag=0;cin>>target[i];for(j=0;j<i;j++)if(target[j]==target[i])flag=1;if(target[i]<0||target[i]>9||flag==1){error1++;}}if(error1!=0)cout<<"输入数据错误!请重新输入!"<<endl;}while(error1!=0);}//实例化初始状态和目标状态,并输出.EightNum start(num),T arget(target);start.parent=start.state_next=start.state_pre=NULL; start.eval_func();cout<<"初始状态为:"<<endl;start.show();cout<<"目标状态为:"<<endl;Target.show();//判断是否有解int m=solve(num,target);if(m==0){cout<<"此状态无解!"<<endl;return 0;}//进入A*算法搜索double time;clock_t startt,finisht;int ok=0;//结束标识位int space=0;//所耗费空间startt=clock();//开始时间EightNum *BestNode=&start,*Node=&start,*New8Num,*r; while(BestNode!=NULL&&ok!=1){BestNode=find(Node);if(*BestNode==Target){//调用"=="操作符ok=1;break;}r=BestNode->state_pre;//生成向上移的节点BestNode->getnum(num);if(moveup(num) && !exist(num,BestNode)){New8Num=new EightNum;New8Num->setnum(num);New8Num->parent=BestNode;New8Num->eval_func();New8Num->state_pre=r;if(r==NULL)Node=New8Num;elser->state_next=New8Num;r=New8Num;space++;}//生成向下移的节点BestNode->getnum(num);if(movedown(num) && !exist(num,BestNode)){ New8Num=new EightNum;New8Num->setnum(num);New8Num->parent=BestNode;New8Num->eval_func();New8Num->state_pre=r;if(r==NULL)Node=New8Num;elser->state_next=New8Num;r=New8Num;space++;}//生成向左移的节点BestNode->getnum(num);if(moveleft(num) && !exist(num,BestNode)){ New8Num=new EightNum;New8Num->setnum(num);New8Num->parent=BestNode;New8Num->eval_func();New8Num->state_pre=r;if(r==NULL)Node=New8Num;elser->state_next=New8Num;r=New8Num;space++;}//生成向右移的节点BestNode->getnum(num);if(moveright(num) && !exist(num,BestNode)){New8Num=new EightNum;New8Num->setnum(num);New8Num->parent=BestNode;New8Num->eval_func();New8Num->state_pre=r;if(r==NULL)Node=New8Num;elser->state_next=New8Num;r=New8Num;space++;}r->state_next=BestNode->state_next;if(BestNode->state_next!=NULL)BestNode->state_next->state_pre=r;BestNode->state_next=BestNode->state_pre=NULL; }finisht=clock();//输出搜索结果if(ok==1){time=(double)(finisht-startt)*1000/CLOCKS_PER_SEC; EightNum *p,*q=NULL;int step=0;for(p=BestNode->parent;p!=NULL;p->parent){if(step==0){i=8;p->show_spec(i);i=p->null_position();}else{p->show_spec(i);i=p->null_position();}if (step==8||step==18||step==28||step==38||step==48) cout<<"\n";step++;}cout<<"\nA*算法处理结果：所耗时间:";cout<<time;cout<<"ms, ";cout<<"所耗空间:";cout<<space;cout<<"块, ";cout<<"最短路径步数:";cout<<step;cout<<"步 !\n";}elsecout<<"\nA*算法无法找到最短路径!\n";}。

一、实验内容和要求八数码问题：在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

例如：图1 八数码问题示意图请任选一种盲目搜索算法（广度优先搜索或深度优先搜索）或任选一种启发式搜索方法（全局择优搜索,加权状态图搜索，A 算法或A＊算法)编程求解八数码问题（初始状态任选）。

选择一个初始状态，画出搜索树，填写相应的OPEN 表和CLOSED表，给出解路径，对实验结果进行分析总结,得出结论。

二、实验目的1. 熟悉人工智能系统中的问题求解过程；2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用；3. 熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验算法A*算法是一种常用的启发式搜索算法.在A＊算法中，一个结点位置的好坏用估价函数来对它进行评估.A＊算法的估价函数可表示为：f'（n）= g’(n）+ h’(n）这里,f'（n)是估价函数,g'(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h’（n）是n到目标的最短路经的启发值。

由于这个f’(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：f（n） = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点的最佳路径的估计代价。

在这里主要是h（n）体现了搜索的启发信息，因为g(n）是已知的。

用f(n）作为f’（n)的近似，也就是用g（n）代替g'(n）,h(n）代替h'(n)。

这样必须满足两个条件：（1）g(n）〉=g’(n）(大多数情况下都是满足的，可以不用考虑）,且f必须保持单调递增。

（2）h必须小于等于实际的从当前节点到达目标节点的最小耗费h（n）<=h'(n).第二点特别的重要。

可以证明应用这样的估价函数是可以找到最短路径的。

二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。

距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。

距离越小, 该节点的效果越好。

某个状态所有将牌到目标位置的距离之和用“h值”表示。

2.主要函数2.1countH（state & st）;countH函数功能是计算st状态的h值。

2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置（位置 = 行下标 * 3 + 列下标）。

2.3f（state * p）;f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。

2.6search(state & start)；在open表不为空时, 按f值由小到大对open表中元素进行排序。

调用findZero()函数找到0值元素的位置。

空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。

确定某方向可走后, 空格移动一步, 生成状态p’。

2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据；检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。

2.8重复的执行这个过程, 直到某状态的h值为零。

2.9dump_solution(state * q)；在终端输出解路径。

// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等（对应位置元素相等）, 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。

#include "Stdio.h"#include "Conio.h"#include "stdlib.h"#include "math.h"void Copy_node(struct node *p1,struct node *p2);void Calculate_f(int deepth,struct node *p);void Add_to_open(struct node *p);void Add_to_closed(struct node *p);void Remove_p(struct node *name,struct node *p);int Test_A_B(struct node *p1,struct node *p2);struct node * Search_A(struct node *name,struct node *temp); void Print_result(struct node *p);struct node // 定义8数码的节点状态{int s[3][3]; //当前8数码的状态int i_0; //当前空格所在行号int j_0; //当前空格所在列号int f; //当前代价值int d; //当前节点深度int h; //启发信息，采用数码"不在位"距离和struct node *father; //指向解路径上该节点的父节点struct node *next; //指向所在open或closed表中的下一个元素} ;struct node s_0={{2,8,3,1,6,4,7,0,5},2,1,0,0,0,NULL,NULL}; //定义初始状态struct node s_g={{1,2,3,8,0,4,7,6,5},1,1,0,0,0,NULL,NULL}; //定义目标状态struct node *open=NULL; //建立open表指针struct node *closed=NULL; //建立closed表指针int sum_node=0; //用于记录扩展节点总数//***********************************************************//********************** **********************//********************** 主函数开始**********************//********************** **********************//***********************************************************void main(){int bingo=0; //定义查找成功标志，bingo=1，成功struct node s; //定义头结点sstruct node *target,*n,*ls,*temp,*same; //定义结构体指针Copy_node(&s_0,&s); //复制初始状s_0态给头结点s Calculate_f(0,&s); //计算头结点的代价值Add_to_open(&s); //将头结点s放入open表while(open!=NULL) //只要open表不为空，进行以下循环{n=open; //n指向open表中当前要扩展的元素ls=open->next;Add_to_closed(n);open=ls; //将n指向的节点放入closed表中if(Test_A_B(n,&s_g)) //当前n指向节点为目标时，跳出程序结束；否则，继续下面的步骤{bingo=1;break;}elseif(n->j_0>=1) //空格所在列号不小于1,可左移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0&&temp->j_0-1==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝n指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0-1]; //空格左移temp->s[temp->i_0][temp->j_0-1]=0;temp->j_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end左移if(n->j_0<=1) //空格所在列号不大于1,可右移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0&&temp->j_0+1==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0+1]; //空格右移temp->s[temp->i_0][temp->j_0+1]=0;temp->j_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end右移if(n->i_0>=1) //空格所在列号不小于1,上移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0-1&&temp->j_0==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0-1][temp->j_0];//空格上移temp->s[temp->i_0-1][temp->j_0]=0;temp->i_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end上移if(n->i_0<=1) //空格所在列号不大于1,下移{temp=n->father;if(temp!=NULL&&temp->i_0==n->i_0+1&&temp->j_0==n->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(n,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0+1][temp->j_0]; //空格下移temp->s[temp->i_0+1][temp->j_0]=0;temp->i_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=n; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end下移}if(bingo=1) Print_result(n); //输出解路径else printf("问题求解失败！");}//主函数结束//************************************************************************* //********************** ********************** //********************** 计算某个节点状态的代价值********************** //********************** ********************** //*************************************************************************void Calculate_f(int deepth,struct node *p){int i,j,temp;temp=0;for(i=0;i<=2;i++) //计算所有"不在位"数码的距离和{for(j=0;j<=2;j++){if((p->s[i][j])!=(s_g.s[i][j]))temp++;}}p->h=temp;p->f=deepth+p->h;}//*************************************************************************//********************** **********************//********************** 添加p指向的节点到open表中********************** //********************** **********************//*************************************************************************void Add_to_open(struct node *p){struct node *p1,*p2;p1=open; //初始时p1指向open表首部p2=NULL;if(open==NULL) //open表为空时，待插入节点即为open表第一个元素，open 指向该元素{p->next=NULL;open=p;}else //open表不为空时，添加待插入节点，并保证open表代价递增的排序{while(p1!=NULL&&p->f>p1->f){p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}if(p2==NULL) //待插入节点为当前open表最小{p->next=open;open=p;}else if(p1==NULL) //待插入节点为当前open表最大{p->next=NULL;p2->next=p;}else //待插入节点介于p2、p1之间{p2->next=p;p->next=p1;}}}//***************************************************************************//********************** **********************//********************** 添加p指向的节点到closed表中**********************//********************** **********************//***************************************************************************void Add_to_closed(struct node *p){if(closed==NULL) //closed表为空时，p指向节点为closed表第一个元素，closed{p->next=NULL;closed=p;}else //closed表不为空时，直接放到closed表首部{p->next=closed;closed=p;}}//************************************************************************************* *************//********************************************//********************** 在open表或closed表中搜索和temp指向的节点相同的节点**********************//********************************************//*************************************************************************************struct node * Search_A(struct node *name,struct node *temp){struct node *p1;p1=name; //p1指向open表或closed表while(p1!=NULL){if(Test_A_B(p1,temp)) //找到相同的节点，返回该节点地址return p1;elsep1=p1->next;}return NULL;}//************************************************************************************* **********//********************************************//********************** 判断两个节点状态是否相同，相同则返回1，否则返回0 **********************//********************************************//************************************************************************************* **********int Test_A_B(struct node *p1,struct node *p2){int i,j,flag;flag=1;for(i=0;i<=2;i++)for(j=0;j<=2;j++){if((p2->s[i][j])!=(p1->s[i][j])) { flag=0; return flag; }else ;}return flag;}//******************************************************************************//********************** **********************//********************** 从open表或closed表删除指定节点********************** //********************** **********************//******************************************************************************void Remove_p(struct node *name,struct node *p){struct node *p1,*p2;p1=NULL;p2=NULL;if(name==NULL) //如果name指向的链表为空，则不需要进行删除return;else if(Test_A_B(name,p)&&name->f==p->f) //指定节点为name指向的链表的第一个元素{open=name->next;name->next=NULL;return;}else{p2=name;p1=p2->next;while(p1){if(Test_A_B(p1,p)&&p1->f==p->f) //找到指定节点{p2->next=p1->next;return;}else{p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}}return;}}//************************************************************************************* *//********************************************//********************** 将p1指向的节点状态拷贝到p2指向的节点中**********************//********************************************//************************************************************************************* *void Copy_node(struct node *p1,struct node *p2){int i,j;for(i=0;i<=2;i++){for(j=0;j<=2;j++){ p2->s[i][j]=p1->s[i][j]; }}p2->i_0=p1->i_0;p2->j_0=p1->j_0;p2->f=p1->f;p2->d=p1->d;p2->h=p1->h;p2->next=p1->next;p2->father=p1->father;}//*********************************************************** //********************** ********************** //********************** 输出结果********************** //********************** ********************** //***********************************************************void Print_result(struct node *p){struct node *path[100];struct node *temp,*temp_father;int i,j,k;for(i=0;i<=99;i++) //初始化路径指针数组path[i]=0;temp=p;printf("总共扩展%d 个节点\n",sum_node);printf("总共扩展%d 层\n",temp->d);printf("解路径如下：\n");for(i=p->d;i>=0;i--) //存储解路径上各节点的地址{path[i]=temp;temp=temp->father;}for(k=0;k<=p->d;k++) //输出解路径{temp=path[k]; //建立节点指点指针printf("第%d步",temp->d);if(k-1>=0) //输出移动策略{temp_father=path[k-1];if(temp->i_0<temp_father->i_0) printf("->上移\n");if(temp->i_0>temp_father->i_0) printf("->下移\n");if(temp->j_0<temp_father->j_0) printf("->左移\n");if(temp->j_0>temp_father->j_0) printf("->右移\n");}elseprintf("\n");printf("当前节点状态为：\n");for(i=0;i<=2;i++){for(j=0;j<=2;j++){printf("%d ",temp->s[i][j]);}printf("\n");}printf("\n");}}THANKS !!!致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求欢迎您的下载，资料仅供参考。

基于A*算法解决把数码问题《人工智能》专业：信息与计算科学班级：101001学号：101001102姓名：陈斌指导老师：时华日期：2013年10月14日一、问题描述8数码问题又称9宫问题，与游戏“华容道”类似。

意在给定的33⨯棋格的8个格子内分别放一个符号，符号之间互不相同，余下的一格为空格。

并且通常把8个符号在棋格上的排列顺序称作8数码的状态。

开始时，规则给定一个初始状态和一个目标状态，并要求被试者对棋格内的符号经过若干次移动由初始状态达到目标状态，这个过程中只有空格附近的符号可以朝空格的方向移动，且每次只能移动一个符号。

为方便编程和表示，本文中8个格子内的符号分别取1—8的8个数字表示，空格用0表示。

并给定8数码的初始状态和目标状态分别如图1、2所示。

图1 初始状态图2 目标状态则要求以图1为初始状态，通过交换0和0的上、下、左、右四个方位的数字（每次只能和其中一个交换），达到图2所示目标状态。

二、算法设计根据任务要求，本文采用A*搜索算法。

但要在计算机上通过编程解决该问题，还应当解决该问题在计算机上表示的方式，并设计合适的启发函数，以提高搜索效率。

①状态的表示在A*算法中，需要用到open表和closed表，特别是在open表中，待扩展节点间有很严格的扩展顺序。

因此在表示当前状态的变量中，必须要有能指向下一个扩展节点的指针，以完成对open表中元素的索引。

从这一点上看，open表中的元素相互间即构成了一个线性表，因此初步选定使用结构体表示问题的状态。

如图3所示，表示问题的结构体包括表示当前节点状态的DATA和指向open 表中下一个待扩展节点的指针NEXT。

图3 结构体现在进一步考虑DATA中包括的内容：如图1、2所示，8数码问题的提出是以一个33⨯数表表示的，因此本文中采用一个33⨯的二维数组s[3][3]表示当前状态的具体信息。

而为了保证在搜索到目标状态后能够顺利复现寻优路径，当前状态的DATA中还应该包括一个指向其父节点的指针father，这样，才能在达到目标状态后，通过指针father逐层回溯到初始状态，即复现寻优路径。

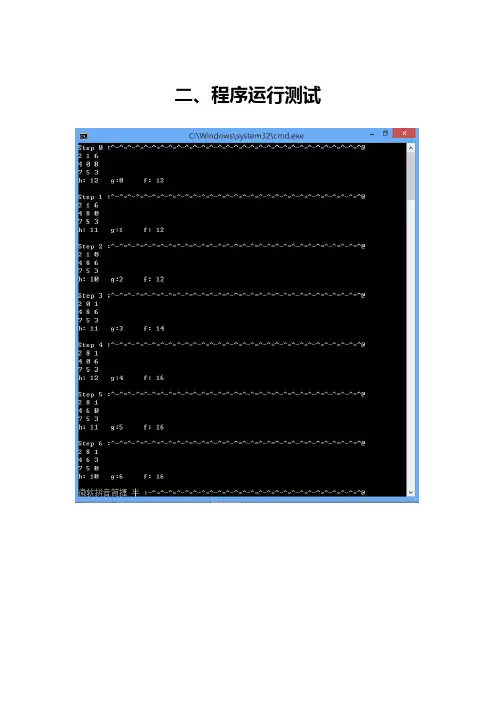
八数码C语言A算法详细代码以下是八数码问题的C语言A*算法的详细代码：```c#include <stdio.h>#include <stdlib.h>#define N 3typedef struct Nodeint board[N][N]; // 八数码局面struct Node *parent; // 父节点指针int f; // f(n) = g(n) + h(n)，g(n)表示起始节点到当前节点的代价，h(n)表示当前节点到目标节点的估计代价int g; // g(n)int h; // h(n)} Node;//目标局面int target[N][N] = {{1, 2, 3}, {8, 0 ,4}, {7, 6, 5}};//计算当前节点到目标节点的曼哈顿距离int manhattanDistance(int board[N][N])int distance = 0;for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)if (board[i][j] != 0)int value = board[i][j] - 1;int targetI = value / N;int targetJ = value % N;distance += abs(i - targetI) + abs(j - targetJ);}}}return distance;//创建一个新节点Node* createNode(int board[N][N], int g, Node* parent) Node* node = (Node*) malloc(sizeof(Node));for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)node->board[i][j] = board[i][j];}}node->parent = parent;node->g = g;node->h = manhattanDistance(board);node->f = node->g + node->h;return node;//判断两个局面是否相等int isBoardEqual(int board1[N][N], int board2[N][N]) for (int i = 0; i < N; i++)for (int j = 0; j < N; j++)if (board1[i][j] != board2[i][j])return 0;}}}return 1;//判断节点是否在开放列表中int isInOpenList(Node *node, Node **openList, int openListSize)for (int i = 0; i < openListSize; i++)if (isBoardEqual(node->board, openList[i]->board))return 1;}}return 0;//判断节点是否在关闭列表中int isInClosedList(Node *node, Node **closedList, int closedListSize)for (int i = 0; i < closedListSize; i++)if (isBoardEqual(node->board, closedList[i]->board))return 1;}}return 0;//比较两个节点的f(n)值Node *a = *(Node **)node1;Node *b = *(Node **)node2;return a->f - b->f;//输出路径void printPath(Node *node)if (node != NULL)printPath(node->parent);printf("Step %d:\n", node->g);for (int i = 0; i < N; i++)printf("%d %d %d\n", node->board[i][0], node->board[i][1], node->board[i][2]);}printf("\n");}//A*算法求解八数码问题void solvePuzzle(int initial[N][N])//创建初始节点Node* initialNode = createNode(initial, 0, NULL);//开放列表和关闭列表Node* openList[N*N*N*N];int openListSize = 0;Node* closedList[N*N*N*N];int closedListSize = 0;//将初始节点放入开放列表openList[openListSize++] = initialNode;while (openListSize > 0)//从开放列表中选择f(n)最小的节点//取出开放列表中f(n)最小的节点作为当前节点Node* currentNode = openList[0];//将当前节点从开放列表中移除for (int i = 1; i < openListSize; i++) openList[i - 1] = openList[i];}openListSize--;//将当前节点放入关闭列表closedList[closedListSize++] = currentNode; //判断当前节点是否为目标节点if (isBoardEqual(currentNode->board, target)) printf("Solution found!\n");printPath(currentNode);return;}//生成当前节点的邻居节点int i = 0, j = 0;for (i = 0; i < N; i++)for (j = 0; j < N; j++)if (currentNode->board[i][j] == 0)break;}}if (j < N)break;}}if (i > 0)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l]; }}newBoard[i][j] = newBoard[i - 1][j];newBoard[i - 1][j] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (i < N - 1)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i + 1][j];newBoard[i + 1][j] = 0;currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (j > 0)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i][j - 1];newBoard[i][j - 1] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}if (j < N - 1)int newBoard[N][N];for (int k = 0; k < N; k++)for (int l = 0; l < N; l++)newBoard[k][l] = currentNode->board[k][l];}}newBoard[i][j] = newBoard[i][j + 1];newBoard[i][j + 1] = 0;if (!isInOpenList(createNode(newBoard, currentNode->g + 1, currentNode), openList, openListSize) &&!isInClosedList(createNode(newBoard, currentNode->g + 1, currentNode), closedList, closedListSize))openList[openListSize++] = createNode(newBoard, currentNode->g + 1, currentNode);}}}printf("Solution not found!\n");int maiint initial[N][N] = {{2, 8, 3}, {1, 6, 4}, {7, 0, 5}};solvePuzzle(initial);return 0;```这个代码实现了八数码问题的A*算法。

*文件Chess.h,包含必要的数据结构,全局变量和类声明*/#ifndef _YLQ_CHESS_#define _YLQ_CHESS_#include <algorithm>#include <iostream>#include <vector>#ifndef N#define N 3#endif#define BLANK 0static int g_iId=1;typedef struct tagNode{int node[N][N];int iF,iH,iG;int id,idParent;}NODE,*PNODE;typedef std::vector<NODE> OPEN;#define CLOSED OPEN#define SUCCERSSOR OPENclass Chess{public:Chess(NODE const &nstar,NODE const &nend); private:OPEN m_vOpen,m_vClosed;NODE m_nStart,m_nEnd;bool NodeEuqal(NODE node1,NODE node2);bool NodeExist(NODE node);bool InOpen(NODE node,int &index);bool InClose(NODE node,int &index);SUCCERSSOR ExplortNode(NODE node); protected:virtual int CaculateHV(NODE &node);//计算h值和f值public:bool Algorithms();void Show(int it);//it=1展示Open,2->Closed};#endif*文件Chess.cpp,包含算法实现*/#include "Chess.h"#include <MA TH.H>bool comp(const NODE &n1,const NODE &n2){return n1.iF>n2.iF;}void Chess::Show(int tp){SUCCERSSOR::iterator it,iend;if (tp==1) {it=m_vOpen.begin();iend=m_vOpen.end();}else{it=m_vClosed.begin();iend=m_vClosed.end();}for (;it!=iend;it++){printf("iF=%d;iG=%d;iH=%d\n",(PNODE)it->iF,(PNODE)it->iG,(PNODE)it->iH);printf("id=%d;idParent=%d\n",(PNODE)it->id,(PNODE)it->idParent);for(int i=0;i<N;i++){for (int j=0;j<N;j++){printf("%d ",(PNODE)it->node[i][j]);}std::cout<<std::endl;}}}Chess::Chess(const NODE &nstar,const NODE &nend){m_nStart = nstar;m_nEnd = nend;m_nStart.idParent=0;//初始结点的父节点设为0m_nStart.id = 1;m_nStart.iG=0;//初始结点G设为0,再次结点扩展一次就+1( 表示深度);CaculateHV(m_nStart);//初始化开始结点h和f以及gm_vOpen.push_back(m_nStart);}int Chess::CaculateHV(NODE &node){//用位置差来计算h值node.iH=0;for (int i=0;i<N;i++){for (int j=0;j<N;j++){bool bget=false;for (int m=0;m<N;m++){for (int n=0;n<N;n++){if (node.node[m][n] == m_nEnd.node[i][j]) {node.iH+=abs(m-i)+abs(n-j);bget=true;break;}}if (bget)break;}}}node.iF =node.iG+node.iH;return node.iH;}bool Chess::NodeEuqal(NODE node1,NODE node2){int sum=0;for (int i=0;i<N;i++)for (int j=0;j<N;j++){if (node1.node[i][j] == node2.node[i][j]) {sum++;}}if (sum==N*N) {return true;}elsereturn false;}bool Chess::InOpen(NODE node,int &index){//查找node是否在Open表中,是的返回true并返回指针位置index OPEN::iterator itOpen=m_vOpen.begin();index=0;for (;itOpen!=m_vOpen.end();itOpen++){if (NodeEuqal(node,*(PNODE)itOpen->node)) {return true;}index++;}return false;}bool Chess::InClose(NODE node,int &index){//查找node是否在InClose表中,是的返回true并返回指针位置index CLOSED::iterator itClosed=m_vClosed.begin();index=0;for (;itClosed!=m_vClosed.end();itClosed++){if (NodeEuqal(node,*(PNODE)itClosed->node)) {return true;}index++;}return false;}bool Chess::NodeExist(NODE node){int i;if (InOpen(node,i) || InClose(node,i)) {return true;}return false;}SUCCERSSOR Chess::ExplortNode(NODE node){//扩展结点,并插入到SUCCERSSOR队列中int i,j;SUCCERSSOR temp;for (i=0;i<N;i++)for (j=0;j<N;j++)if (node.node[i][j]==BLANK){//找到空格,开始扩张,按照空格依次往上下左右扩展,判断其合法性if (j>0) {NODE ntemp=node;ntemp.node[i][j]=ntemp.node[i][j-1];ntemp.node[i][j-1]=BLANK;g_iId++;ntemp.id=g_iId;ntemp.idParent = node.id;ntemp.iG=ntemp.iG+1;CaculateHV(ntemp);temp.push_back(ntemp);}if (j<N-1) {NODE ntemp=node;ntemp.node[i][j]=ntemp.node[i][j+1];ntemp.node[i][j+1]=BLANK;g_iId++;ntemp.id=g_iId;ntemp.idParent = node.id;ntemp.iG=ntemp.iG+1;CaculateHV(ntemp);temp.push_back(ntemp);}if (i>0) {NODE ntemp=node;ntemp.node[i][j]=ntemp.node[i-1][j];ntemp.node[i-1][j]=BLANK;g_iId++;ntemp.id=g_iId;ntemp.idParent = node.id;ntemp.iG=ntemp.iG+1;CaculateHV(ntemp);temp.push_back(ntemp);}if (i<N-1) {NODE ntemp=node;ntemp.node[i][j]=ntemp.node[i+1][j];ntemp.node[i+1][j]=BLANK;g_iId++;ntemp.id=g_iId;ntemp.idParent = node.id;ntemp.iG=ntemp.iG+1;CaculateHV(ntemp);temp.push_back(ntemp);}}return temp;}bool Chess::Algorithms(){NODE nTemp;while (m_vOpen.size()!=0){std::sort(m_vOpen.begin(),m_vOpen.end(),comp);//取出f值最小的进行扩展nTemp = *((PNODE)(m_vOpen.end()-1));m_vOpen.pop_back();m_vClosed.push_back(nTemp);if (NodeEuqal(nTemp,m_nEnd))return true;SUCCERSSOR stemp=ExplortNode(nTemp);SUCCERSSOR::iterator isuc=stemp.begin();for (;isuc!=stemp.end();isuc++){int indexOp,indexCl=0;NODE suc=*(PNODE)isuc,*old;if (InOpen(suc,indexOp)) {old = (PNODE)(m_vOpen.begin()+indexOp);if (suc.iG<old->iG){//若G值比原先的小,则直接修改old结点old->iG = suc.iG;//修改其父节点,指向suc结点old->idParent = suc.idParent;old->iF = old->iG+old->iH;}}else if (InClose(suc,indexCl)){old = (PNODE)(m_vClosed.begin()+indexCl);if (suc.iG<old->iG){//若G值比原先的小,则直接修改old结点old->iG = suc.iG;//修改其父节点,指向suc结点old->idParent = suc.idParent;old->iF = old->iG+old->iH;}}else{m_vOpen.push_back(suc);}}}return false;}/**文件main.cpp,如何使用该类*/#include "Chess.h"#include <IOSTREAM>using namespace std;NODE nStart={{2,8,3,0,1,4,7,6,5},0,0,0,g_iId,0};NODE nEnd={{1,2,3,8,0,4,7,6,5},0,0,0,0,0};int main(int argc,char *argv){Chess *chess=new Chess(nStart,nEnd);if (chess->Algorithms()){cout<<"搜索成功:\n";chess->Show(2);}return 0;}。

二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。

距离的定义为：“某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。

距离越小，该节点的效果越好。

某个状态所有将牌到目标位置的距离之和用“h值”表示。

2.主要函数2.1countH（state & st）;countH函数功能是计算st状态的h值。

计算过程中将会用到rightPos数组，数组里记录的是目标状态下，0~9每个将牌在九宫格里的位置（位置 = 行下标 * 3 + 列下标）。

2.2f（state * p）;f()=h()+level2.3look_up_dup(vector<state*> & vec, state * p);在open表或close表中，是否存在指定状态p，当找到与p完全相等的节点时，退出函数。

2.4search(state & start)；在open表不为空时，按f值由小到大对open表中元素进行排序。

调用findZero()函数找到0值元素的位置。

空格可以向上下左右四个方向移动，前提是移动后不能越过九宫格的边界线。

确定某方向可走后，空格移动一步，生成状态p’。

此时，检查open表中是否已有p’，若有，更新p’数据；检查close表中是否已有p’，若有，将p’从close表中删除，添加到open表中。

重复的执行这个过程，直到某状态的h值为零。

2.5dump_solution(state * q)；在终端输出解路径。

// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数)，这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时，若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等（对应位置元素相等），完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值，对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st，计算它的h值。

一、实验内容和要求八数码问题：在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

例如：图1 八数码问题示意图请任选一种盲目搜索算法（广度优先搜索或深度优先搜索）或任选一种启发式搜索方法（全局择优搜索，加权状态图搜索，A 算法或A* 算法）编程求解八数码问题（初始状态任选）。

选择一个初始状态，画出搜索树，填写相应的OPEN 表和CLOSED表，给出解路径，对实验结果进行分析总结，得出结论。

二、实验目的1. 熟悉人工智能系统中的问题求解过程；2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用；3. 熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验算法A*算法是一种常用的启发式搜索算法。

在A*算法中，一个结点位置的好坏用估价函数来对它进行评估。

A*算法的估价函数可表示为：f'(n) = g'(n) + h'(n)这里，f'(n)是估价函数，g'(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h'(n)是n到目标的最短路经的启发值。

由于这个f'(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点的最佳路径的估计代价。

在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。

用f(n)作为f'(n)的近似，也就是用g(n)代替g'(n)，h(n)代替h'(n)。

这样必须满足两个条件：（1）g(n)>=g'(n)（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增。

（2）h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。

if (dup != open_table.end()){ if (f(q) < f(*dup)){ (*dup)->level = q->level; (*dup)->parent = q->parent; } skip = true;
}
原值小， open表
dup = look_up_dup(close_table, q); if (dup != close_table.end()){ //若q已在close表中，且f值比
} return *this; } };
void dump_panel(state * p){
//将八数码按3*3矩阵形式输出
for (int i = 0; i<GRID; i++){
for (int j = 0; j<GRID; j++)
cout << p->panel[i][j] << " ";
<< f(trace.back()) << endl << endl; trace.pop_back(); count++;
} } int main() {
state p(0); state *q;
p.panel[0][0] = 2;//设置初始状态 p.panel[0][1] = 1; p.panel[0][2] = 6; p.panel[1][0] = 4; p.panel[1][1] = 0; p.panel[1][2] = 8; p.panel[2][0] = 7; p.panel[2][1] = 5; p.panel[2][2] = 3;

一、实验内容和要求八数码问题：在3×3的方格棋盘上，摆放着1到8这八个数码，有1个方格是空的，其初始状态如图1所示，要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。

例如：(a) 初始状态 (b) 目标状态图1 八数码问题示意图请任选一种盲目搜索算法（广度优先搜索或深度优先搜索）或任选一种启发式搜索方法（全局择优搜索，加权状态图搜索，A 算法或 A* 算法）编程求解八数码问题（初始状态任选）。

选择一个初始状态，画出搜索树，填写相应的OPEN 表和CLOSED表，给出解路径，对实验结果进行分析总结，得出结论。

二、实验目的1. 熟悉人工智能系统中的问题求解过程；2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用；3. 熟悉对八数码问题的建模、求解及编程语言的应用。

三、实验算法A*算法是一种常用的启发式搜索算法。

在A*算法中，一个结点位置的好坏用估价函数来对它进行评估。

A*算法的估价函数可表示为：f'(n) = g'(n) + h'(n)这里，f'(n)是估价函数，g'(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h'(n)是n到目标的最短路经的启发值。

由于这个f'(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点的最佳路径的估计代价。

在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。

用f(n)作为f'(n)的近似，也就是用g(n)代替g'(n)，h(n)代替h'(n)。

这样必须满足两个条件：（1）g(n)>=g'(n)（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增。

（2）h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。

#include "Stdio.h"#include "Conio.h"#include "stdlib.h"#include "math.h"void Copy_node(struct node *p1,struct node *p2);void Calculate_f(int deepth,struct node *p);void Add_to_open(struct node *p);void Add_to_closed(struct node *p);void Remove_p(struct node *name,struct node *p);int Test_A_B(struct node *p1,struct node *p2);struct node * Solution_Astar(struct node *p);void Expand_n(struct node *p);struct node * Search_A(struct node *name,struct node *temp);void Print_result(struct node *p);/* 定义8数码的节点状态*/typedef struct node{int s[3][3]; //当前8数码的状态int i_0; //当前空格所在行号int j_0; //当前空格所在列号int f; //当前代价值int d; //当前节点深度int h; //启发信息，采用数码“不在位”距离和struct node *father; //指向解路径上该节点的父节点struct node *next; //指向所在open或closed表中的下一个元素};struct node s_0={{3,8,2,1,0,5,7,6,4},1,1,0,0,0,NULL,NULL}; //定义初始状态struct node s_g={{1,2,3,8,0,4,7,6,5},1,1,0,0,0,NULL,NULL}; //定义目标状态struct node *open=NULL; //建立open表指针struct node *closed=NULL; //建立closed表指针int sum_node=0; //用于记录扩展节点总数int main(void){struct node s,*target;Copy_node(&s_0,&s);Calculate_f(0,&s); //拷贝8数码初始状态，初始化代价值target=Solution_Astar(&s); //求解主程序if(target) Print_result(target); //输出解路径else printf("问题求解失败！");getch();return 0;}/******************************************//* A*算法*//******************************************/struct node * Solution_Astar(struct node *p){struct node *n,*temp;Add_to_open(p); //将s_0放入open表while(open!=NULL) //只要open表中还有元素，就继续对代价最小的节点进行扩展{n=open; //n指向open表中当前要扩展的元素temp=open->next;Add_to_closed(n);open=temp;if(Test_A_B(n,&s_g)) //当前n指向节点为目标时，跳出程序结束；否则，继续下面的步骤return n;Expand_n(n); //扩展节点n}return NULL;}/*******************************************************//* 生成当前节点n通过走步可以得到的所有状态*//*******************************************************/void Expand_n(struct node *p){struct node *temp,*same;if(p->j_0>=1) //空格所在列号不小于1,可左移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0&&temp->j_0-1==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0-1]; //空格左移temp->s[temp->i_0][temp->j_0-1]=0;temp->j_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end左移if(p->j_0<=1) //空格所在列号不大于1,可右移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0&&temp->j_0+1==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0][temp->j_0+1]; //空格右移temp->s[temp->i_0][temp->j_0+1]=0;temp->j_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end右移if(p->i_0>=1) //空格所在列号不小于1,上移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0-1&&temp->j_0==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0-1][temp->j_0]; //空格上移temp->s[temp->i_0-1][temp->j_0]=0;temp->i_0--;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end上移if(p->i_0<=1) //空格所在列号不大于1,下移{temp=p->father;if(temp!=NULL&&temp->i_0==p->i_0+1&&temp->j_0==p->j_0) //新节点与其祖父节点相同;else //新节点与其祖父节点不同，或其父节点为起始节点{temp=(struct node *)malloc(sizeof(struct node)); //给新节点分配空间Copy_node(p,temp); //拷贝p指向的节点状态temp->s[temp->i_0][temp->j_0]=temp->s[temp->i_0+1][temp->j_0]; //空格下移temp->s[temp->i_0+1][temp->j_0]=0;temp->i_0++;temp->d++;Calculate_f(temp->d,temp); //修改新节点的代价值temp->father=p; //新节点指向其父节点if(same=Search_A(closed,temp)) //在closed表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比closed表中相同状态节点代价小，加入open表{Remove_p(closed,same); //从closed表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else;}else if(same=Search_A(open,temp)) //在open表中找到与新节点状态相同的节点{if(temp->f<same->f) //temp指向的节点,其代价比open表中相同状态节点代价小，加入open表{Remove_p(open,same); //从open表中删除与temp指向节点状态相同的节点Add_to_open(temp);sum_node++;}else ;}else //新节点为完全不同的新节点，加入open表{Add_to_open(temp);sum_node++;}}}//end下移}/*******************************************************//* 添加p指向的节点到open表中*//*******************************************************/void Add_to_open(struct node *p){struct node *p1,*p2;p1=open; //初始时p1指向open表首部p2=NULL;if(open==NULL) //open表为空时，待插入节点即为open表第一个元素，open指向该元素{p->next=NULL;open=p;}else //open表不为空时，添加待插入节点，并保证open表代价递增的排序{while(p1!=NULL&&p->f>p1->f){p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}if(p2==NULL) //待插入节点为当前open表最小{p->next=open;open=p;}else if(p1==NULL) //待插入节点为当前open表最大{p->next=NULL;p2->next=p;}else //待插入节点介于p2、p1之间{p2->next=p;p->next=p1;}}}/*******************************************************//* 添加p指向的节点到closed表中*//*******************************************************/void Add_to_closed(struct node *p){if(closed==NULL) //closed表为空时，p指向节点为closed表第一个元素，closed指向该元素{p->next=NULL;closed=p;}else //closed表不为空时，直接放到closed表首部{p->next=closed;closed=p;}}/**************************************************************//* 在open表或closed表中搜索与temp指向节点状态相同的节点，*//* 返回搜索到的节点地址*//**************************************************************/struct node * Search_A(struct node *name,struct node *temp){struct node *p1;p1=name; //p1指向open表或closed表while(p1!=NULL){if(Test_A_B(p1,temp)) //找到相同的节点，返回该节点地址return p1;elsep1=p1->next;}return NULL;}/**********************************************************//* 判断两个节点A、B状态是否相同，相同则返回1，否则返回0 *//**********************************************************/int Test_A_B(struct node *p1,struct node *p2){int i,j,flag;flag=1;for(i=0;i<=2;i++)for(j=0;j<=2;j++){if((p2->s[i][j])!=(p1->s[i][j])) { flag=0; return flag; }else ;}return flag;}/*******************************************************//* 从open表或closed表删除指定节点*//*******************************************************/void Remove_p(struct node *name,struct node *p){struct node *p1,*p2;p1=NULL;p2=NULL;if(name==NULL) //如果name指向的链表为空，则不需要进行删除return;else if(Test_A_B(name,p)&&name->f==p->f) //指定节点为name指向的链表的第一个元素{open=name->next;name->next=NULL;return;}else{p2=name;p1=p2->next;while(p1){if(Test_A_B(p1,p)&&p1->f==p->f) //找到指定节点{p2->next=p1->next;return;}else{p2=p1; //p2始终指向p1指向的前一个元素p1=p1->next;}}return;}}/******************************************//* 计算某个节点状态的代价值*//******************************************/void Calculate_f(int deepth,struct node *p){int i,j,temp;temp=0;for(i=0;i<=2;i++) //计算所有“不在位”数码的距离和{for(j=0;j<=2;j++){switch(p->s[i][j]){case 0: temp+=abs(i-1)+abs(j-1); break;case 1: temp+=abs(i-0)+abs(j-0); break;case 2: temp+=abs(i-0)+abs(j-1); break;case 3: temp+=abs(i-0)+abs(j-2); break;case 4: temp+=abs(i-1)+abs(j-2); break;case 5: temp+=abs(i-2)+abs(j-2); break;case 6: temp+=abs(i-2)+abs(j-1); break;case 7: temp+=abs(i-2)+abs(j-0); break;case 8: temp+=abs(i-1)+abs(j-0); break;}}}p->h=temp;p->f=deepth+p->h;}/********************************************//* 将p1指向的节点状态拷贝到p2指向的节点中*//********************************************/void Copy_node(struct node *p1,struct node *p2){int i,j;for(i=0;i<=2;i++){for(j=0;j<=2;j++){ p2->s[i][j]=p1->s[i][j]; }}p2->i_0=p1->i_0;p2->j_0=p1->j_0;p2->f=p1->f;p2->d=p1->d;p2->h=p1->h;p2->next=p1->next;p2->father=p1->father;}/********************************************//* 输出解路径*//********************************************/void Print_result(struct node *p){struct node *path[100];struct node *temp,*temp_father;int i,j,k;for(i=0;i<=99;i++) //初始化路径指针数组path[i]=0;temp=p;printf("总共扩展%d 个节点\n",sum_node);printf("总共扩展%d 层\n",temp->d);printf("*************************************************\n"); printf("解路径如下：\n");for(i=p->d;i>=0;i--) //存储解路径上各节点的地址{path[i]=temp;temp=temp->father;}for(k=0;k<=p->d;k++) //输出解路径{temp=path[k]; //建立节点指点指针printf("第%d步",temp->d);if(k-1>=0) //输出移动策略{temp_father=path[k-1];if(temp->i_0<temp_father->i_0) printf("—>上移\n");if(temp->i_0>temp_father->i_0) printf("—>下移\n");if(temp->j_0<temp_father->j_0) printf("—>左移\n");if(temp->j_0>temp_father->j_0) printf("—>右移\n");}elseprintf("\n");printf("当前：f=%d，d=%d，h=%d\n",temp->f,temp->d,temp->h);printf("当前节点状态为：\n");for(i=0;i<=2;i++){for(j=0;j<=2;j++){printf("%d ",temp->s[i][j]);}printf("\n");}printf("\n");}}。