相位法激光测距原理及算法详解
- 格式:pdf
- 大小:665.58 KB
- 文档页数:11


相位式激光测距原理
相位式激光测距原理是一种利用光学原理测量物体距离的方法。
其基
本原理是将激光束发送到目标物体,经过反射后接收回来,然后根据
光的相位差计算出物体到激光测距仪的距离。
下面将会逐一讲解相位
式激光测距原理的详细内容。
1. 激光的发射
相位式激光测距仪通过激光器发射一束定向、单色、激光光束,将激
光传输到目标体上。
2. 激光的接收
激光的接收有两种方法,其中一种可以使用普通的接收型光电二极管
来完成,另一种则需要使用相位测量的方法。
3. 相位差的测量
通过对激光发射时和接收时的相位差进行测量,得到目标到发射点的
距离,这个距离与光的波长有关。
4. 数据的处理
将测得的距离进行处理后,即可得到精确的目标距离数据,同时在数
据处理的过程当中,还可以实现自动跟踪,提高了装置的实用性。
总之,相位式激光测距原理是一种非常先进和高精度的测距方法,其
原理也比较复杂,需要参考一定的物理学知识,而在工业、航空航天、军事等领域都有广泛的应用。


相位式激光测距仪原理激光测距是光波测距中的一种测距方式,如果光以速度c在空气中传播在A、B两点间往返一次所需时间为t,则A、B两点间距离D可用下列表示。
D=ct/2 式中:D——测站点A、B两点间距离;c——光在大气中传播的速度;t——光往返A、B一次所需的时间。
由上式可知,要测量A、B距离实际上是要测量光传播的时间t,根据测量时间方法的不同,激光测距仪通常可分为脉冲式和相位式两种测量形式。
相位式激光测距仪相位式激光测距仪是用无线电波段的频率,对激光束进行幅度调制并测定调制光往返测线一次所产生的相位延迟,再根据调制光的波长,换算此相位延迟所代表的距离。
即用间接方法测定出光经往返测线所需的时间,如下图所示。
图为相位式激光测距仪测距原理图相位式激光测距仪一般应用在精密测距中。
由于其精度高,一般为毫米级,为了有效的反射信号,并使测定的目标限制在与仪器精度相称的某一特定点上,对这种测距仪都配置了被称为合作目标的反射镜。
若调制光角频率为ω,在待测量距离D上往返一次产生的相位延迟为φ,则对应时间t 可表示为:t=φ/ω 将此关系代入上式距离D可表示为:D=1/2 ct=1/2 c·φ/ω=c/(4πf) (Nπ+Δφ)=c/4f (N+ΔN)=U(N+)式中:φ——信号往返测线一次产生的总的相位延迟。
ω——调制信号的角频率,ω=2πf。
U——单位长度,数值等于1/4调制波长N——测线所包含调制半波长个数。
Δφ——信号往返测线一次产生相位延迟不足π部分。
ΔN——测线所包含调制波不足半波长的小数部分。
ΔN=φ/ω在给定调制和标准大气条件下,频率c/(4πf)是一个常数,此时距离的测量变成了测线所包含半波长个数的测量和不足半波长的小数部分的测量即测N或φ,由于近代精密机械加工技术和无线电测相技术的发展,已使φ的测量达到很高的精度。
为了测得不足π的相角φ,可以通过不同的方法来进行测量,通常应用最多的是延迟测相和数字测相,目前短程激光测距仪均采用数字测相原理来求得φ。

激光测距的方法及原理激光测距的方法及原理激光测距技术与一般光学测距技术相比具有操作方便、系统简单及白天和夜晚都可以工作的优点。
与雷达测距相比,激光测距具有良好的抗干扰性和很高的精度,而且激光具有良好的抵抗电磁波干扰的能力。
其在探测距离较长时,激光测距的优越性更为明显。
光测距技术是指利用射向目标的激光脉冲或连续波激光束测量目标距离的距离测量技术。
较常用的激光测距方法有三角法、脉冲法和相位法激光测距。
1.三角法激光测距激光位移传感器的测量方法称为激光三角反射法,激光测距仪的精度是一定的,同样的测距仪测10米与100米的精度是一样的。
而激光三角反射法测量精度是跟量程相关的,量程越大,精度越低。
采用激光三角原理和回波分析原理进行非接触位置、位移测量的精密传感器。
广泛应用于位置、位移、厚度、半径、形状、振动、距离等几何量的工业测量。
半导体激光器1被镜片2聚焦到被测物体6。
反射光被镜片3收集,投射到CCD阵列4上;信号处理器5通过三角函数计算阵列4上的光点位置得到距物体的距离。
图1. 激光三角测量原理图激光发射器通过镜头将可见红色激光射向物体表面,经物体反射的激光通过接受器镜头,被内部的CCD线性相机接受,根据不同的距离,CCD线性相机可以在不同的角度下“看见”这个光点。
根据这个角度即知的激光和相机之间的距离,数字信号处理器就能计算出传感器和被测物之间的距离。
同时,光束在接收元件的位置通过模拟和数字电路处理,并通过微处理器分析,计算出相应的输出值,并在用户设定的模拟量窗口内,按比例输出标准数据信号。
如果使用开关量输出,则在设定的窗口内导通,窗口之外截止。
另外,模拟量与开关量输出可设置独立检测窗口。
常用在铁轨、产品厚度、平整度、尺寸等方面。
2.脉冲法激光测距脉冲法测距的过程是这样的:测距仪发射出的激光经被测量物体的反射后又被测距仪接收,测距仪同时记录激光往返的时间。
光速和往返时间的乘积的一半,就是测距仪和被测量物体之间的距离。

激光测距传感器工作原理脉冲和相位的区别
脉冲和相位法测距的区别是什么?
脉冲式激光测距传感器通过发送一束激光脉冲到目标物体,然后测量脉冲往返所需的时间来计算距离。
激光脉冲在发射后经过目标物体反射,返回传感器。
传感器根据脉冲往返的时间计算出目标物体的距离。
脉冲式激光测距传感器适用于长距离测量,其精度受限于脉冲持续时间和计时器的精度。
主要用于机载激光雷达、测距望远镜等远距离测场景。
相位式激光测距传感器通过发送连续激光束,并比较发射和接收激光束的相位差来计算距离。
相位式激光测距传感器在测量过程中,通过调整发射激光的频率或相位,并与接收到的反射激光进行相位比较,从而计算出目标物体的距离。
相位式激光测距传感器适用于中短距离测量,具有较高的精度。
主要用在工业自动化、机器人导航等精度要求高的场景。
在实际应用中,可以根据需求选择适合的激光测距传感器。

相位法激光测距的理论设计(综合最新版)第一篇:相位法激光测距的理论设计(综合最新版)相位法激光测距的理论设计摘要本文介绍了半导体激光技术,并在传统的相位法激光测距原理的基础上, 参考激光测距光学系统设计,运用数字相关检测的测量方法,提出一种把直接数字频率合成(DDS)技术和数字信号处理(DSP)技术相结合的新的相位激光测距理论设计,这种设计有助于简化电路、提高相位测距的精度。
关键词:相位激光测距,数字相关检测,数字信号Phase Type Laser Ranging Theoretical Design This article introduced the semiconductor laser technology, and in the traditional phase laser ranging principle foundation, the reference laser ranging optical system design, Using digital correlation detection measuring technique,proposing one kind the new phase laser ranging theoretical design which(DDS)technical and the digital signal processing(DSP)the technology unifies the direct digital frequency synthesis, for could overcome in the traditional phase range finder method the precision to enhance, the measuring range with difficulty difficulty with increases, the electric circuittoo is complex and so on the shortcoming provides has been possible to supply the reference the theoretical design.Key word:PHASE LASER RANGING,DIGITAL CORRELATION DETECTION,DIGITAL SIGNAL目录第一章引言 (4)第二章国内外研究状况.................................................................................................5 第三章激光测距光学系统 (7)3. 1 激光测距仪的系统结构.........................................................................................7 3.2光学系统图示..........................................................................................................8 3.3 光学系统设计主要部件功能与作用.....................................................................9 3.4 主要参考性能数据...............................................................................................10 第四章数字相关检测技术改进方法设计. (11)4. 1 激光相位式测距的基本原理.............................................................................11 4.2 数字信号处理(DSP)的简述 (13)4.2.1 数字信号处理的主要研究内容....................................................................14 4.2.2 测试信号数字化处理的基本步骤................................................................14 4.2.3 数字处理信号的优势....................................................................................15 4.3 直接数字频率合成技术 (15)4.3.1 DDS的基本工作原理....................................................................................16 4.4 改进的数字测相的框图设计...............................................................................16 第五章小结. (22)参考文献.............................................................................................................23 致谢........................................................................................................................... (24)第一章引言第一章引言激光,是一种自然界原本不存在的,因受激而发出的具有方向性好、亮度高、单色性好和相干性好等特性的光。


相位式激光测距——间接tof法全文共四篇示例,供读者参考第一篇示例:相位式激光测距是一种常用的测距方法,它通过测量光波的相位差来确定物体与传感器之间的距离。
而间接TOF(Time of Flight)法则是一种常见的相位式激光测距方法之一,其原理是通过测量光波往返传播的时间来计算距离。
本文将详细介绍相位式激光测距及间接TOF法的基本原理、应用领域以及优缺点。
一、相位式激光测距的基本原理相位式激光测距利用了光波的波长特性,通过测量光波的相位差来确定距离。
在相位式激光测距中,激光器向目标发射一束光波,光波经过目标反射后返回传感器,传感器接收到反射光波并测量与发射光波的相位差,通过相位差的变化来计算目标与传感器之间的距离。
相位式激光测距的精度通常很高,可以达到亚毫米级别。
二、间接TOF法的原理及优缺点间接TOF法是相位式激光测距的一种常见方法,其原理是通过测量光波往返传播的时间来计算距离。
具体来说,激光器向目标发射一束光波,光波经过目标反射后返回传感器,传感器测量光波往返的时间并将其除以光速来计算距离。
间接TOF法的优点在于测距精度高、测量速度快、适用于长距离测距等特点,但其缺点是受到光波传播速度波动的影响,可能在复杂环境中出现误差。
相位式激光测距在工业、汽车、航空航天等领域有着广泛的应用。
在工业领域,相位式激光测距可以用于精密加工、质量检测等工作中;在汽车领域,相位式激光测距可以用于自动驾驶、停车辅助等功能;在航空航天领域,相位式激光测距可以用于飞行器导航、高精度测绘等应用。
四、结论相位式激光测距是一种精确、高效的测距方法,间接TOF法作为其中一种方法,在实际应用中具有一定优势和局限性。
相位式激光测距在各个领域都有着重要的应用价值,未来随着技术的不断进步和应用领域的拓展,相位式激光测距将会得到更广泛的应用和发展。
【本文2000字,已完整】第二篇示例:相位式激光测距是一种常用的激光测距方法,通过测量激光光束的相位变化来计算目标物体的距离。

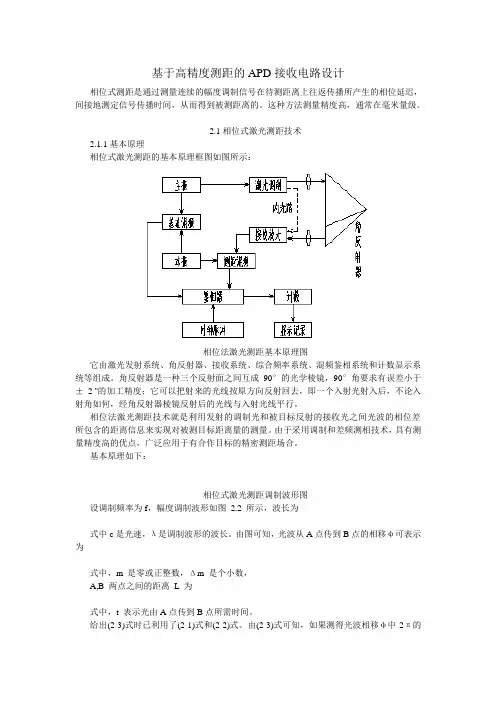
基于高精度测距的APD接收电路设计相位式测距是通过测量连续的幅度调制信号在待测距离上往返传播所产生的相位延迟,间接地测定信号传播时间,从而得到被测距离的。
这种方法测量精度高,通常在毫米量级。
2.1相位式激光测距技术2.1.1基本原理相位式激光测距的基本原理框图如图所示:相位法激光测距基本原理图它由激光发射系统、角反射器、接收系统、综合频率系统、混频鉴相系统和计数显示系统等组成。
角反射器是一种三个反射面之间互成90°的光学棱镜,90°角要求有误差小于±2 ''的加工精度;它可以把射来的光线按原方向反射回去,即一个入射光射入后,不论入射角如何,经角反射器棱镜反射后的光线与入射光线平行。
相位法激光测距技术就是利用发射的调制光和被目标反射的接收光之间光波的相位差所包含的距离信息来实现对被测目标距离量的测量。
由于采用调制和差频测相技术,具有测量精度高的优点,广泛应用于有合作目标的精密测距场合。
基本原理如下:相位式激光测距调制波形图设调制频率为f,幅度调制波形如图 2.2 所示,波长为式中c是光速,λ是调制波形的波长。
由图可知,光波从A点传到B点的相移φ可表示为式中,m 是零或正整数,Δm 是个小数,A,B 两点之间的距离L 为式中,t 表示光由A点传到B点所需时间。
给出(2-3)式时已利用了(2-1)式和(2-2)式。
由(2-3)式可知,如果测得光波相移φ中2π的整数m 和小数Δm ,就可由(2-3)式确定出被测距离L,所以调制光波被认为是相位式激光测距仪测量距离的一把度量标准,可以形象的称之为“光尺”。
不过,用一台测距仪直接测量A和B两点光波传播的相移是非常困难的,因此采用在B点设置一个反射器(即所谓合作目标),使从测距仪发出的光波经反射器反射再返回测距仪,然后由测距仪的测相系统对光波往返一次的相位变化进行测量。
图 2.3示意地表示光波在距离L 上往返一次后的相位变化。
激光测距原理与方法激光测距是一种常见的测量距离的方法,它基于激光的特性来实现高精度的测距。
激光测距广泛应用于建筑、工程、地质勘测等领域,具有快速、准确、非接触等优点。
本文将介绍激光测距的基本原理和常用的测距方法。
一、原理激光测距的基本原理是利用激光器发射出的激光束,并通过接收器接收反射回来的激光束,通过测量激光传播的时间来计算出距离。
具体来说,激光测距仪发射激光束后,激光束会在测量目标上产生反射,反射回来的激光束会被接收器接收到。
通过测量激光从发射到接收的时间间隔,再结合光速的知识,就可以计算出目标物体与测距仪之间的距离。
二、方法1. 直接测量法直接测量法是最常见的激光测距方法,它通过测量激光从发射到接收的时间来计算距离。
该方法适用于目标物体与测距仪之间没有障碍物的情况下。
具体操作上,测距仪会发射一束激光并计时,当激光束反射回来时停止计时,通过计算时间差并结合光速,即可得到距离。
2. 干涉测量法干涉测量法是一种高精度的激光测距方法,它利用激光的干涉现象来实现测量。
该方法适用于需要高精度测距的场景,如光学仪器的校准等。
干涉测量法的原理是将激光束分成两束,一束直接射向目标物体,另一束经过反射后再射向目标物体,通过比较两束激光的相位差来计算距离。
3. 相移测量法相移测量法是一种基于相位差的激光测距方法,它通过改变激光的相位来实现测量。
该方法适用于需要高精度测距和抗干扰能力的场景,如工业制造中的测量和定位。
相移测量法的原理是通过改变激光的相位,使得接收到的激光信号与参考信号之间产生相位差,通过测量相位差来计算距离。
4. 多点测量法多点测量法是一种基于三角测量原理的激光测距方法,它通过同时测量目标物体与测距仪之间的多个点来计算距离。
该方法适用于需要测量目标物体的形状和尺寸的场景,如建筑物的测量和勘测。
多点测量法的原理是通过测量目标物体多个点之间的距离,并结合三角测量原理计算出目标物体与测距仪之间的距离。
总结激光测距是一种高精度、快速、非接触的测量方法,它通过测量激光的传播时间或相位差来计算目标物体与测距仪之间的距离。
相位式激光测距是一种常见的激光测距方式,它采用连续调制的光束。
当这种光束遇到被测物体并反射回来时,通过对比接收到的光束中产生的相位变化,可以换算出测量距离。
这种方式的优点在于,由于是对发射光波的光强进行调制,并通过测量相位差来间接测量时间,所以其处理难度相对于直接测量往返时间的方式降低了许多。
相位式激光测距通常适应于中短距离的测量,其测量精度可以达到毫米、微米级,也是目前测距精度最高的一种方式。
具体的测量公式为:L = ϕ⋅c ⋅T / (2π),其中L为测量距离,c为光在空气中的传播速度,T为调制信号的周期时间,ϕ为发射与接收波形的相位差。
激光测距技术的原理与工程应用激光测距技术是一种利用激光器发射连续或脉冲激光,通过测量激光传播的时间或相位差来确定目标距离的一种测距方法。
它利用激光在空间中的传播速度快、方向性强和散射小等特点,广泛应用于各个领域。
本文将介绍激光测距技术的原理,以及其在工程应用中的实际运用。
激光测距技术的原理是基于光的传播速度和时间的关系。
光在真空中的传播速度为每秒299,792,458米,而光在空气或其他介质中的传播速度则会有所减慢。
通过测量从激光器发射到目标物体反射回来所需的时间,可以计算出目标物体与激光器之间的距离。
这种测距方法称为时间差测距法。
另外一种测距方法是基于激光传播的相位差来计算距离,称为相位差测距法。
在激光测距技术的工程应用中,最常见的应用之一是测量仪器。
激光测距仪是一种采用激光测距技术的仪器,可以用于测量距离、高度、角度等。
它广泛应用于建筑工程、地理测量、工业制造、环境保护等领域。
例如,在建筑工程中,激光测距仪可以用于测量建筑物的高度、距离和角度,帮助工程师进行设计和施工。
在地理测量领域,激光测距仪可以用于制作地形图、测量地表的高程等。
另外一个工程应用的领域是激光雷达。
激光雷达是利用激光测距技术来测量目标物体的距离的雷达系统。
它可以用于无人驾驶汽车、航空航天、地质勘探等领域。
在无人驾驶汽车中,激光雷达可以用于实时检测车辆周围环境的障碍物、行人等,并通过计算距离和速度来实现智能驾驶。
在航空航天中,激光雷达可以用于测量卫星与地面的距离,帮助航空航天工程师进行轨道设计和导航。
除了测量应用之外,激光测距技术还可以用于工程的控制应用。
例如,在机器人控制中,激光测距技术可以用于检测机器人周围的环境,帮助机器人进行导航和避障。
在航空航天工程中,激光测距技术可以用于测量航空器和航天器的姿态和位置,帮助工程师进行飞行控制。
总之,激光测距技术是一种非常重要且广泛应用的技术。
它的原理是基于光的传播速度和时间的关系,并通过测量距离来实现工程应用。
激光相位法测距的原理激光相位测距中,把连续的激光进行幅度调制,调制光的光强随时间做周期性变化,测定调制光往返过程中所经过的相位变化即可求出时间和距离。
图.1 相位式激光测距原理示意图如图1所示,设发射处与反射处(提升容器)的距离为x ,激光的速度为c ,激光往返它们之间的时间为t ,则有:cxt 2设调制波频率为f ,从发射到接收间的相位差为 ,则有:N cfxft 242 (2) 其中,N 为完整周期波的个数, 为不足周期波的余相位。
因此可解出:)(2)22(24N N fcN f c f c x(3) 其中,f c L s 2 称为测尺或刻度,N 即是整尺数, 2 N 为余尺。
根据测得的相位移的大小,可知道N 余尺的大小。
而整尺数N 必须通过选择多个合适的测尺频率才能确定,测尺频率的选择是提升容器精确定位的关键因素之一。
多尺测量方法测量正弦信号相移的方法都无法确定相位的整周期数,即不能确定出相位变化中 2的整倍数N ,而只能测量不足 2的相位尾数 ,因此公式(2.3)中的N 值无法确定,使该式产生多个解,距离D 就不能确定。
解决此缺陷的办法是选用一个较低的测尺频率s f ,使其测尺长度s L 稍大于该被测距离,这种状况下不会出现距离的多值解。
但是由于测相系统的测相误差,会导致测距误差,并且选用的s L 越大则测距误差越大。
因此为了得到较高的测距精度而使用较短的测尺长度,即较大的测尺频率s f ,系统的单值测定距离就相应变小。
为了解决长测程和高精度之间的矛盾,一般使用的解决办法是:当待测距离D 大于基本测尺sb L (精测测尺)时,可再使用一个或几个辅助测尺sl L (又叫粗测测尺),然后将各个测尺测得的距离值组合起来得到单一的和精确的距离信息。
由此可见,用一组测尺共同对距离D 进行测量就可以解决距离的多值解,即用短尺保证精度,用长尺保证量程。
这样就解决高精度和长测程的矛盾[4]。
本系统选用10米作为精尺,1000米作为粗尺,带入公式即可求得精尺频率和粗尺频率:精尺频率 MHz L cf 152510(4) 粗尺频率 kHz L cf 150210001000 (5) 其中,光速s m c /1038 。
一原理:1 相位测距:通过测定连续的调制激光在待测距离d上往返的相位差Φ来间接测量传播时间t计算得出d=1/2c*t.2 差频测相:为了保证一定的测距精度,激光信号的频率必须选得很高(见第4点),一般为十几MHz~几百MHZ.如果在这样高的频率下直接对发射波和接收波进行相位比较,电路中的寄生参量的影响将产生显著的附加相移,降低测相精度;为此,采用差频法来测相,即通过主振频率与本振频率混频,变成中低频信号,由于差频信号仍保持着原高频信号的相位关系,测量中低频信号的相位就等于测量上振信号经2D距离后的相位延迟.3 测试间:t=Φ/2*pi*f4 精度:波长(测尺长度Ls)/1000测尺长度和测尺频率关系:Vs=C/2Ls5 注意:当d>波长时,又需要精度时要用多把尺子,用较长的测尺粗测,用较短的尺子精测。
6 间接测尺:有时各测尺频率的值相差较大,使得放大器,调制器电路难以做到对各种测尺都具有相同的增益及相位稳定性。
间接测尺是采用一种数值接近的调制频率,间接获得各个测尺的方法二方案要求:侧量范围1—15m,精度1cm测尺长度Ls=15m测尺频率Vs=3*108 /2*15=10MHZ比较:典型激光测距的方法有脉冲法、相位法、干涉法等。
脉冲法:是采用测量激光的传输时间的测量方法,由于激光脉冲的能量相对比较集中,能够传输较远的距离,所以该方法适用于较远距离测距,但是测距精度较低。
相位法:是采用激光调制的方法,通过测量载波调制频率的相位,达到测量距离的目的,避免了测量非常短的时间间隔,可以达到较高的测距精度。
其测距精度主要受激光调制的相位测量精度和相位的调制频率的影响,要达到距离的高精度测量,必须提高系统的激光调制频率和相位测量精度。
干涉法:测量精度高,适用于微小位移的测量(一般小于1 m),对测量环境要求非常苛刻,适用于高精度的实验室的实验定标等应用。
激光相位法测距的原理激光相位测距中,把连续的激光进行幅度调制,调制光的光强随时间做周期性变化,测定调制光往返过程中所经过的相位变化即可求出时间和距离。
图.1 相位式激光测距原理示意图如图1所示,设发射处与反射处(提升容器)的距离为x ,激光的速度为c ,激光往返它们之间的时间为t ,则有:cxt 2设调制波频率为f ,从发射到接收间的相位差为 ,则有:N cfxft 242 (2) 其中,N 为完整周期波的个数, 为不足周期波的余相位。
因此可解出:)(2)22(24N N fcN f c f c x(3) 其中,f c L s 2 称为测尺或刻度,N 即是整尺数, 2 N 为余尺。
根据测得的相位移的大小,可知道N 余尺的大小。
而整尺数N 必须通过选择多个合适的测尺频率才能确定,测尺频率的选择是提升容器精确定位的关键因素之一。
多尺测量方法测量正弦信号相移的方法都无法确定相位的整周期数,即不能确定出相位变化中 2的整倍数N ,而只能测量不足 2的相位尾数 ,因此公式(2.3)中的N 值无法确定,使该式产生多个解,距离D 就不能确定。
解决此缺陷的办法是选用一个较低的测尺频率s f ,使其测尺长度s L 稍大于该被测距离,这种状况下不会出现距离的多值解。
但是由于测相系统的测相误差,会导致测距误差,并且选用的s L 越大则测距误差越大。
因此为了得到较高的测距精度而使用较短的测尺长度,即较大的测尺频率s f ,系统的单值测定距离就相应变小。
为了解决长测程和高精度之间的矛盾,一般使用的解决办法是:当待测距离D 大于基本测尺sb L (精测测尺)时,可再使用一个或几个辅助测尺sl L (又叫粗测测尺),然后将各个测尺测得的距离值组合起来得到单一的和精确的距离信息。
由此可见,用一组测尺共同对距离D 进行测量就可以解决距离的多值解,即用短尺保证精度,用长尺保证量程。
这样就解决高精度和长测程的矛盾[4]。
本系统选用10米作为精尺,1000米作为粗尺,带入公式即可求得精尺频率和粗尺频率:精尺频率 MHz L cf 152510(4) 粗尺频率 kHz L cf 150210001000 (5) 其中,光速s m c /1038 。
上面公式计算出的只是个大概的数值,实际上光速要小于s m /1038 ,而且c 还和实际的大气条件(比如矿井温湿度、气体成分、风速等)有关,因此,这些测尺频率需要进一步调整,具体的做法是在现场标定。
混频原理及其在系统中的应用模拟相乘混频器混频是将信号频率由一个量值变换为另一个量值的过程。
如图2.2所示,信号输入和输出的关系分析如下:图2.2 模拟相乘混频器Fig. 2 Frequency mixer设输入信号分别为)cos()(s s sm s t U t U 和)cos()(l l lm l t U t U ,经过模拟乘法器相乘以后得:l s l s lm sm M l s l s lm sm M z t U U K t U U K U)(cos 21)(cos 21(2.6) 由上式可以看出,经过模拟乘法器将两个信号相乘,就实现了两个信号的差频与和频,其中M K 为增益系数。
通过带通滤波器或者低通滤波器后,即可得到差分输出:l s l s lm sm M I t U U K U)(cos 21在相位法测距中使用混频精尺频率15MHz 的正弦信号是中高频信号,对其进行测量是很困难的,这样就要求对信号波形做一定的变化,在保证相位不变的情况下降低信号频率,使后级的模数转换器采样更容易。
在本相位式测距系统中,设由DDS 发出的调制信号和APD 接收到的回波信号分别为1U 、2U :)cos(11 t U (2.7) )cos(22 t U (2.8)其中f 2 ,f 是精尺频率,其值为15MHz ,此时两路信号的相位差是21 。
另外一个DDS 发出的本振信号)cos(313 t U ,其中112f ,1f 为本振频率,其值为MHz 985.14。
将调制信号1U 与本振信号3U 混频:31131131131)(cos )(cos 21)cos()cos( t t t t U U (2.9) 使用低通滤波器保留其低频 kHz 15的正弦信号,得到:311)(cos t U s (2.10)同理可得回波信号2U 与本振3U 混频后的信号:321)(cos t U l (2.11)此时我们可以得到s U 与l U 的相位差:213231)()( (2.12)由此可见,混频前后相位差不变,信号频率降低到了kHz 15。
同理,对于粗尺频率150kHz ,引入的本振频率为135kHz ,经过上述方法,同样可以在相位差不变的情况下将信号频率降低到kHz 15。
基于快速傅里叶变换的相位测量方法相位法激光测距系统的测量精度主要取决于测相的精度,而传统的测相方式通常大量采用模拟电路,无法解决模拟元件固有的缺点(如温漂、零漂严重,抗干扰能力差等),尤其在煤矿开采现场,不仅环境条件十分恶劣(淋水、粉尘等),而且现场有各种大功率机电设备,有很强的电磁串扰,因而这种采用模拟元器件搭建电路的测相方法在稳定性和可靠性方面都很不理想[4]。
用基于信号频谱分析的鉴相方法,需要对采样的信号进行数字信号处理,这就要求将回波信号这样的模拟量转换为数字量,系统中采用模数转换器(ADC )实现,采样过程需要遵循一定的条件,采样后的数据进行快速傅里叶变换(FFT )算法。
采样定理A/D 转换是相位法测距的重要组成部分,是整个数字化处理的基础。
从模拟的连续时域信号得到离散的数字信号应该遵循一定的原则,这就是在数字信号处理领域著名的采样定理。
2 Nyquist 采样定理Nyquist 采样定理是针对基带信号而言的,又称低通采样定理[8]。
设有一个频率带限信号)(t x ,其频带限制在),0(H f 内,如果以不小于H s f f 2 的采样速率对)(t x 进行等间隔采样,得到离散的采样信号)()(s nT x n x 其中s s f T 1 称为采样间隔,则原有信号)(t x 将被得到的采样值)(n x 完全地确定。
采样之后,信号频谱周期化,变为原信号频谱移频后的多个谱叠加,如果原信号)(t x 的频谱如图2.3(a)所示,那么采样后的信号频谱就如图2.3(b)所示[8]。
图3(a) 带限信号)(t x 频谱 3(b) )(t x 经采样后信号频谱Fig. 2.3(a) Spectrum of band-limited signal )(t x Fig. 2.3(b) Spectrum of sampled )(t x由图可见,)(w X s 中包含有)(w X 的频谱成分,如图2.3(b)中虚框部分所示,只要满足H s f f 2 或H s w w 2 (2.13)则虚框部分不会与其它频率部分相混叠。
这时只需要一个带宽大于等于H w 2的低通滤波器,就能滤出原来的信号)(t x 。
Nyquist 采样定理告诉我们,如果以不低于信号最高频率的两倍的采样速率对带限信号进行采样,那么所得到的离散采样值就能准确地确定原信号。
该定理的用意在于,时间上连续的模拟信号可以用时间上离散的采样值来取代,这样就为模拟信号的数字化处理提供了理论依据[8]。
带通信号采样定理带通信号采样定理又称欠采样定理、带通采样定理或中频采样定理[9]。
Nyquist 采样定理只讨论了频谱分布在),0(H f 上的基带信号的采样问题,如果信号的频率分布在某一有限的频带),(H L f f 上时,也需要遵循一定的原则。
当然,根据NyquistHH S HH S S采样定理来进行采样。
但是,当L H H f f B f 时,也就是当信号的最高频率H f 远远大于其信号带宽B 时,如果仍按Nyquist 采样率来采样的话,则其采样率会很高,甚至很难实现,或者后级处理的速度也满足不了要求。
这样的情况下,可以按照带通信号采样定理来采样。
带通信号采样定理:设一个带限信号)(t x ,其频率限制在),(H L f f 内,如果其采样率满足:12)(2n f f f H L s (2.14)式中,n 取满足)(2L H s f f f 的最大正整数(0,1,2,…),则用s f 进行等间隔采样所得到的信号采样值)(s nT x 能准确地确定原信号)(t x [9]。
式(2.14)用带通信号的中心频率0f 和频率带宽B 也可以表示为:1240n f f s (2.15) 式中 20HL f f f,n 取满足B f s 2 (B 为频带宽度)的最大整数。
显然,当20H f f 、H f B 时,取0 n ,式(2.15)就是Nyquist 采样定理,即满足H s f f 2 。
由式(2.15)可见,当确定了频带宽度B ,为了能用最低采样速率即两倍频带宽度速率)2(B f s 对带通信号进行采样,带通信号的中心频率必须满足:B n f 2120(2.16) 或 B n f f H L )12( (2.17) 也即信号的最高和最低频率相加是带宽的整数倍。
带通信号采样前后的频谱示意图如图2.4所示。
(a) 采样前 (b)采样后4 带通信号采样前后的频谱Fig.2.4 Spectrum of bandpass signal before and after samplingL 0H L 0H S S上述带通采样定理适用的先决条件是:只允许在其一个频带上存在信号,但是不允许在许多不同的频带上同时存在信号,否则就将会引起混叠。
但实际的情况是在多个频带上都有信号,为解决这一问题,一般要在采样之前先将信号通过一个带通滤波器,也称抗混叠滤波器[9]。
以上的结论为我们对正弦信号的采样提供了一个总的准则:采样的频率应为信号频率的整数倍,采样的点数应包括整数倍的周期,由于本论文采样过后的信号进行FFT 的处理,基2的FFT 算法要求输入离散数据的点数是2的整数次幂,所以我们这里的采样频率应是正弦信号频率的M 2倍(M 在工程上一般取大于等于2的正整数)[9]。
快速傅里叶变换(FFT ) 离散傅里叶变换(DFT )离散傅里叶变换(DFT )的定义为:设x (n )为N 点有限长序列,其DFT 为1)()(N n nk N W n x k X k =0, 1, …, N -1 (2.18)其中:NjN eW 2 ,称为蝶形因子。
一般说来,x (n )和nk N W 都是复数,)(k X 也是复数,所以每计算一个)(k X 值,需要N 次复数乘法和N-1次复数加法。
而)(k X 一共有N 个点(k 从0取到N-1),所以完成整个DFT 运算总共需要2N 次复数乘法及 1 N N 次复数加法[10]。