分布列及数学期望经典复习

2023年高考数学复习----《求概率及随机变量的分布列与期望》规律方法与典型例题讲解【规律方法】求离散型随机变量的分布列及期望的一般步骤：（1）根据题中条件确定随机变量的可能取值；（2）求出随机变量所有可能取值对应的概率，即可得出分布列；（3）根据期望的概念，结合分布列，即可得出期望（在计算时，要注意随机变量是否服从特殊的分布，如超几何分布或二项分布等，可结合其对应的概率计算公式及期望计算公式，简化计算）【典型例题】例1．（2022·陕西宝鸡·统考一模）甲､乙两个代表队各有3名选手参加对抗赛．比赛规定：甲队的1，2，3号选手与乙队的1，2，3号选手按编号顺序各比赛一场，某队连赢3场，则获胜，否则由甲队的1号对乙队的2号，甲队的2号对乙队的1号加赛两场，胜场多者最后获胜（每场比赛只有胜或负两种结果）．已知甲队的1号对乙队的1，2号选手的胜率分别是0．5，0．6，甲队的2号对乙队的1，2号选手的胜率都是0．5，甲队的3号对乙队的3号选手的胜率也是0．5，假设每场比赛结果相互独立．（1）求甲队仅比赛3场获胜的概率；（2）已知每场比赛胜者可获得200个积分，求甲队队员获得的积分数之和X的分布列及期望．【解析】（1）甲队1，2，3号选手与乙队1，2，3号选手比赛获胜的概率分别为0.5,0.5,0.5，，⨯⨯=；甲队比赛3场获胜的概率为P=0.50.50.50.125（2）X所以可能取得值为0,200,400,600,800；()3500.50.12P X ===，()31213200C 0.50.500..540.5600.07.5P X ==⨯=⨯⨯=⨯，()()11233332400C 0.50.60.50.40.55C 0.50.40.5 2.1050.50.262.P X ==⨯+⨯⨯⨯=⨯+⨯=⨯⨯， ()()31323333 6000.5C 0.50.60.5C 0.50.60.50.40.5 3.40.50.425P X ==+⨯⨯+⨯⨯+⨯=⨯=， ()2333800C 0.50.605.50.900.112.5P X ===⨯⨯=⨯．即所以()00.1252000.0754000.26256000.4258000.1125465E X =⨯+⨯+⨯+⨯+⨯=． 例2．（2022春·云南昆明·高三云南师大附中校考阶段练习）我校举办“学党史”知识测试活动，每位教师3次测试机会，规定按顺序测试，一旦测试合格就不必参加以后的测试，否则3次测试都要参加．甲教师3次测试每次合格的概率组成一个公差为18的等差数列，他第一次测试合格的概率不超过12，且他直到第二次测试才合格的概率为932，乙教师3次测试每次测试合格的概率均为23，每位教师参加的每次测试是否合格相互独立． （1）求甲教师第一次参加测试就合格的概率P ；（2）设甲教师参加测试的次数为m ，乙教师参加测试的次数为n ，求m n ξ=+的分布列．【解析】（1）由甲教师3次测试每次合格的概率组成一个公差为18的等差数列，又甲教师第一次参加测试就合格的概率为P ，故而甲教师参加第二、三次测试合格的概率分别是18P +、14P +，由题意知，19(1)832P P ⎛⎫−+= ⎪⎝⎭，解得14P =或58P =（舍），所以甲教师第一次参加测试就合格的概率为14．（2）由（1）知甲教师参加第二、三次测试合格的概率分别是38、12， 由题意知，ξ的可能取值为2，3，4，5，6，由题意可知121(2)(1,1)436P P m n ξ=====⨯=， 11233235(3)(1,2)(2,1)433483144P P m n P m n ξ⎛⎫⎛⎫====+===⨯⨯+⨯⨯= ⎪ ⎪⎝⎭⎝⎭， (4)(1,3)(2,2)(3,1)P P m n P m n P m n ξ====+==+==1113312352584334833483144⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯⨯+⨯⨯= ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， (5)(2,3)(3,2)P P m n P m n ξ====+==33113512134833483396⎛⎫⎛⎫⎛⎫⎛⎫=⨯⨯⨯+⨯⨯⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， 35115(6)(3,3)483396P P m n ξ⎛⎫⎛⎫=====⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭，所以ξ的分布列为：例3．（2022春·云南曲靖·高三校联考阶段练习）受新冠肺炎疫情的影响，某商场的销售额受到了不同程度的冲击，为刺激消费，该商场开展一项促销活动，凡在商场消费金额满300元的顾客可以免费抽奖一次，抽奖的规则如下：在不透明箱子中装有除颜色外其他都相同的10个小球，其中：红色小球1个，白色小球3个，黄色小球6个，顾客从箱子中依次不放回地摸出3个球，根据摸出球的颜色情况分别进行兑奖．将顾客摸出的3个球的颜色分成以下四种情况：A ：1个红球2个白球；B ：3个白球；C ：恰有1个黄球；D ：至少两个黄球，若四种情况按发生的机会从小到大的顺序分别对应一等奖，二等奖，三等奖，不中奖． （1）写出顾客分别获一､二､三等奖时所对应的概率；（2）已知顾客摸出的第一个球是白球，求该顾客获得二等奖的概率；（3）若五名顾客每人抽奖一次，且彼此是否中奖相互独立．记中奖的人数为X ，求X 的分布列和期望．【解析】（1）由题意可得：()()23331010C 3111,C 12040C 120P A P B =====， ()1264310C C 363=C 12010P C ==，2()1()()()3P D P A P B P C =−−−=所以中一等奖的概率为1120，二等奖的概率为140，三等奖的概率为310 （2）记事件E 为顾客摸出的第一个球是白球，事件F 为顾客获得二等奖，则()111229C C 1C 18P FE ==∣． （3）由（1）知一名顾客中奖的概率为113112040103P =++=． 由题意可得，15,3X B ⎛⎫ ⎪⎝⎭，所以()()5512C 1,2,3,4,533i ii P X i i −⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭则分布列为()15533E X =⨯=。

第49讲 离散型随机变量的分布列及期望一、知识与方法1 随机变量如果随机试验的结果可以用一个变量来表示,那么这样的变量叫作随机变量. 2 离散型随机变量对于随机变量可能的取值,可以按次序一一列出,这样的随机变量叫作离散型随机变量. 3 离散型随机变量的分布列一般地,设离散型随机变量ξ可能取的值为12,,,,,i x x x ξ取每一个值i x (1i =,2,3,) 的概率为()i i P x P ξ==，01i P ，121i P P P ++++=, 则称下表为随机变量ξ的概率分布,简称为ξ的分布列.4 离散型随机变量的期望若离散型随机变量ξ的概率分布列()i i P x P ξ==，1i =, 2,3,，则ξ的数学期望1122i i E x P x P x P ξ=++++5 二项分布在n 次独立重复试验中,某个事件发生的次数ξ是一个随机变量,如果在一次试验中某事件发生的概率是p , 那么这个事件恰好发生k 次的概率是()kkn kn P k C P qξ-==,其中0,1,2,,k n =，1q p =-, 则称ξ服从二项分布,记作(),B n p ξ~. 其中n p 、为参数, 并记 作(),,C kkn kn b k n p p q-=.6 离散型随机变量的方差(1) 若离散型随机变量ξ的概率分布为()i i P x p ξ==，1,2,3,i =, 那么()D ξ=()()2221122()i i x E p x E p x E p ξξξ-⋅+-⋅++-⋅+叫作随机变量ξ的方差,其中E ξ为随机变量的期望.ξ的标准差,记作()σξ.(2) 方差计算的简化公式: ()()()22D E E ξξξ=-.(3) 离散型随机变量的性质: (1) ()0D c =, 其中c 为常数; (2)()()2D c c D ξξ=, 其中c 为常数; (3) ()()2D c b c D ξξ+=, 其中b c 、为常数; (4) 若(),b n p ξ~, 则()1D np p ξ=-.二、典型例题【例1】一个袋子中装有7个小球,其中红球4个, 编号分别为1,2,3,4,黄球3个,编号分别为2,4,6, 从袋子中任取4个小球(假设取到任一小球的可能性相等).（1）求取出的小球中有相同编号的概率;（2）记取出的小球的最大编号为X ,求随机变量X 的分布列和数学期望.【例2】)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立,（1）用X表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X的分布列和数学期望;（2）设M为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2", 求事件M发生的概率.【例3】某人参加射击,击中目标的概率是1 3 .（1）设ξ为他射击6 次击中目标的次数,求随机变量ξ的分布列；（2）设η为他第一次击中目标时所需要射击的次数,求η的分布列;（3）若他连续射击6 次,设ξ为他第一次击中目标时之前射击的次数,求ξ的分布列;（4）若只有 6 颗子弹,他击中目标,则不再射击,否则直到子弹打完,求他射击次数ξ的分布列.三、易错警示【例】甲、乙两人解一道数学奥林匹克问题,甲解出该题的概率为23, 乙解出该题的概率为45, 设ξ为表示解出该题的人数,求E ξ.四、难题攻略【例】设袋子中装有a 个红球,b 个黄球,c 个蓝球,且规定:取出一个红球得1分, 取出一个黄球得2分,取出一个蓝球得3 分.（1）当 3a =，2b =，1c =时, 从该袋子中任取(有放回,且每球取到的机会均等)2 个球,记随机变量ξ为取出此两球所得分数之和,求ξ的分布列;（2）从该袋中任取(每球取到的机会均等) 1个球,记随机变量η为取出此球所得分数. 若53E η=，59D η=, 求 ::a b c .五、强化训练1已知某单位甲、乙丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.（1）应从甲、乙、丙三个部门的员工中分别抽取多少人?（2）若抽出的7 人中有 4 人睡眠不足,3 人睡眠充足,现从这7 人中随机抽取 3 人做进一步的身体检査.①用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;②设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.2 在10件产品中有3件一等品,4件二等品,3件三等品, 从这10件产品中任取3件.求：（1）取出的3件产品中一等品件数X的分布列和数学期望；（2）取出的3件产品中一等品件数多于二等品件数的概率.。

1.【2015高考四川，理17】某市A,B 两所中学的学生组队参加辩论赛，A 中学推荐3名男生，2名女生，B 中学推荐了3名男生，4名女生，两校推荐的学生一起参加集训，由于集训后队员的水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队（1）求A 中学至少有1名学生入选代表队的概率. （2）某场比赛前，从代表队的6名队员中随机抽取4人参赛，设X 表示参赛的男生人数，求X 得分布列和数学期望.【解析】（1）由题意，参加集训的男女生各有6名.参赛学生全从B 中抽取（等价于A 中没有学生入选代表队）的概率为333433661100C C C C =. 因此，A 中学至少1名学生入选的概率为1991100100-=. （2）根据题意，X 的可能取值为1，2，3.1333461(1)5C C P X C ===，2233463(2)5C C P X C ===， 3133461(3)5C C P X C ===，所以X 的分布列为：因此，X 的期望为131()1232555E X =⨯+⨯+⨯=.2.（2016年天津高考）某小组共10人，利用假期参加义工活动，已知参加义工活动次数为1,2,3的人数分别为3,3,4,.现从这10人中随机选出2人作为该组代表参加座谈会.（I ）设A 为事件“选出的2人参加义工活动次数之和为4”，求事件A 发生的概率； （II ）设X 为选出的2人参加义工活动次数之差的绝对值，求随机变量X 的分布列和数学期望.【解析】（Ⅰ）设事件A ：选2人参加义工活动，次数之和为4()112343210C C C 1C 3P A +== （Ⅱ）随机变量X 可能取值 0，1，2()222334210C C C 40C 15P X ++=== ()11113334210C C C C 71C 15P X +=== ()1134210C C 42C 15P X === 所以，X()7811515E X =+=3.【2015高考福建，理16】某银行规定，一张银行卡若在一天内出现3次密码尝试错误，该银行卡将被锁定，小王到银行取钱时，发现自己忘记了银行卡的密码，但是可以确定该银行卡的正确密码是他常用的6个密码之一，小王决定从中不重复地随机选择1个进行尝试.若密码正确，则结束尝试；否则继续尝试，直至该银行卡被锁定. (Ⅰ)求当天小王的该银行卡被锁定的概率；(Ⅱ)设当天小王用该银行卡尝试密码次数为X ，求X 的分布列和数学期望．【解析】（Ⅰ）设“当天小王的该银行卡被锁定”的事件为A ，则5431(A)=6542P（Ⅱ）依题意得，X 所有可能的取值是1，2，3 又1511542(X=1),(X=2),(X=3)1=.6656653P P P 所以X 的分布列为所以1125E(X)1236632．4.（2016年山东高考）甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得3分；如果只有一人猜对，则“星队”得1分；如果两人都没猜对，则“星队”得0分．已知甲每轮猜对的概率是43，乙每轮猜对的概率是32；每轮活动中甲、乙猜对与否互不影响，各轮结果也互不影响．假设“星队”参加两轮活动，求：(Ⅰ) “星队”至少猜对3个成语的概率；(Ⅱ) “星队”两轮得分之和X 的分布列和数学期望EX ．【解析】(Ⅰ) “至少猜对3个成语”包括“恰好猜对3个成语”和“猜对4个成语”．设“至少猜对3个成语”为事件A ；“恰好猜对3个成语”和“猜对4个成语”分别为事件C B ,，则1253232414331324343)(1212=⋅⋅⋅⋅+⋅⋅⋅⋅=C C B P ； 4132324343)(=⋅⋅⋅=C P ．所以3241125)()()(=+=+=C P B P A P ． (Ⅱ) “星队”两轮得分之和X 的所有可能取值为0,1,2,3,4,6 于是144131413141)0(=⋅⋅⋅==X P ；725144103143314131413241)1(1212==⋅⋅⋅+⋅⋅⋅==C C X P ；14425313243413131434332324141)2(12=⋅⋅⋅+⋅⋅⋅+⋅⋅⋅==C X P ； 1211441231413243)3(12==⋅⋅⋅==C X P ； 12514460)31433241(3243)4(12==⋅+⋅⋅⋅==C X P ； 411443632433243)6(==⋅⋅⋅==X P ；X 的分布列为：X 的数学期望62314455264141253121214425172501441==⨯+⨯+⨯+⨯+⨯+⨯=EX ．作业【2015高考重庆，理17】 端午节吃粽子是我国的传统习俗，设一盘中装有10个粽子，其中豆沙粽2个，肉粽3个，白粽5个，这三种粽子的外观完全相同，从中任意选取3个。

课时考点19 统计-----随机变量的分布列和期望高考考纲透析：等可能性的事件的概率,互斥事件有一个发生的概率,相互独立事件同时发生的概率,独立重复试验、离散型随机变量的分布列、期望和方差高考风向标：离散型随机变量的分布列、期望和方差热点题型1 n 次独立重复试验的分布列和期望 [样题1] (2005年高考·全国卷II ·理19) 甲、乙两队进行一场排球比赛.根据以往经验，单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束.设各局比赛互间没有影响.令ξ为本场比赛的局数,求ξ的概率分布和数学期望.（精确到0.0001）本题考查离散型随机变量分布和数学期望等概念，考查运用概率知识解决实际问题的能力。

解：单局比赛甲队胜乙队的概率为0.6，乙队胜甲队的概率为1－0.6＝0.4比赛3局结束有两种情况：甲队胜3局或乙队胜3局，因而P （ξ＝3）＝330.60.40.28+= 比赛4局结束有两种情况：前3局中甲队胜2局，第4局甲队胜；或前3局中乙队胜2局，第4局乙队胜。

因而P （ξ＝4）＝2230.60.40.6C ⨯⨯⨯＋2230.40.60.40.3744C ⨯⨯⨯=比赛5局结束有两种情况：前4局中甲队胜2局、乙队胜2局，第5局甲胜或乙胜。

因而P （ξ＝5）＝22240.60.40.6C ⨯⨯⨯＋22240.40.60.40.3456C ⨯⨯⨯= 所以ξ的概率分布为ξ的期望E ξ＝3×P （ξ＝3）＋4×P （ξ＝4）＋5×P （ξ＝5）＝4.0656变式新题型1.(2005年高考·浙江卷·理19)袋子A 中装有若干个均匀的红球和白球，从A 中摸出一个红球的概率是31． (Ⅰ) 从A 中有放回地摸球，每次摸出一个，共摸5次，求恰好有3次摸到红球的概率． (Ⅱ) 从A 中有放回地摸球，每次摸出一个，有3次摸到红球即停止． (i) 求恰好摸5次停止的概率； (ii )记5次之内(含5次)摸到红球的次数为ξ，求随机变量ξ的分布列及数学期望E ξ．解：(Ⅰ) 333512140333243C ⎛⎫⎛⎫⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭(Ⅱ)（i ）2224121833381C ⎛⎫⎛⎫⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭(ii)随机变量ξ的取值为0，1，2，3，；由n 次独立重复试验概率公式()()1n kk kn n P k C p p -=-，得()50513*******P C ξ⎛⎫==⨯-= ⎪⎝⎭； ()41511801133243P C ξ⎛⎫==⨯⨯-=⎪⎝⎭ ()232511802133243P C ξ⎛⎫⎛⎫==⨯⨯-=⎪ ⎪⎝⎭⎝⎭()323511173133243P C ξ⎛⎫⎛⎫==⨯⨯-=⎪ ⎪⎝⎭⎝⎭（或()328021731243243P ξ+⨯==-=） 随机变量ξ的分布列是ξ的数学期望是32808017012324324324324381E ξ=⨯+⨯+⨯+⨯= 热点题型2 随机变量ξ的取值范围及分布列[样题2]在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求：（Ⅰ）该顾客中奖的概率；（Ⅱ）该顾客获得的奖品总价值ξ（元）的概率分布列和期望ξE . 解法一：（Ⅰ）324515121026=-=-=C C I P ，即该顾客中奖的概率为32.（Ⅱ）ξ的所有可能值为：0，10，20，50，60（元）..151)60(,152)50(,151)20(,52)10(,31)0(2101311210161121023210161321026===============C C C P C C C P C C P C C C P C C P ξξξξξ且故ξ有分布列：从而期望.161516015250151205210310=⨯+⨯+⨯+⨯+⨯=ξE 解法二：（Ⅰ）,324530)(210241614==+=C C C C P （Ⅱ）ξ的分布列求法同解法一由于10张券总价值为80元，即每张的平均奖品价值为8元，从而抽2张的平均奖品价值ξE =2×8=16（元）.变式新题型2.假设一种机器在一个工作日内发生故障的概率为0 2，若一周5个工作日内无故障，可获利润10万元；仅有一个工作日发生故障可获利润5万元；仅有两个工作日发生故障不获利也不亏损；有三个或三个以上工作日发生故障就要亏损2万元 求：（Ⅰ）一周5个工作日内恰有两个工作日发生故障的概率（保留两位有效数字）； （Ⅱ）一周5个工作日内利润的期望（保留两位有效数字）解：以ξ表示一周5个工作日内机器发生故障的天数，则ξ~B （5，0 2）).5,4,3,2,1,0(8.02.0)(55=⨯⨯==-k C k P k k kξ （Ⅰ）.21.08.02.0)2(3225≈⨯⨯==C P ξ（Ⅱ）以η表示利润，则η的所有可能取值为10，5，0，－2.328.08.0)0()10(5≈====ξηP P .410.08.02.0)1()5(4115≈⨯⨯====C P P ξη .205.08.02.0)2()0(3225≈⨯⨯====C P P ξη .7()2(≥=-=ξηP P η∴的概率分布为∴利润的期望=10×0 （万元）[样题3] (2005年高考·江西卷·理19)A 、B 两位同学各有五张卡片，现以投掷均匀硬币的形式进行游戏，当出现正面朝上时A 赢得B 一张卡片，否则B 赢得A 一张卡片.规定掷硬币的次数达9次时，或在此前某人已赢得所有卡片时游戏终止.设ξ表示游戏终止时掷硬币的次数.（1）求ξ的取值范围； （2）求ξ的数学期望E ξ.解：（1）设正面出现的次数为m ，反面出现的次数为n ，则⎪⎩⎪⎨⎧≤≤=+=-915||ξξn m n m ，可得：.9,7,5:;9,7,22,7;7,6,11,6;5,5,00,5的所有可能取值为所以时或当时或当时或当ξξξξ===============n m n m n m n m n m n m（2）;645)21(2)7(;161322)21(2)5(7155=====⨯==C P P ξξ .322756455964571615;64556451611)9(=⨯+⨯+⨯==--==ξξE P变式新题型3.某射手进行射击练习，每射击5发子弹算一组，一旦命中就停止射击，并进行下一组练习，否则一直打完5发子弹后才能进入下一组练习．若该射手在某组练习中射击命中一次，并且他射击一次命中率为0．8，（1）求在这一组练习中耗用子弹ξ的分布列．（2）求在完成连续两组练习后，恰好共耗用了4发子弹的概率。

离散型随机变量的分布列、期望、方差复习指导学习要求：了解随机变量，离散型随机变量的意义，会求简单的离散型随机变量，掌握离散型随机变量的分布列，会求出期望、方差。

知识总结：一、离散型随机变量的分布列1.随机变量：如果一个随机试验的结果可以用一个变量来表示，这样的变量叫做随机变量，可以按一定次序列出的随机变量叫做离散型随机变量，常用ξ，等希腊字母表示2.离散型随机变量的分布列：若离散型随机变量ξ的一切可能取值为：a1, a2, ……, a n, ……, 相应取这些值的概率为：p1，P2，……, P n, ……，则称下表：为离散型随机变量ξ的概率分布列，简称ξ的分布列。

离散型随机变量的分布列具有的两个性质：①P i0(i=1,2,……,n,……) ②P1+P2+……+P n+……=1 一种典型的离散型随机变量的分布列：二项分布：设重复独立地进行n次随机试验A，在每一次试验中，P(A)=P(0<P<1)，ξ为n次试验中A 发生的次数，则ξ的分布列为：称ξ服从二项分布，记作ξ～B(n,P)注：是二项展开式[P+(1-P)]n=++……++……+中的第k+1项。

P1+P2+……+P n=++……+=[P+(1-P)]n=1。

二、离散型随机变量的期望与方差1．期望：设离散型随机变量ξ的分布列是：ξa1a2……a n……p p1p2……p n……称a1p1+a2p2+……+a n p n+……为ξ的数学期望，简称期望，记作Eξ。

期望的性质：①若=aξ+b (a,b均为常数), 则E=aEξ+b。

②E(ξ1+ξ2)=Eξ1+Eξ2。

③若ξ～B(n, p), 则Eξ=np注：期望Eξ是反映随机变量ξ集中趋势的指标，也反映了ξ取值的平均水平。

2．方差:设离散型随机变量ξ的分布列是ξa1a2……a n……p p1p2……p n……称(a1-Eξ)2p1+(a2-Eξ)2p2+……+(a n-Eξ)2p n+……为随机变量ξ的均方差，简称方差，记作Dξ。

【知识点】1.n 次独立重复试验：在相同的条件下，重复地做n 次试验，各次试验的结果相互独立 2.n 次独立重复试验的概率：一般地，事件A 在n 次试验中发生k 次，其有kn C 种情形，由试验的独立性知A 在k 次试验中发生，而在其余k n -次试验中不发生的概率都是kn k p p --)1(，所以由概率加法公式知，如果在一次试验中事件A 发生的概率是p ，那么在n 次独立重复试验中，事件A 恰好发生k次的概率为).,...2,1,0()1()(n k p p C k P kn k k n n =-=-3.二项分布:在上公式中，若将事件A 发生的次数设为X ，事件A 不发生的概率为p q -=1，那么在n次独立重复试验中，事件A 恰好发生k 次的概率是kn k k n q p C k X P -==)(.其中.,...2,1,0n k =于是得到X 的分布列各对应项的值,所以称这样的离散型随机变量X 服从参数为p n ,的二项分布,记作).,(~p n B X4.离散型随机变量X 的数学期望一般地,设一个离散型随机变量X 所有可能取的值是,,...,,21n x x x 这些对应的概率是,,...,,21n p p p ,则n n p x p x p x X E +++=...)(2211叫做这个离散型随机变量X 的均值或数学期望.5.二项分布的数学期望:np x E =)(【经典例题】【例1】在某批次的某种灯泡中，随机地抽取200个样品，并对其寿命进行追踪调查，将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于天的灯泡是优等品，寿命小于天的灯泡是次品，其余的灯泡是正品.（Ⅰ）根据频率分布表中的数据，写出的值；（Ⅱ）某人从灯泡样品中随机地购买了()*∈n n N 个，如果这个灯泡的等级情况恰好与按三．．个等级分层抽样．．．．．．．所得的结果相同，求n 的最小值； （Ⅲ）某人从这个批次的灯泡中随机地购买了3个进行使用，若以上述频率作为概率，用X 表示此人所购买的灯泡中次品的个数，求X 的分布列和数学期望. 1、【答案】（Ⅰ）解：0.15a =，30b =. （Ⅱ）解：由表可知：灯泡样品中优等品有50个，正品有100个，次品有50个， 所以优等品、正品和次品的比例为50:100:501:2:1=. 所以按分层抽样法，购买灯泡数24()*=++=∈n k k k k k N ， 所以n 的最小值为4． （Ⅲ）解：X 的所有取值为0,1,2,3.【例2】甲、乙两位同学进行篮球三分球投篮比赛，甲每次投中的概率为3，乙每次投中的概率为21，每人分别进行三次投篮． （Ⅰ）记甲投中的次数为ξ，求ξ的分布列及数学期望E ξ； （Ⅱ）求乙至多投中2次的概率；（Ⅲ）求乙恰好比甲多投进2次的概率．2.【答案】解：（Ⅰ）ξ的可能取值为：0,1,2,3．ξ的分布列如下表：（Ⅲ）设乙比甲多投中2次为事件A ，乙恰投中2次且甲恰投中0次为事件1B ，乙恰投中3次且甲恰投中1次为事件2B ，则2121,,B B B B A Y =为互斥事件．【例3】某商场一号电梯从1层出发后可以在层停靠.已知该电梯在1层载有4位乘客，假设每位乘客在234、、层下电梯是等可能的.(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率；(Ⅱ) 用X 表示4名乘客在第4层下电梯的人数，求X 的分布列和数学期望.(Ⅱ) X 的可能取值为0,1,2,3,4【易错题】【例1】经调查发现，人们长期食用含高浓度甲基汞的鱼类会引起汞中毒，其中罗非鱼体内汞含量比其它鱼偏高．现从一批数量很大的罗非鱼中随机地抽出15条作样本，经检测得各条鱼的汞含量的茎叶图（以小数点前的数字为茎，小数点后一位数字为叶）如下：《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm ．（Ⅰ）检查人员从这15条鱼中，随机抽出3条，求3条中恰有1条汞含量超标的概率； （Ⅱ）若从这批数量很大的鱼．．．．．．．．中任选3条鱼，记ξ表示抽到的汞含量超标的鱼的条数．以此15条鱼的样本数据来估计．．．这批数量很大的鱼的总体数据，求ξ的分布列及数学期望E ξ． 1.【答案】解：（Ⅰ）记“15条鱼中任选3条恰好有1条鱼汞含量超标”为事件A ，则ξ可能取0，1，2，3.0 1235567889 135567 罗非鱼的汞含量（ppm ）【例2】某学校随机抽取部分新生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0,100]，样本数据分组为[0,20)，[20,40)，[40,60)，[60,80)，[80,100].（Ⅰ）求直方图中x 的值；（Ⅱ）如果上学所需时间不少于1小时的学生可申请在学校住宿，请估计学校600名新生中有多少名学生可以申请住宿；（Ⅲ）从学校的新生中任选4名学生，这4名学生中上学所需时间少于20分钟的人数记为X ，求X 的分布列和数学期望.（以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率） 2、【答案】解：（Ⅰ）由直方图可得：200.025200.0065200.0032201x ⨯+⨯+⨯+⨯⨯=. 所以 0.0125x =.（Ⅱ）新生上学所需时间不少于1小时的频率为：0.0032200.12⨯⨯=，因为6000.1272⨯=，所以600名新生中有72名学生可以申请住宿. （Ⅲ）X 的可能取值为0,1,2,3,4.【例3】国家对空气质量的分级规定如下表：（Ⅰ）写出下面频率分布表中,,,a b x y 的值；（Ⅱ）某人计划今年6月份到此城市观光4天，若将（Ⅰ）中的频率作为概率，他遇到空气质量为优或良的天数用X 表示，求X 的分布列和均值EX .【例4】某市规定，高中学生三年在校期间参加不少于80小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段[)75,80，[)80,85，[)85,90，[)90,95，[]95,100（单位：小时）进行统计，其频率分布直方图如图所示．（Ⅰ）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；（Ⅱ）从全市高中学生（人数很多）中任意选取3位学生，记ξ为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量ξ的分布列和数学期望E ξ．服务时间/小时O4.【答案】解：（Ⅰ）根据题意，参加社区服务时间在时间段[)90,95小时的学生人数为2000.060560⨯⨯=（人）， 参加社区服务时间在时间段[]95,100小时的学生人数为2000.020520⨯⨯=（人）． 所以抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为80人．由已知得，随机变量ξ的可能取值为0,1,2,3．随机变量ξ的分布列为【课后测试】1.乒乓球单打比赛在甲、乙两名运动员间进行，比赛采用7局4胜制（即先胜4局者获胜，比赛结束），假设两人在每一局比赛中获胜的可能性相同. （Ⅰ）求甲以4比1获胜的概率；（Ⅱ）求乙获胜且比赛局数多于5局的概率； （Ⅲ）求比赛局数的分布列.（Ⅲ）解：设比赛的局数为X ，则X 的可能取值为4,5,6,7．2.张先生家住H 小区，他在C 科技园区工作，从家开车到公司上班有12L L ，两条路线（如图），1L 路线上有123A A A ，，三个路口，各路口遇到红灯的概率均为12；2L 路线上有12B B ，两个路口，各路口遇到红灯的概率依次为34，35．（Ⅰ）若走1L 路线，求最多．．遇到1次红灯的概率； （Ⅱ）若走2L 路线，求遇到红灯次数X 的数学期望；（Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．2 122、【答案】解：（Ⅰ）设走1L 路线最多遇到1次红灯为A 事件，则因为EX EY <，所以选择2L 路线上班最好．3.为提高学生学习数学的兴趣,某地区举办了小学生“数独比赛”.比赛成绩共有90,70,60,40,30分分分分分五种,按本次比赛成绩共分五个等级.从参加比赛的学生中随机抽取了名学生,并把他们的比赛成绩按这五个等级进行了统计,得到如下数据表:(Ⅰ),其成绩等级为“A 或B ”的概率;(Ⅱ)根据(Ⅰ)的结论,若从该地区参加“数独比赛”的小学生(参赛人数很多)中任选3人,记X 表示抽到成绩等级为“A 或B ”的学生人数,求X 的分布列及其数学期望EX ; (Ⅲ)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于20分”的概率.显然基本事件的总数为230C .不妨设m n >,当90m =时,60n =或40或30,其基本事件数为111141073()C C C C ⋅++; 当70m =时,n =40或30,其基本事件数为111673()C C C ⋅+;当60m =时,30n =,其基本事件数为11103C C ⋅;4.在某批次的某种灯泡中，随机地抽取200个样品，并对其寿命进行追踪调查，将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级，其中寿命大于或等于500.（Ⅰ）根据频率分布表中的数据，写出的值；（Ⅱ）某人从灯泡样品中随机地购买了()*∈n n N 个，如果这个灯泡的等级情况恰好与按三．．个等级分层抽样．．．．．．．所得的结果相同，求n 的最小值； （Ⅲ）某人从这个批次的灯泡中随机地购买了3个进行使用，若以上述频率作为概率，用X 表示此人所购买的灯泡中次品的个数，求X 的分布列和数学期望. 4.【答案】（Ⅰ）解：0.15a =，30b =. （Ⅱ）解：由表可知：灯泡样品中优等品有50个，正品有100个，次品有50个， 所以优等品、正品和次品的比例为50:100:501:2:1=. 所以按分层抽样法，购买灯泡数24()*=++=∈n k k k k k N ， 所以n 的最小值为4．（Ⅲ）解：X 的所有取值为0,1,2,3.5.为提高学生学习数学的兴趣,某地区举办了小学生“数独比赛”.比赛成绩共有90,70,60,40,30分分分分分五种,按本次比赛成绩共分五个等级.从参加比赛的学生中随机抽取了(Ⅰ)根据上面的统计数据,试估计从本地区参加“数独比赛”的小学生中任意抽取一人,其成绩等级为“A 或B ”的概率;(Ⅱ)根据(Ⅰ)的结论,若从该地区参加“数独比赛”的小学生(参赛人数很多)中任选3人,记X 表示抽到成绩等级为“A 或B ”的学生人数,求X 的分布列及其数学期望EX ; (Ⅲ)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于20分”的概率.显然基本事件的总数为230C .不妨设m n >,当90m =时,60n =或40或30,其基本事件数为111141073()C C C C ⋅++; 当70m =时,n =40或30,其基本事件数为111673()C C C ⋅+;当60m =时,30n =,其基本事件数为11103C C ⋅;【课后作业】1.某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是13，遇到红灯时停留的时间都是2min。

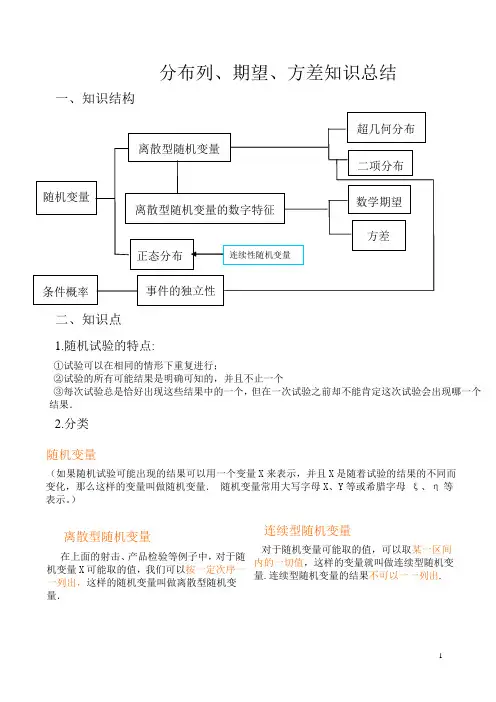
分布列、期望、方差知识总结一、知识结构二、知识点1.随机试验的特点:①试验可以在相同的情形下重复进行；②试验的所有可能结果是明确可知的，并且不止一个③每次试验总是恰好出现这些结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果．2.分类随机变量（如果随机试验可能出现的结果可以用一个变量X来表示，并且X是随着试验的结果的不同而变化，那么这样的变量叫做随机变量．随机变量常用大写字母X、Y等或希腊字母ξ、η等表示。

）离散型随机变量在上面的射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．连续型随机变量对于随机变量可能取的值，可以取某一区间内的一切值，这样的变量就叫做连续型随机变量.连续型随机变量的结果不可以一一列出.3.离散型随机变量的分布列一般的,设离散型随机变量X可能取的值为x1,x2, ,x i , ,x nX取每一个值xi(i=1,2,）的概率P(ξ=x i）＝P i，则称表为离散型随机变量X 的概率分布，简称分布列性质：①pi≥0, i =1，2，…；②p1 + p2 +…+p n= 1．③一般地，离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。

4.求离散型随机变量分布列的解题步骤例题：篮球运动员在比赛中每次罚球命中得1分，不中得0分，已知某运动员罚球命中的概率为0.7，求他罚球一次的得分的分布列.解：用随机变量X表示“每次罚球得的分值”，依题可知，X可能的取值为：1,0且P（X=1）=0.7，P（X=0）=0.3因此所求分布列为：引出二点分布如果随机变量X的分布列为：其中0<p<1，q=1-p，则称离散型随机变量X服从参数p的二点分布二点分布的应用：如抽取彩票是否中奖问题、新生婴儿的性别问题等.超几何分布一般地, 设总数为N 件的两类物品，其中一类有M 件，从所有物品中任取n(n ≤N)件,这n 件中所含这类物品件数X 是一个离散型随机变量，则它取值为k 时的概率为()(0,1,2,,)k n k M N MnNC C P X k k m C --===，其中{}min,m M n =,且*,,,,n N M N n M N N ∈≤≤ 则称随机变量X 的分布列为超几何分布列,且称随机变量X 服从参数N 、M 、n 的超几何分布注意：（1）超几何分布的模型是不放回抽样；（2）超几何分布中的参数是N 、M 、n ，其意义分别是总体中的个体总数、N 中一类的总数、样本容量解题步骤：例题、在某年级的联欢会上设计了一个摸奖游戏，在一个口袋中装有10个红球和20个白球，这些球除颜色外完全相同.游戏者一次从中摸出5个球.至少摸到3个红球就中奖，求中奖的概率解：设摸出红球的个数为X,则X 服从超几何分布,其中30,10,5N M n === X 可能的取值为0，1，2，3，4, 5. 由题目可知，至少摸到3个红球的概率为(3)(3)(4)(5)P X P X P X P X ==+=+=≥324150102010201020555303030C C C C C C C C C =++ ≈0.191答：中奖概率为0.191.nNn MN MCC C -0nNn MN MCC C 11--nNm n MN m MCC C --条件概率1.定义：对任意事件A 和事件B ，在已知事件A 发生的条件下事件B 发生的概率，叫做条件概率P(B|A)，读作A 发生的条件下B 的概率2.事件的交（积）:由事件A 和事件B 同时发生所构成的事件D ，称为事件A 与事件B 的交（或积作D=A ∩B 或D=AB3.条件概率计算公式:P(B|A)相当于把A 看作新的基本事件空间,求Ａ∩Ｂ发生的概率:解题步骤：例题、10个产品中有7个正品、3个次品，从中不放回地抽取两个，已知第一个取到次品，求第二取到次品的概率.解：设 A = {第一个取到次品}， B = {第二个取到次品}，所以，P(B|A) = P(AB) / P(A)= 2/9 答：第二个又取到次品的概率为2/9..0)(,)()()|(>=A P A P AB P A B P .1)|(0)()|()(0)A (P ≤≤⋅=>A B P A P A B P AB P （乘法公式）；，则若.151)(21023==⇒C C AB P .103)(=A P相互独立事件2.相互独立事件同时发生的概率公式两个相互独立事件同时发生的概率，等于每个事件发生的概率的积。

随机变量的数学期望例题和知识点总结在概率论与数理统计中，随机变量的数学期望是一个非常重要的概念。

它反映了随机变量取值的平均水平，具有十分广泛的应用。

接下来，让我们通过一些具体的例题来深入理解随机变量的数学期望，并对相关知识点进行总结。

一、知识点回顾数学期望，简称期望，记作 E(X)。

对于离散型随机变量 X，其概率分布为 P(X ＝ xᵢ) ＝ pᵢ（i ＝ 1, 2, 3,），则数学期望 E(X) ＝Σxᵢpᵢ。

对于连续型随机变量 X，其概率密度函数为 f(x)，则数学期望 E(X) ＝∫xf(x)dx（积分区间为整个定义域）。

数学期望具有以下几个重要性质：1、设 C 为常数，则 E(C) ＝ C。

2、设 X 为随机变量，C 为常数，则 E(CX) ＝ CE(X)。

3、设 X、Y 为两个随机变量，则 E(X ＋ Y) ＝ E(X) ＋ E(Y)。

二、例题解析例 1：掷一枚均匀的骰子，设随机变量 X 表示掷出的点数，求 E(X)。

解：骰子的点数分别为 1, 2, 3, 4, 5, 6，且每个点数出现的概率均为1/6。

则 E(X) ＝ 1×（1/6) ＋ 2×（1/6) ＋ 3×（1/6) ＋ 4×（1/6) ＋ 5×（1/6) ＋ 6×（1/6) ＝ 35例 2：已知离散型随机变量 X 的概率分布如下：｜ X ｜ 0 ｜ 1 ｜ 2 ｜｜｜｜｜｜｜ P ｜ 02 ｜ 05 ｜ 03 ｜求 E(X)。

解：E(X) ＝ 0×02 ＋ 1×05 ＋ 2×03 ＝ 11例 3：设连续型随机变量 X 的概率密度函数为 f(x) ＝ 2x，0 ＜ x ＜1，求 E(X)。

解：E(X) ＝∫0,1 x×2x dx ＝ 2/3例 4：已知随机变量 X 服从参数为λ 的泊松分布，求 E(X)。

解：泊松分布的概率质量函数为 P(X ＝ k) ＝（e^（λ)λ^k) ／ k!E(X) ＝Σk×（e^（λ)λ^k) ／ k! （k 从 0 到正无穷）通过计算可得 E(X) ＝λ三、应用场景数学期望在实际生活中有很多应用。