(完整版)广义胡克定律
- 格式:doc
- 大小:1.03 MB
- 文档页数:10



12 广义虎克定律在弹性力学中,我们由弹性变形过程是一个可逆过程这个前提出发,依据热力学分析,得到了应力分量ij σ是应变分量ij ε的单值函数的结论. 加上小变形的假设,可将应力按泰勒展开,并略去二阶及二阶以上的高阶小量. 我们还假定物体未变形时内部没有应力,得到kl ijkl ij c εσ= (12-1)式中ijkl c 称为广义弹性常数. (12-1)式也可以写成kl ijkl ij b σε= (12-2)式中ijkl b 称为柔性系数.13 各向同性物体的广义虎克定律13.1 一般的表示(12-1)式中ijkl c 为一个四阶张量,共81个元素. 由于形变张量是对称的,所以将指标i 与j , k 与l 互易,或将i ,j 与k ,l 成对地互易之后,乘积kl ij εε并不改变. 由此可见,张量ijkl c 也可以有这个性质,即当指标互易时具有如下的对称性质:klij ijlk jikl ijkl c c c c === (13-1)经计算可证实,四阶张量的分量中具有以上对称性质的分量,在一般情形中有21个. 因此,对极端各向异性的材料,也只有21个独立的弹性常数. 至于具有三个正交的弹性对称面的物体,则具有9个独立的弹性常数,这样的物体称为正交各向异性体. 正交各向异性体的弹性系数矩阵具有如下的形式:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛665544332322131211000000000000c c c c c c c c c 对称对于各向同性体,利用坐标轮换时应变能的不变性和坐标轴选取的任意性可以证明,独立的弹性常数减少到只有2个.各向同性材料的弹性常数矩阵为⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+++G G G G G G000000200020002对称λλλλλλ广义虎克定律可写为.2,2,2,2,2,2121233333131222223231111εσλθεσεσλθεσεσλθεσG G G G G G =+==+==+= (13-2) 或者简写为ij ij ij G λθδεσ+=2 (13-3)其中u div 321332211=++=++==εεεεεεεθii 为体积应变或应变张量的第一不变量,ij δ为Kroneker 符号.广义虎克定律也可以写成以应力分量表示应变分量的形式:⎥⎦⎤⎢⎣⎡⋅⋅+-=ij ij ij I G G δλλσε1)23(21 (13-4) 其中3322111σσσσ++==Θ=ii I 为应力张量的第一不变量.13.2 弹性常数及其相互之间的关系常用的弹性常数有λ、G 、E 、μ、K . 其中λ和G 称为拉梅常数,G 又称为剪切模量或刚性模量. E 称为杨氏弹性模量,μ称为泊松比或横向变形系数,K 称为体积弹性模量.G 可以利用纯剪切试验直接测得, 此时τσ=12, 其余应力分量均为零,根据(13-2),G 2/12τε=. 因此测得τ和12ε即可求得G.E 和μ可以利用单轴拉伸试验测得,此时σσ=11,其余0312*******=====σσσσσ.令11111σEε=, 11113322σE εεεμμ-=⋅-== (13-5)由广义虎克定律(13-2)⎪⎪⎪⎭⎫+=+=+=λθελθελθεσ3322111120202G G G (13-6) 将上三式相加得到)2G 3/(11+=λσθ将上式代入(13-6)的第一式得到GG G E ++=λλ)23( (13-7)代入(13-6)的第二式或第三式得到)(2G +=λλν (13-8)(13-7)、(13-8)也可以化为)21)(1(μμμλ-+=E , )1(2μ+=EG (13-9)利用(13-9)可将虎克定律表示为如下更常用的形式[][][])())(2211333311332222332211111(11σσμσεσσμσεσσμσε+-=+-=+-=EE E ⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+=+=121231312323111σμεσμεσμεE E E(13-10)或ij ij ij EE δσμσμε031-+=(13-11) 其中3/3/3/)(13322110I =Θ=++=σσσσ,1I 为应力张量第一不变量,ij δ为Kroneker 符号.在各向均匀压力试验中,p -===332211σσσ, 0312312===σσσ, 将上述应力分量的值代入广义虎克定律公式(13-2)得到λθε+=-112G p , λθε+=-222G p λθε+=-332G p将上面三式相加就得到θλ)23(3G p +=-定义体积变形模量K 为θ/p K -=就得到G K 32+=λ (13-12)可推出五个弹性常数之间的关系, 结果如下:,9)3(313 )21)(1(323)2(212EK E K K K E G K E G G E G G --=+=-+=-=--=-=μμμμμμμλE K KEK E K G -=+-=+=-=-=93)1(2)21(3 )1(2)(232)21(μμμλμμλ KEK G K G K G E K G 63)3(223 123)(2-=+-=-=-=+=μλλλμ )21(339)1(2 3)(9)21)(1()23(μμλλμμμλλλ-=+=+=--=-+=++=K GK KG G K K K G G G E.)21(3)3(3 )21(3)1(23)1(32μμμμμλλ-=-=-+=+=+=EE G GE G G K (13-13).12+ ,21μμλλμλ-=-=+G G G (13-14)。


材料力学广义胡克定律公式好的,以下是为您生成的关于“材料力学广义胡克定律公式”的文章:在我们探索材料力学这个神奇的领域时,广义胡克定律公式就像一把神奇的钥匙,能帮助我们打开很多未知的大门。
咱先来说说啥是广义胡克定律公式。
简单来讲,它描述了材料在复杂应力状态下的应变与应力之间的关系。
这就好比我们去拉一根橡皮筋,拉得越用力,它就伸得越长,这个伸长的程度和我们用力的大小是有关系的。
广义胡克定律公式就是在告诉我们这个“关系”到底是咋样的。
比如说,有一次我在实验室里做材料力学的实验。
那是一根金属棒,我们要通过施加不同的力来观察它的变形情况。
我小心翼翼地调整着仪器,眼睛紧紧盯着那根金属棒,心里还挺紧张,就怕出啥差错。
当我逐渐增加力的大小,那金属棒开始慢慢地发生了细微的弯曲。
我赶紧记录下每一个数据,心里想着,这不就是广义胡克定律公式在现实中的体现嘛!广义胡克定律公式可以用数学表达式来表示,对于各向同性材料,它通常可以写成这样:\(\epsilon_{x} = \frac{1}{E}[\sigma_{x} - \nu (\sigma_{y} +\sigma_{z})]\)\(\epsilon_{y} = \frac{1}{E}[\sigma_{y} - \nu (\sigma_{x} +\sigma_{z})]\)\(\epsilon_{z} = \frac{1}{E}[\sigma_{z} - \nu (\sigma_{x} +\sigma_{y})]\)这里面的\(\epsilon\)表示应变,\(\sigma\)表示应力,\(E\)是材料的弹性模量,\(\nu\)是材料的泊松比。
可别小看这些公式,它们在工程领域的作用那可大了去了。
就拿建筑来说吧,设计师们在设计高楼大厦的时候,就得靠这些公式来计算材料在各种力的作用下会发生多大的变形,从而确保建筑的安全和稳定。
想象一下,如果没有广义胡克定律公式,那盖出来的房子说不定哪天就歪了或者塌了,多吓人啊!再比如说汽车制造。
第四章 广义胡克定律第四章 广义胡克定律 (1)§4.1节广义胡克定律 (2)§4.2节拉梅常数与工程弹性常数 (5)§4.3节弹性应变能函数 (7)§4.1节 广义胡克定律(一)单向应力状态下胡克定律单向应力状态下,处于线弹性阶段材料,其应力与应变关系可由下式表示:x x E σε=其中E 为材料的弹性模量。
(二)三维广义胡克定律三维条件下,物体应力状态可由6个分量表示,而应变状态也由6个分量表示。
假设应力与应变的各个分量之间均相关,一般地,1111111222133314121523163122211122222333241225232631333111322233333412352336311241114222433344124523463123511152225c c c c c c c c c c c c c c c c c c c c c c c c c c c σεεεεεεσεεεεεεσεεεεεεσεεεεεεσεε=+++++=+++++=+++++=+++++=++33354125523563131611162226333641265236631c c c c c c c c c εεεεσεεεεεε⎧⎪⎪⎪⎪⎨⎪⎪+++⎪=+++++⎪⎩ 或写作111213141516111121222324252622223132333435363333121241424344454623235152535455563131616263646566c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c σεσεσεσεσεσε⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥⎥ 其中,mn C (,1,,6m n =")为弹性常数。
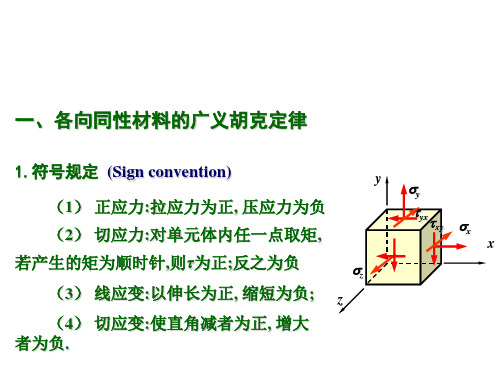
广义胡克定律 强度理论[知识回顾]1、 轴向拉(压)变形在轴向拉(压)杆件内围绕某点截取单元体,单向应力状态(我们分析过)横向变形2)纯剪切[导入新课]胡克定律反映的是应力与应变间的关系,对复杂应力状态,其应力与应变间的关系由广义胡克定律确定。
[新课教学]x x E εσ=E xx y σμμεε-=-=γτG =广义胡克定律 强度理论一、广义胡克定律(Generalized Hooke Law )1、主应力单元体-叠加法只在1σ作用下:1方向只在2σ作用下:1方向 1方向由1σ、2σ、3σ共同作用引起的应变只在3σ作用下:1方向即同理:2、非主应力单元体可以证明:对于各向同性材料,在小变形及线弹性范围内,线应变只与正应力有关,而与剪应力无关; 剪应变只与剪应力有关,而与正应力无关, 满足应用叠加原理的条件。
E11σε='E21σμε-=''E 31σμε-='''111εεεε'''+''+'=()[]32111σσμσε+-=E()[]13221σσμσε+-=E()[]21331σσμσε+-=E [][][]⎪⎪⎪⎭⎪⎪⎪⎬⎫+-=+-=+-=)(1)(1)(1y x z z x z y y z y x x E E E σσμσεσσμσεσσμσε⎪⎪⎪⎭⎪⎪⎪⎬⎫===zx zx yz yz xy xy G G G τγτγτγ111小变形,线弹性范围内,符合叠加原理3、体积应变单元体,边长分别为dx 、dy 和dz 。
在三个互相垂直的面上有主应力1σ、2σ和3σ。
变形前单元体的体积为 变形后,三个棱边的长度变为由于是单元体,变形后三个棱边仍互相垂直,所以,变形后的体积为dxdydz V )1)(1)(1(3211εεε+++=将上式展开,略去含二阶以上微量的各项,得dxdydz V )1(3211εεε+++= 于是,单元体单位体积的改变为 3211εεεθ++=-=VVV θ称为体积应变(或体应变)。
广义胡克定律 强度理论
[知识回顾]
1、 轴向拉(压)变形
在轴向拉(压)杆件内围绕某点截取单元体,单向应力状态(我们分析过)
横向变形
2)纯剪切
[导入新课]
胡克定律反映的是应力与应变间的关系,对复杂应力状态,其应力与应变间的关系由广义胡克定律确定。
[新课教学]
x x E εσ=E x
x y σ
μμεε-=-=γ
τG =
广义胡克定律 强度理论
一、广义胡克定律(Generalized Hooke Law )
1、主应力单元体-叠加法
只在1σ作用下:1方向
只在2σ作用下:1方向 1方向由1σ、2σ、3σ共同作用引起的应变
只在3σ作用下:1方向
即
同理:
2、非主应力单元体
可以证明:对于各向同性材料,在小变形及线弹性范围内,
线应变只与正应力有关,而与剪应力无关; 剪应变只与剪应力有关,而与正应力无关, 满足应用叠加原理的条件。
E
1
1σε=
'E
21σ
με-=''E 31
σ
με-='''111εεεε'''+''+'=()[]
32111
σσμσε+-=E
()[]1322
1
σσμσε+-=E
()[]21331σσμσε+-=E []
[]
[]
⎪⎪⎪
⎭
⎪⎪⎪⎬⎫+-=+-=+-=)(1)(1)(1y x z z x z y y z y x x E E E σσμσεσσμσεσσμσε⎪⎪⎪⎭⎪⎪⎪
⎬⎫===zx zx yz yz xy xy G G G τγτγτγ111小变形,线弹性范围内,符合叠加原理
3、体积应变
单元体,边长分别为dx 、dy 和dz 。
在三个互相垂直的面上有主应力1σ、2σ和3σ。
变形前单元体的体积为 变形后,三个棱边的长度变为
由于是单元体,变形后三个棱边仍互相垂直,所以,变形后的体积为
dxdydz V )1)(1)(1(3211εεε+++=
将上式展开,略去含二阶以上微量的各项,得
dxdydz V )1(3211εεε+++= 于是,单元体单位体积的改变为 3211εεεθ++=-=
V
V
V θ称为体积应变(或体应变)。
它描述了构件内一点的体积变化程度。
5、体积应变与应力的关系
将广义虎克定律(8-22)代入上式,得到以应力表示的体积应变
式中
K 称为体积弹性模量,m σ是三个主应力的平均值。
体积应变θ只与平均应力m σ有 关,或者说只与三个主应力之和有关,而与三个主应力之间的比值无关。
体积应变θ与平均应力m σ成正比,称为体积虎克定律。
dxdydz V =dz
dz dz dy
dy dy dx
dx dx )1()1()1(332211εεεεεε+=++=++=+)21(3μ-=
E K )(31321σσσσ++=m K E m σσσσμθ=
++⋅-==3)21(3321)(21321321σσσμ
εεεθ++-=++=E。