2-6 带通滤波器
- 格式:pptx
- 大小:1.71 MB
- 文档页数:10

《深入理解二阶带通滤波器:中心频率和固有频率的探讨》在探讨二阶带通滤波器的中心频率和固有频率之前,让我们先了解二阶带通滤波器的基本原理和应用。
二阶带通滤波器是一种常见的电子滤波器,它可以通过选择适当的电路元件和参数来实现对特定频率范围内信号的增强,并对其他频率的信号进行抑制。
在讨论中心频率和固有频率之前,我们需要先了解滤波器中的一些基础知识。
1. 二阶带通滤波器的基本原理二阶带通滤波器是由一个高通滤波器和一个低通滤波器级联构成的。
它的传递函数可以表示为:H(s) = k * (s^2) / (s^2 + (s/Q) + 1)其中,s是复频域变量,k是系统增益,Q是品质因数。
二阶带通滤波器可以在选择合适的参数后实现对特定频率范围内信号的增强,是一种非常常用的滤波器。
2. 中心频率的概念中心频率是指带通滤波器增益最大的频率点,也是滤波器响应曲线的中心位置。
在二阶带通滤波器中,中心频率通常由下式计算得出:fc = 1 / (2 * π * √(L * C))其中,fc表示中心频率,L表示电感值,C表示电容值。
中心频率决定了滤波器对特定频率范围内信号的响应程度,是设计带通滤波器时需要考虑的重要参数。
3. 固有频率的意义固有频率是指带通滤波器自身的振荡频率,也是在没有外部输入信号作用时,滤波器自由振荡的频率。
在二阶带通滤波器中,固有频率可以用下式表示:f0 = 1 / (2 * π * √(L * C))与中心频率类似,固有频率也与电感值和电容值有关。
固有频率可以反映出滤波器自身的特性,是分析滤波器稳定性和振荡特性的重要参数。
4. 理论与实际应用在实际应用中,中心频率和固有频率是设计二阶带通滤波器时需要重点考虑的参数。
通过合理选择电感值和电容值,可以实现对特定频率范围内信号的增强,同时保持滤波器的稳定性和响应速度。
在设计滤波器时,需要根据实际需求去调整中心频率和固有频率,以实现最佳的滤波效果。
总结回顾通过以上的讨论,我们对二阶带通滤波器的中心频率和固有频率有了更深入的了解。

二阶带通滤波器工作原理二阶带通滤波器是一种常见的电子滤波器,通过限制特定频率范围内的信号传递,对输入信号进行滤波处理。
它在电子通信、音频处理、图像处理等领域中被广泛应用。
本文将详细介绍二阶带通滤波器的工作原理,包括其结构、频率响应特性、传递函数等方面的内容。
一、二阶带通滤波器的结构二阶带通滤波器通常由电阻、电容、电感等元件构成,它可以使用不同的电路结构来实现。
其中比较常见的是基于运算放大器的二阶带通滤波器。
该结构的基本框图如下所示:(插入二阶带通滤波器的基本框图)从图中可以看出,二阶带通滤波器由两个滤波段组成,每个滤波段都包括一个运算放大器和一组电阻、电容元件。
输入信号经过第一个滤波段进行低频滤波,然后经过第二个滤波段进行高频滤波,最终得到带通滤波效果。
这种结构的二阶带通滤波器在实际应用中具有较好的性能和稳定性。
二、频率响应特性二阶带通滤波器的频率响应特性是描述其滤波效果的重要指标。
在频率响应曲线上,可以清晰地看出滤波器对不同频率的信号的响应情况。
一般而言,二阶带通滤波器的频率响应曲线呈现出一个中心频率(通带中心频率)和一定的带宽。
中心频率是滤波器允许通过的信号的集中频率,而带宽则是中心频率附近信号的传递范围。
二阶带通滤波器的频率响应曲线还包括通带增益、截止频率等重要参数。
通带增益是指在滤波器通过信号时的增益情况,而截止频率则是指在该频率以下或以上的信号被滤波器阻止的情况。
这些参数直接影响着滤波器的性能和实际应用效果。
三、传递函数二阶带通滤波器的传递函数是描述其输入输出之间关系的数学表达式,通常用H(s)表示,其中s是复变量。
传递函数可以准确地描述滤波器的频率响应特性和滤波效果。
常见的二阶带通滤波器传递函数形式为:H(s) = K * (s^2 + ω_0/Q * s + ω_0^2) / (s^2 + ω_0/Q * s + ω_0^2)K是传递函数的增益参数,ω_0是通带中心频率,Q是品质因数。

带通滤波器设计1. 引言在信号处理中,滤波器是一种重要的工具,用于去除或改变信号的特定频率成分。
带通滤波器是一种常用的滤波器,它可以传递一定范围内的频率成分,而抑制其他频率成分。
本文将介绍带通滤波器的基本原理和设计方法。
2. 带通滤波器的原理带通滤波器是一种频率选择性滤波器,它可以传递一定范围内的频率信号,而将其他频率信号抑制。
其基本原理是利用滤波器的频率响应特性,对输入信号进行滤波处理。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联连接而成。
低通滤波器用于抑制高于截止频率的频率成分,而高通滤波器用于抑制低于截止频率的频率成分,从而实现带通滤波效果。
3. 带通滤波器的设计方法带通滤波器的设计通常包括以下几个步骤:在设计带通滤波器之前,需要确定滤波器的一些规格参数,包括中心频率、通带宽度、阻带宽度等。
这些参数决定了滤波器的性能和应用范围。
步骤二:选择滤波器的类型常见的带通滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
根据具体的应用要求和设计指标,选择适合的滤波器类型。
步骤三:计算滤波器的阶数滤波器的阶数决定了滤波器的陡峭程度和相频特性。
根据设计要求和滤波器类型,计算滤波器的阶数。
步骤四:确定滤波器的传输函数根据滤波器的类型和阶数,使用滤波器设计方法计算滤波器的传输函数。
常用的设计方法包括频率折叠法、零极点法等。
根据滤波器的传输函数,采用模拟滤波器的设计方法,设计滤波器的电路结构和参数。
常用的设计方法包括电压法、电流法等。
步骤六:数字滤波器的设计对于数字信号处理系统,需要将模拟滤波器转换为数字滤波器。
常用的设计方法包括脉冲响应法、频率采样法等。
根据系统的采样率和滤波器的性能要求设计数字滤波器。
4. 带通滤波器的应用带通滤波器在信号处理领域有着广泛的应用。
例如,音频处理中常用带通滤波器对音频信号进行频率选择性处理,去除噪声和杂音。
图像处理中常用带通滤波器对图像进行频率域滤波,增强或抑制特定频率成分,实现图像增强、去噪等功能。

滤波器种类作用原理滤波器是一种电子电路,它可以根据频率的不同,选择性地通过或抑制电路中的信号。
根据作用原理和种类的不同,滤波器可以分为多种类型。
1. 低通滤波器(Low-pass filter)低通滤波器是一种能够通过较低频率信号而抑制高频信号的滤波器。
它的作用是削弱或过滤掉输入信号中高于截止频率的频率分量。
低通滤波器广泛应用于音频和通信领域,常用于去除高频噪声。
2. 高通滤波器(High-pass filter)高通滤波器是一种能够通过较高频率信号而抑制低频信号的滤波器。
它的作用是削弱或过滤掉输入信号中低于截止频率的频率分量。
高通滤波器常用于音频和通信领域,常用于削弱或滤除低频噪声。
3. 带通滤波器(Band-pass filter)带通滤波器是一种能够通过一些频率范围内的信号而抑制其他频率范围内的信号的滤波器。
它的作用是只允许通过滤波器中选择的中心频率附近的频率分量,同时抑制其他频率范围的信号。
带通滤波器常用于音频、无线通信和图像处理等领域。
4. 带阻滤波器(Band-stop filter)带阻滤波器是一种能够通过除了一些频率范围内的信号外的其他信号的滤波器。
它的作用是削弱或完全抑制一些频率范围内的信号,同时允许通过其他频率范围的信号。
带阻滤波器常用于音频、无线通信和图像处理等领域。
5. 陷波滤波器(Notch filter)陷波滤波器是一种能够抑制特定频率的信号,但对其他频率相对较不敏感的滤波器。
它的作用是在滤波器的中心频率处产生一个深度抑制的窄带,用于削弱或滤除特定的干扰信号。
陷波滤波器常用于音频、无线通信和图像处理等领域。
滤波器的原理基于信号的频率特性,利用电子器件的非线性特性或通过设计合适的电路,选择性地通过或抑制输入信号中不同频率的分量。
常见的滤波器电路包括电容、电感和电阻等元件的组合。
通过调整元件的数值、组合方式和连接方式,可以实现不同类型的滤波器。
滤波器的工作原理可以根据其类型细分为不同的方法,例如使用RC电路或LC电路来实现滤波效果。
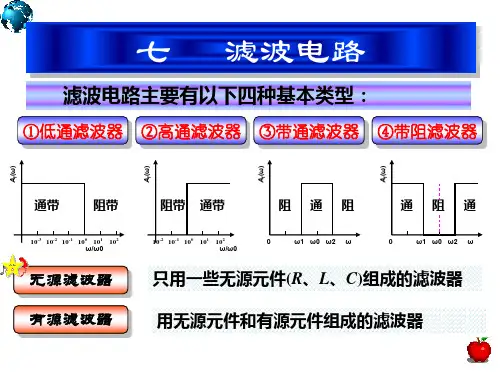

之阳早格格创做滤波器是一种只传输指定频段旗号,压造其余频段旗号的电路.滤波器分为无源滤波器与有源滤波器二种:①无源滤波器:由电感L、电容C及电阻R等无源元件组成②有源滤波器:普遍由集成运搁与RC搜集形成,它具备体积小、本能宁静等便宜,共时,由于集成运搁的删益战输进阻抗皆很下,输出阻抗很矮,故有源滤波器还兼有搁大与慢冲效率. 利用有源滤波器不妨超过有用频次的旗号,衰减无用频次的旗号,压造搞扰战噪声,以达到普及疑噪比或者选频的手段,果而有源滤波器被广大应用于通疑、丈量及统造技能中的小旗号处理.从功能去上有源滤波器分为:矮通滤波器(LPF)、下通滤波器(HPF)、戴通滤波器(BPF)、戴阻滤波器(BEF)、齐通滤波器(APF).其中前四种滤波器间互有通联,LPF与HPF间互为对于奇闭系.当LPF的通戴截行频次下于HPF的通戴截行频次时,将LPF与HPF相串联,便形成了BPF,而LPF与HPF并联,便形成BEF.正在真用电子电路中,还大概共时采与几种分歧型式的滤波电路.滤波电路的主要本能指标有通戴电压搁大倍数AVP、通戴截行频次fP及阻僧系数Q等.戴通滤波器(BPF)(a)电路图(b)幅频个性图1 压控电压源二阶戴通滤波器处事本理:那种滤波器的效率是只允许正在某一个通频戴范畴内的旗号通过,而比通频戴下限频次矮战比上限频次下的旗号均加以衰减或者压造.典型的戴通滤波器不妨从二阶矮通滤波器中将其中一级改成下通而成.如图1(a)所示. 电路本能参数通戴删益核心频次通戴宽度采用性此电路的便宜是改变Rf战R4的比率便可改变频宽而没有效率核心频次.例.央供安排一个有源二阶戴通滤波器,指标央供为:通戴核心频次通戴核心频次处的电压搁大倍数:戴宽:安排步调:1)采用图2电路.2)该电路的传输函数:本量果数:通戴的核心角频次:通戴核心角频次处的电压搁大倍数:与,则:图2 无限删益多路背反馈有源二阶戴通滤波器电路。

一阶带通滤波和二阶带通滤波摘要:一、引言二、一阶带通滤波1.定义与概念2.公式与性质3.应用场景三、二阶带通滤波1.定义与概念2.公式与性质3.应用场景四、总结正文:一、引言在数字信号处理领域,滤波技术是一种重要的方法,用于从噪声和干扰中提取有用信号。
带通滤波器是一种特殊的滤波器,能够通过特定的频率范围内的信号,而阻止其他频率范围内的信号。
本文将介绍一阶带通滤波和二阶带通滤波的相关知识。
二、一阶带通滤波1.定义与概念一阶带通滤波器是一种线性时不变滤波器,它的传递函数具有以下形式:H(s) = A(s) / (1 + ω_c / ω_n * A(s))其中,A(s)是截止频率为ω_c的sinc函数的传输函数,ω_n是噪声带宽。
2.公式与性质一阶带通滤波器的频率响应具有以下特点:- 在ω_c附近,频率响应呈现出一个峰值,表示信号能量集中在ω_c附近;- 在ω_n附近,频率响应逐渐下降,表示滤波器能够有效地抑制噪声。
3.应用场景一阶带通滤波器广泛应用于音频处理、图像处理、通信系统等领域,用于去除噪声和干扰,提高信号质量。
三、二阶带通滤波1.定义与概念二阶带通滤波器是一种具有两个截止频率的带通滤波器,它的传递函数具有以下形式:H(s) = (ω_c^2 / (s^2 + 2 * ζ * ω_c * s + ω_c^2)) * (1 / (1 + ω_n / ω_c))其中,ζ是阻尼比,ω_n是噪声带宽。
2.公式与性质二阶带通滤波器的频率响应具有以下特点:- 在ω_c附近,频率响应呈现出两个峰值,表示信号能量集中在ω_c附近;- 在ω_n附近,频率响应逐渐下降,表示滤波器能够有效地抑制噪声。
3.应用场景二阶带通滤波器在保留信号能量的同时,具有更好的噪声抑制性能,因此广泛应用于音频处理、图像处理、通信系统等领域。
四、总结本文介绍了一阶带通滤波和二阶带通滤波的定义、公式和应用场景。
带通滤波器是一种重要的信号处理技术,能够有效地去除噪声和干扰,提高信号质量。

四种滤波器的幅频特性本次实验是观察四种滤波器(低通、高通、带宽、带阻)的幅频特性,以加强对各种滤波器的功能认知。
本次实验我们选用的放大器为324型,其功能图如下所示:下面我们来逐步观察一下四种滤波器的特性。
1.低通滤波器其电路图如下所示: 图中,电阻R1=R2=R=10KΩ,C1=C2=0.01uF,Ro=0.8R=8Ω,Vcc+=+12V , Vcc-=-12V ,低通滤波器的传递函数20022)(ωαωω++=s s K s H p ,,其中2221102121001111;1;1C R K R R C C C R R RRK K ff p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数据w 。
=10000rad/s ,Kp =1.8,α=1.2,()()2202202225/2425/78.1)(ωωωωω+-=j H ;当w =0时)(ωj H =1.8,;w 增加且w<4800rad/s 时,)(ωj H 增加;当>4800rad/s 时,)(ωj H 减小,;w 趋近无穷时,)(ωj H 趋近于0。
此时wc=1.17rad/s 。
对于不同的α,滤波器的幅频特性也不相同对于实验中的低通,α=1.2,与1.25的相似,我们对于实验数据的测量如下:输入为100mV范围10~6kHz 输出不失真 绘出的幅频特性图如下: 2、高通滤波器 其电路图如下:其中R1=R2=R=10K,C1=C2=0.01uF,Ro=0.8R=8K 高通的传递函数为20022)(ωαω++=s s s K s H p ,()()2022022)(ωαωωωωω+-=p K j H ,1121202121001111;1;1CR K C C R C C R R RR K K f f p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数值后,Kp =1.8,W=0时)(ωj H =0;w<4800rad/s 时)(ωj H 增加;w 趋近于无穷时,)(ωj H 保持不变。

实验二 方波信号的分解与合成及相位、幅度对波形合成的影响(4学时)一 、实验目的1 、通过观察方波信号的分解与合成过程,理解利用傅利叶级数进行信号频谱分析的方法。
2 、了解频率失真和相位失真对方波信号合成波形的影响。
3、 加深理解相位对波形合成中的作用。
4、 加深理解幅值对波形合成的作用。
二 、实验内容1、通过观察方波信号的分解与合成过程,进一步理解信号的频谱分析方法。
2、了解频率失真和相位失真对方波信号合成波形的影响。
3、加深理解相位对波形合成中的作用。
4、加深理解幅值对波形合成的作用。
三、实验原理说明2.1电信号的分解任何电信号都是由各种不同频率、幅度和初相的正弦波迭加而成的。
对周期信号由它的傅里叶级数展开可知,各次谐波为基波频率的整数倍。
而非周期信号包含了从零到无穷大的所有频率成分,每一频率成分的幅度均趋向无限小。
如图4-1所示方波信号的傅里叶级数展开式为 )5sin 513sin 31(sin 4)( +++=t t t A t f ωωωπ (2-1) 其中Tπω2=为方波信号的角频率。
图2-1 方波信号由式(2-1)可知,方波信号中只含奇次谐波的正弦分量。
通过一选频网络可以将方波信号中所包含的各次谐波分量提取出来。
本实验采用有源带通滤波器作为选频网络,共5路。
各带通滤波器的B W =2Hz ,如图2-2所示。
图2-2带通滤波器 u iu 5u 4 u 3 300Hz 400Hz500Hz将被测信号加到选频网络上,从每一带通滤波器的输出端可以用示波器观察到相应频率的谐波分量。
本实验采用的被测信号为100Hz 的方波,通过各滤波器后,可观察到1、3、5次谐波,如图2-3。
而2、4次谐波在理想情况下应该无输出信号,但实际上方波可能有少量失真以及受滤波器本身滤波特性的限制而使偶次谐波分量未能达到理想的情况。
方波激励方波基波方波三次谐波方波五次谐波图2-3 方波的1、2、3次谐波实验电路图2.2.1电路框图图2-4电路框图 由双运放LM324组成带通滤波电路(B W 约2Hz )和射随器;三极管9013组成移相电路,起到相位补偿的作用。

二阶带通滤波器引言滤波器是信号处理中常用的工具,它可以通过改变信号的频谱来实现信号的处理和分析。
在滤波器的分类中,二阶带通滤波器是一种常见且有实际应用的滤波器。
本文将介绍二阶带通滤波器的基本概念、设计方法以及其在信号处理中的应用。
一、二阶带通滤波器的基本概念1.1 二阶滤波器的定义二阶滤波器指的是滤波器的阶数为2的滤波器。
阶数表示滤波器对信号的响应能力,阶数越高,滤波器对信号的处理能力越强。
1.2 带通滤波器的定义带通滤波器是指在一定频率范围内放行信号,而将其他频率范围内的信号抑制掉的滤波器。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联而成。
1.3 二阶带通滤波器的特性二阶带通滤波器具有以下特性:•适用于音频和语音处理等应用;•可以选择滤波器的中心频率、带宽和衰减等参数;•可以实现有源或无源滤波器,适应不同的系统需求;•具有较好的相位响应和幅频特性。
二、二阶带通滤波器的设计二阶带通滤波器的设计过程包括确定滤波器的频率响应和参数。
2.1 选择滤波器类型常见的二阶带通滤波器类型有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
不同的滤波器类型具有不同的特性,选择适合应用场景的滤波器类型是设计过程的第一步。
2.2 确定中心频率和带宽根据需要滤波的信号频率范围,确定带通滤波器的中心频率和带宽。
中心频率是指带通滤波器放行信号的中心频率,带宽是指带通滤波器放行信号的频率范围。
2.3 设计滤波器响应根据选择的滤波器类型和中心频率、带宽的要求,设计带通滤波器的频率响应。
常用的设计方法有频域法和时域法等。
2.4 参数调整和优化根据设计的频率响应,对滤波器的参数进行调整和优化,以满足实际应用的需求。
三、二阶带通滤波器的应用二阶带通滤波器在信号处理中具有广泛的应用。
以下是二阶带通滤波器的一些典型应用:3.1 音频处理在音频处理中,二阶带通滤波器可应用于语音增强、音频均衡和音效处理等环节。
通过控制滤波器的中心频率和带宽等参数,可以选择性地增强或抑制特定频率的音频信号。
二阶带通滤波的标准形式二阶带通滤波器是一种常用的信号处理工具,可以用于滤除不需要的频率成分,保留感兴趣的频率范围。
它的标准形式是一种常见的表示方式,可以方便地描述滤波器的特性和参数。
二阶带通滤波器的标准形式可以表示为:H(s) = K * (s^2 + ω0/Q * s + ω0^2) / (s^2 + ω0/Q * s + ω0^2)其中,H(s)是滤波器的传递函数,s是复频域变量,K是增益系数,ω0是中心频率,Q是品质因数。
在这个标准形式中,分子和分母都是二次多项式,分别表示滤波器的分子传递函数和分母传递函数。
通过调整K、ω0和Q的值,可以实现不同的滤波器特性。
K是增益系数,用于调整滤波器的增益。
通过改变K的值,可以增强或减弱滤波器的输出信号。
ω0是中心频率,决定了滤波器的中心频率位置。
通过调整ω0的值,可以改变滤波器的中心频率,从而选择需要保留的频率范围。
Q是品质因数,决定了滤波器的带宽。
Q的值越大,滤波器的带宽越窄,选择的频率范围越小;Q的值越小,滤波器的带宽越宽,选择的频率范围越大。
通过调整这三个参数的值,可以实现不同的滤波器特性。
例如,当K=1、ω0=1000Hz、Q=0.5时,滤波器可以实现一个中心频率为1000Hz,带宽为2000Hz的带通滤波器。
二阶带通滤波器的标准形式在信号处理领域得到了广泛的应用。
它可以用于音频处理、图像处理、通信系统等领域。
通过调整滤波器的参数,可以实现不同的滤波效果,满足不同应用的需求。
总之,二阶带通滤波器的标准形式是一种常见的表示方式,可以方便地描述滤波器的特性和参数。
通过调整增益系数、中心频率和品质因数的值,可以实现不同的滤波器特性,满足不同应用的需求。
在信号处理领域,二阶带通滤波器被广泛应用于音频处理、图像处理、通信系统等领域。
目录摘要 (2)第一章前言 (3)1.1专业设计任务及要求 (3)1.2M ATLAB简介 (3)1.3M ATLAB下的SIMULINK简介 (3)1.4通信系统模型 (4)第二章 FSK调制解调原理及MATLAB仿真 (5)2.1FSK信号产生原理 (5)2.1.1 2FSK信号的产生: (5)2.1.2 2FSK信号的频谱特性: (6)2.2FSK调制原理 (6)2.3FSK解调原理 (8)2.4仿真思路 (8)2.5仿真程序 (9)2.6输出波形及结果分析 (11)结果分析 (16)第三章用SIMULINK仿真FSK调制解调 (17)3.1用S IMULINK仿真FSK调制 (17)3.1.1 Simulink仿真FSK调制框图 (17)3.1.2参数设置 (17)3.1.3仿真波形 (18)3.2用S IMULINK仿真FSK解调 (20)3.2.1 Simulink仿真FSK解调框图 (20)3.2.2参数设置 (20)3.2.3仿真波形及分析 (22)第五章结论 (24)参考文献 (25)摘要本设计是基于MATLAB来实现调制与解调的仿真。
主要设计思想是利用MATLAB和MATLAB集成环境下Simulink的仿真平台,这个强大的数学软件工具方便快捷灵活的功能实现数字调制解调中的频率调制与解调的设计。
首先,先阐述了通信系统的模型,以及FSK信号的产生原理,调制与解调的基本原理。
然后分别设计了FSK调制框图和解调框图,实现了Matlab程序仿真和Simulink系统仿真,在解调部分各信号都是采用相干解调、非相干解调的方法,同时在没有噪声的情况下和存在噪声的基础上分别对信号进行调制与解调,并且在解调的过程中都对整个系统的误码率在display模块中有所显示,得到了比较准确的结果,进而在存在噪声和不存在噪声时进行对比,对结果进行了详尽而且准确的分析。
最后给出了一些结论:信道中的噪声大小严重影响通信质量。
目录1技术要求 (1)2基本原理 (1)2.1 2ASK定义 (1)2.2 2ASK的调制 (2)2.3 2ASK的解调 (3)2.4 2ASK功率谱密度 (4)2.5 眼图 (5)3 建立模型描述 (5)3.1 SystemView方案 (5)3.2 Simulink方案 (6)4 功能模块分析或源程序代码 (8)4.1 SystemView功能模块分析 (8)4.2 Simulink功能模块分析 (12)5 调试过程及结论 (13)5.1 SystemView调试过程及结论 (13)5.2 Simulink调试过程及结论 (18)6 心得体会 (20)7 参考文献 (21)二进制数字频带传输系统设计——2ASK系统1技术要求设计一个2ASK数字调制系统,要求:(1)设计出规定的数字通信系统的结构;(2)根据通信原理,设计出各个模块的参数(例如码速率,滤波器的截止频率等);(3)用Matlab或SystemView 实现该数字通信系统;(4)观察仿真并进行波形分析;(5)系统的性能评价。
2基本原理2.1 2ASK定义振幅键控是正弦载波的幅度随着数字基带信号而变化的数字调制,当数字基带信号为二进制时,则为二进制振幅键控.。
设发送的二进制符号序列由0、1序列组成,发送0符号的概率为P,发送1符号的概率为1-P,且相互独立。
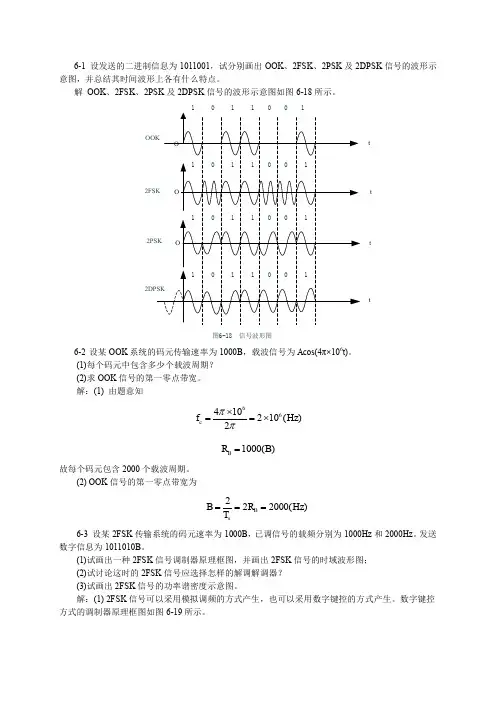
该二进制符号序列可表示S(t)=其中:⎩⎨⎧=P P a n -出现概率为出现概率为110Ts 是二进制基带信号时间间隔,g(t)是持续时间为Ts 的矩形脉冲:则二进制振幅键控信号可表示为:t nT t g a t S c n s n ASK ωcos )()(2⎥⎦⎤⎢⎣⎡-=∑t t S c ωcos )(= 二进制振幅键控信号时间波型如图2-1所示,可以看出2ASK 信号的时间波形S2ASK(t)随二进制基带信号s(t)通断变化,所以又称为通断键控信号(OOK 信号)。
图2-1 2ASK 信号时域波形2.2 2ASK 的调制二进制振幅键控信号的产生方法有两种。
第六次试验生物医学工程班3010202294吴坤亮一、实验内容:搭建滤波器(低通、高通、带通、带阻、全通)加以分析,搭建三运放差分滤波器,并加以分析。
二:(滤波器)简单低通滤波器简单高通滤波器由上图搭建电路,接入负载f H、f H会发生变化,为了减小负载效应,可以在输出端串接一个电压跟随器,因为电压跟随器的输入电阻很大。
(以下电路在此基础构造)1、低通滤波器:电路图如下:f H=1/(2πRC)=1KHZ,放大倍数K=(1+R f/R1)=4.以下图均为(蓝线为输入,黄线为输出)50HZ CH1 CH2200HZ CH1 CH2500HZ CH1 CH2900HZ CH1 CH2 由以上波形比例可知,实验成功。
2、高通滤波器:f l=1/(2πRC)=1KHZ,放大倍数K=(1+R f/R1)=4.200HZ CH1 CH2500HZ CH1 CH21000HZ CH1 CH25KHZ CH1 CH230KHZ CH1 CH275KHZ(失真)CH1 CH2高通电路上限是有限制(不是很理解),正常增益内输入输出信号存在相移。
(以下带通、带阻可以通过低通带通的电路构造出来,我做了尝试误差较大,这里不再试用)3、带通滤波器:(中心频率)f o=1/(2πc(R1R2)1/2)=2022HZ,f BW=1/(R2C)=1000HZ(2.7HZ1.00vpp)数据图如下:4、带阻滤波器:它常用于通信和生物医学仪器中以清除无用的频率分量(如50HZ的电源频率等)f o=1/2πRC=4.423KHZ。
以下为不同频率下的波形:f=1KHZf=4.432KHZf=45KHZ实验测量数据如下:5、全通滤波器:输入信号所有无衰减地通过的一种滤波器。
但它对不同的频率分量提供不同的相移。
传输线(如电话线)常常会引起输入信号的相位移动,故全通滤波器称为相位校正器或延迟均衡器。
∠H(jw)=-2arctan(wRC)以下为调节R所得位移波形:R=834Ω R=19.57kΩR=26.9Ω相位移动明显二、三运放差分滤波器电路图如下:电路分析:差模增益:Avd=(R1+R2+R6)/R6*(R4/R3)=17共模增益:Avc=Rw/( R5+Rw)* (R3+R4)/ R3- R4/R3=0;(R w=16K)所以电路的共模抑制比CMRR为:CMRR= Avd/ Avc=[(R1+R2+Rw)/ Rw*(R4/R3)]/ [Rw/( R5+Rw )* (R3+R4)/ R3- R4/R3]=无穷大(理论上)1、首先调节共模抑制,使其简直最低方法(将两输入端接相同信号)(输入1KHZ、1vpp)(以下为输出波形和数据)R=24.1KR=19.6KR=16K(最好)R=11.96K (又开始变大)R=6.74K(可知R w=R4=16K,共模抑制比最大,实验与理论最大程度的吻合)以下为Vi1接正弦信号,Vi2接地2、输入50mvpp观察频率对其影响(以下为输出)f=50HZf=5KHZf=10.5KHZ(开始发生变化)f=50KHZf=500KHZf=1M(在示波器上显示为失真导出图片只是它的某一帧)3、5KHZ下不同伏值对其影响(蓝线为输入、黄线为输出)30mvpp(无放大)35mvpp40mvpp(很好)50mvpp(很好)160mvpp(失真)600mvpp8vpp以下图形为Vi1用手捏住做输入其他不变(娱乐):。
巴特沃斯二阶带通滤波器simulink实现巴特沃斯二阶带通滤波器的设计和实现在信号处理领域中是非常常见的。
本文将一步一步地回答如何使用Simulink工具来实现巴特沃斯二阶带通滤波器。
第一步:理解巴特沃斯二阶带通滤波器的原理巴特沃斯二阶带通滤波器是一种常用的滤波器类型,可以通过选择适当的截止频率来过滤出特定频率范围内的信号。
它的传递函数表达式为:H(s) = K/[(s^2 + s/Q + 1)]其中,K是增益系数,s是复频域变量,Q是品质因数。
巴特沃斯二阶带通滤波器的特点是通过选择合适的Q值和截止频率来实现带通滤波的效果。
第二步:创建Simulink模型打开MATLAB软件并启动Simulink工具。
然后,创建一个新模型。
第三步:添加输入信号源在模型中添加一个信号源,用于提供待滤波的输入信号。
可以选择Sin波形作为输入信号。
在Simulink库浏览器中,找到"Sources"文件夹,在其中选择"Sine Wave"模块并拖动到模型中。
第四步:添加巴特沃斯二阶带通滤波器在模型中添加一个巴特沃斯二阶带通滤波器。
在Simulink库浏览器中,找到"Continuous"文件夹,在其中选择"Transfer Fcn"模块并拖动到模型中。
双击该模块,打开其参数设置窗口。
在参数设置窗口中,将传递函数的表达式输入框中的表达式设置为H(s) =K/[(s^2 + s/Q + 1)]。
设置增益系数K和品质因数Q的值。
这些值可以根据实际需求进行调整。
第五步:连接信号源和滤波器将信号源模块的输出端口连接到巴特沃斯二阶带通滤波器的输入端口。
在模型中拖动一个连接线,从信号源的输出端口连接到滤波器的输入端口。
第六步:添加输出显示在模型中添加一个显示模块,用于显示滤波器输出的信号。
在Simulink库浏览器中,找到"Sinks"文件夹,在其中选择"Scope"模块并拖动到模型中。