当前位置：文档之家 › 卫生统计学案例分析

卫生统计学案例分析

  • 格式：ppt
  • 大小：447.50 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

第七版_卫生统计学案例讨论2讲述PPT课件

第七版_卫生统计学案例讨论2讲述PPT课件
1,建立检验假设，确定检验水准 H0：即两种抗原检出率阳性概率相等 H1：即两种抗原检出率阳性概率不相等 α=0.05 2，计算检验统计量 观察数据可知b+c<40需要做连续性校正，
16
故：
1 2bc1231 1123.5 bc 311
3，确定P值，作出推断 自由度为1，查x2临界表，x20.050,1=3.84.可 知p>0.05.在α=0.05的水准上接受H0，差别无统 计学意义，两种抗原检出率阳性概率相等。
• 疗效 Z=-4.41 P=0.659 • 住院日 Z=-1.921 P=0.55 • 费用 Z=-1.549 P=0.121 结论
不能认为两年的疗效、住院日及费用不同 ，即；两年的疗效、住院日及费用的差别均 无统计学意义。
7
案例8-2
某研究对140名乙型肝炎患者和ＨＢｓ Ａｇ携带者的唾液中乙肝病毒的前Ｓ１抗原 分别与ＨＢｓＡｇ，ＨＢｅＡｇ和前Ｓ２抗 原检出率进行差别分析，
分析
• 1.该资料为计数资料。 • 2.该资料中的指标分组为有序变量，即定型
变量。 故
X2检验用于检验两个率之间的差别是否有统 计学意义，不适用于有序变量的计数资料。 对于有序的变量， X2检验检验的结果只是说 明各组构成比的差异有无统计学意义。
4
正确检验方法
• 对于等级资料，在比较各组治疗等级时，用 秩和检验更为合适。
案例1 P165
2001—2002年医疗质量进行总体评价与比较，按分 层抽样方法抽取两年内牟冰患者1250例。20012002年间 患者年龄构成与病情的差别没有统计学意义，三项评价 指标分为疗效，住院日，费用。等级“很好，好，一般 ，差”的定义标准见表1-1，病人医疗质量各等级频数分 布见表1-2.

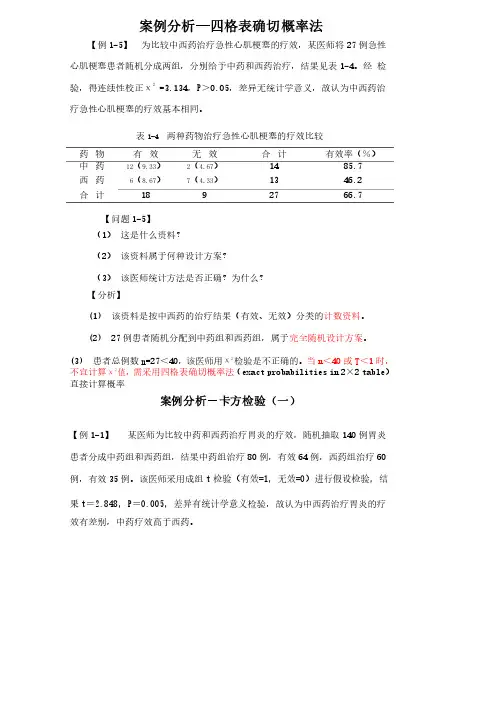
医学统计学案例分析2

医学统计学案例分析2

案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效，某医师将27例急性心肌梗塞患者随机分成两组，分别给予中药和西药治疗，结果见表1-4。

经检验，得连续性校正χ22=3.134，P＞0.05，差异无统计学意义，故认为中西药治疗急性心肌梗塞的疗效基本相同。

表1-4两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率（％）中药12（9.33）2（4.67）1485.7西药6（8.67）7（4.33）1346.2合计1892766.7【问题1-5】（1）这是什么资料？（2）该资料属于何种设计方案？（3）该医师统计方法是否正确？为什么？【分析】(1)该资料是按中西药的治疗结果（有效、无效）分类的计数资料。

该资料是按中西药的治疗结果（有效、无效）分类的计数资料完全随机设计方案。

(2)27例患者随机分配到中药组和西药组，属于例患者随机分配到中药组和西药组，属于完全随机设计方案(3)患者总例数n=27＜40，该医师用χ2检验是不正确的。

当n＜40或T＜1时，不宜计算χ2值，需采用四格表确切概率法（exact probabilities in2×2table）直接计算概率案例分析－卡方检验（一）【例1-1】某医师为比较中药和西药治疗胃炎的疗效，随机抽取140例胃炎患者分成中药组和西药组，结果中药组治疗80例，有效64例，西药组治疗60例，有效35例。

该医师采用成组t检验（有效=1，无效=0）进行假设检验，结果t＝2.848，P＝0.005，差异有统计学意义检验，故认为中西药治疗胃炎的疗效有差别，中药疗效高于西药。

【问题1-1】（1）这是什么资料？（2）该资料属于何种设计方案？（3）该医师统计方法是否正确？为什么？（4）该资料应该用何种统计方法？【分析】(1)该资料是按中西药疗效（有效、无效）分类的该资料是按中西药疗效（有效、无效）分类的二分类资料，即计二分类资料，即计数资料。

(2)随机抽取140例胃炎患者分成西药组和中药组，属于属于完全随机设完全随机设计方案。

第七版__卫生统计学_案例讨论2

第七版__卫生统计学_案例讨论2

1.91
12
n足 n过
12
838 58
v=k-1=3-1=2
查χ²界值表得0.25＜P＜0.50。
3.确定P值，做出推断
P早，足＜0.005，P早，过＜0.005 ，在α=0.05 的水准上，拒绝H0,接受H1，认为早产产妇和足 月产产妇、过期产产妇在产后一个月内泌乳量有 差别 0.25＜P足，过＜0.50 ，在α=0.05的水准上， 尚不能认为 足月产产妇和过期产产妇在产后一 个月内泌乳量有差别
1,建立检验假设，确定检验水准 H0：即两种抗原检出率阳性概率相等 H1：即两种抗原检出率阳性概率不相等 α=0.05 2，计算检验统计量 观察数据可知b+c>40不需要做连续性校正，
故：
1 2 (b c)2 (55 0)2 55 b c 55 0
3，确定P值，作出推断 自由度为1，查x2临界表，x20.005,1=7.88.可 知p<0.005.在α=0.05的水准上拒绝H0，差别有统 计学意义，两种抗原检出率阳性概率不相等。
)C
(395.21 539.83)2 23.07
993(993 1) ( 1 1 )0.04
12
n早 n过
12
97 58
v=k-1=3-1=2
查χ²界值表得P＜0.005。
x2 足,过
(R足 R过 )2 N (N 1) ( 1 1
)C
(505.82 539.83)2 993(993 1) ( 1 1 )0.40
10
60
住院日 2001
180
250
130
40
2002
200
310
120
20
费用
2001

卫生统计学案例

卫生统计学案例

卫生统计学案例引言卫生统计学是一门重要的研究领域，通过对卫生数据的收集、整理和分析，可以为公共卫生政策提供科学依据。

本文将通过一个卫生统计学案例，深入探讨如何使用统计方法分析健康数据，为决策者提供有关公共卫生的信息。

数据收集在卫生统计学中，数据收集是至关重要的一步。

我们需要从可靠的来源获取数据，并确保数据的准确性和完整性。

对于本次案例，我们以一座城市的健康调查数据为例进行分析。

数据整理数据整理包括数据清洗、数据转换和数据标准化等过程。

在清洗过程中，需要删除重复数据、处理缺失值和异常值等。

在转换过程中，可能需要将数据转换为统一的单位或变量类型。

在标准化过程中，可以使不同数据源之间的数据可以进行比较和分析。

数据分析在数据分析阶段，我们可以使用不同的统计方法来探索数据，揭示数据背后的趋势和关联性。

下面是一些常用的统计方法：描述统计描述统计是对数据进行总结和描述的方法。

通过计算均值、标准差、中位数等指标，我们可以了解数据的分布情况和集中趋势。

假设检验假设检验是通过对数据进行统计推断，判断某个假设是否成立。

在卫生统计学中，假设检验可以用来判断两组数据之间是否存在显著差异，或者某个因素对健康影响是否显著。

回归分析回归分析用于研究因变量和一个或多个自变量之间的关系。

在卫生统计学中，回归分析可以用来探究不同因素对人群健康状况的影响，并预测未来趋势。

结果与讨论在本案例中，我们对一座城市的健康调查数据进行了整理和分析。

以下是我们的主要发现：1.饮食习惯与慢性病发病率之间存在显著相关性。

人们饮食不健康的程度越高，慢性病发病率也越高。

2.在不同年龄段中，糖尿病发病率呈现明显的上升趋势。

这提示我们在预防和治疗糖尿病方面需要加大力度。

3.女性与男性在心血管疾病发病率方面存在差异。

女性相对较少患心血管疾病，但一旦患病，症状和疾病进展可能更为严重。

这些结果与我们的假设相符，并对公共卫生政策制定者具有重要意义。

我们应该加强对健康饮食的宣传和教育，以及加大对糖尿病和心血管疾病的防治力度。

卫生统计学案例分析(4-8章)‘’‘’

卫生统计学案例分析(4-8章)‘’‘’
编号 病人 1 2 3 4 5 6 7 8 9 10 11 12 13
健康人 2.7 2.2 4.1 4.3 2.6 1.9 1.7 0.6 1.9 1.3 1.5 1.7 1.3
3.6 3.4 3.7 5.4 3.6 6.8 4.7 2.9 4.8 5.6 4.1 3.3 4.3
（1）请用excel计算健康人和Ⅲ度肺气肿病人痰中抗胰蛋白酶 含量的均数和标准差（请注明步骤）。 （2）欲比较两组抗胰蛋白酶含量是否有差异，可以采用哪些统 计方法？用这些方法的条件是什么？ （3）该研究者的统计处理方法是否正确？为什么？ （4）比较两组抗胰蛋白酶含量是否有差异，请写出分析步骤， 并下结论。
• （1）这是什么资料？该资料属于何种设计方案？ • （2）拟比较三组小鼠细胞免疫功能是否有差异，可以采用哪些 统计方法？用该方法的条件是什么？思想是什么？请写出三组 小鼠细胞免疫功能比较的分析步骤，并下结论。 • （3）如果想知道党参组和黄芪组小鼠细胞免疫功能是否有差异， 可以采用哪些统计方法？ • （4）该研究者的统计处理方法是否正确？为什么？
案例十
• 分别测得13名健康人和13名Ⅲ度肺气肿病人痰中抗胰蛋白酶含 量(g/L)如下表。某研究者根据此资料先计算差值并进行正态性 检验，服从统000,故认为 Ⅲ度肺气肿病人痰中抗胰蛋白酶含量高于健康人。 • 表2 13名健康人和13名Ⅲ度肺气肿病人痰中抗胰蛋白酶含量 (g/L)
案例六
为研究不同药物对肥胖患者的疗效，将BMI≥28的肥胖患 者随机分成两组，每组10人，测得他们服药前及服药2个月后 体重的变化（下表）。试评价：①A、B两种药物对肥胖患者是 否有效。②A、B两种药物的疗效有无差别。
两组肥胖患者服药前后体重变化/kg 药 物 A 服药前 服药后 B 服药前 服药后 1 75.6 73.0 69.4 60.8 2 61.2 60.2 89.9 95.5 3 67.8 63.6 66.8 61.6 4 77.2 72.0 63.4 62.0 5 73.2 74.6 70.0 69.4 6 65.4 60.8 86.6 78.0 7 80.0 69.4 90.4 71.0 8 74.4 77.4 74.8 76.6 9 82.6 79.6 67.4 58.2 10 68.6 63.4 84.4 75.4

卫生统计学案例

卫生统计学案例

以下是一则卫生统计学案例：
某市区卫生局对该区域内的糖尿病患者进行了一次调查，共有1000人参与了调查。

调查结果如下：
1.男性患者占总患者人数的60%，女性患者占40%。

2.年龄在40岁以下的患者占总患者人数的30%，年龄在40岁至60岁之间的患者占总患者人数的50%，年龄在60岁以上的患者占总患者人数的20%。

3.有高血压病史的患者占总患者人数的40%，有心脏病史的患者占总患者人数的30%，有肾病病史的患者占总患者人数的20%，有视网膜病变的患者占总患者人数的10%。

根据以上数据，可以进行如下的卫生统计学分析：
1.男性患者比女性患者多，说明男性更容易患糖尿病，需要针对男性进行更多的预防宣传和治疗。

2.年龄在40岁至60岁之间的患者最多，说明这个年龄段的人更容易患糖尿病，需要针对这个年龄段的人进行更多的预防宣传和治疗。

3.有高血压病史、心脏病史、肾病病史的患者比例较高，说明这些疾病与糖尿病有一定的关联性，需要针对这些疾病的患者进行更多的糖尿病筛查和预防宣传。

同时，对于已经患有糖尿病的患者，还需要加强针对这些疾病的治疗和管理。

医学统计学案例分析.


• Pearson积矩相关系数，是定量描述两个变量间线性关系密切程度和相关方向的统计 指标。
• 适用于等级资料的一些统计学方法：非参数统计的秩和检验、有序变量的Logistic回 归分析、线性趋势卡方分析等。
• (2).应该使用多组有序变量资料的秩和检验。
• (3).分析：①.建立假设检验，确定检验水准
住院日、费用。等级“很好、好、一般、差”的定义见表一，病人医 疗质量各等级频数分布见下表二。
指标
表一 很好、好、一般、差的标准
很好
好
一般
疗效
治愈
显效
好转
住院日（天）
≤15
16-20
21-25
差 无效 ＞25
费用（元）
≤1400 1400-1800 1800-2200
＞2200
• 1.本题的研究员用卡方检验对本题做了统计推断而我们知道卡方检验 用于计数或计量资料，而本题是一个等级资料。
b c 2 10
• 以上三个值对应的p值见表，请讨论是否正确？
• 分析该资料得出本案例是配对R*R列连及资料的卡方检验，由于他组内是配对 设计，而组间是多个样本配对设计，因此我们将R*R联表分割成为多个四格表 ，即分割或配对2*2列联表资料，然后进行卡方检验。对于配对2*2列联表资 料的卡方检验，其计算公式为
释疑：原作者目的是为了观察s1a在各种疾病中的表达是否 存在差异。根据资料的类型应选用一般χ2检验进行统计分 析，但是由于理论频数<5的格子数大于总格子数的1/5，因 而并不适合直接进行χ2检验，如果直接进行fisher的精确检
•
验，由于计算量太大，程序长时间运行不能得出
•
结果来。
• 因而考虑根据专业知识，对表中的数据进行合并，CSG和CAG均属于胃 炎，经fisher的精确检验，CSG、A、IM、Dys的各基因表达构成之间的 差别无显着意义，因而将各行的数据求和。同样道理GU和DU均属于溃 疡，检验后将各行的数据也加在一起，重新整理成表，见表2。

卫生统计学案例分析


谢 谢！
芪两组差异没有统计学意义（P＞0.05），其余两组间差异有统 计学意义（P＜0.05）。
• 对照组 14 10 12 16 13 14 12 10 13 9 党参组 21 24 18 17 22 19 18 23 20 18 黄芪组 24 20 22 18 17 21 18 22 19 23
• （1）这是什么资料？该资料属于何种设计方案？ • （2）拟比较三组小鼠细胞免疫功能是否有差异，可以采用哪些
•（4）该研究者采用的统计方法是否恰当？为什么？
案例六
某地随机抽样调查了部分健康成人的血红蛋白含量 （g/L），结果见表1.
• 表1 某地健康成人的血红蛋白含量（g/L）
性别 例数
均数 标准差 标准值
男
360
134.5 7.21 140.2
女
255
117.6 10.2 124.7
（1）有人认为该地男女性血红蛋白含量均低于上表的标准值（若 测定方法相同）且男性血红蛋白含量低于女性，你是否同意该结论？ （2）可采用什么方法比较男和女血红蛋白含量是否有差异？如果 男和女血红蛋白含量有差异，是否有实际意义？ （3）请制定该人群的参考值范围？制定参考值范围需要注意什么？ 总体均数的置信区间和参考值范围有何区别？
统计方法？用该方法的条件是什么？思想是什么？请写出三组 小鼠细胞免疫功能比较的分析步骤，并下结论。 • （3）如果想知道党参组和黄芪组小鼠细胞免疫功能是否有差异， 可以采用哪些统计方法？ • （4）该研究者的统计处理方法是否正确？为什么？
案例三
• 分别测得13名健康人和13名Ⅲ度肺气肿病人痰中抗胰蛋白酶含 量(g/L)如下表。某研究者根据此资料先计算差值并进行正态性
检验，服从统计后应用配对t检验：t=-5.276,P=0.000,故认为

第七版 卫生统计学 课后案例讨论1


回顾：
1.poisson分布的特征：有其参数λ唯一确定。 2.poisson分布和二项分布的一个前提条件是事件 发生的概率不变，每 个事件的发生与否是相 互独立的。 3. 传染性疾病首列出现后便成为传染源，会增加 该区后续病例出现的概率，且随着病例的增加， 其他易感人群感染的概率也会增加，因此传染病 的病例数的分布不能看做二项分布和poison 分布。
检
验
1，建立假设检验，确定检验水准 H0：1
2
H1：三个总体方差不全相等
= 2 = 3
2
2（即三个总体方差全相等）
α=0.10
2.计算检验统计量 2
= 13.18 v=2
3.确定P值，做出推断。 以自由度V=2，查附表8的 ×2 界值表，得 P<0.005,按α=0.10的水准，拒绝H0，接受H1,即三 个总体方差不全相等。
案例七 （7-2） P142
对该资料进行分析，可以得出该资 料属于计量资料，该统计学设计属于 完全随机设计资料，并使用方差分析 法进行了统计分析。
• • • •
方差分析适用条件： 1.各样本是来自正态分布的总体 2.两个样本是相互独立的随机样本 3.样本均数所在总体方差具有齐性
2 • 故我们首先因对资料进行方差齐性的
案例一 P78
2000年某地艾滋病病毒的感染率为10/10万，该地10万人口， 2001年感染 艾滋病病毒的人口人数为17人，有人说，该地2001 年总体上艾滋病病毒感染率与200年持平，是这样的话，该地 2001年感染艾滋病病毒的人数为17人 这种情况发生的概率为
P ( x 17) e
7
（2）计算统计检验量 n1=8,X1=19.75 S1=8.35 n2=8,X2=51.88 S1=19.63 t=

医学统计学案例分析

医学统计学案例分析医学统计学是应用数理统计学原理和方法对医学研究进行分析的学科。

下面介绍一个医学统计学案例分析。

某医院开展了一项针对心脏病患者的新药临床实验。

实验分为两组，A组为接受新药治疗的患者，B组为接受常规治疗的患者。

为了评估新药的疗效，研究者采集了每组患者的治疗前和治疗后的心脏功能数据。

实验结果如下表所示：组别治疗前心脏功能治疗后心脏功能A组 70 85B组 65 80为了分析和评估新药的疗效，可以采用配对样本T检验进行统计分析。

配对样本T检验是一种适用于两个相关样本的统计检验方法。

首先，可以计算出每组患者的差值（治疗后心脏功能-治疗前心脏功能）：差值A组 = 85-70 = 15差值B组 = 80-65 = 15接下来，计算这些差值的平均值和标准差：平均值差值A组 = 15/1 = 15平均值差值B组 = 15/1 = 15标准差差值A组= sqrt(Σ(xi-平均值差值A组)²/(n-1)) = 0标准差差值B组= sqrt(Σ(xi-平均值差值B组)²/(n-1)) = 0然后，可以计算T值：T = (平均值差值A组-平均值差值B组)/sqrt((标准差差值A组²/样本容量)+(标准差差值B组²/样本容量))T = (15-15)/sqrt((0²/1)+(0²/1)) = 0最后，根据自由度和显著性水平可以查找T值对应的临界值。

假设显著性水平为0.05，查表可得临界值为1.96。

由于计算得到的T值为0，小于临界值1.96，所以可以得出结论：新药治疗和常规治疗在心脏功能上没有显著差异。

通过以上医学统计学案例分析，我们可以对新药的疗效进行客观评估，为临床医学提供科学依据。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6（8.67）
两种药物治疗急性心肌梗塞的疗效比较 无 效 2（4.67）
7（4.33）
合 计 14 13 27
有效率（％） 85.7 46.2 66.7
18
9
【问题 1-5】 （1） 这是什么资料？ （2） 该资料属于何种设计方案？ （3） 该医师统计方法是否正确？为什么？
【分析】 (1) 该资料是按中西药的治疗结果（有效、无效）分类的计数资料。 (2) 27 例患者随机分配到中药组和西药组，属于完全随机设计方案。 (3) 患者总例数 n=27＜40， 该医师用χ 2 检验是不正确的， 需采用四格表确切概率法 （exact probabilities in 2×2 table） 直接计算概率
• 不正确
案例五
某地随机抽样调查了部分健康成人的血红蛋白含量 （g/L），结果见表1. • 表1 某地健康成人的血红蛋白含量（g/L） 性别 例数 均数 标准差 标准值 男 360 134.5 7.21 140.2
女
255
117.6
10.2
124.7
（1）有人认为该地男女性血红蛋白含量均低于上表的标准值（若 测定方法相同）且男性血红蛋白含量低于女性，你是否同意该结论？ （2）可采用什么方法比较男和女血红蛋白含量是否有差异？如果 男和女血红蛋白含量有差异，是否有实际意义？ （3）请制定该人群的参考值范围？制定参考值范围需要注意什么？ 总体均数的置信区间和参考值范围有何区别？
编号 病人 1 2 3 4 5 6 7 8 9 10 11 12 13
健康人 2.7 2.2 4.1 4.3 2.6 1.9 1.7 0.6 1.9 1.3 1.5 1.7 1.3
3.6 3.4 3.7 5.4 3.6 6.8 4.7 2.9 4.8 5.6 4.1 3.3 4.3
（1）请计算健康人和Ⅲ度肺气肿病人痰中抗胰蛋白酶含量的均 数和标准差（请注明步骤）。 （2）欲比较两组抗胰蛋白酶含量是否有差异，可以采用哪些统 计方法？用这些方法的条件是什么？ （3）该研究者的统计处理方法是否正确？为什么？ （4）比较两组抗胰蛋白酶含量是否有差异，请写出分析步骤， 并下结论。
• 健康人：均数2.15，标准差1.06；Ⅲ度肺 气肿病人：均数4.32，标准差1.11 • 两独立样本t检验、两独立样本秩和检验， 应用条件略 • 该研究者结论错误，首先应该做正态及方 差齐性检验。满足正态方差齐，可用两独 立样本t检验做统计推断。 • 服从正态、方差齐，用两独立样本t检验做 统计推断。T=-5.09,P=0.000,差异有统计 学意义。
卫生统计学案例分析
2015.05
案例一
• 中药治疗再生障碍性贫血，治疗前后血红蛋白结果 见下面数据。某医生计算出治疗前后的差值，均数 为35，故认为治疗后血红蛋白含量高于治疗前。
• • • • • • • •
患者编号 1 2 3 4 5 6 7 8 9 治疗前 68 65 55 75 50 70 76 65 72 治疗后 128 82 80 112 125 110 85 80 105 （1）该资料属于什么资料类型？ （2）该资料属于何种设计方案？ （3）比较治疗前后血红蛋白是否有差别可采用什么统计方法？ 用这些方法的条件是什么？ （4）该医生的结论是否正确？为什么？ （5）请比较治疗前后血红蛋白是否有差别，写出分析步骤， 并下结论。
案例七
谢 谢！
• 定量资料，完全随机设计 • 完全随机设计方差分析，多个独立样本秩 和检验。应用条件略。思想略。经检验服 从正态分布，方差齐，F=25.49，P=0.000. • 多个样本均数的两两比较，LSD,SNK • 不正确，方法错误。三组均数比较用t检验 增大犯一类错误概率。
案例三
• 分别测得13名健康人和13名Ⅲ度肺气肿病人痰中抗胰蛋白酶含 量(g/L)如下表。某研究者根据此资料先计算差值并进行正态性 检验，服从统计后应用配对t检验：t=-5.276,P=0.000,故认为 Ⅲ度肺气肿病人痰中抗胰蛋白酶含量高于健康人。 • 表2 13名健康人和13名Ⅲ度肺气肿病人痰中抗胰蛋白酶含量 (g/L)
案例二
• 研究2种单味中药对小鼠细胞免疫功能的影响，并设一个空白对 照组，将30只小鼠随机分为3组，每组10只，雌雄各半，用药15 天后，测定E-玫瑰结形成率（%），结果如下。研究者对该资料 采用了两样本均数的t检验进行两两比较，得结论为除党参与黄 芪两组差异没有统计学意义（P＞0.05），其余两组间差异有统 计学意义（P＜0.05）。 • 对照组 14 10 12 16 13 14 12 10 13 9 党参组 21 24 18 17 22 19 18 23 20 18 黄芪组 24 20 22 18 17 21 18 22 19 23
案例四
• 已知正常成年男子血红蛋白均值为 140g/L ，今随机调 查某厂成年男子 60 人，测其血红蛋白均值为 125g/L ， 标准差15g/L。故认为该厂成年男子血红蛋白均值低于 一般成年男子。 • （1）该结论是否正确？为什么？ • （2）有研究者根据该资料估计该地成年男子血红蛋白 均值为125g/L，该结论是否正确？为什么？ • （3）解决此类问题可采用哪些统计分析方法？这些方 法有什么区别和联系？ • （4）拟比较该厂成年男子血红蛋白均值与一般成年男 子是否有差异，请写出分析步骤，并下结论。
• 结论不完全正确，研究者想通过抽样调查了解总 体特征，但是没有考虑抽样误差，直接用样本均 数作为总体的估计值，用单样本t检验或通过置信 区间回答。 • 假设检验、两组大样本均数比较，用u检验，假设 检验只能说明有无统计学意义，不能说明实际意 义。 • 制定参考值范围需要注意： 1、所谓正常人指的是排除了影响所研究指标的疾病 和有关因素的同质人群。 2、选择有足够大的人群作为调查对象 样本数理足够大 3、确定单侧还是双侧正常值范围；选择适当的百分 界限，选择正确的方法（百分位数或近似正态法
• （1）这是什么资料？该资料属于何种设计方案？ • （2）拟比较三组小鼠细胞免疫功能是否有差异，可以采用哪些 统计方法？用该方法的条件是什么？思想是什么？请写出三组 小鼠细胞免疫功能比较的分析步骤，并下结论。 • （3）如果想知道党参组和黄芪组小鼠细胞免疫功能是否有差异， 可以采用哪些统计方法？ • （4）该研究者的统计处理方法是否正确？为什么？
案例六
【例 1-5】 为比较中西药治疗急性心肌梗塞的疗效，某医师将 27 例急性 心肌梗塞患者随机分成两组，分别给予中药和西药治疗，结果见表 1-4。经 检 验，得连续性校正 χ
2
=3.134，P＞0.05，差异无统计学意义，故认为中西药治
疗急性心肌梗塞的疗效基本相同。 表 1-4 药 物 中 药 西 药 合 计 有 效 12（9.33）
• 定量资料 • 自身配对设计 • 差值服从正态分布，配对t检验；不服从正 态分布，配对设计秩和检验；应用条件略 • 错误，没有进行统计推断，直接用样本信 息下结论。该资料首先检验差值是否服从 正态分布，然后选择合适检验方法进行统 计推断 • 本题差值服从正态分布，用配对t检验吧， t=4.78,p=0.001,治疗前后血红蛋白差别有 统计学意义。