二叉树各种基本运算与遍历算法

二叉树基本运算二叉树基本运算二叉树是计算机科学中最基础的数据结构之一，它由节点和指向其左右子节点的指针组成。

在实际应用中，二叉树作为一种重要的数据结构，可以用于解决各种问题。

在进行二叉树的操作时，常见的有插入节点、删除节点、查找节点以及遍历。

这些操作都是二叉树的基本运算。

第一类运算是插入节点的操作。

插入节点到二叉树中，需要根据一定的规则将新节点放置在合适的位置。

例如，若新节点的值比当前节点的值小，则将其放在当前节点的左侧；若新节点的值大，则将其放在当前节点的右侧。

这样，可以保持二叉树的有序性。

插入节点的运算可以通过递归或迭代的方式实现。

无论是哪种方式，重要的是要保证插入后的二叉树仍然是一棵二叉树。

第二类运算是删除节点的操作。

删除节点的操作相对比较复杂，需要考虑被删除节点的子节点情况。

若被删除节点没有子节点，则直接删除即可；若被删除节点只有一个子节点，则将其子节点连接到被删除节点的父节点上即可；若被删除节点有两个子节点，则需找到其右子树的最小节点，用该最小节点替代被删除节点，并删除该最小节点。

删除节点的运算同样可以通过递归或迭代的方式实现。

第三类运算是查找节点的操作。

查找节点的操作可以用于判断二叉树中是否存在某个特定值的节点。

查找节点的运算可以通过递归或迭代的方式实现。

在递归实现中，从根节点开始，若当前节点的值等于目标值，则返回该节点，否则分别在左子节点和右子节点中进行查找。

在迭代实现中，可以借助栈或队列等数据结构来辅助查找。

最后一类运算是遍历二叉树的操作。

二叉树的遍历有三种方式：前序遍历、中序遍历和后序遍历。

前序遍历先访问根节点，然后依次遍历左子树和右子树；中序遍历先遍历左子树，然后访问根节点，最后遍历右子树；后序遍历先遍历左子树，然后遍历右子树，最后访问根节点。

这三种遍历方式均可以通过递归或迭代的方式实现。

在二叉树的基本运算中，不同的操作可以根据具体的需求进行选择。

其中，插入节点、删除节点和查找节点操作都涉及到对二叉树结构的修改，需要小心处理，以保证操作的正确性。

二叉树的建立与基本操作二叉树是一种特殊的树形结构，它由节点（node）组成，每个节点最多有两个子节点。

二叉树的基本操作包括建立二叉树、遍历二叉树、查找二叉树节点、插入和删除节点等。

本文将详细介绍二叉树的建立和基本操作，并给出相应的代码示例。

一、建立二叉树建立二叉树有多种方法，包括使用数组、链表和前序、中序、后序遍历等。

下面以使用链表的方式来建立二叉树为例。

1.定义二叉树节点类首先，定义一个二叉树节点的类，包含节点值、左子节点和右子节点三个属性。

```pythonclass Node:def __init__(self, value):self.value = valueself.left = Noneself.right = None```2.建立二叉树使用递归的方法来建立二叉树，先构造根节点，然后递归地构造左子树和右子树。

```pythondef build_binary_tree(lst):if not lst: # 如果 lst 为空，则返回 Nonereturn Nonemid = len(lst) // 2 # 取 lst 的中间元素作为根节点的值root = Node(lst[mid])root.left = build_binary_tree(lst[:mid]) # 递归构造左子树root.right = build_binary_tree(lst[mid+1:]) # 递归构造右子树return root```下面是建立二叉树的示例代码：```pythonlst = [1, 2, 3, 4, 5, 6, 7]root = build_binary_tree(lst)```二、遍历二叉树遍历二叉树是指按照其中一规则访问二叉树的所有节点，常见的遍历方式有前序遍历、中序遍历和后序遍历。

1.前序遍历前序遍历是指先访问根节点，然后访问左子节点，最后访问右子节点。

```pythondef pre_order_traversal(root):if root:print(root.value) # 先访问根节点pre_order_traversal(root.left) # 递归访问左子树pre_order_traversal(root.right) # 递归访问右子树```2.中序遍历中序遍历是指先访问左子节点，然后访问根节点，最后访问右子节点。

实验三二叉树的基本运算一、实验目的1、使学生熟练掌握二叉树的逻辑结构和存储结构。

2、熟练掌握二叉树的各种遍历算法。

二、实验内容1、问题描述建立一棵二叉树，试编程实现二叉树的如下基本操作：(1). 按先序序列构造一棵二叉链表表示的二叉树T；(2). 对这棵二叉树进行遍历：先序、中序、后序以及层次遍历，分别输出结点的遍历序列；(3). 求二叉树的深度/结点数目/叶结点数目；(选做)(4). 将二叉树每个结点的左右子树交换位置。

（选做）2、基本要求从键盘接受输入（先序），以二叉链表作为存储结构，建立二叉树（以先序来建立）。

3、测试数据如输入：abc00de0g00f000（其中ф表示空格字符）则输出结果为：先序：a->b->c->d->e->g->f中序：a->b->c->d->e->g->f后序：a->b->c->d->e->g->f三、程序代码#include<malloc.h>#include<iostream.h>#define OK 1#define ERROR -1typedef char TElemType;int i;typedef struct BiTNode{TElemType data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;int CreateBiTree(BiTree&T) //创建二叉树{char a;cin>>a;if(a=='0') T=NULL;else{if(!(T=(BiTNode*)malloc(sizeof(BiTNode)))) {return ERROR;}T->data=a;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}return OK;}int PreOrderTraverse(BiTree&T) //先序遍历二叉树{if(T){//cout<<"此为先序遍历"<<endl;cout<<T->data<<"->";if(PreOrderTraverse(T->lchild))if(PreOrderTraverse(T->rchild))return OK;return ERROR;}else return OK;}int InOrderTraverse(BiTree&T) //中序遍历二叉树{if(T){//cout<<"此为中序遍历"<<endl;if(InOrderTraverse(T->lchild)){cout<<T->data<<"->";if(InOrderTraverse(T->rchild))return OK;}return ERROR;}else return OK;}int PostOrderTraverse(BiTree&T) //后序遍历二叉树{if(T){//cout<<"此为后序遍历"<<endl;if (PostOrderTraverse(T->lchild))if(PostOrderTraverse(T->rchild)){cout<<T->data<<"->";i++;return (OK);}return (ERROR);}elsereturn (OK);}int CountDepth(BiTree&T) //计算二叉树的深度{if(T==NULL){return 0;}else{int depl=CountDepth(T->lchild);int depr=CountDepth(T->lchild);if(depl>depr){return depl+1;}else{return depr+1;}}}void main() //主函数{BiTree T;cout<<"请输入二叉树节点的值以创建树"<<endl;CreateBiTree(T);cout<<"此为先序遍历";PreOrderTraverse(T);cout<<"end"<<endl;cout<<"此为中序遍历";InOrderTraverse(T);cout<<"end"<<endl;cout<<"此为后序遍历";PostOrderTraverse(T);cout<<"end"<<endl<<"此树节点数是"<<i<<endl<<"此树深度是"<<CountDepth(T)<<endl;}四、调试结果及运行界面：五、实验心得通过这次程序上机实验让我认识到了以前还不太了解的二叉树的性质和作用，这次实验的的确确的加深了我对它的理解。

软件技术基础实验四--二叉树的各种基本运算的实现班级：电信0901学号：0703090106姓名：蒋玮珂实验四二叉树的各种基本运算的实现（1）实验题目:编写一个程序，实现二叉树的各种基本运算，并在此基础上设计一个主程序完成如下功能：（1）创建二叉树btree（2）求出二叉树btree的树高（3）中序遍历二叉树btree（4）统计二叉树btree的叶结点数（5）输出二叉树btree的所有叶结点（2）实验目的：（1）掌握二叉树的递归操作与运算；（2）加深对二叉树的建立，先序中序遍历方法以及树高的理解与应用（3）调试通过并正确执行给定功能要求的实验代码#include "stdafx.h"#include <fstream.h>struct bitree{char data;bitree *lchild;bitree *rchild;};bitree *createtree(char a[],char b[],int l1,int h1,int l2,int h2) {btree *root;int i,lhigh,rhigh;root=(btree*)malloc(sizeof(btree));root->data=a[l1];if(i=h1,(b[i]!=(root->data)),i++){lhigh=i-h1;rhigh=h2-i;if(lhigh)root->lchild=createtree(a,b,l1+1,l1+lhigh,h1,h1+lhigh-1);elseroot->lchild=NULL;if(rhigh)root->rchild=createtree(a,b,l2-rhigh+1,l2,h2-rhigh+1,h2);elseroot->rchild=NULL;}return root;}int treehigh(bitree *q)if(q==NULL)return 0;else{int lhigh,rhigh;lhigh=treehigh(q->lchild);rhigh=treehigh(q->rchild);if(lhigh>=rhigh)return lhigh+1;elsereturn rhigh+1;}}void inorder(bitree *q){j=0;if(q!=NULL){inorder(q->lchild,str1+(++j));*(str1+j)=q->data;inorder(q->rchild,str1+(++j));}}int countleaf(bitree *q, int count,int flag,char *str2) {k=0;if(q==0)return NULL;else if (q->lchild==NULL &&q->rchild==NULL){count ++;while (flag)*(str2+(k++))=q->data;return count;}else{countleaf(q->lchild ,count,flag,str2+(++k));countleaf(q->rchild ,count,flag,str2+(++k));if(!flag)return count;elsereturn NULL;}}void main()bitree *q;int high,flag,n=0,i=0;char x,y;ifstream infile("e:\\ProgramFiles\\MSDev98\\MyProjects\\jwk\\infile.txt");ofstream outfile("e:\\ProgramFiles\\MSDev98\\MyProjects\\jwk\\outfile.txt");char a[20],b[20],str2[20],str1[20];while(infile.get(x)){infile>>x;a[i++]=x;n++;}i=0;while(infile.get(y)){infile>>y;b[i++]=y;}q=createtree(a,b,1,n,1,n);high=treehigh(q);outfile<<"The height of the bitree is："<<high<<endl;outfile<<"The sequence of the bitree by the way of inorder："<<endl; inorder(q,str1);i=0;while(str1[i])outfile<<str1[i++];count=0;flag=0;count=countleaf(q,count,flag,str2);cout<<"The number of the leaves is："<<endl<<count<<endl;flag=1;cout<<"The leaves of the bitree is："<<endl;i=0;while(str2[i])outfile<<str2[i++];infile.close();outfile.close();}（4）实验结果截图。

信息学奥赛培训之『树——二叉树』树——二叉树为何要重点研究二叉树？ 引 ： 为何要重点研究二叉树 ？ （1）二叉树的结构最简单，规律性最强； （2）可以证明，所有树都能转为唯一对应的二叉树，不失一般性。

一、二叉树基础1. 二叉树的定义 二叉树是一类非常重要的树形结构，它可以递归地定义如下： 二叉树 T 是有限个结点的集合，它或者是空集，或者由一个根结点以及分别称为左 子树和右子树的两棵互不相交的二叉树。

因此，二叉树的根可以有空的左子树或空的右子树，或者左、右子树均为空。

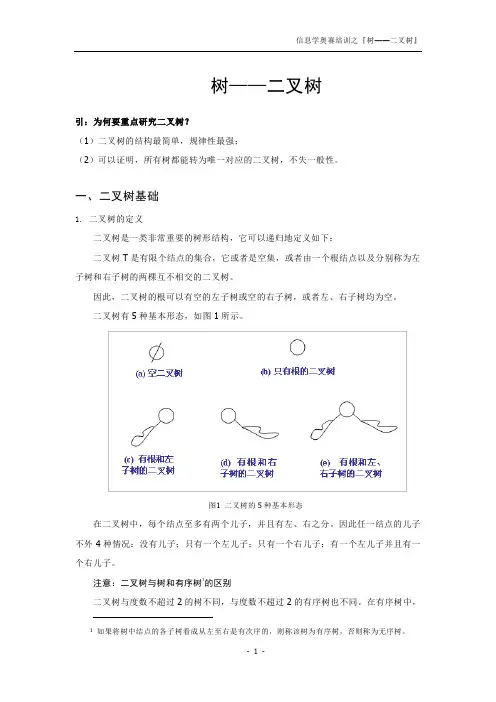
二叉树有 5 种基本形态，如图 1 所示。

图1 二叉树的 5 种基本形态在二叉树中，每个结点至多有两个儿子，并且有左、右之分。

因此任一结点的儿子 不外 4 种情况：没有儿子；只有一个左儿子；只有一个右儿子；有一个左儿子并且有一 个右儿子。

注意：二叉树与树和有序树 的区别 二叉树与度数不超过 2 的树不同，与度数不超过 2 的有序树也不同。

在有序树中，11如果将树中结点的各子树看成从左至右是有次序的，则称该树为有序树，否则称为无序树。

-1-信息学奥赛培训之『树——二叉树』虽然一个结点的儿子之间是有左右次序的，但若该结点只有一个儿子时，就无须区分其 左右次序。

而在二叉树中，即使是一个儿子也有左右之分。

例如图 2-1 中(a)和(b)是两棵 不同的二叉树。

虽然它们与图 2-2 中的普通树(作为无序树或有序树)很相似，但它们却 不能等同于这棵普通的树。

若将这 3 棵树均看作是有序树，则它们就是相同的了。

图2-1 两棵不同的二叉树图2-2 一棵普通的树由此可见，尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。

不是 ．．2. 二叉树的性质图3 二叉树性质１： 在二叉树的第 i 层上至多有 2 i −1 结点(i>=1)。

性质２： 深度为 k 的二叉树至多有 2 k − 1 个结点(k>=1)。

性质３： 对任何一棵二叉树 T，如果其终端结点数为 n0,度为 2 的结点数为 n2,则 n0=n2+1。

二叉树的各种基本运算的实现实验报告
一、实验目的
实验目的为了深入学习二叉树的各种基本运算，通过操作实现二叉树的建立、存储、查找、删除、遍历等各种基本运算操作。

二、实验内容
1、构造一个二叉树。

我们首先用一定的节点来构建一棵二叉树，包括节点的左子节点和右子节点。

2、实现查找二叉树中的节点。

在查找二叉树中的节点时，我们根据二叉树的特点，从根节点开始查找，根据要查找的节点的值与根节点的值的大小的关系，来决定接下来查找的方向，直到找到要查找的节点为止。

3、实现删除二叉树中的节点。

在删除二叉树节点时，我们要做的是找到要删除节点的父节点，然后让父节点的链接指向要删除节点的子节点，有可能要删除节点有一个子节点，有可能有两个极点，有可能没有子节点，我们要根据每种情况进行处理，来保持二叉树的结构不变。

4、对二叉树进行遍历操作。

二叉树的遍历有多种方法，本实验使用的是先序遍历。

首先从根节点出发，根据先序遍历的顺序，先访问左子树，然后再访问右子树，最后访问根节点。

三、实验步骤
1、构建二叉树：
我们用一个数组代表要构建的二叉树，第一项为根节点，第二项和第三项是根节点的子节点。

实验四二叉树的操作班级：计算机1002班姓名：唐自鸿学号：201003010207 完成日期：2010.6.14 题目：对于给定的一二叉树，实现各种约定的遍历。

一、实验目的：（1）掌握二叉树的定义和存储表示，学会建立一棵特定二叉树的方法；（2）掌握二叉树的遍历算法（先序、中序、后序遍历算法）的思想，并学会遍历算法的递归实现和非递归实现。

二、实验内容：构造二叉树，再实现二叉树的先序、中序、后序遍历，最后统计二叉树的深度。

三、实验步骤：(一) 需求分析1. 二叉树的建立首先要建立一个二叉链表的结构体，包含根节点和左右子树。

因为树的每一个左右子树又是一颗二叉树，所以用递归的方法来建立其左右子树。

二叉树的遍历是一种把二叉树的每一个节点访问并输出的过程，遍历时根结点与左右孩子的输出顺序构成了不同的遍历方法，这个过程需要按照不同的遍历的方法，先输出根结点还是先输出左右孩子，可以用选择语句来实现。

2．程序的执行命令为：1）构造结点类型，然后创建二叉树。

2）根据提示，从键盘输入各个结点。

3）通过选择一种方式（先序、中序或者后序）遍历。

4）输出结果，结束。

(二)概要设计1.二叉树的二叉链表结点存储类型定义typedef struct Node{DataType data;struct Node *LChild;struct Node *RChild;}BitNode,*BitTree;2.建立如下图所示二叉树：void CreatBiTree(BitTree *bt)用扩展先序遍历序列创建二叉树，如果是当前树根置为空，否则申请一个新节点。

3.本程序包含四个模块1) 主程序模块：2)先序遍历模块3)中序遍历模块4)后序遍历模块4.模块调用关系：主程序模块（三）详细设计1.建立二叉树存储类型//==========构造二叉树=======void CreatBiTree(BitTree *bt)//用扩展先序遍历序列创建二叉树，如果是当前树根置为空，否则申请一个新节点//{char ch;ch=getchar();if(ch=='.')*bt=NULL;else{*bt=(BitTree)malloc(sizeof(BitNode));//申请一段关于该节点类型的存储空间(*bt)->data=ch; //生成根结点CreatBiTree(&((*bt)->LChild)); //构造左子树CreatBiTree(&((*bt)->RChild)); //构造右子树}}2. 编程实现以上二叉树的前序、中序和后序遍历操作，输出遍历序列1）先序遍历二叉树的递归算法如下：void PreOrder(BitTree root){if (root!=NULL){Visit(root ->data);PreOrder(root ->LChild); //递归调用核心PreOrder(root ->RChild);}}2）中序遍历二叉树的递归算法如下：void InOrder(BitTree root){if (root!=NULL){InOrder(root ->LChild);Visit(root ->data);InOrder(root ->RChild);}}3）后序遍历二叉树的递归算法如下：void PostOrder(BitTree root){if(root!=NULL){PostOrder(root ->LChild);PostOrder(root ->RChild);Visit(root ->data);}}4）计算二叉树的深度算法如下：int PostTreeDepth(BitTree bt) //求二叉树的深度{int hl,hr,max;if(bt!=NULL){hl=PostTreeDepth(bt->LChild); //求左子树的深度hr=PostTreeDepth(bt->RChild); //求右子树的深度max=hl>hr?hl:hr; //得到左、右子树深度较大者return(max+1); //返回树的深度}else return(0); //如果是空树，则返回0}四、调试分析及测试结果1. 进入演示程序后的显示主界面：请输入二叉树中的元素；先序、中序和后序遍历分别输出结果。

二叉树的各种遍历算法及其深度算法一、二叉树的遍历算法二叉树是一种常见的数据结构，遍历二叉树可以按照根节点的访问顺序将二叉树的结点访问一次且仅访问一次。

根据遍历的顺序不同，二叉树的遍历算法可以分为三种：前序遍历、中序遍历和后序遍历。

1. 前序遍历（Pre-order Traversal）：首先访问根节点，然后遍历左子树，最后遍历右子树。

可以用递归或者栈来实现。

2. 中序遍历（In-order Traversal）：首先遍历左子树，然后访问根节点，最后遍历右子树。

可以用递归或者栈来实现。

3. 后序遍历（Post-order Traversal）：首先遍历左子树，然后遍历右子树，最后访问根节点。

可以用递归或者栈来实现。

二、二叉树的深度算法二叉树的深度，也叫做高度，指的是从根节点到叶子节点的最长路径上的节点数目。

可以使用递归或者层次遍历的方式来计算二叉树的深度。

1.递归算法：二叉树的深度等于左子树的深度和右子树的深度的较大值加一、递归的终止条件是当节点为空时，深度为0。

递归的过程中通过不断递归左子树和右子树，可以求出二叉树的深度。

2.层次遍历算法：层次遍历二叉树时，每遍历完一层节点，深度加一、使用一个队列来辅助层次遍历，先将根节点加入队列，然后依次取出队列中的节点，将其左右子节点加入队列，直到队列为空，完成层次遍历。

三、示例为了更好地理解二叉树的遍历和求深度的算法，我们以一个简单的二叉树为例进行说明。

假设该二叉树的结构如下：A/\BC/\/\DEFG其中，A、B、C、D、E、F、G分别代表二叉树的结点。

1.前序遍历：A->B->D->E->C->F->G2.中序遍历：D->B->E->A->F->C->G3.后序遍历：D->E->B->F->G->C->A4.深度：2以上是针对这个二叉树的遍历和深度的计算示例。

树遍历算法实现策略概述树遍历算法是计算机科学中常用的一种算法，用于遍历树形数据结构，并按照一定的顺序访问树的节点。

树遍历算法是解决许多与树相关的问题的基础，包括二叉搜索树的查找、排序、删除等操作。

本文将概述树遍历算法的实现策略，旨在帮助读者全面理解和掌握这一常用算法。

1. 深度优先搜索（DFS）深度优先搜索是一种递归的树遍历算法。

该算法从根节点开始，递归地遍历树的每个子树，直到遍历完整棵树或达到终止条件。

在深度优先搜索中，我们可以使用前序、中序或后序三种遍历顺序。

- 前序遍历：先访问根节点，然后再按照左子树、右子树的顺序遍历。

- 中序遍历：先按照左子树、根节点、右子树的顺序遍历。

- 后序遍历：先按照左子树、右子树、根节点的顺序遍历。

2. 广度优先搜索（BFS）广度优先搜索是一种迭代的树遍历算法。

该算法使用队列将树的节点按照层次顺序依次入队和出队，以此实现对整棵树的遍历。

3. 二叉树遍历算法二叉树是一种特殊的树形结构，每个节点最多有两个子节点，即左子节点和右子节点。

针对二叉树的遍历，常用的算法有：- 前序遍历：先访问根节点，再遍历左子树和右子树。

- 中序遍历：先遍历左子树，再访问根节点，最后遍历右子树。

- 后序遍历：先遍历左子树和右子树，最后访问根节点。

4. 多叉树遍历算法多叉树是一种每个节点可以有多个子节点的树形结构。

对于多叉树的遍历，可以使用深度优先搜索或广度优先搜索算法。

5. 树遍历算法的应用场景树遍历算法广泛应用于各种领域，包括图像处理、自然语言处理、编译原理等。

其中，图像处理中的图像分割、自然语言处理中的依存句法分析、编译原理中的语法分析等都依赖于树遍历算法来实现。

总结：树遍历算法是计算机科学中常用的一种算法，用于按照一定顺序访问树结构中的各个节点。

深度优先搜索和广度优先搜索是树遍历的两种基本策略，而针对二叉树和多叉树的遍历有相应的算法。

树遍历算法在各个领域都有广泛的应用场景，深入理解和掌握这些算法，对于解决与树相关的问题具有重要意义。

《数据结构与数据库》实验报告实验题目二叉树的基本操作及运算一、需要分析问题描述：实现二叉树（包括二叉排序树）的建立，并实现先序、中序、后序和按层次遍历，计算叶子结点数、树的深度、树的宽度，求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目，以及二叉树常用运算。

问题分析：二叉树树型结构是一类重要的非线性数据结构，对它的熟练掌握是学习数据结构的基本要求。

由于二叉树的定义本身就是一种递归定义，所以二叉树的一些基本操作也可采用递归调用的方法。

处理本问题，我觉得应该：1、建立二叉树；2、通过递归方法来遍历（先序、中序和后序）二叉树；3、通过队列应用来实现对二叉树的层次遍历；4、借用递归方法对二叉树进行一些基本操作，如：求叶子数、树的深度宽度等；5、运用广义表对二叉树进行广义表形式的打印。

算法规定：输入形式：为了方便操作，规定二叉树的元素类型都为字符型，允许各种字符类型的输入，没有元素的结点以空格输入表示，并且本实验是以先序顺序输入的。

输出形式：通过先序、中序和后序遍历的方法对树的各字符型元素进行遍历打印，再以广义表形式进行打印。

对二叉树的一些运算结果以整型输出。

程序功能：实现对二叉树的先序、中序和后序遍历，层次遍历。

计算叶子结点数、树的深度、树的宽度，求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目。

对二叉树的某个元素进行查找，对二叉树的某个结点进行删除。

测试数据：输入一：ABC□□DE□G□□F□□□（以□表示空格）,查找5,删除E预测结果：先序遍历ABCDEGF中序遍历CBEGDFA后序遍历CGEFDBA层次遍历ABCDEFG广义表打印A（B（C,D（E（,G）,F）））叶子数3 深度5 宽度2 非空子孙数6 度为2的数目2 度为1的数目2查找5，成功，查找的元素为E删除E后，以广义表形式打印A（B（C,D（,F）））输入二：ABD□□EH□□□CF□G□□□（以□表示空格）,查找10,删除B预测结果：先序遍历ABDEHCFG中序遍历DBHEAGFC后序遍历DHEBGFCA层次遍历ABCDEFHG广义表打印A（B(D,E(H)),C(F(,G))）叶子数3 深度4 宽度3 非空子孙数7 度为2的数目2 度为1的数目3查找10，失败。

二叉树的基本操作实验报告二叉树的基本操作实验报告引言：二叉树是一种常见的数据结构，它由节点组成，每个节点最多有两个子节点。

二叉树的基本操作包括创建、遍历、插入和删除等。

本实验旨在通过实践来深入了解二叉树的基本操作，并通过实验结果验证其正确性和有效性。

一、创建二叉树创建二叉树是二叉树操作中的第一步。

在本实验中，我们使用了递归算法来创建二叉树。

递归算法是一种重要的算法思想，通过将问题划分为更小的子问题来解决复杂的问题。

在创建二叉树时，我们首先创建根节点，然后递归地创建左子树和右子树。

二、遍历二叉树遍历二叉树是对二叉树中的每个节点进行访问的过程。

常见的遍历方式有前序遍历、中序遍历和后序遍历。

前序遍历先访问根节点，然后递归遍历左子树和右子树；中序遍历先递归遍历左子树，然后访问根节点，最后递归遍历右子树；后序遍历先递归遍历左子树和右子树，最后访问根节点。

三、插入节点插入节点是向二叉树中添加新节点的操作。

插入节点的过程需要遵循二叉树的特性，即左子节点的值小于父节点的值，右子节点的值大于父节点的值。

在插入节点时，我们需要找到合适的位置，将新节点插入到正确的位置上。

四、删除节点删除节点是从二叉树中移除节点的操作。

删除节点的过程相对复杂，需要考虑多种情况。

如果要删除的节点是叶子节点，直接删除即可。

如果要删除的节点只有一个子节点，将其子节点连接到父节点上。

如果要删除的节点有两个子节点，我们需要找到其后继节点或前驱节点来替代被删除的节点。

实验结果：通过实验，我们成功地实现了二叉树的基本操作。

创建二叉树的递归算法能够正确地创建出符合要求的二叉树。

遍历二叉树的算法能够按照指定的顺序遍历每个节点。

插入节点和删除节点的操作也能够正确地修改二叉树的结构。

讨论与总结：二叉树的基本操作是数据结构中的重要内容，对于理解和应用其他数据结构具有重要意义。

通过本次实验，我们深入了解了二叉树的创建、遍历、插入和删除等操作，并通过实验验证了其正确性和有效性。

二叉树基本运算算法的实现
二叉树是一种常见的数据结构，基本运算算法包括二叉树的遍历、查找、插入、删除等操作。

下面是这些算法的实现：
1. 二叉树遍历：二叉树遍历有三种方式，分别是前序遍历、中序遍历和后序遍历。

其中，前序遍历先访问根节点，再访问左子树和右子树；中序遍历先访问左子树，再访问根节点和右子树；后序遍历先访问左子树，再访问右子树和根节点。

遍历可以使用递归算法或栈实现。

2. 二叉树查找：二叉树查找可以使用递归算法或循环算法实现。

递归算法通过比较节点值实现查找，如果查找值小于当前节点值，则在左子树中查找，否则在右子树中查找。

循环算法使用二叉树的特性，比较查找值和当前节点值的大小，根据大小关系不断移动到左子树或右子树中进行查找，直到找到目标节点或遍历到叶子节点为止。

3. 二叉树插入：二叉树插入需要先查找到插入位置，然后在该位置插入一个新节点。

插入操作可以使用递归算法或循环算法实现。

4. 二叉树删除：二叉树删除分为三种情况：删除叶子节点、删除只有一个孩子的节点和删除有两个孩子的节点。

删除叶子节点很简单，只需要将其父节点的指针设为NULL即可。

删除只有一个孩子的节点需要将父节点的指针指向该节点的
孩子节点。

删除有两个孩子的节点需要找到该节点的后继节点（或前驱节点），将后继节点的值复制到该节点中，然后删除后继节点。

上述算法的实现需要根据具体的编程语言进行调整和实现。

二叉树的基本参数计算二叉树是一种特殊的树结构，其中每个节点最多有两个子节点，分别称为左子节点和右子节点。

在二叉树中，节点可以包含各种不同类型的数据，而节点之间的连接由指向子节点的链接表示。

二叉树在计算机科学中有广泛的应用，包括排序算法、算法、解析表达式等。

在二叉树中，有许多基本参数可以用来描述和计算二叉树的特性。

下面将介绍一些常见的二叉树基本参数。

1.节点数量：指二叉树中节点的总数。

可以通过遍历二叉树并计数的方式来获得节点数量。

2.深度/高度：指二叉树中从根节点到最远叶子节点的距离。

每个节点的深度等于其父节点的深度加1、根节点的深度通常为0。

树的深度等于根节点的深度。

3.完全二叉树：指二叉树中除了最后一层外，其他层的节点数量都达到了最大值，并且最后一层的节点都尽可能靠左排列的二叉树。

4.平衡二叉树：指二叉树中每个节点的左子树和右子树的高度差不超过1的二叉树。

5.叶子节点数量：指二叉树中没有子节点的节点数量。

6.度数：指二叉树中每个节点的子节点数量。

二叉树中每个节点的度数最多为27.层数：指二叉树中从根节点到叶子节点的层数。

根节点所在的层数为18.前序遍历：指以根节点-左子树-右子树的顺序遍历二叉树。

9.中序遍历：指以左子树-根节点-右子树的顺序遍历二叉树。

10.后序遍历：指以左子树-右子树-根节点的顺序遍历二叉树。

11.层序遍历：指按树的层次从上到下、从左到右的顺序遍历二叉树。

除了这些基本参数外，还有一些常用的计算方式可以用来分析和计算二叉树的特性。

1.二叉树的最大深度可以使用递归的方式计算。

对于二叉树中的每个节点，将节点的深度加1，并将其左子节点和右子节点深度较大的值作为节点的深度。

2.二叉树的最小深度可以使用递归的方式计算。

对于二叉树中的每个节点，将节点的深度加1，并将其左子节点和右子节点深度较小的值作为节点的深度。

3.二叉树的前序遍历可以使用递归的方式实现。

对于每个节点，先访问根节点，然后递归遍历左子树，最后递归遍历右子树。

c语言实现二叉树各种基本运算的算法二叉树是一种常见的数据结构，可以应用于许多算法和问题中。

在C语言中，我们可以使用指针和结构体来实现二叉树的各种基本运算。

本文将详细介绍二叉树的创建、插入、删除、查找以及遍历等基本操作的算法。

1.创建二叉树创建二叉树可以通过递归的方式来实现。

首先定义一个表示二叉树节点的结构体，包含一个值和左右子节点指针。

然后，通过递归地创建左右子树来构建整个二叉树。

```ctypedef struct TreeNode {int data;struct TreeNode* left;struct TreeNode* right;} TreeNode;//创建二叉树TreeNode* createBinaryTree() {int data;scanf("%d", &data);if (data == -1) { // -1表示空节点return NULL;}TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode)); node->data = data;node->left = createBinaryTree();node->right = createBinaryTree();return node;}```2.插入节点在二叉树中插入节点可以按照二叉搜索树的性质进行。

如果要插入的值小于当前节点的值，则将其插入到左子树中，否则插入到右子树中。

如果子树为空，则直接创建一个新节点作为子树。

```c//插入节点TreeNode* insertNode(TreeNode* root, int data) {if (root == NULL) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;}if (data < root->data) {root->left = insertNode(root->left, data);} else {root->right = insertNode(root->right, data);}return root;}```3.删除节点删除二叉树中的节点可以分为三种情况：删除叶子节点、删除只有一个子节点的节点、删除有两个子节点的节点。