【精】灰色系统理论与建模
- 格式:ppt
- 大小:3.77 MB
- 文档页数:95

数学建模讲稿-------灰色系统分析五步建模思想研究一个系统,一般应首先建立系统的数学模型,进而对系统的整体功能、协调功能以及系统各因素之间的关联关系、因果关系、动态关系进行具体的量化研究。
这种研究必须以定性分析为先导,定量与定性紧密结合。
系统模型的建立,一般要经历思想开发、因素分析、量化、动态化、优化五个步骤,故称为五步建模。
第一步:开发思想,形成概念,通过定性分析、研究,明确研究的方向、目标、途径、措施,并将结果用准确简练的语言加以表达,这便是语言模型。
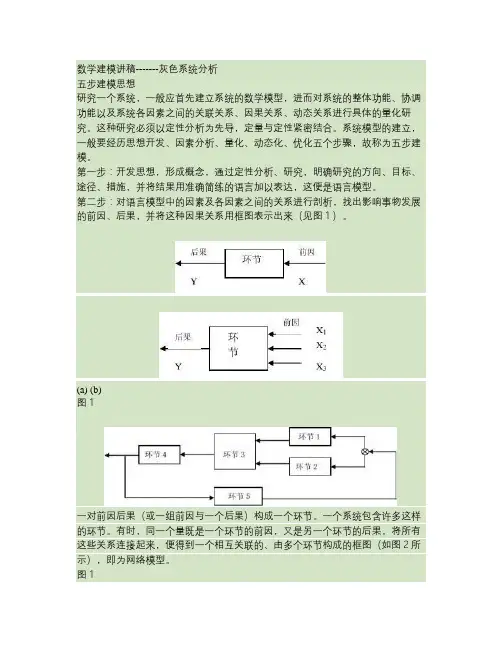
第二步:对语言模型中的因素及各因素之间的关系进行剖析,找出影响事物发展的前因、后果,并将这种因果关系用框图表示出来(见图1)。
(a) (b)图1一对前因后果(或一组前因与一个后果)构成一个环节。
一个系统包含许多这样的环节。
有时,同一个量既是一个环节的前因,又是另一个环节的后果,将所有这些关系连接起来,便得到一个相互关联的、由多个环节构成的框图(如图2所示),即为网络模型。
图1第三步:对各环节的因果关系进行量化研究,初步得出低层次的概略量化关系,即为量化模型。
第四步:进一步收集各环节输入数据和输出数据,利用所得数据序列,建立动态GM模型,即动态模型。
动态模型是高层次的量化模型,它更为深刻地揭示出输入与输出之间的数量关系或转换规律,是系统分析、优化的基础。
第五步:对动态模型进行系统研究和分析,通过结构、机理、参数的调整,进行系统重组,达到优化配置、改善系统动态品质的目的。
这样得到的模型,称之为优化模型。
五步建模的全过程,是在五个不同阶段建立五种模型的过程:网络模型优化模型在建模过程中,要不断地将下一阶段中所得的结果回馈,经过多次循环往复,使整个模型逐步趋于完善。
数学建模讲稿-------灰色系统分析灰色系统建模的基本思路可以概括为以下几点:1科学实验数据;○2经验数据;○3生产数据;○4决策数据。
(1)建立模型常用的数据有以下几种:○(2)序列生成数据是建立灰色模型的基础数据。


数学建模讲稿-------灰色系统分析五步建模思想研究一个系统,一般应首先建立系统的数学模型,进而对系统的整体功能、协调功能以及系统各因素之间的关联关系、因果关系、动态关系进行具体的量化研究。
这种研究必须以定性分析为先导,定量与定性紧密结合。
系统模型的建立,一般要经历思想开发、因素分析、量化、动态化、优化五个步骤,故称为五步建模。
第一步:开发思想,形成概念,通过定性分析、研究,明确研究的方向、目标、途径、措施,并将结果用准确简练的语言加以表达,这便是语言模型。
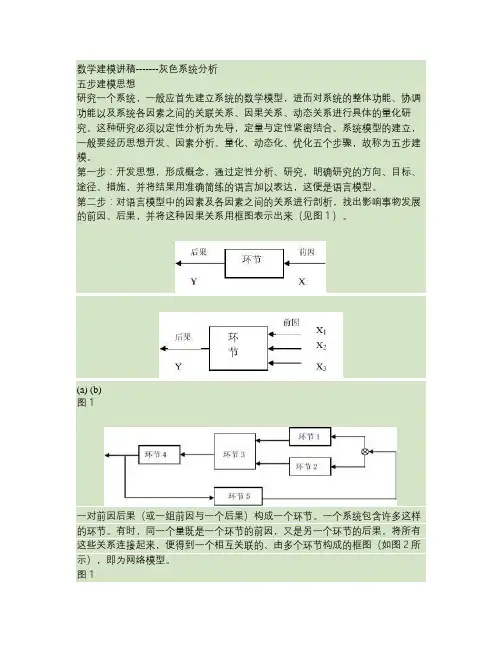
第二步:对语言模型中的因素及各因素之间的关系进行剖析,找出影响事物发展的前因、后果,并将这种因果关系用框图表示出来(见图1)。
(a) (b)图1一对前因后果(或一组前因与一个后果)构成一个环节。
一个系统包含许多这样的环节。
有时,同一个量既是一个环节的前因,又是另一个环节的后果,将所有这些关系连接起来,便得到一个相互关联的、由多个环节构成的框图(如图2所示),即为网络模型。
图1第三步:对各环节的因果关系进行量化研究,初步得出低层次的概略量化关系,即为量化模型。
第四步:进一步收集各环节输入数据和输出数据,利用所得数据序列,建立动态GM模型,即动态模型。
动态模型是高层次的量化模型,它更为深刻地揭示出输入与输出之间的数量关系或转换规律,是系统分析、优化的基础。
第五步:对动态模型进行系统研究和分析,通过结构、机理、参数的调整,进行系统重组,达到优化配置、改善系统动态品质的目的。
这样得到的模型,称之为优化模型。
五步建模的全过程,是在五个不同阶段建立五种模型的过程:网络模型优化模型在建模过程中,要不断地将下一阶段中所得的结果回馈,经过多次循环往复,使整个模型逐步趋于完善。
数学建模讲稿-------灰色系统分析灰色系统建模的基本思路可以概括为以下几点:1科学实验数据;○2经验数据;○3生产数据;○4决策数据。
(1)建立模型常用的数据有以下几种:○(2)序列生成数据是建立灰色模型的基础数据。






§3 灰色模型GM(1,N)及其应用客观系统无论本征非灰,还是本征灰,一般都存在能量吸收、储存、释放等过程,加之生成数列一般都有较强的指数变化趋势,所以灰色系统理论指出用离散的随机数,经过生成变为随机性被显著削减的较有规律的生成数,这样便可以对变化过程做较长时间的描述,进而建立微分方程形式的模型。
建模的实质是建立微分方程的系数。
设有N 个数列N i n X X X X i i i i ,,2,1))(,),2(),1(()0()0()0()0( == 对)0(i X 做累加生成,得到生成数列Ni n X n X X X X m X m XXXi i i i i nm i m iii,,2,1))()1(,),2()1(),1(())(,,)(),1(()0()1()0()1()1(1)0(21)0()0()1( =+-+==∑∑==我们将数列)1(i X 的时刻n k ,,2,1 =看作连续的变量t ,而将数列)1(i X 转而看成时间t 的函数)()1()1(t X X i i =。
如果数列)1()1(3)1(2,,,NX X X 对)1(1X 的变化率产生影响,则可建立白化式微分方程)1(1)1(32)1(21)1(1)1(1N N X b X b X b aX dtdX -+++=+ (1) 这个微分方程模型记为GM (1,N )。
方程(1)的参数列记为T N b b b a ),,,(121-= α,再设T N n X X X Y ))(,),3(),2(()0(1)0(1)0(1 =,将方程(1)按差分法离散,可得到线性方程组,形如αˆB Y N = (2)按照最小二乘法,有N T T Y B B B 1)(ˆ-=α (3)其中,利用两点滑动平均的思想,最终可得矩阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+--+-+-=)()())()1((21)3()3())3()2((21)2()2())2()1((21)1()1(2)1(1)1(1)1()1(2)1(1)1(1)1()1(2)1(1)1(1n X n X n X n X X X X X X X X X B N N N 求出αˆ后,微分方程(1)便确定了。