下载文档原格式
第一章绪论第三节数学的魅力（第一课时）教学目标通过一些实例，让学员初步感受数学的魅力。
教学过程一、导入你可能喜欢音乐，因为它有优美和谐的旋律；你可能喜欢图画，因为它从视觉上反映人和自然的美；那么，你应该更喜欢数学，因为它像音乐一样和谐，像图画一样美丽，而且它在更深的层次上，揭示自然界和人类社会内在的规律，用简洁的、漂亮的定理和公式描述世界的本质。
数学，是无声的音乐；数学，是无色的图画。
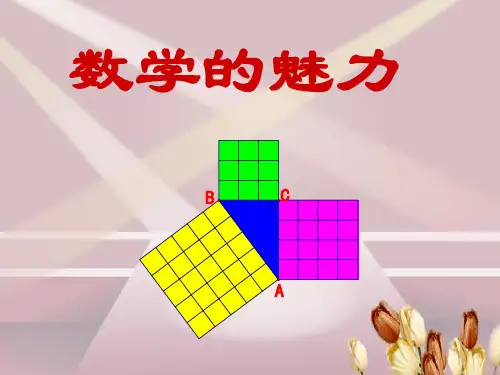
数学，有无穷的魅力！二、新授（一）渔网的几何规律用数学方法可以证明，无论你用什么绳索织一片网，无论你织一片多大的网，它的结点数(V)，网眼数(F)，边数(E)都必定适合下面的公式：V + F – E = 1（二维情形）多面体的欧拉公式V + F – E = 2（二）任何一个省会城市至少有两个人头发根数一样多标题中的这个命题是一个“存在性命题”，可以叙述为：任何一个省会城市中，一定存在两个头发根数一样多的人。
通常有两类证明方法：一类是构造性的证明方法，即把需要证明存在的事物构造出来，便完成了证明；一类是纯存在性证明，并不具体给出存在的事物，而是完全依靠逻辑的力量，证明事物的存在。
这里介绍一个事实：任何一个人的头发根数都不会多于20万根的，省会城市中的人数则远远大于20万。
例如设为70万人。
把头发根数为1至头发根数为20万分别当作20个抽屉，把70万个人放到20万个抽屉里，根据抽屉原理，则至少一个抽屉里有两个或者两个以上的人，而同一个抽屉里的人，就是头发根数一样多的人。
这里并没有具体给出哪两个人头发根数一样多，但是依靠逻辑推理，让你不得不承认，确实存在两个头发根数一样多的人。
这就是纯存在性证明的方法，这就是数学推理的力量。
（三）圆的魅力圆是一种几何图形，指的是平面中到一个定点距离为定值的所有点的集合。
这个给定的点称为圆的圆心。
作为定值的距离称为圆的半径。
当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹就是一个圆。
第一章绪论第三节数学的魅力（第二课时）教学目标通过一些实例，让学员初步感受数学的魅力。
教学过程（六）素数的奥秘自然数是整个数学最重要的元素。
自然数中有一种特别基本又特别重要的数，称为“素数”。
素数是大于1的自然数中，只能被自己和1整除的数；大于1的自然数中不是素数的都称为“合数”；1则既不是素数也不是合数。
由于在大于1的自然数中，素数的因子最少，所以素数是特别简单的数。
又由于一切大于1的自然数都能够从素数通过乘法得到，所以素数又是特别基本的数。
素数很早就被古希腊的数学家所研究。
2300多年前欧几里得的几何《原本》第9卷的定理20，就给出了“素数有无穷多个”的漂亮证明但是，素数的有些规律，表述出来很容易听懂，研究起来却出人意料地困难。
（当然，素数的有些规律表述出来也是相当复杂的。
）关于素数的规律，人类有许多的“猜想”。
至今还有不少关于素数的重要猜想，既没有被证明，也没有被否定。
有的猜想的解决，现在看来可能会十分遥远。
有人甚至预言，“人类探寻素数规律的历史，将等同于人类的整个文明史”。
三个关于素数规律的问题从加法的角度研究素数两个猜想：每个足够大的偶数都是两个素数的和；每个足够大的奇数都是三个素数的和。
后一个猜想现在已被证明；前一个猜想至今却既没有人举出反例，也没有人给出证明。
前者就是著名的“哥德巴赫猜想”。
从乘法的角度研究素数算术基本定理：任一个大于1的自然数，都可以被表示为有限个素数（可以重复）的乘积，并且如果不计次序的话，表法是唯一的。
算术基本定理早已被证明，但不是采用“构造性”的证明。
未解之谜：这个问题是：对任一个大于1的自然数，试给出一个一般的方法，以便较快地找到有限个素数（可以重复），使它们的乘积等于那个预先写出的大于1的自然数。
解决问题的本质困难，也在这两个步骤。
虽然现在有了高速计算机，但是对于很大的数a，例如200位的数a，这两步的计算仍然很费时日，以至于实际上是不可能解决问题的。
这样的困难，反倒给密码通讯提供了思路。
