浙江省台州市天台、椒江、玉环三区2013年九年级第一次模拟考试

##区第二中初三数学模拟卷一、选择题〔本大题共10小题,每小题4分,共40分〕 1. 若〔 〕×〔﹣2〕=1,则括号内填一个实数应该是〔 〕 A ．21 B ． 2C ． ﹣2D ．21-2. 光速约为300000千米/秒,将数字300000用科学记数法表示为〔 〕 A ．3×104B ．3×105C ．3×106D ．30×1043.如图是某个几何体的三视图,则该几何体的形状是〔 〕 A ．长方体B ． 圆锥C ．圆柱D ．三棱柱4. 作业时间是中小学教育质量综合评价指标的考查要点之一,腾飞学习小组五个同学每天课外作业时间分别是〔单位：分钟〕：60,80,75,45,120．这组数据的中位数是〔 〕 A ．45B ．75C ．80D ．605. 下列计算正确的是〔 〕 A ．325=-B ．24±=C ．326a a a =÷D ．()632a a -=-6. 将〔a ﹣1〕2﹣1分解因式,结果正确的是〔 〕A ．a 〔a ﹣1〕B ．a 〔a ﹣2〕C ．〔a ﹣2〕〔a ﹣1〕D ．〔a ﹣2〕〔a+1〕 7.已知⎩⎨⎧=-=21y x 是二元一次方程组⎩⎨⎧=-=+123y nx my x 的解,则m ﹣n 的值是〔 〕 A ．1 B ．2 C ．3 D ．48. 将抛物线y=x 2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是〔 〕A ．y=〔x ﹣4〕2﹣6B ．y=〔x ﹣4〕2﹣2C ．y=〔x ﹣2〕2﹣2D ．y=〔x ﹣1〕2﹣39. 如图,在四边形ABCD 中,AD ∥BC,DE ⊥BC,垂足为点E,连接AC 交DE 于点F,点G 为AF 的中点,∠ACD=2∠ACB ．若DG=3,EC=1, 则DE 的长为〔 〕 A ．32B ．10C ．22D ．610. 如图,Rt △AOB ∽△DOC,∠AOB=∠COD=90°,M 为OA 的中点,OA=6,OB=8,将△COD 绕O 点旋转,连接AD,CB 交于P 点,连接MP,则MP 的最大值〔 〕A ．7B ．8C ．9D ．10二、填空题〔本大题共6小题,每小题5分,共30分〕 11.函数11-+=x x y 的自变量x 的取值范围为． 12. 如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针 的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针 所指的位置〔指针指向两个扇形的交线时,当作指向右边的扇形〕,则指 针指向红色的概率为． 13. 不等式组⎩⎨⎧≤--+<4)1(2312x x x x 的解集为．14. 如图,在△ABC 中,点D 是BC 的中点,点E,F 分别在线段AD 与其延长线上,且DE=DF ．给 出下列条件：①BE ⊥EC ；②BF ∥CE ；③AB=AC ；从中选择一个条件使四边形BECF 是菱形,你认为这个条件是〔只填写序号〕．第14题 第15题 第16题 15. 如图,在平行四边形ABCD 中,以点A 为圆心,AB 的长为半径的圆恰好与CD 相切于点C,交AD 于点E,延长BA 与⊙A 相交于点F ．若的长为,则图中阴影部分的面积为．16．如图,在平面直角坐标系中,△A 1A 2A 3,△A 3A 4A 5,△A 5A 6A 7,△A 7A 8A 9,…,都是等边三角形,且点A 1,A 3,A 5,A 7,A 9的坐标分别为A 1〔3,0〕,A 3〔1,0〕,A 5〔4,0〕,A 7〔0,0〕,A 9〔5,0〕,依据图形所反映的规律,则A 100的坐标为．三、解答题〔本题共8题,第17 、18、19、20每题8分,第21题10分,第22、23题每题12分,第24 题14分,共80分〕 17. 计算与解分式方程．〔1〕121845sin 21-⎪⎭⎫⎝⎛+-︒-〔2〕13231=--++x x x18．阅读以下材料,并按要求完成相应的任务．几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形﹣﹣筝形．所谓筝形,它的形状与我们生活中风筝的骨架相似．定义：两组邻边分别相等的四边形,称之为筝形,如图,四边形ABCD是筝形,其中AB=AD,CB=CD判定：①两组邻边分别相等的四边形是筝形②有一条对角线垂直平分另一条对角线的四边形是筝形显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点如果只研究一般的筝形〔不包括菱形〕,请根据以上材料完成下列任务：如果只研究一般的筝形〔不包括菱形〕,请根据以上材料完成下列任务：〔1〕请说出筝形和菱形的相同点和不同点各两条；〔2〕请仿照图1的画法,在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下：①顶点都在格点上；②所涉与的图案既是轴对称图形又是中心对称图形；③将新图案中的四个筝形都图上阴影〔建议用一系列平行斜线表示阴影〕．19．我市民营经济持续发展,2015年城镇民营企业就业人数突破20万．为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2015年月平均收入随机抽样调查,将抽样的数据按"2000元以内"、"2000元～4000元"、"4000元～6000元"和"6000元以上"分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图．由图中所给出的信息解答下列问题：〔1〕本次抽样调查的员工有人,在扇形统计图中x的值为,表示"月平均收入在2000元以内"的部分所对应扇形的圆心角的度数是；〔2〕将不完整的条形图补充完整,并估计我市2015年城镇民营企业20万员工中,每月的收入在"2000元～4000元"的约多少人？〔3〕统计局根据抽样数据计算得到,2016年我市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理？20.如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点．〔1〕求证：AB平分∠OAC；〔2〕延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长．21.如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的、高〔AB,CD均与水平面垂直,结果保留根号〕．22.神仙居景区门票价格80元/人,景区为吸引游客,对门票价格 进行动态管理,非节假日打a 折,节假日期间,10人以下〔包 括10人〕不打折,10人以上超过10人的部分打b 折,设游客 为x 人,门票费用为y 元,非节假日门票费用y 1〔元〕与节假日门票费用y 2〔元〕与游客x 〔人〕之间的函数关系如图所示． 〔1〕a=,b=；〔2〕直接写出y 1、y 2与x 之间的函数关系式；〔3〕导游小王6月10日〔非节假日〕带A 旅游团,6月20日〔端午节〕带B 旅游团到神仙居景区旅游,两团共计50人,两次 共付门票费用3040元,求A 、B 两个旅游团各多少人？23．在矩形ABCD 中,ADAB=a,点G,H 分别在边AB,DC 上,且HA=HG,点E 为AB 边上的一个动点,连接HE,把△AHE 沿直线HE 翻折得到△FHE ．〔1〕如图1,当DH=DA 时,①填空：∠HGA=度；②若EF ∥HG,求∠AHE 的度数,并求此时的最小值；〔2〕如图3,∠AEH=60°,EG=2BG,连接FG,交边DC 于点P,且FG ⊥AB,G 为垂足,求a 的值．24．定义：如果一个y 与x 的函数图象经过平移后能与某反比例函数的图象重合,则称这个函数是y 与x 的"反比例平移函数"．例如:121+-=x y 的图象向左平移2个单位,再向下平移1个单位得到xy 1=的图象,则121+-=x y 是y 与x 的"反比例平移函数"．〔1〕若矩形的两边分别是2cm 、3cm,当这两边分别增加x cm 、y cm 后,得到的新矩形的面积为82cm ,求y 与x 的函数表达式,并判断这个函数是否为"反比例平移函数"．〔2〕如图,在平面直角坐标系中,点O 为原点,矩形OABC 的顶点A 、C 的坐标分别为<9,0>、<0,3> ．点D 是OA 的中点,连接OB 、CD 交于点E,"反比例平移函数"6-+=x kax y 的图象经过B 、E 两点．则这个"反比例平移函数"的表达式为；这个"反比例平移函数"的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式．〔3〕在〔2〕的条件下, 已知过线段BE 中点的一条直线l 交这个"反比例平移函数"图象于P 、Q 两点<P 在Q 的右侧>,若B 、E 、P 、Q 为顶点组成的四边形面积为16,请求出点P 的坐标．参考答案1～10,DBDBD BDBCC 11．1≠x 12．73 13．21≤<-x 14．③ 15．22π- 16．⎪⎭⎫ ⎝⎛3251-25， 17．<1>2-1 <2>x=0 经检验是原方程的解18．解：〔1〕相同点：①两组邻边分别相等；②有一组对角相等；③一条对角线垂直平分另一条对角线；④一条对角线平分一组对角；⑤都是轴对称图形；⑥面积等于对角线乘积的一半；不同点：①菱形的对角线互相平分,筝形的对角线不互相平分； ②菱形的四边都相等,筝形只有两组邻边分别相等； ③菱形的两组对边分别平行,筝形的对边不平行； ④菱形的两组对角分别相等,筝形只有一组对角相等； ⑤菱形的邻角互补,筝形的邻角不互补；⑥菱形的既是轴对称图形又是中心对称图形,筝形是轴对称图形不是中心对称图形； 〔共4分〕 〔2〕如图所示：〔4分〕19．解：〔1〕本次抽样调查的员工人数是：=500〔人〕,D 所占的百分比是：×100%=14%,则在扇形统计图中x 的值为14；"月平均收入在2000元以内"的部分所对应扇形的圆心角的度数是360°×=21.6°；故答案为：500,14,21.6°；〔3分〕〔2〕C的人数为：500×20%=100,补全统计图如图所示,"2000元～4000元"的约为：20万×60%=12万；〔3分〕〔3〕∵2000元～4000元的最多,占60%,∴用月平均收入为4872元反映月收入情况不合理．〔2分〕20．〔1〕证明：连接OC,∵∠AOB=120°,C是AB弧的中点,∴∠AOC=∠BOC=60°,∵OA=OC,∴△ACO是等边三角形,∴OA=AC,同理OB=BC,∴OA=AC=BC=OB,∴四边形AOBC是菱形,∴AB平分∠OAC；〔4分〕〔2〕解：连接OC,∵C为弧AB中点,∠AOB=120°,∴∠AOC=60°,∵OA=OC,∴OAC是等边三角形,∵OA=AC,∴AP=AC,∴∠APC=30°,∴△OPC是直角三角形,∴．〔4分〕21．解：过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,在Rt△BFD中,∵∠DBF=30°,sin∠DBF==,cos∠DBF==,∵BD=6,∴DF=3,BF=3,〔4分〕∵AB∥CD,CE⊥AB,BF⊥CD,∴四边形BFCE为矩形,∴BF=CE=3,CF=BE=CD﹣DF=1,在Rt△ACE中,∠ACE=45°,∴AE=CE=3,〔4分〕∴AB=3+1．答：铁塔AB的高为〔3+1〕m．〔2分〕22．解：〔1〕由y1图象上点〔10,480〕,得到10人的费用为480元,∴a=×10=6；由y2图象上点〔10,800〕和〔20,1440〕,得到20人中后10人费用为640元,∴b=×10=8；〔4分〕〔2〕设y1=k1x,∵函数图象经过点〔0,0〕和〔10,480〕,∴10k1=480,∴k1=48,∴y1=48x；0≤x≤10时,设y2=k2x,∵函数图象经过点〔0,0〕和〔10,800〕,∴10k2=800,∴k2=80,∴y2=80x,x＞10时,设y2=kx+b,∵函数图象经过点〔10,800〕和〔20,1440〕,∴,∴,∴y2=64x+160；∴y2=；〔4分〕〔3〕设A团有n人,则B团的人数为〔50﹣n〕,当0≤n≤10时,48n+80〔50﹣n〕=3040,解得n=30〔不符合题意舍去〕,当n＞10时,48n+64〔50﹣n〕+160=3040,解得n=20,则50﹣n=50﹣20=30．答：A团有20人,B团有30人．故答案为：6,8．〔4分〕23．解：〔1〕①∵四边形ABCD是矩形,∴∠ADH=90°,∵DH=DA,∴∠DAH=∠DHA=45°,∴∠HAE=45°,∵HA=HG,∴∠HAE=∠HGA=45°；故答案为：45°；〔2分〕②分两种情况讨论：第一种情况：∵∠HAG=∠HGA=45°；∴∠AHG=90°,由折叠可知：∠HAE=∠F=45°,∠AHE=∠FHE,∵EF∥HG,∴∠FHG=∠F=45°,∴∠AHF=∠AHG﹣∠FHG=45°,即∠AHE+∠FHE=45°,∴∠AHE=22.5°,此时,当B与G重合时,a的值最小,最小值是2；〔2分〕第二种情况：∵EF∥HG,∴∠HGA=∠FEA=45°,即∠AEH+∠FEH=45°,由折叠可知：∠AEH=∠FEH,∴∠AEH=∠FEH=22.5°,∵EF∥HG,∴∠GHE=∠FEH=22.5°,∴∠AHE=90°+22.5°=112.5°,此时,当B与E重合时,a的值最小,设DH=DA=x,则AH=CH=x,在Rt△AHG中,∠AHG=90°,由勾股定理得：AG=AH=2x,∵∠AEH=∠FEH,∠GHE=∠FEH,∴∠AEH=∠GHE,∴GH=GE=x,∴AB=AE=2x+x,∴a的最小值是=2+；〔2分〕〔2〕如图：过点H作HQ⊥AB于Q,则∠AQH=∠GOH=90°, 在矩形ABCD中,∠D=∠DAQ=90°,∴∠D=∠DAQ=∠AQH=90°,∴四边形DAQH为矩形,∴AD=HQ,〔2分〕设AD=x,GB=y,则HQ=x,EG=2y,由折叠可知：∠AEH=∠FEH=60°,∴∠FEG=60°,在Rt△EFG中,EG=EF×cos60°,EF=4y,在Rt△HQE中,EQ==x,∴QG=QE+EG=x+2y,∵HA=HG,HQ⊥AB,∴AQ=GQ=x+2y,∴AE=AQ+QE=x+2y,〔2分〕由折叠可知：AE=EF,∴x+2y=4y,∴y=x,∴AB=2AQ+GB=2〔x+2y〕+y=x,∴a==．〔2分〕另解：如图：过点H作HQ⊥AB于Q,则∠AQH=∠GOH=90°, 在矩形ABCD中,∠D=∠DAQ=90°,∴∠D=∠DAQ=∠AQH=90°,∴四边形DAQH为矩形,∴AD=HQ,〔2分〕设GB=x,则EG=2x,由折叠可知：∠AEH=∠FEH=60°,∴∠FEG=60°,在Rt△EFG中,EG=EF×cos60°,EF=4x,∴AG=6x∵HA=HG,HQ⊥AB,∴AQ=GQ=3x∴EQ=x在Rt△HQE中,∵∠AEH=60°y=3xy=2x -9x -6FNP 1M QPyxEABCO ∴HQ=3x 〔2分〕∴a==．〔2分〕24．解：〔1〕8)3)(2(=++y x ,∴328-+=x y 328-+=x y 向右平移2个单位,再向上平移3个单位得到x y 8=．∴328-+=x y 是 "反比例平移函数"．〔4分〕〔2〕"反比例平移函数"的表达式为692--=x x y .变换后的反比例函数表达式为xy 3=. 〔4分〕〔3〕如图,当点P 在点B 左侧时,设线段BE 的中点为F ,由反比 例函数中心对称性,四边形PEQB 为平行四边形. ∵四边形PEQB 的面积为16,∴PFB S ∆=4, ∵B <9,3>,F <6,2>.692--=x x y 是xy 3=的 "反比例平移函数", ∴PFB S ∆=OE P S 1∆=4,E <3,1> 〔2分〕过E 作x 轴的垂线,与BC 、x 轴分别交于M 、N 点.111EMP ONE OCP ONMC E OP S S S S S ∆∆∆∆---=四边形.设),(001y x P ,∴⎪⎩⎪⎨⎧=---⨯⨯--=.4)3)(1(213121213,30000000x y y x y y x 即⎩⎨⎧=-=.83,30000x y y x∴⎩⎨⎧==.3,100y x∴1P <1,3>,∴点P 的坐标为〔7,5〕.〔2分〕 当点P 在点B 右侧时,同理可得点P 的坐标为〔15,37〕. 〔2分〕 解法不唯一。

2024年浙江省台州市中考数学一模试卷一、选择题（本题共有10小题，每小题3分，共30分：在每小题给出的四个选项中，只有一项符合题目要求）1．根据计划，我国将在2030年前实现中国人首次登陆月球，开展月球科学考察及相关技术试验等，地月距离的平均值大约为384400公里，数据384400用科学记数法表示为（）A．0.3844×106B．38.44×104C．3.844×105D．3.844×1062．下列运算，结果正确的是（）A．a3+a3＝a6B．（a3）2＝a5C．a3÷2＝a D．3．下面四个古典园林中的花窗图案，既是轴对称图形仅是中心对称图形的是（）A．B．C．D．4．若一件礼物的外包装，其主视图是正方形，则该礼物的外包装不可能是（）A．三棱锥B．圆柱C．正方体D．长方体5．学校随机调查了部分学生一周平均每天的睡眠时间，统计结果如图，则在这组数据中，这些被调查学生睡眠时间的众数和中位数分别是（）A．8，9B．8，8.5C．16，13D．16，14.56．用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，…，按此规律排列下去，则第⑩个图案用的木棍根数是（）A．49B．54C．55D．647．如图，AB切圆O于点B，连接OA交圆O于点C，BD∥OA交圆O于点D，连接CD，若∠A＝34°，则∠OCD的大小为（）A．68°B．56°C．34°D．28°8．《算学启蒙》中记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之？其大意是：快马每天行240里，慢马每天行150里，慢马先行12天，快马几天可追上慢马？若设快马天可追上慢马，由题意得（）A．240x＝150（x+12）B．240（x﹣12）﹣150xC．D．9．小函研究二次函数（a0，a为整数）时，发现下列说法中只有一个是错误的，你认为错误的是（）A．函数与x轴的一个交点为（﹣1，0）B．对称轴为直线x＝1C．a＞0时，函数的最小值为3D．点（2，8）在函数图象上10．如图，四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH，连接BD交CH，EG，AF于点M，O，N，若M，O，N是BD的四等分点，则的值为（）A．B．C．D．二、填空题（本题共有6小题，每小题3分，共18分）11．分解因式：a2+4a＝．12．直角坐标系中，点（3，﹣4）关于坐标原点O成中心对称的点的坐标是．13．一个不透明的袋子里装有1个黑球，2个白球，3个红球，4个绿球，它们除颜色外其余都相同袋中任意摸出一个球是绿球的概率为．14．如图是凸透镜成像示意图，CD是蜡烛AB通过凸选镜N所成的虚像已知蜡烛的高AB 为4.8cm，蜡烛AB离凸透镜MN的水平距离OB为6cm，该凸透镜的焦距OF为10cm，AE∥OF，则像CD的高为cm．15．如图，一次函数y＝x+b的图象分别与x轴，y轴交于点A，B，以线段AB为边向第一象限内作等边三角形ABC，反比例函数y＝（k≠0）图象恰好经过BC边的中点D，与AC边交于点E．若△ODE的面积为，则k的值为．16．已知四边形ABCD是平行四边形，∠ABC＝60°，AB＝4，BC＝6，点E是AD边上一个动点，连接BE，沿BE将△ABE翻折至△BEF（如图1），EF所在的直线与BC交于点H．（1）当点E与点D重合时（如图2），则CH的长为；（2）当CH取最大值时，EF的长为．三、解答题（本题共有8小题，第17～18小题每小题6分，第19～20小题每小题6分，第21～22小题每小题6分，第23～24小题每小题6分，共72分.请务必写出解答过程）17．计算：6÷（﹣+）．玲玲同学的计算过程为：原式＝6÷（）+6÷＝﹣12+18＝6．请你判断玲玲的计算过程是否正确，若不正确，请你写出正确的计算过程．18．在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的三角形为整点三角形．如图，已知整点A（1，3），B（3，4），请在所给网格区域（含边界）上按要求画整点三角形．（1）在图1中画一个等腰三角形ABC，使得点C的横、纵坐标之和为偶数；（2）在图2中画一个Rt△ABP，使得点P在坐标轴上．19．在数学综合实践课上，某学习小组计划制作一个款式如图1所示的风筝：图2是其示意图，已知两条侧翼AB，AC的长为60cm，夹角为100°，AD平分，求B，C两点间的距离．（参考数据：sin50°≈0.64，cos50°≈0.77，tan50°≈0.87）20．青少年体重指数（BMI）是评价青少年营养状况、肥胖的一种衡量方式．其中体重指数BMI计算公式：BMI＝（kg/m2），其中G表示体重（kg），h表示身高（m）．《国家学生体质健康标准》将学生体重指数（BMI）分成四个等级（如表），为了解学校学生体重指数分布情况，八年级某数学综合实践小组开展了一次调查．等级偏瘦（A）标准（B）超重（C）肥胖（D）男BMI≤15.715.7＜BMI≤22.522.5＜BMI≤25.4BMI＞25.4女BMI≤15.415.4＜BMI≤22.222.2＜BMI≤24.8BMI＞24.8【数据收集】小组成员从本校学生中随机抽取部分学生进行问卷调查，并收集数据：【数据整理】调查小组根据收集的数据，绘制了两组不完整的统计图．【问题解决】根据以上信息，解决下列问题：（1）若一位男生的身高为1.6m，体重为51.2kg，则他的体重指数（BMI）属于等级；（填“A”，“B”，“C”，“D”）（2）求本次调查的总人数，并补全条形统计图；（3）求扇形统计图中表示体重指数（BMI）“A”等级的扇形的圆心角的度数；（4）若该校共有2000名学生，估计全校体重指数为“肥胖”的学生约为多少人？21．金师傅购买了一辆某型号的新能源车，其电池电量为60千瓦时．目前有两种充电方案供选择（如表），经测算金师傅发现电池剩余电量y（千瓦时）与已行驶里程x（千米）有如图关系．方案安装费用每千瓦时所需费用方案一：私家安装充电桩2700元0.6元方案二：公共充电桩充电0 1.8元（含服务费）（1）已知新能源车充电时一般损耗率为1.2，电池剩余电量为零时，使用家用充电桩一次性充满电需要费用为60×1.2×0.6＝43.2（元），则电池剩余电量为零时到公共充电桩一次性充满电需要多少费用？（2）当已行驶里程大于300千米时，求出电池剩余电量y（千瓦时）与已行驶里程（千米）的函数表达式，当电池剩余电量为10%时，会提示充电，此时理论上还能继续行驶多少千米？（3）金师傅都是在电池剩余电量不低于30千瓦时就开始充电，请问累计行驶里程为多少千米时，选择私家安装充电桩充电（含安装费用）更合算．22．已知点A（m，p），B（3，q），C（m+2，p）都在二次函数y＝2x2+bx+4的图象上．（1）若m＝1，求该二次函数的表达式；（2）求p+q的最大值；（3）若p＜q＜4，求m的取值范围．23．定义：在四边形内，如果有一点和一组对边组成的两个三角形都是以对边为斜边的等腰直角三角形，那么这个四边形叫做蝴蝶四边形．例如图1，在四边形ABCD中，∠AMB ＝∠CMD＝90°，MA＝MB，MC＝MD，则四边形ABCD为蝴蝶四边形．（1）【概念理解】如图2，正方形ABCD中，对角线AC与BD相交于O．求证：正方形ABCD为蝴蝶四边形；（2）【性质探究】如图3，在蝴蝶四边形ABCD中，∠AMB＝∠CMD＝90°．求证：AC ＝BD；（3）【拓展应用】如图3，在蝴蝶四边形ABCD中，∠AMB＝∠CMD＝90°，MA＝MB ＝，MC＝MD＝1．当△ACD是等腰三角形时，求此时以BD为边的正方形的面积．24．如图，点C在AB为直径的圆O上，连接AC，BC，∠ACB的角平分线交AB于点E，交圆O于点P．G是BP上一点，且PG＝BC，连接AG并延长交CB的延长线于点F，连接EG．（1）求证：AC＝CF；（2）若BC＝3，AC＝4，①求AG的长度；②求△AEG的面积．（3）设＝x，tan∠AGE＝y，求y关于x的函数表达式．。

浙江省台州市天台、椒江、玉环三区2013年九年级第一次模拟考试英语试卷亲爱的考生：欢迎参加考试！请你认真审题，积极思考，仔细答题，发挥最佳水平。

答题时，请注意以下几点：1.全卷共10页。

满分120分。

考试时间100分钟。

2.答案必须写在答题纸相应的位置上,写在试题卷、草稿纸上无效。

3.答题前，认真阅读答题纸上的《注意事项》，按规定答题。

祝你成功！卷一说明: 本卷共四大题, 55小题,满分80分。

第一部分听力部分一、听力（本题有15小题，第一节每小题1分，第二、三节每小题2分，共计25分）第一节：听小对话，请从A、B、C三个选项中选出符合对话内容的图片。

第二节：听下面两段长对话,每段对话后有2-3个问题。

请从A、B、C三个选项中选择正确的答案。

听下面一段较长对话，回答第6-7小题。

6. What is James busy doing?A. Making a travel plan.B. Visiting his pen friends.C. Studying for his final exam.7. Why does James suggest going camping?A. It’s cheaper than staying at a hotel.B. The woman has never camped before.C. It is an exciting experience.听下面一段较长对话，回答第8-10小题。

8. When does the boy want to see a movie?A. This Friday.B. This Saturday.C. This Sunday.9. Which movie can the boy watch?A. The sound of Music.B. My Father’s Birthday.C. Black September.10. How much is the ticket?A. 15 yuan.B. 30 yuan.C. 50 yuan.第三节：听独白，请从A、B、C三个选项中选出正确的选项，完成下面的信息记录表。

2024-2025学年九年级数学上学期期中模拟卷（浙教版）（考试时间：120分钟试卷满分：120分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

4．测试范围：浙教版九上第1~4章（二次函数+简单事件的概率+圆的基本性质+相似三角形）。

5．难度系数：0.65。

第一部分（选择题共30分）一、选择题（本大题共10小题，每小题3分，满分30分．在每个小题给出的四个选项中，只有一项符合题目要求的）1．已知线段a、b，如果a：b＝2：3，那么下列各式中一定正确的是（ ）A．2a＝3b B．a+b＝5C．a+ba =52D．a+3b+2=12．关于二次函数y＝﹣（x+1）2的图象，下列说法错误的是（ ）A．开口向下B．对称轴为直线x＝﹣1C．当x＜﹣1时，y随x的增大而增大D．当x＝﹣1时，函数有最小值，最小值为y＝33．如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB＝CD，已知CE＝2，ED＝8，则⊙O的半径是（ ）A．3B．4C．5D4．如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连接EF．若EF＝BD ＝8，则菱形ABCD 的周长为（ ）A ．8B ．C ．D ．5．如图，身高1.5米的小明（AB ）在太阳光下的影子AG 长1.8米，此时，立柱CD 的影子一部分是落在地面的CE ，一部分是落在墙EF 上的EH ．若量得CE ＝1.2米，EH ＝1.5米，则立柱CD 的高为（ ）A ．2.5mB ．2.7mC ．3mD ．3.6m6．“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”．小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（　）A ．16B ．18C ．23D ．127．如图，在△ABC 中，点D 在AB 上，BD ＝2AD ，DE ∥BC 交AC 于E ，则下列结论不正确的是（ ）A ．BC ＝3DEB ．BD BA =CE CAC ．△ADE ∽△ABCD ．S △ADE =13S △ABC8．已知二次函数y ＝﹣3x 2+12x ﹣9与直线y ＝m ，以下说法不正确的是（ ）A ．若方程﹣3x 2+12x ﹣9＝m 有实数根，则m ≤3B ．若二次函数y ＝﹣3x 2+12x ﹣9与直线y ＝m 交于点E ，F ，若EF ＝6，则m ＝﹣24C ．若x 1，x 2（x 1＜x 2）是方程﹣3x 2+12x ﹣9＝m （m ＜0）的两个根，则x 1＜1＜x 2＜3D ．二次函数y ＝﹣3x 2+12x ﹣9﹣m 图象实质是将二次函数y ＝﹣3x 2+12x ﹣9的图象向下平移m 个单位长度9．如图，点A ，B ，C 是圆O 上的三点，且四边形ABCO 是平行四边形，OF ⊥OC 交⊙O 于点F ，则∠BAF 的度数为（ ）A ．12.5°B ．15°C ．20°D ．22.5°10．如图是二次函数y ＝ax 2+bx +c （a ≠0）图象的一部分，图象过点A （﹣3，0），对称轴为直线x ＝﹣1，给出四个结论：①b 2＞4ac ；②b ﹣2a ＝0；③a +b +c ＞0；④若点B(―52，y 1)，C(―12，y 2)为函数图象上的两点，则y 1＜y 2．其中正确结论是（ ）A ．①②④B ．①④C ．①③④D ．②④第二部分（非选择题 共90分）二、填空题（本大题共6小题，每小题3分，满分18分）11．已知线段AB ＝10，C 为AB 的黄金分割点（AC ＞BC ），则AC ＝ ．12．如图，四边形ABCD 为⊙O 的内接四边形，已知∠BOD ＝140°，则∠BCD 的度数为 ．13．如图，在Rt△ABC中，∠ABC＝90°，AB＝2，∠BCA＝30°，以点B为圆心，AB的长为半径作弧，分别交AC，BC于点D，E，则图中阴影部分的面积为．14．如图，D、E分别是△ABC的边上AB、BC上的点，DE∥AC，若S△BDE ：S△CDE＝1：3，当S△DOE＝1时，则S△AOC的值为．15．已知二次函数y＝ax2+bx+c，当x＝2时，该函数取最大值12．设该函数图象与x轴的一个交点的横坐标为x1，若x1＞4，则a的取值范围是．16．如图1是护眼学习台灯，该台灯的活动示意图如图2所示．灯柱BC＝6cm，灯臂AC绕着支点C可以旋转，灯罩呈圆弧形（即AD和EF）．在转动过程中，AD（EF）总是与桌面BH平行．当AC⊥BH时，AB＝46cm，DM⊥MH，测得DM＝37.5cm（点M在墙壁MH上，且MH⊥BH）；当灯臂AC转到CE 位置时，FN⊥MH测得FN＝13.5cm，则点E到桌面BH的距离为cm．若此时点C，F，M在同一条直线上，EF的最低点到桌面BH的距离为35cm，则EF所在圆的半径为cm．三、解答题（本大题共8小题，满分72分．解答应写出文字说明，证明过程或演算步骤）17．（8分）已知：二次函数y ＝ax 2+bx +c 的图象与x 轴相交于A （﹣4，0），B （2，0）两点，与y 轴相交于点C （0，﹣4），点D 为抛物线的顶点．（1）求二次函数的解析式；（2）求S △ABC ：S △ACD 的值．18．（8分）对垃圾进行分类投放，能提高垃圾处理和再利用的效率，减少污染，保护环境．为了检查垃圾分类的落实情况，某居委会成立了甲、乙两个检查组，采取随机抽查的方式分别对辖区内的A ，B ，C ，D 四个小区进行检查，并且每个小区不重复检查．（1）甲组抽到A 小区的概率是 ；（2）请用列表或画树状图的方法求甲组抽到A 小区，同时乙组抽到C 小区的概率．19．（8分）如图，⊙O 的直径AB 垂直于弦CD ，垂足为E ，AE ＝2，CD ＝8．（1）求⊙O 的半径长；（2）连接BC，作OF⊥BC于点F，求OF的长．20．（8分）如图，在△ABC中，点D在BC边上，点E在AC边上，且AD＝AB，∠DEC＝∠B．（1）求证：△AED∽△ADC；（2）若AE＝1，EC＝3，求AB的长．21．（8分）在平面直角坐标系中，设二次函数y=―12(x―2m)2+3―m（m是实数）．（1）当m＝2时，判断函数图象与x轴有几个交点；（2）小明说二次函数图象的顶点在直线y=―12x+3上，你认为他的说法对吗？为什么？（3）已知点P（a+1，c），Q（4m﹣5+a，c）都在该二次函数图象上，求证：c≤13 8．22．（10分）如图，△ABC内接于⊙O，∠ABC＞90°，△ABC的外角∠EAC的平分线交⊙O于点D，连接DB，DC，DB交AC于点F．（1）求证：△DBC是等腰三角形．（2）若DA＝DF．①求证：BC2＝DC•BF．②若⊙O的半径为5，BC＝6，求S△BCFS△ADF的值．23．（10分）跳台滑雪是冬季奥运会比赛项目之一．如图，运动员通过助滑道后在点A处起跳经空中飞行后落在着陆坡BC上的点P处，他在空中飞行的路线可以看作抛物线的一部分．这里OA表示起跳点A到地面OB的距离，OC表示着陆坡BC的高度，OB表示着陆坡底端B到点O的水平距离．建立如图所示的平面直角坐标系，从起跳到着陆的过程中，运动员的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y=―116x2+bx+c．已知OA＝70m，OC＝60m，落点P的水平距离是40m，竖直高度是30m．（1）点A的坐标是，点P的坐标是；（2）求满足的函数关系y=―116x2+bx+c；（3）运动员在空中飞行过程中，当他与着陆坡BC竖直方向上的距离达到最大时，直接写出此时的水平距离．24．（12分）在⊙O中，半径为8．（1）如图一，若B为AC上一个点（不与A、C重合），且ABC的度数为90°，①求∠ABC的度数；②若E为弦AB的中点，F为弦BC的中点，求线段EF的长度．（2）如图二，若AB的度数为60°，CD的度数为120°，BD的度数为60°，点E为弦AB的中点，点F为弦CD的中点，求线段EF的长度．。

2024年初中毕业生适应性考试语文亲爱的考生：欢迎参加考试!请你认真审题，仔细答题，发挥最佳水平。

答题时，请注意以下几点：1.全卷共6页，17小题。

满分120分，其中卷面书写3分。

考试时间120分钟。

2.答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上无效。

3.答题前，请认真阅读答题纸上的“注意事项”,按规定答题。

4.要求书写规范、工整，保持卷面整洁。

一、学校开展“传承汉字文化”主题活动，请你参与。

(68分)【活动缘起】网络时代，文字记录方式发生革命性变化，jiàn①▲盘代替了书写，音频、视频取代了原有的文字表达。

许多人只能大致记住汉字的形态，渐渐提笔忘字，“汉字失写症”màn② ▲延。

互联网已成为错别字的温床，“账与帐很多人分不清”“登陆和登录，也让人很抓狂”,这样的现象很常见，如右侧易错词词云图所示。

日曰很不俱程事落#湘器天燃气仔象1.结合语境，根据拼音正确书写汉字。

(2分)jiàn.①▲_盘màn②▲延2.从上面词云图中，任选一个不规范用词加以改正，并从词义角度分析原因。

(3分)示例：“帐号”改为“账号”,因为“贝”字旁与钱物有关，而“巾”字旁与纺织物有关，“账号”本用于金钱往来，所以应该是“贝”字旁。

▲改为▲, 因为【汉字溯源】在距今大约六千年的半坡遗址等地方，已经出现刻划符号，共达五十多种。

它们整齐规范，并且有一定的规律性，具备了简单文字的特征，学者们认为这可能是汉字的萌芽。

汉字形成为系统的文字是公元前16世纪的商朝。

考古证实，在商朝早期，中国文明已发展到相当高的水平，其主要特征之一就是甲骨文的出现。

甲骨文是刻在龟甲和兽骨上的古老文字。

【汉字比较】中国汉字与其他文明古国文字比较表文字出现时期数量字体状态中国汉字公元前3000年约4500个(甲骨文)甲骨文、金文、小篆、隶书、草书、楷书、行书等全世界至今有16亿人使用巴比伦楔形文字公元前3200年640个基本字刻符、岩画、文字画、图画字消失了2100年埃及圣书字公元前3000年2000多个符号碑铭体、僧侣体、大众体消失了500多年古印度哈拉巴文字公元前2300年500个符号印章文字消失了3800年【汉字守护】传承中国文字，庵续汉字之美，需要我们规范使用汉字。

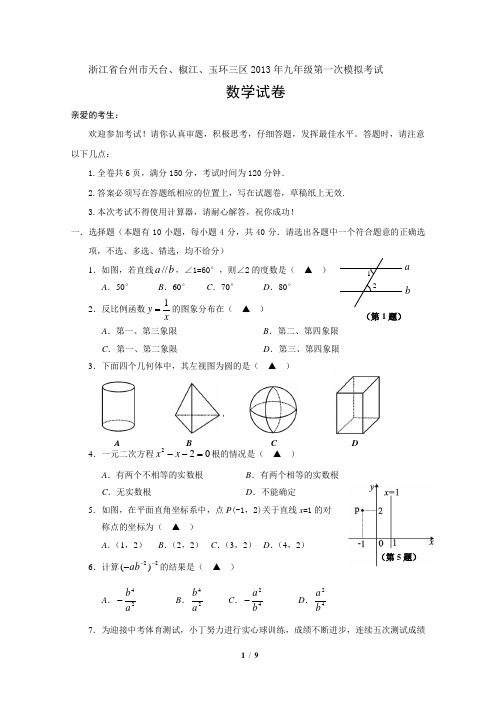
浙江省台州市天台、椒江、玉环三区2013年九年级第一次模拟考试数学试卷亲爱的考生：欢迎参加考试！请你认真审题，积极思考，仔细答题，发挥最佳水平。

答题时，请注意以下几点：1.全卷共6页，满分150分，考试时间为120分钟．2.答案必须写在答题纸相应的位置上，写在试题卷，草稿纸上无效.3.本次考试不得使用计算器，请耐心解答，祝你成功！一．选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）1．如图，若直线b a //，∠1=60°，则∠2的度数是（ ▲ ）A ．50°B ．60°C ．70°D ．80° 2．反比例函数xy 1=的图象分布在（ ▲ ） A ．第一、第三象限 B ．第二、第四象限 C ．第一、第二象限D ．第三、第四象限3．下面四个几何体中，其左视图为圆的是（ ▲ ）4．一元二次方程022=--x x 根的情况是（ ▲ ）A ．有两个不相等的实数根B ．有两个相等的实数根C ．无实数根D ．不能确定5．如图，在平面直角坐标系中，点P (-1，2)关于直线x =1的对 称点的坐标为（ ▲ ） A ．（1，2）B ．（2，2）C ．（3，2）D ．（4，2）6．计算22)(---ab 的结果是（ ▲ ）A ．24ab -B ．24a bC ．42b a -D ．42ba7．为迎接中考体育测试，小丁努力进行实心球训练，成绩不断进步，连续五次测试成绩21ba （第1题）A B C D（第5题）分别为6分，7分，8分，9分，10分，那么数据6，7，8，9，10的方差为（ ▲ ） A ．40B ．8C ．10D ．28．如图，AD 是△ABC 的角平分线，下列结论中错误．．的是（ ▲ ） A ．CDBDS S ACD ABD ＝∆∆ B ．ACAB S S ACD ABD ＝∆∆ C ．CD BD AC AB = D ．AC ADAD AB = DCABAO（第8题图） （第9题图） （第10题图）9．我们把弧长等于半径的扇形叫等边扇形．如图，扇形OAB 是等边扇形，设OA ＝R ，下列结论中：①∠AOB ＝60°；②扇形的周长为3R ；③扇形的面积为221R ；④点A 与半径OB 中点的连线垂直OB ；⑤设OA 、OB 的垂直平分线交于点P ，以P 为圆心，P A 为半径作圆，则该圆一定会经过扇形的弧AB 的中点．其中正确的个数为（ ▲ ） A ．1个B ．2个C ．3个D ．4个10．如图，半径为3cm 的⊙O 从斜坡上的A 点处沿斜坡滚动到平地上的C 点处，已知∠ABC =120°，AB =10 cm ，BC =20cm ，那么圆心O 运动所经过的路径长度为（ ▲ ） A ．30 cmB ．29 cmC ．28 cmD ．273cm二．填空题（本题有6小题，每小题5分，共30分）11．分解因式：=-92x ▲ ．12．台州市是中国黄金海岸线上一个年轻的滨海城市，因其境内有天台山而得名，她拥有约745 000米长的海岸线，占浙江省海岸线总长度的28%．数据745 000用科学记数法表示为 ▲ ．13．若点P （m ，n ）在一次函数12-=x y 的图象上，则=-n m 21▲ ． 14．已知四边形ABCD 内一点E ，若EA =EB =EC =ED ，∠BAD =70°，则∠BCD 的度数为▲ ．EDBA（图2）A'F EAD（第14题图） （第15题图）15．如图，矩形ABCD 中，AB =4，BC =8.若将它沿EF 折叠，使点B 与点D 重合，点A落在点A ′处，则tan ∠EFD = ▲ ．16．如图1，R t △ABC 中，∠ACB =90°，AC =1，BC =2，将△ABC 放置在平面直角坐标系中，使点A 与原点重合，点C 在x 轴正半轴上.将△ABC 按如图2方式顺时针滚动(无滑动)，则滚动2013次后，点B 的坐标为 ▲ ．（第16题图1） （第16题图2）三．解答题（本题有8小题，第17~20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）17．计算：()023201328--+-.18．解不等式组 ，并把解集在数轴上表示出来.19．在Rt △ABC 中，AB =4，∠ACB =90°，∠ABC =30°，将△ABC 放在平面直角坐标系中（如图），使点C 与坐标原点O 重合，A ，B 分别在y 轴和x 轴的正半轴上． （1）分别求点A ，B 的坐标；（2）将△ABC 向左平移，使平移距离等于线段BC 的长度，此时点A 刚好落在反比例函数xky =的图象上，求k 的值.EDC⎩⎨⎧--+2312x x ＞ 3420．如图，AB 是⊙O 的直径，D ，E 是⊙O 上的两点，AE 和BD 的延长线交于点C ，连接DE .（1）求证：△CDE ∽△CAB ； （2）若∠C =60°，求证：DE =21AB .21．如图是一同学设计的一个电路图，K 1、K 2、K 3、K 4为四个开关. （1）当闭合四个开关中的任意一个时，求灯泡会亮的概率；（2）当闭合四个开关中的任意两个时，请用列表法或画树形图，求出灯泡会亮的概率．22．请仔细阅读下面两则材料，然后解决问题：材料1：小学时我们学过，任何一个假分数都可以化为一个整数与一个真分数的和的形式，同样道理，任何一个分子次数不低于分母次数的分式都可以化为一个整式与另一个分式的和（或差）的形式，其中另一个分式的分子次数低于分母次数.如： . 材料2：对于式子2132x ++，因为 ≥ ，所以21x +的最小值为1，所以213x +的最 大值为3，所以2132x++的最大值为5．根据上述材料，解决下列问题： 问题1：把分式 化为一个整式与另一个分式的和（或差）的形式，其中另一个分式的分子次数低于分母次数.问题2：当x 的值变化时，求分式 的最小值． 23．我们把三角形内部的一个点到这个三角形三边所在直线距离的最小值叫做这个点到这个三角形的距离．如图1，PD ⊥BC 于D ，PE ⊥AC 于E ，PF ⊥AB 于F ，如果PE ≥PF ≥PD ，则称PD 的长度为点P 到△ABC 的距离.如图2、图3，在平面直角坐标（第19题） （第20题） （第21题）2x 012178422++++x x x x 15)1(1)5()1()(14222---=--++-+-=---x x x x x x x x x 12178422++++x x x x系中，已知A （6，0），B （0，8），连接AB .（1）若P 在图2中的坐标为（2，4），则P 到OA 的距离为 ▲ ，P 到OB 的距离为▲ ，P 到AB 的距离为 ▲ ，所以P 到△AOB 的距离为 ▲ ； （2）若点Q 是图2中△AOB 的内切圆圆心，求点Q 到△AOB 距离的最大值； （3）若点R 是图3中△AOB 内一点，且点R 到△AOB 的距离为1，请画出所有满足条件的点R 所形成的封闭图形，并求出这个封闭图形的周长.（画图工具不限）24．已知，在平面直角坐标系xoy 中，点A 的坐标为（0，2），点P （m ，n ）是抛物线上的一个动点． （1）如图1，过动点P 作PB ⊥x 轴，垂足为B ，连接P A ，请通过测量或计算，比较P A与PB 的大小关系：P A ▲ PB （直接填写“>”“<”或“=”，不需解题过程）； （2）请利用（1）的结论解决下列问题：①如图2，设C 的坐标为（2，5），连接PC ， AP +PC 是否存在最小值？如果存在，求点P 的坐标；如果不存在，简单说明理由；②如图3，过动点P 和原点O 作直线交抛物线于另一点D ，若AP =2AD ，求直线OP 的解析式.（第24题图1） （第24题图2） （第24题图3）（第23题图1） （第23题图2） （第23题图3）1412+=xy数学参考答案及评分标准一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）二、填空题（本题有6小题，每小题5分，共30分） 11.()()33-+x x ； 12. 7.45×105； 13.21； 14. 110°；15. 2；16. ()256712014，+.三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）17.解：原式=-2+4-1………………………………………………6分（每项化简正确得2分）=1…………………………………………………………2分18.解： 由①得x ≤1……………………………………………………2分由②得x ＜-2……………………………………………………2分 ∴原不等式组的解集为：x ＜-2………………………………2分 解集在数轴上表示：略………………………………………2分19.解：（1）∵AB =4，∠ACB =90°，∠ABC =30° ∴OA =AB sin30°=2，OB =AB cos30°=32…………2分∴A （0，2），B （0，32）……………………………2分天台 椒江 玉环2013年九年级第一次模拟考试（2）∵平移距离为32∴平移后A 的坐标为（32-，2）……………………2分∴34232-=⨯-=k …………………………………2分20.证明：（1）∵四边形ABDE 内接于⊙O ，∴∠CDE =∠A ，………………2分又∵∠C =∠C∴△CDE ∽△CAB ………………………………………………2分 （2）连接AD∵AB 是⊙O 的直径，∴∠ADC =∠ADB =90°又∵∠C ＝60°，∴2160cos =︒=AC CD ……………………2分 由（1）已证△CDE ∽△CAB ，∴21==AC CD AB ED ∴AB ED 21=………………………………………………2分21.解：（1）闭合四个开关中的任意一个共有4种等可能结果，而灯炮会亮的结果有1个，∴P （灯炮会亮）=41………………………………………4分（2）根据题意可以列出表格（或画出树形图）（略）………2分从表格（或树形图）可以看出，所有可能出现的结果共有12个，这些结果出现的可能性相等，灯炮会亮的结果有6个，∴P （灯炮会亮）=21126=……………………………………4分 22.问题1：解：原式=222822216168222++-=++-++x x x x x x ………………………5分1)1(282++-=x ……………………………………………2分问题2：解：∵0)1(2≥+x ，∴1)1(2++x 的最小值为1，∴1)1(22++x 的最大值为2，∴1)1(282++-x 的最小值为6，即12178422++++x x x x 的最小值为6. ………………………………………5分23.解：（1）P 到OA 的距离为 4 ，P 到OB 的距离为 2 ，P 到AB 的距离为 0.8 ，所以P 到△AOB 的距离为 0.8 ；………………………………4分 （2）当点Q 到△AOB 三边距离相等即Q 为△AOB 的内心时，Q 到△AOB 的距离最大.…………………………………………………2分 设这个最大值为h ，则86211021821621⨯⨯=⨯⨯+⨯⨯+⨯⨯h h h ，解得h =2.∴点Q 到△AOB 距离的最大值为2.……………………………………2分（3）设点Q 为△AOB 的内心，连接QA ，QB ，QO ，分别取QA ，QB ，QO 的中点E ，F ，G ，连接EF ，FG ，GE ，则△EFG 即为所要画的图形.（只要画图正确即可，不必书写画图过程）……2分由画图可知，△EFG ∽△ABO ，由上题及已知条件可知，△EFG 与△ABO 的相似比为21，因为△ABO 的周长为24，所以△EFG 的周长为12.……………………2分24.解：（1）P A ＝ PB …………………………………………………………2分 （2）①过点P 作PB ⊥x 轴于B ，由（1）得P A =PB ， 所以要使AP +CP 最小，只需当BP +CP 最小，因此当C ，P ，B 共线时取得，此时点P 的横坐标等于点C （2，5）的横坐标，所以点P 的坐标为（2，2）……………………………………………4分②当点P 在第一象限时，如图，作DE ⊥x 轴于E ，作PF ⊥x 轴于F ， 由（1）得：DA =DE ，P A =PF ∵P A =2DA ，∴PF =2DE ，∵△ODE ∽△OPF ，∴21==PF DE OF OE设P （m ，1412+m ），则D （m 21，21812+m ）∵点D 在抛物线1412+=x y 上， ∴12141218122+⎪⎭⎫⎝⎛=+m m ，解得22±=m 此时P （22，3），直线OP 的解析式为x y 823=………………6分 当P 在第二象限时，同理可求得直线OP 的解析式为x y 823-=………………………2分 综上，所求直线OP 的解析式为x y 823=或x y 823-=.（负舍去）。

台州市2024年九年级教学质量评估试题语文亲爱的考生：欢迎参加考试！请你认真审题，仔细答题，发挥最佳水平。

答题时，请注意以下几点：1.全卷共6页，17小题。

满分120分，其中卷面书写3分。

考试时间120分钟。

2.答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上无效。

3.答题前，请认真阅读答题纸上的“注意事项”，按规定答题。

4.要求书写规范、工整，保持卷面整洁。

学习语文，可以在课堂上，也可以在课外生活中。

班级开展“我的语文生活”综合性学习活动，邀请你一起参与。

活动一：拟新年书单1. 阅读《新周刊·新年的第一份书单》的序言，完成各题。

为什么要坚持阅读？这是老生cháng 谈的话题。

当热搜频繁更新，短视频高度qīn 占人们的时间，直播成为最大的公共话题策源地……阅读似乎退到了国人精神生活的角落。

但如果仔细聆听，还是能在公共cáo 杂的背后，听到流动的文学性。

诗人韩东的一首《温柔的部分》，大概能概括书本对我们精神世界的锚(A. máo B. miáo)定作用：“我有过寂寞的乡村生活，它形成了我生活中温柔的部分，每当厌倦的情绪来临，就会有一阵风为我解脱，至少我不那么无知，我知道粮食的由来。

”书页是( ) ，字行是( ) ，书写是耕耘，阅读是收获，这永远是“精神粮食”的重要由来。

（1）根据拼音写汉字。

老生cháng ____ 谈qīn ____ 占cáo _____ 杂（2）给文段中的加点字“锚”选择正确的读音（）A. máoB. miáo（3）根据语境，为空白处选出恰当的词语（）A. 田垄田地B. 田地田垄【答案】（1）①. 常②. 侵③. 嘈（2）A （3）B【解析】【小问1详解】本题考查字形。

老生常谈，lǎo shēng cháng tán，原指老书生经常讲的话。

后指人们听惯了的没有新意的话。

2024年浙江省初中毕业生学业模拟考试（台州卷）数 学 试题卷亲爱的考生：欢迎参加考试！请你认真审题，仔细答题，发挥最佳水平. 答题时，请注意以下几点：1. 全卷共4页，满分120分，考试时间120分钟.2. 答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上无效.3. 答题前，请认真阅读答题纸上的“注意事项”，按规定答题.4. 本次考试不得使用计算器.一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）1. “中国空间站”入选了2023年全球十大工程成就．空间站离地球的距离约为380 000米，数据380 000用科学计数法可表示为（ ▲ ）.A. 38×104B.3.8×106C.3.8×105D.0.38×106 2.下列四个2024年巴黎奥运会项目图标中，既是轴对称图形又是中心对称图形的是（ ▲ ）.A. B. C. D.3. 下列计算正确的是（ ▲ ）.A ．32x x xB ．523)(x xC ．33)x x （D ．326x x x4. 如图，直线AB ∥CD ，BC 平分∠ABD ，若∠1＝55°，则∠2＝（ ▲ ）.A ．70°B ．65°C ．60°D ．55°5. 对于平面图形上的任意两点P ，Q ，如果经过某种变换得到新图形上的对应点P ′，Q ′，保持PQ ＝P ′Q ′，我们把这种变换称为“保距变换”，下列变换中不一定是“保距变换”的是（ ▲ ）. A . 平移 B. 旋转 C. 轴对称 D. 位似 6. 小明的期中与期末测试成绩如下表：A.小明期末与期中总分相同B.小明英语期末名次一定在中等以上C.小明数学期末成绩比期中有进步D.小明语文期末成绩比期中有退步(第4题) (第7题) （第10题）DC B AG FE D C B A 2 1 D C B A7. 如图，Rt △ABC 中，∠ABC ＝90°，AB ＝3，BC ＝2，以点C 为圆心，BC 长为半径作圆弧交AC 于点D ，则AD 长在（ ▲ ）.A. 0与1之间 B . 1与2之间 C. 2与3之间 D. 3与4之间8. 有如下数列：a 1，a 2，a 3，a 4，a 5，a 6，...，a n-2，a n-1，a n ，...，满足a n -2·a n ＝2a n -1，已知a 1＝1，a 3＝4， 则a 2024＝（▲）.A.8B.6C.4D.29. 学校要制作一块广告牌，请来两名工人，已知甲单独完成需4天，乙单独完成需6天，若先由乙做1天，再两人合作，完成任务后共得到报酬900元，若按各人的工作量计算报酬，则分配方案为（ ▲ ）. A ．甲360元，乙540元B ．甲450元，乙450元C ．甲300元，乙600元D ．甲540元，乙360元10. 如图，在Rt △ABC 中，∠ACB ＝90°，以AB 为边向三角形外作正方形ABDE ，作EF ⊥BC 于点F ，交对角线AD 于点G ，连接BG. 要求△BFG 的周长，只需要知道（ ▲ ）. A.线段BF 的长度 B.线段AC 的长度 C.线段FG 的长度 D.线段BC 的长度 二、填空题（本题有6小题，每小题4分，共24分） 11. 分解因式：x 2 xy ＝ ▲ ．12. 一个不透明的口袋中有3个质地相同的小球，其中2个红色，1个蓝色. 随机摸取一个小球是红色小球的概率是 ▲ ．13. 小明用刻度尺（单位：cm ）测量某三角形部件的尺寸．如图所示，已知∠ACB=90°，D 是AB 的中点，点A ，B 对应的刻度分别是1，8，则CD ＝ ▲ cm ．14. 某绿化队原来用漫灌方式浇绿地，a 天用水m 吨，现改用喷灌方式，可使这些水所用的天数为2a 天，现在比原来每天节约用水 ▲ 吨．（用含a ，m 的代数式表示）15. 在平行四边形ABCD 中，点E ，F 在BC 边上，把△ABE 沿直线AE 折叠，△CDF 沿直线DF 折叠，使点B ，C 落在对角线AC 上的点G 处，若∠AGD ＝110°，则∠B 的度数为 ▲ ．(第13题) (第15题)16. 已知抛物线k x a y +=2)2(－上有A （－2，y 1），B （1，y 2），C （4，y 3），D （5，y 4）四个点，某数学兴趣小组研究后得到三个命题：①若y 1＋y 3 > y 2＋y 4，则a > 0；②若y 2－y 3 > 0，则y 1－y 4 > 0； ③若y 2 y 3 = 0，则y 1 y 4 > 0. 属于真命题是 ▲ ．（填写序号）三、解答题（本题有8小题，第17～19题每题6分，第20，21题每小题8分，第22，23题每题10分，第24题12分，共66分） 17.π0(2)2 .18. 解不等式组：14,23.x x xEGFDCBAA BC D19. 图1是太阳能路灯的实物图，图2是其示意图，AB 垂直于地面l ，AB ＝800 cm ，BC ＝105 cm ，∠ABC＝108°，求点C 离地面的高度. (结果精确到1cm ，参考数据：sin18°≈0.31，cos18°≈0.95 ，tan18°≈0.31 )20. 如图，一次函数b kx y 与反比例函数xcy的图象相交于A ，B 两点，A ，B 的坐标分别为(2，n )，(－4，－2).（1）分别求出一次函数和反比例函数的解析式；（2）已知点M (m ，c )，B (m ，d )，分别在一次函数和反比例函数上，当c ＞d 时，直接写出m 的取值范围．（第20题） （第21题）21. 如图，在△ABC 中，∠ABC 的平分线BD 交AC 边于点D ，已知∠ADB ＝2∠ABD ．（1）求证：AB ²＝AD AC ；（2）若DC ＝2AD ＝2，求∠A 的度数．22. 某中学开展专家讲座，帮助学生合理规划周末使用手机的时间，并在讲座前后对本校学生周末手机使用时间情况进行随机抽样调查，制成如下统计图表（数据分组包含左端值不包含右端值）．（1）在讲座开展前抽取的学生中周末使用时长在哪个区间的人数最多？占抽取人数的百分之几？ （2）该校共有学生1500人，请估计讲座开展后全校周末使用手机8小时以上的学生人数；（3）小军认为，活动开展后的样本中周末使用手机6小时以上的人数与讲座前相比变化不大，所以讲座并没有起到效果．请结合统计图表，对小军分析数据的方法及讲座宣传活动的效果谈谈你的看法．DCBAlD BCA图1 图223. 图1是某校园的紫藤花架，图2是其示意图，它是以直线AB 为对称轴的轴对称图形，其中曲线AC ，AD ，BE ，BF 均是抛物线的一部分.图1 图2 图3素材1：某综合实践小组测量得到点A ，B 到地面距离分别为5米和4米.曲线AD 的最低点到地面的距离是4米，与点A 的水平距离是3米；曲线BF 的最低点到地面的距离是289米，与点B 的水平距离是4米．素材2：按图3的方式布置装饰灯带GH ，GI ，KL ，MN ，HJ ，布置好后成轴对称分布，其中GI ，KL ，MN ，HJ 垂直于地面， GI 与HJ 之间的距离比KL 与MN 之间的距离多2米．任务一：（1）在图２中建立适当的平面直角坐标系，求曲线AD 的函数解析式； 任务二：（2）若灯带GH 长度为d 米，求 MN 的长度．（用含ｄ的代数式表示）； 任务三：（3）求灯带总长度的最小值．24. 如图，半圆O 的直径AB ＝6.点C 在半圆O 上，连结AC ，BC ，过点O 作OD ∥AC 分别交BC ， AB于点E ，D ，连结AD 交BC 于点F . （1）求证：点D 是 BC的中点； （2）将点O 绕点F 顺时针旋转90 °到点G .①当点G 在线段AD 上，求AC 的长；②当点G 在线段AC 上，求sin ∠ABC 的值.(第24题)FBOA E CDBO备用图A数学答案第1页共5页2024年浙江省初中毕业生学业模拟考试（台州卷）数学参考答案和评分细则一、选择题（本题有10小题，每小题3分，共30分）题号12345678910答案CACADBBDBD二、填空题(本题有6小题，每小题4分，共24分)11．x (x -y )12．2313．3.514．2m a15．75°16．①③三、解答题(本题有8小题，第17～19题每题6分，第20，21题每小题8分，第22，23题每题10分，第24题12分，共66分)17.（6分）解：原式=3+1－4…3分=0…6分18．（6分）解：由①得：5x <-…2分由②得：1x <…4分∴不等式组的解集为：5x <-.…6分19.（6分）解：过点C 作CE ⊥AD ，垂足为E∵CE ⊥AD ，∴∠CEB ＝90°∴∠C ＝∠ABC －∠AEC ＝18°…2分∵BE ＝BC sin ∠C ，∴BE ＝105×0.31＝32.55≈33（cm ）…4分AE ＝AB ＋BE ＝833cm…6分答：点C 距离地面的高度是833cm20.（8分）解：（1）将B （－4，－2）代入xcy =42-=-c 得解得c=8…2分∴反比例函数的解析式：xy 8=令x=2代入得y=4∴A(2,4)将点A （2，4），点B （-4，-2）代入y =kx +b 得⎩⎨⎧+-=-+=bk b k 4224…4分数学答案第2页共5页解得⎩⎨⎧==21b k ∴一次函数的解析式为y =x +2…6分（2）-4<m <0或m >2（写对一个一分共2分）21.（8分）解证明：（1）∵BD 平分∠ABC ∴∠ABC ＝2∠ABD ＝2∠DBC∵∠ADB ＝2∠ABD ∴∠ABC ＝2∠ADB ……………1分∵∠ADB ＝∠DBC ＋∠C ∴∠ABD ＝∠C………………2分∴△ABD ∽△ACB ………………3分∴ACABAB AD =即AB ²＝AD ⋅AC ………………4分（2）由（1）得∠DBC ＝∠C ∴BD ＝CD ＝2……………1分∵2AD =2∴AD =1∴AC ＝3∵AB ²＝AD ⋅AC ∴AB=3……………2分∴AB ²＋AD ²＝BD ²……………3分∴∠A =90°……………4分22.（10分）（1）在开展前周末手机使用时长为4～6小时的同学最多．……2分5＋8＋15＋12＋10＝50（人）15÷50×100％＝30％……4分（2）16＋24＋40＋16＋4＝100（人）4÷100×100％＝4％1500×4％＝60（人）……2分由样本估计总体，全校讲座开展后周末使用手机8小时以上大约有60人……3分（3）因为忽略了两次样本容量的差异，所以小军分析的方法不合理……1分样本中周末使用手机时长6小时以上的人数由44％下降为20％，所以此次讲座宣传活动是有效果的．……2分（未运用统计量说明的给1分）23.（10分）（1）如图，以地面所在直线为x 轴，AB 所在直线为y 轴，建立如图所示的直角坐标系.设()234y a x =-+，代入()05A ,得：()25034a =-+，解得:19a =，()21349y x =-+ (3)分数学答案第3页共5页（2）2H d x =,12M d x =-,2113492M d y ⎛⎫=--+ ⎪⎝⎭214523699d d =-+214523699MN d d =-+…4分(3)设曲线BF 的函数解析式为：()22849y a x =-+，代入()04B ,得：()2284049a =-+解得：118a =，()21284189y x =-+设灯带总长度为w ,GH d =,22w MN HJ GH=++22145212822436991829d d d d⎡⎤⎛⎫⎛⎫=-++-++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦2111761239d d =-+,当2x =时，1739w =最小值.…3分24．（12分）解：（1）解法一：∵AB 是半圆O 直径∴∠C ＝90°……………………2分∵OD ∥AC∴∠OEB ＝∠C ＝90°，即OD ⊥BC……………………3分∴ BD＝ CD ，即点D 是 BC 的中点……………………4分解法二：∵OD ∥AC ∴∠D ＝∠CAD ……………………1分∵OA ＝OD ∴∠D ＝∠OAD …………………2分∴∠OAD ＝∠CAD……………………3分∴ BD＝ CD ，即点D 是 BC 的中点……………………4分解法三：连结CO ∵AB 是半圆O 直径∴∠ACB ＝90°……………………2分∵OD ∥AC ∴∠OEB ＝∠ACB ＝90°，即OD ⊥BC……………………3分∵OB ＝OC ，OE ＝OE ∴Rt △BOE ≌Rt △COE （HL ）∴∠BOD ＝∠COD ∴ BD ＝ CD ，即点D 是 BC的中点……………………4分（说明：各种方法合理均可.）（2）①解法一：连结OF ，作FG ＝OF∵点O 绕点F 顺时针旋转90°到点G ∴∠OFG ＝90°∴AF ＝DF……………………1分FBOAE CDF OAEC D G数学答案第4页共5页又∵OD ∥AC∴∠D ＝∠CAD ，∠C ＝∠DEC ∴△ACF ≌△DEF （AAS ）……………………2分（由平行线直接得△ACF ∽△DEF 也给分.）∴AC ＝DE ∵O 是AB 中点，OD ∥AC ∴AC ＝2OE ……………………3分∵直径AB ＝6∴OE ＋DE ＝OD ＝3∴AC ＝2……………………4分解法二：连结OF ，BD ，作FG ＝OF ∵点O 绕点F 顺时针旋转90°到点G ∴∠OFG ＝90°∴AF ＝DF……………………1分又∵AB 是半圆O 直径∴∠ADB ＝90°∴OF ∥BD∴△OEF ∽△DEB ，OF :BD ＝1:2……………………2分∴DE ＝2OE ∵直径AB ＝6∴OE ＝1……………………3分∵O 是AB 中点，OD ∥AC ∴AC ＝2OE ＝2……………………4分（2）②解法一：如图，构造对应图形易证△CFG ≌△EOF………………1分∴OE ＝CF 由①得，AC ＝2OE ，△ACF ∽△DEF .设OE ＝CF ＝x ，则AC ＝2x ，DE ＝3－x ∴CF :AC ＝EF :DE ＝1:2∴EF ＝……………………2分∴CE ＝BE ＝CF ＋EF ＝∴在Rt △BOE 中，解得：x ＝1.8……………………3分∴sin ∠ABC ＝＝0.6……………………4分（说明：各种方法合理均可.如：连结BD，通过比例和勾股定理求BD 的长等也可解决问题）解法二：如图，构造对应图形，作FH ⊥AB 于点H 易证△CFG ≌△EOF……………………1分∴OE ＝CF ，EF ＝CG ，∠OFE ＝∠CGF 易证△CFG ≌△HFO ，△CFA ≌△HFA ∴AC ＝AH ＝3，∠OFE ＝∠CGF ＝∠BOF ∴AG ＝AO ＝BO ＝BF ＝3……………………2分F B OAEC DGFBO AECD GF B O AE C DGH由①得，AC＝2OE.设OE＝CF＝x，EF＝CG＝y，则AC＝2x ∴2x－y＝AG＝3，x＋y＋y＝BF＝3（BC＝2CE＝2x＋2y，再由AC2＋BC2＝AB2也可）解得：x＝1.8……………………3分∴sin∠ABC＝＝0.6……………………4分数学答案第5页共5页19．（本题满分6分）(第19题)21．（本题满分8分）（1）（4分）(第21题)（2）（4分）考号[0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9]20．（本题满分8分）（1）（6分）（2）（2分）.(第20题)一、选择题（本题有10小题，每小题3分，共30分，请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）18．（本题满分6分）解不等式组：1423.x x x ⎧⎨⎩＋＜－，＜＋2024年中考模拟考试（一）数学答题卷学校班级姓名说明1、准考证号和选择题请用2B 铅笔填涂；2、除选择题外请用0.5mm 黑色中性笔答题；3、保持答题卷整洁，请勿折叠.缺考标记：[](考生不得填涂)二、填空题（本题有6小题，每小题4分，共24分）11．．12．．13．．14．．15．．16．．.17．（本题满分6分）计算：9＋（π-2）0＋|－2|．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每小题8分，第22，23题每题10分，第24题12分，共66分）◤□■◤◥24．（本题满分12分）（1）（4分）(第24题)（2）①（4分）②（4分）22．（本题满分10分）（1）（4分）（2）（3分）（3）（3分）23．（本题满分10分）（1）（3分）（图2）（2）（4分）（图3）（3）（3分）模拟（一）数学答题卷第3页共4页模拟（一）数学答题卷第4页共4页。

台州市2024年九年级教学质量评估试题数学参考答案和评分细则一、选择题（本题共10小题，每小题3分，共30分）题号12345678910答案BDACCD DACC二、填空题（本题共6小题，每小题4分，共24分）11.2(答案不唯一)12.x (x -2y )13.3114.13215.27°16.a1三、解答题（本题共8小题，第17～19题每小题6分，第20，21题每小题8分，第22，23题每小题10分，第24题12分，共66分）17.（1）计算：2)2(163-+--=3−4+4…………………………（3项计算，错一项扣1分）=3；…………………………3分（2）解不等式组：⎩⎨⎧>+>-．21;813x x 解不等式①得：x >3；…………………………1分解不等式②得：x >1；…………………………1分⸫不等式组的解集为：x >3.…………………………1分18.作法如图所示.（说明：尺规作图作出AC 的中点O 得4分，连接BO 得2分，共6分.其它合理作法均给分.）…………………………6分19.在Rt △OBD 中，cos20°=OBOD，…………………………3分⸫OB ≈940.OD≈10.6cm.…………………………3分答：折射光线OB 长约为10.6cm.20.（1）解：设线段BC 的解析式为：v =kt +b .…………………………1分把B （230，40），C （270，0）代入解析式得：⎩⎨⎧=+=+027040230b k b k ，…………………………1分解得：⎩⎨⎧==2701-b k .…………………………1分∴v =−t +270.…………………………1分（2）设线段OA 的解析式为：v =k 't .把A （90，40）代入，得k '=94.∴49v t =.…………………………1分把30v =代入v =-t +270得240t =.…………………………1分把30v =代入49v t =得1352t =.…………………………1分∴列车速度不低于30米/秒的行驶时间为：13534524022-=（秒）.……………1分21.（1）解：∵△BCE 是等边三角形，∴∠BCE =60︒，在正方形ABCD 中，∠BCD =90︒，∴∠DCE =BCD BCE ∠-∠=30︒，………………………2分又∵EC =BC =CD ，∴∠DEC =（180°−∠DCE ）÷2=（180°−30°）÷2=75°.………………………2分（2）证明：∵CE =CD ，∴∠DEC =∠CDE =75°，………………………1分∴BD 是正方形的对角线，∴∠CDF =45°，∴∠DFE =∠DCE+∠CDF=30°+45°=75°，…………………………1分∴∠DFE =∠CDE ，又∵∠DEF =∠CED ，∴△EDF ∽△ECD ，…………………………1分∴DE EFEC DE=，即：2DE EF EC =⋅.…………………………1分22.解：（1）解法一：1号饲料效果较好，理由如下：13.4106.37.35.49.47.36.33.57.38.35.4=+++++++++=A x （kg ），……2分71.3102.33.36.35.44.39.37.34.45.36.3=+++++++++=B x （kg ），……2分A 水池样本平均重量大于B 水池样本平均重量，因此，1号饲料效果较好.……1分解法二：如果学生用中位数判断饲料效果，且计算正确，结论正确，扣2分，因为中位数不能准确判断饲料的喂养效果.具体得分点如下：1号饲料效果较好，理由如下：A 水池样本重量的中位数为3.75kg ，……………………1分B 水池样本重量的中位数为3.6kg.……………………1分A 水池样本重量的中位数大于B 水池样本重量的中位数，因此，1号饲料效果较好.……………………1分（2）A 水池符合出售标准的条数为：200104⨯=80（条）.……………………2分B 水池符合出售标准的条数为：160102⨯=32（条）.……………………2分80+32=112（条）.根据样本估计总体得：估计此时这360条鱼中符合出售标准的鱼大约有112条.………………1分23.（1）解：当p =10时，C 坐标为（10，40），由对称得点A 坐标为（-10，40），…………………………1分∴抛物线AB 的解析式为：()211040.20y x =-++…………………………2分（2）①解：根据题意，设)3511y E ，（，)3022y E ，（.∵21L L <，∴213035y y +<+，即：35+()21355020p p ⎡⎤--+-⎢⎥⎣⎦<30+()21305020p p ⎡⎤--+-⎢⎥⎣⎦，……………2分化简得：65-2p >20，∴245<p ，…………………………1分∴2458<≤p .…………………………1分②解：设EF −AC =2d ，三段塑料管总长度为L .根据题意可得：），（p d d p E -+-+502012，∴）（p d d p L -+-++=502012222，化简得：110101012+--=）（d L ，…………………………1分当d =10时，L 有最大值110.∴当EF 与AC 的差为20m 时，三段塑料管总长度最大，最大值为110m.……2分24.（1）解：设和美角的度数为x .根据题意可得：x +90°+x +x =180°，…………1分解得：x =30°，∴和美角的度数为30°.……………2分（2）证明：如图1，作BD ⊥AB 交AC 于D ，∴∠ABD =90°，∵△ABC 是和美三角形，∠ABC 是钝角，∠A 是和美角，∴∠ABC =∠ABD +∠DBC=90°+∠DBC =90°+∠A ，∴∠DBC =∠A ，又∵∠C =∠C ，∴△ABC ∽△BDC ，……………………2分∴A ABBDAC BC tan ==.……………………1分（如图2，作CD ⊥AC 交AB 延长线于D ，也可证.其它证法，合理均给分.）（3）①如图3，当∠EAC 为和美角时，由（2）得：ACBCAC CE BAC ==∠tan ，∴CE =BC =5，∵∠CEB =∠AED ，∠ADE =∠ABC ，∴AD =AE ，作CF ⊥AB 于F ，图1图2∴∠ACB =∠CFB ，∴△ABC ∽△CBF ，∴EF =FB =13252=AB BC ，∴AD =AE =13－EB =13119.……………………2分如图4，当∠ACE 为和美角时，∵△AEC ∽△DEB ，∴∠EBD 为和美角，由（2）得：DBADDB DE ABD ==∠tan ，∴AD =DE ，∴∠DAE =∠AED=∠CEB =∠DCB ，∴BE =BC =5，作DH ⊥AB 于H ，∴AH =HE =42513=-，由△ADH ∽△ABD ，∴522=⋅=AB AH AD ，∴AD =13252=.……………………2分②22或215-.……………………2分解析：设∠CAB =a.图5图6图7图8ⅰ.如图5，若∠CAB 与∠CDB 是和美角，则∠ACD =∠BCD =45°，CE =CB ，a =22.5°.所以22==OD CG ED CE .ⅱ.如图6，若∠CAB 与∠DCB 是和美角，则∠CEA =90°+a ，∠ACE =90−2a ，∠DCB =2a ，∠CBD =90°+2a ，由△BDC 内角和可得a =18°.所以215-==ED OE ED CE .ⅲ.如图7，若∠ACD 与∠CDB 是和美角，则∠CEA =135°−0.5a ，∠ACE =45°−0.5a ，∠DCB =45°+0.5a ，∠CBD =90°+a ，由△BDC 内角和可得a =18°.所以215-==ED GE ED CE .ⅳ.如图8，若∠ACE 与∠DCB 是和美角，则∠CEA =135°−0.5a ，∠ACE =45°-0.5a ，∠DCB =45°−0.5a ，由∠ACB =90°可得a =0°，这种情形不存在.图4。

2023年浙江省台州市椒江五中中考语文模拟试卷一、积累与运用（17分）1．（4分）阅读下面文段，完成任务。

二十秒钟的① （shùn ）息间，整个夜空露出笑脸，金色的新月像一把镰钩高高挂在空中，一朵淡淡的云彩② （ zh ē）住了它的笑容，显现出一个若隐若现的月晕．；星星眨巴着亮晶晶的小眼睛，熙熙攘攘，③ （zhuì）满天空，一直连接上银河的明亮光带。

（1）（3分）根据拼音写出汉字。

①②③（2）（1分）加点字在文中的正确读音是A.yùnB.y ūn2．（10分）根据提示，写出最恰当的古诗文名句。

最美不如初相遇。

“忽如一夜春风来，① ”，这是岑参在塞外遇见的奇丽雪景。

“② ，风正一帆悬”，这是王湾在北固山下遇见的壮观江景。

“③ ，并怡然自乐”，这是武陵人误入桃花源，遇见的老幼同乐、幸福和谐的美好场景。

“箫鼓追随春社近，④ ”，这是陆游出游农家遇见的古朴风俗的生动画卷。

“⑤ ， ”，这是苏轼在《水调歌头》中与中秋圆月相遇时，发出的对亲友的思念与祝福。

虽然前路障碍重重，但李白还是在黑暗的现实中，遇见了“理想之光”，在《行路难》中唱出了满怀信心的强音：“⑥ ， 。

”面对疫情来袭，我们遇见了临危受命的医护人员，这让我想到诸葛亮在《出师表》中所说的“⑦ ， ”；茫茫诗海中，与你邂逅，是我今生最美的相遇。

3．（3分）下列文学常识的说法，表述有误的一项是（ ）A ．《孟子》是孟子及其门人所作，是儒家经典著作，记录了孟子的仁政、民本等政治主张。

B ．《儒林外史》是清代吴敬梓的长篇讽刺小说，深刻揭露了封建科举制度的虚伪腐败，范进、严监生、孔乙己等都是其中的艺术典型。

C．老舍，原名舒庆春，杰出的语言大师，人民艺术家。

代表作有《骆驼祥子》《四世同堂》《茶馆》等。

D．“一门父子三词客，千古文章四大家”中的“三词客”指苏洵、苏轼、苏辙父子三人。

“四大家”指韩愈、柳宗元、欧阳修、苏轼。

二、阅读（64分）4．（9分）阅读回答问题。