下载文档原格式
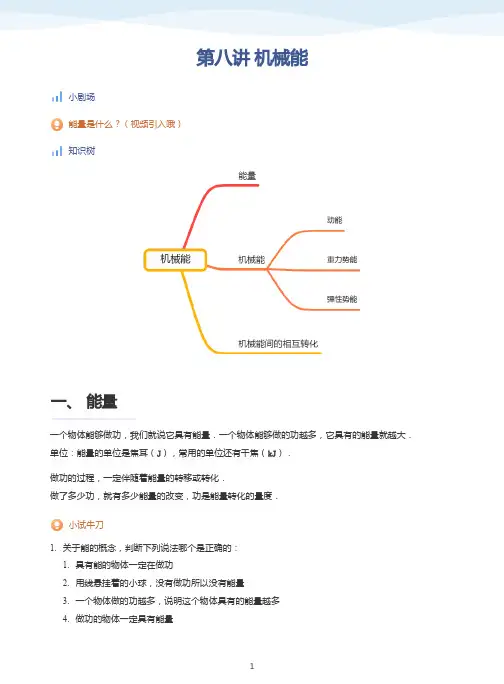
第八讲 机械能小剧场能量是什么？（视频引入哦）知识树一、能量一个物体能够做功，我们就说它具有能量．一个物体能够做的功越多，它具有的能量就越大．单位：能量的单位是焦耳（），常用的单位还有千焦（）．做功的过程，一定伴随着能量的转移或转化．做了多少功，就有多少能量的改变，功是能量转化的量度．小试牛刀1.2.3.4.1.关于能的概念，判断下列说法哪个是正确的：具有能的物体一定在做功用线悬挂着的小球，没有做功所以没有能量一个物体做的功越多，说明这个物体具有的能量越多做功的物体一定具有能量5. 6. 7.物体具有的能量多，说明这个物体做的功一定多绷紧的弓能射出去箭，所以具有能量做功可以引起能量改变，根据做功的多少可以衡量能量变化的多少反转课堂推荐题目A.B.C.D.2.下列关于能量的说法中正确的是（ ）做功的物体具有能量，不做功的物体没有能量做功多的物体能量就多，做功少的物体能量就少能够做功的物体具有能量，但不一定就做功能量多的物体所做的功一定就多二、机械能1.动能影响动能的因素决定动能大小的两个因素是物体的质量和物体的运动速度。
要研究动能的大小与质量的关系时，应保证小球在平面上具有相同的速度。
把质量不同的小球放在斜面的同一高度由静止开始滚下。
结论：质量相同的物体，运动的速度越大，物体的动能就越大；要研究动能的大小与速度的关系时，应保证小球的质量相同。
把同一个小球分别放在同一斜面的不同高度由静止开始滚下。
结论：运动速度相同的物体，质量越大，物体的动能就越大。
总结：物体的质量越大、运动的速度越大，动能就越大；而速度对物体动能大小的影响比较显著。
运动的物体可以对外做功，我们说它具有能量．物体由于运动而能够做功，它具有的能量叫做动能．动能的大小与物体的质量、速度有关．小试牛刀（1）（2）3.在探究“物体动能大小跟哪些因素有关”时，某同学用质量分别是和的两个钢球（）从同一斜面的不同高度和静止滑下，如图所示．实验中需要通过观察木块移动的距离来判断小球的动能大小，这种研究物理问题的方法是 （选填“控制变量法”“转换法”或“等效替代法”），若水平面是绝对光滑的，你认为该实验 （选填“能”或“不能”）达到目的．由甲丙两图得出“物体的动能大小与质量有关”的实验结论，你认为这个结论正确还是不正确，理由是 ．百步穿杨（1）（2）（3）（4）4.如图所示，某小组设计了一组装置来探究“物体的动能大小与哪些因素有关”，小球按图示位置由静止释放，当小球摆动到竖直位置时，恰好与静止在水平面上的木块发生碰撞，木块都会在水平面上滑行一定距离后停止．三张图所示的三次实验中，摆线的长保持不变，小球、的质量，悬线与竖直方向的夹角．图甲中将摆球从图示位置由静止释放，摆球向下摆动的过程中，动能逐渐 ，重力势能逐渐 （均填“增大”或“减小”）．本实验中通过 反映小球撞击木块前的动能大小．第一组实验：对比甲、乙图所示实验可得出初步结论： ．（5）在图丙实验中，木块被撞后滑出了木板，现在需要重做实验，甲同学建议是换用一个较大的木块，乙同学建议换同样材料的较长木板，丙同学建议降低小球下摆的角度．你认为应当采用（选填“甲”“乙”“丙”）同学的建议．本实验中用到了、这两个常用的物理实验思维方法．反转课堂推荐题目（1）（2）5.如图所示是探究动能大小与哪些因素有关的实验装置：实验中通过观察木块在同一水平面上被推动的距离来比较．在探究动能与速度大小的关系时，要保持小球的不变，让小球从斜面（选填“相同”或“不同”）的高度滚下，以不同的速度推动木块移动．下列研究实例中运用了这种物理研究方法的是．A．探究“平面镜成像的特点”B．探究“通过电阻的电流跟电阻两端电压的关系”C．探究磁场时，引入“磁感线”2. 重力势能物体由于被举高而具有的能量叫做重力势能．重力势能与物体的质量（）、所处的高度（）有关．小试牛刀6.如图是一小球从桌面滚落后的运动轨迹，、两处高度相同．点的重力势能点的重力势能；点的动能点的动能．（均选填“大于”“小于”或“等于”）7.如图所示，学习小组的同学在探究“物体的重力势能的大小跟哪些因素有关”时，设计了以下实验：（1）（2）（3）实验方案：三个相同的木桩插在沙坑里，露出沙坑的高度相同，如甲图所示．取三个铁块从空中静止释放后撞击木桩，木桩陷入沙坑，如乙图所示．在此实验中，我们可以通过观察 来比较铁块重力势能的大小．若，，如图乙所示：比较、情况，说明．比较、情况，说明 ．实验得出的结论是：物体重力势能的大小跟物体的有关．百步穿杨A.B. C.D.8.如图所示，在空中以相同速度水平匀速直线飞行的加油机和受油机，在加油的过程中，下列说法正确的是（ ）加油机动能减小，重力势能减小，机械能减小受油机动能减小，重力势能不变，机械能不变加油机动能减小，重力势能不变，机械能减小受油机动能减小，重力势能增大，机械能增大A.球在点时受平衡力作用B.球在点时速度最大C.从到，球的动能减少D.从到，球的势能增加9.如图，细线上端固定，下端拉着小球在竖直平面内摆动，、是球摆动过程中的最高点，是最低点，不计空气阻力，则（ ）反转课堂推荐题目A.B.C.D.10.小明同学踢足球，如图所示为球离开脚后向上运动到一定高度又落回地面的运动轨迹，不计空气阻力，关于足球离开脚后的运动过程，下列说法中正确的是（）足球上升过程中，足球受力方向是竖直向下的足球上升过程中，小明对足球做功足球运动到最高点时，其动能为零足球下落过程中，动能转化为重力势能3. 弹性和弹性势能物体在外力的作用下，它的形状会发生变化，称为形变．如果外力撤消，物体的形变能够完全消失，恢复原状，这种形变称为弹性形变，这种性质叫做弹性．我们把发生弹性形变的物体具有的能量叫做弹性势能．物体的弹性形变越大，具有的弹性势能越大．小试牛刀A.B.C.D.11.下列关于弹性势能的说法，正确的是（ ）橡皮泥的形变越大，它具有的弹性势能越大弹簧的弹性越大，它具有的弹性势能越大弹簧越长，它具有的弹性势能越大对于给定的弹簧来说，它的弹性形变越大，它具有的弹性势能越大12.图右是玩弹弓的情景．经验表明，橡皮筋拉得越长，同样的“子弹”射得越远，这说明橡皮筋的弹性势能与 有关；橡皮筋把“子弹”射出是 能变为能．百步穿杨A.B.C.D.13.如图所示，将木块放在压缩了的弹簧旁，释放弹簧，木块沿水平地面向右运动，离开弹簧后，木块运动一段距离后停下来，下列说法中不正确的是（）此装置可以用来探究弹性势能和弹簧形变大小的关系木块离开弹簧之前，弹簧的弹性势能一直在减小木块离开弹簧之后，木块的动能逐渐减少木块运动时，木块所受的重力对木块做了功独步天下（1）（2）（3）（4）14.在探究弹性势能的大小跟哪些因素有关时，小志提出了如下猜想：猜想一：弹性势能的大小与弹簧被压缩的程度有关；猜想二：弹性势能的大小与弹簧的材料有关；猜想三：弹性势能的大小与弹簧的长度有关；猜想四：弹性势能的大小与弹簧的粗细有关．为验证猜想一，他设计了如图所示实验，实验时将同一弹簧压缩 （相同/不同）的长度（弹簧被压缩后未超过其弹性限度），将小球置于弹簧的右端，松开后小球碰到同一位置的相同木块上，分析比较，从而比较弹性势能的大小．为验证猜想二，需选用 的两根弹簧，实验时将两根弹簧压缩 （相同/不同）的长度，将小球置于弹簧的右端，松开后小球碰到同一位置的相同木块上，对数据进行比较分析时，若 ，说明弹性势能的大小与弹簧的材料有关；若水平面绝对光滑，本实验将 （能/不能）达到探究目的；小志根据实验现象认为：小球和木块移动一段距离后都要停下来，所以弹簧、小球和木块所具有的动能和势能最终都消失了，你认为小志的观点是 （正确/不正确）的．4. 机械能动能和势能统称为机械能．一个物体可以具有动能，又可以具有势能，动能和势能之和称为机械能．A.他在下滑过程中没有力做功B.他的势能转化为动能，机械能不变C.他在下滑过程中，重力势能转化为动能D.他的重力势能减小，动能不变，机械能减少15.小朋友沿着滑梯匀速滑下，下列说法中正确的是（ ）A.B.C.D.16.如图所示，用轻质弹簧（弹簧质量和空气阻力忽略不计）把小球挂在天花板上，当小球从如图水平位置放手后摆动到最低点的过程中，下列说法正确的是（）小球的机械能守恒小球的重力势能的减少量等于小球动能的增加量小球的重力势能的减少量大于弹簧弹性势能的增加量小球的重力势能的减少量小于小球动能的增加量5.机械能转化的模型动能和势能统称为机械能，动能和势能可以相互转化． 如下图所示滚摆，在下降过程中，越转越快，它的重力势能越来越小，动能越来越大，重力势能转化为动能；滚摆上升过程中，越转越慢，重力势能越来越大，动能越来越小，动能转化为重力势能．如上图所示的单摆，小球从A 点摆向最低点B 时，位置越来越低，重力势能减小，动能增大，重力势能转化为动能；从B 点摆向C 点时，小球上升，位置升高，动能减小，重力势能增大，动能转化为重力势能．③蹦床运动，是动能与势能的转化④人造地球卫星许多人造地球卫星沿椭圆轨道绕地球运行。
流体机械能转换实验流体机械能转换实验⼀、实验⽬的熟悉流动流体中各种能量和压头的概念及其互相转换关系，在此基础上掌握柏努利⽅程。
⼆、实验原理1. 流体在流动时具有三种机械能：即①位能，②动能，③压⼒能。
这三种能量可以互相转换。
当管路条件改变时（如位置⾼低，管径⼤⼩），它们会⾃⾏转换。
如果是粘度为零的理想流体，由于不存在机械能损失，因此在同⼀管路的任何⼆个截⾯上，尽管三种机械能彼此不⼀定相等，但这三种机械能的总和是相等的。
2. 对实际流体来说，则因为存在内摩擦，流动过程中总有⼀部分机械能因摩擦和碰撞⽽消失，即转化成了热能。
⽽转化为热能的机械能，在管路中是不能恢复的。
对实际流体来说，这部分机械能相当于是被损失掉了，亦即两个截⾯上的机械能的总和是不相等的，两者的差额就是流体在这两个截⾯之间因摩擦和碰撞转换成为热的机械能。
因此在进⾏机械能衡算时，就必须将这部分消失的机械能加到下游截⾯上，其和才等于流体在上游截⾯上的机械能总和。
3. 上述⼏种机械能都可以⽤测压管中的⼀段液体柱的⾼度来表⽰。
在流体⼒学中，把表⽰各种机械能的流体柱⾼度称之为“压头”。
表⽰位能的，称为位压头；表⽰动能的，称为动压头（或速度头）；表⽰压⼒的，称为静压头；已消失的机械能，称为损失压头（或摩擦压头）。
这⾥所谓的“压头”系指单位重量的流体所具有的能量。
4. 当测压管上的⼩孔（即测压孔的中⼼线）与⽔流⽅向垂直时，测压管内液柱⾼度（从测压孔算起）即为静压头，它反映测压点处液体的压强⼤⼩。
测压孔处液体的位压头则由测压孔的⼏何⾼度决定。
5. 当测压孔由上述⽅位转为正对⽔流⽅向时，测压管内液位将因此上升，所增加的液位⾼度，即为测压孔处液体的动压头，它反映出该点⽔流动能的⼤⼩。
这时测压管内液位总⾼度则为静压头与动压头之和，我们称之为“总压头”。
6. 任何两个截⾯上位压头、动压头、静压头三者总和之差即为损失压头，它表⽰液体流经这两个截⾯之间时机械能的损失。
机械能转换实验重力势能与动能转化实验机械能转换实验：重力势能与动能转化实验摘要：本实验旨在通过观察重力势能与动能之间的转化过程，进一步理解机械能转换的基本原理。
通过实验操作，可观察到物体从重力势能转化为动能的过程，并测量物体的质量、高度和速度等参数，验证机械能守恒定律的成立。
1. 实验目的通过实验操作，验证机械能守恒定律，重点观察和测量物体从重力势能转化为动能的过程。
2. 实验器材- 实验台- 物体（如小球、弹簧等）- 条形测量标尺- 秤盘- 记时器- 计算器3. 实验原理机械能转换实验涉及到重力势能和动能的转化。
当一个物体在高度为h处具有重力势能E_p时，其动能E_k为零。
而当该物体由高度h滑落到高度为0时，其重力势能为零，而动能不为零。
根据机械能守恒定律，机械能守恒定律可以表达为：E_p + E_k = 常数。
4. 实验步骤（注：实验步骤可根据实际情况进行适当调整，以下仅供参考）步骤1：准备实验装置在实验台上放置一条直标尺，将物体放置于起始位置，确保其高度为h。
步骤2：测量物体质量使用秤盘将物体放在平衡位置，记录物体的质量m。
步骤3：测量起始高度使用直标尺测量物体的起始高度h，记录结果。
步骤4：测量初始速度将物体从起始位置释放，并使用记时器记录物体滑落至终点所需的时间t。
根据公式 v = h / t，计算物体在滑落过程中的初始速度v。
步骤5：测量动能根据动能公式E_k = 0.5 * m * v^2，计算物体在滑落过程中的动能。
步骤6：测量重力势能根据重力势能公式 E_p = m * g * h，计算物体在起始位置所具有的重力势能。
步骤7：比较与分析将动能和重力势能的结果进行比较，并观察它们之间的关系。
验证机械能守恒定律是否成立。
5. 实验数据记录与处理记录实验中测得的物体质量、起始高度、滑落时间、初始速度、动能和重力势能等数据，并进行适当的数据处理与分析。
6. 实验结果与讨论根据实验数据计算得到的动能和重力势能之间进行比较，并观察它们之间的变化规律。
化工原理实验讲义专业:环境工程应用化学教研室2015.3实验一 流体机械能转化实验一、实验目的1、了解流体在管内流动情况下，静压能、动能、位能之间相互转化关系，加深对伯努利方程的理解。
2、了解流体在管内流动时，流体阻力的表现形式。
二、实验原理流动的流体具有位能、动能、静压能、它们可以相互转换。
对于实际流体， 因为存在内摩擦，流动过程中总有一部分机械能因摩擦和碰撞，而被损失掉。
所以对于实际流体任意两截面，根据能量守恒有：2211221222f p v p v z z H g g g g ρρ++=+++上式称为伯努利方程。
三、实验装置（d A =14mm ，d B =28mm ，d C =d D =14mm ，Z A -Z D =110mm ）实验装置与流程示意图如图1-1所示，实验测试导管的结构见图1-2所示：图1-1 能量转换流程示意图图1-2实验导管结构图四、操作步骤1.在低位槽中加入约3/4体积的蒸馏水，关闭离心泵出口上水阀及实验测试导管出口流量调节阀和排气阀、排水阀，打开回水阀后启动离心泵。
2.将实验管路的流量调节阀全开，逐步开大离心泵出口上水阀至高位槽溢流管有液体溢流。
3.流体稳定后读取并记录各点数据。
4.关小流量调节阀重复上述步骤5次。
5.关闭离心泵出口流量调节阀后，关闭离心泵，实验结束。
五、数据记录和处理五、结果与分析1、观察实验中如何测得某截面上的静压头和总压头，又如何得到某截面上的动压头？2、观察实验，对于不可压缩流体在水平不等径管路中流动，流速与管径的关系如何？3、实验观测到A、B截面的静压头如何变化？为什么？4、实验观测到C、D截面的静压头如何变化？为什么？5、当出口阀全开时，计算从C到D的压头损失？六、注意事项1．不要将离心泵出口上水阀开得过大以免使水流冲击到高位槽外面，同时导致高位槽液面不稳定。
2．流量调节阀开大时，应检查一下高位槽内的水面是否稳定，当水面下降时应适当开大泵上水阀。
实验13 流体机械能转换实验—、实验目的1.1熟悉流动流体中各种能量和压头的概念及其相互转换关系，进一步理解伯努利方程的含义；1.2 观察流体的变化规律；1.3 观察各项压头的变化规律。
二、基本原理2.1 流体能量的形式流体在流动时有3种机械能，即位能、动能、压强能。
这3种能量是可以相互转换的。
当管路条件改变时，它们会自行转化。
如果是理想流体，因不存在因摩擦和碰撞而产生的机械能损失，因此同一管路的任何两个截面上，尽管3种机械能彼此不一定相等，但这3种机械能的总和是相等的。
对实际流体来说，因为存在内摩擦，流动过程中总有部分机械能因摩擦和碰撞而损失，即转化为热能。
转化为热能的机械能在管路中是不能恢复的，因此对实际流体来说，两个截面上的机械能的总和不相等，两者之差就是流体在这两个截面之间因摩擦和碰撞转化成为了热的机械能，即机械能损失。
2.2 液体柱表示流体机械能流体机械能可用测压管中的一段液体柱的高度来表示。
在流体力学中，把表示各种机械能的流体柱高度称之为“压头”。
表示位能的称为位压头，表示动能的称为动压头，表示压力能的称为静压头，表示已消失的机械能的称为损失压头。
当测压管上的小孔（即测压孔的中心线）与水流方向垂直时，测压管内的液位高度即为静压头，它反映测压点处液体的压强大小。
测压孔处液体的位压头则由测压孔的几何高度决定。
当测压孔由上述方位转为正对水流方向时，测压管内液位将因此上升，所增加的液位高度即为测压孔处液体的动压头，它反映出该点水流动能的大小。
这时测压管内液位总高度则为静压头与动压头之和。
任何两个截面上，位压头、动压头、静压头三者总和之差即为损失压头，它表示流体流过这两个截面之间的机械能的损失。
三、实验装置的基本情况（流程图见图一）不锈钢离心泵 WB50/025 型低位槽 700×453×496 材料不锈钢高位槽 445×445×500 材料有机玻璃实验测试导管的结构尺寸见图二中标绘四、实验的操作方法：1.将低位槽灌有一定数量的蒸馏水，关闭离心泵出口调节阀门及实验测试导管出口调节阀门而后启动离心泵。
机械能转化演示实验资料机械能转化是一个科学严谨而又实用性极强的学科。
在生产生活中，机械能转化已经成为不可或缺的一部分。
为了更好地学习和掌握机械能转化相关的知识，我们进行了一系列的实验。
实验1：利用轮轴原理制作手摇发电机实验材料：木板、电机、电池、随动轮、手摇轴、电线、螺丝、手摇碗、LED灯等。
实验过程：利用轮轴原理，将手摇碗链接到手摇轴上，再通过随动轮的运动带动电机产生电能，最后通过电线连接到LED灯中，实现手摇发电。
实验结果：手摇发电器可以有效地将机械能转化为电能，并且可以通过LED灯来展示转化效果。
实验2：通过弹簧振动实现机械能转化实验材料：弹簧、弹簧架、根据需要选择不同大小的物块实验过程：将物块放到弹簧上，让弹簧受到压缩变形，然后释放弹簧，让弹簧反弹并带动物块振动。
实验3：利用滑轮原理实现机械能转化实验材料：木板、滑轮、金属线、重物（如水瓶）等。
实验过程：将重物挂在金属线上，通过滑轮原理将金属线绕过滑轮，使得重物得以升高，并实现机械能到重力势能的转化。
实验材料：压缩弹簧、斜面、柱体、逆向垂直轴等。
实验过程：将柱体放置在斜面上，然后压缩弹簧，使其在斜面上滑动，在滑动过程中，机械能被转化为重力势能和动能并保持平衡。
实验结果：利用机械结构可以实现机械能的转化，并且通过柱体滑动的过程来展示转化效果。
以上实验均通过不同的实验材料和装置实现了机械能的转化，每个实验都展示了机械转化效果并形象生动地展示了相关原理和应用。
通过这些实验，我们不仅能够更好地理解机械能转化的原理和应用，还能够更加深入地学习与掌握相关知识，不断提高自己的科学实验能力。
机械能转化演示实验
一、实验目的
1.观测动、静、位压头随管径、位置、流量的变化情况，验证连续性方程和柏努利方程。
2.定量考察流体流经收缩、扩大管段时，流体流速与管径关系。
3.定量考察流体流经直管段时，流体阻力与流量关系。
4.定性观察流体流经节流件、弯头的压损情况。
二、基本原理
化工生产中，流体的输送多在密闭的管道中进行，因此研究流体在管内的流动是化学工程中一个
重要课题。
任何运动的流体，仍然遵守质量守恒定律和能量守恒定律，这是研究流体力学性质的基本
出发点。
1.连续性方程
对于流体在管内稳定流动时的质量守恒形式表现为如下的连续性方程：
⎰⎰⎰⎰=2211vdA dA v ρρ （1－1） 根据平均流速的定义，有 222111A u A u ρρ= （1－2）
即 21m m = （1－3）
而对均质、不可压缩流体，常数==21ρρ，则式（1－2）变为
2211A u A u = （1－4）
可见，对均质、不可压缩流体，平均流速与流通截面积成反比，即面积越大，流速越小；反之，
面积越小，流速越大。
对圆管，4/2
d A π=，d 为直径，于是式（1－4）可转化为 2
22211d u d u = （1－5） 2.机械能衡算方程
运动的流体除了遵循质量守恒定律以外，还应满足能量守恒定律，依此，在工程上可进一步得到
十分重要的机械能衡算方程。
对于均质、不可压缩流体，在管路内稳定流动时，其机械能衡算方程（以单位质量流体为基准）
为：
f e h g
g u z h g g u z +++=+++ρρ22
221211p 2p 2 （1－6） 显然，上式中各项均具有高度的量纲，z 称为位头，g u 2/2称为动压头（速度头），g ρ/p 称为
静压头（压力头），e h 称为外加压头，f h 称为压头损失。
关于上述机械能衡算方程的讨论：
（1）理想流体的柏努利方程
无黏性的即没有黏性摩擦损失的流体称为理想流体，就是说，理想流体的0=f h ，若此时又无外
加功加入，则机械能衡算方程变为： g
g u z g g u z ρρ22
221211p 2p 2++=++ （1－7） 式（1－7）为理想流体的柏努利方程。
该式表明，理想流体在流动过程中，总机械能保持不变。
（2）若流体静止，则0=u ，0=e h ，0=f h ，于是机械能衡算方程变为 g
z g z ρρ2211p p +=+ （1－8） 式（1－8）即为流体静力学方程，可见流体静止状态是流体流动的一种特殊形式。
3.管内流动分析
按照流体流动时的流速以及其它与流动有关的物理量（例如压力、密度）是否随时间而变化，可
将流体的流动分成两类：稳定流动和不稳定流动。
连续生产过程中的流体流动，多可视为稳定流动，
在开工或停工阶段，则属于不稳定流动。
流体流动有两种不同型态，即层流和湍流，这一现象最早是由雷诺（Reynolds ）于1883年首先发
现的。
流体作层流流动时，其流体质点作平行于管轴的直线运动，且在径向无脉动；流体作湍流流动
时，其流体质点除沿管轴方向作向前运动外，还在径向作脉动，从而在宏观上显示出紊乱地向各个方
向作不规则的运动。
流体流动型态可用雷诺准数（Re ）来判断，这是一个无因次数群，故其值不会因采用不同的单位
制而不同。
但应当注意，数群中各物理量必须采用同一单位制。
若流体在圆管内流动，则雷诺准数可
用下式表示：
μρdu =
Re （1－9）
式中：Re —雷诺准数，无因次；
d —管子内径，m ； u —流体在管内的平均流速，m ／s ；
ρ—流体密度，kg ／m 3；
μ—流体粘度；Pa·s 。
式（1－9）表明，对于一定温度的流体，在特定的圆管内流动，雷诺准数仅与流体流速有关。
层
流转变为湍流时的雷诺数称为临界雷诺数，用Re c 表示。
工程上一般认为，流体在直圆管内流动时，
当Re≤2000时为层流；当Re>4000时，圆管内已形成湍流；当Re 在2000至4000范围内，流动处于
一种过渡状态，可能是层流，也可能是湍流，或者是二者交替出现，这要视外界干扰而定，一般称这
一Re 数范围为过渡区。
三、装置流程
该装置为有机玻璃材料制作的管路系统，通过泵使流体循环流动。
管路内径为30mm ，节流件变
截面处管内径为15mm 。
单管压力计1和2可用于验证变截面连续性方程，单管压力计1和3可用于
比较流体经节流件后的能头损失，单管压力计3和4可用于比较流体经弯头和流量计后的能头损失及
位能变化情况，单管压力计4和5可用于验证直管段雷诺数与流体阻力系数关系 ，单管压力计6与5
配合使用，用于测定单管压力计5处的中心点速度。
在本实验装置中设置了两种进了方式：1、高位槽进料；2、直接泵输送进料，设置这两种方式是为了让学生有对比，当然直接泵进料液体是不稳定的，会产生很多空气，这样实验数据会有波动，所以一般在采集数据的时候建议采用高位槽进料。
四、实验操作
1.关闭管路排水阀、出口阀，在下水槽中加满清水。
2、通过循环泵将水打入上水槽中，使整个管路中充满流体，并保持上水槽液位一定高度，观察并记录流体静止状态时各管段高度。
3、通过出口阀调节管内流量，注意保持上水槽液位高度稳定（即保证整个系统处于稳定流动状态），并尽可能使转子流量计读数在刻度线上。
观察并记录各单管压力计读数和流量值。
4、改变流量，观察各单管压力计读数随流量的变化情况。
注意每改变一个流量，需给予系统一定的稳流时间，方可读取数据，记录各单管压力计读数。
5、结束实验，关闭循环泵，全开出口阀排尽系统内流体，之后打开排水阀排空管内沉积段流体。
6、注意：
1）若不是长期使用该装置，对下水槽内液体也应作排空处理，防止沉积尘土，否则可能堵塞测速管。
2）每次实验开始前，也需先清洗整个管路系统，即先使管内流体流动数分钟，检查阀门、管段有无堵塞或漏水情况。
7、数据记录表
五、数据分析
1. h1和h2的分析
由转子流量计流量读数及管截面积，可求得流体在1处的平均流速u1（该平均流速适用于系统内其他等管径处）。
若忽略h1和h2间的沿程阻力，适用柏努利方程即式（1－7），且由于1、2处等高，则有：
g
u g g u g 2p 2p 222211+=+ρρ （1－10） 其中，两者静压头差即为单管压力计1和2读数差（mH 2O ），由此可求得流体在2处的平均流速u 2。
令u 2代入式（1－5），验证连续性方程。
2. h1和h3的分析
流体在1和3处，经节流件后，虽然恢复到了等管径，但是单管压力计1和3的读数差说明了能头的损失（即经过节流件的阻力损失）。
且流量越大，读数差越明显。
3. h3和h4的分析
流体经3到4处，受弯头和转子流量计及位能的影响，单管压力计3和4的读数差明显，且随流量的增大，读数差也变大，可定性观察流体局部阻力导致的能头损失。
4. h4和h5的分析
直管段4和5之间，单管压力计4和5的读数差说明了直管阻力的存在（小流量时，该读数差不明显，具体考察直管阻力系数的测定可使用流体阻力装置），根据
g
u d L h f 22
λ= （1－11） 可推算得阻力系数，然后根据雷诺准数，作出两者关系曲线。
5. h5和h6的分析
单管压力计5和6之差指示的是5处管路的中心点速度，即最大速度u c ，有
g
u h c 22
=∆ （1－12） 考察在不同雷诺准数下，与管路平均速度u 的关系。
