清华大学博弈论3
- 格式:pdf
- 大小:582.33 KB
- 文档页数:64


《博弈论:原理与模型》参考文献mnsliul@国内出版的有关博弈论方面的专门书籍,大致分为两类:一类只介绍von Neumann经典理论、Nash均衡与存在性、联盟博弈等内容,不涉及Nash均衡向动态系统、不完全信息系统、不对称信息系统的引申,这一类书多为应用数学工作者尤其是运筹学专家所著。
另一类书的内容则恰好相反,只介绍Nash均衡以及它向多种经济系统的引申,基本上不介绍上面列举的其它内容,这一类书强调概念的引申以及对于案例极其繁琐拖沓的分析,大多是经济学家或博弈论专家所著。
一、沦为病夫,一切免谈:通晓医书,以确保身心之康健1、吴阶平.中国大百科全书(现代医学卷I、卷II)(M). 北京:中国大百科全书出版社,1992年4月第1版.二、逻辑,最高、最彻底的智慧1、王宪钧. 数理逻辑引论(M). 北京:北京大学出版社,1982年6月第1版.2、吴家国. 《普通逻辑》教学参考书(M). 上海:上海人民出版社,1983年5月第1版.三、科学(S)与信念(B):做人,与做学问1、[日]新渡户稻造,宗建新译.武士道(M). 济南:山东画报出版社,2006年6月第1版.2、程麻.零距离的日本(M). 北京:人民文学出版社,2007年9月第1版.3、[日]千岛佑郎,姜乃明等译.犹太人为什么优秀(M). 北京:中央编译出版社,2006年10月第2版.四、本课程的直接辅助教材1.谢识予.经济博弈论(第二版)(M).上海:复旦大学出版社,2002年1月第2版.2.谢识予.经济博弈论习题指南(M).北京:中国人民大学出版社,2003年1月第1版.五、博弈论入门教材1.王则柯.人人博弈论(M).北京:中信出版社,2007年5月第1版.点评:数学家出身的王则柯教授,是博弈论方面具有跨国知名度的学者。
他的这本《人人博弈论》是其《博弈论平话》的扩充版,概念准确,引伸广泛,委实是博弈论科普方面的一部力作。
2.张峰.博弈逻辑(M).北京:中国社会出版社,2008年1月.3.潘天群.博弈生存—社会现象的博弈论解读(第二版)(M).北京:中央编译出版社,2004年10月第2版.4.孙恩棣.生活中的博弈论(M).北京:京华出版社,2006年8月第2版.六、博弈论初级教材1.王则柯,李杰.博弈论教程(M).北京:中国人民大学出版社,2004年11月第1版.2.汪贤裕,肖玉明.博弈论及其应用(M).北京:科学出版社,2008年2月第1版.3.范如国,韩民春.博弈论(M).武汉:武汉大学出版社,2006年4月第1版.点评:基本为谢识予版本的通俗化改写,行文罗嗦、冗长泛味之极!七、偏于数学味的博弈论1.姜殿玉.带熵博弈论及其应用(M).北京:科学出版社,2008年8月第1版.2.俞建.博弈论与非线性分析(M).北京:科学出版社,2008年2月第1版.3.高红伟,[俄]彼得罗相.动态合作博弈(M).北京:科学出版社,2009年3月第1版.4.侯定丕.博弈论导论(M).合肥:中国科技大学出版社,2004年2月第1版.5.李登峰.微分对策及其应用(M).北京:国防工业出版社,2000年4月第1版.6.谢政.对策论(M).长沙:国防科技大学出版社,2004年3月第1版.7.于维生,朴正爱.博弈论及基在经济管理中的应用(M).北京:清华大学出版社,2005年1月第1版.8.于维生.博弈论与经济(M).北京:高等教育出版社,2007年4月第1版.9.[加]杨荣基,[俄]彼得罗香,[香港]李颂志.动态合作—尖端博弈论(M).北京:中国市场版社,2007年2月第1版.。

大国博弈教材
关于大国博弈的教材有很多,以下列举了一些经典著作:
1. 《博弈论入门》作者:葛泽慧,于艾琳,赵瑞,冯世豪等著出版社:清华大学出版社 ISBN:
2. 《博弈论教程》作者:罗云峰著出版社:清华大学出版社 ISBN:
3. 《博弈论通识十八讲》作者:常金华,陈梅著出版社:北京大学出版社 ISBN:
4. 《博弈论》作者:王力哲著出版社:民主与建设出版社 ISBN:
5. 《博弈论:最高级思维和生存策略》作者:刘庆财著出版社:北京联合出版公司 ISBN:
6. 《博弈论》作者:翟文明著出版社:中国华侨出版社 ISBN:
以上书籍内容仅供参考,可以根据自己的兴趣和需求选择合适的教材。


关于博弈论,推荐你读这些书2022年春季学期,丘成桐数学科学中⼼郑绍远教授即将开设通识课程《博弈论》。
介绍博弈论基本概念如:组合博奕,扩展型博奕,双⼈零和博奕,双矩阵博奕,纳什均衡,相关均衡,进化博奕论,重复囚徒博奕,谈判理论,联盟型博奕,Shapley 值,核仁,两边配对问题等。
郑教授特别为同学们推荐了⼏本博弈论经典教材,欢迎各位同学阅读学习!A Course in Game TheoryThomas Ferguson01博弈⽆处不在、代价多种多样。
本书包含博弈背后的不同数学模型及相关研究。
通过对数学模型的分析,或讨论最佳应对策略,或是尝试更准确地预测未来。
Game Theory, a multi-levelled approachHans Peters02本书深⼊浅出地讲授了博弈论的基础理论内容,适合本科⽣、研究⽣通读。
Game TheoryMichael Maschler, Eilon Solan, Shmuel Zamir03本书介绍博弈论达到了相当的⼴度,⽆出其右。
不仅包含技术性讲解,完整数学证明,也有丰富的例⼦和练习,带领本科⽣深⼊了解博弈论及相关跨学科课题,包括经济学、数学、计算机科学、⼯程学、⽣命科学等等。
Fun and GamesKen Binmore04这本突破性的著作讨论了当理性个体⾯对利益冲突时应如何应对,简明扼要地介绍了博弈论的主要发展历程,也深⼊探讨了其中⼀些颇为严肃的问题。
作者独特的写作⽅式,便于读者学习如何⽤理论知识解决简单问题。
Game Theory and StrategyPhilip D. Straffin05本书介绍了博弈论在跨学科领域中的应⽤,其范围和深度均值得称道。
只需有⾼中代数知识便可阅读,并可在阅读中培养复杂的数学思维。
Game TheoryGuillermo Owen06本书被视为博弈论的标准教科书之⼀。
新版本包括最新的研究⽅向,讨论了富有争议的三门问题,增加了介绍诺奖级⼯作的章节,涉及Hurwicz, Maskin和Myerson的机制设计理论以及Roth的匹配理论等。

UOJ266.【清华集训2016】Alice和Bob⼜在玩游戏(博弈论+01-trie)UOJ266. 【清华集训2016】Alice和Bob⼜在玩游戏(博弈论+01-trie)题⽬⼤意有 n 个节点,m 条边(0≤m≤n−1),构成若⼲棵有根树,每棵树的根节点是该连通块内编号最⼩的点。
Alice 和 Bob 轮流操作(Alice 先⼿),每回合选择⼀个没有被删除的节点 x,将 x 及其所有祖先全部删除,不能操作的⼈输。
需要注意的是,树的形态是在⼀开始就确定好的,删除节点不会影响剩余节点⽗亲和⼉⼦的关系。
⽐如:1-3-2 这样⼀条链,1 号点是根节点,删除 1 号点之后,3 号点还是 2 号点的⽗节点。
假设 Alice 和 Bob 都⾜够聪明,问 Alice 有没有必胜策略。
数据范围对于10%的数据,m=0;对于20%的数据,1≤n≤20;对于40%的数据,1≤n≤102;对于60%的数据,1≤n≤103;对于100%的数据,1≤T≤10,1≤n≤105,∑n≤2×105,0≤m≤n−1,输⼊数据保证不会形成环,且每棵树的⼤⼩≤5×104。
解题思路⾸先可以看出这是⼀个博弈论问题,考虑⽤ SG 函数解决如何算出⼀个⼦树的 SG 值?枚举删除的第⼀个点 x,将根节点到 x 的路径删掉,发现树变成了森林,也就是当前局⾯的⼀个后继状态,那么森林中所有的树 SG 值异或起来插⼊集合中即可,最后对集合中的数取 mex 即可,时间复杂度 Θ(N2)考虑数据结构优化考虑⼀个⼦树向上合并的过程,发现只需将⼦树异或上其他⼦树的 SG 值并加⼊到集合,并加⼊删除根节点的 SG 值,也就是维护整体异或,合并,插⼊,不难发现可以⽤ 01-trie 解决代码#include <queue>#include <vector>#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#define MP make_pair#define ll long long#define fi first#define se secondusing namespace std;template <typename T>void read(T &x) {x = 0; bool f = 0;char c = getchar();for (;!isdigit(c);c=getchar()) if (c=='-') f=1;for (;isdigit(c);c=getchar()) x=x*10+(c^48);if (f) x=-x;}template<typename F>inline void write(F x){static short st[30];short tp=0;if(x<0) putchar('-'),x=-x;do st[++tp]=x%10,x/=10; while(x);while(tp) putchar('0'|st[tp--]);putchar('\n');}template <typename T>inline void Mx(T &x, T y) { x < y && (x = y); }template <typename T>inline void Mn(T &x, T y) { x > y && (x = y); }const int N = 400500; int vis[N];int tag[N*8], ch[N*10][2], cnt, n, m, T;int siz[N*8], h[N], ne[N<<1], to[N<<1], tot;inline void add(int x, int y) {ne[++tot] = h[x], to[h[x] = tot] = y;}#define ls ch[x][0]Processing math: 100%#define rs ch[x][1]inline void spread(int x, int dep) {if ((tag[x] >> dep) & 1) swap(ls, rs);tag[ls] ^= tag[x], tag[rs] ^= tag[x];tag[x] = 0;}void insert(int x, int p) {int pp = p;for (int i = 16;i >= 0; i--) {int di = (x >> i) & 1; spread(p, i);if (!ch[p][di]) ch[p][di] = ++cnt;p = ch[p][di];}if (siz[p]) return; p = pp;for (int i = 16;i >= 0; i--) {int di = (x >> i) & 1;p = ch[p][di]; siz[p]++;}}int merge(int x, int y, int dep) {if (!x || !y) return x | y;if (dep == -1) return siz[x] = 1, x;spread(x, dep), spread(y, dep);ls = merge(ls, ch[y][0], dep - 1);rs = merge(rs, ch[y][1], dep - 1);siz[x] = siz[ls] + siz[rs];return x;}int query(int x, int dep) {if (!x) return 0; spread(x, dep);if (siz[ls] >= (1 << dep)) return query(rs, dep - 1) + (1 << dep); return query(ls, dep - 1);}int res[N], sg[N], Rt[N];void dfs2(int x, int fa) {vis[x] = 1, tag[x] = res[x] = 0, Rt[x] = x;for (int i = h[x]; i; i = ne[i]) {int y = to[i]; if (y == fa) continue;dfs2(y, x); res[x] ^= sg[y];}insert(res[x], Rt[x]);for (int i = h[x]; i; i = ne[i]) {int y = to[i]; if (y == fa) continue;tag[Rt[y]] ^= res[x] ^ sg[y];Rt[x] = merge(Rt[x], Rt[y], 16);}sg[x] = query(Rt[x], 16);}void work(void) {read(n), read(m); cnt = n, tot = 0;memset(vis, 0, sizeof(vis));memset(h, 0, sizeof(h));memset(ch, 0, sizeof(ch));memset(siz, 0, sizeof(siz));for (int i = 1, x, y;i <= m; i++)read(x), read(y), add(x, y), add(y, x);int ans = 0;for (int i = 1;i <= n; i++)if (!vis[i]) dfs2(i, 0), ans ^= sg[i];puts(ans ? "Alice" : "Bob");}int main() {for (read(T); T--; ) work();return 0;}。


进化博弈 Evolutionary Games第13章 Chapter 13进化博弈 Evolutionary Games目前为止我们学过了具有多种不同特征的博弈: We have so far studied games with many different features:同时和序贯博弈 Simultaneous and sequential moves 零和与非零和博弈 Zero-sum and non-zero-sum payoffs 操纵未来博弈规则的策略性行动 Strategic moves to manipulate rules of games to come 一次性和重复博弈 One-shot and repeated play 许多人同时进行的集体博弈 Games of collective action in which a large number of people play simultaneouslySlide 2进化博弈 Evolutionary Games所有这些博弈中的参与者都是理性的:每个参 与者…… All the players in all these games are rational: each player…………具有内在一致的价值体系 has an internally consistent value system ……能够计算其策略选择的后果 can calculate the consequences of her strategic choices ……作出最符合其利益的选择 makes choice that best favors her interestsSlide 3进化博弈 Evolutionary Games对理性可能的替代方法可以从生物学的进化和进化动 力学中找到,在那里…… One possible alternative to rationality can be found in the biological theory of evolution and evolutionary dynamics, where…………好的策略可以得到更多的奖励 good strategies will be rewarded with higher payoffs ……参与者可以观察或模仿成功者并试验新的策略 players can observe or imitate success and experiment with new strategies ……随着参与者在参加博弈中获得经验,好的策略将会得到 更经常的使用,坏的策略得到更少的使用。

计算机科学与技术专业(计算机科学实验班)本科培养方案一、培养目标本专业培养具有良好科学素养和创新精神、德智体全面发展,且计算机理论及应用基础扎实、熟悉计算机科学前沿领域、科研实践能力强,能够从事计算机科学研究的领跑国际拔尖创新计算机科学人才。
“计算机科学与技术(计算机科学实验班)”专业致力于培养与美国麻省理工学院、普林斯顿大学等世界一流高校本科生具有同等、甚至更高竞争力的领跑国际拔尖创新计算机科学人才。
二、基本要求计算机科学与技术专业(计算机科学实验班)本科毕业生应达到如下知识、能力和素质的要求:具有扎实的计算机科学理论基础,全面了解计算机科学的前沿领域。
具有较高的计算机科研实践能力,具备成为国际一流计算机科学研究人才的良好综合素质。
三、学制与学位授予学制:本科学制四年,按照学分制管理机制,实行弹性学习年限。
授予学位:工学学士学位。
四、基本学分学时本科培养总学分不少于165。
其中春、秋季学期课程总学分127,夏季学期实践环节14学分,第七学期在清华或各著名研究院所从事计算机科学研究实践9学分,第八学期综合论文训练15学分。
五、专业核心课程计算机科学实验班特设全英文教学的专业及核心课程25门,覆盖计算机科学的前沿领域,学生可以根据自身研究兴趣在专业核心课中按要求进行选择性修读。
其中大一、大二专业核心课开设13门,以“通才教育”为主,涉及计算机科学基本专门知识,帮助学生全面了解计算机科学前沿领域;大三、大四专业核心课开设12门,以“专才教育”为主,分别面向两个专业方向“理论和安全”以及“系统和应用”。
25门专业及核心课程如下:计算机入门(3学分),计算机应用数学(3学分),普通物理(1)英(4学分),信息物理(2学分),算法设计(4学分),普通物理(2)英,计算理论(4学分),网络科学(4学分),密码学基础(4学分),博弈论(4学分),近代物理(1)英,计算机安全的理论及实践(2学分),Java程序设计基础(2学分),分布式计算(基础与系统)(4学分),量子信息(4学分),大数据算法与模型(4学分),机器学习(4学分),高等计算机图形学(3学分),近代物理(2)英,计算机网络基础(3学分),操作系统(4学分),计算生物学(3学分),信息论与网络编码(3学分),专题训练实践(5学分),计算机科学研究实践(9学分)。

《博弈论:原理与模型》参考文献mnsliul@国内出版的有关博弈论方面的专门书籍,大致分为两类:一类只介绍von Neumann经典理论、Nash均衡与存在性、联盟博弈等内容,不涉及Nash均衡向动态系统、不完全信息系统、不对称信息系统的引申,这一类书多为应用数学工作者尤其是运筹学专家所著。
另一类书的内容则恰好相反,只介绍Nash均衡以及它向多种经济系统的引申,基本上不介绍上面列举的其它内容,这一类书强调概念的引申以及对于案例极其繁琐拖沓的分析,大多是经济学家或博弈论专家所著。
一、沦为病夫,一切免谈:通晓医书,以确保身心之康健1、吴阶平.中国大百科全书(现代医学卷I、卷II)(M). 北京:中国大百科全书出版社,1992年4月第1版.二、逻辑,最高、最彻底的智慧1、王宪钧. 数理逻辑引论(M). 北京:北京大学出版社,1982年6月第1版.2、吴家国. 《普通逻辑》教学参考书(M). 上海:上海人民出版社,1983年5月第1版.三、科学(S)与信念(B):做人,与做学问1、[日]新渡户稻造,宗建新译.武士道(M). 济南:山东画报出版社,2006年6月第1版.2、程麻.零距离的日本(M). 北京:人民文学出版社,2007年9月第1版.3、[日]千岛佑郎,姜乃明等译.犹太人为什么优秀(M). 北京:中央编译出版社,2006年10月第2版.四、本课程的直接辅助教材1.谢识予.经济博弈论(第二版)(M).上海:复旦大学出版社,2002年1月第2版.2.谢识予.经济博弈论习题指南(M).北京:中国人民大学出版社,2003年1月第1版.五、博弈论入门教材1.王则柯.人人博弈论(M).北京:中信出版社,2007年5月第1版.点评:数学家出身的王则柯教授,是博弈论方面具有跨国知名度的学者。
他的这本《人人博弈论》是其《博弈论平话》的扩充版,概念准确,引伸广泛,委实是博弈论科普方面的一部力作。
2.张峰.博弈逻辑(M).北京:中国社会出版社,2008年1月.3.潘天群.博弈生存—社会现象的博弈论解读(第二版)(M).北京:中央编译出版社,2004年10月第2版.4.孙恩棣.生活中的博弈论(M).北京:京华出版社,2006年8月第2版.六、博弈论初级教材1.王则柯,李杰.博弈论教程(M).北京:中国人民大学出版社,2004年11月第1版.2.汪贤裕,肖玉明.博弈论及其应用(M).北京:科学出版社,2008年2月第1版.3.范如国,韩民春.博弈论(M).武汉:武汉大学出版社,2006年4月第1版.点评:基本为谢识予版本的通俗化改写,行文罗嗦、冗长泛味之极!七、偏于数学味的博弈论1.姜殿玉.带熵博弈论及其应用(M).北京:科学出版社,2008年8月第1版.2.俞建.博弈论与非线性分析(M).北京:科学出版社,2008年2月第1版.3.高红伟,[俄]彼得罗相.动态合作博弈(M).北京:科学出版社,2009年3月第1版.4.侯定丕.博弈论导论(M).合肥:中国科技大学出版社,2004年2月第1版.5.李登峰.微分对策及其应用(M).北京:国防工业出版社,2000年4月第1版.6.谢政.对策论(M).长沙:国防科技大学出版社,2004年3月第1版.7.于维生,朴正爱.博弈论及基在经济管理中的应用(M).北京:清华大学出版社,2005年1月第1版.8.于维生.博弈论与经济(M).北京:高等教育出版社,2007年4月第1版.9.[加]杨荣基,[俄]彼得罗香,[香港]李颂志.动态合作—尖端博弈论(M).北京:中国市场版社,2007年2月第1版.。
博弈论第三版课后习题答案
《博弈论第三版课后习题答案:深入理解博弈论的精髓》
博弈论是一门研究决策制定者在有限理性条件下进行决策的学科。
它不仅仅是
一门数学理论,更是一门涉及经济学、政治学、社会学等多个领域的交叉学科。
在博弈论第三版课后习题答案中,我们可以深入理解博弈论的精髓,探讨博弈
论在现实生活中的应用。
首先,博弈论的基本概念包括博弈参与者、策略、收益和信息。
在博弈论中,
参与者为决策制定者,他们根据自身利益选择不同的策略,并根据不同的策略
组合获取相应的收益。
而信息则是影响参与者决策的重要因素,不同的信息可
以导致不同的决策结果。
其次,博弈论的经典模型包括囚徒困境、合作博弈和非合作博弈等。
囚徒困境
是博弈论中最经典的模型之一,它描述了两个囚犯在被捕前是否应该合作或者
背叛的情景。
这个模型揭示了合作和背叛之间的利益冲突,以及如何在有限理
性条件下做出最优决策。
另外,博弈论在现实生活中有着广泛的应用。
在经济学领域,博弈论可以用来
分析市场竞争、价格战略和合作博弈等问题;在政治学领域,博弈论可以用来
分析国际关系、选举竞争和政策制定等问题;在社会学领域,博弈论可以用来
分析合作与冲突、社交网络和社会规范等问题。
总之,博弈论第三版课后习题答案为我们提供了深入理解博弈论的机会,它不
仅可以帮助我们理解博弈论的基本概念和经典模型,更可以帮助我们将博弈论
应用到现实生活中的各种问题中。
希望我们可以通过学习博弈论,更好地理解
和解决现实生活中的种种挑战。
清华851西方经济学考研真题(一)
我们给大家整理的是清华851西方经济学考研真题(回忆版),为准备参加清华大学考研的相关专业学生提供参考复习。
1清华851西方经济学考研判断说理题(10×3分)
涉及到的知识点有收入效应,公共物品,垄断,汇率升降,永久收入假说,经济衰退时的货币供应量等
2清华851西方经济学考研简答题(共8题,每题5分)
(1)契约曲线
(2)停止营业点
(3)风险溢价
(4)宏观经济的长期表现与短期表现
(5)财政政策与货币政策的异同
(6)信息不对称及方法
(7)李嘉图等价
3清华851西方经济学考研计算题:(共4题)
(1)求利润最大化时的劳动供给
(2)博弈论,求均衡结果
(3)求法定准备金率下降后,M的变化率
(4)索罗模型,求各种增长率
4清华851西方经济学考研论述题:(共2题)
(1)用经济人假设和委托代理机制分析如何预防腐败
(2)外汇储备的由来,以及怎么实现中国的外部经济平衡
盛世清北—专注清华大学考研|保研|考博辅导。
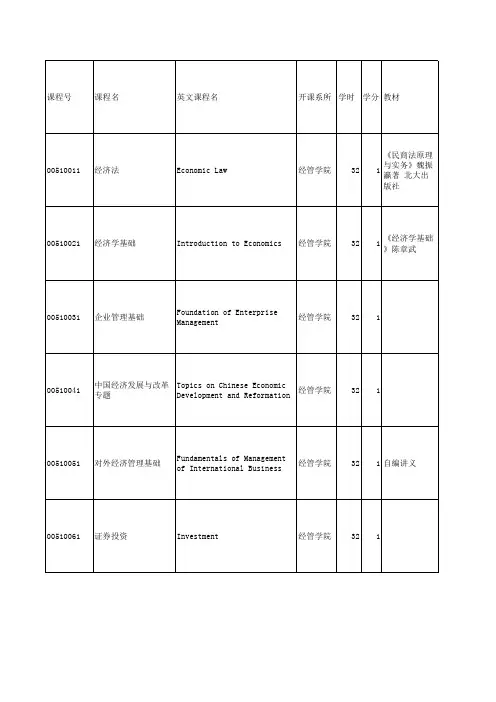
经济管理学院本科培养方案一、培养目标清华经管学院遵循清华大学的基本方针,把人才培养作为学院的根本任务。
经管学院本科生教育的理念是:培养每一位学生成为有良好素养的现代文明人,同时创造一种环境使得杰出人才能够脱颖而出。
学院实现这一理念的途径是通识教育与个性发展相结合,并由此确定本科培养方案包括通识课程、专业课程和任选课程三部分。
信息管理与信息系统专业培养掌握数字经济时代商务活动规律,能够有效驾驭信息通信技术以提升绩效、引领创新的复合型管理人才。
会计学专业培养既掌握国际前沿的会计理论研究方法,通晓全球会计准则和会计制度发展趋势,又熟悉国际国内经济发展与资本市场运作规律的,复合型高端会计研究和实践人才。
经济与金融专业(含保险方向)培养既掌握系统的经济学和金融学理论和分析方法,又具备解决现代经济特别是金融领域中实际问题的技能,既具有国际视野同时也了解中国国情的高素质复合型经济和金融人才。
二、基本要求本科培养方案中的通识教育课程包括思想政治理论课和体育课,中文、英语和数学三种基础技能课,通识教育核心课(即文化素质教育核心课),以及新生研讨课等课程。
专业课程包括三个专业的共同专业基础课、各专业的专业必修课以及专业选修课。
在完成专业课学习的同时,根据个人兴趣可跨越专业界限,选修任选课程。
三个专业开设的专业课程对毕业生的要求为:信息管理与信息系统专业培养学生具有坚实的数学基础、系统的管理学基础、必要的经济学知识和较强的中英文沟通能力,掌握计算机专业知识,并有一定的信息系统和数据分析以及信息资源开发利用的技能。
会计学专业不仅需要学习大量的会计、审计、财务、税务、会计信息系统等专业知识,还要学习经济学、金融学、战略管理、市场营销、法律以及数学、计算机等课程。
毕业后应具备在企业管理和资本市场中运用现代会计学知识分析问题、解决问题的能力,和从事研究型工作的能力。
经济与金融专业的特点是更好地融合经济学与金融学教学,将学生对金融学的分析技巧和操作方法的掌握,建筑在更加全面和扎实的经济学基础之上,使之更加深入和灵活;而金融学专业知识与技能的训练,也为经济学的学习提供用武之地,达到理论和实践的融合。
爱考机构考研-保研-考博高端辅导第一品牌社会科学学院理论经济学专业招生目录院系所、专业及研究方向招生人数考试科目备注070社会科学学院9 含深圳研究生院2名010100哲学01科学技术哲学①101思想政治理论②201英语一或202俄语或203日语③302数学二或648科学技术概论④850科学技术史本专业分为科技哲学、科技社会学、科技传播和科技政策四个研究方向;承认我校任何理工专业的考试;复试时专业综合考试内容:自然辩证法初阶。
020100理论经济学01政治经济学①101思想政治理论②201英语一③303数学三④851西方经济学复试时专业综合考试内容:政治经济学02经济史同上复试时专业综合考试内容:经济史03西方经济学同上复试时专业综合考试内容:西方经济学04人口与资源经济学同上复试时专业综合考试内容:人口与资源经济学030200政治学01政治学理论与方法02国际关系03比较政治04中国政府与政治①101思想政治理论②201英语一或202俄语或203日语或241德语或242法语③649政治学概论④864历史综合考试(国际关系史、政治思想史、中外政治制度史)复试时专业综合考试内容:小论文030300社会学01社会学①101思想政治理论②201英语一③610社会学理论④853社会研究方法复试时专业综合考试内容:应用社会学040200心理学01应用心理学①101思想政治理论②201英语一③312心理学专业基础综合复试时专业综合考试内容:应用心理学、统计学040300体育学01体育人文社会学①101思想政治理论②201英语一或202俄语或203日语或241德语或242法语③634体育学专业基础综合复试时专业综合考试内容:体育社会学02运动人体科学同上复试时专业综合考试内容:运动生物化学03体育教育训练学同上复试时专业综合考试内容:运动训练学071200科学技术史01科学技术史①101思想政治理论②201英语一或202俄语或203日语③302数学二或648科学技术概论④850科学技术史(本专业承认我校任何理工专业的考试)复试时专业综合考试内容:科技写作035200社会工作 2 专业学位01社会工作硕士①101思想政治理论②202俄语或203日语或204英语二③331社会工作原理④437社会工作实务全部以委托培养形式在职攻读,不提供住宿,周末或集中授课。