高数第一章1节
- 格式:ppt
- 大小:2.01 MB
- 文档页数:75


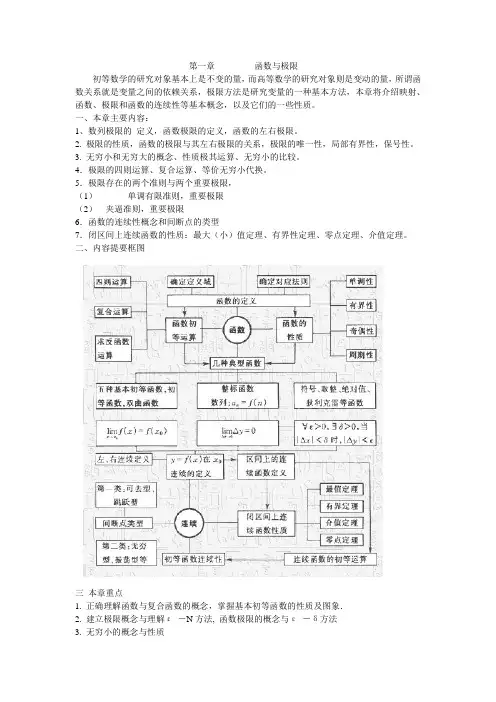
第一章函数与极限初等数学的研究对象基本上是不变的量,而高等数学的研究对象则是变动的量,所谓函数关系就是变量之间的依赖关系,极限方法是研究变量的一种基本方法,本章将介绍映射、函数、极限和函数的连续性等基本概念,以及它们的一些性质。
一、本章主要内容:1、数列极限的定义,函数极限的定义,函数的左右极限。
2. 极限的性质,函数的极限与其左右极限的关系,极限的唯一性,局部有界性,保号性。
3. 无穷小和无穷大的概念、性质极其运算、无穷小的比较。
4.极限的四则运算、复合运算、等价无穷小代换。
5.极限存在的两个准则与两个重要极限,(1)单调有限准则,重要极限(2)夹逼准则,重要极限6.函数的连续性概念和间断点的类型7.闭区间上连续函数的性质:最大(小)值定理、有界性定理、零点定理、介值定理。
二、内容提要框图三本章重点1. 正确理解函数与复合函数的概念,掌握基本初等函数的性质及图象.2. 建立极限概念与理解ε-N方法, 函数极限的概念与ε-δ方法3. 无穷小的概念与性质4. 单调有界法则与两个重要极限及其应用5. 初等函数的连续性及其应用四本章难点1. 反函数概念,由实际问题建立函数关系式与求分段的复合函数的关系式.2. ε-N, ε-δ极限定义证明法3. 理解无穷小,无穷小与任意小、充分小、很小的数的区别4. 两个重要极限公式,分清各公式的特点及适用时机.5. 闭区间上连续函数的几条性质.第一节映射与函数学习指导1.教学目的读者应理解集合、映射的概念;理解函数概念,了解函数的有界性、单调性、奇偶性和周期性,了解反函数概念。
2.基本练习会求函数的定义域,会求函数的反函数。
会判断函数的有界性、单调性、奇偶性和周期性;熟练掌握基本初等函数的图形和性质。
会把复合函数分解成基本初等函数的组合。
3.应注意的事项本节内容大多数中学阶段已经学过,此处为了教学方便,将中学阶段的内容加以归纳,扩充,提高。
学生可根据自己的知识结构进行复习、有重点地学习,对教材上的练习题,先阅读题目,再适当选做部分练习题。


第一章:第1节: 1A 。
2D 。
3A 。
4x y =。
5.21)(nxx x f n +=。
6.当2/10<<a 时,定义域为]1,[a a -;当2/1>a 时,定义域为空集;当2/1=a 时,定义域2/1=x 。
7.)1ln()(x x -=ϕ,定义域为}0|{≤x x 。
第2节: 1D 。
2C 。
3B 。
4.证明:由定义知0>∀ε,N N ∈∃,使得当n N >时,有||n u a ε-<成立。
注意到a u a u n n -≤-。
因此当n N >时,有ε<-≤-a u a u n n 。
即||||lim a u n n =∞→。
反过来若1||lim =∞→n n u ,则n n u ∞→lim 不一定存在。
比如(1),n n u =-则n n u ∞→lim 不存在,但1||lim =∞→n n u 。
若0||lim =→∞n n u ,则由00-=-n n u u 知0lim =∞→n n u 。
第3节:1A 。
2B 。
3D 。
4C 。
5C 。
第4节: 1D 。
2D 。
3D 。
4C 。
5D 。
6.证:假设函数xx y 1sin 1=在区间]1,0(上有界,则0,M ∃>使得函数11sin y M x x =≤。
若取2/)1]([21ππ++=M x ,则有M M y >++=2/)1]([2ππ矛盾。
所以在区间]1,0(上无界,但也不是+→0x 时的无穷大。
因为若取πk x 21=(N k ∈),则当+∞→k 时,+→0x ,而此时0≡y 不是无穷大。
第5节: 1A 。
2C 。
3B 。
4B 。
5.1。
6.21。
7。
a 21-。
8.1。
9.2。
10.21。
11.6。
12.1,1-==b a 第6节: 1C 。
2D 。
3B 。
4.3。
5.3/5。
6.0 。
7.由于()nnn n11333213⋅<++<,所以由夹逼定理可得()3321lim 1=++∞→nn nn 。





第一章 函数.极限和连续第一节 函数1. 决定函数的要素:对应法则和定义域2. 基本初等函数:(六类)(1) 常数函数(y=c );(2)幂函数(y=x a );(3)指数函数(y=a x ,a>0,a ≠1);(4)对数函数(y=log a x ,a>0,a ≠1)(5)三角函数;(6)反三角函数。
注:分段函数不是初等函数。
特例:y =√x 2是初等函数3.构成复合函数的条件:内层函数的值域位于外层函数的定义域之内。
4.复合函数的分解技巧:对照基本初等函数的形式。
5.函数的几种简单性质:有界性,单调性,奇偶性,周期性。
第二节 极限1.分析定义∀&>0(任意小) ∃∂>0当|x |>ð(或0<|x −x 0|<ð )时总有 |f (x )−A |<&称 lim x→∞f (x )=0 (或lim x→x0f (x )=A)2.极限存在的充要条件lim x→x0f (x )=A ↔lim x→x 0+f (x )=lim x→x 0−f (x )=A 3.极限存在的判定准则(1)夹逼定理f 1(x )≤f(x)≪f 2(x) ,且 lim x→x0f 1(x )=A = lim x→x0f 2(x ) 所以lim x→x0f (x )=A(2)单调有界准则单调有界数列一定有极限。
4.无穷小量与无穷大量,则称 时,f (x )为无穷小量 , 则称 时,f (x )为无穷大量 注:零是唯一的可作为无穷小的常数。
性质1 有限多个无穷小的代数和或乘积还是无穷小。
注:无限个无穷小量的代数和不一定是无穷小量性质2 有界变量或常数与无穷小的乘积还是无穷小。
5. 定义 设 是同一极限过程中的无穷小, 则若 则称 α 是β比高阶的无穷小,记作若 则称α是比β 低阶的无穷小∞=→)(lim 0x f x x )(或∞→→x x x 00)(lim 0=→x f x x )(或∞→→x x x 0)(,)(x x ββαα==,0)(≠x β且,0lim =βα);(βαo =,lim ∞=βα,0lim ≠=C βα若 则称 α 是β的同阶无穷小;特别地,当c=1 时,则称α 是β的等价无穷小,记作若 则称α是关于β 的 k 阶无穷小。
高数大一第一节知识点总结大学的高数课程对于很多理科生来说都是一个巨大的挑战。
无论是对于数学基础薄弱的同学,还是对于数学领域有所了解的同学来说,高数都是一门需要认真学习和掌握的课程。
在大一的第一节高数课上,我们学习了一些基础的数学概念和方法,下面就对这些知识点进行总结和归纳。
第一部分:数列与数列极限数列是高数中一个非常基础也非常重要的概念。
数列可以看作是按照一定规律排列的一系列数值。
在第一节课中,我们学习了数列的概念以及常见的一些数列类型,如等差数列和等比数列。
我们还学习了数列极限的概念。
数列极限可以理解为当数列中的项数趋近于无穷大时,数列的值会趋近于一个确定的值。
数列极限的计算可以使用一些特定的方法,如极限的四则运算法则、夹逼定理等。
第二部分:函数及其基本性质在高数课程中,函数是一个核心概念。
函数可以看作是一种输入和输出之间的映射关系。
在第一节课中,我们学习了函数的定义和性质。
函数的定义包括定义域、值域和对应关系等。
函数的性质包括奇偶性、周期性、单调性等。
我们还学习了函数的图像和函数的图像的基本变换。
在高数课程中,函数的图像是非常重要的,通过观察函数的图像可以更好地理解函数的性质和行为。
第三部分:极限与连续极限是高数课程中一个非常重要的概念。
极限可以理解为当自变量趋于一个确定的值时,函数的值会趋近于一个确定的值。
在第一节课中,我们学习了函数的极限和无穷小的概念。
无穷小可以理解为当自变量趋于一个确定的值时,函数值与这个确定值之间的差异非常小。
我们还学习了极限的四则运算法则和夹逼定理。
连续是一个和极限密切相关的概念。
在高数课程中,连续可以理解为函数在某一点处的极限与函数在该点的函数值相等。
第四部分:导数与微分导数是高数课程中一个重要且难点的内容。
导数可以理解为函数在某一点处的切线的斜率。
导数的计算可以使用一些特定的方法,如导数的基本公式、导数的运算法则等。
在第一节课中,我们学习了导数的定义和性质。
我们还学习了一阶导数和二阶导数的概念。