年金的终值和现值

一、年金终值：年金终值是指在一段时间内，定期支付一定金额的现金流，经过一定的利率增长后所积累的总金额。

年金终值计算的目的是评估未来一段时间内现金流的价值。

年金终值的计算可以通过如下的公式进行：FV=P*((1+r)^n-1)/r其中，FV表示年金终值，P表示每期支付的金额，r表示每期支付的利率，n表示支付的期数。

例如，每年支付1000元，利率为5%，持续支付10年，则年金终值的计算为：年金终值的计算方法可以应用于各种不同的现金流情况，如每月、每季度、每半年等的现金支付。

二、年金现值：年金现值是指将未来一段时间内的现金流按照一定的利率折算到现在的价值，将未来的现金流所得到的总金额。

年金现值的计算的目的是评估未来现金流的现值，以便做出更加准确的投资决策。

年金现值的计算可以通过如下的公式进行：PV=P*(1-(1+r)^(-n))/r其中，PV表示年金现值，P表示每期支付的金额，r表示每期支付的利率，n表示支付的期数。

例如，每年支付1000元，利率为5%，持续支付10年，则年金现值的计算为：所以，每年支付1000元，利率为5%，持续支付10年，年金现值为7721.73元。

年金现值的计算方法也可以适用于各种不同的现金流情况。

三、年金终值和年金现值的应用：在投资决策中，投资者可以利用年金终值和年金现值来比较不同投资方案的收益。

通过计算不同方案的年金终值和年金现值，可以判断哪种投资方案更加有利可图，从而做出更加明智的决策。

在退休规划中，个人可以利用年金终值和年金现值来评估自己的退休金需求和储蓄目标。

通过计算所需的年金终值和现值，可以规划合理的退休储蓄计划，确保在退休时有足够的资金支持。

总之，年金终值和年金现值是评估一定时间内或一系列现金流价值的重要工具。

通过运用年金终值和年金现值的计算方法，可以帮助人们做出更加准确的投资决策和退休规划。

年金现值与终值的比较年金现值与终值是财务管理中两个重要的概念，用于评估不同时期的现金流量的价值。

年金现值是指在未来一段时间内产生的现金流量，在当下的价值，而年金终值则是指在未来一段时间内产生的现金流量的未来价值。

在财务决策中，对于年金现值和终值的比较是至关重要的。

本文将就年金现值与终值的比较进行探讨。

首先，我们来看看年金现值的计算方法。

年金现值是指未来一系列现金流量在当下的价值。

计算年金现值的方法可以用现值公式来表示，即PV = PMT × [(1 - (1 + r)^-n) / r]，其中PV代表年金现值，PMT代表每期现金流量，r代表折现率，n代表期数。

通过这个公式，我们可以计算出不同时期的现金流量在当下的价值，帮助我们做出更明智的决策。

然后，我们来看看年金终值的计算方法。

年金终值是指未来一系列现金流量在未来的价值。

计算年金终值的方法可以用终值公式来表示，即FV = PV × (1 + r)^n，其中FV代表年金终值，PV代表现值，r代表折现率，n代表期数。

通过这个公式，我们可以计算出未来一系列现金流量的未来价值，帮助我们更好地规划未来的财务安排。

接着，我们来比较年金现值和终值在财务决策中的作用。

年金现值可以帮助我们评估不同时期的现金流量在当下的价值，有助于我们做出投资决策、贷款决策等。

而年金终值则可以帮助我们评估未来一系列现金流量的未来价值，有助于我们规划未来的财务安排和退休计划等。

因此，在财务管理中，年金现值和终值都扮演着重要的角色，需要根据具体情况灵活运用。

最后，需要注意的是，在比较年金现值和终值时，我们应该根据具体情况综合考虑两者的影响因素。

在实际应用中，我们可能需要同时考虑年金现值和终值，综合分析现金流量在不同时间点的价值，以便做出更全面的财务决策。

综上所述，年金现值与终值的比较在财务管理中具有重要意义。

通过对年金现值和终值的计算和比较，我们可以更好地评估现金流量的价值，帮助我们做出明智的财务决策。

终值和现值的计算公式是什么？
公式如下：
1、年金终值计算公式为：F=A*(F/A，i，n)=A*(1+i)n-1/i
其中(F/A，i，n)称作“年金终值系数”。

2、年金现值计算公式为：P=A*(P/A，i，n)=A*[1-(1+i)-n]/i
其中(P/A，i，n)称作“年金现值系数”。

扩展资料：
如果年金的期数n很多，用上述方法计算现值显然相当繁琐。

由于每年支付额相等，折算现值的系数又是有规律的，所以，可找出简便的计算方法。

先付年金现值：是其最后一期期末时的本利和，相当于各期期初等额收付款项的复利现值之和。

n期先付年金与n期普通年金的收付款次数相同，但由于付款时间不同，n期先付年金现值比n期普通年金的现值多计算一期利息。

因此在n期普通年金现值的基础上乘以（1+i）而将分母加1就得出n期先付年金的现值了。

六、年金终值和年金现值的计算（一）年金的含义年金是指一定时期内每次等额收付的系列款项。

通常记作A 。

具有两个特点：一是金额相等；二是时间间隔相等。

也可以理解为年金是指等额、定期的系列收支。

在现实工作中年金应用很广泛。

例如，分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款、每年相同的销售收入等，都属于年金收付形式。

老师手写板：①②年、月、半年、2年1年 2年 3年1年 1年 1年（二）年金的种类年金按其每次收付款项发生的时点不同，可以分为四种：普通年金（后付年金）：从第一期开始每期期末收款、付款的年金。

预付年金（先付年金、即付年金）：从第一期开始每期期初收款、付款的年金。

与普通年金的区别仅在于付款时间的不同。

递延年金：从第二期或第二期以后开始每期期末收付的年金。

永续年金：无限期的普通年金。

注意：各种类型年金之间的关系（1）普通年金和即付年金区别：普通年金的款项收付发生在每期期末，即付年金的款项收付发生在每期期初。

联系：第一期均出现款项收付。

【例题1·单选题】2007年1月1日，甲公司租用一层写字楼作为办公场所，租赁期限3年，每年12月31日支付租金10万元，共支付3年。

该租金有年金的特点，属于（ ）。

(2010年考试真题)A ．普通年金B ．即付年金C ．递延年金D ．永续年金【答案】A【解析】每年年末发生等额年金的是普通年金。

（2）递延年金和永续年金二者都是在普通年金的基础上发展演变起来的，它们都是普通年金的特殊形式。

它们与普通年金的共同点有：它们都是每期期末发生的。

区别在于递延年金前面有一个递延期，也就是前面几期没有现金流，永续年金没有终点。

在年金的四种类型中，最基本的是普通年金，其他类型的年金都可以看成是普通年金的转化形式。

【提示】1.这里的年金收付间隔的时间不一定是1年，可以是半年、一个季度或者一个月等。

A A A A A A A A A A 300万 200万 100万2.这里年金收付的起止时间可以是从任何时点开始，如一年的间隔期，不一定是从1月1日至12月31日，可以是从当年7月1日至次年6月30日。

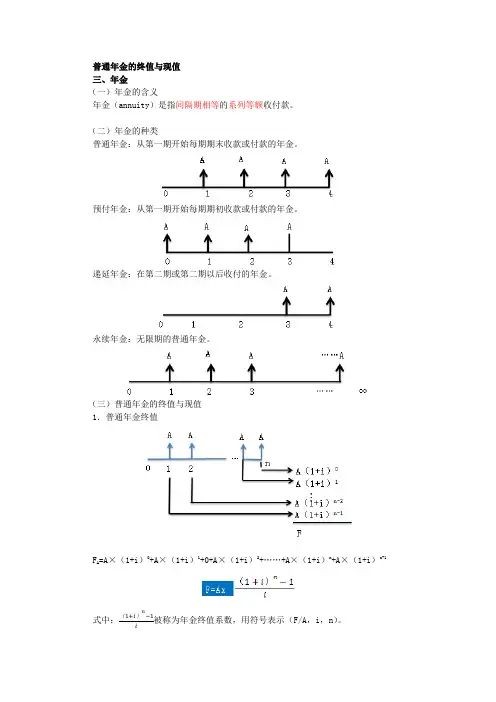
终值和现值1.年金终值和年金现值（1）年金现值（普通年金现值）普通年金现值是指将在一定时期内按相同时间间隔在每期期末收付的相等金额折算到第一期期初的现值之和。

根据复利现值的方法计算年金现值的公式为：P A=A（1+i）-1+A（1+i）-2+A（1+i）-3+···+A（1+i）-n=A式中称为“年金现值系数”记做（P/A,i,n）【例题】某投资项目于2017年年初完工，假定当年投产，从投产之日起每年末可获得收益100000元。

按年利率5%计算，预期5年收益的现值是多少元？（P/A，5%，5）=4.3295【答案】P A=A×（P/A，i，n）=100000×（P/A，5%，5）=100000×4.3295=432950（元）。

【例题·单选题】2017年1月1日，某企业的投资项目正式投入运营，从运营之日起，该企业每年年末可从该项目中获得收益200000元，预计收益期为4年。

假设年利率6%，已知（P/A，6%，4）=3．4651。

不考虑其他因素，2017年1月1日该项目预期4年总收益的现值为（）元。

（2018年）A．693020B．200000C．2772080D．800000【答案】A【解析】P A=200000×（P/A，6%，4）=200000×3.4651=693020（元）。

【例题·单选题】下列各项中，属于普通年金形式的是（）。

（2018年）A．企业在某中学设立奖励基金，用于每年发放等额奖学金B．企业租房2年，每个月初向出租方支付等额房租C．企业生产线使用年限为5年，从年初投产之日起每年年末获得等额现金收益D．企业设立一项公益基金，连续10年于每年年初投入等额奖金【答案】C【解析】普通年金是年金的最基本形式，它是指从第一期起，在一定时期内每期期末等额收付的系列款项，又称为后付年金，即选项C正确。

年金是指一定时期内定期支付的固定金额的现金流，可以分为年金的终值和现值两种计算方式。

一、年金的终值计算年金的终值是指在一定时期内，以固定利率计算，连续不断地进行定期支付的现金流的总金额。

假设有一个年金，每年支付2000元，年利率为5%，计算5年后的年金终值需要使用以下公式：FV=PMT×[(1+r)^n-1]/r其中FV表示年金的终值；PMT表示每年支付的金额；r表示年利率；n表示年数。

将数据代入计算公式，得到年金的终值：FV=2000×[(1+0.05)^5-1]/0.05=2000×[1.276-1]/0.05=2000×0.276/0.05二、年金的现值计算年金的现值是指在一定时期内，以固定利率计算，连续不断地定期支付的现金流的当前金额。

假设有一个年金，每年支付2000元，年利率为5%，计算当前的年金现值需要使用以下公式：PV=PMT×[1-(1+r)^-n]/r其中PV表示年金的现值；PMT表示每年支付的金额；r表示年利率；n表示年数。

将数据代入计算公式，得到年金的现值：PV=2000×[1-(1+0.05)^-5]/0.05=2000×[1-0.7835]/0.05=2000×0.2165/0.05=8659所以，当前该年金的现值为8659元。

年金的终值和现值的计算是财务管理中常用的计算方法，可以帮助人们进行投资决策和规划个人财务。

通过计算年金的终值，可以了解到未来收益的总金额，帮助人们判断投资的价值和收益能力；而通过计算年金的现值，可以了解到当前年金的价值，帮助人们做出合理的投资决策。

在实际应用中，可以使用电子表格软件（如Excel）中的相应函数或者金融计算器来进行年金的终值和现值的计算，这样更加简便和快捷。

不过，理解计算公式的推导过程对于掌握计算方法和理解计算结果的正确性是很重要的。

年金是指在一定期限内定期支付的一系列等额现金流。

年金可以分为两类：年金终值和年金现值。

年金终值是指在未来一些特定时间点的一系列等额现金流的总和。

计算年金终值的公式如下：FV=PMT*[(1+r)^n-1]/r其中FV是年金终值PMT是每期支付的金额r是每期的利率n是支付期数。

我们可以通过以下例子来说明如何计算年金终值：假设你决定每个月从现在开始存入500元，存款期限是10年，年利率是5%。

现在我们来计算这个年金的终值。

PMT=500,r=0.05/12,n=10*12=120。

带入公式计算得到：FV=500*[(1+0.05/12)^120-1]/(0.05/12)年金现值是指将未来的一系列等额现金流折算到现在的总金额。

计算年金现值的公式如下：PV=PMT*[1-(1+r)^(-n)]/r其中PV是年金现值PMT是每期支付的金额r是每期的利率n是支付期数。

以下是一个年金现值的实例：假设你决定每个月从现在开始存入500元，存款期限是10年，年利率是5%。

现在我们来计算这个年金的现值。

PMT=500,r=0.05/12,n=10*12=120。

带入公式计算得到：PV=500*[1-(1+0.05/12)^(-120)]/(0.05/12)在计算年金终值和现值时，需要注意以下几个要点：1.利率的表示方式：通常利率是年利率，需要根据支付频率进行调整。

例如，如果利率是年利率，而支付频率是每个月，则利率需要除以122.支付期数的计算：支付期数等于存款期限乘以支付频率。

例如，如果存款期限是10年，支付频率是每个月，则支付期数为10乘以12，即120期。

3.利率和支付期数的单位要一致：利率和支付期数的单位要保持一致，比如，如果利率是年利率，支付期数应该是年份；如果利率是月利率，支付期数应该是月份。

4.汇率调整：如果计算的是国际性的年金，涉及到不同货币的转换，需要根据汇率进行调整。

综上所述，年金终值和现值的计算可以通过相应的公式进行完成。

现值（Present Value，PV）是指一笔未来的现金流量在现在的价值。

终值（Future Value，FV）是指一笔现金流量在未来的价值。

年金（Annuity）是指在固定时间间隔内，按照固定利率计算的一系列等额现
金流。

现值、终值和年金之间的关系可以通过现值终值年金计算公式来表示。

这个公式如下：
PV=P*(1-(1+r)^(-n))/r
其中，PV为现值，P为每期的支付金额，r为利率，n为总期数。

这个公式的推导可以通过数学的复利公式得到。

假设我们有一个固定的现金流量P，每期支付一次，支付期数为n。

那么，在第一期结束时，这笔现金流量的价值为P/(1+r)，其中r为利率。

在第二期结束时，这笔现金流量的价值为P/(1+r)^2、依此类推，在第n
期结束时，这笔现金流量的价值为P/(1+r)^n。

现值（PV）是指这个现金流量在现在的价值。

因此，我们可以将每期
的现金流量除以(1+r)^n，然后将所有的现金流量相加，来计算现值。

终值（FV）是指这个现金流量在未来的价值。

因此，我们可以直接将
每期的现金流量相加，来计算终值。

年金（Annuity）是指在固定时间间隔内，按照固定利率计算的一系
列等额现金流。

因此，我们可以将每期的现金流量用一个普通年金公式来
计算，然后将结果相加，来计算现值或者终值。

综上所述，现值终值年金计算公式是一种灵活和广泛应用的工具，用于计算金融和投资问题中的现值和终值。

通过这个公式，我们可以更加准确地评估和比较不同的投资选择，从而做出最优的决策。

（三）年金终值和现值——定期、等额的系列收支款项的复利终值和复利现值的合计数 1.年金：等额、定期的系列收支款项。

（1）系列——通常是指多笔款项，而不是一次性款项； （2）定期——每间隔相等时间（未必是1年）发生一次； （3）等额——每次发生额相等。

2.普通年金终值和现值 （1）普通年金（后付年金）：从第一期起，各期期末等额收付的年金，其特征为： ①n期内共发生n笔年金（n个A）； ②第1笔年金发生在第一期期末（时点1），最后1笔年金发生在最后一期期末（时点n）。

（2）普通年金终值——一定时期内每期期末等额收付款项的复利终值的合计数。

已知年金A（系列定期等额款项的每笔发生额）、每期复利1次的利率i、期数n（年金A的个数），求年金终值F（“n个A”的复利终值合计）。

以等额收付4次的普通年金为例，推导普通年金终值计算公式如下： F＝A+A（1+i）+A（1+i）2+A（1+i）3 推广成为一般形式，有： F＝A+A（1+i）+A（1+i）2+A（1+i）3+……+A（1+i）n－1 【示例】 A公司计划未来10年每年底将50000元存入银行，已知：存款年利率为2％，（F/A，2％，10）＝10.950，则第10年底这10笔存款的本利和合计为： F＝50000×（F/A，2％，10）＝50000×10.950＝547500（元） （3）普通年金现值——一定时期内每期期末等额收付款项的复利现值的合计数。

已知年金A（系列定期等额款项的每笔发生额）、每期复利1次的利率i、期数n（年金A的个数），求年金现值P（“n个A”的复利现值合计）。

以等额收付4次的普通年金为例，推导普通年金现值计算公式如下： P=A（1+i）－1+A（1+i）－2+A（1+i）－3+A（1+i）－4 推广成为一般形式，有： P=A（1+i）－1+A（1+i）－2+A（1+i）－3+A（1+i）－4+……+A（1+i）－n 【示例】 某企业年初存入银行一笔款项，计划用于未来10年每年底发放职工奖金10000元，已知：存款年利率为2％，(P/A，2％，10)＝8.9826，则现在应存入的款项可计算如下： P＝10000×（P/A，2％，10）＝10000×8.9826＝89826（元） （四）货币时间价值原理在财务决策中的应用 1.证券价值评估原理 （1）证券价值是证券所获未来现金流量按投资者的必要收益率所折成的现值，其中，投资者的必要收益率取决于等风险投资的预期收益率。

年金现值与终值的区别与联系在金融学中，年金是指一种定期给付固定数额的资金流，通常可以分为年金现值和终值两种形式。

年金现值是指未来一段时间内，每期支付一定金额的资金在当前时点的价值，而年金终值则是将未来所有支付的资金在未来特定时点的总价值。

接下来，我将详细介绍年金现值与终值的区别与联系。

首先，年金现值与终值的主要区别在于时间点的不同。

年金现值是在未来一段时间内每期支付的资金在当前时点的价值，而年金终值则是将所有未来支付的资金在特定时点的总价值。

因此，年金现值强调的是当前时点的价值，而年金终值则更注重未来时点的总价值。

其次，年金现值与终值的计算方式也有所不同。

年金现值的计算是通过现值公式来实现，该公式会考虑到每期支付的金额、利率以及期数，从而计算出未来支付的所有金额在当前时点的价值。

而年金终值则是通过终值公式来计算，该公式会考虑到每期支付的金额、利率以及期数，从而计算出未来所有支付的金额在未来特定时点的总价值。

此外，年金现值与终值之间也存在一定的联系。

首先，年金现值和终值都是预测未来一段时间内资金流的工具，能够帮助人们更好地规划资金的使用和投资。

其次，通过计算年金现值和终值，可以帮助人们更好地评估投资项目的价值和收益，从而做出更明智的投资决策。

总的来说，年金现值与终值虽然在时间点和计算方式上存在一定的区别，但它们也有着密切的联系，都可以作为评估资金流的重要工具。

通过深入了解年金现值与终值的概念和计算方法，可以帮助人们更好地管理自己的资金，并实现财务目标。

希望以上内容能够对您有所帮助，谢谢！。

3.年金终值与年金现值的计算香港首富李嘉诚说过“一个人从此刻开始，每年存 1.4 获取每年均匀 20%的投资回报率， 40 年后财产会增加为万元，并都能投资到股票或房地产，1 亿零 281 万元”。

（ 1 ）年金的含义和种类年金是指间隔期相等的系列等额收付款，往常记作 A 。

如间隔期固定、金额相等的分期付款赊购、分期偿还贷款、发放养老金、分期支付工程款以及每年同样的销售收入等。

一般年金预支年金递延年金永续年金【提示】一般年金和付年金都是从第一期开始生等收付，二者的区是付年金生在期初。

一般年金生在期末，（ 2 ）一般年金和年基金的算①一般年金F=A+A （ 1+i ） +A （ 1+i）2+⋯ +A（ 1+i ）n-1（ 1 ）将此公式两都乘以（1+i），F （ 1+i ） =A （ 1+i） +A （ 1+i）2+⋯ +A（ 1+i）n（ 2 ）（2）-（1）F i =A （ 1+i ）nA ，整理后得【】①称作“年金系数”，作：（F/A，i， n ）当 n ＞ 1 ，年金系数与折率或期数同方向。

② 年金终值系数与复利终值系数关系以下：=【应用举例】【例题】 2018 年 1 月 16 日，某人拟订了一个存款计划，计划从2019 年 1 月 16 日开始，每年存入银行 10 万元，合计存款 5 次，最后一次存款时间是2023 年 1 月 16 日。

每次的存款限期都是1年，到期时利息和本金自动续存。

假定存款年利率为2%，打算在2024 年 1 月 16 日拿出所有本金和利息，则届时本利和共为多少？（F/A ， 2%， 5 ） =5.2040 ，（ F/P ， 2%， 1 ） =1.02 。

【剖析】依据题干描绘，画出此题表示图以下：依据图形及要求此题解题步骤以下：第一步： 2018 年 1 月 16 日 -2023 年 1 月 16日的存进款切合一般年金的形式，因此可先将这5个 10 万元依据一般年金的形式折算到2023年 1月 16 日。