递延年金终值与现值的计算(有图解)

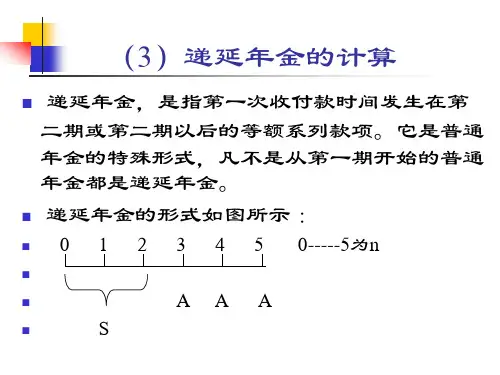
财务管理》第二章重难点讲解及例题：递延年金终值和现值递延年金终值和现值（1）递延年金终值（已知从第二期或第二期以后等额收付的普通年金A，求FA）递延年金是指第－次等额收付发生在第二期或第二期以后的普通年金。

图示如下：求递延年金的终值与求普通年金的终值没有差别（要注意期数），递延年金终值与递延期无关。

如上图中，递延年金的终值为：FA＝AX（F／A，i，n），其中，“n，，表示的是A的个数，与递延期无关。

（2）递延年金现值（已知从第二期或第二期以后等额收付的普通年金A，求PA）方法－：把递延期以后的年金套用普通年金公式求现值，这时求出的现值是第－次等额收付前－期的数值，再往前推递延期期数就得出递延年金的现值。

图示如下：PA＝AX（P／A，i，n）×（P／F，i，m）方法二：把递延期每期期末都当作有等额的收付，把递延期和以后各期看成是－个普通年金，计算这个普通年金的现值，再把递延期多算的年金现值减去即可。

图示如下：PA＝AX（P／A，i，m＋n）－A×（P／A，i，m）【提示】方法－、方法二求递延年金现值的思路是把递延年金的现值问题转换为普通年金的现值问题，再求递延年金现值。

方法三：先求递延年金的终值，再将终值换算成现值，图示如下：PA＝A×（F／A，i，n）×（P／F，i，m＋n）【提示】递延年金现值计算公式中的“n”指的是等额收付的次数，即A的个数；递延期“m”的含义是，把普通年金（第－次等额收付发生在第1期期末）递延m期之后，就变成了递延年金（第－次等额收付发生在第W期期末，W>1）。

因此，可以按照下面的简便方法确定递延期m的数值：（1）确定该递延年金的第－次收付发生在第几期末（假设为第W期末）（此时应该注意“下－期的期初相当于上－期的期末”）；（2）根据（W－1）的数值确定递延期m的数值。

【例题7.单选题】下列关于递延年金的说法中，错误的是（）。

A.递延年金是指隔若干期以后才开始发生的系列等额收付款项B.递延年金没有终值C.递延年金现值的大小与递延期有关，递延期越长，现值越小D.递延年金终值与递延期无关【答案】B【解析】递延年金是指隔若干期以后才开始发生的系列等额收付款项；递延年金存在终值，其终值的计算与普通年金是相同的；终值的大小与递延期无关；但是递延年金的现值与递延期是有关的，递延期越长，递延年金的现值越小，所以选项B的说法是错误的。

终值F ＝P ＋P ×n ×i ＝P ×（1＋i ×n ）现值P ＝F/(1＋i ×n ）终值F=P ×(1+i)n ＝P ×（F/P ，i ，n ）现值P=F ×(1+i)-n =F ×（P/F ，i ，n ）F=A ×[(1+i)n -1]/i ＝A ×（F/A ，i ，n ）在普通年金终值计算公式中，如果已知年金终值求年金，则求出的年金被称为“偿债基金”。

年偿债基金A=F*i/[(1+i)n -1]=F*(A/F,i,n)即：偿债基金＝普通年金终值×偿债基金系数“偿债基金系数”与“年金终值系数”互为倒数。

P=A ×[1-(1+i)-n ]/i ＝A ×（P/A ，i ，n ）在普通年金现值计算公式中，如果已知年金现值求年金，则求出的年金被称为“资本回收额”。

资本回收额A=P*i/[(1-(1+i)-n ]=P*(A/P,i,n)即：资本回收额＝普通年金现值×资本回收系数“资本回收系数”与“年金现值系数”互为倒数。

F ＝A ×（F/A ，i ，n ）×（1＋i ）＝A ×[（F/A ，i ，n ＋1）-1]P ＝A ×（P/A ，i ，n ）×（1＋i ）＝A ×[（P/A ，i ，n －1）＋1]终值F ＝A ×（F/A ，i ，n ），其中n 是指A 的个数，与递延期无关。

计算方法一：先将递延年金视为n 期普通年金，求出在m 期末普通年金现值，然后再将此年金现值按求复利现值的方法折算到第一期期初。

P ＝A ×（P/A ，i ，n ）×（P/F ，i ，m ）计算方法二：先计算m ＋n 期年金现值，再减去m 期年金现值。

P ＝A ×[（P/A ，i ，m ＋n ）-（P/A ，i ，m ）］计算方法三：先求递延年金终值，再折现为现值。

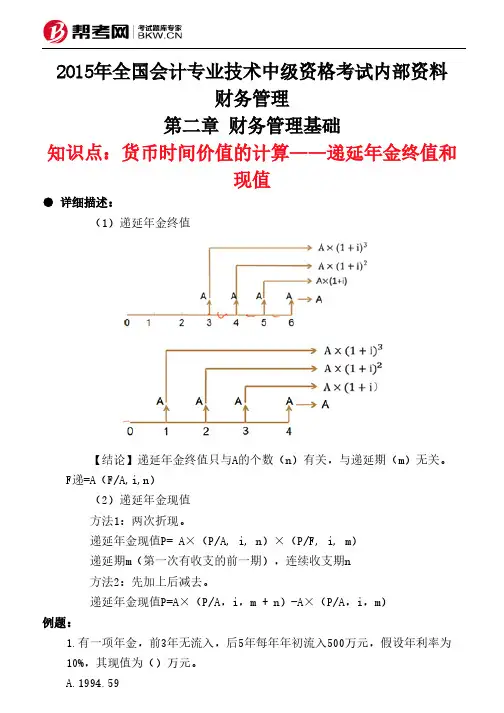
2015年全国会计专业技术中级资格考试内部资料财务管理第二章 财务管理基础知识点：货币时间价值的计算——递延年金终值和现值● 详细描述：（1）递延年金终值【结论】递延年金终值只与A的个数（n）有关，与递延期（m）无关。

F递=A（F/A,i,n）（2）递延年金现值方法1：两次折现。

递延年金现值P= A×（P/A, i, n）×（P/F, i, m）递延期m（第一次有收支的前一期），连续收支期n方法2：先加上后减去。

递延年金现值P=A×（P/A，i，m + n）-A×（P/A，i，m）例题：1.有一项年金，前3年无流入，后5年每年年初流入500万元，假设年利率为10%，其现值为（）万元。

A.1994.59B.1566.36C.1813.48D.1423.21正确答案：B解析：现值＝500×（P/A，10%，5）×（P/F，10%，2）＝1566.36（万元）2.某递延年金，前3年没有现金流入，后5年每年年初有等额的现金流入100万元，折现×率为10%，下列关于该递延年金现值的表达式中，不正确的是（） 。

A.100×(P/A,10%,5)×(P/F,10%,2)B.100×(P/A,10%,5)×(P/F,10%,3)C.100×[(P/A,10%,4)+1]×(P/F,10%,3)D.100×(F/A,10%,5)×(P/F,10%,7)正确答案：B解析：本题中，第一次现金流入发生在第4年初，相当于第3年末。

100×(P/A,10%,5)表示的是第3年初的现值，进一步折现到第1年初，还需要折现2期，因此，选项A的表达式正确，选项B的表达式不正确；100×[(P/A,10%,4)+1]表示的是第4年初的现值，进一步折现到第1年初，还需要折现3期，因此，选项C的表达式正确；100×(F/A，10%,5)表示的是第7年末的终值，进一步折现到第1年初，需要折现7期，因此，选项D的表达式正确。

答：
1.定义递延年金：递延年金是指以未来的货币价值来确定的一种金融产品，即受益人的金融权利在未来一些特定的时点上才发放的金融付款。

2.递延年金现值的计算方法：递延年金现值是指投资者在当前时点上将未来收取的延迟支付的金融付款转换为现在价值的过程，可以用贴现现值公式来表示：
V=P/(1+i)^n
其中：
V表示现值；
P表示未来可能收取的金融付款金额；
i表示贴现率；
n表示未来支付延期的时间。

3.根据贴现原理，同样本金及利息水平的情况下，贴现现值越高，说明未来支付的延迟时间越长，同时也是投资者收益越低。

因此，投资者在计算递延年金现值时，应根据投资的期望收益率合理设定贴现率，以确定贴现现值大小。

4.投资者不仅应根据未来可能收取的金融付款金额、未来延期支付的时间和贴现率来计算递延年金现值，而且还应根据自身的投资能力和投资目标，计算出最佳的递延年金现值，以实现投资的最佳收益。

第四节递延年金终值与现值的计算第四节递延年金终值与现值的计算钭志斌丽水职业技术学院一、递延年金递延年金（Deferred Annuity）是指第一次年金收付形式发生在第二期或第二期以后的年金。

递延年金的支付形式如图2-8所示。

12 …mm+1m+2 …m+n递延期递延年金发生的期数二、递延年金终值计算由于递延期m与终值无关只需考虑递延年金发生的期数n。

计算公式如下：12 …mm+1m+2 …m+n递延期递延年金发生的期数【例2-11】农庄的累计净收益为多少？假设江南公司拟一次性投资开发某农庄，预计该农庄能存续15年，但是前5年不会产生净收益，从第6年开始，每年的年末产生净收益5万元。

在考虑资金时间价值的因素下，若农庄的投资报酬率为10%，该农庄给企业带来累计收益为多少？12 …55+15+2 …5+10递延期5递延年金发生的期数10求该农庄给企业带来的累计收益，实际上就是求递延年金终值。

根据＝50000×（F/A，10%，10）＝50000×153>.937＝796850（元）12 …55+15+2 …5+10递延期5递延年金发生的期数10三、递延年金现值的计算递延年金的现值与递延期数相关，递延的期数越长，其现值越低。

递延年金的现值计算有三种方法：方法1：把递延期以后的年金套用普通年金公式求现值，然后再向前折现。

即：12 …mm+1m+2 …m+n递延期递延年金发生的期数方法2：把递延期每期期末都当作有等额的年金收付A，把递延期和以后各期看成是一个普通年金，计算出这个普通年金的现值再把递延期虚增的年金现值减掉即可。

即：12 …mm+1m+2 …m+n假设递延期内每期都有A收付方法3：先求递延年金终值，再折现为现值即12 …mm+1m+2 …m+n【例2-12】农庄的累计投资限额为多少？接例2-11，假设江南公司决定投资开发该农庄，根据其收益情况，该农庄的累计投资限额为多少？实质上，求现值12 …55+15+2 …5+10递延期5递延年金发生的期数10按第一种方法计算：P＝50000×（P/A，10%，10）×（P/F，10%，5）＝50000×6.1446×0.6209＝190759.11（元）按第二种方法计算：P＝50000×（P/A，10%，15）－50000×（P/A，10%，5）＝50000×7.6061－50000×3.7908＝190765.00（元）按第三种方法计算：P＝50000×（F/A，10%，10）×（P/F，10%，15）＝50000×15.9370×0.2394＝190765.89（元）计算结果表明，该农庄的累计投资限额为190759.11元。

（5）递延年金终值和现值的计算递延年金由普通年金递延形成，递延的期数称为递延期，用m表示（m为大于0的整数）。

递延年金的第一次收付发生在第（m+1）期期末。

递延年金的形式如下图：递延年金终值递延年金的终值=A×（F/A，i，n），只与年金期有关，与递延期无关。

递延年金的现值递延年金的现值，与递延期有关。

递延年金的现值计算方法【应用举例】【例题】某递延年金为从第4期开始，每期期末支付10万元，共计支付6次，假设利率为4%，相当于现在一次性支付的金额是多少？（P/A，4%，6）=5.2421，（P/F，4%，3）=0.8890，（P/A，4%，9）=7.4353，（P/A，4%，3）=2.7751。

【分析】从图上可看出，递延期m=3，年金A=10万元，n=6。

第一种方法分段折现：将6个10万元按普通年金求现值的方法折算到第3期期末，再将6年期的普通年金现值由按复利现值的方法折算到第0年。

递延年金现值P=10×（P/A，4%，6）×（P/F，4%，3）=10×5.2421×0.8890=46.60（万元）第二种方法用减法：假设递延期每期期末也都有年金10万元，这样在0时点看就构成了普通年金的形式，一共有9个10万元，可将这9个10万元求普通年金的现值，然后再减去递延期3个10万元的普通年金现值，就可求出本题递延年金的现值。

即：递延年金现值P=10×（P/A，4%，9）-10×（P/A，4%，3）=10×7.4353-10×2.7751=46.602（万元）【例题】某递延年金为从第4期开始，每期期初支付10万元，共计支付6次，假设利率为4%，相当于现在一次性支付的金额是多少？（P/F，4%，2）=0.9246，（P/A，4%，6）=5.2421。

【分析】从图上可看出，递延期m=3，年金A=10万元，n=6。

递延年金现值P=10×（P/A，4%，6）×（P/F，4%，2）=10×5.2421×0.9246=48.47（万元）递延年金现值P=10×（P/A，4%，8）-10×（P/A，4%，2）=48.47（万元）递延年金的现值计算方法【应用举例】【例题】DL公司2019年12月10日欲购置一批电脑，销售方提出三种付款方案，具体如下：方案1：2019年12月10日付款10万元，从2021年开始，每年12月10日付款28万元，连续支付5次。

终值现值系数公式终值和现值系数公式，这俩家伙在财务和金融领域那可是相当重要！咱先来说说啥是终值。

简单来讲，终值就是一笔钱在未来某个时间点的价值。

比如说，你现在有 1000 块钱，存到银行里年利率是 5%，存 3 年，那 3 年后这笔钱会变成多少呢？这就得用到终值系数公式来算一算啦。

终值系数公式是：F = P × (1 + i)^n 。

这里的 F 就是终值，P 是现值，也就是你最初的那笔钱，i 是利率，n 是期数。

举个例子哈，我有个朋友小李，他特别想攒钱买一辆心仪已久的摩托车，价格大概是 2 万块。

他现在手里有 1 万块，他想着把这 1 万块存到银行里，银行年利率是 4%。

那他得存几年才能攒够买摩托车的钱呢？咱们用终值系数公式来算算。

P = 10000，i = 4% = 0.04，F = 20000，代入公式就是 20000 = 10000 × (1 + 0.04)^n 。

先化简一下，2 = (1.04)^n 。

这时候就得用到对数来求解啦，n = log₁.₀₄ 2 。

算出来 n 大概是17.67 年。

哎呀，小李一看，这可不行，得想办法多赚点钱或者找个更高利率的存钱方式。

再来说说现值。

现值呢，就是未来的一笔钱在现在的价值。

比如说，你知道 3 年后能收到 5000 块钱，年利率还是 5%，那这 5000 块钱在现在值多少钱呢？这就用到现值系数公式：P = F / (1 + i)^n 。

还是我那朋友小李，他听说有个投资项目，3 年后能给他带来15000 块的收益，但是需要他现在投入 12000 块。

他就犯愁了，不知道这投资划不划算。

咱们用现值系数公式来帮他算算。

F = 15000，i = 5%，n = 3，P = 15000 / (1 + 0.05)^3 ，算出来 P 大概是 12957.58 块。

这说明，如果按照 5%的利率来算，3 年后的 15000 块钱在现在只值 12957.58 块，而他现在要投入 12000 块，看起来还是有点小赚的。

递延年金推导公式
摘要：
1.递延年金现值计算公式
2.递延年金现值的概念
3.递延年金现值的计算方法
4.递延年金终值计算方法
5.递延年金在财务规划中的应用
正文：
一、递延年金现值计算公式
递延年金现值计算公式为：PV(1+(r/m))^(-mn)[(A/i)(1+(r/m))^(-n)]，其中PV 代表年金的现值，r 代表折现率，m 代表折现率的分割次数，n 代表距今的年份数，A 代表支付的金额，i 代表时期。

二、递延年金现值的概念
递延年金现值是指间隔一定时期后每期期末或期初收付的系列等额款项，按照复利计息方式折算的现时价值，即间隔一定时期后每期期末或期初等额收付资金的复利现值之和。

三、递延年金现值的计算方法
递延年金现值的计算方法包括三种：
1.直接计算法：根据公式PV(1+(r/m))^(-mn)[(A/i)(1+(r/m))^(-n)]，将给定的参数代入计算即可。

2.间接计算法：先求出m 期后付年金现值，减去没有付款的前m 期后
付年金现值，二者之差便是延期m 期的n 期后付年金现值。

3.折现法：将未来每期支付的金额折现到现在，求和即可得到递延年金现值。

四、递延年金终值计算方法
递延年金终值计算方法与普通年金终值计算一样，计算公式为：
FA(FA,i,n)，其中"n"表示的是A 的个数，与递延期无关。

五、递延年金在财务规划中的应用
递延年金在企业家庭财务规划中可以提升个人财务安全性和抗风险能力。

中级经济师递延年金现值计算方法嘿，咱今儿个就来唠唠中级经济师递延年金现值计算方法这档子事儿。

你说这递延年金现值，就好像是一个藏起来一部分的宝藏，咱得想办法把它给挖出来，算出它到底值多少钱。

想象一下啊，年金就像是一条稳定流淌的小河，每年都给你带来一定的财富。

但这递延年金呢，它不是一开始就给你，而是过了一段时间才开始流出来。

那怎么算它的现值呢？咱可以把它分成两段来看。

一段是从开始递延到真正开始有年金流入的这一段，这就像是一段空白期；另一段就是从开始有年金流入之后的那段正常年金。

咱先看这空白期，这时候其实就相当于一个普通的复利现值问题。

就好比你把钱存在银行里，过了几年后再取出来，得算一下现在值多少钱。

然后呢，再看后面正常年金那段。

这时候就可以用普通年金现值的计算方法啦。

比如说，有个递延年金，从第 3 年开始每年末流入 100 元，一共流5 年，利率是 5%。

那咱先算前面两年的复利现值，把第三年年初的价
值算出来。

然后再用普通年金现值的方法，把后面 5 年的年金现值算
出来。

最后把这两个加起来，可不就得到递延年金的现值啦！
这计算过程中可得仔细点，一个数算错了，那结果可就全错咯！就
像盖房子，一块砖没放好，整座房子都可能不稳当。

其实啊，中级经济师考试里，这递延年金现值计算虽然有点小复杂，但只要咱多练练，多琢磨琢磨，也没啥难的。

你说是不是？咱可不能
被这点小难题给吓住了呀！咱得鼓起劲来，把它拿下！
总之，递延年金现值计算方法就是这么个事儿，咱得好好掌握，这
样在考场上才能应对自如，取得好成绩呀！加油吧！。

递延年金的计算方法
递延年金呢，就是有个小延迟的年金。

比如说，你在未来的某个时间点才开始收到或者支付年金。

咱先说说递延年金现值的计算。

有两种常见的方法哦。

一种是分段法。

你可以把递延年金的现金流分成两段。

第一段呢，是前面没有年金收付的那段时间，就像在等待期一样。

第二段就是开始有年金收付的那段时间啦。

计算的时候呢，先把后面那段年金按照普通年金现值的计算方法算出在开始收付那年的现值，然后再把这个现值往前折现到最开始的时间点。

就好像你先把后面的钱在那个开始收钱的时间点算个总价值，然后再把这个总价值折回到现在，是不是有点像穿越时空算钱钱呀，哈哈。

还有一种方法是补全法。

你就想象把前面缺的那些年金都补上，这样就变成一个完整的普通年金啦。

然后按照普通年金现值算出这个完整年金的现值。

接着呢，再把你补上的那部分年金的现值减掉。

这就好比你先多算了一些钱，然后再把多算的部分去掉，剩下的就是递延年金的现值啦。

再说说递延年金终值的计算。

这个就比较简单啦。

因为递延年金终值的计算和普通年金终值的计算方法是一样的，只要按照普通年金终值的公式，用年金的金额、利率和收付的期数来计算就好啦。

就像你不管前面等了多久，只要后面收钱或者付钱的方式是一样的，那最后算总的钱数的时候，就和普通年金算最后的总数一样呢。

递延年金的计算公式递延年金是指在最初若干期没有收付款项的情况下，后面若干期等额的系列收付款项。

咱们先来说说递延年金的计算公式，这个公式看起来有点复杂，但是别怕，跟着我一步步来，保证能搞明白。

我先给您举个例子啊。

比如说，小王打算从第 3 年末开始，每年年末存入银行 1000 元，年利率为 5%，连续存 5 年。

那这就是一个递延年金的问题。

递延年金的计算方法有两种，一种是先把递延年金视为普通年金，求出递延期末的现值，然后再将此现值调整到第一期期初。

另一种是假设递延期中也进行收付，先求出（m＋n）期的年金现值，然后扣除实际并未收付的递延期（m）的年金现值。

咱就用上面小王的例子，先用第一种方法算算。

先把第 3 年末到第7 年末这 5 年的年金看作普通年金，按照普通年金现值的计算公式，P = A×（P/A，i，n），其中 A 是年金金额，也就是 1000 元；i 是年利率5%；n 是年金期数 5 年。

计算得出这 5 年年金在第 3 年初（也就是第 2 年末）的现值，然后再把这个现值按照复利现值的计算公式，P = F×（P/F，i，m），折回到第 1 年初。

这里的 F 就是刚才算出的第 2 年末的现值，m 是递延期 2 年。

再用第二种方法算算，假设从第 1 年初就开始收付，那就是一个 7 年期的年金，按照普通年金现值的计算公式算出（m＋n）期的现值。

然后再减去前 2 年实际没有收付的年金现值。

您看，通过这两种方法都能算出递延年金的现值。

不过在实际运用的时候，得根据具体的题目情况选择更简便的方法。

我记得有一次，在给学生们讲递延年金的计算公式时，有个学生特别迷糊，怎么都搞不明白。

我就又给他举了个例子，把每一步都详细地写在黑板上，还让他自己动手算。

最后他终于恍然大悟，那脸上露出的笑容，让我觉得自己的努力特别值得。

其实啊，学习递延年金的计算公式就像是走迷宫，刚开始可能会觉得晕头转向，但只要耐心点儿，多练习几个例子，就能找到出口，搞清楚其中的门道。