《幂的乘方与积的乘方》ppt课件

格式：ppt
大小：945.00 KB
文档页数：22

下载文档原格式

幂的乘方与积的乘方 ppt课件4

(3) (am)2 =am· am =am+m =a2m ;
n个am
…· (4) (am)n =am· a m· am（幂的意义）
n个 m
… +m m+m+ =a
（同底数幂的乘法性质）
=amn （乘法的意义） (am)n=amn (m,n都是正整数). 幂的乘方，底数不变，相乘指数 .
例1 计算：
…· …· am · an =(a· a· a) (a· a· a) …· = a· a· a =am+n
m个 a
n个 a
(m+n)个a
问题1. 乙正方体的边长是2cm, 则乙正方体的体积V乙= 8 cm3
甲正方体的边长是乙正方体的5倍，则甲正方体的体积 V甲= 1000 cm3 V甲是V乙的 125 即 53 倍倍
第四章整式的乘法
4. 幂的乘方与的运算性质的过程，进一步体会幂的意义，发展推理能力和有条理的表达能力。
2. 了解幂的乘方与积的乘方的运算性质，并能解决一些实际问题。
复习
幂的意义: n个 a
…· a· a· a =an
同底数幂乘法的运算性质： am · an =am+n（m,n都是正整数）
木星地球太阳
(102)3=106，为什么？
(102)3
幂的意义 2 2 2 ( 根据 =10 ×10 ×10
). ).
2+2+2 (根据同底数幂的乘法性质 =10
=106 2 × 3 =10
太棒了！
做一做
计算下列各式，并说明理由 .
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n . 62· 62· 62 解：(1) (62)4 = 62· =62+2+2+2 =68 =62×4 ; (2) (a2)3 = a2· a2· a2 =a2+2+2 =a6 =a2×3 ;

北师大版数学七年级下册幂的乘方与积的乘方——幂的乘方课件(第一课时20张)

拓展与延伸
已知16m=4×22n-2，27n=9×3m+3 ，求 m，n 的值.
解：因为16m=4×22n-2，所以24m =22×22n-2 . 所以24m=22n，即4m=2n，2m=n. ① 因为 27n=9×3m+3 ，所以(33)n=32×3m+3 . 所以33n=3m+5，即3n=m+5. ② 由①②得，m=1，n=2.
解：a4n-a6n = (a2n)2- (a2n)3 = 32-33 = -18 .
把指数是积的情势的幂写成幂的乘方，amn=(am)n （m，n都是正整数），然后整体代入，求出式子的值.
课堂小结
幂的乘方
性质：幂的乘方，底数不变，指数相乘.
(am)n=amn （m，n为正整数）
当堂小练
1.计算(x3)3的结果是（ D ）
新课导入
视察计算结果，你能发现什么规律？ (1) (x2)2 = x2∙x2 = x2+2= x4 ;
(2) (x2)3 = x2∙x2∙x2 = x2+2+2= x6 .
结论 (1) (x2)2 = x2∙2= x4 ; (2) (x2)3 = x2∙3= x6 .
新课导入
视察计算结果，你能发现什么规律？（m，n为正整数）
A. x5
B. x6
C. x8
D. x9
2. 下列运算正确的是（ B ）
A. a2·a3=a6 a5
B. (a2)3=a6
C. a5·a5=a25 a10
D. (3x)3=3x3 27x3
当堂小练
3. （1）若2x+y=3，则4x·2y= 8 . （2）已知3m·9m·27m·81m=330，求m的值. 解：3m·32m·33m·34m=330 310m=330 m=3

北师大版数学七年级下册幂的乘方与积的乘方——积的乘方课件(第二课时20张)

第一章整式的乘除
2 幂的乘方与积的乘方课时2 积的乘方
学习目标
1.了解并掌握积的乘方的法则，熟练运用幂的乘方的运算法则进行实际计算.（重点） 2.掌握积的乘方的运算法则的推导.（难点） 3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
新课导入
思考边长为 x 的正方形面积为 x2 ，将边长扩大3倍后，新的正方形的面积为多少呢？
(2)1 [(-a3)2]2 ;
3
解：(1) (-3×102)3 =(-3)3×(102)3=-27×106=-2.7×107 ;
(2)
1
[(-3
a3)2]2
1
=(9
)2·(a6)2=811
a12 ;
(3) (-a2b3)3 =(-1)3·(a2)3·(b3)3=-a6b9 .
(3) (-a2b3)3 .
） B. m2·m3=m6
C. (mn)3=mn3
分析：选项A中，m2和2m3不是同类项，不能合并，故而错误；选项B中，m2·m3=m5，故而错误；选项D中，(mn)3=m3n3，故而错误.
拓展与延伸
若(4am+nbm)3=64a15b9成立，则（ A ）
A. m=3，n=2
B. m=n=2
C. m=6，n=2
思考：你能总结出积的乘方的运算法则吗?
新课讲授
知识点1 积的乘方
性质：积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘
一. 般地，对于任意底数a，b与任意正整数 n.
（ab）n （ab）（ ab）（ ab）
符号表示： (ab)n=anbn （n为正整数）.
n个ab
（a a a）（ b b b）

课件114幂的乘方与积的乘方.ppt

证明
=am+m+ … +m （同底数幂的乘法性质）
=amn （乘法的意义）
幂的乘方法则
(am)n=amn (m,n都是正整数)
幂的乘方，底数不变，指数相乘.
阅读体验 ☞例题解析
【例1】计算：
(1) (102)3 ;
(2) (b5)5 ;
(4) -(x2)m ; (5) (y2)3 ·y ;
V球
4 3
R3
甲球的半径是乙球的10倍，则甲球的体积V甲= 36000 cm3 .
V甲是 V乙的 1000 倍
即 103 倍
如果甲球的半径是乙球的n 倍，那么甲球体积是乙球体积的 n3倍。
地球、木星、太阳可以近似地看作球体。木星、太阳
的半径分别约是地球的10倍和102倍，它们的体积分别约
是地球的 103 倍和 106 倍. (102)3=106，为什么？
底数不变，指数相加 .
作作业业

(6) 2(a2)6 – (a3)4 =2a2×6 - a3×4 =2a12-a12 =a12.
随随堂堂练练习习
1、计算： (1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 ·x2 ; (4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 ·x3 .
解：(1) (62)4 = 62·62·62·62=62+2+2+2 =68 =62×4 ;
(2) (a2)3 = a2·a2·a2 =a2+2+2 =a6 =a2×3 ;
(3) (amm)22=am·am =am+m=a2m ;

幂的乘方与积的乘方(2)课件PPT

5、若ａ 2＋ａ＝ 0，（ａ0）求ａ 2003＋ａ 2002＋ 12的值。
27
6、如果 28ｎ16ｎ＝ 222，求ｎ的值。
7、如果9ｎ2＝ 316，求ｎ的值。
28
8 、已知ａｘ＝ 3 ，ａｙ＝ 2 ，求下列各式的值。（1 ）ａ2ｘ＋ 3ｙ（ 2 ）ａ3ｘ＋ 2ｙ
(am)n = am ·am ·… ·am
n个am
（幂的意义）
= am+m+…+m
n个m （同底数幂的乘法性质）
结论
= amn (m，n都是正整数).
(am)n=amn(m，n都是正整数).
7
幂的乘方法则
(am)n=amn (m,n都是正整数)
幂的乘方，底数不变，指数相. 乘
8
例4 计算：（1）(105)2；
(2) (a 2)5
(7)(a2)3·(a3)4
( 3 )( x 3 ) 4 x 2
(8)(am+3)2
( 4 )( a 3 ) 2 n
(9)[(x-3y)m]3
(5)(am)4
(10)9m·27n
注1：幂的底数和指数不仅仅是单独字母或数字，
也可以是某个单项式和多项式. 17
练习2、判断下列各式的对错，并改正
(1)(a5)2=a7 (4)x3m+1=(x3)m+1 (2)a5·a2=a10 (5)a6·a4=a24 (3)(x3)3=x6 (6)4m·4n=22(m+n)
注2：幂的乘方法则与同底数幂的乘法法则的异同
(am)n amn(m,n都是正整 ). 数
aman amn(m,n都是正整 ). 数

初中数学北师大版七年级下册《幂的乘方与积的乘方(第2课时)》课件

（2）－(－2x3y4)3 ＝－(－2)3(x3)3(y4)3 ＝－(－8)x9y12 ＝8x9y12
4．计算：
（1）a2·(－a)3·(－a2)4；（2）(3x4y2)2＋(－2x2y)4；
＝a2·(－a3)·a8 ＝－a2·a3·a8 ＝－a13
＝9x8y4＋16x8y4 ＝25x8y4
（3）
探究新知（1）(3×5)4＝(3×5)×(3×5)×(3×5)×(3×5)×＝(3×3×3×3) ×(5×5×5×5)＝3( ) ×5( )；
4
4
（2）(ab)4＝
＝
＝a( )b( )；
（3）(ab)n＝
＝
＝a( )b( )．
解：（2）(ab)4＝(ab)·(ab)·(ab)·(ab)＝(a·a·a·a)·(b·b·b·b)＝a4b4；
1.2
幂的乘方与积的乘方
数学北师大版七年级下
学习目标 1.掌握积的乘方的运算法则，并能利用法则进行计算和解决一些实际问题．
2.探索积的乘方的法则，进一步体会幂的意义，发展推理能力和有条理的表达能力，培养从特殊到一般，从具体到抽象的逐步概括抽象的认识能力．
1．同底数幂的乘法的运算性质：同底数幂相乘，底数不变，指数相加． 2．幂的乘方的运算性质：幂的乘方，底数不变，指数相乘．
( n )个ab
(ab)n (ab) (ab) (ab)
( n )个a
( n )个b
aa abb b
a( n )b( n )；
(ab)n =a( n )b( n （) n是正整数）．
2.把你发现的规律用文字语言表述，再用符号语言表达．积的乘方的结果是把积的每一个因式分别乘方，再把所得的
＝－8a6·a3＋16a2·a7－125a9

教学课件：七下湘教2.幂的乘方与积的乘方(第1课时幂的乘方)

知识讲授
做一做请根据乘方的意义及同底数幂的乘法填空，
视察计算结果，你能发现什么规律？
2
3
2
3
( 2 ) = ___________ ；
( ) = ___正整数）.
2
知识讲授
2
3
2
2
2
2+2+2
( 2 ) = 2 ·2 ·2 = 2

m n
知识讲授
练一练：
20
10
2
5
2
2
y
(y
)
[(y ) ] =______=________；
x5mn
(x5m)n
[(x5)m]n=______=______.
知识讲授
幂的乘方法则的逆用
a
mn
(a ) (a )
m n
n m
(m，n都是正整数）
幂的乘方的逆运算：
(1)13·7=（20）=( 4 )5=( 5 )4=( 2 )10
随堂训练
1. 下列各式中，与 5+1相等的是（
A.（ 5)+1
B.（+1)5
C.·( 5)
D. · 5 ·
2. 14不可以写成（
c
c
）
）
A. 5·( 3)3
B. (-) ·(- 2) ·(- 3) ·(- 8)
C.( 7)7
D. 3 · 4 · 5 · 2
解： (1) (103)5=103×5 =1015 ;
(2) (4)4=4×4=16;
(3) ()2=×2= 2 ;
(4) -(4)3 =-4×3=-12 .
(4)-(4)3.

人教版八年级上册课件 14.1.2 幂的乘方和积的乘方 (共48张PPT)

2018/8/1
温故知新
1.幂的乘方的法则语言叙述幂的乘方，底数不变，指数相乘.
符号叙述 ( a ) a
m n
m n
(m、n都是正整数） .
公式中的a可表示一个数、字母、式子等 .
2.幂的乘方的法则可以逆用.即
a
mn
(a ) (a )
m n
n m
3.多重乘方也具有这一性质.如
[(a ) ] a
已知：am=2， an=3.
m+n 求a
= ？.
=2 × 3=6
解： am+n = am · an
2018/8/1
1.( x) （ -x） ( x)
6 5
2.( y x) （ x-y）
3 4
2018/8/1
判断下面计算是否正确，如有错误请改正。
a +a a
6 6
12
(×)
2018/8/1
(3) (am)2= a mΧ 2 = a 2m ; (4) -(x4)3 = - x 4Χ3 = - x12 .
计算： (1) (103)3; (2) (x3)2;
(3) - ( xm )5 ; ⑸ ( y 3 )2
(4) (a2 )3∙ a5;
⑹
[(a b) 3 ]4
幂的乘方法则(重点) 例 2：计算： (1)(x2)3； (3)(a3)2－(a2)3; (2)－(x9)8； (4)(a2)3· a5.
a
6
a a
6
2a
2018/8/1
6
2、
(1) [(x y) ]
3 4
⑵ (a-b)3［(a-b)3］2
⑶［(x-y)2］2［(y-x)2］3

幂的乘方与积的乘方PPT课件

知识回顾
1、同底数的幂相乘法则：同底数的幂相乘，底数不变，指数相加。
数学符号表示： am • an amn
（其中m、n为正整数）
练习：判断下列各式是否正确。
a3 • a3 2a3,b4 b4 b8, m2 m2 2m2 (x)3 • (x)2 • (x) (x)6 x6
2、幂的乘方法则：幂的乘方，底数不变，指数相乘。
c ·c3 = c4
y5 ·y5 =y10 （6）m + m3 = m4 (×)
m + m3 = m + m3
基础演练
(1) a ·a7- a4 ·a4 = 0
；
(2)(1/10)5 ×(1/10)3 = (1/10)8 ； (3)(-2 x2 y3)2 = 4x4y6 ；
(4)(-2 x2 )3 = -8x6 ；
(5)求代数式的值 1、已知10m=4，10n=5．求103m+2n+1的值．
2、已知162×43×26=22a+1， (102)b=1012，求a+b的值。
能力挑战:
若xm3 x2 x7则m的值为 ___2__
已知2x 2 y 25 , 则正整数 x, y 的值有（D）
（A）1对（B）2对（C）3对（D）4对
)
=p6+10 ( 同底数幂的乘法法则 )
=p16
例、木星是太阳系九大行星中最大的一颗,木星可以近似地看作球体.已知木星的半径大约是7×104km,木星的体积大约是多少km3(∏取3.14)?
分析:球体体积公式 v 4 R3 解: v 4 (7 104 )3 3
3
4 73 1012
数学符号表示： (a m )n a mn

北师大版七年级数学下册课件：1.2 幂的乘方与积的乘方(共25张PPT)

(1) (ab4)4 = ab8 ;
(2) (-3pq)2 = –6p2q2
解：（1）错误，结果应为a4b16；（2）错误，结果应为9p2q2
2. 计算：
(1) (- 3n)3 ; (2) (5xy)3 ; (3) –a3 +(–4a)2 a
解（1）(-3n)3=（-3）3n3=-27n3；（2）(5xy)3=53x3y3=125x3y3；（3）–a3 +(–4a)2 a=–a3+16a2a=–a3+16a3=15a3
运用积的乘方法则时要注意：
公式中的a、b代表任何代数式；每一个因式
都要“乘方”；注意结果的符号、幂指数及其逆向运用（混合运算要注意运算顺序）
n个a m
=am+m+…+m
n个m
同底数幂的乘法法则
=amn
乘法的定义
幂的乘方的计算公式：
(am)n=amn（m，n都是正整数）
幂的乘方，底数_不__变___，指数__相__乘____.
例1 计算：
(1) (102)3； (2) (b5) 5 ； (3) (an) 3
(4) －(x2)m；(5) (y2)3 • y ； (6)2 (a2)6 － ( a3) 4
3
3
那么，(6×103)3=？这种运算有什么特征？
填空，看看运算过程用到哪些运算律，从运算结果看能发现什么规律？（1）（ab）2=(ab)·(ab)=（a·a）·（b·b） =a(2)b(2 ). （2）（ab）3=（__a_b_）__·（__a_b_）__·_（__ab）
=（_a_a_a_）__·（_b_b_b_）_ =a( 3 )b( 3 ) .
解：(1) (102)3= 102×3 = 106; (2) (b5)5 = b5×5 = b25 ; (3) (an) 3 = an×3 = a3n ; (4) －(x2)m = －x2×m = －x2m ; (5) (y2)3 • y = y2×3 • y = y7 ;

幂的乘方与积的乘方课件

04
THANKS
[ 感谢观看 ]
注意处理负指数和分数指数
在进行积的乘方运算时，应注意处理负指数和分数指数的情况，如 $a^{-m} = frac{1}{a^m}$， $a^{frac{1}{n}} = sqrt[n]{a}$。
CHAPTER 03
幂的乘方与积的乘方的关系
幂的乘方与积的乘方的相同点
两者都是基于乘法的运算性质
幂的乘方和积的乘方都是基于乘法运算的性质进行推导的，是数学中指数运算的一部分。
CHAPTER 04
幂的乘方与积的乘方的练习题
基础练习题
1. $(a^m)^n = ?$
总结词：考察基本概念和运算规则
பைடு நூலகம்
01
02
03
2. $a^{m times n} = ?$
3. $(ab)^n = ?$
04
05
4. $a^m times a^n = ?$
进阶练习题
总结词：增加难度，考察理解和应用能力
幂的乘方与积的乘方课件
CONTENTS 目录
• 幂的乘方 • 积的乘方 • 幂的乘方与积的乘方的关系 • 幂的乘方与积的乘方的练习题
CHAPTER 01
幂的乘方
幂的乘方运算规则
幂的乘方运算法则
$(a^m)^n = a^{m times n}$
运算步骤
先计算指数的乘积，再对底数进行幂运算。
注意事项
两者都涉及到指数的运算
无论是幂的乘方还是积的乘方，都涉及到指数的运算，这是理解两者关系的基础。
幂的乘方与积的乘方的不同点
定义不同
幂的乘方是指数相乘，底数不变；而积的乘方是将几个相同的因式相乘，每个因式的指数相加。

幂的乘方与积的乘方课件数学北师大版七年级下册

(3)(－a2)3=－a2×3=－a6；
(4)x2·x4+(x2)3=x6+x6=2x6.
当出现混合运算时，先算乘
方，再算乘法，最后算加法.
感悟新知
知1－练
1-1. 下列式子正确的是( D )
A. a2·a2=(2a)2
B. (a3)2=a9
C. a12=(a5)7
D. (a8)2=(a2)8
感悟新知
·(a6)2=
12
a ；

(4)(－a2b3)3=(－1)3·(a2)3·(b3)3=－a6b9.
系数乘方时，要带前面的符号，特别是系
数为－1 时，不要漏掉.
感悟新知
知2－练
3-1. 计算：
(1)(2ab)3；
(2)

－ 4；

解：原式=8a3b3；

原式= x4；
(3)(xmyn)2；
别乘方，不要漏掉任何一个.
感悟新知
知2－讲
2. 法则的拓展运用
(1)积的乘方法则的推广：(abc)n=anbncn(n为正
整数)；
(2)积的乘方法则也可以逆用，逆用时anbn=
(ab)n(n为正整数).
感悟新知
知2－练
例 3 计算：
(1)(x·y3)2；
(3)
(2)(－3×102)3；
2
原式=x2my2n
(4)(－3×102)4.
原式=8.1×109
感悟新知
知2－练
例4 计算：
(1)48×0.258
； (2)
2 024
－
×

2 024

.

解题秘方：紧扣“两底数互为倒数(或负倒数)，

幂的乘方与积的乘方(课件)八年级数学上册(人教版)

（4） − 2
3
= 9 ⋅ 12 = 21
+1 2
= −2
2+2
⋅ 4 3 ； (4) − 2
+1 2
.
12．在比较216 和312 的大小时，我们可以这样来处理：
∵216 =(24 )4 =164 ，312 = 33 4 =274 ，16＜27，
∴164 ＜274 ，即216 ＜312 ．
解：原式＝
4
=
5
5
4
2019
= ．
5
×
4
4 2019
5
2019
×
×
5
4
5 2020
−
4
(2) (−8)2020 × (−0.125)2022
解：原式=82020 × 0.1252022
=(8 × 0.125)2020 × 0.1252
=0.1252
=
1
64
三种幂的运算法则逆运用的规律
逆用公式(以下m，n都是
C．c>a>b
D．a<b<c
7．计算：（ 2 ）3 ⋅ 2 − （ 4 ）2 + 2 ⋅ 6 ＝_____．
x8
8．已知2 = ，32 = ，则23+10 =______．
a3b2
9．已知，满足方程3 + 2 = 4，则8 ⋅ 4 =______．
16
10．比较大小：230 ______3
同理：
( ab )
(ab) (ab) (ab)
3
(a a a) (b b b)
a b
3 3
推理验证

《幂的乘方与积的乘方》课件(共26张PPT)【推荐】

2
2
16
（4）（3a4bm）n＝3n（a4）n（bm）n＝3na4nbmn.
经典例题
题型一几种幂的综合运算
例1 计算:（1）（-2x2）3＋（-3x3）2＋（-x）6；（2）x2·x4·x6＋（x3）2＋［（-x）4］3. 、
题型一几种幂的综合运算
例1 计算:（1）（-2x2）3＋（-3x3）2＋（-x）6；（2）x2·x4·x6＋（x3）2＋［（-x）4］3. 分析按照先算乘方，再算乘除，最后算加减，若有小括号先算小括号里的原则进行计算. 、
题型二幂的运算法则的逆用
例2 计算:（1）已知2×8x×16x＝222，求x的值；（2）已知2m＝3，2n＝4，求22m＋n的值.
题型二幂的运算法则的逆用
例2 计算:（1）已知2×8x×16x＝222，求x的值；（2）已知2m＝3，2n＝4，求22m＋n的值.
解析（1）因为2×8x×16x＝222，所以2×（23）x×（24）x＝222，所以2×23x×24x＝222，所以,21＋3x＋4x＝222，所以1＋3x＋4x＝22，解得x＝3. （2）因为2m＝3，2n＝4，所以22m＋n＝（2m）2·2n＝9×4＝36.
题型一几种幂的综合运算
例1 计算:（1）（-2x2）3＋（-3x3）2＋（-x）6；（2）x2·x4·x6＋（x3）2＋［（-x）4］3. 分析按照先算乘方，再算乘除，最后算加减，若有小括号先算小括号里的原则进行计算. 解析（1）原式＝-8x6＋9x6＋x6＝2x6. （2）原式＝x12＋x6＋x12＝2x12＋x6. 、
（3）
1
3
3
1
9
.
3 3
（4）（x4）3-2（x3）4＝x12-2x12＝-x12.

沪科版七年级数学下册幂的乘方与积的乘方课件

例3 已知2x＝8y＋1，9y＝3x－9，则代数式1 x＋1 y的值为________．
32
解析：由2x＝8y＋1，9y＝3x－9得2x＝23(y＋1)，32y＝3x－9，则x＝
11
3(y＋1)，2y＝x－9，解得x＝21，y＝6，故代3 数式2 x＋ y＝7 ＋3＝10.
新知运用
例4 计算： (1)(－2a2)3·a3＋(－4a)2·a7－(5a3)3； (2)(－a3b6)2＋(－a2b4)3. 解析：(1)先进行积的乘方，然后根据同底数幂的乘法法则求解； (2)先进行积的乘方和幂的乘方，然后合并．
(2)a6·a4=a24
(3)(ab4)4=ab8
(4)(-3pq)2=-6p2q2
2.计算:
(1)(103)3
(2)-(a2)5
(3)(x3)4·x2
(4)[(-x)2]3
(5)(-a)2(a2)2
(6)x·x4-x2·x3
课堂小结
这节课你学到了哪些新知识呢？
1.幂的乘方:(am)n=amn(其中m,n都是正整数) 即:幂的乘方,底数不变,指数相乘. 2.积的乘方:(ab)n=anbn(n是正整数) 即:积的乘方等于乘方的积
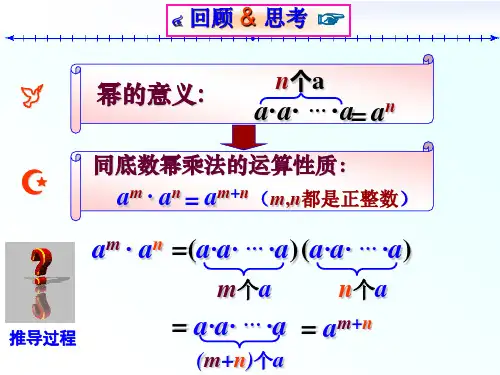
探究新知
(2)计算下列各式,并说明理由. ①(62)4;②(a2)3;③(am)2;④(am)n. 仿照前面,来研究以上四个题目的运算情况,实际上做到(3)题时可以猜想(4)题的结果,也为后面幂的乘方的法则推导带来指点性. 结论1: 幂的乘方:(am)n=amn(其中m,n都是正整数) 即:幂的乘方,底数不变,指数相乘.
解：(1)原式＝－8a6·a3＋16a2·a7－125a9＝－8a9＋16a9－125a9＝－ 117a9； (2)原式＝a6b12－a6b12＝0.

(新版)湘教版七年级数学下册：2.幂的乘方与积的乘方课件

底数的积容易计算
适用法则同底数幂的乘法
幂的乘方
积的乘方
【题组训练】 1.计算 ( 1 ab2c3)3 的结果为____21_7_a_3b_6_c9___.
3
2.计算:0.1253×(-0.25)3×26×(-2)12=_____-_8_.
3.计算:(1)(-a3b6)2-(-a2b4)3. (2)2(anbn)2+(a2b2)n.
(2)2(a5)2·(a2)2-(a2)4·(a3)2 =2a10·a4-a8·a6 ……………………幂的乘方运算 =2a14-a14 ……………………同底数幂的乘法运算 =a14. ……………………………………合并同类项
【学霸提醒】幂的乘方运算的“两点注意”
(1)同底数幂的乘法与幂的乘方的区分:前者指数相加, 后者指数相乘. (2)幂的乘方中底数可以是一个数字,也可以是字母或式子等.
4.计算: (1)(3xy)3+(2xy)3. (2)(-3a3)2·a2+(-4a)2·a6-(-2a4)2.
解:(1)(3xy)3+(2xy)3 =27x3y3+8x3y3=35x3y3. (2)(-3a3)2·a2+(-4a)2·a6-(-2a4)2 =9a8+16a8-4a8=21a8.
【题组训练】
1.计算(-x3)8·(-x4)2的结果为
A.x32
B.-x32
C.x17
D.-x17
(A)
2.已知3x=m,3y=n,则32x+3y= ( D )
A.6mn
B.2m+3n
C.m2+n3
D.m2n3
3.计算(-x)3·(x2)5-(-x4)2·(-x)5的结果为_____0_. 4.若(72)3·7m=79,则m的值为______.3

苏科版七年级下册数学《幂的乘方与积的乘方》课件

苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
结束寄语：
只有不断思考,才有新的发现; 只有量的变化,才有质的进步。
祝同学们学有所得!
x3 x5 x8
(a)2 a4 a6
(a b)2 (a b)3 (a b)5
苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
( 23)2
苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
1、能说出幂的乘方的运算性质，会用符号表示。 2、会用幂的乘方法则进行运算，并知道每一步运算的根据。
上(33面)2 各 3式3 括33 号中都是33幂2 的情势，
然(a4后)3再乘a4 方 a．4 你a4能给这种a运43算起(am个)5名 a字m 吗a？m am am am
am5
从上面的计算中，你发现了什么？
苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
“行家”看“门道”
猜想：(am)n 等于什么？(am)n = amn
8.2 幂的乘方与积的乘方（1）
苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
☆同底数幂相乘，底数不变，指数相加。
am·an=am+n（m、n是正整数）。
am·an＝ (a·a·… ·a) (a·a·… ·a) m个a n个a
= a·a·… ·a = am+n
(m+n)个a
苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
苏科版数学教科书
8.2 幂的乘方与积的乘方（1）
我思我进步
思考：已知2a＝3, 2b ＝6, 2c ＝12 , 则a、b、c的关系（ C ）
A. a+b>2c

2.幂的乘方和积的乘方PPT课件(3份打包)

2.1 整式的乘法
——2.1.2 幂的乘方与积的乘方
幂的乘方
动脑筋幂的意义:
n个a a·a·… ·a
= an
同底数幂乘法的运算性质： am ·an = am+n(m，n都是正整数)
am ·an = (a ·a·… ·a) (a ·a ·… ·a)
推导过程
m个a
n个a
= a ·a ·… ·a = a m+n
(3)由特殊的 (ab)3=a3b3 出发，你能想到一般的公式
吗？
(ab)3=ab·ab·ab
=a·a·a ·b·b·b
=a3·b3
猜想
(ab)n=anbn
说一说 (4) 在(ab)3运算过程中你用到了哪些知识？
(ab)3 =(ab)·(ab)·(ab) (幂的意义)
3个ab =(a ·a ·a)(b ·b ·b) (乘法交换律和结合律)
(2)(-4xyቤተ መጻሕፍቲ ባይዱ2 ；
(4)
.
-
1 2
xy2z3
4
(1) (-2x)3 解：(-2x)3 =(-2)3x3 = -8x3 ；
(2) (-4xy)2 解：(-4xy)2 = (-4)2x2y2 = 16x2 y2 ；
(3) (xy2)3 解： (xy2)3
= (x)3(y2)3 =x3 y6 ；
结论
积的乘方法则
(ab)n = an·bn (m，n都是正整数)
积的乘方
乘方的积
结论
用自己的语言叙述一下积的乘方法则？
积的乘方法则
积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘.
你能说出法则中“因式”这两个字的意义吗？
公式的拓展 (7)三个或三个以上的积的乘方，是否也具有上面的性质？ (8)怎样用公式表示？

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章整式的乘除
1.2 幂的乘方与积的乘方（一）
学习目标
1.经历探索幂的乘方的运算性质的过程，进一步体会幂的意义。
2.了解幂的乘方的运算性质，并能解决一些简单问题。
3.体会类比、归纳等方法的作用，发展运算能力和有条理的思考和表达能力。
探究新知
你知道(102)3等于多少吗？
(102)3 =102×102×102 (根据幂的意义 ). =102+2+2 (根据同底数幂的乘法 ). =106 =102×3
联系拓广
⑴ a12 ＝（a3）( ) ＝（a2）( )
＝a3 a( )＝（）3 ＝（）4
(2) y3n ＝3, y9n ＝
.
(3) （a2）m+1 ＝
.
(4) 32﹒9m ＝3( )
想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？
幂的乘方法则：
(am )n amn
同底数幂的乘法法则：
am • an amn
其中m , n都是正整数.
运算种类
公式
法则
计算结果
中运算底数指数
同底数幂乘法
am an amn
乘法
指数不变相加
指数
幂的乘方（am）n amn 乘方不变相乘
同底数幂相乘
am • an amn
指数相加
其中m , n都是正整数
底数不变
指数相乘
(am )n amn
(1) (102)3 ;
(2) (b5)5 ;
(4) -(x2)m ; (5) (y2)3 ·y ;
(3) (an)3;
(6) 2(a2)6 - (a3)4 .
解：(1) (102)3 =102×3 =106 ;
(2) (b5)5 = b5×5 = b25 ; (3) (an)3 = an×3 =a3n ;
同底数幂相乘,底数不变,指数相加.
2. (am)n=amn (m,n都是正整数)
幂的乘方，底数不变，指数相乘.
作业
• 完成课本习题1.2中1、2 • 拓展作业：
你能尝试运用今天所学的知识解决下面的问题吗
(1)填空： [（a－b）3 ]2＝（b－a ）( )
(2)若4﹒8m﹒16m ＝29 ，求m的值
(4) -(x2)m = -x2×m =பைடு நூலகம்-x2m ;
(5) (y2)3 ·y= y2×3 ·y = y6 ·y = y7;
(6) 2(a2)6 – (a3)4 =2a2×6 - a3×4 =2a12-a12 =a12.
幂的乘方法则的逆用
amn (am )n (an )m
幂的乘方的逆运算： (1)x13·x7=x（20 ）=( x4 )5=( x5 )4=( x2 )10； (2)a2m =( am )2 =( a2 )m （m为正整数）.
落实基础
随堂练习：
1. 判断下面计算是否正确？如果有错误
请改正：
(1) (x3)3 = x6 ;
(2)a6 ·a4 = a24 .
2. 计算： (1) (103)3 ; (2) －(a2)5 ; (4) [(－x)2 ]3 ; (5) (－a)2(a2)2;
(3) (x3)4 ·x2 ; (6) x·x4 – x2 ·x3 .
x x （3）x2 x3 x4
9；
（4）(x)3 (x)5
8
；
（5）(x)3 x3 x6；（6）a2 a3 a4 a 2a5 .
2．下面的计算对不对？如果不对应该怎样改正？
⑴ x3 x3 2x3;错 ⑵ x3 x3 x6;错
⑶ x3 x3 x6; 对 ⑷ x3 x3 x9;错
探究新知
做一做：计算下列各式，并说明理由 .
(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ; (4) (am)n .
解：(1) (62)4 = 62·62·62·62=62+2+2+2 =68 =62×4 ;
(2) (a2)3 = a2·a2·a2 =a2+2+2 =a6=a2×3 ;
幂的意义:
n个a
a·a·… ·a = an
同底数幂的乘法的运算性质：am·an= am+n
am ·an = (a·a·… ·a) ·(a·a·… ·a)
m个a
n个a
= a·a·… ·a = am+n
(m+n)个a
同底数幂相乘,底数不变,指数相加.
1.计算（口答）：
（1） 93 95 98 ；
（2）a6 a2 a8 ；
(3) (am)2 =am·am =am+m =a2m ;
n 个am (4) (am)n =am·am·… ·am
n 个m =am+m+ … +m =amn
(a m )n a mn
探究新知
幂的乘方法则
(am)n=amn (m,n都是正整数) 幂的乘方，底数不变，指数相乘 .
【例1】计算：
（C） x ·(x5)m （D） x ·x5 ·xm
C 3．x14不可以写成（）
（A）x5 ·(x3)3 （B） (－x) ·(－x2) ·(－x3) ·(－x8)
（C）(x7)7
（D）x3 ·x4 ·x5 ·x2
4.已知，44•83=2x，求x的值.
解: 44 83 (22 )4 (23 )3
⑸ a a3 a3; 错
3．计算： x yx y2 x y3 x y6
情境引入
地球、木星、太阳可以近似地看做是球体 . 木星、太阳的半径分别约是地球的10倍和102倍，它们的体积分别约是地球的多少倍？
103倍
V球= —34 πr3 ，
其中V是体积、r 是球的半径
(102)3倍
你知道(102)3等于多少吗？
28 29
217
所以x 17
5. 已知3×9n=37，求：n的值．
6. 已知a3n=5，b2n=3，求：a6nb4n的值．
7. 设n为正整数，且x2n=2，求9(x3n)2的值．
8. 已知2m=a，32n=b，求：23m+10n．
小结
a • a a 1. amm an anmn m, nm都n是正整数
幂的乘方
达标测评
1.下列各式对吗？请说出你的观点和理由：
(1) (a4)3=a7
( ×)
(2) a4 a3=a12
( ×)
(3) (a2)3+(a3)2=(a6)2 (4) (－x3)2=(－x2)3
( ×)
( ×)
c 2．下列各式中，与x5m+1相等的是（）
（A）（x5)m+1 （B）（xm+1)5

《军神》课件(第一课时)

页数:18
军神第一课时课件

页数:12
《军神》-课件(第一课时)

页数:24
部编新人教版小学五年级语文下册《军神》优质课件(第一课时)

页数:24
语文五年级下册第一课时.军神-PPT课件

页数:2
部编版小学五年级语文下册第四单元第11课《军神》教学课件(第一课时)

页数:23
新部编五年级语文下册第11课《军神》公开课PPT课件【护眼版】

页数:46
优质课军神第一课时课件

页数:13
部编版五年级语文下册第11课《军神》精品课件

页数:88
部编版语文五年级下册《军神》第一课时教学课件

页数:12