2 T
(3-13)’、(3-15a)代入(3-12a) 2 2 2 (T 2 )[ E (u1 , u2 ) Z ( z )] k E (u1 , u2 ) Z ( z ) z 2 d Z ( z) 2 2 [T E (u1 , u2 ) k E (u1 , u2 )] Z ( z ) E (u1 , u2 ) d z2 2 2 2 E ( u , u ) k E ( u , u ) 1 d Z ( z ) 1 2 1 2 E (u1 , u2 ) Z ( z ) T 2 Z ( z ) d z E ( u , u ) 1 2
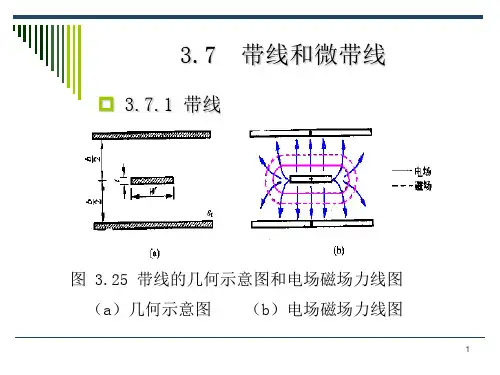
3. 波导 同轴线损耗的主要矛盾在内导体上,如果拔掉同轴 线的内导体,既可减少电流的热损耗,又可避免使用介 质支撑固定,将会大大降低传输损耗,提高功率容量。 然而,这种空心的金属管能传送微波吗? 只要金属管的截面尺寸与波长比足够大, 可以传输 电磁波,称这种金属管为“波导”。 用长线理论作定性分析:以矩形波导为例, 可将其 视为由平行双线演变来的:
2 T
(3 16b)
令 k k (3 20) 2 2 得 T E (u1 , u2 ) kc E (u1 , u2 ) 0 2 2 同理 T H (u1 , u2 ) kc H (u1 , u2 ) 0
2 2 2 c
(3 19)'
• 请注意: 为书写方便, 今后场强复变量符号上的 “ ” 将被略去。
E j 0 H H j 0 E (3-4)’ E 0 H 0
2 E k E 0 (3 12) 2 2 H k H 0