下载文档原格式
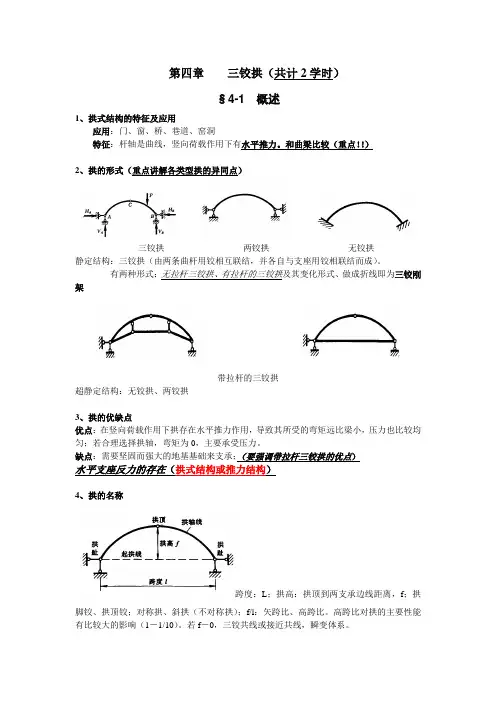
第四章三铰拱（共计2学时）§4-1 概述1、拱式结构的特征及应用应用：门、窗、桥、巷道、窑洞特征：杆轴是曲线，竖向荷载作用下有水平推力。
和曲梁比较（重点！！）2、拱的形式（重点讲解各类型拱的异同点）三铰拱两铰拱无铰拱静定结构：三铰拱（由两条曲杆用铰相互联结，并各自与支座用铰相联结而成）。
有两种形式：无拉杆三铰拱、有拉杆的三铰拱及其变化形式、做成折线即为三铰刚架带拉杆的三铰拱超静定结构：无铰拱、两铰拱3、拱的优缺点优点：在竖向荷载作用下拱存在水平推力作用，导致其所受的弯矩远比梁小，压力也比较均匀；若合理选择拱轴，弯矩为0，主要承受压力。
缺点：需要坚固而强大的地基基础来支承；（要强调带拉杆三铰拱的优点）水平支座反力的存在（拱式结构或推力结构）4、拱的名称跨度：L；拱高：拱顶到两支承边线距离，f；拱脚铰、拱顶铰；对称拱、斜拱（不对称拱）；f/l：矢跨比、高跨比。
高跨比对拱的主要性能有比较大的影响（1－1/10）。
若f－0，三铰共线或接近共线，瞬变体系。
平拱：两拱趾在同一水平线上的拱；斜拱：两拱趾不在同一水平线上的拱5、计算方法数解法、图解法§4-2 三铰拱的数解法（以竖向荷载作用下三铰平拱为例，本章重点）重点推导竖向荷载作用下三铰平拱的支座反力和内力的计算公式，并和相应简支梁进行比较。
一、支座反力的推导（此图要解释含义）三铰平拱承受竖向荷载作用：三铰拱相当梁：对三铰拱及相当梁结构，根据静力平衡条件（解释三铰结构的静力平衡方程形式）：∑===H B AHF H F FX ,0结论：（这是重点，帮助学生理解记忆，并要活用）（1）在竖向荷载作用下，三铰平拱的竖向反力与相当梁的竖向力相同，与拱轴形状及拱高无关；（2）三铰平拱在竖向荷载作用下，水平推力F H 等于相应梁C 截面的弯矩除以拱高而得。
F H 仅与荷载及三个铰的位置有关，而与拱轴无关。
（推广到三铰刚架在竖向荷载作用下水平支反力的计算）（即只与拱的矢跨比f/l 有关，f/l ↑，H ↓；f/l ↓，H ↑）和拱轴形状无关。
（完整版）结构⼒学最全知识点梳理及学习⽅法第⼀章绪论§1-1 结构⼒学的研究对象和任务⼀、结构的定义:由基本构件（如拉杆、柱、梁、板等）按照合理的⽅式所组成的构件的体系，⽤以⽀承荷载并传递荷载起⽀撑作⽤的部分。
注：结构⼀般由多个构件联结⽽成，如：桥梁、各种房屋（框架、桁架、单层⼚房）等。
最简单的结构可以是单个的构件，如单跨梁、独⽴柱等。
⼆、结构的分类：由构件的⼏何特征可分为以下三类1．杆件结构——由杆件组成，构件长度远远⼤于截⾯的宽度和⾼度，如梁、柱、拉压杆。
2．薄壁结构——结构的厚度远⼩于其它两个尺度，平⾯为板曲⾯为壳，如楼⾯、屋⾯等。
3．实体结构——结构的三个尺度为同⼀量级，如挡⼟墙、堤坝、⼤块基础等。
三、课程研究的对象材料⼒学——以研究单个杆件为主弹性⼒学——研究杆件（更精确）、板、壳、及块体（挡⼟墙）等⾮杆状结构结构⼒学——研究平⾯杆件结构四、课程的任务1．研究结构的组成规律，以保证在荷载作⽤下结构各部分不致发⽣相对运动。
探讨结构的合理形式，以便能有效地利⽤材料，充分发挥其性能。
2．计算由荷载、温度变化、⽀座沉降等因素在结构各部分所产⽣的内⼒，为结构的强度计算提供依据，以保证结构满⾜安全和经济的要求。
3．计算由上述各因素所引起的变形和位移，为结构的刚度计算提供依据，以保证结构在使⽤过程中不致发⽣过⼤变形，从⽽保证结构满⾜耐久性的要求。
§1-2 结构计算简图⼀、计算简图的概念：将⼀个具体的⼯程结构⽤⼀个简化的受⼒图形来表⽰。
选择计算简图时，要它能反映⼯程结构物的如下特征：1．受⼒特性（荷载的⼤⼩、⽅向、作⽤位置）2．⼏何特性（构件的轴线、形状、长度）3．⽀承特性（⽀座的约束反⼒性质、杆件连接形式）⼆、结构计算简图的简化原则1．计算简图要尽可能反映实际结构的主要受⼒和变形特点．．．．．．．．．．．．．．，使计算结果安全可靠；2．略去次要因素，便于．．。
．．分析和．．．计算三、结构计算简图的⼏个简化要点1．实际⼯程结构的简化：由空间向平⾯简化2．杆件的简化：以杆件的轴线代替杆件3．结点的简化：杆件之间的连接由理想结点来代替（1）铰结点：铰结点所连各杆端可独⾃绕铰⼼⾃由转动，即各杆端之间的夹⾓可任意改变。
目前解决曲线桥梁计算方法有以下几种：1、空间梁元模型法2、空间薄壁箱梁元模型法3、空间梁格模型法4、实体、板壳元模型法第一种方法，是不能考虑桥梁的横向效应的，使用时要求桥梁的宽跨比不易太大。
第二种方法，是第一种方法的改进，主要区别是采用了不同的单元模型，考虑了横向作用如翘曲和畸变。
第四种方法，是解决问题最有效的方法，能够考虑各种结构受力问题。
第三种方法，是目前设计及科研中常采用的方法，其特点是容易掌握，且对设计能保证足够的精度，其中采用比较多的方法是剪力-柔性梁格法，能充分考虑弯桥横向的受力特性。
剪力-柔性梁格法的原理是当梁格节点与结构重合的点承受相同挠度和转角时，由梁格产生的内力局部静力等效与结构的内力。
其实质是将传统的一维杆单元计算模式推进到二维计算模型，用一个二维的空间网格来模拟结构的受力特性。
对于梁格法的讨论这里也有不少帖子进行了讨论，实际与梁格之间的等效关系，主要表现在梁格各个构件的刚度计算上，理论上，原型和等效梁格承受相等的外荷载时，必须具有恒等的挠曲和扭转，等效梁格中每一构件的内力也必须等于该构件所代表的原型截面的，事实上这种理想状况是达不到的，模拟也是近似的，但事实是按梁格计算能把握住结构的总体性能，对于设计来说应该是能满足精度的。
梁格也是近似的模拟，只要计算者能够和好的模拟了横向纵向的特性，应该是可以作为设计依据的。
你在这里说的横向的切分使得预应力产生的次内力问题我不太清楚你指的什么，但是只要横向的刚度业等效了原型，对于计算应该不会出现逆所说的结构内力失真，这条可以通过结果验证。
当然任何结构，只要不怕麻烦都可以用实体单元来分析，只要正确模拟，实体分析也是最精确的，但是对于这种模型要准确模拟可不是一件容易的事，并且预应力的损失计算，施加等等都非常麻烦，还有最后结果的查看也不方便，因此除了结构局部的分析，一般是没有拿实体来进行全桥的整体分析的，至于说单梁我也说了，有些时候精度是可以的，但是对于这种结构相对于梁格来说单梁的精度是不如梁格的。
2.1 几何可变系统和几何不变系统工程结构是用来承受和传递外载荷的系统。
一个工程结构通常是由若干个构件用某种方法联结而成的。
它在承受载荷作用时，各构件只允许发生材料的弹性变形，而不应发生构件间相对的机械运动。
如图2.1(a)所示的系统，如果不考虑弹性变形，系统也未发生破坏，则其几何形状与位置均保持不变，这样的系统，我们称之为几何不变系统。
但是，对如图2.1（b）所示的系统，在载荷作用下，即使不考虑弹性变形，它的形状和位置也将改变，这样的系统，我们称之为几何可变系统，它是不能用来承受和传递外载荷的。
所以，凡是工程结构必须是几何不变系统。
图2.1对系统进行几何组成分析的目的在于：判断该系统是否为几何不变系统，以决定其能否作为工程结构使用；研究并掌握几何不变系统的组成规则，以便合理安排构件，设计出合理的结构；根据系统的组成规则，确定结构的性质（静定系统还是静不定系统），以便选用相应的计算方法。
3.2 静定桁架的内力桁架是由某些杆系结构经过简化而得到的计算模型，其特点是：（1）各元件均为直杆；（2）各杆两端均用没有摩擦的理想铰链相连接；（3）杆的轴线通过铰心，称铰心为桁架的结点；（4）载荷和支座反力仅作用在各结点上。
由于理想铰链没有摩擦力，故不能传递力矩。
显然，在载荷仅作用在结点上时，若不计杆的自重，各杆都只受到两端结点的作用力，且在此二力作用下处于平衡。
因此，桁架的杆件均为“二力杆”，即杆两端受到大小相等、方向相反、沿着杆轴线的两个力作用。
杆子横截面上只有轴力，这些轴力就是所要计算的桁架内力。
静定桁架是一种没有多余约束的结构，它的内力计算原则上，只要把桁架分解为若干自由体（结点）和约束（杆），用未知力代替约束的作用，对所有的自由体列出全部静力平衡方程式，所得方程式数与包含的未知力数相等。
由于结构是几何不变的，方程组有唯一解。
解这联立方程组就可得到静定桁架的内力。
但在工程实际中，往往可以运用下述两种方法：结点法和截面法。
总第３１８期交 通 科 技ＳｅｒｉａｌＮｏ．３１８ ２０２３第３期ＴｒａｎｓｐｏｒｔａｔｉｏｎＳｃｉｅｎｃｅ＆ＴｅｃｈｎｏｌｏｇｙＮｏ．３Ｊｕｎｅ．２０２３ＤＯＩ１０．３９６３／ｊ．ｉｓｓｎ．１６７１ ７５７０．２０２３．０３．０１２收稿日期：２０２２ １１ １６第一作者：刘昊林（１９９９－），男，硕士生。
曲线梁桥有限元法与解析法计算结果对比分析刘昊林（重庆交通大学土木工程学院 重庆 ４０００７４）摘 要 为研究曲线梁桥在有限元法与解析法下的计算结果特性，采用ｍｉｄａｓＣｉｖｉｌ２０２０建立有限元模型进行数值计算，文中根据不同方法建立３个有限元模型，分别为单梁法模型，基于顶、底板划分的梁格法模型和基于腹板划分的梁格法模型，解析法是根据纯扭转理论进行计算。
对比３个有限元模型与解析法在自重及集中力作用下的内力和反力计算结果。
研究表明，根据不同方法建立的有限元模型与解析法在自重和集中力作用下的弯矩、剪力及竖向支反力计算结果是一致的，在扭矩的计算结果上有所差异，梁格法计算出的扭矩比单梁法和解析法偏大；且梁格法有限元模型可以反映曲线桥在犉犡和犉犢方向的支座反力结果，而单梁法有限元模型不能；有限元法与解析法在支承处的内力计算结果有差异。
关键词 曲线桥 有限元法 解析法 梁格法 单梁法中图分类号 Ｕ４４８．２１＋３ Ｕ４４１ 曲线梁桥因其可适应不同地形、建筑限制等优点被广泛修建。
我国桥梁学者对于曲线桥进行了大量研究。
于长鰑等［１］对双箱单室曲线钢箱梁的横向内力计算方法进行了研究；李林等［２］研究了温度作用下曲线桥的位移情况；傅中秋等［３］研究了横隔板变形对曲线钢箱梁焊缝疲劳的影响；罗建群等［４］研究了不同的桥面纵坡在温度等荷载下对曲线桥铺装层受力的影响；柳苗等［５］研究了检测曲线桥线形的方法；王一光等［６］对曲线桥墩梁连接方式进行了研究；谢铠泽等［７］对曲线桥桥墩横向刚度进行了研究。
本文以一跨径为２５ｍ的单跨静定曲线箱梁桥为例，对其进行了解析计算与有限元分析。
曲线梁桥的受力特点和分析方法摘要：由于在经济和审美上的优势，曲线梁桥被广泛应用于现代公路立交系统。
曲线梁的竖曲和扭转耦合，由于结构上的特点，相对于直梁桥而言，曲线梁的分析更为复杂。
本文对弯道梁桥的受力特点进行了介绍，并总结了分析弯道梁桥的有关理论。
关键词：曲线梁桥；弯扭耦合；支承体系；有限元法引言曲线梁桥是指主梁本身为弧形的弯曲桥梁。
由于其独特的线形，曲线梁桥突破了多种地形的限制，同时在高速公路、山地公路、城市桥梁等方面，由于其优美的曲线造型而得到了更快的发展。
曲线梁桥具有现实意义，发展前景非常看好，无论从几何角度、美学角度，还是从经济角度，都是如此。
1曲线桥梁受力特性1.1弯扭耦合作用由于受弯曲率的影响，当竖向弯曲时，曲线梁截面必然会产生扭转，而这种扭转又会导致梁的挠曲变形，这种挠曲变形被称为“弯扭耦合作用”。
对于弯道梁桥的设计，相对于直线型梁桥来说，要特别注意，因为弯道扭力耦合作用所产生的附加扭力，会使梁体结构产生较不利的受力条件，从而增加结构的挠曲变形。
值得注意的是，由于自重在使用荷载下占绝大多数，对于混凝土曲线箱梁桥而言，也会导致更明显的弯扭耦合。
由于弯道梁桥沿弯梁的线形布置支承不成直线，因此由于弯道外侧较重，导致桥体恒载重心相对于形心向外偏移。
曲线梁在自重的作用下，也会产生扭转和扭曲的变形，从而使曲线桥发生翻转，出现匍匐的现象，这就是曲线梁在自重的作用下产生的变形[1]。
1.2曲线梁内外侧受力不均匀曲线桥因弯曲和扭动耦合作用，变形大于同跨径的直线桥，且曲率半径越小、桥越宽，因此其简支曲线梁外缘的挠度比内缘大，这种变化趋势是显而易见的。
曲线梁桥体具有向外扭转的较大扭力、弯曲扭力耦合和偏载作用的可能。
扭转作用会越来越明显，曲率半径越小、跨度越大的曲线梁桥甚至会引起抗扭支座内侧支座产生空心现象，这种情况在抗扭转支座的内部支座上会产生空心现象，这种情况的发生曲线桥的支点反力与直线桥相比，有一种倾向，它的外侧会变大、内侧会变小，甚至在内侧产生负反力。
