曲线拟合的数值计算方法实验
- 格式:docx
- 大小:157.97 KB
- 文档页数:28

曲线拟合问题的数值试验一、算法要求已知数据:x=5,y=1.OO29;x=1O,y=1.OO23;x=15,y=1.OOOO;x=2O,y=O.999O; x=25,y=O.9983; x=3O,y=O.9979; x=35,y=O.9978;x=4O,y=O.9981 x=45,y=O.9987 x=5O,y=O.9996;拟合多项式:P(X)=aO+a1x+a2x^2+•…+an x A n分别对n=2,3,4,5,6 进行数值计算,且根据各自偏差平方和分析拟合效果。
二、源代码及注释#include <stdio.h>#include <conio.h>#include <math.h>#include <process.h>#define N 1O//N 个点#define T 2 //T 次拟合#define W 1//权函数#define PRECISION O.OOOO1float pow_n(float a,int n){int i;if(n==O) return(1);float res=a;for(i=1;i<n;i++){ res*=a;// 自己相乘} return(res);// 返回 a 的平方}void mutiple(float a[][N],float b[][T+1],float c[][T+1]) {float res=O;int i,j,k;for(i=O;i<T+1;i++)for(j=O;j<T+1;j++){res=O;for(k=O;k<N;k++){res+=a[i][k]*b[k][j]; c[i][j]=res;// 返回ab 的内积} } } void matrix_trans(float a[][T+1],float b[][N]) { int i,j;for(i=0;i<N;i++){ for(j=0;j<T+1;j++){ b[j][i]=a[i][j];// 交换}}}void init(float x_y[][2],int n){int i;printf("请输入%d个已知点:\n",N);for(i=0;i<n;i++) { printf("(x%d y%d):",i,i);scanf("%f %f",&x_y[i][0],&x_y[i][1]);}}void get_A(float matrix_A[][T+1],float x_y[][2],int n) { int i,j; for(i=0;i<N;i++){ for(j=0;j<T+1;j++){matrix_A[i][j]=W*pow_n(x_y[i][0],j);// 获取输入矩阵}}}void print_array(float array[][T+1],int n){int i,j;for(i=0;i<n;i++) {for(j=0;j<T+1;j++){printf("%-g",array[i][j]);}printf("\n");}}void convert(float argu[][T+2],int n){int i,j,k,p,t;float rate,temp;for(i=1;i<n;i++){for(j=i;j<n;j++){ if(argu[i-1][i-1]==0){ for(p=i;p<n;p++){if(argu[p][i-1]!=0)break;}if(p==n){printf(" 方程组无解!\n");} for(t=0;t<n+1;t++){ temp=argu[i-1][t];argu[i-1][t]=argu[p][t]; argu[p][t]=temp;}} rate=argu[j][i-1]/argu[i-1][i-1]; for(k=i-1;k<n+1;k++){ argu[j][k]-=argu[i-1][k]*rate; if(fabs(argu[j][k])==PRECISION) argu[j][k]=0;}}}}void compute(float argu[][T+2],int n,float root[]) {float temp;for(i=n-1;i>=0;i--){ temp=argu[i][n];for(j=n-1;j>i;j--){temp-=argu[i][j]*root[j];}root[i]=temp/argu[i][i];}}void get_y(float trans_A[][N],float x_y[][2],float y[],int n){int i,j;float temp;for(i=0;i<n;i++){temp=0;for(j=0;j<N;j++){temp+=trans_A[i][j]*x_y[j][1];}y[i]=temp;}}void cons_formula(float coef_A[][T+1],float y[],float coef_form[][T+2]) {int i,j;for(i=0;i<T+1;i++){for(j=0;j<T+2;j++){if(j==T+1) coef_form[i][j]=y[i];elsecoef_form[i][j]=coef_A[i][j];}}}void print_root(float a[],int n){int i,j;printf("%d个点的%d次拟合的多项式系数为:\n",N,T);for(i=0;i<n;i++){printf("a[%d]=%g,",i+1,a[i]);}printf("\n");printf(" 拟合曲线方程为:\ny(x)=%g",a[0]);for(i=1;i<n;i++){printf(" + %g",a[i]);for(j=0;j<i;j++){printf("*X");}}printf("\n");}void process(){floatx_y[N][2],matrix_A[N][T+1],trans_A[T+1][N],coef_A[T+1][T+1],coef_formu[T+1][T+2 ], y[T+1],a[T+1];init(x_y,N);get_A(matrix_A,x_y,N);printf(" 矩阵 A 为:\n");print_array(matrix_A,N);matrix_trans(matrix_A,trans_A);mutiple(trans_A,matrix_A,coef_A);printf(" 法矩阵为:\n");print_array(coef_A,T+1);get_y(trans_A,x_y,y,T+1);cons_formula(coef_A,y,coef_formu);convert(coef_formu,T+1);compute(coef_formu,T+1,a);print_root(a,T+1);}void main(){ process();}三、调试:本程序在调试时,因为代码中的T声明是通过宏定义#define T 2,所以欲达到能对n=2,3,4,5,6切换的目的,还需程序员在代码中修改T的值四、计算结果如图:1.004d1.0021.001口099S0.93®0.957五、说明:本题用C++语言编程,用matlab作图,以此来使报告更加形象,直观。

![曲线拟合实验报告[优秀范文5篇]](https://uimg.taocdn.com/ed56c4cd0342a8956bec0975f46527d3240ca6e1.webp)
曲线拟合实验报告[优秀范文5篇]第一篇:曲线拟合实验报告数值分析课程设计报告学生姓名学生学号所在班级指导教师一、课程设计名称函数逼近与曲线拟合二、课程设计目的及要求实验目的: ⑴学会用最小二乘法求拟合数据的多项式,并应用算法于实际问题。
⑵学会基本的矩阵运算,注意点乘与叉乘的区别。
实验要求: ⑴编写程序用最小二乘法求拟合数据的多项式,并求平方误差,做出离散函数与拟合函数的图形;⑵用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差,并用MATLAB的内部函数plot作出其图形,并与(1)结果进行比较。
三、课程设计中的算法描述用最小二乘法多项式曲线拟合,根据给定的数据点,并不要求这条曲线精确的经过这些点,而就是拟合曲线无限逼近离散点所形成的数据曲线。
思路分析 : 从整体上考虑近似函数)(x p 同所给数据点)(i iy x , 误差i i iy x p r -=)(的大小,常用的方法有三种:一就是误差i i iy x p r -=)(绝对值的最大值im ir≤≤ 0max ,即误差向量的无穷范数;二就是误差绝对值的与∑=miir0,即误差向量的 1成绩评定范数;三就是误差平方与∑=miir02的算术平方根,即类似于误差向量的 2 范数。
前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑 2 范数的平方,此次采用第三种误差分析方案。
算法的具体推导过程: 1、设拟合多项式为:2、给点到这条曲线的距离之与,即偏差平方与:3、为了求得到符合条件的 a 的值,对等式右边求偏导数,因而我们得到了:4、将等式左边进行一次简化,然后应该可以得到下面的等式5、把这些等式表示成矩阵的形式,就可以得到下面的矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====niininiiknikinikinikinikiniiniinikiniiyyyaax x xx x xx x11i11012111111211 1an MMΛM O M MΛΛ 6.将这个范德蒙得矩阵化简后得到⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡n kkn nkkyyyaaax xx xx x M MΛM O M MΛΛ21102 21 1111 7、因为 Y A X = * ,那么 X Y A / = ,计算得到系数矩阵,同时就得到了拟合曲线。

Lab04.曲线拟合的最小二乘法实验【实验目的和要求】1.让学生体验曲线拟合的最小二乘法,加深对曲线拟合的最小二乘法的理解;2.掌握函数ployfit和函数lsqcurvefit功能和使用方法,分别用这两个函数进行多项式拟合和非多项式拟合。
【实验内容】1.在Matlab命令窗口,用help命令查询函数ployfit和函数lsqcurvefit功能和使用方法。
2.用多项式y=x3-6x2+5x-3,产生一组数据(x i,y i)(i=1,2,…,n),再在y i上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用randn产生N(0,1)均匀分布随机数),然后对x i和添加了随机干扰的y i用Matlab提供的函数ployfit用3次多项式拟合,将结果与原系数比较。
再作2或4次多项式拟合,分析所得结果。
3.用电压V=10伏的电池给电容器充电,电容器上t时刻的电压为τt eVVVtv ---=)()(,其中V0是电容器的初始电压,τ是充电常数。
对于下面的一组t,v数据,用Matlab提供的函数lsqcurvefit确定V和τ。
【实验仪器与软件】1.CPU主频在1GHz以上,内存在128Mb以上的PC;2.Matlab 6.0及以上版本。
实验讲评:实验成绩:评阅教师:年月日Lab04.曲线拟合的最小二乘法实验1.在Matlab命令窗口,用help命令查询函数ployfit和函数lsqcurvefit功能和使用方法。
在MATLAB中,用polyfit函数来求得最小二乘拟合多项式的系数,polyfit函数的调用格式为:[P,S]=polyfit(X,Y,m)。
函数根据采样点X和采样点函数值Y,产生一个m次多项式P及其在采样点的误差向量S。
其中X,Y是两个等长的向量,P是一个长度为m+1的向量,P的元素为多项式系数,得到的多项式为降序。
同样可以用lsqcurvefit函数来求得最小二乘拟合多项式的系数,调用格式为:x = lsqcurvefit(fun,x0,xdata,ydata)。

数值计算方法实验报告5―温度分布的曲线拟合本报告是关于温度分布的曲线拟合的,望对大家有所帮助!!!数值计算方法实验报告标题:温度分布的曲线拟合1.实验描述:在科学技术工程和实验中,经常需要从大量的实验数据中寻找拟合曲线,最简单的是一维情形(一元函数),此时数据的形式为x和y坐标的有序对,如:(x1,y1),...,(xN,yN),这里的横坐标{x}是明确的。
数值计算方法的目的之一是求解一个将自变量与因变量联系起来的拟合函数。
求解拟合函数的方法有多种,常见的方法有:线性最小二乘拟合、多项式拟合(最小二乘抛物线拟合)、样条插值拟合(三次样条拟合)、三角多项式拟合、贝塞尔曲线拟合这五种方法。
本次实验分别利用上述五种方法对一组温度数据进行拟合,通过拟合的结果比较这五种方法的优缺点(主要考虑误差)。
2.实验内容:已知某地区一天的温度数据如下:时间,p.m***-**********午夜***-********-********-*****温度时间,a.m***-**********正午***-********-********-*****温度分别利用:线性最小二乘拟合、多项式拟合(最小二乘抛物线拟合)、样条插值拟合(三次样条拟合)、三角多项式拟合、贝塞尔曲线拟合这五种方法对这组温度数据进行拟合,通过拟合的结果比较这五种方法的优缺点。
3.实验原理及分析:本报告是关于温度分布的曲线拟合的,望对大家有所帮助!!!①线性最小二乘拟合法:设{(x,y)}有N个点,其中横坐标{x}是确定的。
最小二乘拟合曲线为:kkk=1kk=1y=Ax+B,其系数满足如下正规方程:(∑x)A+(∑xk)B=∑xkyk 2kNNNNNk=1k=1(∑xk)A+NB=∑yk k=1k=1N解得:A=N∑xk=1Nk=1Nkyk Nxy2k∑xkNxN2=∑(xNNkx)(yk y),B=y Axk∑(xk=1kx)2其中:x=∑xk=1N,y=∑yk=1N线性最小二乘法的本质是:多元函数(均方根误差函数)求极值问题。

数值分析曲线拟合的最小二乘法实验报告数值分析曲线拟合的最小二乘法实验报告篇一:数值分析设计曲线拟合的最小二乘法曲线拟合的最小二乘法一、目的和意义在科学实验的统计方法研究中,往往要从一组实验数据?xi,yi??i?0,1,2,?,m?中,寻找自变量x与因变量y之间的函数关系y?F?x?。
由于观测数据往往不准确,因此不要求y?F?x?经过所有点?xi,yi?,而只要求在给定点xi上误差而只要求所在所有给定点xi上的误差?i?F(xi)?yi ?i?0,1,2,?,m?按某种标准最小。
若记????0,?1,?2,?,?m?,就是要求向量?的范数如果用最大范数,计算上困难较大,通常采用欧式范数?最小。
2T 作为误差度量的标准。
F?x?的函数类型往往与实验的物理背景以及数据的实际分布有关,它一般含有某些待定参数。
如果F?x?是所有待定参数的线性函数,那么相应的问题称为线性最小二乘问题,否则称为非线性最小二乘问题。
最小二乘法还是实验数据参数估计的重要工具。
这是因为这种方法比其他方法更容易理解,即使在其他方法失效的情况下,用最小二乘法还能提供解答,而且从统计学的观点分析,用该方法求得各项估计具有最优统计特征,因此这一方法也是系统识别的重要基础。
线性最小二乘问题可以借助多元微分学知识通过求解法方程组得到解答。
用最小二乘法求拟合曲线时,首先要确定S?x?的形式。
这不单纯是数学问题,还与所研究问题的运动规律以及所得观测数据?xi,yi?有关;通常要从问题的运动规律以及给定数据描图,确定S?x?的形式,并通过实际计算选出较好的结果。
为了使问题的提法更有一般性,通常把最小二乘法中的? 22 都考虑为加权平方和22 ? ????xi???S?xi??f?xi??? i?0 m 2 这里??xi??0是?a,b?上的加权函数,它表示不同点?xi,f?xi?处的数据比重不同。
?二、计算方法在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量y与时间t的拟合曲线。


实验报告
实验项目名称拟合实验所属课程名称数学建模实验类型综合性实验实验日期
班级
学号
姓名
成绩
【实验目的】
1、直观了解拟合基本内容。
2、掌握用数学软件求解拟合问题。
【实验原理】
1. 曲线拟合问题最常用的解法——线性最小二乘法的基本思路 第一步:先选定一组函数 r 1(x), r 2(x), …,r m (x), m<n, 令
f(x)=a 1r 1(x)+a 2r 2(x)+ …+a m r m (x) (1) 其中 a 1,a 2, …,a m 为待定系数.
第二步: 确定a 1,a 2, …,a m 的准则(最小二乘准则): 使n 个点(x i ,y i ) 与曲线 y=f(x) 的距离
i 的平方和最小 .
22
1211
2
1
1
(,,
)[()][()](2)
n
n
m i i i i i n
m
k k i i i k J a a a f x y a r x y δ======-=-∑∑∑∑
MATLAB 函数: p=polyfit(x,y,n) [p,s]= polyfit(x,y,n)
多项式曲线求值函数:polyval( ) 调用格式: y=polyval(p,x)
p 为幂次从高到低的多项式系数向量p 。
s 用于生成预测值的误差估计。

数据拟合与曲线拟合实验报告【数据拟合与曲线拟合实验报告】1. 实验介绍数据拟合与曲线拟合是数学和统计学中非常重要的概念和方法。
在科学研究、工程技术和数据分析中,我们经常会遇到需要从一组数据中找到代表性曲线或函数的情况,而数据拟合和曲线拟合正是为了解决这一问题而存在的。
2. 数据拟合的基本原理数据拟合的基本思想是利用已知的一组数据点,通过某种数学模型或函数,找到一个能够较好地描述这组数据的曲线或函数。
常见的数据拟合方法包括最小二乘法、最小二乘多项式拟合、指数拟合等。
在进行数据拟合时,我们需要考虑拟合的精度、稳定性、可行性等因素。
3. 曲线拟合的实验步骤为了更好地理解数据拟合与曲线拟合的原理与方法,我们进行了一组曲线拟合的实验。
实验步骤如下:- 收集一组要进行拟合的数据点;- 选择合适的拟合函数或模型;- 利用最小二乘法或其他拟合方法,计算拟合曲线的参数;- 对拟合结果进行评估和分析;- 重复实验,比较不同的拟合方法和模型。
4. 数据拟合与曲线拟合的实验结果通过实验,我们掌握了数据拟合和曲线拟合的基本原理与方法。
在实验中,我们发现最小二乘法是一种简单而有效的数据拟合方法,能够较好地逼近实际数据点。
我们还尝试了多项式拟合、指数拟合等不同的拟合方法,发现不同的拟合方法对数据拟合的效果有着不同的影响。
5. 经验总结与个人观点通过这次实验,我们对数据拟合和曲线拟合有了更深入的理解。
数据拟合是科学研究和实践工作中不可或缺的一部分,它能够帮助我们从一堆杂乱的数据中提炼出有用的信息和规律。
曲线拟合的精度和稳定性对研究和实践的结果都有着重要的影响,因此在选择拟合方法时需要慎重考虑。
6. 总结在数据拟合与曲线拟合的实验中,我们深入探讨了数据拟合和曲线拟合的基本原理与方法,并通过实验实际操作,加深了对这一概念的理解。
数据拟合与曲线拟合的重要性不言而喻,它们在科学研究、工程技术和信息处理中发挥着重要的作用,对我们的日常学习和工作都具有重要的指导意义。
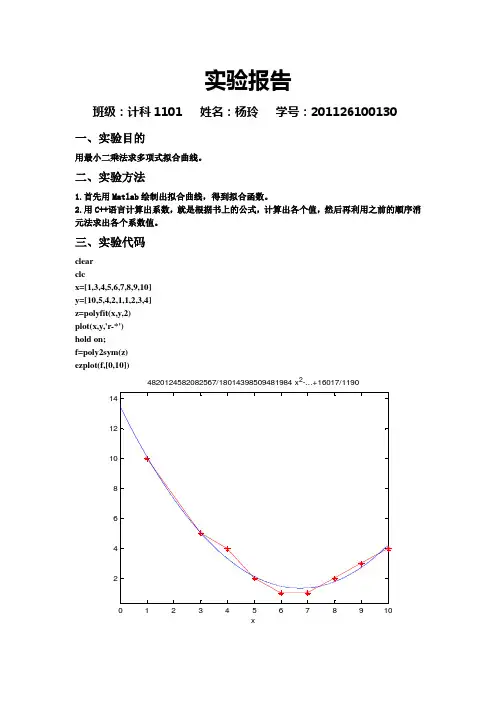
实验报告班级:计科1101 姓名:杨玲 学号:201126100130一、实验目的用最小二乘法求多项式拟合曲线。
二、实验方法1.首先用Matlab 绘制出拟合曲线,得到拟合函数。
2.用C++语言计算出系数,就是根据书上的公式,计算出各个值,然后再利用之前的顺序消元法求出各个系数值。
三、实验代码clearclcx=[1,3,4,5,6,7,8,9,10]y=[10,5,4,2,1,1,2,3,4]z=polyfit(x,y,2)plot(x,y,'r-*')hold on;f=poly2sym(z)ezplot(f,[0,10])0123456789102468101214x 4820124582082567/18014398509481984 x 2-...+16017/1190#include <iostream>#include <iomanip>using namespace std;void main(){int x[9]={1,3,4,5,6,7,8,9,10},y[9]={10,5,4,2,1,1,2,3,4}; double sum1=0;for(int p=0;p<9;p++){sum1+=x[p];}double sum2=0;for(int q=0;q<9;q++){sum2+=x[q]*x[q];}double sum3=0;for(int g=0;g<9;g++){sum3+=x[g]*x[g]*x[g];}double sum4=0;for(int w=0;w<9;w++){sum4+=x[w]*x[w]*x[w]*x[w];}double sum5=0;for(int r=0;r<9;r++){sum5+=y[r];}double sum6=0;for(int t=0;t<9;t++){sum6+=x[t]*y[t];}double sum7=0;for(int f=0;f<9;f++){sum7+=x[f]*x[f]*y[f];}//===================================================floata[3][4]={9,sum1,sum2,sum5,sum1,sum2,sum3,sum6,sum2,sum3,sum4,sum7},XX[3];//---------------------------------------for (int k=0;k<2;k++){for (int i=k+1;i<3;i++){float l=a[i][k]/a[k][k];for (int j=k+1;j<4;j++){a[i][j]=a[i][j]-l*a[k][j];}}} //消元for (int m=2;m>=0;m--){float sum=0;for (int j=m+1;j<3;j++){sum+=a[m][j]*XX[j];}XX[m]=(a[m][3]-sum)/a[m][m];} //计算//===========================================for (int h=0;h<3;h++){cout<<"XX["<<h+1<<"]="<<XX[h]<<endl;}cout<<"y="<<XX[2]<<"x^2"<<XX[1]<<"x+"<<XX[0]<<endl;cout<<"最低点位置:("<<(-1)*XX[1]/(2*XX[2])<<","<<(4*XX[0]*XX[2]-XX[1]*XX[1])/(4*XX[2])<<")"<< endl;}四、实验结果及其讨论实验结果有很小的误差,这是计算机本身的保留的小数位引起的五、总结通过本次实验,我开始会使用了Matlab软件,并且产生了浓厚的兴趣!另外,这次实验的代码,可能有点笨拙,不是很技巧,因为是直接计算出各个值在进行计算的,循环的次数很多,效率不是很高。

实验三 函数逼近一、实验目标1. 掌握数据多项式拟合的最小二乘法。
2. 会求函数的插值三角多项式。
二、实验问题(1)由实验得到下列数据jx 0.00.10.20.30.50.81.0jy 1.00.410.500.610.912.022.46试对这组数据进行曲线拟合。
(2)求函数在区间上的插值三角多项式。
()2cos f x x x =[,]ππ-三、实验要求1. 利用最小二乘法求问题(1)所给数据的3次、4次拟合多项式,画出拟合曲线。
2. 求函数在区间上的16次插值三角多项式,并画出插值多项()2cos f x x x =[,]ππ-式的图形,与的图形比较。
()f x 3.对函数,在区间上的取若干点,将函数值作为数据进行适()2cos f x x x =[,]ππ-当次数的最小二乘多项式拟合,并计算误差,与上题中的16次插值三角多项式的结果进行比较。
《数值分析》实验报告【实验课题】利用最小二乘法求上述问题所给数据的2次,3次、4次拟合多项式,画出拟合曲线【实验目标】(1)加深对用最小二乘法求拟合多项式的理解(2)学会编写最小二乘法的数值计算的程序;【理论概述与算法描述】在函数的最佳平方逼近中,如果只在一组离散点集()[,]f x C a b ∈()f x 上给出,这就是科学实验中经常见到的实验数据{,0,1,,}i x i m =⋅⋅⋅的曲线拟合,这里,要求一个函数{(,),0,1,,}i i x y i m =⋅⋅⋅(),0,1,,i i y f x i m ==⋅⋅⋅与所给数据拟合,若记误差*()y S x ={(,),0,1,,}i i x y i m =⋅⋅⋅,,设是上*()(0,1,,)ii i S x y i m δ=-=⋅⋅⋅()01,,,Tm δδδδ=⋅⋅⋅01(),(),,()n x x x ϕϕϕ⋅⋅⋅[,]C a b 的线性无关函数族,在中找一个函数,使误差平01{(),(),,()}n span x x x ϕϕϕϕ=⋅⋅⋅*()S x 方和|2222*2()0|||[()][()]min mmmii i i i S x i i i S x y S x y ϕδδ∈=====-=-∑∑∑这里0011|()()()()()n n S x a x a x a x n m ϕϕϕ=++⋅⋅⋅+<这就是一般的最小二乘逼近,用几何语言说,就称为曲线拟合的最小二乘法。
实验三曲线拟合最小二乘法一、实验目的(1)掌握最小二乘法,(2)熟练掌握求函数的近似最小二乘拟合多项式(3)掌握数据拟合的思想,清楚数据拟合与插值法的区别及最小二乘法原理在数据拟合中的重要作用及最小二乘法解的求法。
二、实验(或算法)原理最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法拟合:对给定数据点{(Xi,Yi)}(i=0,1,…,m),在取定的函数类Φ中,求p(x)∈Φ ,使误差的平方和E^2最小,E^2=∑[p(Xi)-Yi]^2。
从几何意义上讲,就是寻求与给定点 {(XiYi)}(i=0,1,…,m)的距离平方和为最小的曲线y=p(x)。
函数p(x)称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为曲线拟合的最小二乘法。
三、实验步骤(1)根据算法事先写出相应程序。
(2)启动PC机,进入vc集成环境,输入代码。
(3)编译调试。
(4)调试通过,计算出正确结果。
四、代码#include<stdio.h>#include<math.h>#include<conio.h>float cf(int i,float f){float g=1.0;while(i--)g*=f;return g;}void ColPivot(float a[99][99], int n, float b[99][1],float x[99]){float max,m,temp;int k,q=0,i,j,I;for(k=0;k<n && q==0;k++){max=a[k][k];for(i=k+1;i<n;i++)if(fabs(max)<fabs(a[i][k])){max=a[i][k];I=i;}if(max==0)q=1;else{if(I!=k){temp=b[I][0]; b[I][0]=b[k][0];b[k][0]=temp;for(j=k;j<n;j++){temp=a[I][j]; a[I][j]=a[k][j];a[k][j]=temp;}}for(i=k+1;i<n;i++){m=a[i][k]/a[k][k];b[i][0]=b[i][0]-b[k][0]*m;for(j=0;j<n;j++)a[i][j]=a[i][j]-a[k][j]*m;}}}for(i=n-1;i>=0;i--){for(j=n-1;j>=i+1;j--)b[i][0]=b[i][0]-a[i][j]*x[j];x[i]=b[i][0]/a[i][i];}}void main(){float x[99],y[99],z[99],s[99][99],t[99][1]; int n,m,i,j,k;printf("n=");scanf("%d",&n);printf("m=");scanf("%d",&m);printf("y[%]=",n);for(i=0;i<n;i++)scanf("%f",&y[i]);printf("z[%d]=",n);for(i=0;i<n;i++)scanf("%f",&z[i]);for(i=0;i<=m;i++){for(j=0;j<=m;j++){s[i][j]=0.0;for(k=0;k<=n-1;k++)s[i][j]+=cf(i+j,y[k]);}t[i][0]=0.0;for(j=0;j<=n-1;j++)t[i][0]+=z[j]*cf(i,y[j]);}for(i=0;i<=m;i++)s[i][m+1]=t[i][0];for(i=0;i<=m;i++){for(j=0;j<=m+1;j++) printf("%f\t",s[i][j]);printf("\n");}ColPivot(s,m+1,t,x);printf("\n\n");for(i=0;i<=m;i++)printf("\na[%d]=%f",i,x[i]); printf("\n\n");}四、实验结果、实验体会通过实验的验证,可以更深刻地理解曲线拟合最小二乘法在数值计算的重要性,同时了解了其基本原理在计算机数值拟合的应用,更深刻地理解了曲线拟合最小二乘法的计算原理。
数值计算(分析)实验报告2南昌航空大学数学与信息科学学院实验报告课程名称:《数值计算方法》实验名称:曲线拟合实验类型:验证性■综合性□设计性□实验室名称:数学实验室班级学号: 09072113学生姓名:邢宪平任课教师(教师签名):成绩:一、实验目的实验目的:实验目的:了解函数逼近与曲线拟合的基本原理,并且运用MATLAB 软件进行实践操作。
二、实验原理、程序框图、程序代码等 实验题目:题目1:试分别用抛物线2y a bx cx =++和指数曲线bxy ae =拟合下列数据并比较两个拟合函数的优劣。
题目2:已知实验数据如下:试用形如2y a bx =+的抛物线进行最小二乘拟合。
实验原理:1、逼近方式 假设()[,]f x C a b ∈,2{1,,,...,}n nHspan x x x =,()nnP x H ∈,称(,)|||||()()|max n n n a x bf P F P f x P x ≤≤=-=-V 为()f x 与()|nP x 在[,]a b 上的偏差。
若存在*()nnP x H ∈,使得**(,)|||||()()|max inf n nn nn P H a x bf P f Pf x P x ∞∈≤≤=-=-V 则称*()nP x 是()f x 在[,]a b 上的最佳一致逼近多项式。
假设()[,]f x C a b ∈及[,]C a b 的一个子集01{(),(),,...()}nspan x x x ϕ=ϕϕϕ,若存在*()S x ϕ∈,使*22222()()||()()||||()()||()[()()]min min bS x S x af x S x f x S x x f x S x dxϕϕρ∈∈-=-=-⎰则称*()S x 是()f x 在子集[,]C a b ϕ⊂中的最佳平方逼近数。
2、曲线拟合上述函数的最佳平方逼近法中,若()f x 是以一组离散点集的形式给出的,即给出了函数()f x 在一些离散点上的值{(,),0,1,...,}iix y i m =,则该方法就是所说的曲线拟合。
数值分析上机作业实验报告专业:建筑与土木工程姓名:学号:联系电话:课题四 曲线拟合的最小二乘法一、问题提出从随机的数据中找出其规律性,给出其近似表达式的问题,在生产实践和科学实验中大量存在,通常利用数据的最小二乘法求得拟合曲线。
在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量 y 与时间t 的拟合曲线。
二、要求1 、用最小二乘法进行曲线拟合;2 、近似解析表达式为()t ϕ=a 1t+a 2t 2+a 3t 33 、打印出拟合函数()t ϕ,并打印出()tj ϕ与()y tj 的误差,j=1,2...,12:4 、另外选取一个近似表达式,尝试拟合效果的比较;5 、* 绘制出曲线拟合图﹡。
三、目的和意义1 、掌握曲线拟合的最小二乘法;2 、最小二乘法亦可用于解超定线代数方程组;3 、探索拟合函数的选择与拟合精度间的关系。
四、实验结果:1.用最小二乘法做出的曲线拟合为三次多项式a1= -0.0052 ,a2= 0.2634 ,a3= 0.0178。
()tϕ= (-0.0052) t+ (0.2634) t2 + (0.0178) t3三次多项式的误差平方和=0.2583。
图形为:图形上红线表示拟合曲线,*表示实验所给的点。
源代码为:x=[0,5,10,15,20,25,30,35,40,45,50,55];y=[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.02,4.64]; a1=polyfit(x,y,3) %三次多项式拟合%b1= polyval(a1,x)r1= sum((y-b1).^2) %三次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%(说明本程序调用了MATLAB中的函数polyfit、polyval、plot)2.另外选取几个近似表达式:主要选取6次、9次和12次的拟合表达式。
两条曲线拟合率自动计算方法摘要:一、引言1.背景介绍2.研究目的二、曲线拟合方法概述1.曲线拟合的基本概念2.常见曲线拟合方法简介三、两条曲线拟合率自动计算方法1.算法原理2.计算步骤3.算法优缺点分析四、实证分析1.数据来源及处理2.拟合结果展示3.结果分析与讨论五、结论与展望1.研究结论2.研究局限3.未来研究方向正文:一、引言1.背景介绍在科学研究、工程应用等领域,经常需要对实验数据进行曲线拟合,以揭示数据之间的关系。
两条曲线的拟合更是常见,如线性拟合、多项式拟合等。
对于多条曲线拟合,已有成熟的自动计算方法。
然而,针对两条曲线的拟合,尚未有统一的自动计算方法。
2.研究目的本文旨在提出一种针对两条曲线的拟合率自动计算方法,以满足实际应用中的需求。
二、曲线拟合方法概述1.曲线拟合的基本概念曲线拟合是指在给定数据点的基础上,通过一定的数学模型来描述数据之间的关系。
2.常见曲线拟合方法简介常见的曲线拟合方法包括线性拟合、多项式拟合、指数拟合等。
三、两条曲线拟合率自动计算方法1.算法原理本文提出的两条曲线拟合率自动计算方法,基于最小二乘法原理,通过求解误差平方和最小的一组参数,实现对两条曲线的拟合。
2.计算步骤(1)确定拟合函数形式;(2)构建误差平方和目标函数;(3)求解目标函数最小值对应的参数;(4)根据求解得到的参数,绘制拟合曲线。
3.算法优缺点分析优点:计算简便,易于实现自动化;缺点:对初始参数敏感,可能出现局部最优解。
四、实证分析1.数据来源及处理本文以某实验数据为例,共有10个数据点。
首先对数据进行预处理,包括去除异常值、填补缺失值等。
2.拟合结果展示采用本文提出的自动计算方法,对两条曲线进行拟合。
拟合结果如图所示,红色点为实际数据点,蓝色线为拟合曲线。
3.结果分析与讨论由拟合结果可知,本文提出的自动计算方法能够较好地拟合两条曲线。
同时,通过比较拟合曲线与实际数据点的误差,评估拟合效果。
>> PIot(x,y,'*r',x1,y1,'-b')% 比较拟合曲线效果实验10曲线拟合与插值运算、实验目的学会曲线拟合与插值运算的方法. 、实验内容与要求 1. 曲线拟合定义:已知数据集[(X l ,y i ),(X 2,y 2),…,(X n ,y n )],求一解析函数y=f(x),使f(x)在原离散点X i 上尽可能接近给定 y i 的值,这一过程叫曲线拟合.最小二乘法曲线拟合,拟合结果可使误差的平方和最小,即找出使最小的f(x).【例】>>x = [0.5,1.0,1.5,2.0,2.530];>>y = [1.75,2.45,3.81,4.80,7.00,8.60]; % 给出数据点的 y 值 >>p = Polyfit(x,y,2) %求出2阶拟合多项式f(x)的系数 >>x1 = 0.5:0.05:3.0; % 给出x 在0.5~3.0之间的离散值 >>y1 = polyval(p,x1); % 求出 f(x)在 x1 上的值方法: f (X i )i 1y i格式: p=polyfit( x,Y,n).注意: 已知数据x 必须是单调的.%给出数据点的x 值62基于MATLAB 的数学实验-0注 意:该命令用指定的算法对数 Y:原始数据点i :插值点7据点之间计算内插值,它找出 元函数f (X )在中间点的数值,其 f /」/r i-0••中函数f (X )由所给数据决定,各d 1 X :原始数据点工□ X :插值点计算结果为: P=0.5614 0.8287 1.1560即用f (X )=0.5614X 2+0.8287X +1.1560拟合已知数据,拟合曲线 效果如图1.31所示.2. 一维插值定义:已知离散点上的数据集 [(X l ,y i ),(X 2,y 2),…,(x n ,y n )],找出一解的数值,这一过程叫插值 interp1(1-D interpolation格式一:yi = interp1(X,Y,xi,method) 析函数连接自变量相邻的两个点(X i , X i +1),并求得两点间内插法)第一章MATLAB软件操作实验63个参量之间的关系如图所示'nearest'最近邻点插值,直接完成计算’linear'线性插值(缺省方式),直接完成计算.'spline '三次样条函数插值.'cubic ':三次函数插值.对于超出x范围的x i的分量,执行外插值算法格式二:yi = interp1(X,Y,xi,method, ‘extrap ' ) % 对于超出围的X i中的分将执行特殊的外插值法extra p.yi = inter p1(X,Y,xi,method,extra pval) %确定超出围的xi 中的分量的外插值extra pval ,其值通常取NaN或0.【例】>> year = 1900:10:2010;>> product = [75.995,91.972,105.711,123.203,131.669,…150.697,179.323,203.212,226.505,249.633,256.344,267.893];>>p2005 = interp1(year, product,2005) >>x = 1900:1:2010;>>y= inter p1(year, product,x,'cubic');>>pl ot(year, product,'o',x,y)插值结果为:p2005 =262.118564 基于MATLAB 的数学实验250 200 150 100 . r r 50 _I 1900 I 19201940 1960 1980 2000 20203. 二维插值格式:ZI = interp2(X,Y, Z, XI ,YI ,method)说明:用指定的算法 method 计算二维插值.返回矩阵Z i ,其元素对应于参量 X I 与Y i 的元素.用户可以输入行向量 和列向量X i 与Y i ,此时,输出向量 乙与矩阵meshgrid( X i ,y i ) 是同型的.参量X 与丫必须是单调的,且相同的划分格 式,就像由命令 meshgrid 生成的一样.method 有: 'linear ':双线性插值算法(缺省算法) ‘nearest '最临近插值 . 'spline '三次样条插值. 'cubic ': 双三次插值 . 【例】>>years = 1950:10:1990; >>service = 10:10:30;>>wage = [150.697,199.592,187.625,179.323,195.072,250,287,插值图形如图1.33所示.300 .尸■*第一章MATLAB软件操作实验65 203.212,179.092,322.767, 226.505,153.706,426.730,249.633,120.281,598.243];>>w = inter p2(service,years,wage,15,1975)插值结果为:190.6288【例】>>x=1:6;y=1:4; %给出自变量数据>>t=[12,10,11,11,13,15;16,22,28,35,27,20;18,21,26,32,28,25;20,25,30,33,32,30]; %给出对应自变量的温度值,注意t的维数和x,y的维数之间的关系>>sub plot(1,2,1)>>mesh(x,y,t) %画出插值前的温度分布图>>x1=1:0.1:6; %将x细化为51个点>>y1=1:0.1:4; %将y细化为51个点>>[x2,y2]=meshgrid(x1,y1); %产生51 行51 列网格数据点,这一步不可省>>t1=interp2(x,y,t,x2,y2,'cubic');>>sub plot(1,2,2)>>mesh(x1,y1,t1) ; %画出插值后的温度分布图66 基于MATLAB 的数学实验并做出拟合曲线及sinx 函数曲线图.练习:1.已知 x=[0.1,0.8,1.3,1.9,2.5,3.1],用不同的方法求x=2点的插值,并分析所得的结果有何不同x=[1.2,1.8,2.1,2.4,2.6,3.0,3.3]y=[4.85,5.2,5.6,6.2,6.5,7.0,7.5],求对 x 和 y 进行 6 阶多项式拟合 的系数.3.分别用2, 3, 4, 5阶多项式来逼近[0,3]上的正弦函数sinx , y=[121.6,2.7,2.0,1.3,0.5],2.图形结果如图1.34所示.。
曲线拟合的数值计算方法实验Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】曲线拟合的数值计算方法实验【摘要】实际工作中,变量间未必都有线性关系,如服药后血药浓度与时间的关系;疾病疗效与疗程长短的关系;毒物剂量与致死率的关系等常呈曲线关系。
曲线拟合(curve fitting)是指选择适当的曲线类型来拟合观测数据,并用拟合的分析两变量间的关系。
曲线直线化是曲线拟合的重要手段之一。
对于某些非线性的资料可以通过简单的变量变换使之直线化,这样就可以按原理求出变换后变量的,在实际工作中常利用此直线方程绘制资料的标准工作曲线,同时根据需要可将此直线方程还原为,实现对资料的曲线拟合。
常用的曲线拟合有最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束。
关键词曲线拟合、最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束一、实验目的1.掌握曲线拟合方式及其常用函数指数函数、幂函数、对数函数的拟合。
2.掌握最小二乘法、线性插值、三次样条插值、端点约束等。
3.掌握实现曲线拟合的编程技巧。
二、实验原理1.曲线拟合曲线拟合是平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。
用解析表达式逼近的一种方法。
在或社会活动中,通过实验或观测得到量x 与y 的一组数据对(X i ,Y i )(i=1,2,...m ),其中各X i 是彼此不同的 。
人们希望用一类与数据的背景材料规律相适应的解析表达式,y=f(x ,c )来反映量x 与y 之间的依赖关系,即在一定意义下“最佳”地逼近或拟合已知数据。
f(x ,c)常称作拟合模型 ,式中c=(c 1,c 2,…c n )是一些待定参数。
当c 在f 中出现时,称为线性模型,否则称为。
有许多衡量拟合优度的标准,最常用的一种做法是选择参数c 使得拟合模型与实际在各点的(或),c)-f (f y e k k k 的平方和达到最小,此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线。
有许多求解拟合曲线的成功方法,对于线性模型一般通过建立和求解来确定参数,从而求得拟合曲线。
至于,则要借助求解非线性方程组或用最优化方法求得所需参数才能得到拟合曲线,有时称之为非线性。
曲线拟合:与路径转化时的误差。
值越大,误差越大;值越小,越精确。
2.最小二乘法拟合:最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
函数曲线为:y=Ax+B其中系数满足下列的正规方程:∑∑∑====⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛Nk kk N k k N k k y x B x A x 1112∑∑===+⎪⎭⎫⎝⎛Nk kN k k y NB A x 113.幂函数拟合:函数曲线为:设(){}Νk k ,k y x 1=有N 个点,其中横坐标是确定的。
最小二乘幂函数拟合曲线的系数A 为:)/()(121∑∑===Nk Mk Nk k Mk x y x A 、4.对数函数拟合:对数函数(lograrithmic function )的标准式形式为=XXb)0+Y>ln(ab>0时,Y随X增大而增大,先快后慢;b<0时,Y随X增大而减少,先快后慢,见图(c)、(d)。
当以Y和lnX绘制的散点图呈直线趋势时,可考虑采用对数函数描述Y与X之间的非线性关系,式中的b和a 分别为斜率和截距。
更一般的对数函数Y=a+bln(X+k)式中k为一常量,往往未知。
(a)lnY=lna+bX(b)lnY=lna-bX(c)Y=a+blnX(d)Y=a-blnX5.线性插值:在代数插值中,为了提高插值多项式对函数的逼近程度一般是增加节点的个数,即提高多项式的次数,但这样做往往不能达到预想的效果。
如下图所示:f(x) = 1 / (1 + x2)如果在区间[-5,5]上取7个等距节点:x k =5*(k/3-1) (k=0,1,2,...,6),由lagrange 插值公式可得到f(x)的次L7(x)。
如图所示:L7(x)仅在区间的中部能较好的逼近函数f(x), 在其它部位差异较大,而且越接近端点,逼近效果越差。
可以证明,当节点无限加密时,Ln(x)也只能在很小的范围内收敛,这一现象称为Runge 现象。
它表明通过增加节点来提高逼近程度是不适宜的,因而不采用高次多项式插值。
如果我们把以上的点用直线连接起来,显然比L7(x)要更逼近f(x)。
这就是分段线性插值。
而在实际应用中通常采用分段低次插值来提高近似程度,比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数,但它们的总体光滑性较差。
为了克服这一缺点,一种全局化的分段插值方法——三次样条插值成为比较理想的工具。
6.三次样条插值:设(){}Nk k k ,y x 0=有N+1个点,其中b x ...x x x a N =<<<<=210。
如果存在N 个三次多项式x )S k (,系数为3210k ,k ,k ,k ,,S,S ,S S 满足如下性质:33,22,1,0,)()()()()(k k k k k k k k x x s x x s x x s s x S x S -+-+-+==1,....,1,0],,[1-=∈+N k x x x k k)('')('')(')(')()()(111111111+++++++++====k k k k k k k k k kk x S x S x S x S x S x S y x S 2,....1,02,....1,02,....1,0,....1,0-=-=-==N k N k N k N k则成函数S(x)为三次样条函数。
7.端点约束:紧压样条:存在唯一的三次样条曲线,其一阶导数的边界条件是:N d b S d a S ==)(',)('0natural 样条:存在唯一的三次样条曲线,它的自由边界条件是:0)('',0)(''==b S a S外推样条:存在唯一的三次样条曲线,其中通过对点x1和x2进行外推得到 ()a S '',同时通过对点X(n-1)和X(N-2)进行外推得到()b S ''。
端点曲率调整:存在唯一的三次样条曲线,其中二阶导数的边界条件()a S ''和()b S ''是确定的。
抛物线终结样条:存在唯一的三次样条曲线,其中二阶在区间[X 0,X 1]内0x S ≡''')(,而在[Xn-1,Xn]内0x S ≡''')(。
三、实验内容1.P202 1胡克定律指出F=kx ,其中F 是拉伸弹簧的拉力(单位为盎司),x 为拉伸的长度(单位为英寸)。
根据下列试验数据,求解拉伸常量k 的近似值。
(a )(b )2.P215 1洛杉矶(美国城市)郊区11月8日的温度记录入下表所示,其中共有24个数据点。
(a )根据例中的处理过程(使用fmins 命令),对给定的数据求解最小二乘曲线E Dx C Bx A x f ++=)sin()cos()(。
(b )求。
)(2f E(c )在同一坐标系下画出这些点集和(a)得出的最小二乘曲线。
3.P229 1一个轿车在时间T k 时经过的距离d k ,如下表所示。
使用程序,并根据一阶导数边界条件98)8(',0)0('==S S ,求这些数据的三次紧压样条插值。
4.P238 5美国洛杉矶郊区11月9日的温度(华氏温度)如表所示。
采用24小时制。
(a )求三角多项式)(7x T(b )在同一坐标系下,画出图)(7x T 和24个数据点。
(c )使用本地的温度情况重新求解问题(a)和问题(b)。
5.P246 1编写Matlab 程序,生成并绘制组合贝塞尔曲线。
利用该程序生成和绘制过3个控制点集{(0,0),(1,2),(1,1),(3,0)},{(3,0),(4,-1),(5,-2),(6,1),(7,0)},{(7,0),(4,-3),(2,-1),(0,0)}的贝塞尔曲线。
四、实验结果及分析1实验描述:由题意可知,此题需要用最小二乘法进行计算,因为已知函数的5个插点并且知道它们的x,y 的值。
且函数的表达式为F=kx ,所以只需用方程中∑∑===Nk k Nk k y A x 11)(便可计算出k 的数值。
定义一个动态数组[]a,用来依次存取x和y的插值。
其中x,y的插值通过键盘手动输入并赋予给a中的元素。
然后通过相应的求和和基本运算便可以得到相应插值下的最小二乘法的函数表达式。
(其中k保留小数点后4位)具体函数运行效果如下:(a)请在此输入x的各插值请在此输入y的各插值此函数的最小二乘法曲线表达式为Y=*x请按任意键继续。
(b)请在此输入x的各插值请在此输入y的各插值此函数的最小二乘法曲线表达式为Y=*x请按任意键继续。
结果分析:易得,最小二乘法多项式计算可以很好的做出较为精确的最小二乘法拟合曲线,并且程序通用性高,只要输入相应的插值便可以计算出结果,结果系数的小数点有效位同时也可以自己确定。
1实验描述:给出的最小二乘曲线表达式为:sin(=)))(cos(+DxEf+CBxxA其中变量有5个,而给出的数据点有24个,在C语言中可以用牛顿-拉夫森算法迭代计算分别得出5个变量的值,但是方法繁琐,且迭代计算量庞大,因此这里采用Matlab进行相关的计算,调用fminsearch函数,求得当5个参量都为1附近时候多项式的最小值,此时便可求出此5个参变量的值.然后继续通过Matlab,将得到的公式以及各点,用plot函数,便可以求得。
实验结果:运行matlab结果如下:>> fminsearch('fiveOne',[1 1 1 1 1])ans =此时的所求值便为函数的待定系数。
所以可得最小二乘曲线的表达式为:15.)cos(7225.1fx=x+(+.2768)37173579.160)15.sin(5359然后进行相应的绘制图形便可以求出所要求出的结果。
结果分析:通过最小二乘法多项式同样可以绘制出三角函数的曲线。
并且程序通用性高,只要输入相应的插值便可以计算出结果,结果系数的小数点有效位同时也可以自己确定。
1实验描述:由题意可知,由于这里涉及到了样条线的运算,计算较为复杂。