安徽师范大学《702信号与系统》考研专业课真题试卷

安徽大学2014—2015学年第 2 学期《信号与系统 》考试试卷（A 卷）（闭卷 时间120分钟）考场登记表序号一、填空题（每小题1分，共10分）1．利用单位冲激信号)(t δ的性质，有()=-⎰+∞∞--dt t e t 23δ ； 2．描述离散时间系统输入输出关系的数学模型是 方程； 3．已知信号()t f 的单边拉普拉斯变换()21++=s s s F ，则该信号的傅里叶变换为 ； 4．全通系统的系统函数()as s s F +-=2，则a 的取值为 ； 5．根据响应产生的原因，完全响应等于零输入响应与 响应相加； 6．()()()t f t f t y 211*=，则()()()=-*-=22112t t f t t f t y ；7．离散时间系统的单位样值响应为()n h ，则该系统因果稳定的充分必要条件为 ；8．根据傅里叶变换的性质可知，当信号在时域中压缩时，其频谱将会 ； 9．s 平面上的虚轴对应z 平面上的 ；10．设激励信号为)(t e ，响应信号为)(t r ，则无失真传输条件为 。

二、选择题（每小题2分，共10分）1．一个线性定常系统，若要使其稳定，则它的极点不该出现在（ ） A . 实轴 B . 虚轴 C . 右半平面 D . 左半平面院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------2．已知()()11+=s s s F ，则)(∞f 等于（ ）A. 0B. 1C. 2D. 33．已知连续系统二阶微分方程的零输入响应()t y zi 的形式为t t Be Ae 2--+，则其2个特 征根为（ ）。

安徽大学2006—2007学年第二学期 《 信号与系统 》考试试卷（A 卷）（时间120分钟）1． 系统的激励是)t (e ，响应为)t (r ，若满足dt)t (de )t (r =，则该系统为 线性、时不变、因果。

（是否线性、时不变、因果？） 2． 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。

3． 当信号是脉冲信号f(t)时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。

4． 若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5． 信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。

6． 系统阶跃响应的上升时间和系统的 截止频率 成反比。

7．若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8． 为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的 左半平面 。

9． 已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10． 若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1.单位冲激函数总是满足)()(t t -=δδ （ √ ）2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（ × ） 3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

安徽大学2011—2012学年第2学期《信号与系统》（B 卷）考试试题参考答案及评分标准一、 选择题1.C2.A3.D4.B5. B 每小题2分，共计10分 二、 填空题1. 0()f t2. 1(/3)3F w 3. 零状态响应 4. ()(0)sF s f --5. X(z)H(z)每小题2分，共计10分 三、 简述题1、调制过程将信号频谱搬移到任何所需的较高频率范围，这就容易以电磁波形式辐射出去。

（+2分）调制作用的实质是把各种信号的频谱搬移，使它们互不相重叠地占据不同的频率范围，也即信号分别托附于不同频率的载波上，接收机就可以分离出所需频率的信号，不致互相干扰。

（+3分）2、连续时间域就是以连续时间t 为自变量，频率域则是以变化的频率w 对其进行研究，傅里叶变换就是将连续的时间域信号转变到频率域，拉氏变换是傅里叶变换的推广，是将连续的时间域信号变换到复频率域（拉氏变换，此时看成仅在j Ω轴）；而z 变换则是连续信号经过理想采样之后的离散信号的拉氏变换，再令STz e =时的变换结果，所对应的域为数字复频率域，此时数字频率ω=ΩT 。

（+5分）3、系统零状态响应的拉式变换与激励的拉式变换之比称为“系统函数”，以(s)H 表示。

在S 域中，系统函数非常重要，系统函数零、极点分布与冲激响应的有着对应关系。

利用()H s 在s 平面的零极点分布情况可以分析系统的时域特性。

由()H s 可直接写出系统的微分方程，因而系统也就可以用具有微分方程特性的网络来实现。

可研究()H s 的零极点分布对()h t 的影响。

（+10分）四、计算题1、解：()()()-(t)y t h t *x t =*()d tdh x dtττ∞=⎰ （+1分）()()()()()()=[t 1t 2][t 2u t 2t 4u t 4]δδ---*-----（+1分）=(3)(3)(4)(4)(5)(5)(6)(6)t u t t u t t u t t u t --------+--（+1分）2、解：(n)*y(n)={4,3,2,1}*{2,3,4}={8,18,29,20,11,4}x（+5分）3、解：由图可得：0,(),t t f t tt τττττ<->⎧⎪=⎨-<≤⎪⎩或 （+3分）令1(),tf t t τττ=-<≤，2()0,f t t t ττ=<->或，则1()1/[()()]1/[()()()()]df t u t u t dtu t u t u t u t ττττττ=+--=+-+-- （+3分）122()11()(/2)(/2)j j df t F Sa e Sa e dt ττωωωτωτττ-=+（+2分）所以频谱 1()()()(0)()df t F dt F F j ωπδωω=+ 2211(/2)(/2)2j j Sa e Sa ej ττωωωτωτπττωτ-+=+（+2分）4、解：（1）211()3+2(s 2)(s 1)F s s s ==--- =111()s 12s -∙--- （+2分）⇒ 2(t )=e tt f e -（+3分）（2）由于收敛域为0.5Z ＞，因此(n)x 为右边序列（+1分）2(z )=(z 0.5)(z 0.3)z X --=2.5 1.50.50.3z zz z --- （+2分）⇒ ()x (n )=[2.5(0.5)1.50.3]u (n )nn -（+2分）五、综合题1、 解：（1）由于2()(1)()t g t e u t -=-则系统的冲击响应为2()()2t dg t h t e dt-== （+2分）所以，系统函数2()2H s s =+ （+3分）（2）2()2H j j ωω=+，得到其幅频特性如图1所示 （+2分）()arctan ϕωω=-，得到其相频特性如图2所示（+2分）图1 图2（3）由2111()11/22(2)()()22R s s s s E s H s s s s --++===-++ （+3分）可得：21()(1)()2t e t e u t -=-（+3分）2、解：（1）(n)+0.2y(n 1)0.24y(n 2)=x(n)+x(n 1)y ---- 对差分方程表达式进行Z 变换，得：121()0.2(z)0.24(z)=X(z)+X(z)Y z z Y z Y z ---+-（+2分）⇒12122()1+()=()10.20.24+0.20.24Y Z z z zH Z X Z z z z z ---+==+-- 22()(z+1)()=()+0.20.24(z 0.4)(z+0.6)Y Z z z z H Z X Z z z +==-- （+2分）()H Z 的两个极点分别位于0.4和—0.6，它们都在单位圆内，对此因果系统的收敛域为0.6z ＞，且包含=z ∞点，是一个稳定的因果系统。

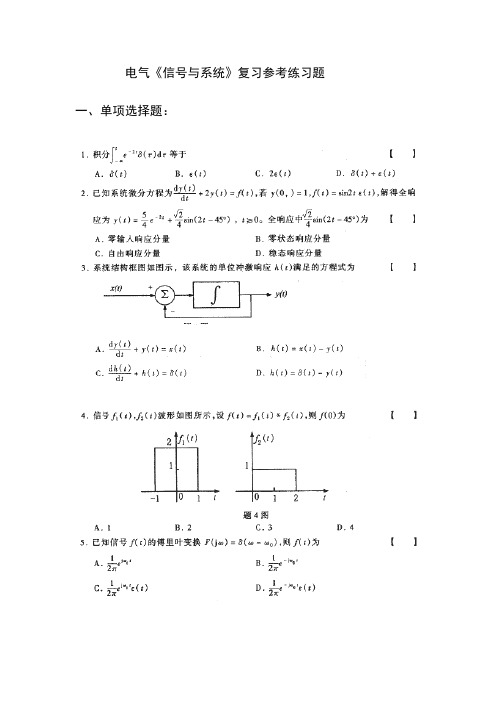
电气《信号与系统》复习参考练习题一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／sf如下图（a）所示，其反转右移的信号f1(t) 是（ d ）15、已知信号)(tf如下图所示，其表达式是（）16、已知信号)(1tA、ε（t）＋2ε(t－2)－ε(t－3)B、ε(t－1)＋ε(t－2)－2ε(t－3)C、ε(t)＋ε(t－2)－ε(t－3)D、ε(t－1)＋ε(t－2)－ε(t－3)17、如图所示：f（t）为原始信号，f1(t)为变换信号，则f1(t)的表达式是（）A、f(－t+1)B、f(t+1)C、f(－2t+1)D、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ c ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（ ）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ ）A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ ）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( ) A )0(f B )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应 D .全响应与强迫响应之差2A 、1-eB 、3eC 、3-e D 、1 27.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+，则其2个特征根为( )A 。