空间中平行关系知识点小结

空间几何的平行与垂直关系知识点总结空间几何是研究点、线、面等几何形体在空间中的相互关系和特性的学科。

在空间几何中，平行和垂直是两种重要的关系。

本文将总结空间几何中的平行与垂直关系的知识点。

一、平行关系平行是指两条直线或两个平面在空间中永远不会相交的关系。

平行关系在日常生活和工程建设中经常被应用到。

1. 平行关系的性质- 平行线与同一平面内的直线交线的两个内角是同位角，即两个内角之和等于180度。

- 平行线与同一平面外的直线交线的两个内角也是同位角，同位角性质适用于平行于同一平面内的两条直线。

2. 判定平行关系的方法- 平行线的判定：如果两条直线上有一点与第三条直线上的两个点重合，并且这两条直线分别与第三条直线平行，则这两条直线是平行线。

- 平行面的判定：如果两个平面上有一条直线与第三个平面上的两条直线重合，并且这两个平面分别与第三个平面平行，则这两个平面是平行面。

3. 平行线的性质- 平行线投影性质：平行于同一平面内的两条直线的等角投影相等。

- 平行线的方向性：平行线有确定的方向，可以延长或缩短，但方向不会改变。

二、垂直关系垂直是指两条直线或两个平面相交成直角的关系。

垂直关系在几何学、建筑学和物理学中都有广泛应用。

1. 垂直关系的性质- 垂直关系性质一：两个直角相等。

- 垂直关系性质二：两个互相垂直的直线或两个互相垂直的平面，其中一个与第三个垂直，则它们与第三个也是垂直关系。

- 垂直关系性质三：垂直于同一面的直线与该面的交线垂直。

2. 判定垂直关系的方法- 判定直线垂直关系的方法：如果两条直线上有一点与第三条直线上的两个点重合，并且这两条直线分别与第三条直线垂直，则这两条直线是垂直的。

- 判定面垂直关系的方法：如果两个平面上有一条直线与第三个平面上的两条直线相交成直角，并且这两个平面分别与第三个平面垂直，则这两个平面是垂直的。

三、平行和垂直关系的应用平行和垂直关系在日常生活和工程建设中具有广泛的应用。

空间中的平行与垂直例题和知识点总结在立体几何的学习中，空间中的平行与垂直关系是非常重要的内容。

理解和掌握这些关系，对于解决相关的几何问题具有关键作用。

下面我们通过一些例题来深入探讨，并对相关知识点进行总结。

一、平行关系（一）线线平行1、定义：如果两条直线在同一平面内没有公共点，则这两条直线平行。

2、判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

例 1：在正方体 ABCD A₁B₁C₁D₁中，E，F 分别是 AB，BC 的中点，求证：EF∥A₁C₁。

证明：连接 AC，因为 E，F 分别是 AB，BC 的中点，所以 EF∥AC。

又因为正方体中，AC∥A₁C₁，所以 EF∥A₁C₁。

（二）线面平行1、定义：如果一条直线与一个平面没有公共点，则称这条直线与这个平面平行。

2、判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

例 2：已知四棱锥 P ABCD 的底面是平行四边形，M 是 PC 的中点，求证：PA∥平面 MBD。

证明：连接 AC 交 BD 于 O，连接 MO。

因为四边形 ABCD 是平行四边形，所以 O 是 AC 的中点。

又因为 M 是 PC 的中点，所以MO∥PA。

因为 MO⊂平面 MBD，PA⊄平面 MBD，所以 PA∥平面MBD。

（三）面面平行1、定义：如果两个平面没有公共点，则称这两个平面平行。

2、判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

例 3：在正方体 ABCD A₁B₁C₁D₁中，求证：平面 A₁BD∥平面 B₁D₁C。

证明：因为 A₁B∥D₁C，A₁D∥B₁C，且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线，D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线，所以平面 A₁BD∥平面 B₁D₁C。

二、垂直关系（一）线线垂直1、定义：如果两条直线所成的角为 90°，则这两条直线垂直。

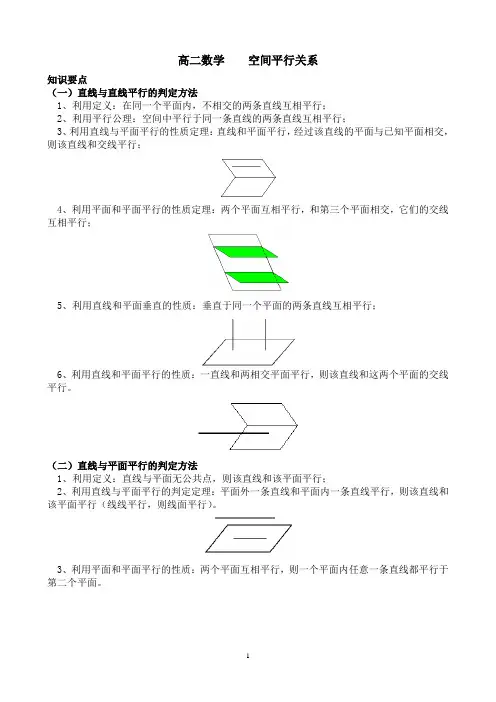
高二数学空间平行关系知识要点（一）直线与直线平行的判定方法1、利用定义：在同一个平面内，不相交的两条直线互相平行；2、利用平行公理：空间中平行于同一条直线的两条直线互相平行；3、利用直线与平面平行的性质定理：直线和平面平行，经过该直线的平面与已知平面相交，则该直线和交线平行；4、利用平面和平面平行的性质定理：两个平面互相平行，和第三个平面相交，它们的交线互相平行；5、利用直线和平面垂直的性质：垂直于同一个平面的两条直线互相平行；6、利用直线和平面平行的性质：一直线和两相交平面平行，则该直线和这两个平面的交线平行。

（二）直线与平面平行的判定方法1、利用定义：直线与平面无公共点，则该直线和该平面平行；2、利用直线与平面平行的判定定理：平面外一条直线和平面内一条直线平行，则该直线和该平面平行（线线平行，则线面平行）。

3、利用平面和平面平行的性质：两个平面互相平行，则一个平面内任意一条直线都平行于第二个平面。

（三）平面和平面平行的判定方法1、利用定义：两个平面没有公共点，则这两个平面平行；2、利用平面与平面平行的判定定理：一个平面内有两条相交直线分别与另一个平面内两条相交直线平行，则这两个平面平行；3、利用平面与平面平行的判定：一个平面内有两条相交直线分别平行于另一个平面，则这两个平面平行；4、利用平面与平面平行的传递性：平行于同一个平面的两个平面互相平行．5、利用直线与平面垂直的性质：垂直于同一条直线的两个平面互相平行；（四）直线与平面平行的性质1、性质定理：直线和平面平行，经过该直线的平面与已知平面相交，则该直线和交线平行；2、直线和平面平行的性质：一直线和两相交平面平行，则该直线和这两个平面的交线平行。

（五）平面与平面平行的性质1、平面与平面平行的性质定理：如果两个平行平面同时与第三个平面相交，那么它们的交线平行。

2、平面与平面平行的性质：两个平面互相平行，则一个平面内任意一条直线均平行于第二个平面。

平行线与平面的关系知识点总结平行线与平面是几何学中重要的基本概念，它们之间有着密切的关系。

本文将对平行线与平面的相关知识点进行总结。

一、基本定义平行线：在平面内，如果两条直线在同一个平面内永不相交，则它们是平行线。

平面：平面是由无数平行线构成的。

平面也可以用一个曲面无限延伸在空间中形成。

二、平行线的性质1. 平行线的唯一性：在平面内，通过一点可以且只可以画出一条与已知直线平行的直线。

2. 平行线的传递性：若直线l与m平行，m与n平行，则l与n平行。

3. 平行线的对应角性质：当两条直线被一条截线所切割时，所得到的对应角相等。

4. 平行线的同位角性质：当两条直线被一条截线所切割时，所得到的同位角相等。

三、平行线与平面的关系1. 平行线与平面的交点：平行线与同一个平面相交于无穷远点。

2. 平面与平行线的位置关系：一个平面内的两条平行线，它们所在的平面也平行于它们。

四、平行线与平面的判定方法平行线与平面的判定方法主要有以下几种：1. 垂直线判定法：若一条直线与平面内一直线垂直，则该直线与该平面上的另一条直线平行。

2. 平行线判定法：当两线的斜率相等且截距不相等时，可以确定两条线平行。

3. 同一平面内两直线垂直于同一直线时，这两直线平行。

4. 平面内有两直线和另一条直线垂直，则这两直线平行。

五、平面与平面之间的关系平面与平面之间的关系主要有以下几种情况：1. 平面平行于另一平面。

2. 平面垂直于另一平面。

3. 平面与平面之间存在夹角。

六、应用示例平行线与平面的概念和性质在实际应用中具有广泛的运用。

以下是一些应用示例：1. 在建筑设计中，需要考虑平行线与平面的关系，以确定建筑物的结构和平面布局。

2. 在地图测量和导航系统中，平行线和平面的概念被用于确定地理位置和路线规划。

3. 在工程制图和机械设计中，平行线与平面的关系用于确定零件位置和装配要求。

综上所述，平行线与平面是几何学中的重要概念，它们之间有着密切的关系。

空间几何中的平行与垂直关系空间几何是研究空间中点、线、面及其相关性质和关系的数学学科。

在空间几何中，平行和垂直是两个基本的关系。

本文将介绍平行和垂直的概念、性质以及它们在空间几何中的应用。

一、平行关系平行是指两条直线或两个面永远不会相交的关系。

在空间几何中，我们可以通过以下方式判断两条直线是否平行：1. 直线的斜率相等：如果两条直线的斜率相等，那么它们是平行的。

这是因为两条直线的斜率相等，意味着它们的倾斜角度相同，在空间中永远不会相交。

2. 直线的方向向量平行：如果两条直线的方向向量平行，那么它们是平行的。

我们可以通过计算两条直线的方向向量，并判断它们是否平行。

3. 直线的截距比相等：如果两条直线的截距比相等，那么它们是平行的。

我们可以通过计算两条直线的截距比，并判断它们是否相等。

平行的性质：1. 平行具有传递性：如果直线l1与直线l2平行，直线l2与直线l3平行，那么直线l1与直线l3平行。

2. 平行具有对称性：如果直线l1与直线l2平行，那么直线l2与直线l1平行。

平行的应用：1. 平行线在平面图形中的应用：平行线在平面图形中有着重要的应用，如矩形、平行四边形等。

在这些图形中，平行线的存在使得我们可以推导出图形的性质和定理。

2. 平行线在建筑设计中的应用：建筑设计中常常需要使用平行线来确定建筑物的边界、墙壁等。

二、垂直关系垂直是指两条直线或两个面之间存在直角的关系。

在空间几何中，我们可以通过以下方式判断两条直线是否垂直：1. 直线斜率之积为-1：如果两条直线的斜率之积为-1，那么它们是垂直的。

这是因为两条直线的斜率之积为-1，意味着它们相互垂直。

2. 直线的方向向量垂直：如果两条直线的方向向量垂直，那么它们是垂直的。

我们可以通过计算两条直线的方向向量，并判断它们是否垂直。

3. 直线的斜率之和为0：如果两条直线的斜率之和为0，那么它们是垂直的。

这是因为两条直线的斜率之和为0，意味着它们相互垂直。

空间平行方法总结
平行关系：线线平行、线面平行、面面平行
线线平行：两直线平行必定共面，所以线线平行问题在空间中只是作为证明线面平行或者面面平行的工具使用，不会直接考查。

常见的线线平行有：（1）平行四边形对边平行；（2）三角形的中位线平行对应边；（3）两平行平面与第三个平面相交，则两条交线平行（面面平行的性质定理）；（4）垂直于同一平面的两直线平行；（5）如果一条直线和一个平面平行，经过这条直线的平面和这条直线相交，那么这条直线和交线平行（线面平行的性质定理）；（6）平行的传递性；
线面平行：线面平行判定定理为，平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

所以线面平行的核心归结为证明线线平行。

面面平行：面面平行的判定定理为，一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

既证明两平面平行只需证明两条相交线与一个平面平行即可，所以面面垂直归结为线线垂直。

总结：在空间平行关系中主要为:线线平行、线面平行、面面平行，考查题目主要类型为线面平行和面面平行，面面平行通过证明两组线面平行，线面平行通过证明线线平行，所以要熟练掌握线线平行的证明，也是空间中平行的核心内容。

空间中的平行一、知识梳理<一>线线平行与线面平行1.线线平行：定义：空间中两直线共面且没有交点，则两直线平行.证明两直线平行的主要方法是：①三角形中位线平行并等于底边的一半；②平行四边形两组对边分别平行；③梯形的一组对边平行；④直线平行的传递性：若a//b,b//c,则a//c.2.线面平行定义：若直线和平面没有交点，则称直线和平面平行.判定1：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.（只需在平面内找一条直线和平面外的直线平行就可以）////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭判定2:两平面平行，一平面上的任一条直线与另一个平面平行.a a a a αβαββααβ⇒⇒⊂⊂⎫⎫⎬⎬⎭⎭或线面平行的性质：如果一条直线平行于一个平面，经过这条直线的平面与这个平面相交，那么这条直线和它们的交线平行.<二>面面平行1.定义：若两个平面没有交点，则两个平面平行2.判断：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行.,,a b a b A a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭,,,a b a b A a a b b a b ααββ⊂⎫⎪=⎪⇒⎬''⎪⎪''⊂⎭判定定理的推论： 一个平面内的两条相交直线与另一个平面上的两条直线分别平行，两平面平行.3.两平面平行的性质： 性质Ⅰ：如果一个平面与两平行平面都相交，那么它们的交线平行.a ab b αβαγβγ=⇒=⎫⎪⎬⎪⎭性质Ⅱ：平行于同一平面的两平面平行；性质Ⅲ：夹在两平行平面间的平行线段相等；,,A C AC BD B D AB CD αβαβ∈⇒=∈⎫⎪⎪⎬⎪⎪⎭二、典例精析【例1】如图所示的几何体中，△ABC 是任意三角形，AE ∥CD ，且AE ＝AB ＝2a ，CD ＝a ，F 为BE 的中点．求证：DF ∥平面ABC .【练习】如图，已知P 是平行四边形ABCD 所在平面外一点，M 、N 分别是AB 、PC 的中点．求证：MN ∥平面P AD .【例2】已知正方形ABCD 所在的平面和正方形ABEF 所在的平面相交与AB ，M 、N 分别是AC 、BF 上的中点.求证：MN//平面BCE .【练习】如图，在四棱锥P-ABCD 中，底面ABCD 为矩形，E 为PD 的上一点，且PE=2ED ．若F 为PE 的中点.求证：BF ∥平面AEC .【例3】如图，四棱锥P-ABCD 中，底面ABCD 为梯形，AB ∥DC ，AB ⊥BC ．AB =BC=22AD ，点E 在棱PB 上，且PE=2EB ．求证：PD ∥平面EAC .【练习】如图，正四棱锥P-ABCD 中，PA=AB ，点M ，N 分别在PA ，BD 上，且31==BD BN PA PM .求证：MN ∥平面PBC .2【例4】a ，b ，c 为三条不重合的直线，α，β，γ为三个不重合平面，现给出六个命题①a ∥c ，b ∥c ⇒a ∥b ②a ∥γ ，b ∥γ ⇒a ∥b ③α∥c ，β∥c ⇒α∥β④ α∥γ ，β∥γ ⇒α∥β ⑤α∥c ，a ∥c ⇒α∥a ⑥α∥γ ，a ∥γ ⇒α∥a其中正确的命题是（ ）A.①②③⑥ B ．①④⑤ C ．①④ D ．①④⑥【练习】下面六个命题中正确命题的个数是（ ）①如果a 、b 是两条直线，b a //，那么a 平行于经过b 的任何一个平面；②如果直线a 和平面α满足a //α,那么a 与平面α内的任何一条直线平行；③如果直线a //α,b //α,那么b a //；④如果直线a 、b 和平面α满足b a //，a //α，α⊄b ，那么b //α；⑤如果直线a 与平面α上的无数条直线平行，则a //α；⑥如果平面α的同侧有两点A 、B 到平面α的距离相等，则AB //α.A. 0B. 1C. 2D. 3【例5】一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（ ）A ．异面B ．相交C ．平行D ．不能确定【练习】直线a //平面α，α内有n 条直线交于一点，这n 条直线直线中与直线a 平行的直线（ ）A.至少有一条 B ．至多有一条 C ．有且只有一条 D ．没有三、课后练习1．已知直线a ∥平面α，P α∈，那么过点P 且平行于α的直线（ ）A ．只有一条，不在平面α内B ．有无数条，不一定在α内C ．只有一条，且在平面α内D ．有无数条，一定在α内 2．若夹在两个平面间的三条平行线段相等，则这两个平面位置关系是（ ）A ．平行B ．相交C ．相交或平行D ．以上答案都不对3．下列结论中正确的是（ ） ①α∥β，β∥γ，则α∥γ；②过平面外一条直线有且只有一个平面与已知平面平行；③平面外的两条平行线中，如果有一条和平面平行，那么另一条也和这个平面平行；④如果一条直线与两个平行平面中一个相交，那么它与另一个必相交.A ．①②③B ．②③④C ．①③④D ．①②③④4．a ，b 是两条异面直线，A 是不在a ，b 上的点，则下列结论成立的是( )A ．过A 且平行于a 和b 的平面可能不存在B ．过A 有且只有一个平面平行于a 和bC ．过A 至少有一个平面平行于a 和bD ．过A 有无数个平面平行于a 和b5．如果平面α外有两点A 、B ，它们到平面α的距离都是a ，则直线AB 和平面α的位置关系是( )A ．平行B ．相交C ．平行或相交D ．AB ⊂α6.如图所示，在棱长为a 的正方体1111ABCD A BC D -中，E ，F ，P ，Q 分别是BC ，11C D ，1AD ，BD 的中点.(1)求证：PQ //平面11DCC D ；(2)在DC 上找一点H ，使EFH //平面11BB D D .7.如图，在空间四边形ABCD 中，P 、Q 分别是ABC ∆和BCD ∆的重心.求证：PQ ∥平面ACD .8.如图所示，已知三棱锥BCD A -被一平面所截，截面为平行四边形EFGH ，求证：（1）//EF 平面BCD ；（2）CD EF //.。

空间中的平行与垂直关系一、知识梳理1、 平行关系（1）直线与平面平行的判定定义：直线与平面没有公共点，称这条直线与这个平面平行。

判定定理：若l α⊄，a α⊂，l ∥a ，则l ∥α。

（2）直线与平面的平行性质定理：判定定理：若l ∥α，l β⊂，a αβ=，则l ∥a 。

（3）平面与平面的平行的判定定义：没有公共点的两个平面叫做平行平面。

判定定理1：若, a b αα⊂⊂，a b P =，a ∥β，b ∥β，则α∥β；判定定理2：若, l l αβ⊥⊥，则α∥β；判定定理3：若α∥β，β∥γ，则α∥γ。

（4）平面与平面的平行性质定理：性质定理1：若α∥β，a α⊂，则a ∥β；性质定理2：若α∥β，且a γα=，b γβ=，则a ∥b ；性质定理3：若α∥β，且l α⊥，则l β⊥。

2、补充结论：如果一个平面内的两条相交直线分别平行于另一个平面内的两条直线，那么这两个平面平行。

3、线线平行的常用证明方法（1）利用平面几何的结论，如三角形的中位线平行于底边、平行四边形的对边平行、利用比例，等；（2）利用公理4：平行于同一条直线的两条直线平行；（3）利用线面平行的性质定理、面面平行的性质定理、线面垂直的性质定理4、垂直关系（1）直线与平面垂直的判定定义：如果一条直线和一个平面相交，并且和这个平面内的所有直线垂直。

判定定理：若, , m n mn P αα⊂⊂=，, l m l n ⊥⊥，则l α⊥。

（2）直线与平面的垂直性质定理：符号表示：若l α⊥，对任意的a α⊂，都有l a ⊥。

（3）平面与平面的垂直的判定定义：两个平面所成的二面角为直角，那么这两个平面垂直。

判定定理：若, a a αβ⊂⊥，则l α⊥。

（4）平面与平面的垂直性质定理：性质定理1：若, , , l a a l αβαβα⊂=⊂⊥，则a β⊥。

性质定理2：若, , l αβαγβγ=⊥⊥，则l γ⊥。

5、补充定理（1）若, l αα⊥∥β，则l β⊥；（2）若, l a α⊥∥l ，则a α⊥。

知识点一 基本事实4平行于同一条直线的两条直线平行． 知识点二 等角定理如果空间中两个角的两条边分别对应平行，那么这两个角相等或互补．如图，空间四边形ABCD 中，E ，F 分别是AB ，AD 边上的中点，G ，H 分别是BC ，CD 边上的点，且CG GB ＝CH HD ＝12 .求证：四边形GHFE 是梯形．知识点 直线与平面平行位置关系定理符号表示 图形表示线 面 平 行判定如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行⎭⎪⎬⎪⎫a ∥b a ⊄αb ⊂α ⇒a ∥α性质 一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直线与交线平行⎭⎪⎬⎪⎫a ∥αa ⊂βa ∩β＝b ⇒a ∥b[线线平行 ――――――→在平面内作或找一直线 线面平行 ――――――――→经过直线作或找平面与平面的交线线线平行 (1)如果一条直线和平面内一条直线平行，那么这条直线和这个平面平行．( ) (2)若直线l 上有两点到平面α的距离相等，则l ∥平面α.( )(3)若直线l 与平面α平行，则l 与平面α内的任意一条直线平行．( ) (4)若直线a ∥平面α，直线a ∥直线b ，则直线b ∥平面α.( )(5)若直线a ∥平面α，则直线a 与平面α内任意一条直线都无公共点．( ) 2．能保证直线a 与平面α平行的条件是( ) A ．b ⊂α，a ∥b B ．b ⊂α，c ∥α，a ∥b ，a ∥cC ．b ⊂α，A ，B ∈a ，C ，D ∈b ，且AC ∥BD D ．a ⊄α，b ⊂α，a ∥b3.如图，四棱锥P -ABCD 中，M ，N 分别为AC ，PC 上的点，且MN ∥平面P AD ，则( ) A ．MN ∥PDB ．MN ∥P AC ．MN ∥AD D ．以上均有可能4.若在四棱锥S -ABCD 中，底面ABCD 为平行四边形，E 是SA 上的一点，当点E 满足条件________时，SC ∥平面EBD .探究点一 直线与平面平行的判定如图，四边形ABCD 是平行四边形，P 是平面ABCD 外一点，M ，N 分别是AB ，PC 的中点．求证：MN ∥平面P AD .应用判定定理证明线面平行的步骤 如图所示，在三棱柱ABC -A 1B 1C 1中，点D 是AB 的中点．求证：AC 1∥平面CDB 1.探究点二 直线与平面平行性质的应用角度一证明问题如图，P是平行四边形ABCD所在平面外的一点，M是PC的中点，在DM上取一点G，过点G和AP作平面，交平面BDM于GH.求证：AP∥GH.应用线面平行的性质定理解题的步骤角度二计算问题如图，在四棱锥S-ABCD中，底面ABCD是菱形，点E是棱AD的中点，点F在棱SC上，且SFSC＝λ，SA∥平面BEF.求实数λ的值．1．如图，用平行于四面体ABCD的一组对棱AB，CD的平面截此四面体．求证：截面MNPQ是平行四边形．2．如图，在正方体ABCD-A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上，若EF∥平面AB1C，求线段EF的长度．探究点三直线与平面平行的判定、性质定理的综合应用如图所示，AB是圆O的直径，点C是圆O上异于A，B的点，P为平面ABC外一点，E，F分别是P A，PC的中点．记平面BEF与平面ABC的交线为l.求证：直线l∥平面P AC.如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．求证：AB∥平面EFGH.1．圆台底面内的任意一条直径与另一个底面的位置关系是()A．平行B．相交C．在平面内D．不确定2．(多选)在梯形ABCD中，AB∥CD，AB⊂平面α，CD⊄平面α，则直线CD与平面α内的直线的位置关系可能是()A．平行B．异面C．相交D．共面3．已知m，n是平面α外的两条直线，给出下列三个论断：①m∥n；②m∥α；③n∥α.以其中两个为条件，余下的一个为结论，写出你认为正确的一个________．1．已知直线a∥平面α，直线b⊂平面α，则()A．a∥b B．a与b异面C．a与b相交D．a与b无公共点4．如图，已知S为四边形ABCD外一点，G，H分别为SB，BD上的点，若GH∥平面SCD，则() A．GH∥SA B．GH∥SD C．GH∥SC D．以上均有可能5.(多选)如图所示，P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，下列四个结论正确的是()A．OM∥PD B．OM∥平面PCD C．OM∥平面PDA D．OM∥平面PB 知识点平面与平面平行位置关系定理符号表示图形表示面面平行判定如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行⎭⎪⎬⎪⎫a⊂β，b⊂βa∥α，b∥αa∩b＝P⇒β∥α性质两个平面平行，如果另一个平面与这两个平面相交，那么两条交线平行⎭⎪⎬⎪⎫α∥βα∩γ＝aβ∩γ＝b⇒a∥b[点拨]在判断与证明空间中的平行关系时要注意线线、线面、面面平行关系的转化过程：1．判断正误(正确的打“√”，错误的打“×”)(1)若平面α∥平面β，l⊂平面β，m⊂平面α，则l∥m.()(2)如果一个平面内有无数条直线与另一个平面平行，那么这两个平面平行．()(3)若α∥β，则平面α内有无数条互相平行的直线平行于平面β.()(4)如果两个平面平行，那么其中一个平面内的直线与另一个平面内的直线异面．()2．已知a，b，c，d是四条直线，α，β是两个不重合的平面，若a∥b∥c∥d，a⊂α，b⊂α，c⊂β，d⊂β，则α与β的位置关系是()A．平行B．相交C．平行或相交D．以上都不对3．已知长方体ABCD-A′B′C′D′，平面α∩平面ABCD＝EF，平面α∩平面A′B′C′D′＝E′F′，则EF与E′F′的位置关系是()A．平行B．相交C．异面D．不确定4．如图，过正方体ABCD-A1B1C1D1的顶点B1，D1与棱AB的中点P的平面与底面ABCD所在平面的交线记为l，则l与B1D1的位置关系为________．探究点一平面与平面平行的判定如图所示，已知正方体ABCD-A1B1C1D1.(1)求证：平面A1BD∥平面B1D1C；(2)若E，F分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD.探究点二平面与平面平行性质定理的应用角度一证明问题如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD为梯形，AD∥BC，平面A1DCE与B1B交于点E.求证：EC∥A1D.利用平面与平面平行的性质定理的基本步骤角度二计算问题设平面α∥平面β，A，C∈α，B，D∈β，直线AB与CD交于点S，且S位于平面α，β之间，AS＝8，BS＝6，CS＝12，求SD的长．2．如图，已知α∥β，点P是平面α，β外的一点(不在α与β之间)，直线PB，PD分别与α，β相交于点A，B和C，D.(1)求证：AC∥BD；(2)已知P A＝4 cm，AB＝5 cm，PC＝3 cm，求PD的长；(3)若点P在α与β之间，试在(2)的条件下求CD的长．探究点三平行关系的综合问题如图所示，P为▱ABCD所在平面外一点，M，N分别为AB，PC的中点，平面P AD∩平面PBC＝l.(1)求证：BC∥l.(2)判断MN与平面P AD是否平行？并证明你的结论．1．下列说法正确的个数是()①两平面平行，夹在两平面间的平行线段相等；②两平面平行，夹在两平面间的相等的线段平行；③如果一条直线和两个平行平面中的一个平行，那么它和另一个平面也平行；④平行直线被三个平行平面截得的线段对应成比例．A．1B．2C．3D．42．平面α∥平面β，点A，C∈α，B，D∈β，则直线AC∥直线BD的充要条件是()A．AB∥CD B．AD∥CB C．AB与CD相交D．A，B，C，D四点共面1．已知平面α∥平面β，a⊂α，b⊂β，则直线a，b的位置关系是()A．平行B．相交C．异面D．平行或异面2．已知平面α∥平面β，直线a∥平面α，直线b∥平面β，则a与b的位置关系可能是()A．平行或相交B．相交或异C．平行或异面D．平行、相交或异面3．在长方体ABCD-A1B1C1D1中，E，F，G，H分别为棱A1B1，BB1，CC1，C1D1的中点，则下列结论中正确的是()A．平面AA1D1D∥平面EFGH B．BD1∥GH C．BD∥EF D．平面EFGH∥平面A1BCD16．已知a，b表示两条直线，α，β，γ表示三个不重合的平面，给出下列命题：①若α∩γ＝a，β∩γ＝b，且a∥b，则α∥β；②若a，b相交且都在α，β外，a∥α，b∥β，则α∥β；③若a∥α，a∥β，则α∥β；④若a⊂α，a∥β，α∩β＝b，则a∥b.其中正确的是________．(填序号)9．如图所示，在长方体ABCD-A1B1C1D1中，E，F，G，H，分别是BC，CC1，C1D1，A1A的中点，求证：(1)EG∥平面BB1D1D；(2)平面BDF∥平面B1D1H.。