样本函数与统计量
- 格式：ppt
- 大小：381.01 KB
- 文档页数：14
下载文档原格式
合集下载
第五章《概率论与数理统计教程》课件
试决定常数 3.
X ,Y
C
使得随机变量 cY 服从分布
2
分布。
相互独立，都与 N ( 0 , 9 ) 有相同分布， X 分别是来自总体
X ,Y
1
, X 2 , , X 9和
Y1 ,Y 2 , ,Y 9
的样本，
Z
9
X
i
i1
6 - 23
Y
i1
9
则Z 服从—— ，自由度为——。
2 i
4.
X1, X 2, X 3, X 4
是来自总体
X ~ N ( , )
2
的样本，则随机变
量 Y
X3 X4
服从——分布，其自由度为———。
2
(X i )
i1
2
5.
设
X 1 , X 2 , , X 10
是来自总体 X
~ N ( ,4 )
2
的样本， ( S 2 P
a ) 0 .1
一. 单个正态总体的统计量的分布
X 1 , X 2 , X n是来自正态总体 ~ N ( , 2 )的样本, X
X , S 分别是样本均值和样本 方差
2
定理1
X
n
1
n
X i ~ N ( ,
n
2
);
i1
定理2 U
1
X
/
~ N ( 0 ,1 );
n
定理3
6 - 18
定理7
当 1
2
2 2
2 2 时, 令 S w
( n1 1) S 1 ( n 2 1) S 2
2
样本和统计量
样本和统计量1. 样本空间随机试验E的所有基本结果组成的集合为E的样本空间。
样本空间中的数据元素具有唯⼀性，不能重复。
2. 总体所研究对象的某项数量指标取值的全体称为总体，⽤随机变量X表⽰。
⽐如我们要研究亚洲⼈的⾝⾼分布，那所有亚洲⼈的⾝⾼数据就构成总体。
总体中数据个数⼤于等于样本空间中的数据个数，⽐如 100 个⼈⾝⾼全为 2m，那么总体就是 100 个 2m，⽽样本空间就只有⼀个2m。
3. 个体总体中的⼀个元素称为个体。
⽐如某⼀个⼈的⾝⾼。
4. 简单随机样本由于总体太过庞⼤，我们总不能真的统计全部亚洲⼈的⾝⾼，于是我们采⽤抽样的⼿段，在亚洲⼈中抽出 10000 ⼈，⽤这 10000 ⼈的⾝⾼分布来代表总体的⾝⾼分布，这 10000 次抽样相互独⽴。
我们现在只研究⼀次抽样：假如总体是\left \{ 0.1, 0.2, 0.2, 0.3, 0.3, 0.3 \right \}，那么可以认为我们抽取出的这⼀个⼈有\frac{1}{6}的概率⾝⾼为 0.1，有\frac{1}{3}的概率⾝⾼为 0.2，有\frac{1}{2}的概率⾝⾼为 0.3。
由于每次抽样之前，不会知道抽样的结果，所以⽤⼀个随机变量来表⽰，将这 10000 次的抽样结果记为随机变量X_{1},X_{2},...X_{n}，称为简单随机样本，简称样本，它们的具体观察值x_{1},x_{2},...x_{n}称为样本值。
样本与总体同分布,每⼀个个体都是⼀维随机变量,所以样本是多维,总体是⼀维。
这就和投硬币⼀样.投⼀次是⼀维随机变量.投多次是多维随机变量。
注意：总体是概率分布⾓度，是理论上的，样本是统计⾓度，是实际观察到的，两者是不同的。
5. 统计量样本X_{1},X_{2},...X_{n}不含参数的函数T = T(X_{1},X_{2},...X_{n})称为统计量，也称样本统计量。
常见的样本统计量有：样本均值、样本⽅差等。
我们需要认识到样本统计量本⾝也是⼀个随机变量，这是因为每次抽样的结果具有不确定性，即样本具有不确定性，那么样本的函数当然也具有不确定性。
统计量简介
n
X
1 n
Xi
i1
x
1 n
n
xi
i1
S 2 1 n n 1 i1
X X i
2
1 n n 1 i1
X i2 n X
2
s 2 1
n
2
xi x
1
n
x
2 i
n x 2
n 1 i1
n 1 i1
常用的统计量
3. 样本标准差
n
S
S2
1 n 1 i1
Xi X
0;
B2
n 1 S 2. n
2. 若总体X的k阶矩 E X k 存在，则由大数定律有 k
Ak P k
(k 1, 2,)， B P E X E ( X )k
k
k
(k 1, 2,)
这是下一章矩估计法的理论依据.
童鞋们，课 后记得复习
巩固哦！
统计量
统计量的概念
Def.
设 X1, X 2,, Xn为 总 体 X的 一 个 样 本 ，g是 n元 连 续 函 数 ,
若 g X 1 , X 2 , , X n 中 不 含 任 何 未 知 参 数 ， 则 称 样 本 函
数 g ( X 1 , X 2 , , X n )为 统 计 量 .
Note: 1. 统计量实质上是特殊地样本函数.
2
其观测值 为
4. 样本k 阶原点矩
Ak
1 n
n
X
k i
,
i1
其观测值为
k 1,2,
5.样本k阶中心矩 其观测值为
n
B k
1 n
i 1
X X k
i
,
1 n
统计量
2
12
)
5
0.2923
几个常用的统计量
样本均值
X
1 n
n i 1
Xi
样本方差
S 2
1 n 1
n i பைடு நூலகம்1
(Xi
X )2
样本均方差
S
1 n 1
n i 1
(Xi
X
)2
样本k阶原点矩
Ak
1 n
n i 1
X
k i
k 1,2,
样本k阶中心矩
Bk
1 n
解：P (max(X1, X 2 X5 ) 15) 1 P( X1 15, X 2 15, X5 15)
1 P( X1 15)P( X 2 15)P( X 5 15)
1 P( X 15)5 1 F (15)5
1
(15
1 P (min(X1, X 2 X n ) x) 1 P( X1 x, X 2 x, X n x)
1 P(X1 x)P(X 2 x)P(X n x)
1 1 F (x)n
例.从 总 体N (12,4)中 随 机 抽 取 一 容 量 为5的 样 本 X1, X 2, X3, X 4, X 5,求P{max(X1, X 2, X3, X 4, X 5 ) 15}
(1.7143) (1.1429) 0.8239
P157 X ~ N(72 ,100),为使样本均值大于70
的概率不小于90%,则样本容量至少取多少?
解 设样本容量为 n , 则 X ~ N (72,100)
故 P(X 70) 1 P(X 70)
样本及其抽样分布基本概念
概率论与数理统计优质学案
第六章
样本及抽样分布
第1，2节 基本概念
一、总体、个体 二、随机样本、直方图 三、样本函数与统计量 四、小结
一、总体与个体
一个统计问题总有它明确的研究对象.
研究对象的全体称为总体(母体)， 总体中每个成员称为个体.
总体
总体 …
研究某批灯泡的心每个 个体的一项(或几项)数量指标和该数量指标 在总体中的分布情况. 这时，每个个体具有 的数量指标的全体就是总体.
直方图
5
8
4.5
7
4 6
3.5 5
3
2.5
4
2
3
1.5 2
1
1 0.5
0
0
140
150
160
170
180
190
200
147
157
167
177
187
197
三、统计量
由样本推断总体特征,需要对样本进行 “加工”,“提炼”.这就需要构造一些样本的 函数,它把样本中所含的信息集中起来.
1. 代表性： X1,X2,…, Xn中每一个与所考察的 总体X有相同的分布. 2. 独立性： X1,X2,…, Xn是相互独立的随机变量.
满足上述两条性质的样本称为简单随机样本. 获得简单随机样本的抽样方法称为简单随机抽样.
为了使大家对总体和样本有一个明确的 概念,我们给出如下定义:
定义 一个随机变量X或其相应的分布 函数F(x)称为一个总体.
4. 直方图 4.1 频数--频率分布表
样本数据的整理是统计研究的基础，整理数据的最 常用方法之一是给出其频数分布表或频率分布表。
例3 为研究某厂工人生产某种产品的能力， 我们随机调查了20位工人某天生产的该种产品 的数量，数据如下
第六章
样本及抽样分布
第1，2节 基本概念
一、总体、个体 二、随机样本、直方图 三、样本函数与统计量 四、小结
一、总体与个体
一个统计问题总有它明确的研究对象.
研究对象的全体称为总体(母体)， 总体中每个成员称为个体.
总体
总体 …
研究某批灯泡的心每个 个体的一项(或几项)数量指标和该数量指标 在总体中的分布情况. 这时，每个个体具有 的数量指标的全体就是总体.
直方图
5
8
4.5
7
4 6
3.5 5
3
2.5
4
2
3
1.5 2
1
1 0.5
0
0
140
150
160
170
180
190
200
147
157
167
177
187
197
三、统计量
由样本推断总体特征,需要对样本进行 “加工”,“提炼”.这就需要构造一些样本的 函数,它把样本中所含的信息集中起来.
1. 代表性： X1,X2,…, Xn中每一个与所考察的 总体X有相同的分布. 2. 独立性： X1,X2,…, Xn是相互独立的随机变量.
满足上述两条性质的样本称为简单随机样本. 获得简单随机样本的抽样方法称为简单随机抽样.
为了使大家对总体和样本有一个明确的 概念,我们给出如下定义:
定义 一个随机变量X或其相应的分布 函数F(x)称为一个总体.
4. 直方图 4.1 频数--频率分布表
样本数据的整理是统计研究的基础，整理数据的最 常用方法之一是给出其频数分布表或频率分布表。
例3 为研究某厂工人生产某种产品的能力， 我们随机调查了20位工人某天生产的该种产品 的数量，数据如下
概率论与数理统计第6章
第六章6.4 在例6.2.3 中, 设每箱装n 瓶洗净剂. 若想要n 瓶灌装量的平均阻值与标定值相差不超 过0.3毫升的概率近似为95%, 请问n 至少应该等于多少？ 解：因为1)3.0(2)/3.0|/(|)3.0|(|-Φ≈<-=<-n nnX P X P σσμμ依题意有,95.01)3.0(2=-Φn ，即)96.1(975.0)3.0(Φ==Φn于是 96.13.0=n ，解之得 7.42=n 所以n 应至少等于43.6.5 假设某种类型的电阻器的阻值服从均值 μ=200 欧姆， 标准差σ=10 欧姆的分布, 在一个电子线路中使用了25个这样的电阻.（1) 求这25个电阻平均阻值落在199 到202 欧姆之间的概率; （2) 求这25个电阻总阻值不超过5100 欧姆的概率. 解:由抽样分布定理，知nX /σμ-近似服从标准正态分布N （0，1)，因此(1) )25/10200199()25/10200202()202199(-Φ--Φ≈≤≤X P)5.0(1)1()5.0()1(Φ+-Φ=-Φ-Φ=5328.06915.018413.0=+-= (2) )204()255100()5100(≤=≤=≤X P X P X n P 9772.0)2()25/10200204(=Φ=-Φ≈6。
8 设总体X ~N （150,252), 现在从中抽取样本大小为25的样本, {140147.5}P X ≤≤。
解： 已知150=μ，25=σ，25=n ，)25/25150140()25/251505.147()5.147140(-Φ--Φ≈≤≤X P)5.0()2()2()5.0(Φ-Φ=-Φ--Φ= 2857.09615.09772.0=-=第六章《样本与统计量》定理、公式、公理小结及补充：。
数理统计--参数估计、假设检验、方差分析(李志强) (3)讲解
教学单元案例： 参数估计与假设检验北京化工大学 李志强教学内容：统计量、抽样分布及其基本性质、点估计、区间估计、假设检验、方差分析 教学目的：统计概念及统计推断方法的引入和应用（1）理解总体、样本和统计量等基本概念；了解常用的抽样分布；（2）熟练掌握矩估计和极大似然估计等方法； （3）掌握求区间估计的基本方法； （4）掌握进行假设检验的基本方法； (5) 掌握进行方差分析的基本方法；（6）了解求区间估计、假设检验和方差分析的MA TLAB 命令。
教学难点：区间估计、假设检验、方差分析的性质和求法 教学时间：150分钟教学对象：大一各专业皆可用一、统计问题 引例例1 已知小麦亩产服从正态分布，传统小麦品种平均亩产800斤，现有新品种产量未知，试种10块，每块一亩，产量为：775,816,834,836,858,863,873,877,885,901问：新产品亩产是否超过了800斤？例2 设有一组来自正态总体),(2σμN 的样本0.497, 0.506, 0.518, 0.524, 0.488, 0.510, 0.510, 0.512. (i) 已知2σ=0.012，求μ的95%置信区间； (ii) 未知2σ，求μ的95%置信区间； (iii)求2σ的95%置信区间。
例3现有某型号的电池三批, 分别为甲乙丙3个厂生产的, 为评比其质量, 各随机抽取5只电池进行寿命测试, 数据如下表示, 这里假设第i 种电池的寿命),(.~2σμi i N X .(1) 试在检验水平下,检验电池的平均寿命有无显著差异? (2) 利用区间估计或假设检验比较哪个寿命最短.二 统计的基本概念: 总体、个体和样本（1）总体与样本总体 在数理统计中,我们将研究对象的某项数量指标的值的全体称为总体,总体中的每个元素称为个体比如，对电子元件我们主要关心的是其使用寿命.而该厂生产的所有电子元件的使用寿命取值的全体，就构成了研究对象的全体，即总体，显然它是一个随机变量，常用X 表示 为方便起见，今后我们把总体与随机变量X 等同起来看，即总体就是某随机变量X 可能取值的全体.它客观上存在一个分布，但我们对其分布一无所知，或部分未知，正因为如此，才有必要对总体进行研究.简单随机样本对总体进行研究，首先需要获取总体的有关信息. 一般采用两种方法：一是全面调查.如人口普查，该方法常要消耗大量的人力、物力、财力.有时甚至是不可能的，如测试某厂生产的所有电子元件的使用寿命. 二是抽样调查. 抽样调查是按照一定的方法，从总体X 中抽取n 个个体.这是我们对总体掌握的信息.数理统计就是要利用这一信息，对总体进行分析、估计、推断.因此，要求抽取的这n 个个体应具有很好的代表性.按机会均等的原则随机地从客观存在的总体中抽取一些个体进行观察或测试的过程称为随机抽样.从总体中抽出的部分个体,叫做总体的一个样本.从总体中抽取样本时,不仅要求每一个个体被抽到的机会均等,同时还要求每次的抽取是独立的,即每次抽样的结果不影响其他各次的抽样结果,同时也不受其他各次抽样结果的影响.这种抽样方法称为简单随机抽样.由简单随机抽样得到的样本叫做简单随机样本.往后如不作特别说明,提到“样本”总是指简单随机样本.从总体X 中抽取一个个体,就是对随机变量X 进行一次试验.抽取n 个个体就是对随机变量X 进行n 次试验,分别记为X1,X2,…,Xn.则样本就是n 维随机变量(X1,X2,…,Xn).在一次抽样以后, (X1,X2,…,Xn)就有了一组确定的值(x1,x2,…,xn),称为样本观测值.样本观测值(x1,x2,…,xn)可以看着一个随机试验的一个结果,它的一切可能结果的全体构成一个样本空间,称为子样空间.（2）样本函数与统计量设n x x x ,,,21 为总体的一个样本，称ϕϕ= （n x x x ,,,21 ）为样本函数，其中ϕ为一个连续函数。
概率论数理统计基础知识第五章
C
]
（A）Y ~ 2 (n). （B）Y ~ 2 (n 1). （C）Y ~ F (n,1). （D）Y ~ F (1, n).
【例】设 随机变量X和Y都服从标准正态分布，则[ C ]
（A）X+Y服从正态分布.
2 2 2
（B）X2 +Y2服从 2分布. Y
2
2 X （C）X 和Y 都服从 分布. （D）
(X ) ~ t ( n 1) S n
客、考点 10，正态总体的抽样分布
33/33
34/33
35/33
【例】设总体 X ~ N (0,1)，X 1 , X 2 , X1 X 2
2 2 X3 X4
, X n 是简单随机
2 X i. i 4 n
样本 , 试问下列统计量服从什么分布？ （1 ） ; （2 ） n 1X1
记：F分布是两个卡方分布的商
2. F 分布的上侧分位数
设 F ~ F (k1 , k2 ) ，对于给定的 a (0,1) ，称满足条件
P{F Fa (k1 , k2 )}
Fa ( k1 ,k2 )
f F ( x)dx a
的数 Fa (k1 , k2 ) 为F 分布的上侧a 分位数。
服从F分布.
§5.5 正态总体统计量的分布
一、单个正态总体情形 总体
X ~ N ( , 2 ) ，样本 X1 , X 2 , , Xn ，
1 n 样本均值 X X i n i 1
n 1 2 样本方差 S 2 ( X X ) i n 1 i 1
1. 定理1 若设总体X~N(μ,σ2), 则统计量
有一约束条件
(X
i 1
解释总体与样本、参数和统计量的含义
总体与样本、参数和统计量1. 介绍在统计学中，研究对象通常被称为总体。
总体是指研究者感兴趣的特定群体或现象，可以是人群、产品、事件等。
然而，由于取得总体数据的成本和时间都非常昂贵，因此研究者经常只能从总体中选择一部分数据进行分析，这部分数据被称为样本。
样本是总体的一个子集，它代表了总体的某些特征。
通过对样本进行研究和分析，研究者可以得出关于总体的结论或推断，以及对总体未知特征的估计。
2. 参数和统计量2.1 参数参数是描述总体特征的数值度量，它通常用希腊字母来表示。
例如，总体的平均值用μ表示，总体的标准差用σ表示。
参数是基于总体数据的固定值。
以人群身高为例，如果我们想了解某人群的平均身高，将全体人群的身高加起来再除以总人数就是该人群平均身高的参数。
2.2 统计量为了对总体进行研究和推断，我们需要从样本中计算数值度量，这些度量被称为统计量。
统计量是基于样本数据计算得到的，用拉丁字母来表示。
以人群身高为例，从人群中抽取一个样本，计算样本的平均身高作为样本的平均身高统计量。
样本统计量是样本数据的函数，通过样本研究和推断可以估计总体的参数。
3. 总体与样本的关系总体和样本是密切相关的，通过样本可以了解总体的特征。
在实际研究中，样本是从总体中随机选取的，因此样本应该能够代表总体。
样本收集需要注意一些问题，如样本的大小和抽样方法的合理性。
样本大小对于统计推断的准确性非常重要。
样本越大，通常可以提供更准确的估计和推断。
抽样方法的合理性涉及到随机性和无偏性的问题，确保选择的样本能够代表总体。
总体和样本之间的关系可以用下式表示：总体数据→ 样本选择→ 样本数据→ 统计量计算→ 参数估计和推断→ 总体特征估计和推断4. 参数估计和假设检验通过样本统计量，我们可以对总体参数进行估计和推断。
常见的估计方法包括点估计和区间估计。
点估计是使用样本统计量直接估计总体参数的数值。
例如，样本的平均值可以作为总体平均值的点估计。
然而，点估计存在估计误差的问题，可能导致估计结果偏离真实参数。
几种常用统计量的分布
P{
χ2
χ
2 a
(n)
}
f
a2 (n)
x dx a
的点χa 2(n)称为 χ2 分布单侧 分位点或双侧临界值，如图11-5 所示 .
图11-5
几种常用统计量的分布
定义4
设X ~ N ( ， 2 ) ，样本方差为S 2，则统计量χ2
(n
1)S 2
2
服从自由度为n
1
的χ 2分布，记作
χ2
n
/ n
几种常用统计量的分布
证明
X ~ N ( ， 2 ) ，( X1.，X 2 ， ，X n )是来自总体 X 的样本 ，
X
~
N ( ， 2 )(i 1，2 ，
，n) ，其线性函数 X
1 n
n i 1
Xi
也服从正态分布，即
E X
E1 n
n i 1
Xi
1n E
n i1
Xi
1 n n
(
EX i i 1，2
n) ，
1 n
1
DX
D n
i 1
Xi
n2
n
D Xi
i 1
1 n2 2 (
n2
n
X1 ，X 2 ， X n相互独立) ，
则X ~ N ( ， 2 ) ，故 X ~ N (0 ，1) .
n
/ n
几种常用统计量的分布
例1
解
因为总体 X 服从正态分布N 5 ，9 ，所以 X 服从正态分布N (5 ，9 ) ，故
图11-2
几种常用统计量的分布
显然，f x随着n不同而不同，且f x为偶函数 . 当n 时，有
lim f x
统计3：样本和统计量
统计3：样本和统计量统计推断是指，在数理统计中，我们研究的随机变量，其分布是未知的，或者是不完全知道的，⼈们是通过对所研究的随机变量进⾏重复独⽴的观察，得到许多观察值，对这些数据进⾏分析，从⽽对所研究的随机变量的分布做出种种推断。
⼀，随机样本总体和个体在数理统计中，研究对象是某⼀项数量指标（例如，学⽣的⾝⾼，体重等），对这⼀项数量指标进⾏观察。
把试验的全部可能的观察值称为总体，每⼀个可能的观察值称为个体。
总体中的每⼀个个体是随机试验的⼀个观察值，因此，它是某⼀随机变量X的值。
⼀个总体就对应⼀个随机变量X，对总体的研究就是对⼀个随机变量X的研究。
样本在实际中，总体的分布⼀般是未知的，或只知道它具有某种形式⽽其中包含了未知参数。
在数理统计中，⼈们都是通过从总体中抽取⼀部分个体，根据获得的数据对总体分布做出推断，被抽出的部分个体叫做总体的⼀个样本。
所谓从总体抽取⼀个个体，就是对总体X进⾏⼀次观察并记录观察结果。
在相同的条件下对总体X进⾏n次重复的，独⽴的观察，把n次观察的结果按照试验的次序记为：X1,X2,...,Xn，由于X1,X2,...,Xn是对随机变量X观察的结果，且各次观察是在相同的条件下独⽴进⾏的，所以有理由认为X1,X2,...,Xn是相互独⽴的，且都与X具有相同分布的随机变量，把X1,X2,...,Xn 称为来⾃总体X的⼀个简单随机样本。
当n次观察⼀经完成，得到⼀组实数x1,x2,...,xn，它们依次是随机变量X1,X2,...,Xn的观察值，称为样本值。
样本定义，设X是具有分布函数F的随机变量，若 X1,X2,...,Xn 是具有同⼀分布函数F的，相互独⽴的随机变量，则称 X1,X2,...,Xn 为从分布函数F（或总体F，总体X）得到的简单随机样本，简称样本。
它们的观察值 x1,x2,...,xn称为样本值，⼜称为X的n个独⽴的观察值。
若 X1,X2,...,Xn 为总体X的⼀个样本，则X1,X2,...,Xn相互独⽴，且它们的分布函数都是F(x)，所以(X1,X2,...,Xn)的分布函数是：⽩话：随机变量X1,X2,...,Xn同时发⽣的概率是单独发⽣的概率之积。
5.2样本函数与统计量
答案: (B)
( n 1) S 2
2
(D)
n( X ) S
统计量中不含任何未知参数.
由以上定义得下述结论:
若总体 X 的k 阶矩 E ( X k ) 记成 k 存在, P V k , k 1, 2,. 则当n 时, k
证明 因为 X 1 , X 2 ,, X n 独立且与X 同分布,
k k 所以 X 1k , X 2 , , X n 独立且与X k 同分布, k E( X ) E( X ) E ( X n ) k .
该段时间内通过的 汽车数所在区间
区间中点值x( i )
225 235 245 255 265 275 285
频数 mi
1 3 6 14 4 1 1 30
（220，230] （230，240] （240，250] （250，260] （260，270] （270，280] （280，290] 总 计
数据只需分7次输入计算器即可算得，
1 7 x mi x(i ) 253 , 30 i 1
7 1 s 2 mi ( x(i ) x ) 2 147.59 , 29 i 1
7 1 2 ~2 m ( x x ) 142.67 . i (i ) 30 i 1
小结
1.有关概念： 样本函数与统计量（注意两者的区别）
n 1 2 S2 ( X X ) , i n 1 i 1 n 1 2 s2 ( x x ) . i n 1 i 1
其观测值记作
1 n 2 s ( x x ) . i n 1 i 1
4.样本 k 阶原点矩
1 n k Vk X i n i 1
38.2 40.0 42.4 37.6 39.2 41.0 44.0 43.2 38.8 40.6
( n 1) S 2
2
(D)
n( X ) S
统计量中不含任何未知参数.
由以上定义得下述结论:
若总体 X 的k 阶矩 E ( X k ) 记成 k 存在, P V k , k 1, 2,. 则当n 时, k
证明 因为 X 1 , X 2 ,, X n 独立且与X 同分布,
k k 所以 X 1k , X 2 , , X n 独立且与X k 同分布, k E( X ) E( X ) E ( X n ) k .
该段时间内通过的 汽车数所在区间
区间中点值x( i )
225 235 245 255 265 275 285
频数 mi
1 3 6 14 4 1 1 30
（220，230] （230，240] （240，250] （250，260] （260，270] （270，280] （280，290] 总 计
数据只需分7次输入计算器即可算得，
1 7 x mi x(i ) 253 , 30 i 1
7 1 s 2 mi ( x(i ) x ) 2 147.59 , 29 i 1
7 1 2 ~2 m ( x x ) 142.67 . i (i ) 30 i 1
小结
1.有关概念： 样本函数与统计量（注意两者的区别）
n 1 2 S2 ( X X ) , i n 1 i 1 n 1 2 s2 ( x x ) . i n 1 i 1
其观测值记作
1 n 2 s ( x x ) . i n 1 i 1
4.样本 k 阶原点矩
1 n k Vk X i n i 1
38.2 40.0 42.4 37.6 39.2 41.0 44.0 43.2 38.8 40.6
统计学 第6版 课后答案
第一章统计量是用来描述样本特征的概括性数字度量，它是根据样术数据计算出来的一个量，由于抽样是随机的，因此统计量是样本的函数。
研究者所关心的统计量主要有样本平均数、样本标准总、样本比例等。
3,变量(D变量，变量值①变量:说明现象某种特征的概念，其特点是从一-次观察到下一-次观察结果会呈现出差别成变化。
②变量值:变量的几体取值。
(2)变量的类型①分类变量是说明事物类别的一个名称，其取值是分类数据。
②顺序变量是说明事物有序类别的一一个名称，其取值足顺序数据。
③数值型变量是说明事物数字特征的一一个名称，其取值是数值型数据。
根据其取值的不同，又可以分为:..离散型变量:只能取可数值的变量，它只能取有限个值，而且其取值都以整位数断开，可以一一列举:b.连续型变量:可以在一个或多个区间中取任何值的变量，它的取值是连续不断的，不能-列举。
(3)变量的其他分类①随机变量、非随机变量②经验变量，理论变量经验变量所措述的是周围环境中可以观察到的事物:理论变量是由统计学家用数学方法所构造出来的一些变什么是统计学?答: 统计学是关于数据的科学，它所提供的是一套有关数据收集、处理，分析。
解释并从数据中得出结论的方法，统计研究的是来自各领域的数据。
数据收集也就是取得统计数据:数据处理是将数据用图表等形式展示出来:数据分析则是选择适当的统计方法研究数据，井从数据中提取有用信息进而得出结论。
.解释描述统计和推断统计。
答:数据分析所用的方法可分为描述统计方法和推断统计方法。
(1)描述统计研究的是数据收集、处理、汇总、图表措述，概括与分析等统计方法。
(2)推断统计是研究如何利用样本数据来推断总体特征的统计方法。
比如，对产品的质量进行检验，往往是破坏性的，不可能对每个产品进行测量。
这就需要抽取部分个体即样本进行测量。
然后根据获得的样本数据对来:数据分析则是选择适当的统计方法研究数据，井从数据中提取有用信息进而得出结论。
3.统计数据可分为哪几种类型?不同类型的数据各有什么特点?答:统计数据是对现象进行测量的结果，可以从不同角度对统计数据进行分类:(1) 按照所采用的计量尺度不同，可以将统计数据分为分类数据、顺序数据和数值型数据。
考研数学备考：概率论各章节知识点梳理
考研数学备考：概率论各章节知识点梳理考研数学备考：概率论各章节知识点梳理第一局部：随机事件和概率(1)样本空间与随机事件(2)概率的定义与性质(含古典概型、几何概型、加法公式)(3)条件概率与概率的乘法公式(4)事件之间的关系与运算(含事件的独立性)(5)全概公式与贝叶斯公式(6)伯努利概型其中：条件概率和独立为本章的重点，这也是后续章节的难点之一，请各位研友务必重视起来。
第二局部：随机变量及其概率分布(1)随机变量的概念及分类(2)离散型随机变量概率分布及其性质(3)连续型随机变量概率密度及其性质(4)随机变量分布函数及其性质(5)常见分布(6)随机变量函数的分布其中：要理解分布函数的定义，还有就是常见分布的分布律抑或密度函数必须记好且纯熟。
第三局部：二维随机变量及其概率分布(1)多维随机变量的概念及分类(2)二维离散型随机变量结合概率分布及其性质(3)二维连续型随机变量结合概率密度及其性质(4)二维随机变量结合分布函数及其性质(5)二维随机变量的边缘分布和条件分布(6)随机变量的独立性(7)两个随机变量的简单函数的分布其中：本章是概率的重中之重，每年的解答题定会有一道与此知识点有关，每个知识点都是重点，务必重视!第四局部：随机变量的数字特征(1)随机变量的数字期望的概念与性质(2)随机变量的方差的概念与性质(3)常见分布的数字期望与方差(4)随机变量矩、协方差和相关系数其中：本章只要清楚概念和运算性质，其实就会显得很简单，关键在于计算。
第五局部：大数定律和中心极限定理(1)切比雪夫不等式(2)大数定律(3)中心极限定理其中：其实本章考试的可能性不大，最多以选择填空的形式，但那也是十年前的事情了。
第六局部：数理统计的根本概念(1)总体与样本(2)样本函数与统计量(3)样本分布函数和样本矩其中：本章还是以概念为主，清楚概念后灵敏运用解决此类问题不在话下第七局部：参数估计(1)点估计(2)估计量的优良性(3)区间估计。
统计量的定义并举例
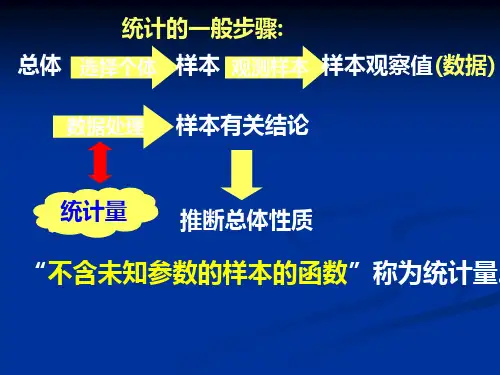
统计量的定义并举例
统计量的定义如下：
样本的已知函数；其作用是把样本中有关总体的信息汇集起来；是数理统计学中一个重要的基本概念。
统计量依赖且只依赖于样本x1,x2,…xn；它不含总体分布的任何未知参数。
统计量是统计理论中用来对数据进行分析、检验的变量。
宏观量是大量微观量的统计平均值，具有统计平均的意义，对于单个微观粒子，宏观量是没有意义的．相对于微观量的统计平均性质的宏观量也叫统计量。
统计量的分布
统计量的分布叫抽样分布。
它与样本分布不同，后者是指样本x1,x2，…，xn的联合分布。
统计量的性质以及使用某一统计量作推断的优良性，取决于其分布。
所以抽样分布的研究是数理统计中的重要课题。
寻找统计量的精确的抽样分布，属于所谓的小样本理论（见大样本统计）的范围，但是只在总体分布为正态时取得比较系统的结果。
对一维正态总体，有三个重要的抽样分布，即Ⅹ分布、t分布和F分布。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
计算样本均值、样本方差及样本二阶中心矩的观测值.
解： 数据进行如下分组，
该段时间内通过的 汽车数所在区间
（220，230] （230，240] （240，250] （250，260] （260，270] （270，280] （280，290]
总计
区间中点值x(i )
225 235 245 255 265 275 285
观测值 x(1) 频 数 m1
x(2)
m2
x(l )
总计
ml
n
则
x
1 n
l
mi x(i)
i1
,
s2
1 n 1
l i1
mi
( x(i )
x)2
,
~2
1 n
l i1
mi
( x(i )
x)2
.
注：对于连续随机变量或者某些离散随机变量抽样得 到的样本观测值，分成若干个子区间整理后，通常把
各个子区间的中点值取作 x(i) , 样本观测值落在对应区 间的频数取作 mi 进行计算.
若总体 X 的k阶矩 E( X k ) 记成 k 存在, 则当n 时, Vk P k , k 1, 2, .
证明 因为 X1, X2 , , Xn 独立且与X 同分布,
所以 X1k ,
X
k 2
,
,
X
k n
独立且与X k 同分布,
故有
E(
X1k
)
E
(
X
k 2
)
E
(
X
k n
)
k
.
再根据第三章大数定律知
统计量 ：不依赖任何未知参数的样本函数.
例1 设 X1, X2, X3是来自总体N (, 2 )的一个 样本, 其中 为已知, 2 为未知, 判断下列各式哪
些是统计量, 哪些不是?
T1 X1,
T2 X1 X2e X3 ,
T3
1 3
(
X
1
X2
X 3 ),
是
T4 max( X1, X 2 , X 3 ), T5 X1 X2 2,
x
)2
.
3其.S样样2观本本测n方标S1值2差准1记(可差innnn作111化1X111i简(2(iiinnn1为Ss11n(XXXX：iii222nn)n1,12Xs2112XXi2inn1i1i)n(X(n1xXi1Xi1iXx(X)inn221))X.x2i.22
)
nx
2
).
4.样本 k 阶原点矩
[例2] 观测某交通路口每天上午8:00~8:30这段时间内
通过的汽车车辆数，共观测30天，得到如下观测值：
234 260 241 259 256 241 261 257 277 255 244 249 238 269 250 268 256 253 226 256 235 256 251 258 246 255 257 282 251 261
T6
1 2
(
X
2 1
X
2 2
X 32 ).
不是
2.常用统计量
设X1, X 2,是,取X n自总体X 的一组样本, 计量有：
1.样本均值
X
1 n
n i1
Xi ,
其观测值记作
x
1 n
n i1
xi
.
常用统
2.样本方差
S 2
1 n 1
n i1
(Xi
X
)2
,
其观测值记作
s2
1 n 1
n i1
( xi
计算样本均值、样本方差及样本二阶中心矩的观测值.
解：把上述10个数据逐个输入电子计算器或计算机中，
不难求得：
x
1 10
10 i1
xi
40.5.
s2
1 9
10 i1
( xi
x) 2
4.66.
~2
1 10
10 i1
( xi
x) 2
4.194.
注：当样本容量很大时，可使用统计计算软件在计算 机上进行计算.而相同的数据往往可能重复出现，为了 使计算简化，应先把所得的数据整理，设得到下表：
第五章 数理统计的基本知识
§5.2 样本函数与统计量
1.样本函数与统计量
设X1, X 2,是,取X n自总体X 的一组样本,
x1 , x2 , ,
xn 是观测值.
样本函数 ：以样本为自变量的函数.记 g ( X1 , X 2 , , X n ).
样本函数也是随机变量. 称 g ( x1 , x2 , , xn ) 为样本函 数 g ( X1 , X 2 , , X n ) 的观测值.
Vk
Байду номын сангаас1 n
n i1
X
i
k
其观测值记作 vk . 特别地， V1 X .
5.样本 k 阶中心矩
其观测值记作 uk .
U k
1 n
n
(Xi
i1
X
)k
特别地， U1 0 , U2
n 1S2 , n
记样本二阶中心矩的观测值为
~ 2
u2
n 1s2. n
若n充分大，~2 s2 .
由以上定义得下述结论:
频数 mi
1 3 6 14 4 1 1
30
数据只需分7次输入计算器即可算得，
x
1 30
7 i1
mi x(i)
253,
s2
1 29
7
mi
i1
( x(i )
x)
2
147.59
,
~2
1 30
7 i1
mi
(
x(i
)
x
)2
142.67
.
小结
1.有关概念：样本函数与统计量（注意两者的区别）
2.学会用计算器算出常用统计量的样本观测值.
1
n
n i 1
X
k i
P k
,
k 1, 2, ;
从而有
g(V1,V2 , ,Vk ) P g(1, 2 , , k ),
其中g 是连续函数. 以上结论是下一章所要介绍的矩估计法的理
论根据.
[例1] 设抽样得到样本观测值如下：
38.2 40.0 42.4 37.6 39.2 41.0 44.0 43.2 38.8 40.6
思考题
设总体 X ~ N,其中, 2和 都未 知,
从 X中抽取
样本X1 , X 2 , , X n ,则下列随机变量中为统计量的是:
n
(A) ( Xi ) 2 i1
n
(B) ( Xi X ) 2 i1
(C)
(n
1)S
2
2
(D)
n(X )
S
答案: (B) 统计量中不含任何未知参数.
解： 数据进行如下分组，
该段时间内通过的 汽车数所在区间
（220，230] （230，240] （240，250] （250，260] （260，270] （270，280] （280，290]
总计
区间中点值x(i )
225 235 245 255 265 275 285
观测值 x(1) 频 数 m1
x(2)
m2
x(l )
总计
ml
n
则
x
1 n
l
mi x(i)
i1
,
s2
1 n 1
l i1
mi
( x(i )
x)2
,
~2
1 n
l i1
mi
( x(i )
x)2
.
注：对于连续随机变量或者某些离散随机变量抽样得 到的样本观测值，分成若干个子区间整理后，通常把
各个子区间的中点值取作 x(i) , 样本观测值落在对应区 间的频数取作 mi 进行计算.
若总体 X 的k阶矩 E( X k ) 记成 k 存在, 则当n 时, Vk P k , k 1, 2, .
证明 因为 X1, X2 , , Xn 独立且与X 同分布,
所以 X1k ,
X
k 2
,
,
X
k n
独立且与X k 同分布,
故有
E(
X1k
)
E
(
X
k 2
)
E
(
X
k n
)
k
.
再根据第三章大数定律知
统计量 ：不依赖任何未知参数的样本函数.
例1 设 X1, X2, X3是来自总体N (, 2 )的一个 样本, 其中 为已知, 2 为未知, 判断下列各式哪
些是统计量, 哪些不是?
T1 X1,
T2 X1 X2e X3 ,
T3
1 3
(
X
1
X2
X 3 ),
是
T4 max( X1, X 2 , X 3 ), T5 X1 X2 2,
x
)2
.
3其.S样样2观本本测n方标S1值2差准1记(可差innnn作111化1X111i简(2(iiinnn1为Ss11n(XXXX：iii222nn)n1,12Xs2112XXi2inn1i1i)n(X(n1xXi1Xi1iXx(X)inn221))X.x2i.22
)
nx
2
).
4.样本 k 阶原点矩
[例2] 观测某交通路口每天上午8:00~8:30这段时间内
通过的汽车车辆数，共观测30天，得到如下观测值：
234 260 241 259 256 241 261 257 277 255 244 249 238 269 250 268 256 253 226 256 235 256 251 258 246 255 257 282 251 261
T6
1 2
(
X
2 1
X
2 2
X 32 ).
不是
2.常用统计量
设X1, X 2,是,取X n自总体X 的一组样本, 计量有：
1.样本均值
X
1 n
n i1
Xi ,
其观测值记作
x
1 n
n i1
xi
.
常用统
2.样本方差
S 2
1 n 1
n i1
(Xi
X
)2
,
其观测值记作
s2
1 n 1
n i1
( xi
计算样本均值、样本方差及样本二阶中心矩的观测值.
解：把上述10个数据逐个输入电子计算器或计算机中，
不难求得：
x
1 10
10 i1
xi
40.5.
s2
1 9
10 i1
( xi
x) 2
4.66.
~2
1 10
10 i1
( xi
x) 2
4.194.
注：当样本容量很大时，可使用统计计算软件在计算 机上进行计算.而相同的数据往往可能重复出现，为了 使计算简化，应先把所得的数据整理，设得到下表：
第五章 数理统计的基本知识
§5.2 样本函数与统计量
1.样本函数与统计量
设X1, X 2,是,取X n自总体X 的一组样本,
x1 , x2 , ,
xn 是观测值.
样本函数 ：以样本为自变量的函数.记 g ( X1 , X 2 , , X n ).
样本函数也是随机变量. 称 g ( x1 , x2 , , xn ) 为样本函 数 g ( X1 , X 2 , , X n ) 的观测值.
Vk
Байду номын сангаас1 n
n i1
X
i
k
其观测值记作 vk . 特别地， V1 X .
5.样本 k 阶中心矩
其观测值记作 uk .
U k
1 n
n
(Xi
i1
X
)k
特别地， U1 0 , U2
n 1S2 , n
记样本二阶中心矩的观测值为
~ 2
u2
n 1s2. n
若n充分大，~2 s2 .
由以上定义得下述结论:
频数 mi
1 3 6 14 4 1 1
30
数据只需分7次输入计算器即可算得，
x
1 30
7 i1
mi x(i)
253,
s2
1 29
7
mi
i1
( x(i )
x)
2
147.59
,
~2
1 30
7 i1
mi
(
x(i
)
x
)2
142.67
.
小结
1.有关概念：样本函数与统计量（注意两者的区别）
2.学会用计算器算出常用统计量的样本观测值.
1
n
n i 1
X
k i
P k
,
k 1, 2, ;
从而有
g(V1,V2 , ,Vk ) P g(1, 2 , , k ),
其中g 是连续函数. 以上结论是下一章所要介绍的矩估计法的理
论根据.
[例1] 设抽样得到样本观测值如下：
38.2 40.0 42.4 37.6 39.2 41.0 44.0 43.2 38.8 40.6
思考题
设总体 X ~ N,其中, 2和 都未 知,
从 X中抽取
样本X1 , X 2 , , X n ,则下列随机变量中为统计量的是:
n
(A) ( Xi ) 2 i1
n
(B) ( Xi X ) 2 i1
(C)
(n
1)S
2
2
(D)
n(X )
S
答案: (B) 统计量中不含任何未知参数.