高一物理匀变速直线运动
- 格式:docx
- 大小:33.96 KB
- 文档页数:12


高一物理匀变速直线运动例题1. 什么是匀变速直线运动匀变速直线运动,听起来是不是有点拗口?其实它就是一种运动状态,简单来说,就是物体在一段时间内加速或减速的运动方式。
比如说,想象你在马路上骑自行车,刚开始你可能慢慢蹬,后来越蹬越快,这就是在做匀变速运动。
这里的“匀”指的是加速度保持不变,所以在这段时间里,你的速度是逐渐变化的,而不是一开始就飞速。
简单来说,匀变速直线运动就是让物体的速度以均匀的方式变化。
2. 匀变速直线运动的基本公式2.1 速度公式我们在学习匀变速直线运动时,首先要知道几个基本公式。
第一个公式就是关于速度的:( v = u + at )。
这里的 ( v ) 是末速度,( u ) 是初速度,( a ) 是加速度,( t ) 是时间。
这个公式就像是数学中的开门大吉,一旦掌握了,你就能轻松解决很多问题。
2.2 位移公式接下来,咱们要聊聊位移公式:( s = ut + frac{1{2at^2 )。
这个公式的意思是,位移( s ) 是由初速度 ( u ) 和加速度 ( a ) 共同决定的。
听起来有点复杂,但其实只要把这些字母代入数值,跟着公式走,结果就会乖乖出来。
3. 例题解析3.1 例题一:小明的自行车咱们来看看一个例子,想象一下,小明骑着他的自行车,起初速度是 0 m/s,随后每秒加速2 m/s²,问他在 5 秒后速度是多少?按照刚才的公式,我们把数据代进去:( v = 0 + 2 times 5 = 10 ) m/s。
哇哦,小明飞起来了,感觉就像风一样,真是爽到不行。
3.2 例题二:火车的旅程再来个稍微复杂一点的例子,假设一列火车起始速度是20 m/s,每秒加速1 m/s²,问它在 10 秒内行驶的距离。
首先算速度:( v = 20 + 1 times 10 = 30 ) m/s。
接下来,代入位移公式:( s = 20 times 10 + frac{1{2 times 1 times 10^2 = 200 + 50 = 250 ) m。

高一物理匀变速直线运动知识点沿着一条直线,且加速度方向与速度方向平行的运动,叫做匀变速直线运动。
如果物体的速度随着时间均匀减小,这个运动叫做匀减速直线运动。
如果物体的速度随着时间均匀增加,这个运动叫做匀加速直线运动。
s(t)=1/2·at^2+v(0)t=【v(t)^2-v(0)^2】/(2a)={【v(t)+v(0)】/2}*tv(t)=v(0)+at其中a为加速度,v(0)为初速度,v(t)为t秒时的速度 s(t)为t秒时的位移速度公式:v=v0+at位移公式:x=v0t+1/2at²位移---速度公式:2ax=v2;-v02;条件:物体作匀变速直线运动须同时符合下述两条:⑴受恒外力作用⑵合外力与初速度在同一直线上。
高一物理匀变速直线运动考点问题一匀变速直线运动的基本应用解答运动学问题的基本思路[典题1](2016·南昌调研)出租车载客后,从高速公路入口处驶入高速公路,并从10时10分55秒开始做初速度为零的匀加速直线运动,经过10 s时,速度计显示速度为54 km/h。
求:(1)这时车离出发点距离;(2)车继续做匀加速直线运动,当速度计显示速度为108 km/h 时,车开始做匀速直线运动。
10时12分35秒时计价器里程表示数应为多少米?(车起动时,计价器里程表示数为零)[答案](1)75 m(2)2 700 m问题二两类特殊的匀减速直线运动1.刹车类问题。
汽车匀减速到速度为零后即停止运动,加速度a突然消失,求解时要注意确定其实际运动时间。
如果问题涉及最后阶段(到停止运动)的运动,可把该阶段看成反向的初速度为零、加速度不变的匀加速直线运动。
[典题2](2016·湛江模拟)以36 km/h的速度沿平直公路行驶的汽车,遇障碍物刹车后获得大小为a=4 m/s2的加速度,刹车后第三个2 s内,汽车走过的位移为()A.12.5 mB.2 mC.10 mD.0[答案]D2.双向可逆类问题。

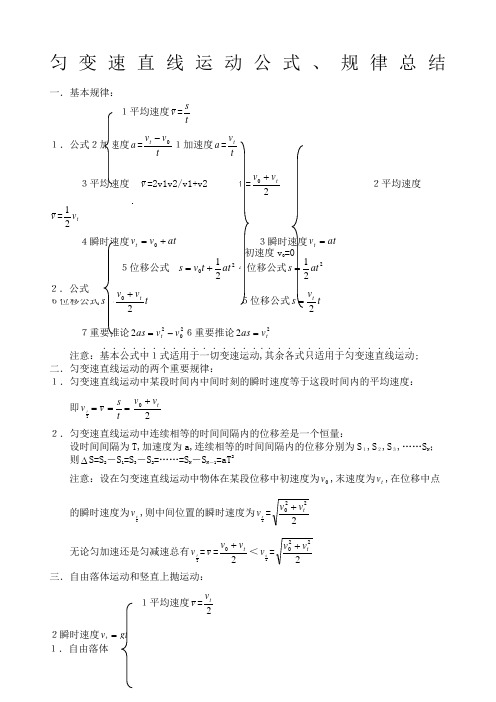
匀变速直线运动公式、规律总结一.基本规律:1平均速度v =tsa =tv v t 0-1加速度a v =2v1v2/v1+v2 2平均速度v =t v 21at v v t +=0 at =5位移公式021t v s +=2t v v t 20+ 2022v v as t -=6重要推论22t v as =注意:基本公式中1式适用于一切变速运动................,.其余各式只适用于匀变速直线运动...............; 二.匀变速直线运动的两个重要规律:1.匀变速直线运动中某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:即2t v =v ==ts 20tv v + 2.匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量:设时间间隔为T,加速度为a,连续相等的时间间隔内的位移分别为S 1,S 2,S 3,……S N ; 则∆S=S 2-S 1=S 3-S 2=……=S N -S N -1=aT 2 注意:设在匀变速直线运动中物体在某段位移中初速度为0v ,末速度为t v ,在位移中点的瞬时速度为2s v ,则中间位置的瞬时速度为2s v =2220t v v +无论匀加速还是匀减速总有2t v =v =20t v v +<2s v =2220t v v +三.自由落体运动和竖直上抛运动:1平均速度v =2tv3位移公式s =212gt 4重要推论22t v gs =总结:自由落体运动就是初速度0v =0,加速度a =g 的匀加速直线运动. 1瞬时速度gt vt =2021gt t v s -= 3重要推论2022v v t --总结:竖直上抛运动就是加速度g a -=的匀变速直线运动.四.初速度为零的匀加速直线运动规律: 设T 为时间单位,则有: 11s 末、2s 末、3s 末、……ns 末的瞬时速度之比为: v1∶v2∶v3∶……:vn =1∶2∶3∶……∶n同理可得:1T 末、2T 末、3T 末、……nT 末的瞬时速度之比为: v1∶v2∶v3∶……:vn =1∶2∶3∶……∶n 21s 内、2s 内、3s 内……ns 内位移之比为: S 1∶S 2∶S 3∶……:S n =12∶22∶32∶……∶n 2同理可得:1T 内、2T 内、3T 内……nT 内位移之比为:S 1∶S 2∶S 3∶……:S n =12∶22∶32∶……∶n 23第一个1s 内,第二个2s 内,第三个3s 内,……第n 个1s 内的位移之比为: S Ⅰ∶S Ⅱ∶S Ⅲ∶……:S N =1∶3∶5∶……∶2n -1同理可得:第一个T 内,第二个T 内,第三个T 内,……第n 个T 内的位移之比为: S Ⅰ∶S Ⅱ∶S Ⅲ∶……:S N =1∶3∶5∶……∶2n -1 4通过连续相等的位移所用时间之比为:t 1∶t 2∶t 3∶……:t n =1∶12-∶23-∶………∶1--n n。

高一物理 匀变速直线运动练习及解析一、匀变速直线运动的基本规律1.速度与时间的关系式:v =v0+at. 2.位移与时间的关系式:x =v0t +12at2. 3.位移与速度的关系式:v2-v20=2ax.二、匀变速直线运动的推论 1.平均速度公式:v =v t 2=v0+v 2. 2.位移差公式:Δx =x2-x1=x3-x2=…=xn -xn -1=aT2. 可以推广到xm -xn =(m -n)aT2. 3.初速度为零的匀加速直线运动比例式(1)1T 末,2T 末,3T 末……瞬时速度之比为: v1∶v2∶v3∶…∶vn =1∶2∶3∶…∶n. (2)1T 内,2T 内,3T 内……位移之比为:x1∶x2∶x3∶…∶xn =1∶22∶32∶…∶n2.(3)第一个T 内,第二个T 内,第三个T 内……位移之比为: x Ⅰ∶x Ⅱ∶x Ⅲ∶…∶xn =1∶3∶5∶…∶(2n -1). (4)通过连续相等的位移所用时间之比为:t1∶t2∶t3∶…∶tn =1∶(2-1)∶(3-2)∶…∶(n -n -1). 三、自由落体运动和竖直上抛运动的规律 1.自由落体运动规律 (1)速度公式: v =gt. (2)位移公式: h =12gt2. (3)速度—位移关系式: v2=2gh. 2.竖直上抛运动规律(1)速度公式: v =v0-gt. (2)位移公式: h =v0t -12gt2. (3)速度—位移关系式: v2-v20=-2gh. (4)上升的最大高度: h =v202g . (5)上升到最大高度用时: t =v0g.适应性训练 (一)(45分钟)单项选择题1.关于质点和参考系,下列说法正确的是( )A .AK -47步枪子弹速度很快,杀伤力大,什么时候都能认为是质点B .研究男子3米板跳水运动员在空中的跳水动作时,不能把他看成质点C .研究物体的运动时不一定要选择参考系D .歼-15在“辽宁号”航母上的起飞速度大约为300 km/h ,是相对航母甲板来说的 答案:B 2.(2015·苏州模拟)物体做匀加速直线运动,已知加速度为5 m/s2,那么任意1 s 内( ) A .物体的末速度一定等于初速度的5倍 B .物体的末速度一定比初速度大5 m/sC .物体的初速度一定比前1 s 内的末速度大5 m/sD .物体的末速度一定比前1 s 内的初速度大5 m/s 答案:B3.一物体做匀加速直线运动,在第一个Δt 的时间内通过的位移为x1,在第三个Δt 的时间内通过的位移为x2,则物体运动的加速度为( ) A.x1+x2Δt2 B.x2-x1Δt2C.x2-x12Δt2D.x2-x13Δt2解析:选C.由逐差公式得:x2-x1=2a(Δt)2,所以a =x2-x12Δt2,故C 正确.4.两位杂技演员,甲从高处自由落下的同时乙从蹦床上竖直跳起,结果两人同时落到蹦床上,若以演员自己为参考系,此过程中他们各自看到对方的运动情况是( ) A .甲看到乙先朝上、再朝下运动 B .甲看到乙一直朝上运动C .乙看到甲先朝下、再朝上运动D .甲看到乙一直朝下运动解析:选B.乙上升过程,甲、乙间距越来越小,故甲看到乙向上运动;乙下降过程,因甲的速度大于乙的速度,甲、乙间距仍然变小,故甲看到乙还是向上运动,只有B 项正确. 5.(2014·高考广东卷)如图是物体做直线运动的v -t 图象.由图可知,该物体( ) A .第1 s 内和第3 s 内的运动方向相反 B .第3 s 内和第4 s 内的加速度相同 C .第1 s 内和第4 s 内的位移大小不相等 D .0~2 s 和0~4 s 内的平均速度大小相等解析:选B.第1 s 内和第3 s 内的速度均为正值,方向相同,选项A 错误;v -t 图象的斜率代表加速度,第3 s 内和第4 s 内斜率相同,所以加速度相同,选项B 正确;图象与时间轴所围面积在数值上等于位移的大小,第1 s 内的位移x1=12×1×1 m =0.5 m ,第4 s 内的位移x4=-12×1×1 m =-0.5 m ,两段时间内位移大小相等,选项C 错误;0~2 s 内的平均速度:v =x t =1.52 m/s =0.75 m/s ,0~4 s 内的平均速度v -′=x′t′=1.54 m/s =0.375 m/s ,选项D 错误.6.(2015·福建福州质检)某物体做直线运动的v -t 图象如图所示,根据图象提供的信息可知,该物体( )A .在0~4 s 内与4~6 s 内的平均速度相等B .在0~4 s 内的加速度大于7~8 s 内的加速度C .在6 s 末离起始点最远D .在4 s 末离起始点最远解析:选C.根据平均速度的公式v =v0+v2可知,在0~4 s 内的平均速度是6 m/s ,在4~6 s 内的平均速度是4 m/s ,A 错误.根据加速度的公式a =ΔvΔt ,在0~4 s 内的加速度是1 m/s2,在7~8 s 内的加速度是4 m/s2,B 错误.在6 s末,物体运动方向改变,离起始点最远,C 正确,D 错误.7.做匀减速直线运动的物体经4 s 停止,若在第1 s 内的位移是14 m ,则最后1 s 内位移是( )A .3.5 mB .2 mC .1 mD .0解析:选B.各秒内物体的位移之比为7∶5∶3∶1,由于第1 s 内位移为14 m ,故最后1 s 内的位移为2 m ,B 正确. 8.一辆以20 m/s 的速度行驶的汽车,突然采取急刹车,加速度大小为8 m/s2,汽车在刹车后的3秒内的位移和3秒时的速度分别为( )A .24 m,4 m/sB .25 m,4 m/sC .24 m ,-4 m/sD .25 m,0 答案:D 9.(2015·福建福州一模)一名宇航员在某星球上完成自由落体运动实验,让一个质量为2 kg 的小球从一定的高度自由下落,测得在第5 s 内的位移是18 m ,则( ) A .物体在2 s 末的速度是20 m/sB .物体在第5 s 内的平均速度是3.6 m/sC .物体在第2 s 内的位移是20 mD .物体在5 s 内的位移是50 m解析:选D.根据x =12gt2可得,12g×(5 s)2-12g×(4 s)2=18 m ,因此星球上的重力加速度g =4 m/s2,因此2 s 末的速度v =gt =8 m/s ,A 错误;第5秒内的平均速度v =181 m/s =18 m/s ,B 错误;第2 s 秒内的位移x2=12gt22-12gt21=12×4×22 m -12×4×12 m =6 m ,C 错误;物体在5 s 内的位移x =12gt2=12×4×52 m =50 m ,D 正确. 10.(2015·贵州贵阳十校联考)一条悬链长7.2 m ,从悬挂点处断开,使其自由下落,不计空气阻力,则整条悬链通过悬挂点正下方20 m 处的一点所需的时间是(g 取10 m/s2)( ) A .0.3 s B .0.4 s C .0.7 s D .1.2 s解析:选B.链条上、下端到达该点用时分别为: t 上=2h 上g=2×2010s =2 s ,t 下=2h 下g =2×20-7.210s =1.6 s ,则Δt =t 上-t 下=0.4 s ,故B 正确. 11.(2015·威海模拟)从16 m 高处每隔一定时间释放一球,让它们自由落下,已知第一个球刚好落地时,第五个球刚释放,这时第二个球离地面的高度是(g 取10 m/s2)( ) A .15 m B .12 m C .9 m D .7 m解析:选D.第一个小球落地时,从上到下相邻两球之间的距离之比为:1∶3∶5∶7,因此第1、2两球间距离为:71+3+5+7×16 m =7 m ,故D 正确.二、多项选择题 1.(2015·长沙模拟)对加速度的理解,下列说法正确的是( ) A .加速度增大,速度可能减小B .速度变化量Δv 越大,加速度就越大C .物体有加速度,速度就增大D .物体速度很大,加速度可能为零解析:选AD.当a 与v 同向时,不论加速度是否增大,速度必增大,当a 与v 反向时,不论加速度是否增大,速度必减小,故A 正确C 错.速度变化率越大,加速度越大,而速度变化量大,加速度不一定大,B 错.速度很大,若不变,加速度等于零,故D 正确. 2.(2015·潍坊模拟)甲、乙两个物体在同一直线上沿正方向运动,a 甲=4 m/s2,a 乙=-4 m/s2,那么对甲、乙两物体判断正确的是( )A .甲的加速度大于乙的加速度B .甲做加速直线运动,乙做减速直线运动C .甲的速度比乙的速度变化快D .甲、乙在相等时间内速度变化的大小相等 答案:BD3.(高考改编题)一物体自t =0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )A .在0~6 s 内,物体离出发点最远为30 mB .在0~6 s 内,物体经过的路程为40 mC .在0~4 s 内,物体的平均速率为7.5 m/sD .在4 s ~6 s 内,物体的平均速度为0解析:选BCD.物体0~5 s 内的位移x1=12×(2+5)×10 m =35 m,5 s ~6 s 内的位移x2=-12×1×10 m =-5 m ,即物体先沿正方向运动35 m ,然后反向运动5 m ,故t =5 s 时物体离出发点最远,最远距离为35 m,0~6 s 内经过的路程为40 m ,A 错误,B 正确.同理,可求出0~4 s 内物体的路程为30 m ,故此段时间内物体的平均速率v =7.5 m/s ,C 正确.物体在4 s ~5 s 与5 s ~6 s 内的位移大小相等、方向相反,总位移为0,故D 正确.4.(2015·郑州模拟)在塔顶上将一物体竖直向上抛出,抛出点为A ,物体上升的最大高度为20 m ,不计空气阻力,设塔足够高,则物体位移大小为10 m 时,物体通过的路程可能为( ) A .10 m B .20 m C .30 m D .50 m解析:选ACD.物体在塔顶上的A 点抛出,位移大小为10 m 的位置有两处,如图所示,一处在A 点之上,另一处在A 点之下,在A 点之上时,通过位移为10 m 处又有上升和下降两种过程,上升通过时,物体的路程s1等于位移x1的大小,即s1=x1=10 m ;下降通过时,路程s2=2h -x1=2×20 m -10 m =30 m .在A 点之下时,通过的路程s3=2h +x2=2×20 m +10 m =50 m .故A 、C 、D 正确,B 错误.5.做初速度不为零的匀加速直线运动的物体,在时间T 内通过位移x1到达A 点,接着在时间T内又通过位移x2到达B 点,则以下判断正确的是( ) A .物体在A 点的速度大小为x1+x22TB .物体运动的加速度为2x1T2C .物体运动的加速度为x2-x1T2D .物体在B 点的速度大小为2x2-x1T解析:选AC.根据匀变速直线运动规律,中间时刻的瞬时速度等于该段时间内的平均速度,故A 正确;根据x2-x1=aT2,C 正确,B 错误;根据v =v0+aT ,物体在B 点的速度大小为3x2-x12T,D 错误.☆6.(2015·河北石家庄质检)酒后驾驶会导致许多安全隐患,这是因为驾驶员的反应时间变长.反应时间是指驾驶员从发现情况到采取制动的时间.下表中“思考距离”是指驾驶员发现情况到采取制动的时间内汽车的行驶距离;“制动距离”是指驾驶员发现情况到汽车停止行驶的距离(假设汽车制动加速度都相同).速度(m/s) 思考距离(m) 制动距离(m) 正常 酒后 正常 酒后 15 7.5 15.0 22.5 30.0 20 10.0 20.0 36.7 46.7 2512.525.054.266.7分析上表可知,下列说法正确的是( ) A .驾驶员正常情况下反应时间为0.5 s B .驾驶员酒后反应时间比正常情况慢0.5 sC .驾驶员采取制动措施后汽车加速度大小为3.75 m/s2D .当车速为25 m/s 时,发现前方60 m 处有险情,酒驾者不能安全停车 解析:选ABD.反应时间=思考距离÷车速,因此正常情况下反应时间为0.5 s ,酒后反应时间为1 s ,故A 、B 正确;设汽车从开始制动到停车的位移为x ,则x =x 制动-x 思考,根据匀变速直线运动公式:v2=2ax ,解得a =v22x 制动-x 思考=7.5 m/s2,C 错;根据表格,车速为25 m/s 时,酒后制动距离为66.7 m>60 m ,故不能安全停车,D 正确. 三、非选择题10.在一次低空跳伞训练中,当直升机悬停在离地面224 m 高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5 m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5 m/s ,求:(取g =10 m/s2)(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下? (2)伞兵在空中的最短时间为多少?解析:(1)设伞兵展伞时,离地面的高度至少为h ,此时速度为v0,着地时相当于从h1高处自由落下, 则有v2-v20=-2ah , 又v20=2g(224 m -h)联立解得h =99 m ,v0=50 m/s以5 m/s 的速度落地相当于从h1高处自由落下,即2gh1=v2,所以 h1=v22g =5220m =1.25 m.(2)设伞兵在空中的最短时间为t , 则有v0=gt1,t1=v0g =5010 s =5 s ,t2=v -v0a =5-50-12.5s =3.6 s , 故所求时间t =t1+t2=(5+3.6)s =8.6 s. 答案:(1)99 m 1.25 m (2)8.6 s11.(2015·广州模拟)做匀加速直线运动的物体途中依次经过A 、B 、C 三点,已知AB =BC =l2,AB 段和BC 段的平均速度分别为v1=3 m/s 、v2=6 m/s ,则: (1)物体经B 点时的瞬时速度vB 为多大?(2)若物体运动的加速度a =2 m/s2,试求AC 的距离l.解析:(1)设加速度大小为a ,经A 、C 的速度大小分别为vA 、vC.由匀加速直线运动规律可得: v2B -v2A =2a×l2①v2C -v2B =2a×l2②v1=vA +vB2③ v2=vB +vC2④ 解①②③④式得:vB =5 m/s. (2)解①②③④式得: vA =1 m/s ,vC =7 m/s 由v2C -v2A =2al ,得:l =12 m. 答案:(1)5 m/s (2)12 m ☆12.(2014·高考山东卷)研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)t0=0.4 s ,但饮酒会导致反应时间延长.在某次试验中,志愿者少量饮酒后驾车以v0=72 km/h 的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L =39 m .减速过程中汽车位移s 与速度v 的关系曲线如图乙所示,此过程可视为匀变速直线运动.取重力加速度的大小g =10 m/s2.求:(1)减速过程汽车加速度的大小及所用时间;(2)饮酒使志愿者的反应时间比一般人增加了多少;(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值.解析:(1)设减速过程中汽车加速度的大小为a,所用时间为t,由题可得初速度v0=20 m/s,末速度vt=0,位移s =25 m,由运动学公式得v20=2as①t=v0 a②联立①②式,代入数据得a=8 m/s2③t=2.5 s.④(2)设志愿者反应时间为t′,反应时间的增加量为Δt,由运动学公式得L=v0t′+s⑤Δt=t′-t0⑥联立⑤⑥式,代入数据得Δt=0.3 s.⑦(3)设志愿者所受合外力的大小为F,汽车对志愿者作用力的大小为F0,志愿者质量为m,由牛顿第二定律得F=ma⑧由平行四边形定则得F20=F2+(mg)2⑨联立③⑧⑨式,代入数据得F0 mg=41 5.答案:(1)8 m/s2 2.5 s(2)0.3 s(3)41 5。
高一物理匀变速直线运动的公式推导整理物理中的运动是我们生活中不可避免的一部分,而了解不同运动下的公式推导对于我们理解和解决问题非常重要。
本文将针对高一物理中的匀变速直线运动公式进行推导整理,帮助读者更好地理解和应用相关内容。
一、物理背景介绍运动是物体位置随时间的变化。
匀变速直线运动是指物体在直线上做匀速运动或者做匀速变速运动。
二、匀速直线运动公式推导1. 位移公式推导根据定义,位移是物体从初始位置到终止位置的直线距离。
假设物体初始位置为s0,结束位置为s,时间为t,速度为v,则根据匀速直线运动的特点,位移可以表示为s = s0 + v * t2. 速度公式推导在匀速直线运动中,速度恒定不变。
速度的定义为位移对时间的导数,即v = ds/dt根据位移公式,可以将其改写为v = (s - s0) / t3. 时间公式推导根据位移公式,可以进一步推导出时间公式,即t = (s - s0) / v三、匀变速直线运动公式推导1. 位移公式推导在匀变速直线运动中,物体速度随时间变化,位移也会随之变化。
根据定义,位移仍表示物体从初始位置到终止位置的直线距离。
假设物体初始位置为s0,结束位置为s,时间为t,初始速度为v0,结束速度为v,加速度为a,则位移可以表示为s = s0 + v0 * t + (1/2) * a * t^22. 速度公式推导在匀变速直线运动中,速度随时间的变化。
速度的定义为位移对时间的导数,即v = ds/dt根据位移公式,可以将其改写为v = v0 + a * t3. 加速度公式推导加速度定义为速度对时间的导数,即a = dv/dt根据速度公式,可以将其改写为a = (v - v0) / t四、公式应用示例以一个实际问题为例进行公式应用示范。
问题:某车以5 m/s的初速度匀减速停下,加速度为-2 m/s^2,求车辆的停止时间和停止位置。
解答:1. 根据速度公式 v = v0 + a * t,代入已知数据,得到0 = 5 + (-2) * t解方程可得,t = 2.5 s2. 根据位移公式 s = s0 + v0 * t + (1/2) * a * t^2,代入已知数据,得到s = 0 + 5 * 2.5 + (1/2) * (-2) * (2.5^2)解方程可得,s = 6.25 m因此,车辆停止的时间为2.5秒,停止位置为6.25米。
高一物理匀变速直线运动知识点总结一、匀变速直线运动概述匀变速直线运动是指物体在直线上做匀速运动和变速运动的组合。
匀变速直线运动的特点是速度的大小和方向都在不断变化,但变化的方式是规律的,可以通过数学模型进行描述和分析。
二、匀变速直线运动的描述1. 位置-时间图匀变速直线运动的位置-时间图是一条曲线,用来描述物体在不同时间点的位置。
曲线的斜率代表物体的速度,斜率越大表示速度越大。
2. 速度-时间图匀变速直线运动的速度-时间图是一条直线,用来描述物体在不同时间点的速度。
直线的斜率代表物体的加速度,斜率越大表示加速度越大。
3. 加速度匀变速直线运动的加速度是指速度的变化率。
加速度可以是正值、负值或零,分别表示物体在增速、减速或匀速运动。
三、匀变速直线运动的基本公式1. 位移公式匀变速直线运动的位移公式为:△x = v0t + 1/2at²其中,△x表示位移,v0表示初始速度,t表示时间,a表示加速度。
2. 速度公式匀变速直线运动的速度公式为:v = v0 + at其中,v表示速度,v0表示初始速度,t表示时间,a表示加速度。
3. 时间公式匀变速直线运动的时间公式为:t = (v - v0) / a其中,v表示速度,v0表示初始速度,t表示时间,a表示加速度。
四、匀变速直线运动的相关概念和定理1. 位移、速度和加速度的关系匀变速直线运动中,位移与速度和加速度之间存在一定的关系。
当加速度为常数时,位移与速度呈线性关系,位移与加速度呈二次函数关系。
2. 平均速度和瞬时速度匀变速直线运动中,平均速度是指在一段时间内物体行驶的平均速度,用来描述物体的整体运动情况。
瞬时速度是指物体在某一时刻的瞬时速度,用来描述物体的瞬时运动情况。
3. 速度的变化率和加速度匀变速直线运动中,速度的变化率就是加速度。
加速度的正负值表示速度增加或减少的方向,绝对值表示速度变化的快慢。
4. 运动图像的分析通过分析匀变速直线运动的位置-时间图和速度-时间图,可以得到物体的运动情况。
高一物理 第5单元 匀变速直线运动一、内容黄金组1.掌握匀变速直线运动的速度公式.知道它是如何推导出的,知道它的图象的物理 意义.会应用这一公式分析和计算.2 .掌握匀变速直线运动的位移公式.会应用这一公式对问题进行分析和计算.3 .会推出匀变速直线运动的位移和速度的关系式,并会应用它进行计算.4 .会用打点计时器测匀变速直线运动的瞬时速度和加速度.二、要点大揭秘1.作匀变速直线运动的物体在相邻相等时间内的位移差相等.设A 、B 、C 为作匀变速直线运动的物体所经过的三点,且从A 到B 和从B 到C 所经时 间均为T .若A 、B 相距S1,B 、C 相距S2,则△$ = % —S1即为相邻相等时间内的位移差.由位 移公式,有S, =v A T+iaT2 ……①s J T2②=v E T+ — aT 2 ................... ②②式减①式:AS=S2—S1= (vg -v^)T 又因 v E =v ft +aT ,故 AS=aT 2.即相邻相等时间内的位移差为恒量.2.作匀变速直线运动的物体在一段位移的中间时刻的瞬时速度等于它在该段位移的平 均速度.这一性质,也可简单地叙述为:中间时刻点速度等于平均速度.设作匀变速直线运动 的物体从A 到B 和从B 到C 所用时间均为T ,显然B 为AC 段的中间时刻点.由速度公式,有 ;v E =v A +aT7 寸匚=v E +aT两式相激:v B —Vc = V A —可解出在匀变速直线运动中,故2V R = V. E-3.作匀变速直线运动的物体在一段位移中点的瞬时速度恒大于物体在该段位移的中间时 刻的瞬时速度(物体加速度不为零).这一性质可简述为:中点速度恒大于中间时刻速度.设线段AB 是加速度为a 的匀变速直线运动的一段位移,C 为AB 中点,D 为物体在AB 段中间时刻所经过的点.为简化证明过程,我们先假定物体的速度方向没有发生变化,艮Pv A、VB 同向(未发生减速至停止后又返回的运动).我们用以下两种方法来证明这一性质.方法I (过程分析法)物体在前一半时间内的位c移必定小于物体在后一半时间内的位移,因而物体一定先经X ~ 1D点再经C点,如图1所示.因速度随时间增大,故V C>VD.图1若a<0,则物体速度不断增小,物体在前一半时间的位移一定工 ------- 1——「大于在后一半时间的位移,因而物体一定先经C点,再经图2D点,如图2所示.因速度随时间减小,故仍有V C>VD.方法2 (解析法)根据基本公式v t2 =v o2 + 2as,可列出方程组\ v c2=第J + 2as[vg2 =v c2 +2as两式相减:2 2 2 2V c -v B =V A -v c ,.解出“卜尸如前所述,我们已知% =注产.故要证明.玩4班,只要证明^V A2+V B2 V A +VB …… ③将③式两边同时平方,并整理为2(屐+VB2) >(V A+ VB)2=v A2+VB2+2V A VE 此式即相当于(v A—V B)2>0 ...... ④因aW0,故V A W V B,④式显然成立,从而③式亦成立,即V C>VD.现在我们来说明,即使发生了减速至速度为零后又返回的运动V C>VD仍然成立.以VA方向为正方向,若发生了返回,则V B<0.在③式中,若V B<0,只使左边减小,故不等式仍然成立,即V C>V D 仍然成立.4.对于初速度为零的匀加速直线运动,有以下3个常用性质:(1)前Ts;前2Ts,前3Ts,……,前nTs内的位移比为S1:S2 :S3:…:S n= 1 :4 :9 :…:n2.⑵第一个Ts内,第二个Ts内,第三个Ts内,……,第n个Ts内的位移比为S ' :S ’ :S ’ :…:S ’ =1 :3 :5 :…:(2n-1), 123 n⑶通过第一个L长,第二个L长,第三个L长,……,第n个L长所用时间比为t : t : t :…t = 1: 22一1: <3 一\;2 …7n一nn一 1三、好题解给你1.本课预习题:(1)下列说法中,正确的是: ( )A.物体在一条直线上运动,如果在相等的时间里变化的位移相等,则物体的运动就是匀变速直线运动B.加速度大小不变的运动就是匀变速直线运动C.匀变速直线运动是加速度不变的运动D.加速度方向不变的运动一定是匀变速直线运动(2)对于作匀变速直线运动的物体,下列说法中正确的是( )A.若加速度方向和速度方向相同,虽然加速度很小,物体的速度还是要增丸.若加速度方向和速度方向相反,虽然加速度很大,物体的速度还是要减小C.不管加速度方向和速度方向的关系怎样,物体的速度都是增大的D.因为物体作匀变速直线运动,所以它的加速度是均匀变化的(3) 一质点作直线运动,当时W=t0时,位移s>0,速度v>0,其加速度a>0,此后a逐渐减小,则它的( )A.速度的变化越来越慢B.速度逐渐减小C.位移继续增大D.位移、速度始终为正值(4)物体在直线上作加速运动,从开始计时起,第1s内的位移是1m,第2s内的位移是2m…第ns内的位移是n m,由此可知( )A.物体肯定是作匀加速直线运动B.物体的初速度为0C.物体的加速度是1m/s2D.物体在前5s内的平均速度是3m/s(5)物体作匀加速直线运动,已知加速度为2m/s2,那么在任意1s内 ( )A.物体的末速度一定等于初速度的2倍B.物体的未速度一定比初速度大2m/sC.物体的初速度一定比前1s内的末速度大2m/sD.物体的末速度一定比前1s内的初速度大2m/s预习题参考答案:(1)、C (2)、AB (3) ACD (4) D(5) B.在匀加速直线运动中,加速度为2m/s2,表示每秒内速度变化(增加)2m/s,即末速度比初速度大2m/s,并不表示末速度一定是初速度的2倍.在任意1s内,物体的初速度就是前1s的末速度,而其末速度相对于前1s的初速度已经过2s,当a=2m/s2时,应为4m/s.2.基础题(1)自由落体运动在任何两个相邻的1s内,位移的增量为( )A.1mB.5mC.10mD.不能确定(2)作匀加速直线运动的物体,设它运动全程的平均速度是v1,运动到中间时刻的速度是v2,经过全程一半位置时的速度是v3,则下列关系中正确的是( )A.V1>V2>V3B.V1<V2=V3C.V1=V2<V3D.V1>V2=V3(3)几个作匀变速直线运动的物体,在相同时间内位移最大的是 ( )A.加速度最大的物体B.初速度最大的物体C.末速度最大的物体D.平均速度最大的物体基础题参考答案:(1) B.用A s=aT 2可知自由落体运动中任何两个相邻的1s内的位移差为10m.(2)C.分析过程见“要点大揭秘" 3 (3) D.3.应用题(1)汽车甲沿着平直的公路以速度v做匀速直线运动,当它通过某处时,该处恰有汽0车乙正开始做初速为0的加速运动去追甲车,根据上述已知条件()A.可求出乙车追上甲车时乙车的速度B.可求出乙车追上甲车时乙车所走的路程C.可求出乙车从起动到追上甲车所用的时间D.不能求出上述三者的任何一个(2)甲物体的重量比乙物体大5倍,甲从H高处自由落下,乙从2H高处与甲物体同时自由落下,在它们落地之前,下列说法中正确的是()A.两物体下落过程中,在同一时刻甲的速度比乙的速度大B.下落1s末,它们的速度相同0各自下落1m时,它们的速度相同D.下落过程中甲的加速度比乙的加速度大(3)一辆沿平直路面行驶的汽车,速度为36km/h.刹车后获得加速度的大小是4m/s2,求:(1)刹车后3s末的速度;(2)从开始刹车至停止,滑行一半距离时的速度.应用题参考答案:(1)C (2)BC(3)分析:汽车刹车后作匀减速滑行,其初速度v0=36km/h=10m/s,v t=0,加速度f =10m/^ a=_4m/E E7777777777777777777777777Z¥777777777777777777777V77A B C* ----- E/2 ---------------- J* --------------- s/2 --------------- *a=-4m/s2.设刹车后滑行t s停止,滑行距离为S,其运动示意图如图所示.解:①由速度公式v t=v0+at得滑行时间:即刹车后经2.5s即停止,所以3s末的速度为零.②由位移公式得滑行距离.即S = v 0t + 1at 2 = 10X2,5m + 1(-4)X 2.52m =12.5m设滑行一半距离至B 点时的速度为v B ,由推论说明:①不能直接把t=3 s 代入速度公式计算速度,因为实际滑行时间只有2.5s.凡刹车滑行一类问题,必须先确定实际的滑行时间(或位移);②滑行一半距离时的速度不等于 滑行过程中的平均速度.4.提高题:(1) 一石块从楼房阳台边缘向下做自由落体运动,到达地面,把它在空中运动的时间 分为相等的三段,如果它在第一段时间内的位移是1.2m,那么它在第三段时间内的 位移是()A 、1.2mB 、 3.6mC 、 6.0mD 、 10.8m (2)如图所示,小球沿斜面向上运动,依次经a 、b 、c 、d 到达最高点e.已知ab=bd=6m,bc=1m,小球从a 到c 和从c 到d 所用的时间都是2s,设小球经b 、c 时的速度分别为 v b 、V c ,则向前行驶,司机突然发现正前方同一轨道上距离为s 处有另一火 车,正以较小的速率v 2沿同方向做匀速运动,于是司机立刻使火车做匀减速运动,要使两 列火车不相撞,加速度a 的大小至少应是多少?提高题参考答案:(1)C (2)ABC (3)解:从以速度L 行驶的火车发现另一 火车开始刹车时计时:设在t 时间内追上,应有s 「s 2,追上要不相撞,则应有追上时vj W v 2,.以v 2行驶的火车在这段时间内通过的位移为x,则有:v i 2-v 22=2a (s+x ) (1)V - V(V 一 V )2x=vt (2)t= T 一2 (3)解出:a= 1 c 2,要满足 v ′<v ,则应有 a2a 2s1 2A 、v b<10 msB 、 v c =3m/sC 、 de=3mD 、从d 到e 所用时间为4s(3)火车正以速率 v E = 7vo + aS = 7102 + (-4) X 12.5m / s=/ s = 7.05m / s(v v )2三四、课后演武场1、甲、乙两辆汽车速度相等,在同时制动后,设均做匀减速运动,甲经3s停止,共前进了36m,乙经1.5s停止,乙车前进的距离为( )A、9mB、18mC、36mD、27m2、皮球从3m高处落下,被地板弹回,在距地面1m高处被接住,则皮球通过的路程和位移的大小分别是( )A、4m、4mB、3m、1mC、3m、2mD、4m、2m3、物体的位移随时间变化的函数关系是S=4t+2t2(m), 则它运动的初速度和加速度分别是()A、0、4m/s2B、4m/s、2m/s2C、4m/s、1m/s2D、4m/s、4m/s24、甲和乙两个物体在同一直线上运动,它们的v-t图像分别如图中的a和b所示.在t1 时刻( )A、它们的运动方向相同B、它们的运动方向相反C、甲的速度比乙的速度大D、乙的速度比甲的速度大5、物体由静止开始以恒定的加速度a向东运动t s后,加速度变为向西,大小不变,再经过t s时,物体的运动情况是()A、物体位于出发点以东,速度为零B、物体位于出发点以东,继续向东运动C、物体回到出发点,速度为零D、物体回到出发点,运动方向向西6、由静止开始做匀加速直线运动的物体当经过S位移的速度是v时,那么经过位移为2S 时的速度是( )A、2vB、4vC、2V vD、2c2 v7、一个物体从某一高度做自由落体运动, 已知它第一秒内的位移恰为它最后一秒内位移的一半,g取10m/s2,则它开始下落时距地面的高度为()A、5mB、11.25mC、20mD、31.25m8.一颗子弹沿水平方向射来,恰穿透三块相同的木板,设子弹穿过木板时的加速度恒定,则子弹穿过三块木板所用的时间之比为______ 。